Introduction

Fresh food logistics distribution refers to the process of delivering fresh products to various regions while maximizing the preservation of their freshness. As living standards improve, there is an increasing demand for perishable fresh products such as meat, seafood, and fruits and vegetables. Consequently, the requirements for cold chain distribution services for perishable fresh products have been increasing. The demand data for cold chain in China from 2016 to 2023 is shown in Fig. 1. Despite the impact of the COVID-19 pandemic in 2020, the demand for cold chain logistics in China has maintained a high level of development1.

Fig. 1
figure 1

The cold chain logistics demand in China from 2016 to 2023 (billion tons, %).

Full size image

Moreover, since the industrial age, global carbon emissions have surged dramatically, leading to severe air pollution and an increased burden on the ecological environment. The escalating environmental issues have garnered attention from all sectors worldwide. Energy conservation, emission reduction, and transitioning to a low-carbon economy have become trends in societal development. In March 2011, China’s 12th Five-Year Plan outlined a target to reduce carbon emission intensity by 17%2. In recent years, the country has also been actively implementing carbon trading policies, enhancing the carbon market. This allows carbon emission rights to be traded as commodities, facilitating the control of carbon emissions at lower costs.

However, cold chain distribution is highly susceptible to weather and traffic conditions, leading to increased distribution costs and transportation times. Accurately quantifying the impact of road conditions on speed is a critical issue to address in the development of urban distribution models. Moreover, the increasing number and complexity of customer orders further escalate the operational costs of cold chain enterprises. Additionally, due to the varying temperature requirements of fresh goods, traditional single-vehicle distribution models fail to meet the actual needs of businesses3. This necessitates the adoption of multi-vehicle distribution models to overcome these challenges. China has been closely monitoring carbon tax policies, and although not yet implemented, they are expected to be introduced in the future. Therefore, considering the carbon emissions of different types of vehicles during distribution and striving to minimize both emissions and costs will become a research focus. Generally, energy consumption is directly proportional to carbon emissions, which increase with higher energy usage. The goal of low-carbon logistics is to save energy and reduce emissions, creating a conflict of interest with the development of cold chain logistics, as both exhibit an inherent paradox4. Overall, the inability of cold chain logistics companies to accurately quantify the impacts of complex road conditions and multi-vehicle carbon emissions on distribution costs restricts further development and affects the construction of efficient, green, and intelligent logistics systems.

Essentially, cold chain distribution challenges are similar to those encountered in vehicle routing problem based on delivery deadlines. Vehicle routing problem (VRP) can be described as ensuring that all required delivery nodes are serviced by vehicles of various types within their permissible delivery times, under constraints such as vehicle capacity, and before a set delivery deadline. On this basis, a vehicle routing plan for all participating vehicles is developed to minimize the generalized costs of the entire distribution scheme. Unlike conventional VRP, cold chain distribution must fully consider the time-varying characteristics of road conditions and the quality degradation of fresh products during transport. Thus, the problem studied in this paper essentially involves time-dynamic vehicle scheduling and route optimization. An important prerequisite for the proposed optimization method to function correctly is that the delivery demand at each delivery point is known and fixed. Furthermore, the locations of these delivery points and warehouses, the number of delivery vehicles, their load capacities, and the delivery deadlines are also given. The main contributions of this paper are demonstrated in the following areas:

  1. (1)

    This paper advances the study of distribution organization and route optimization for fresh food logistics by considering the conflict of interest between carbon emissions and fresh food logistics. Additionally, this study takes into account the delivery deadlines of fresh logistics and the damage caused by the reduction in freshness during transportation, making the research more aligned with practical situations.

  2. (2)

    An integer programming model for the fresh food logistics distribution scheme has been developed, targeting vehicle transportation costs, fuel consumption costs, carbon emission costs, refrigeration costs, and damage costs.

  3. (3)

    A combined optimization algorithm of Tabu Search and Genetic Algorithm is proposed, demonstrating strong applicability in solving distribution problems through the synergistic use of Tabu-Genetic algorithm.

  4. (4)

    The effectiveness of the scheduling schemes and distribution routes generated by this algorithm has been proven through computational examples involving different network scales. Additionally, comparisons with traditional methods have confirmed the superiority of this algorithm.

The remainder of this paper is organized as follows: “Literature review” section reviews related literature. “Problem description” section formally describes the problem. “Model formulation” section presents the mathematical optimization model for this issue, and “Solution algorithm” section designs the Tabu-Genetic algorithm. “Numerical experiments” section provides the experimental results of the distribution route schemes under different scales. “Sensitivity analysis” section conducts sensitivity analysis. “Implication” section develops an implication. Finally, conclusions and future work are discussed in “Conclusion and future direction” section.

Literature review

The logistics distribution issue is a part of the vehicle routing problems, commonly known as the VRP. It is widely considered in academia to be complex and classified as an NP-hard problem. Moreover, the consideration of factors such as carbon emissions and cargo damage in this paper adds layers of complexity, necessitating the evaluation of appropriate transport routes. Currently, there has been extensive research conducted on fresh food logistics distribution both domestically and internationally.

In 2018, Stellingwerf proposed a vehicle routing model with the minimum load target constraints for quantifying carbon emissions under controlled temperature conditions5. In the same year, a computational model for joint route optimization between suppliers and customer points was proposed, demonstrating that adopting this model in cold chain logistics distribution not only saves costs but also minimizes pollutant emissions6. Tsang considered the delivery handling needs of different goods and applied the Internet of Things routing system to cold chain logistics distribution schemes, achieving real-time monitoring of multi-category goods and optimization of vehicle routing7. Amorim studied the impact of perishability during the distribution of agricultural products and established a multi-objective planning model that minimizes distribution costs while maximizing product freshness8. Wang constructed a multi-objective optimization model for the lowest total cost and maximum freshness, solved using a two-stage heuristic algorithm that initially employs the K-means clustering method for generating initial solutions, followed by further optimization using variable neighborhood search and genetic algorithms9. Zhang Yaming, based on the analysis of cold chain distribution costs, constructed single-vehicle type and multi-vehicle type cold chain logistics distribution route optimization models under time and quality satisfaction constraints, revealing the trends of satisfaction with cost optimization and showing that the satisfaction-constrained multi-vehicle transportation route model is more suitable for cold chain distribution scheduling10. Chen considered the different needs of products for freezing temperatures and humidity, established a multi-compartment vehicle routing problem (MCVRP) model for fresh agricultural products, and modified the international standard examples of VRP to obtain 28 MCVRP standard examples, finally solving the model using a particle swarm algorithm integrated with a neighborhood search algorithm, achieving a 2% reduction in total route11. Zhang Qian established a fresh e-commerce optimization model considering distribution costs, product freshness, and carbon emissions. The model calculates product freshness using distance and time factors and carbon emissions based on transportation distance and load. It includes total costs, product freshness, and carbon emissions in its multi-objective optimization model, and uses the fruit fly optimization algorithm for solving12. Wang considered the strong timeliness characteristic of fresh goods distribution and constructed a dual-objective optimization model for minimizing logistics costs and fresh goods value loss. By establishing a logistics cost model including transportation costs of fresh distribution vehicles, temperature control costs, and penalties for violating time windows, and a value loss model based on temperature control, he compared the value loss of fresh goods under different temperature controls. An optimized model that includes both distribution costs and goods value loss as objectives was built, and an improved K-means clustering algorithm considering customer spatial location, product temperature control requirements, and time window constraints was designed13. In the two-stage problem of location and route optimization for vehicle logistics systems, Soumen optimized total financial cost and customer satisfaction levels. Some uncertain parameters in the model were represented as triangular Type-2 neutrosophic numbers, and a new ranking method was used to convert the fuzzy model into a deterministic one14. Satyajit and Soumen considered total transportation cost, procurement cost, recycling cost, maintenance cost, and carbon emissions in the logistics distribution problem, formulating it as a bi-objective mixed-integer linear programming problem15. He established a vehicle routing optimization model with the objective of minimizing the sum of vehicle fixed costs, driver costs, fuel consumption, and carbon emission costs, while considering time window constraints16. Zhou analyzed the relationship between vehicle speed and time, optimizing vehicle routes in logistics distribution by minimizing the sum of vehicle usage costs, fuel consumption, and carbon emission costs17.

Additionally, a group of scholars has focused their research on solving optimization problems using heuristic algorithms. Kok incorporated factors affecting urban traffic congestion and local driving time regulations into consideration and proposed using the Tabu Search algorithm to address related VRP18. Zhang adopted the Ant Colony algorithm to solve the minimum carbon emissions model for cold chain logistics. Chen employed neighborhood search to solve the multi-temperature co-distribution cold chain model. Du Chen utilized the Simulated Annealing algorithm to solve the cold chain distribution route model based on customer satisfaction and minimum loss. Ji used an improved genetic algorithm to solve the dual-objective model of cost and satisfaction for cold chain fruit transportation. Ruan employed a bipartite matrix to classify customer value and solve a multi-objective planning model that maximizes customer value and minimizes total costs19,20,21,22,23, achieving certain optimization results.

In the domain of scheduling algorithms used for solving models, Talouki proposed a hybrid metaheuristic workflow scheduling algorithm based on GA (Genetic Algorithm) and SA (Simulated Annealing). This method benefits from the global optimization capabilities of the Genetic Algorithm and the local search capabilities of the Simulated Annealing, achieving a good balance between exploration and exploitation of the search space24. Ekhlas designed a new Discrete Grey Wolf Algorithm (D-GWA) for the combinatorial k-coverage problem, which gains from deploying the most experienced available candidates while introducing new acceptance rules to avoid local optima25. Alaie proposed a Hybrid Dual Objective Discrete Cuckoo Search Algorithm (HDCSA) for the combinatorial optimization problem of scheduling scientific workflows on cloud platforms. This hybrid algorithm utilizes novel Levy flight operators adapted to discrete search spaces, effectively balancing exploration and exploitation during the optimization process26. Seifhosseini introduced a Multi-objective Cost-aware Discrete Grey Wolf Optimization Algorithm (MoDGWA) for a multi-objective cost-aware bag-of-tasks scheduling model. This algorithm includes a load-balancing process that offloads overburdened fog nodes to underutilized ones, potentially reducing total execution time27.

Table 1 provides a comprehensive comparison between the current study and previous research related to vehicle distribution route optimization. Existing research in the area of fresh food logistics distribution has yielded substantial results, and significant progress has been made in the study of route planning under time-varying road networks. However, the focus of these studies on optimizing routes in time-varying networks has primarily been limited to cost and customer satisfaction. These studies consider the time-varying characteristics of road traffic as well as the quality degradation of fresh products during transport over these networks, highlighting a gap in research on multi-vehicle joint distribution issues. Moreover, as competition in the fresh food logistics market intensifies, businesses pursuing cost reduction through minimizing actual expenditure alone can no longer satisfy the current practical needs. Only by fully integrating multiple objectives such as carbon emissions and time efficiency into models can businesses enhance their competitive edge in the market and achieve long-term, stable development.

Table 1 Comparison of research contributions with existing studies.
Full size table

This paper focuses on the problem of multi-vehicle type fresh food logistics distribution routes under a time-varying network environment, with varying energy consumption. It considers multiple factors affecting fresh food logistics distribution such as transportation costs, energy consumption, carbon emissions, and time efficiency, to construct an optimization model. By designing a Tabu Search-Genetic Algorithm hybrid (TS-GA) to solve this model, the paper analyzes distribution results of varying scales and compares them with other optimization algorithms, thereby studying the effectiveness and superiority of the hybrid algorithm. This also provides a theoretical reference for decision-making in fresh food logistics distribution enterprises.

Problem description

Notations

The parameters designed in the model are shown in Table 2.

Table 2 Parameter table.
Full size table

Problem descriptions

In the distribution process, if temperature control is not adequately maintained, it can accelerate the freshness decay of fresh agricultural products, leading to unnecessary waste and increased cold chain costs. To effectively control temperature variations throughout the cold chain transport and reduce the rate of freshness loss, it is essential to consider factors such as carbon emissions, customer service time constraints, and refrigeration costs to perform rational transport scheduling.

Firstly, cargo damage constrains the cold chain logistics VRP, aiming to ensure that cargo damage remains below a certain level while seeking optimal overall costs, allowing for some cost to be sacrificed to enhance transportation efficiency and reduce cargo damage. The main factor affecting cargo damage in the VRP is the timeliness of delivery. Secondly, there is a significant variation in customer demand for fresh goods (for example, higher demand for fruits and vegetables compared to meats, eggs, dairy, and seafood); using a single vehicle type for delivery could likely result in underutilization, leading to increased delivery costs28,29. Therefore, adopting a multi-vehicle delivery mode is feasible. Lastly, cold chain logistics is an industry within the entire logistics system that has very high energy consumption and carbon emissions, which conflicts with the current advocacy for a “low-carbon economy”. Thus, incorporating low-carbon factors into the model is a trend. In summary, the issue that the model construction needs to solve is how to reasonably schedule vehicles and plan routes in a multi-vehicle mode, so as to minimize the total delivery cost while maximizing customer satisfaction.

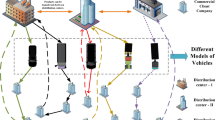
This paper studies the problem of time-varying transportation routes in urban fresh food cold chain logistics based on generalized costs. The problem can be described as follows: there is one distribution center, several customer demand points, and transport vehicles. Every customer’s demand needs to be satisfied; vehicle speeds are variable, affected by traffic conditions; vehicles need to arrive within the customer-specified time windows. By considering transportation costs, energy consumption, time-varying road networks, and other issues, the optimal vehicle driving routes are planned to achieve the lowest overall cost, energy consumption, cargo damage, and shortest transportation time. The problem is illustrated in Fig. 2.

Fig. 2
figure 2

Diagram of time-varying path model for fresh food logistics distribution.

Full size image

During the distribution process, due to the time-varying nature of road network transport, the speed of vehicles varies at different times. The transportation time between delivery nodes depends on the actual transportation speed on the route at the time of departure and the distance between the delivery nodes. For simplicity in analysis and computation, the variation in transportation speed can be represented by a piecewise continuous function, assuming that the vehicle speed is constant over a certain period. As illustrated in Fig. 3, there is a set of time segments \(T=\{ {T_0},{T_1}, \ldots ,{T_{n - 1}},{T_n}\}\). And for any time segment \([{T_{n - 1}},{T_n}]\), there is a corresponding transportation segment\((i,j)\). During the transport process on this segment, the vehicle’s speed at time t is denoted as \({v_{ij}}(t)\).

At this point, the total transportation time on segment \((i,j)\) is calculated using the formula:

$${T_{ij}}({d_i},t)=\left\{ {\begin{array}{*{20}{c}} {{t_{re}}+{T_{ij}}({d_i}+{d_{re}},{t_{re}}+t)}&{{d_i}+{d_{re}}<{d_{ij}}} \\ {{{{d_{ij}}} \mathord{\left/ {\vphantom {{{d_{ij}}} {{v_{ij}}(t)}}} \right. \kern-0pt} {{v_{ij}}(t)}}}&{{d_i}+{d_{re}} \geqslant {d_{ij}}} \end{array}} \right.$$
(1)

Where \({T_{ij}}({d_i},t)\) represents the time required for a vehicle to complete the remaining distance on a road segment at time t, given that the vehicle has already traveled a distance \({d_i}\). The variable \({t_{re}}\)denotes the remaining time in the interval \([{T_{n - 1}},{T_n}]\) at time t, calculated as \({t_{re}}={T_n} - t\), where \(t \in [{T_{n - 1}},{T_n}]\). \({d_{re}}\) represents the distance that can be covered in the remaining time at the transport speed \({v_{ij}}(t)\) at time t, satisfying\({d_{re}}={v_{ij}}(t) \cdot {t_{re}}\).

Fig. 3
figure 3

Schematic diagram of time-varying speed.

Full size image

Model formulation

Assumption

This paper makes the following assumptions:

  1. (1)

    There is only one distribution center within the region, with multiple delivery points. The distribution center has sufficient supplies to meet all delivery demands and is equipped with several models of refrigerated vehicles.

  2. (2)

    Each distribution point can only be served by a single type of delivery vehicle, ensuring that at least one vehicle has a carrying capacity greater than the total demand of the individual distribution point.

  3. (3)

    All delivery vehicles start from the distribution center, pass through all delivery points without repetition, and ultimately return to the distribution center.

  4. (4)

    During the delivery process, the driving speed of the vehicles is influenced only by road congestion and is related solely to the traffic congestion coefficient, but not affected by any other unforeseen circumstances.

  5. (5)

    The fresh products being transported are of uniform initial quality, and their freshness decay follows an exponential function.

  6. (6)

    The location, demand, and time window constraints of each distribution point are given and remain unchanged over the delivery period.

Objective function

This article investigates the issue of fresh produce logistics and distribution, focusing on optimizing the delivery route. The objective function of the distribution path optimization model is to minimize the total cost. The components of the total cost include.

Vehicle operating cost

Vehicle operating costs comprise both fixed and variable costs. Fixed costs include regular operational expenses such as employee salaries and maintenance fees.

$$FC=\sum\limits_{{k=1}}^{k} {{f_k}}$$
(2)

Variable costs cover expenses incurred during delivery, such as tolls and fuel costs.

$$TC=\sum\limits_{{k=1}}^{k} {\sum\limits_{{i,j=1}}^{n} {{X_{ijk}}} } \cdot {d_{ij}} \cdot {\alpha _k}+{C_{Oil}} \cdot \sum\limits_{{k=1}}^{k} {\sum\limits_{{i=1}}^{j} {\sum\limits_{{j=1}}^{n} {{X_{ijk}} \cdot {d_{ij}} \cdot {w_i} \cdot } } } {P_k}(w)$$
(3)

The fuel cost for vehicle k carrying a load w over a unit distance, denoted by\({P_k}(w)\), is calculated as follows:

$${P_k}(w)={P_{k0}}+\frac{{({P_{k1}} - {P_{k0}})}}{{{W_k}}} \cdot w$$
(4)

Dual carbon cost

Dual carbon costs encompass refrigeration costs of vehicles and carbon emission costs. Refrigeration costs arise from pre-cooling refrigerated vehicles at the beginning of delivery and maintaining cooling due to temperature differences during transport. Carbon emission costs refer to the expenses associated with mitigating the carbon emitted due to energy consumption during delivery. The formula for dual carbon costs is as follows:

$$CC=\sum\limits_{{k=1}}^{k} {T_{O}^{k}} \cdot {\eta _{\sigma in,\sigma out}}+\beta \cdot \gamma \cdot \sum\limits_{{k=1}}^{k} {\sum\limits_{{i,j=1}}^{n} {{X_{ijk}}} } \cdot {d_{ij}} \cdot {P_k}(w)$$
(5)

Goods damage cost

Goods damage costs are incurred due to spoilage and deterioration of fresh goods, even when refrigerated. As the delivery time extends, the spoilage can accelerate, affecting other goods within the refrigerated vehicle. The cost associated with this spoilage is referred to as the goods damage cost. The expressions for freshness, denoted by \(fr(t_{i}^{k})\), and goods damage cost \(HC\), are defined as follows:

$$fr(t_{i}^{k}){\text{=}}\sum\limits_{{k=1}}^{k} {\sum\limits_{{i,j=1}}^{n} {{X_{ijk}}} } \cdot {e^{\varphi (t_{i}^{k} - t_{o}^{k})}}$$
(6)
$$HC{\text{=}}\theta \cdot \sum\limits_{{k=1}}^{k} {\sum\limits_{{i,j=1}}^{n} {{X_{ijk}}} } \cdot {w_i} \cdot [1 - {e^{\varphi (t_{i}^{k} - t_{o}^{k})}}]$$
(7)

Time penalty cost

Due to the strict timing requirements of fresh produce delivery, a specific time window is set to ensure the freshness upon arrival. If the delivery falls outside the optimal time window \([A_{i}^{{best}},B_{i}^{{best}}]\), no penalty cost is incurred; if it falls outside the optimal but within the permissible window \([{A_{allow}},{B_{allow}}]\), early or late penalty costs are applied. Deliveries outside the permissible window are not allowed and are assigned an infinite penalty cost. The penalty cost \(EC\) is defined as follows:

$$EC=\sum\limits_{{i=1}}^{n} {{e_i}}$$
(8)

And the time penalty cost \({e_i}\) for delivery point i is defined as follows:

$${e_i}=\left\{ {\begin{array}{*{20}{c}} \infty &{a_{i}^{k}<A_{i}^{{best}},a_{i}^{k}>B_{i}^{{best}}} \\ {{\eta _1}(A_{i}^{{best}} - a_{i}^{k})}&{A_{i}^{{allow}}<a_{i}^{k}<A_{i}^{{best}}} \\ 0&{A_{i}^{{best}} \leqslant a_{i}^{k} \leqslant B_{i}^{{best}}} \\ {{\eta _2}(a_{i}^{k} - B_{i}^{{best}})}&{B_{i}^{{best}}<a_{i}^{k}<B_{i}^{{allow}}} \end{array}} \right.$$
(9)

Constraint condition

Vehicle payload constraint

Due to assumption (2), there is only one vehicle serving at any delivery point i.

$$\sum\limits_{{k=1}}^{k} {{y_{ik}}} =1$$
(10)

For any vehicle k, the total amount of delivered goods is less than its load limit.

$$\sum\limits_{{i=1}}^{n} {{q_i}{y_{ik}}} \leqslant {W_k}$$
(11)

Delivery point service constraint

Considering that there is only one front delivery point and one rear delivery point for any delivery point.

$$\sum\limits_{{i{\text{=}}0,i \ne j}}^{n} {{X_{ijk}}{\text{=}}{Y_{jk}}}$$
(12)

Where \(j=\{ 1,2, \ldots ,n\} ,i \ne j,\forall k\).

$$\sum\limits_{{j=0,i \ne j}}^{n} {{X_{ijk}}{\text{=}}{Y_{ik}}}$$
(13)

Where, \(i=\{ 0,1, \ldots ,n\} ,i \ne j,\forall k\).

Meanwhile, each delivery point requires vehicles for service.

$$\sum\limits_{{i{\text{=}}1}}^{n} {\sum\limits_{{k=1}}^{k} {{Y_{ik}}} } =n$$
(14)

No sub-loops are allowed to form on the route executed by any vehicle.

$$\sum\limits_{i} {\sum\limits_{j} {{X_{ijk}}} } \leqslant |S| - 1$$
(15)

Delivery point time constraint

When a vehicle arrives at a distribution point to load goods, it must meet the following two types of time constraints.

  1. (1)

    The arrival time of vehicle k at distribution point i must be earlier than its departure time from that point.

    $$a_{i}^{k}<t_{i}^{k};\forall i=\left\{ {1, \cdots ,n} \right\},\forall k \in K$$
    (16)
  2. (2)

    If vehicle k travels from distribution point i to distribution point j, the following constraint must be satisfied.

    $$t_{i}^{k}+{{{d_{ij}}} \mathord{\left/ {\vphantom {{{d_{ij}}} {{v_0}}}} \right. \kern-0pt} {{v_0}}} - M(1 - {X_{ijk}}) \leqslant t_{j}^{k}$$
    (17)

The model

The model is constructed with the objective function being the sum of all costs, as described above.

$$\begin{array}{*{20}l} ob.\hbox{min} C=FC+TC+CC+HC+EC \hfill \\ s.t\left\{ \begin{gathered} \sum\limits_{{k=1}}^{k} {{y_{ik}}} =1 \hfill \\ \sum\limits_{{i=1}}^{n} {{q_i}{y_{ik}}} \leqslant {W_k};\forall k \in K \hfill \\ \sum\limits_{{i{\text{=}}0,i \ne j}}^{n} {{X_{ijk}}{\text{=}}{Y_{jk}}} ;\forall j=\left\{ {1,2, \cdots ,n} \right\},i \ne j,\forall k \in K \hfill \\ \sum\limits_{{j=0,i \ne j}}^{n} {{X_{ijk}}{\text{=}}{Y_{ik}}} ;\forall i=\left\{ {0,1, \cdots ,n} \right\},i \ne j,\forall k \in K \hfill \\ \sum\limits_{{i{\text{=}}1}}^{n} {\sum\limits_{{k=1}}^{k} {{Y_{ik}}} } =n; \hfill \\ a_{i}^{k}<t_{i}^{k};\forall i=\left\{ {1, \cdots ,n} \right\},\forall k \in K \hfill \\ {X_{ijk}}=\{ 0,1\} ;\forall i \ne j,\forall i,j,k \hfill \\ {Y_{ik}}=\{ 0,1\} ;\forall i,k \hfill \\ \end{gathered} \right. \hfill \\ \end{array}$$

Solution algorithm

The model discussed in this paper is characterized by its NP-hard nature and is designed as an optimization model for fresh food logistics distribution with time windows, damage rates, and time-varying transportation speeds. It involves numerous variables, objectives, and constraints, with a large solution scale and multiple objective functions. Given these complexities, a heuristic search algorithm suitable for solving this model is proposed.

The Genetic Algorithm (GA) is a population-based search algorithm inspired by the concept of “survival of the fittest”, known for its strong parallel computing and global search capabilities, and its ease of implementation in large-scale combinatorial optimization problems. However, when applied to the layout optimization model for shared bicycle parking zones with multiple constraints, the basic GA encounters several issues due to the increased complexity from the additional constraints in formulas (2) through (17):

  1. 1.

    Poor Local Search Capability: After several generations of evolution, the similarity between individuals increase, leading to new individuals that are highly similar and thus failing to generate truly new solutions.

  2. 2.

    Premature Convergence: GA tends to converge prematurely, often struggling to reach the optimal solution.

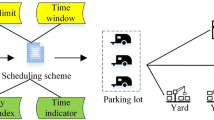
Tabu Search (TS) starts with an initial feasible solution and explores a series of specific search directions, selecting the move that maximizes changes in the objective function. The key feature of TS is its strong local search capability, achieved through local neighborhood search and the introduction of tabu lists and aspiration criteria, which prevent redundant searches and allow rapid convergence to a local optimum. To address the limitations of the traditional GA, this study introduces a TS mechanism into the GA framework, creating a TS-GA Hybrid Algorithm that combines GA’s global search capability with TS’s neighborhood search capability. By incorporating local search improvements and tabu strategies, the hybrid algorithm avoids the drawbacks of getting trapped in local optima, thereby enhancing global optimization capability. This approach reduces the reliance on an optimal initial population, effectively preventing premature convergence, and is more suitable for solving large-scale, complex multi-constraint combinatorial optimization problems. Consequently, this paper proposes a TS-GA Hybrid Algorithm with K-means clustering to solve the previously constructed model. The algorithm steps are shown in Fig. 4.

Fig. 4
figure 4

TS-GA hybrid algorithm process.

Full size image

Design of time-varying path

In practical distribution processes, road network traffic speed often has time-varying characteristics. However, for simplicity and feasibility of calculation, the total daily time is subdivided into \(\rho\) periods, denoted as \(P=\{ {d_p}|p=1, \ldots ,\rho \}\). The start and end times for period \({d_p}\) are \([{O_{p - 1}},{O_p}]\). During the p-th period, the driving speed \({v_p}\) of all vehicles is constant, calculated as \({v_p}={{{v_o}} \mathord{\left/ {\vphantom {{{v_o}} {{\gamma _p}}}} \right. \kern-0pt} {{\gamma _p}}}\), where \({v_o}\) is the ideal vehicle speed and \({\gamma _p}\) is the traffic congestion delay coefficient for the p-th period. The relationship between speed and time is depicted in Fig. 5.

Fig. 5
figure 5

Schematic diagram of the relationship between speed and time.

Full size image

If the total duration of period p is \({H_p}\), then the feasible driving time for that period is \({K_p}\), satisfying\({K_p}={O_p} - {O_{p - 1}}\), and the feasible driving distance is \({L_p}\). The shortest distance between delivery points i and j during period p is \(d_{{ij}}^{p}\), satisfying \({d_{ij}}{\text{=}}\sum\nolimits_{p} {d_{{ij}}^{p}}\), where \(d_{{ij}}^{p}\) is the effective driving distance for period p. Additionally, \(D_{{ij}}^{p}\) represents the remaining distance to be covered after period p along the route \((i,j)\), and \(T_{{ij}}^{p}\) is the effective driving time within period p. The steps for calculating the travel time in a time-varying road network are as follows.

Step 1 Calculate the initial travel distance for the vehicle during its initial period as \(d_{{ij}}^{p}={v_p}{K_p}\). If \(d_{{ij}}^{p} \geqslant {d_{ij}}\), then \(T_{{ij}}^{p}={{{d_{ij}}} \mathord{\left/ {\vphantom {{{d_{ij}}} {{v_p}}}} \right. \kern-0pt} {{v_p}}}\) and proceed to Step 4. Otherwise, \(D_{{ij}}^{p}={d_{ij}} - d_{{ij}}^{p}\) and \(T_{{ij}}^{p}={K_p}\).

Step 2 Set a constant \(\zeta =1\).

Step 3 The vehicle travels during period \(p+\zeta\) with \(d_{{ij}}^{{p+\zeta }}={K_{p+\zeta }} \cdot {v_{p+\zeta }}\). If \(d_{{ij}}^{{p+\zeta }} \leqslant D_{{ij}}^{{p+\zeta - 1}}\), then \(T_{{ij}}^{p}={K_{p+\zeta }}\), \(D_{{ij}}^{{p+\zeta }}=D_{{ij}}^{{p+\zeta - 1}} - d_{{ij}}^{{p+\zeta }}\), iterate \(\zeta\) by setting \(\zeta =\zeta +1\), and repeat Step 3. Otherwise, \(T_{{ij}}^{{p+\zeta }}={{{D_{ij}}} \mathord{\left/ {\vphantom {{{D_{ij}}} {{v_p}}}} \right. \kern-0pt} {{v_p}}}\) and proceed to Step 4.

Step 4 Calculate the total travel time T for the entire route, denoted as \(T=\sum\limits_{{p \in P}} {T_{{ij}}^{p}}\).

Clustering design of Tabu search

To address the challenge of searching through a large number of customer nodes in VRP studied in this paper, and to further improve the solution quality, the tabu Search algorithm incorporates the K-means clustering algorithm. This clustering technique groups customer nodes that are close in spatial location and time windows, allowing the delivery route planning process to consider clusters of customers as a single delivery unit.

Based on the design of the TS-GA hybrid algorithm, the tabu search component is constructed utilizing a tabu search algorithm based on K-means clustering. The specific implementation process is as follows:

Fig. 6
figure 6

Customer point clustering graph based on time and space.

Full size image

Utilizing an enhanced K-means algorithm based on penalty functions associated with customer spatial location, time window constraints, and freshness, we conduct clustering operations on customer points. Determine q clustering units. Taking into account customer spatial location and time constraints, construct the customer point clustering graph as illustrated in Fig. 6. Divide the delivery timeline into 4 time slots, denoted as\({t_1},{t_2},{t_3},{t_4}\) (representing \({A^{allow}},{A^{best}},{B^{best}},{B^{allow}}\) respectively). Represent geographical locations and temperature control ranges on the X-axis and Y-axis, respectively. Establish a tabu set R containing customer time windows. When a customer does not satisfy the tabu set R, consider conducting customer clustering operations. Within each layer of ellipses’ spatial regions, if the customer’s time window requests fall within the same time slot, consider clustering the customers into a single delivery unit.

The enhanced K-means algorithm process is described as follows:

  • Step 1: Establish an initial taboo set R. Customers whose attributes do not satisfy the conditions of set R are eligible to participate in clustering.

  • Step 2: Import the relevant customer data.

  • Step 3: Convert the data matrix into a data vector.

  • Step 4: Determine the initial number of clustering units q, based on the K-means clustering algorithm and select q initial clustering centers.

  • Step 5: Assess whether the clustering criteria between prospective and already clustered customers meet the conditions of the taboo set R. If the conditions are not fully met, assign each customer to the clustering unit whose center is closest to that customer; otherwise, proceed to Step 7.

  • Step 6: Update the centers of each clustering unit.

  • Step 7: Increase the number of clustering units to \(q \to q+1\) and generate new clustering units and centers.

  • Step 8: Repeat Steps 6 and 7 until the cluster affiliations of each customer no longer change.

Algorithm design for the genetic part

Encoding method

In general, the solution is typically encoded as a natural array with specific design rules, when applying genetic algorithms to optimization problems.

This paper uses an integer sequence vector to represent the fresh food logistics delivery route scheme. The initial chromosome, denoted as ‘\(chrom\)’, is designed as follows:

$$chrom=[{x_1},{x_2}, \ldots ,{x_i}, \ldots {x_n}]$$

Where, each gene locus in the chromosome takes on a random integer value between 1 and n, with the constraint that no two gene loci have the same value, i.e., \({x_i} \ne {x_j},i \ne j\). Since a single chromosome ‘\(chrom\)’ contains the routes for multiple vehicles, during decoding, it is possible to decompose the chromosome into several segments based on the cargo demands of different customer sites and the load capacities of various vehicle types. Each segment represents the route of a delivery vehicle, and the number of segments corresponds to the number of deployed delivery vehicles.

Fitness function

The fitness of a chromosome is determined by the combined costs of transportation, energy consumption, carbon emissions, refrigeration, freshness-related cargo loss, and penalties for violating delivery deadlines. During the execution of the genetic algorithm, some chromosomes in the population may not satisfy all constraints. To account for such cases, a penalty function is introduced in the fitness function of the chromosome.

In this paper, when calculating the fitness value of a chromosome, a penalty coefficient M and a step function \(J(x)\) are introduced for gene values that exceed limits or are infeasible. Specifically, if the delivery route scheme x corresponding to the chromosome satisfies all constraints, then \(J(x)=0\). Otherwise, \(J(x)=1\).

The penalty coefficient and the step function are incorporated into the objective function as follows:

$$F(x)=M \cdot J(x)+C(x)$$
(18)

Genetic operators

The selection operator is based on the roulette wheel principle, where high-quality individuals are selected to be carried over to the next generation.

The crossover and mutation operators are illustrated in Fig. 7. Specifically, the crossover operator uses an inversion mechanism with a predefined crossover probability \({P_c}\). The mutation operator employs a swapping mechanism with a predefined mutation probability \({P_m}\).

Fig. 7
figure 7

Schematic diagram of crossover operator and mutation operator.

Full size image

TS-GA hybrid algorithm steps

The fundamental steps of the TS-GA Hybrid Algorithm are as follows:

  • Step 1 Utilize an improved K-means algorithm based on factors such as customer coordinates, demand, and time windows to cluster customer points, thereby assigning all customers into q cluster units.

  • Step 2 Generate an initial population through chromosomal encoding derived from the clustering process, specifying the population size as \(inn\), the maximum number of iterations as \(maxgen\), crossover probability \({P_c}\), mutation probability \({P_m}\), and the length of the Tabu list as l.

  • Step 3 Calculate the fitness values of individuals within the population. The objective functions in this study aim to minimize transportation costs for delivery vehicles, minimize penalty costs for exceeding time windows, and reduce delivery mileage. The fitness function \(f(x)\) is defined accordingly.

  • Step 4 Account for the time window constraints of customer points. Select elite individuals from the population to serve as parents for the next generation using a roulette wheel selection method.

  • Step 5 Perform crossover and mutation operations on the population according to the defined probabilities Pc and Pm to form a new population. For offspring that violate time window constraints, generate new fitness values \(f(x)\) incorporating penalty costs.

  • Step 6 Apply the Genetic Algorithm (GA) procedures to the chromosomes, conduct Tabu Search to generate initial neighborhood solutions, identify candidate solutions, and update the Tabu list, iterating to optimize the solutions.

  • Step 7 Repeat the processes in Steps 3 and 6 in a cycle. Continue iterations until the algorithm reaches the maximum number of iterations \(maxgen\). Conclude the algorithm and output the optimal results.

Time complexity analysis

In this paper, the time complexity of the algorithm is expressed as a function of the number of nodes nn, which describes the number of basic operations required to complete the computational tasks when the number of nodes is nn. Traditional genetic algorithms often struggle to converge to the global optimum and are typically assumed to terminate when the maximum number of iterations is reached. Therefore, the time complexity of traditional genetic algorithms can be approximately described as \(O(maxgen \times inn)\), indicating that it is constant with respect to the number of iterations allowed.

In the paper, the Tabu Search algorithm mainly includes operations such as generating initial solution, creating neighborhoods, assessing Tabu list, and lifting bans. Each step’s time complexity is listed in Table 3 as follows:

Table 3 Tabu search algorithm operation.
Full size table

In the TS-GA hybrid algorithm, the time spent on generating neighborhoods and evaluating fitness values significantly exceeds the time consumed by other operations. As such, the computational time required for generating initial solutions, forming candidate sets, and updating the Tabu list can be disregarded. The TS-GA algorithm employs genetic mutation operators to generate neighborhoods for the initial solutions. These mutation operators are inherently stochastic, and the time complexity of the TS-GA algorithm is determined using methods suitable for analyzing the complexity of random algorithms, resulting in a time complexity of \(O[maxgen \times (in{n^2}+inn+l)]\)30.

Numerical experiments

This section presents the numerical experimental results of the problem example. Part A presents the numerical experimental results of the problem instance based on actual data received by Zhongtong Cold Chain Logistics Company in Pidu District, Chengdu City. Part B reports the computational results on instances of logistics enterprises. Part C designs a set of instances to evaluate the model and algorithm proposed based on this data, providing experimental results to demonstrate the effectiveness of the TS-GA hybrid algorithm.

Real data and generation of instances logistic company

Logistics company A includes one distribution center (\({D_0}\)) and 30 customer sites (\({D_1}\) to \({D_{30}}\)). An example case is generated based on the data received from the operations of a specific day, assuming that the unloading time at each demand point is 10 min. Detailed information on the locations and requirements of the customer sites is on the Gaode Map satellite map available in Fig. 8; Table 4.

Fig. 8
figure 8

Schematic diagram of logistics distribution network in Pidu District.

Full size image
Table 4 Delivery center and customer information table.
Full size table

The information on available delivery vehicles is presented in Table 5. It is assumed that there is a sufficient initial stock of three types of refrigerated trucks.

Table 5 Basic parameters of refrigerated trucks.
Full size table

During the transportation process, the traffic congestion delay coefficients for different time periods are shown in Table 6. These coefficients represent the factors by which travel time is increased due to congestion on the road network during these periods.

Table 6 Traffic congestion delay coefficient at different time periods.
Full size table

Given the varying temperature control requirements of different types of goods, refrigerated trucks adjust their cooling temperatures according to the characteristics of the products being transported. Taking into account the characteristics of heat transfer, the Coefficient of Performance (\(COP\)) is used to represent the conversion ratio between energy and heat.

$$COP=\frac{{{T_L}}}{{{T_H} - {T_L}}}$$
(17)

Where, \({T_H}\) represents the ambient external temperature, measured in Kelvin (K). \({T_L}\) denotes the target temperature set for temperature-controlled regulation, also measured in Kelvin (K).

Assuming the external ambient temperature is 25 °C, the cooling cost at 5 °C is set as unit 1. Consequently, the cooling cost coefficient \({\theta _w}\) at 4 °C is calculated to be 13.9/13.19 = 1.05. Using the same method, cooling cost coefficients for other temperatures can also be calculated. Furthermore, the unit temperature control cost \({g_w}\) under different temperature conditions can be calculated using the formula provided, detailed in Table 7.

Table 7 Values of COP, Q, and g under different temperature control conditions31.
Full size table

Considering the complexity of calculating certain costs, the following parameters are simplified for ease of calculation: the price of fuel is set at 8.5 RMB per liter, the carbon emission coefficient is \(\gamma =2.68\;{\text{kg}}/{\text{L}}\), the carbon tax rate is \(\beta =0.0528\;{\text{yuan}}/{\text{kg}}\), the unit refrigeration cost is \(PC=50\;{\text{yuan}}/{\text{h}} \cdot {\text{t}}\), the ideal vehicle speed is \({v_o}=50\;{\text{km}}/{\text{h}}\), the unit value of the goods is \(\theta =100\;{\text{yuan}}/{\text{t}}\), and the early and late arrival penalty cost coefficient is \({\eta _1}=10\;{\text{yuan}}/{\text{h}}\) and \({\eta _2}=40\;{\text{yuan}}/{\text{h}}\). The decay rate of perishable goods is set at \(\varphi =0.002\).

Computational results for the case

To solve the proposed model, the MATLAB software is employed with specific settings for the Genetic Algorithm (GA) and the Tabu Search (TS) algorithm. The GA parameters are set as follows: population size \(inn=150\), maximum number of iterations at \(maxgen=300\), a crossover probability \({P_c}=0.8\), and a mutation probability \({P_m}=0.05\). The TS algorithm parameters include a search step count of 50 and a Tabu length \(l=5\).

It is evident that the TS-GA hybrid algorithm demonstrates good convergence in solving the model, with gradually stabilizing optimization results depicted in Fig. 9. The total runtime of the algorithm is approximately 16.3 s, and the algorithm stabilizes after about 180 generations. The total cost of the entire distribution system is approximately 12,934.02 RMB.

Fig. 9
figure 9

Convergence curve with the objective ofTS-GA.

Full size image

The convergence of each sub-objective function value through iterations of the algorithm is illustrated in Fig. 10. Figure 10(a) shows the convergence of the number of delivery vehicles as the algorithm progresses, with the algorithm stabilizing at a total of 5 vehicles. Figure 10(b) shows the penalty costs for delivery vehicles arriving either late or early as the algorithm iterates towards convergence. After the algorithm converges, the total penalty time for delivery vehicles is 449 min for early arrivals and 76 min for late arrivals. It can be observed that the penalty cost curve exhibits significant fluctuations in the early stages of the algorithm’s iteration. This is because the penalty costs constitute a relatively small proportion of the overall cost, thus having a minor impact on the fitness values. Consequently, the penalty costs show limited correlation with the overall trend of the total system cost curve. Figure 10(c) shows the convergence of the total mileage covered by the delivery vehicles; upon stabilization, the vehicles cover approximately 283.79 km. From the convergence patterns of these three objectives, it can be observed that the convergence curve of the delivery mileage is most similar to the total cost convergence curve of the delivery system. This similarity arises because, in the total costs of the delivery system, increases in delivery mileage lead to higher transportation variable costs, fuel consumption costs, and carbon emission costs, which collectively constitute the largest proportion of the incurred expenses. This detailed analysis highlights the significant impact that mileage has on the overall cost effectiveness of the logistics operation. The delivery result is shown in Fig. 11; Table 8.

Fig. 10
figure 10

Convergence of the three objectives.

Full size image
Fig. 11
figure 11

Schematic diagram of optimized delivery route plan.

Full size image
Table 8 Delivery plan results.
Full size table

Algorithm validation

To further validate the performance of the model and algorithm, the TS-GA algorithm employed in this study was compared with traditional genetic algorithms and the CPLEX software. The parameters of the TS-GA algorithm were set according to references32,33, aligning with the parameter settings of traditional genetic algorithms. Additionally, six sets of case studies on fresh food logistics distribution routes optimization were created. These cases were referenced in the form of n-k-d, where n represents the number of distribution centers, k represents the number of customer nodes, and d represents the number of types of vehicles for distribution. For instance, 1-30-3 corresponds to a scenario with one distribution center, 30 customer nodes, and three types of vehicles for distribution. In each set of artificial instances, based on the distribution network of Zhongtong Cold Chain Company in Chengdu city, considerations were made for future development and gradual expansion of customer nodes due to increasing demand.

Table 9 presents a comparison of the solution quality and CPU runtime for urban fresh produce logistics distribution route optimization problems, using the improved TS-GA algorithm, a traditional GA algorithm, and CPLEX software.

Table 9 Performance comparison of these methods.
Full size table

As shown in Table 6, the optimization solutions obtained with the improved TS-GA algorithm exhibit superior quality compared to those obtained through the traditional GA, with quality gaps ranging from 2.94 to 7.68%. These results are slightly inferior to those obtained using CPLEX software, which shows quality gaps ranging from 1.53 to 6.52%. However, in terms of computational efficiency, the TS-GA algorithm’s performance is slightly lower than that of the traditional GA, though the difference is not significant. Both intelligent optimization algorithms are far more efficient than CPLEX software. Moreover, when the problem size increases to a certain extent, CPLEX software fails to find the optimal solution. These findings validate the effectiveness of the proposed improved TS-GA algorithm and demonstrate its superiority in finding optimal solutions for large-scale problems.

Sensitivity analysis

The sensitivity analysis in this study includes two aspects: cost sensitivity analysis and traffic environment sensitivity analysis. The cost sensitivity analysis examines how changes in factors such as cooling costs, fuel costs, and time window penalty costs affect the final optimization solution and objective function. Traffic environment sensitivity analysis primarily investigates how changes in road and environmental conditions impact vehicle transportation speeds, which in turn affect factors such as the number of vehicles used in the optimization solution and the accumulation of time beyond the time window.

In terms of sensitivity to the main costs, this study uses the base data from the case as a comparison for research. For cooling costs, different perishable goods have varying temperature requirements. According to the base data in Table 4, considering conventional cold chain transport typically ranges from − 2 °C to 5 °C, the sensitivity of cooling costs to temperature changes in delivery vehicles can be observed, as shown in Fig. 12.

Fig. 12
figure 12

Sensitivity analysis of temperature changes.

Full size image

Figure 12 reveals that as the transportation temperature changes, both cooling costs and carbon emissions costs vary accordingly. When the transportation temperature is 5 °C, the cooling cost is the lowest and the carbon emissions cost is also minimal. Conversely, at a transportation temperature of -2 °C, the cooling cost is highest. Since the damage rate designed in this study is only related to transportation time and not temperature, cooling costs do not affect product damage.

Regarding traffic environment sensitivity analysis, the study simplifies the actual traffic situation by assuming all roads have a speed limit of 50 km/h. Given that urban traffic conditions are difficult to model with simple mathematical methods, an impedance factor is added to the road transport speed to adjust the clustering range of nodes. Based on the contents of “Design of time-varying path” and “Clustering design of Tabu search” sections, all nodes are reclustered, and four of these clusters are compared with the case solution calculated in this study, as shown in Table 10.

Table 10 Sensitivity analysis of different clustering schemes.
Full size table

Table 10 shows that as transportation speed decreases, the permissible range for node clustering reduces, leading to an increase in the number of clusters. Consequently, the number of vehicles required rises, which effectively reduces the accumulated time of time window violations. When the clustering schemes are set to 1 or 2, although the number of vehicles used matches that in this study’s case, the total time of time window violations is longer, resulting in a higher overall system cost. When clustering schemes are 2 or 3, they exhibit a certain degree of comparability with the optimal solution in this study. However, considering the Pareto optimization theory, the final result obtained in this study is superior. For clustering schemes 3 and 4, the accumulated time of time window violations is less than that of the optimal solution obtained, but due to the relatively small design coefficient for penalty costs, the reduction in penalty costs does not offset the increases in fixed and transportation costs.

Implication

The findings of this study have significant practical implications for logistics and transportation companies, offering the following management insights:

  • Cost reduction: The proposed model substantially reduces both production and operational costs for logistics companies, while also effectively minimizing losses due to spoilage and deterioration of goods during transportation.

  • Environmental impact: The model’s optimization towards dual-carbon goals effectively reduces vehicle energy consumption and carbon emissions during the logistics delivery process, contributing to the mitigation of global warming.

  • Cost sensitivity and traffic environment sensitivity: The analysis of cost sensitivity and traffic environment sensitivity included in this study discusses the impact of key parameters on the objective function. This analysis enhances the understanding of how different parameter values affect the overall system cost response mechanisms.

  • Implementation and practical application: The proposed model and algorithm are straightforward to implement, facilitating the development of information systems and decision support systems for industry researchers. This supports logistics professionals in designing efficient delivery route plans.

Conclusion and future direction

This study builds upon traditional cold chain logistics route optimization by addressing the path optimization problem for multi-type fresh food logistics under time-varying conditions. The model constructs a mathematical optimization framework with the objective of minimizing comprehensive costs, considering vehicle operational costs, dual-carbon costs, cargo loss costs, and time penalty costs. Additionally, the TS-GA hybrid algorithm is designed to effectively avoid premature convergence, providing satisfactory solutions within an acceptable time frame for various scale problems. The primary goal is to minimize the total cost, and the problem is formulated as an integer programming model.

The contributions of this research are multifaceted. Firstly, a novel integer programming model for fresh food logistics Vehicle Routing Problem (VRP) is proposed, addressing the trade-offs between carbon emissions and fresh food logistics. The model incorporates delivery time constraints, quantifies cargo loss due to reduced freshness, and accounts for time-varying transportation speeds, thereby optimizing fresh food delivery routes and enhancing management of actual fresh food logistics processes. Secondly, in response to the large-scale and challenging nature of the problem, the study introduces a TS-GA hybrid algorithm tailored for solving this model, effectively mitigating premature convergence and achieving satisfactory optimization results.

Future research could expand in several directions: (1) Including a broader range of influencing factors such as customer acceptance, uncertain demand quantities, and the freshness of perishable goods to enrich the research content and extend its applicability to more realistic environments. (2) Addressing the time-varying urban road background environment, which is not covered due to space and complexity constraints in this study. Future research could consider real-time traffic and weather data, analyzing their direct impact on fresh food delivery vehicle routes. (3) Improving the solution algorithms by enhancing the parallel processing of crossover and mutation operators to reduce time complexity, making the algorithm applicable to more complex logistics networks. (4) Focusing on integrating emerging technologies such as machine learning and artificial intelligence, including analyzing the impact of time-varying weather conditions and road conditions on inter-node transportation times using big data technology, and optimizing vehicle route selection with deep reinforcement learning techniques, to extend the model’s applicability to more realistic scenarios.