3-D intrinsic attenuation tomography using ambient seismic noise applied to La Palma Island (Canary Islands)

Abstract

The potential of the island of La Palma (Canary Islands) to host geothermal resources is very high, mainly due to its high volcanic activity. The primary goal of this study is to get a tridimensional image of the seismic intrinsic attenuation using ambient seismic noise and to identify anomalies that may be linked to active geothermal reservoirs on La Palma island. For this purpose, we developed a new Ambient Noise Attenuation Tomography (ANAT) technique, which uses seismic ambient noise for imaging intrinsic attenuation in 3-D at a local scale down to 5 km depth. Our research identifies two areas with high attenuation in the island’s southern region. One area could be associated with hydrothermal alteration zones beneath the Cumbre Vieja volcanic complex. Another high-attenuation zone was observed in the island’s southern part, which could be associated with extensively fractured rocks that might facilitate the circulation of heated fluids. Furthermore, we discuss the geothermal relevance of such anomalies, making a comparison with previous resistivity, S-wave velocity and density models. This study confirms that intrinsic attenuation retrieved from the coda of Rayleigh waves is more sensitive to the presence of fluids than velocity. Fluids being a key component of active geothermal reservoirs, it is reasonable to expect intrinsic attenuation anomalies in these systems. Therefore, we conclude that ANAT can be useful for geothermal exploration.

Introduction

Elastic waves experience energy loss as they travel through a medium, resulting in a reduction in amplitude as they move away from the source. This decrease in amplitude can be attributed to two factors: either the geometrical spreading of the wavefront or the scattering and intrinsic attenuation of elastic energy, which converts it into different forms such as heat. Various mechanisms can produce intrinsic attenuation, such as frictional dissipation¹, fluid flow in the pore space², or squirting mechanism and local scale fluid motion³. For this reason, the characterization of seismic attenuation is useful for studying the structure of volcanoes (e.g⁴.,) and hydrothermal systems (e.g⁵.,). One of the ways to measure the attenuation is through the coda quality factor $(Q_{c})$, which can be determined by measuring the decay of seismic energy with time⁶. Calvet et al⁷. demonstrated that in the later stages of the seismic coda, the dependency of $Q_{c}^{-1}$ on anisotropy and scattering attenuation diminishes notably. As a result, in this scenario $Q_{c}^{-1}$ can be considered as a direct assessment of intrinsic attenuation ( $Q_{c}^{-1}=Q_{i}^{-1}$).

Seismic attenuation plays an important role in geophysical exploration. Specifically, seismic attenuation tomography is a dependable and valuable tool for imaging the Earth’s internal structure. Many case studies have highlighted the usefulness of seismic attenuation tomography using earthquakes. Hence, Martínez-Arevalo et al⁴. and Castro-Melgar et al⁸. observed a high-consolidated body in the central structure of the Etna volcano that modifies the path of the ascent of new magma. Also, Del Pezzo et al⁵. and De Siena et al⁹. used earthquake-based attenuation tomography to study the Vesuvius and Campi Flegrei, revealing high-attenuation anomalies related to hydrothermal systems and partial melt materials. Furthermore, Calvet et al⁷. used the $Q_{c}$to observe spatial variations of seismic attenuation in the Pyrenees. In general, applying seismic attenuation tomography is useful for revealing the presence of magmatic and hydrothermal fluids^{10,11,12,13,14,15,16}. Seismic attenuation tomography can also be achieved by using active seismic sources. This kind of study was applied to different volcanoes, revealing attenuation anomalies related to the carbonate basement of the Merapi volcano¹⁷or a cracked medium and historical volcanic activity in Vesuvius and Tenerife volcanoes^{5,18,19,20,21,22}.

Recently, several researchers have highlighted the possibility of extracting seismic attenuation through interferometric measurements of surface-wave Empirical Green’s Functions (EGFs)²³. Weemstra et al²⁴. noted that the relationship between quality factor and frequency indicates a depth-dependent variation in attenuation, correlating with the geological characteristics of the surveyed area. Using numerical approaches, other studies demonstrated that the intrinsic attenuation can be successfully retrieved from the EGF^25,26,27,28. The extraction of attenuation from EGFs was used for Ambient Noise Attenuation Tomography (ANAT) in regional-scale seismic networks (approximately 100-1000 km)^23,29,30. Prieto et al²⁹. demonstrated how 1-D depth profiles of phase velocity and quality factor can be effectively derived from stacked cross-correlations of ambient noise. This approach was extended to the 3-D velocity/quality factor case by Lawrence and Prieto³⁰, who reconstructed phase velocity and attenuation coefficient maps at periods of 8-32 s for the western United States. Lin et al²³. employed a different approach, assessing the amplitude decay of time-domain cross-correlations. Furthermore, Liu et al³¹. studied the Los Angeles Basin structure using ambient seismic noise interferometry to infer the near-surface attenuation structure. In addition, Borleanu et al³². obtained 2-D intrinsic attenuation maps at different frequencies of the Eastern-Europe region, revealing heterogeneous structures within the upper crustal sedimentary layer that they related to fluids and high-temperature anomalies of water-content mineralogy. Note that all these studies were focused on regional scales (covering areas larger than 4000 $km^{2}$ approximately).

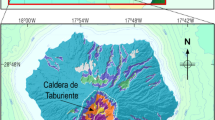
In this study, we conducted the first-ever 3-D intrinsic attenuation tomography at a local scale using seismic ambient noise. Indeed, in previous works dealing with attenuation imaging, 3-D models were obtained using active or passive seismic sources^{10,11,12,13,14,15,16,22}, while noise-based studies were limited to 2-D maps at a regional scale^30,31,32. Our research is dedicated to unravelling the geological structure of La Palma island ($\approx$700 $km^{2}$, Fig. 1) through a novel ANAT method, specifically identifying intrinsic attenuation anomalies that could be linked to geothermal reservoirs. To enrich our comprehension, we compared the 3-D intrinsic attenuation model with previous resistivity³³, S-wave velocity³⁴, and density models^35,36.

Fig. 1

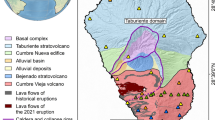
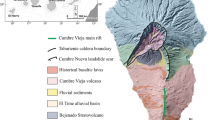
Geological map of La Palma island (adapted from Padrón et al⁵⁵.). The white star on the map denotes the site of the Tajogaite eruption, the most recent volcanic event that occurred on the island from September 19th to December 13th, 2021. Triangles on the map indicate the positions of both temporary and permanent seismic stations, with their colors indicating distinct phases as detailed in the caption. The digital elevation model and historical lava flow data were obtained from GRAFCAN’s public graphic repository (www.grafcan.es ). The 2021 lava flow data was sourced from the Copernicus Emergency Management Service, operated by the European agency (https://emergency.copernicus.eu/mapping/list-of-components/EMSR546). The figure was created using QGIS 3.22 software (https://www.qgis.org).

Geological context

La Palma island, covering an area of $706\hbox { km}^{2}$, is located in the north-westernmost part of the Canary Islands archipelago. The geological structure of La Palma is composed of two main units: the central Taburiente Domain in the north, which dates from 2.0 to 0.51 million years ago, and the southern Dorsal Domain, which has been active from 0.81 million years ago to the present day³⁷.

The island’s formation began 4 My ago with the emissions of submarine lava. Then, 1.77 My ago, the first subaerial material was emitted, forming the Taburiente stratovolcano. After the formation of the Taburiente stratovolcano (between 0.77 and 0.56 My), another volcanic complex, named Cumbre Nueva, was formed in the central part of the island. During the formation process of this volcanic edifice, the western part of the edifice suffered a landslide, creating a large Aridane valley in the central part of the island. Then, within this valley, the Bejenado stratovolcano was formed between 0.56 and 0.49 My. Finally, 0.12 Years ago, the Cumbre Vieja volcanic complex started its formation and gave rise to a complex volcanic rift that stretches 20 km along and rises 1950 m high along an N-S direction. This volcanic system covers an area of $220\hbox { km}^{2}$ and it is characterized by multiple cinder cones and cracks formed during volcanic activity aligned in a N-S direction. This area currently represents the most volcanic active part of the island, where all historical eruptions took place.

The most recent volcanic eruption on La Palma island, the Tajogaite eruption, started on September 19th, 2021 and persisted until December 13th (Tajogaite eruption). The Tajogaite eruption was preceded in 2017 by low-magnitude but relatively deep seismic activity (25-35 km)³⁸. One week before the eruption began, a notable seismic unrest and ground deformation started on September 11th, 2021^38,39. The seismicity and deformation indicated an upward dike intrusion process³⁹. On September 19th, at 14:00 UTC, there started a fissural eruption that involved mainly strombolian activity and occasional phreatomagmatic pulses. These phreatomagmatic pulses emitted an intense eruptive column, reaching a maximum height of 8.500 m⁴⁰. This last eruption served as a reminder of the island’s potential to harbour geothermal resources.

Methods

The methodology we employed for Ambient Noise Attenuation Tomography consists of several key steps. First, $Q_{c}$is measured using the lapse-time dependence method⁷, which involves assessing $Q_{c}$ as a function of the coda window length ($L_{w}$) for different onset times of the coda ($t_{w}$). Second, a 2-D spatial attenuation inversion is performed using a linear inversion scheme with specific sensitivity kernels considering diffusion as the dominant scattering regime⁹. Finally, a 1-D depth inversion is conducted utilizing a linear inversion scheme and sensitivity kernels of the Rayleigh wave fundamental mode extracted from an existing S-wave velocity model³⁴. Detailed information on these steps are described in the following paragraphs.

Data acquisition

Between June and August 2018, we installed 23 seismic stations in the southern part of the island during two phases of one month, specifically focusing on investigating the Cumbre Vieja volcanic complex. In July 2020, we deployed 15 stations distributed throughout the whole island during two months. The primary objective of this expansion was to characterize areas not previously sampled during the initial 2018 campaigns. Furthermore, our temporary campaigns were supplemented by utilizing six permanent stations operated by the Instituto Volcanológico de Canarias (INVOLCAN) for volcano monitoring (Fig. 1).

Since both temporary networks were deployed in summer, there are no significant seasonal effects. Furthermore, we believe that there are no potential temporal variations in the attenuation that could influence the overall attenuation pattern. Previous studies on seismic attenuation tomography, such as those by Prudencio et al¹⁴., utilized datasets spanning several years (between 1984 and 2014). Therefore, we consider the assumption of largely time-invariant attenuation to be reasonable.

Based on the distribution of the seismic stations, the Cumbre Vieja volcano (see Fig. S1 in the supplementary materials) has the greatest concentration of stations and anisotropy in ray paths. This area is the most active part of the island in terms of volcanic activity and the most interesting from a geothermal exploration point of view.

Intrinsic attenuation measurement from ambient noise ($Q_{i}^{-1}$)

To extract the $Q_{i}$from the Empirical Green’s Function (EGF), we used the results obtained by Cabrera-Pérez et al³⁴.. Seismic ambient noise data were pre-processed to obtain the Empirical Green’s functions (EGFs). Initially, in order to identify and remove time windows containing earthquake signals, we applied an automated network-based method. The method relies on analyzing the network covariance matrix, in which the width of the eigenvalues distribution (referred to as spectral width) serves as an indicator of the number of seismic sources composing the wavefield⁴¹. Applying this analysis to each five-minute time window of our data automatically determines whether a coherent signal, such as an earthquake, is present within that specific time window.

Subsequently, we applied a bandpass filter in the frequency range 0.01-5.00 Hz. Then, we employed a standard ambient noise pre-processing including temporal one-bit normalization and spectral whitening⁴²to enhance data quality and reduce non-stationarity in the remaining data. Cupillard et al⁴³. demonstrated theoretically that temporal and spectral normalization methods, like one-bit normalization and spectral whitening, do not affect the relative decay of amplitude when noise sources are evenly distributed. This was also demonstrated by Lin et al²³. in a practical case.

Following these pre-processing steps, we computed cross-correlations for all station pairs using five-minute-long windows and stacked them over one month for the 2018 campaigns and two months for the 2020 campaign. The utilization of a short time window (five minutes instead of one day) for cross-correlation provides more precise information regarding the amplitude of EGFs²⁹. Specifically, we focused on the vertical-vertical components of 578 station pairs. The resulting cross-correlations are presented in Figure 2.A, revealing the presence of coherent wavetrains of dispersive Rayleigh waves.

Fig. 2

Noise-based dataset used for intrinsic attenuation measurement. (A) Empirical Green’s functions sorted according to the distance between stations. The blue solid and dashed lines represent velocities of 1.0 and 3.0 km/s, respectively. (B) and (C) represent the measured values of $Q_{c}^{-1}$ with respect to the frequency (mean and standard deviation marked by red points and blue lines, respectively) and interstation distance, respectively.

Fig. 3

Retrieved 2-D maps of $Q_{c}^{-1}$at different frequencies (indicated at the top-right of each panel). Black triangles represent the seismic stations. The digital elevation model was obtained from GRAFCAN’s repository (www.grafcan.es). The figure was created using the Matplotlib Python package⁵⁷.

For each EGF, we determined the $Q_{c}^{-1}$ for different central frequencies between 0.3 Hz and 3.3 Hz (Fig. 2.B). We used this frequency range because it is the same that Cabrera-Pérez et al³⁴. used for the 2-D inversion of group velocity maps in this region. They selected this frequency range using a criterion of at least 50 measurements of group velocity for the tomographic inversion. The $Q_{c}^{-1}$was measured using the lapse-time dependence method⁷, considering a range of values for both the length of the coda window ($L_{w}$) and the onset time of the coda ($t_{w}$). As suggested by Calvet and Margerin⁷, to ensure that the measured $Q_{c}$ represents the physically meaningful intrinsic quality factor ($Q_{i}$), we need to consider the variation of $Q_{c}$ as a function of $L_{w}$ for different $t_{w}$ (named $Q_{c}$ function) and to extract its mean value in the range when the function stabilizes at sufficiently large $L_{w}$ values (Fig. S2.B in the supplementary materials). This also ensures that the estimate of $Q_{c}$is not hampered by transient phenomena like earthquakes⁷. We applied a positive exponent $(\alpha )$of 2 to parameterize the coda decay, based on the recommendation by Calvet and Margerin⁷. Nonetheless, the influence of the $\alpha$ value has only a minor impact on the estimation of $Q_{c}$⁷. We employed a window-sliding algorithm⁴⁴ to automatically determine the EGF coda and the $Q_{c}$ function’s stabilised segment, facilitating the automated measurement of $Q_{c}^{-1}$ values (Fig. S3 in the supplementary materials). As shown in Figure 2.B, the mean value of the observed $Q_{c}^{-1}$decreases as the frequency increases, consistently with findings from previous studies^45,46. Figure 2.C displays $Q_{c}^{-1}$ measurements as a function of the distance between stations, for all the possible station pairs. Notably, no discernible correlation emerges between $Q_{c}^{-1}$ values and the interstation distance, suggesting that the intrinsic attenuation is not governed by dispersion effects.

2-D intrinsic attenuation maps

The 2-D spatial attenuation inversion at a given frequency is achieved through linear inversion with heuristic sensitivity kernels assuming diffusion as the dominant scattering regime⁴⁷. The analytical expression of these sensitivity kernels governing the propagation of scattered waves between each station pair, is given as follows⁴⁷:

$$\begin{aligned} K_{num}(x,y,x_{i},y_{i},x_{j},y_{j} )= & \frac{1}{6\pi (D\delta )^{2}} \exp {\left( -\left( \frac{\left( x-\frac{x_{i}+x_{j}}{2}\right) ^{2}}{2(\delta D)^{2}}+\frac{\left( y-\frac{y_{i}+y_{j}}{2}\right) ^{2}}{2(\delta D)^{2}}\right) \right) } \nonumber \\ & + \frac{1}{2\pi (\delta D)^{2}} \left[ \exp {\left( -\left( \frac{\left( x-\frac{x+x_{i}}{2}\right) ^{2}}{2(\delta D)^{2}}+ \frac{\left( y-\frac{y+y_{i}}{2}\right) ^{2}}{2(\delta D)^{2}}\right) \right) }\right. \nonumber \\ & \left. +\exp {\left( -\left( \frac{\left( x-\frac{x+x_{j}}{2}\right) ^{2}}{2(\delta D)^{2}}+ \frac{\left( y-\frac{y+y_{j}}{2}\right) ^{2}}{2(\delta D)^{2}}\right) \right) }\right] , \end{aligned}$$

(1)

where ($x_{i},y_{i}$) and ($x_{j},y_{j}$) represent the coordinates of the (virtual) sources and receivers, $\delta$ represents the spatial aperture of the weighting function, and D represents the source-receiver distance. Following previous studies, a value of 0.2 was selected for the parameter $\delta$⁴⁷. An example of a sensitivity kernel corresponding to a specific station pair can be seen in Figure S4 in the supplementary materials. Del Pezzo and Ibáñez⁴⁷ previously used these kernels for imaging the spatial distribution of the intrinsic attenuation parameter $Q_{i}$, while Cabrera-Pérez et al⁴⁸. used the same kernels to map relative velocity variations during the pre-eruptive phase of the 2021 La Palma eruption.

With these sensitivity kernels, the forward model relating the observed attenuation at a given frequency for a given station pair $Q_{c}^{-1}(s_{i},s_{j})$ to the 2-D model of attenuation $Q_{c}^{-1}(x,y)$, can be expressed as:

$$\begin{aligned} Q_{c}^{-1}(s_{i},s_{j}) = n^{-1}\iint K_{num}(x,y,x_{i},y_{i},x_{j},y_{j})\ Q_{c}^{-1}(x,y)\ dx\ dy, \end{aligned}$$

(2)

where, n represents a normalization factor:

$$\begin{aligned} n=\iint K_{num}(x,y,x_{i},y_{i},x_{j},y_{j})\ dx\ dy. \end{aligned}$$

(3)

The forward model (2) is discretized on a 29 $\times$ 48 km mesh with regular tiles of size 0.6 $\times$1.0 km⁴⁹. The linear inversion is performed using a damped least squares approach. The L-curve criterion was used to select the proper damping parameter.

We performed different checkerboard and spike tests to determine the spatial resolution of the tomographic images. We used three different checkerboard sizes of $0.05^{\circ } \times 0.05^{\circ }$, $0.08^{\circ } \times 0.08^{\circ }$ and $0.1^{\circ } \times 0.1^{\circ }$, corresponding appro$\times$imately to sizes of 5.5 km $\times$ 5.5 km, 8.8 km $\times$ 8.8 km and 11.1 km $\times$ 11.1 km, respectively. Furthermore, we used different spike sizes with diameters of 7 km, 4 km and 2 km. Maximum and minimum values of 0.02 and 0.01 were used for $Q_{c}^{-1}$ in the checkerboard tests (Fig. S5 and S6 in the supplementary materials). The model with a resolution of $0.1^{\circ } \times 0.1^{\circ }$ and 7 km of diameter were correctly retrieved in the whole island (Figs. S5.A-B and S6.A-B). Conversely, the checkerboard tests with a resolution of $0.08^{\circ } \times 0.08^{\circ }$ and $0.05^{\circ } \times 0.05^{\circ }$ as well as the spike tests with a diameter of 4 km and 2 km were not correctly retrieved in the island’s northern part (Figs. S5.C-F and S6.C-F), due to a lower ray path density in this zone (see Fig. S1 in the supplementary materials). However, the models were correctly retrieved in the southern part of the island (Figs. S5.C-F and S6.C-F), where the ray path density is higher, which is the main zone of interest of the study.

Depth inversion for 1-D intrinsic attenuation profiles

The last step in the 3-D attenuation imaging process involves inverting the 2-D attenuation maps to obtain 1-D attenuation profiles at depth. First, a $Q_{c}^{-1}$value is extracted in 347 points of each 2-D attenuation map associated with a specific frequency. These points correspond to those where 1-D S-wave velocity models were obtained by ambient noise tomography by Cabrera-Pérez et al³⁴.. Second, we calculated the depth sensitivity kernel at each frequency for each 1-D velocity model ($K_{f}(z)$), covering a frequency range between 0.3 Hz and 3.3 Hz. The depth sensitivity kernels $K_{f}(z)$were calculated using the disba software⁵⁰. This software is a computationally efficient Python library for modeling surface wave dispersion, enabling the calculation of forward modeling (to compute Rayleigh and Love waves phase or group dispersion curves) and the computation of Rayleigh-wave ellipticity sensitivity kernels with respect to layer thickness, P- and S-wave velocities, and density. With these depth sensitivity kernels, the forward problem relating the observed attenuation values at distinct frequencies $Q_{c}^{-1}(f)$ to the 1-D model of attenuation at depth $Q_{c}^{-1}(z)$, can be expressed as:

$$\begin{aligned} Q_{c}^{-1}(f) = \frac{\int |K_{f}(z)|Q_{c}^{-1}(z) dz}{\int |K_{f}(z)|dz}, \end{aligned}$$

(4)

where f denotes the central frequency used for calculating the depth sensitivity kernels $K_{f}(z)$. The resulting discrete inverse linear problem is solved using damped least squares. Figure S7 in the supplementary materials shows an example of depth sensitivity kernels at different frequencies for a specific 1-D velocity model obtained by ambient noise tomography³⁴ (Fig. S7.A), together with the retrieved 1-D attenuation profile at depth (Fig. S7.B).

Fig. 4

Horizontal cross-section of the 3D checkerboard test with dimensions of approximately 9 km $\times$ 9 km $\times$1.5 km in width, height and depth, respectively. The synthetic maps at different depths are shown in panels (A), (C), (E), (G) and (I). The corresponding recovered Qc-1 maps at different depths are shown in panels (B), (D), (F), (H) and (J), respectively. The digital elevation model was sourced from GRAFCAN’s repository (www.grafcan.es), and the figure was generated using the Matplotlib Python package⁵⁷.

Fig. 5

Vertical cross-sections (cf. A-A’ and B-B’ in Fig. 4.B) of the 3-D synthetic (left panel) and retrieved (right panel) model.

Fig. 6

Retrieved 2-D maps of $Q_{c}^{-1}$ at different depths (indicated at the top-right of each panel). The white and black dots in panels B and C represent high (> 316 $\Omega .m$) and low (< 3.16 $\Omega .m$) resistivity zones³³, respectively. The white lines in panels A, B and C represent low-density (-200 $kg/m^{3}$) anomalies³⁶. The digital elevation model was sourced from GRAFCAN’s public graphic repository (www.grafcan.es), and the figure was produced using QGIS 3.22 software (https://www.qgis.org).

To assess the depth resolution of our intrinsic attenuation model, we conducted a 3D checkerboard test with dimensions of approximately $9\hbox { km} \times 9 km \times 1.5\hbox { km}$ in width, height and depth, respectively. This test involved maximum attenuation values of 0.02 and minimum one of 0.01. By following the method previously described, we utilized 347 control points to reconstruct the 3D checkerboard pattern. Figures 4 and 5 show the horizontal and vertical cross-sections of the resulting 3D resolution test. Our model generally achieves a resolution down to a depth of 2 km across most of the study area, effectively resolving attenuation values and the checkerboard pattern (Fig. 5). Furthermore, between 2 km and 3 km depth, we can retrieve the geometry of the checkerboard pattern but not the attenuation values. Below a depth of 3 km, our model lacks sensitivity. For this reason, we determine that the maximum resolution in depth is up to 2 km, although we can still have some sensitivity down to 3 km.

Results and discussion

Figure 3 shows six 2-D maps of $Q_{c}^{-1}$ obtained for frequencies between 0.3 Hz and 3.3 Hz. The mean value of $Q_{c}^{-1}$ decreases with frequency, from 0.039 to 0.012, consistently with the global trend of the average $Q_{c}^{-1}$ curve shown in Figure 2.B. Some important attenuation contrasts appear across the island, which evolve with the frequency. The image shows a high attenuation zone in the southern part of the island, mainly at low frequencies corresponding to deeper penetration depths (Figs. 3A-C). This high attenuation anomaly decreases significantly at frequencies higher than 1.50 Hz, except in the two flanks of the Cumbre Vieja volcanic complex at 3.30 Hz corresponding to superficial layers (Fig. 3F). Frequencies between 2.10 Hz and 2.70 Hz show the lowest attenuation levels in the whole island, with $Q_{c}^{-1}$ values down to 0.012 (Figs. 3D-E). Conversely, the northern part of the island shows low levels of attenuation in general.

Figure 6 shows four horizontal cross-sections of the 3-D model of $Q_{c}^{-1}$ at different depths. The main anomalies observed in the $Q_{c}^{-1}$ model are marked as high (H) attenuation zones in Fig. 6B and C. It appears that the island shows a very strong heterogeneity in the attenuation distribution, with the principal anomalies located in the southern part of the island. Figure 7 shows three vertical cross-sections of the 3-D model of $Q_{c}^{-1}$, whose positions are indicated in Fig. 6A. A high-attenuation zone (H1) extends from the surface to 2000 m b.s.l. (below sea level) in the island’s southern part, with $Q_{c}^{-1}$ values reaching 0.20 (Fig. 7A and C). Another high-attenuation zone (H2) is present between 0 m b.s.l. and 2000 m b.s.l. in the eastern part of the Cumbre Vieja volcanic complex (Fig. 7B and C). The last high-attenuation zone (H3) is located in the island’s southernmost tip, at depths above 2000 m b.s.l. (Fig. 7A and B).

Fig. 7

Vertical cross-sections (cf. A-A’, B-B’ and C-C’ in Fig. 6.A) of the 3-D model of $Q_{c}^{-1}$. The horizontal black dashed line represents the depth at which the model resolution is maximum and below which it starts to decrease. White and red triangles represent the historical and Tajogaite eruption sites, respectively. The white dashed contour represents the hydrothermal zone imaged in the S-wave velocity model obtained by ambient noise tomography by Cabrera-Pérez et al³⁴.

The 3-D $Q_{c}^{-1}$ model of La Palma island exposed in Figs. 6 and 7provides a detailed view of some upper crustal geological structures, revealing three main attenuation anomalies within the Cumbre Vieja volcanic complex in the southern part of the island. In the following, we discuss the volcanological and geothermal relevance of such anomalies, comparing them with the resistivity model of Di Paolo et al³³., the density models of Camacho et al³⁵. and Montesinos et al³⁶., and the S-wave velocity models of Cabrera-Pérez et al³⁴. (ambient noise tomography) or D’Auria et al³⁸. and Serrano et al⁵². (local earthquake tomography). Table S1 in the supplementary material is a summary table comparing the intrinsic attenuation model with other geophysical models.

From a geothermal point of view, the most noteworthy features are the high-attenuation anomalies H1 and H2 (Figs. 6 and 7). These anomalies align with low-resistivity zones, low S-wave velocity zones, and low-density areas, for which various studies have proposed different interpretations. Camacho et al³⁵. associated these low-density anomalies with shallow fractures following the N-S rift structure of Cumbre Vieja, while Montesinos et al³⁶. interpreted them as highly fractured and altered structures related to an active hydrothermal system. Di Paolo et al³³. suggested that these low-resistivity anomalies could be related to clay alteration caps (illite and illite-smectite). Similarly, Cabrera-Pérez et al³⁴. attributed these low-velocity anomalies to a potential hydrothermal zone. Furthermore, D’Auria et al³⁸. and Serrano et al⁵². observed low-velocity and high Vp/Vs values in the same areas, which they related to hydrothermal alteration ascribed to the activity of the geothermal system of the Cumbre Vieja volcanic complex.

Therefore, we believe these high-attenuation anomalies H1 and H2 could be associated with a hydrothermal alteration zone, possibly linked to an active or fossil hydrothermal system in the Cumbre Vieja volcanic complex. This hypothesis is supported by velocity variations (dv/v) observed by Cabrera-Pérez et al⁴⁸., who indirectly confirmed the existence of a potential geothermal reservoir in this zone through ambient noise interferometry during the pre-eruptive phase of the Tajogaite eruption. Indeed, these authors observed a drop in dv/v values 9.5 days prior to the eruption, which they explained by the ascent of hydrothermal fluids towards the surface through this hydrothermal zone. On the other hand, Cabrera-Pérez et al³⁴. noted that the hypocenters of the pre-eruptive seismicity of the Tajogaite eruption were significantly reduced in this low-velocity and high-attenuation zone. This could be a consequence of the presence of hydrothermally altered material characterized by a lower rigidity and/or a more ductile rheology. This latter observation corroborates similar findings by Del Pezzo et al⁹., who identified high attenuation structures associated with gas or fluid reservoirs beneath other volcanic regions.

Another high-attenuation anomaly, H3, is located in the southern part of the island (Figs. 6 and 7), below the historical eruptions of San Antonio (1677) and Teneguía (1971) volcanoes (Fig. 7A and B). Notably, this high attenuation zone does not correspond to any known resistivity or density anomaly reported in previous studies. Nevertheless, Cabrera-Pérez et al³⁴. imaged a low-velocity zone in this area, which they associated with high-temperature rocks and a network of fractures through which hydrothermal fluids and gases ascend to the surface, particularly under the Teneguía and San Antonio volcanoes. This hypothesis aligns with the subsidence detected by InSAR beneath Teneguía volcano by Prieto et al⁵³., which they attributed to a thermal source. Additionally, Padrón et al⁵⁴. recorded diffuse $CO_{2}$ emissions exceeding 800 $g\ m^{-2} day^{-1}$ and anomalous temperatures between $90^{\circ }\hbox {C}$ and $130^{\circ }\hbox {C}$ at a depth of 40 cm in the Teneguía volcano area before the Tajogaite eruption (2001–2013). Notably, a hot spring (Fuente Santa) in the southern part of La Palma island exhibits water temperatures reaching $40^{\circ }\hbox {C}$ and elevated $HCO_{3}^{-}$ and $SO_{4}^{2-}$levels exceeding 2000 mg/L⁵⁵, suggesting underground water circulation through high-temperature rocks. As a result, the high-attenuation anomaly H3 may be associated with fracture zones allowing fluids to migrate to the surface, coinciding with the observed geochemical anomalies^54,55, subsidence zone⁵³, and low-velocity zone³⁴.

Conclusion

Using ANAT, we obtained a 3-D intrinsic attenuation model of La Palma island. Analyzing data from 44 broadband seismic stations and determining $Q_{c}^{-1}$ values for 424 station pairs, we used a linear inversion with appropriate sensitivity kernels to generate 2-D maps of intrinsic attenuation at different frequencies. Subsequently, we used some specific depth sensitivity kernels to create 1-D depth profiles of intrinsic attenuation at 347 points of the 2-D maps. This last step allowed obtaining a full 3-D intrinsic attenuation model of the island of La Palma.

The 3-D model reveals three areas with significant attenuation, termed H1, H2, and H3. The high-attenuation anomalies H1 and H2 are interpreted as hydrothermal alteration zones associated with the presence of an active or fossil hydrothermal system in the Cumbre Vieja volcanic complex. The anomaly H3 is associated with fractured rocks favouring the ascent of hot fluids toward the surface in the island’s southern part. This hypothesis is also supported by geophysical and geochemical anomalies observed in previous studies^34,53,54,55.

The novel passive seismic attenuation tomography method proposed in this work (named ANAT) was revealed to be highly appropriate for attenuation studies at a local scale in areas with low seismicity. This method does not require active sources and, for this reason, is convenient for various scientific and industrial applications. We maintain that its application, jointly with classical ambient noise tomography, provides an excellent tool for surface geothermal exploration and, in general, for imaging upper crustal structures.