Energy efficient mobile sink driven data collection in wireless sensor network with nonuniform data

Abstract

In wireless sensor network, mobile sink is used to collect data from sensor nodes by periodically traversing the network to prevent hotspot problem. However, when sensor nodes generate data non-uniformly, the efficiency of data collection is constrained by rendezvous points and network topology. It becomes more challenging under network energy consumption constraint. Thus, this paper investigates non-uniform data generation in wireless sensor network and proposes an innovative approach: Optimal Clustering and Network Topology for Mobile Sink-Driven Data Collection, called OCNTMS. It focuses on determining optimal rendezvous points and their associated clusters. Through innovative methods such as weight-balanced clustering, cost function optimization, load-balanced link construction, and node forwarding selection, the OCNTMS can efficiently construct link sets within clusters and accurately plan the mobile sink’s traversal of rendezvous points. Simulation results show that the OCNTMS reduces energy consumption by 18% and increases network lifetime by 40% compared with existing approaches under the constraint of non-uniform data generation. This greatly improves the network energy efficiency and data transmission efficiency.

Introduction

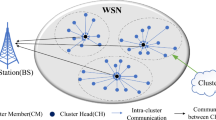
Wireless Sensor Network (WSN) has become essential technologies in today’s world, incorporating recent advancements in robust control and security^1,2. It is widely deployed in various fields such as military, automation, the Internet of Things, and ecological environment monitoring for system observation and control³. In WSN, the sensor nodes collect data from the environment and forward it to base stations through direct or multi-hop communication⁴. Typically, sensor nodes operate with limited battery power. While the data transmission consumes a significant portion energy of sensor node. Moreover, due to the heavy forwarding of data packets, sensor nodes near the base station consume more energy than others, leading to their rapid depletion. This issue is known as the hotspot problem^5,6. To address this issue, the concept of Mobile Sink (MS) has been introduced. The MS periodically traverses the network to collect data from sensors, thereby preventing or minimizing the hotspot problem.

However, if MS attempts to visit each node, it can lead to unacceptable delay. Worse, sensor nodes might drop data packets if the MS does not reach them in time due to memory overflow or other constraints. To minimize delay, the MS visits a few specific locations or sensor nodes, called Rendezvous Points (RPs)^7,8, and the remaining nodes send their data to the nearest RP. Thus, the configuration of RPs is a critical issue in MS-based WSN. Poor RP configuration can lead to inefficient data transmission paths. As illustrated in Fig. 1(a), too few RPs can result in long-distance multi-hop communications, increasing node energy consumption and causing network load imbalances.

Fig. 1

WSN, RPs, MS and travel path.

Additionally, constructing an optimal set of links within each cluster governed by the RP to support efficient data transmission is another critical issue. An ideal link set should ensure that data forwarding between nodes is evenly distributed, reducing energy consumption at specific nodes and avoiding network congestion and energy bottlenecks due to heavy local loads. This is particularly critical when dynamic network changes.

Lastly, the MS’s path strategy plays a decisive role in the overall network performance. A well-planned MS must balance reducing delays and conserving energy. As shown in Fig. 1b, poorly planned MS traversal paths can lead to unnecessary delays in the data collection process, especially when there are numerous RPs.

Worse, the above three critical issues pose more significant challenges for non-uniform data generation in WSN^9,10. When sensor nodes generate data at different rates due to varying sensing tasks, environmental changes, or event occurrences, the fixed RP locations and MS path strategies struggle to adapt to these variations. This leads to uneven energy consumption, inefficient data transmission, and insufficient response to non-uniform data generation patterns¹¹. These issues are particularly pronounced near nodes with high data generation rates. It necessitates new strategies to dynamically adjust RPs and MS paths to accommodate non-uniform data generation, effectively allocating and managing network resources.

Despite the prevalence of non-uniform data generation in practical WSN applications, most existing data collection methods for MS-based WSNs assume uniform data generation rates among sensor nodes. Thus, there is a noticeable research gap on data collection strategies that need to be adjusted to accommodate non-uniform data generation. This gap results in suboptimal network performance, especially in terms of energy efficiency and network lifetime. In addition, WSNs are integral components of the Internet of Things (IoT), where numerous heterogeneous devices generate and transmit data at varying rates. Thus, the challenges posed by non-uniform data generation and energy constraints are also prevalent in IoT. By addressing the research gap in WSNs, it can have significant implications for optimizing IoT networks, enhancing their efficiency, scalability, and reliability. Therefore, this paper proposes the OCNTMS approach to effectively enhance network energy efficiency and data transmission efficiency under the constraint of non-uniform data generation. It is crucial not only for WSNs but also for the broader context of IoT. The contributions of this work are summarized as follows:

• 1. This paper constructs three models for designing OCNTMS approach, including WSN model, energy model and node non-uniform data generation model.

• 2. The node weight assignment mechanism is introduced in OCNTMS. It iteratively optimizes the cost function to balance the node’s data generation rate and its remaining energy, thus achieving reasonable allocation of network resources.

• 3. To find the optimal number of clusters, the OCNTMS balances node distances to cluster centers by designing the weight-balanced k-medoids clustering algorithm. Then, the cost function-driven optimal clustering algorithm in OCNTMS is designed to determine the optimal cluster number k, balancing network traversal length and energy consumption, and node weight.

• 4. After determining the optimal cluster number, the OCNTMS optimizes the network topology to improve network performance and energy efficiency. It implements a load-balanced optimal forwarding node selection (LB-OFNS) strategy to optimize data transmission paths in each cluster. Then the OCNTMS optimizes the MS path between clusters by using GA-MARL¹².

The rest of this paper is organized as follows: Sect. “Related work” provides a review of related work, discussing the application of MS in WSN, data collection strategies, and adaptive network configuration and optimization strategies. Sect. “Model building” introduces the model building of this study. Sect. “Proposed work” details the design of the proposed OCNTMS. Section 5 presents the performance evaluation. Finally, Sect. 6 summarizes the main findings of this paper.

Related work

The realization of energy-efficient data collection is a challenging issue in WSN. In recent years, numerous researchers have proposed various approaches for utilizing MS. This section will discuss some of the literature related to the application of MS in WSN, with a particular focus on environments with non-uniform data generation.

For the uniform data generation environment, various data collection schemes for WSN based on mobile aggregation points have been proposed in recent research. These schemes aim to address challenges like energy consumption, data delivery delay, and network lifetime. Notable approaches included Tunca et al.’s¹³ ring routing protocol, which constructed a virtual ring for easy access and changeability; Zhu et al.¹⁴ proposed a tree-cluster-based data gathering algorithm, which used a weighted tree to collect data efficiently; Khan et al.¹⁵ developed the virtual grid-based dynamic routes adjustment scheme, partitioning the sensor field into virtual grids to streamline data collection; By using MS, Wang et al.¹⁶ proposed the energy-efficient cluster-based dynamic routes adjustment scheme to create multiple clusters for efficient data collection; Liu et al.¹⁷ proposed a hierarchical routing protocol that utilized multiple MSs to enhance coverage and data collection efficiency; Basumatary et al.¹⁸ introduced a centroid-based routing protocol, which moved the sink to an energy-dependent centroid point, improving network lifetime and data transmission efficiency.

Other significant methods include Agrawal et al.s¹⁹ grid cycle routing protocol, which combined grid and chain structures for efficient data transmission; Habib et al.²⁰ proposed the starfish routing protocol, constructing a backbone inspired by the water vascular system of a starfish; Jain et al.²¹ developed the delay aware green routing protocol, which constructed multiple rings for efficient data delivery; Jain et al.²² extended their work with the event-driven virtual wheel-based data dissemination mechanism to reduce the overhead of acquiring sink location information; Jain et al.²³ used the dynamic route adjustment rules and heterogeneous sensor nodes to optimize data aggregation and minimize data delivery delay; Mazumdar et al.²⁴ designed the adaptive hierarchical data dissemination mechanism to support dynamic topology changes.

In addition, several other approaches have utilized metaheuristic algorithms to optimize WSNs, which are considered state-of-the-art in energy-efficient data collection. For instance, Zivkovic et al.²⁵ proposed an enhanced grey wolf optimization algorithm for energy-efficient WSN, improving cluster head selection to extend network lifetime; Zivkovic et al.²⁶ introduced an enhanced dragonfly algorithm adapted for WSN lifetime optimization. It addressed the clustering problem to reduce energy consumption; Bacanin et al.²⁷ developed an energy efficient clustering method using the opposition-based initialization bat algorithm, enhancing the algorithm’s initialization phase to balance exploration and exploitation; Saemi and Goodarzian²⁸ presented an energy-efficient routing protocol for underwater WSN using a hybrid metaheuristic algorithm. It combined the lobal and local search strategies to optimize routing paths; Barnwal et al.²⁹ proposed an improved African buffalo optimization-based energy-efficient clustering in WSNs using a metaheuristic routing technique. It aimed to optimize both clustering and routing processes to enhance energy efficiency and network lifetime.

However, the proposed data collection methods mentioned above have certain limitations. They are only applicable to uniform data generation environments.

Extensive literature research reveals that there are few studies specifically addressing scenarios where nodes generate non-uniform data constraints. For example, Kumar et al.³⁰ proposed a MS path determination method using ant colony optimization to optimize the MS’s path by simulating ant foraging behavior. This method reduced energy consumption and improved data collection efficiency by dynamically adjusting the path in response to changing network conditions; Neogi³¹ employed the intelligent water drops algorithm to optimize MS paths, simulating natural water droplet flow to balance network load and reduce energy consumption in dynamic and uneven data generation scenarios. However, these methods also have limitations. Kumar’s method might struggle with rapid network topology changes and high computational overhead. Neogi’s method might face challenges due to the complexity of simulating natural water flow, potentially leading to increased processing time and energy consumption.

Model building

WSN model

In this paper, WSN is modeled as G = (V, E), where V and E represent the set of nodes and the set of communication links, respectively. Nodes are randomly deployed throughout the sensor field, which has dimensions L × H. Each sensor node has the same transmission range (TR) and initial energy ($e{r}_{init}$). The remaining energy of node ${n}_{i}$ is denoted as ${e}_{i}$. Each sensor node monitors its surrounding area and generates data at different rates depending on the occurrence of nearby events, leading to non-uniform data generation over time.

In WSN model, the MS is used for data collection. It assumes that the MS has unlimited energy and can move freely throughout the network. While the energy of sensor node is limited (it is calculated by energy model in 3.2). The sensor nodes are grouped into $k$ clusters, with cluster head (CH) nodes serving as RPs. The RP is a node that the MS visits on its path to collect data sent by other sensor nodes in the cluster. Each RP has sufficient memory to buffer the data sensed by its cluster members.

After clustering is established, a tour is constructed over the RPs. The MS moves along this tour and collects data from the RPs as it approaches them. The MS is equipped with a GPS system to determine its location. Additionally, the MS’s dwell time at each RP is sufficient to retrieve the stored data. Let $T{L}_{k}$ denote the length of the MS tour constructed over $k$ RPs. And $E{N}_{k}$ represents the energy consumption for collecting data generated in the k clusters.

Energy model

An energy model is constructed by using the free space energy model proposed in³². The ${E}_{tx}\left(i,j\right)$ is the energy consumed by sensor node ${n}_{i}$ to transmit a data packet of B bits to sensor node ${n}_{j}$:

$$\begin{array}{*{20}c} {E_{tx} \left( {i,j} \right) = \left( {\alpha_{tx} + \varepsilon_{fs} d_{ij}^{2} } \right)B} \\ \end{array}$$

(1)

where the ${\alpha }_{tx}$ represents the energy dissipated in transmitting one bit respectively, the ${\varepsilon }_{fs}$ is the energy consumed by the transmitter amplifier per bit per square meter, the ${d}_{ij}$ is the Euclidean distance between sensor nodes ${n}_{i}$ and ${n}_{j}$, and the $B$ is the size of the data packet in bits.

The ${E}_{rx}\left(i\right)$ is the energy consumed by sensor node n_i to receive a data packet of B bits from sensor node ${n}_{j}$:

$$\begin{array}{*{20}c} {\begin{array}{*{20}c} {E_{i} = \left( {E_{tx} \left( {i,j} \right) \times FL_{i} } \right) + \left( {E_{rx} \left( i \right) \times \left( {FL_{i} - np_{i} } \right)} \right)} \\ \end{array} } \\ \end{array}$$

(2)

where the ${\alpha }_{rx}$ represents the energy dissipated in receiving one bit respectively.

The total energy E_i consumed by node n_i while forwarding packets during a single round trip of the MS is calculated as:

$$\begin{array}{*{20}c} {E_{i} = \left( {E_{tx} \left( {i,j} \right) \times FL_{i} } \right) + \left( {E_{rx} \left( i \right) \times \left( {FL_{i} - np_{i} } \right)} \right)} \\ \end{array}$$

(3)

where the ${FL}_{i}$ is the forwarding load of sensor node ${n}_{i}$ and the np_i is the number of data packets generated by sensor node n_i. The term ${E}_{tx}\left(i,j\right)\times {FL}_{i}$ represents the energy used by node n_i to transmit all packets in its forwarding load to its parent node n_j. While the ${E}_{rx}\left(i\right)\times \left({FL}_{i}-{np}_{i}\right)$ accounts for the energy consumed by node ${n}_{i}$ to receive packets from its child nodes.

The forwarding load ${FL}_{i}$ of sensor node ${n}_{i}$ is determined by:

$$\begin{array}{*{20}c} {FL_{i} = \left\{ {\begin{array}{*{20}c} {\mathop \sum \limits_{{j\smallint C_{i} }} FL_{j} + np_{i} iff C_{i} \ne \emptyset } \\ {np_{i} Otherwise} \\ \end{array} } \right.} \\ \end{array}$$

(4)

where the ${C}_{i}$ is the set of child nodes of node ${n}_{i}$. The term $\sum_{j\epsilon {C}_{i}}{FL}_{j}$ aggregates the forwarding loads of all child nodes. If node ${n}_{i}$ has no child nodes, its forwarding load equals its own generated packets ${np}_{i}$.

Node non-uniform data generation model

To simulate the non-uniform data generation behavior of nodes between two data collection intervals of the MS in the WSN model, a node non-uniform data generation model is established based on a common base data generation rate and a random deviation. The base data generation rate ${\lambda }_{i}$ of node ${n}_{i}$ is defined as:

$$\begin{array}{*{20}c} {\lambda_{i} = \lambda \cdot \left( {1 + r_{i} } \right)} \\ \end{array}$$

(5)

where the $\lambda$ is the common base data generation rate, and the ${r}_{i}$ is a random variable uniformly distributed over the interval $\left[ { - \Delta ,\Delta } \right]$, simulating variability in data generation among nodes. And the $\Delta$ represents the maximum deviation proportion from the base rate.

The number of data packets ${np}_{i}$ generated by node ${n}_{i}$ during the MS data collection interval $T$ follows the Poisson distribution with parameter $\lambda_{i} T$. The probability mass function is:

$$\begin{array}{*{20}c} {P\left( {np_{i} = p} \right) = \frac{{\left( {\lambda_{i} T} \right)^{p} e^{{ - \lambda_{i} T}} }}{p!}} \\ \end{array}$$

(6)

where the $p$ represents the number of data packets generated by node ${n}_{i}$ within the time interval $T$, and the ${\lambda }_{i}T$ is the expected number of packets generated during $T$. The Poisson distribution models the random nature of packet generation over time.

By introducing the random deviation ${r}_{i}$, this model captures the non-uniform data generation characteristics among nodes caused by environmental conditions, varying monitoring tasks, or other relevant factors.

Proposed work

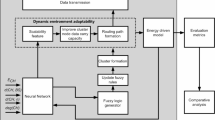
This section details the approach OCNTMS, which is aimed to balance energy consumption and data transmission requirements in scenario where nodes generate non-uniform data. As shown in Fig. 2, OCNTMS is divided into three stages: weight assignment, cluster selection, path planning.

Fig. 2

Flowchart of OCNTMS.

In the weight assignment stage, a weight is assigned to each sensor node based on the node’s remaining energy and data generation rate. The weight assignment stage aims to balance energy consumption and data transmission requirements, providing a foundation for subsequent clustering and path planning.

Next, in the clustering selection stage, the weight-balanced k-medoids clustering algorithm is applied to divide the network into k clusters. Following this, a lightweight network construction strategy is employed to quickly and efficiently establish the link structure for each cluster. Subsequently, the cost function $c{s}_{k}$ for the current cluster number $k$ is calculated by considering the MS traversal length, energy consumption, and clustering weight factors. The $c{s}_{k}$ is then compared with the optimal $cs$. If $c{s}_{k}$ is less than the current optimal $cs$, the cluster number $k$ is updated, and the optimal cost is set to $c{s}_{k}$. This process iteratively updates the value of k until the termination condition is met, thereby ensuring the network is optimally clustered to balance energy consumption and load distribution.

Once the optimal clustering is determined, network topology optimization begins. The LB-OFNS algorithm is designed to further refine the network structure within each cluster, ensuring the optimization of data transmission paths. Finally, the GA-MARL algorithm is applied for the MS’s path planning optimization. This approach achieves global optimization and adaptive adjustment of the MS’s path, further improving data collection efficiency and reducing energy consumption.

Node weight assignment stage

This section discusses in detail how to carry out weight calculation and achieve reasonable allocation of network resources in the weight assignment stage. The key to weight calculation lies in balancing two aspects: the data generation rate of the nodes and their remaining energy. This balance is achieved through the following Eq. (7).

$$\begin{array}{*{20}c} {w_{i} = \mu \cdot np_{i} \cdot f\left( {e_{i} } \right) + \nu \cdot e_{i} } \\ \end{array}$$

(7)

where the W_i represents the weight of node ${n}_{i}$ and the ${e}_{i}$ signifies the remaining energy of node ${n}_{i}$. The coefficients $\mu$ and $\nu$ are adjustment factors that balance the influence of the data generation rate and the remaining energy in the weight calculation, respectively. The $f\left({e}_{i}\right)$ is a function of the remaining energy, defined as shown in Eq. (8).

$$\begin{array}{*{20}c} {f\left( {e_{i} } \right) = \left\{ {\begin{array}{*{20}c} {1 if e_{i} \ge E_{thresh} } \\ {\frac{{e_{i} }}{{E_{thresh} }} if e_{i} < E_{thresh} } \\ \end{array} } \right.} \\ \end{array}$$

(8)

where the ${E}_{thresh}$ represents the energy threshold, indicating whether a node has sufficient energy to participate in data transmission. The function $f\left({e}_{i}\right)$ adjusts the contribution of the data generation rate to the node’s weight based on the ratio of the node’s remaining energy to ${E}_{thresh}$. This mechanism ensures that nodes with lower energy contribute less to the network load, promoting a balanced allocation of network resources.

Weight assignment must consider the actual operating environment of the network and the real-time status of the nodes. It includes a comprehensive evaluation of network load, energy consumption patterns, and data transmission requirements. Thus, the adjustment coefficients $\mu$ and $\nu$ are not static in Eq. (7). They need to be dynamically adjusted according to the different stages of network operation and the energy status of the nodes. For example, when the network is initialized, optimizing data collection efficiency might be prioritized, so $\mu$ could be set higher. As the network runs, the overall energy of the nodes decreases, the value of $\nu$ will gradually increase to ensure effective energy utilization and continuous network operation.

Optimal cluster selection stage

Weight-balanced k-medoids clustering

Traditional clustering methods cannot efficiently handle the rapid energy depletion of nodes and the imbalance of data transmission in WSNs. To improve network lifetime and data transmission efficiency, the weight-balanced k-medoids clustering algorithm is designed. It balances network load and minimizes energy consumption by optimizing the weight differences between nodes and adjusting data transmission paths.

Objective function optimization

In the weight-balanced k-medoids clustering algorithm, optimizing the objective function is a pivotal step. The objective function aims to balance the total distance from nodes to their cluster centers with the sum of weights within each cluster. This optimization is expressed by Eq. (9).

$$\begin{array}{*{20}c} {O\left( x \right) = \gamma \cdot D\left( x \right) + \left( {1 - \gamma } \right) \cdot W\left( x \right)} \\ \end{array}$$

(9)

where the $O(x)$ represents the objective function to be minimized. The parameter $\gamma$ serves as a trade-off factor between 0 and 1, balancing the importance of minimizing the total distance $D\left(x\right)$ and achieving balanced cluster weights $W\left(x\right)$. The total distance $D\left(x\right)$ is calculated as Eq. (10).

$$D\left(x\right)=\sum_{i=1}^{N}\Vert {x}_{i}-{m}_{c(i)}\Vert$$

(10)

where the $N$ denotes the total number of nodes, the ${x}_{i}$ is the position of node ${n}_{i}$, and the ${m}_{c(i)}$ is the medoid of the cluster to which node ${n}_{i}$ belongs. The Euclidean distance $\Vert {x}_{i}-{m}_{c(i)}\Vert$ measures the distance between node ${n}_{i}$ and its cluster center. The weight difference $W\left(x\right)$ is calculated as Eq. (11).

$$W\left(x\right)=\sum_{i=1}^{k}\left|{Wc}_{i}-{Wc}_{average}\right|$$

(11)

where the ${Wc}_{i}$ is the sum of weights of nodes in cluster $i$, and the ${Wc}_{average}$ is the average sum of weights across all clusters. The absolute difference $\left|{Wc}_{i}-{Wc}_{average}\right|$ measures how much the weight of cluster $i$ deviates from the average, aiming to achieve balanced weights across clusters.

The parameter $\gamma$ plays a crucial role in Eq. (9) by determining the balance between minimizing intra-cluster distances and balancing cluster weights. To dynamically adjust $\gamma$ based on the optimization progress, the following equation is introduced:

$$\begin{array}{*{20}c} {\gamma_{new} = \gamma + \delta \cdot \left( {D\left( {x_{new} } \right) - W\left( {x_{new} } \right)} \right)} \\ \end{array}$$

(12)

where the ${\gamma }_{new}$ is the updated trade-off parameter for the next iteration, and the $\delta$ is the adjustment step size controlling the extent of $\gamma$ change; The $D\left({x}_{new}\right)$ and $W\left({x}_{new}\right)$ are the two loss components from the current and previous iterations. If the value of $D\left({x}_{new}\right)-W\left({x}_{new}\right)$ is large, it indicates that $D\left(x\right)$ has changed significantly, necessitating an increase in $\gamma$ to give more weight to the distance optimization in the cost function. Conversely, if $D\left({x}_{new}\right)-W\left({x}_{new}\right)$ is small or negative, it indicates that $W\left(x\right)$ has changed significantly, requiring a decrease in $\gamma$ to enhance the optimization of weight sums. In addition, the step size $\delta$ should be selected appropriately—not too large to cause oscillations, not too small to slow down convergence. This way flexibly adjusts the clustering strategy according to network conditions at different iteration stages. Through the subsequent simulation verification, the parameter $\gamma$ and $\delta$ are set to 0.4 and 0.2, respectively.

To ensure the consistency in the magnitude of $D\left(x\right)$ and $W\left(x\right)$, these two parts have been normalized. This step is necessary to ensure that the algorithm can fairly consider both distance and weight differences during optimization, without bias towards one aspect due to large magnitude differences.

Selection and update of medoids

In the weight-balanced k-medoids clustering algorithm, the selection of initial medoids has a significant impact on the effectiveness of the entire clustering process. Medoids are the central points within clusters, serving as representative nodes for the entire cluster. Thus, the appropriate initial medoids is crucial for ensuring the quality of the clustering results.

Initial medoids are typically selected based on the density and weight of the nodes. Density can be measured by considering the number of neighboring nodes around a node. This paper prefers to select those in denser areas as initial medoids. Moreover, the nodes with higher weights are more likely to be chosen as initial medoids. To incorporate both density and weight into the clustering process, the weighted density ${\rho }_{i}$ at node ${n}_{i}$ is defined as:

$${\rho }_{i}=\sum_{j=1}^{N}{w}_{j}\times \chi (\Vert {x}_{j}-{x}_{i}\Vert -{d}_{c})$$

(13)

where the $\chi$ is the unit step function, the ${d}_{c}$ is the cutoff distance for neighborhood consideration, and the $\Vert {x}_{j}-{x}_{i}\Vert$ is the Euclidean distance between nodes ${n}_{j}$ and ${n}_{i}$. The weighted density ${\rho }_{i}$ measures the cumulative weight of nodes within the neighborhood of node ${n}_{i}$, promoting the selection of nodes that are both densely connected and possess higher weights.

During the clustering process, the medoid update considers a weight-based distance metric to ensure that nodes with higher weights exert a greater influence on medoid selection. The weighted distance metric ${D}_{{x}_{i}{m}_{j}}$ between node ${n}_{i}$ and medoid ${m}_{j}$ is represented by the following equation:

$$\begin{array}{*{20}c} {D_{{x_{i} m_{j} }} = w_{i} \cdot x_{i} - m_{j} } \\ \end{array}$$

(14)

where the $\Vert {x}_{i}-{m}_{j}\Vert$ denotes the Euclidean distance between node ${n}_{i}$ and medoid ${m}_{j}$. This metric emphasizes nodes with higher weights during medoid selection, ensuring that they have a more substantial impact on clustering decisions.

The position of the cluster center ${C}_{m}$ is calculated using the weighted mean, as shown in the following equation:

$$\begin{array}{*{20}c} {C_{m} = \frac{{\mathop \sum \nolimits_{j = 1}^{{N_{c} }} w_{j} \cdot x_{j} }}{{\mathop \sum \nolimits_{j = 1}^{{N_{c} }} w_{j} }}} \\ \end{array}$$

(15)

where the ${N}_{c}$ is the number of nodes in the cluster, the ${x}_{j}$ is the position of node ${n}_{j}$ within the cluster. By utilizing the weighted mean, the cluster center accurately reflects the positions and weights of all nodes in the cluster, ensuring a balanced and representative medoid.

Through the concept of initial medoid selection and the incorporation of weighted metrics, the weight-balanced k-medoids clustering algorithm is designed, as illustrated in Algorithm 1. It aims at optimizing clustering in datasets with unevenly distributed weights. This algorithm clusters nodes based on both spatial coordinates and weights. It selects the initial medoids M based on $\rho$, preferring denser areas and nodes with higher weights. The nodes are assigned to the nearest medoid using the weight-adjusted distance. Then, it iteratively updates medoids by minimizing the weighted distance metric ${D}_{{x}_{i}{m}_{j}}$, recalculates cluster centers using the weighted mean ${C}_{m}$, and adjusts the cost function $O(x)$ using γ, $D\left(x\right)$, and $W\left(x\right)$. This process repeats until convergence or maximum iterations are reached. The output of algorithm 1 is the clusters C with balanced weights $W\left(x\right)$ and minimized intra-cluster distances $D\left(x\right)$.

Algorithm 1

Weight-balanced k-medoids clustering.

Cost function-driven optimal clustering

Determining the CH number is crucial for optimizing network performance. The parameter k directly impacts the travel length and energy depletion rate in WSN. The energy depletion rate is proportional to the total number of hops from the sensors to their respective CH nodes. Therefore, the proposed OCNTMS approach for determining the CH number aims to minimize the MS path length and the network’s energy consumption.

First, a lightweight link set is built within each cluster, aiming for simplicity and efficiency in optimizing the cost function and accelerating the iteration process. In this phase, multiple k values need to be evaluated rapidly to find the optimal number of clusters. This requires an optimization algorithm that balances computational speed with acceptable solution quality.

In this paper, the Breadth-First Search (BFS) spanning tree algorithm³³ is applied to construct the link set from all non-cluster head nodes to the cluster head node within each cluster. The Ant Colony Optimization (ACO) algorithm³⁴ is chosen for constructing the MS path during the cost function optimization process. ACO is a biologically inspired meta-heuristic algorithm known for its efficiency in solving combinatorial optimization problems like the Traveling Salesman Problem, which is analogous to MS path planning. ACO offers a good trade-off between computational efficiency and solution quality, making it suitable for scenarios where quick approximations are needed. While there are more recent optimization algorithms such as the Grey Wolf Optimizer²⁵, Dragonfly Algorithm²⁶, and Red Fox Optimization³⁵. These optimization algorithms usually involve high computational complexity or long convergence times. Given the need for rapid evaluations of multiple k values, these algorithms may not be as practical for the initial optimization in OCNTMS.

According to Wolpert’s No Free Lunch theorem³⁶, no single optimization algorithm is superior to all others on all possible problems. This theorem implies that the effectiveness of an algorithm is problem-specific. Therefore, the choice of ACO is justified for this specific application, as it provides efficient convergence and satisfactory solutions within the computational constraints of the iterative process.

Assumed that ${m}_{ant}$ ants explore the solution space. Each ant starts from an arbitrary RP. After several iterations, the ants identify the shortest tour path across the RPs. The transition probability ${p}_{ij}^{r}$ used by ant $r$ to select the next unvisited RP is defined by Eq. (16).

$${p}_{ij}^{r}=\left\{\begin{array}{c}\frac{{\tau }_{ij}^{{\alpha }_{ant}}{\eta }_{ij}^{{\beta }_{ant}}}{{\sum }_{u\in {J}_{r}}{\tau }_{iu}^{{\alpha }_{ant}}{\eta }_{iu}^{{\beta }_{ant}}} R{P}_{i}\in {J}_{r}\\ 0 otherwise\end{array}\right.$$

(16)

where the ${\tau }_{ij}$ and ${\eta }_{ij}$ represent the pheromone concentration and heuristic value of edge $(i, j)$, respectively. The constants ${\alpha }_{ant}$ and ${\beta }_{ant}$ determine the relative importance of pheromone concentration and heuristic value in the transition probability. Moreover, the ${J}_{r}$ contains the RPs that ant $r$ has not yet visited. To encourage shorter tour lengths, the ${\eta }_{ij}$ is inversely proportional to the distance ${d}_{ij}$, as defined in Eq. (17)

$${\eta }_{ij}=\frac{1}{{d}_{ij}}$$

(17)

where the ${d}_{ij}$ represents the Euclidean distance between $R{P}_{i}$ and $R{P}_{j}$. After the ants complete their tours, the pheromone level ${\tau }_{ij}$ on each edge $(i, j)$ is updated using Eq. (18).

$$\begin{array}{*{20}c} {\tau_{ij} = \left( {1 - \rho } \right)\tau_{ij} + \Delta \tau_{ij} } \\ \end{array}$$

(18)

where the $\rho$ is the pheromone evaporation coefficient, and $\Delta {\tau }_{ij}$ denotes the amount of pheromone added to edge $(i, j)$. The variable $\Delta {\tau }_{ij}$ is further defined by Eq. (19).

$$\Delta {\tau }_{ij}=\left\{\begin{array}{c}\frac{Q}{STL} \left(i, j\right)\in ST\\ 0 otherwise\end{array}\right.$$

(19)

where the $ST$ represents the shortest tour path discovered by the ants, and the $STL$ denotes its length. The $Q$ is a constant value used in the pheromone update process.

The lightweight tour construction process using the ACO algorithm involves initializing the ACO parameters and pheromone levels on all paths. Ants then probabilistically select the next cluster head and iterate to construct the path. After all ants complete their tours, pheromone levels are updated based on the shortest path identified by the ants. Finally, the shortest path among all constructed paths is selected as the lightweight path planning solution for the MS.

Through an iterative process, the optimal CH number k is precisely determined. After each iteration, the current clustering scheme is evaluated, and the cost function $c{s}_{k}$ is used to decide whether CH number needs to be adjusted. For example, 250 sensor nodes are deployed in a 250 m × 250 m area in WSN. Assuming k equals 5, the travel length and total number of hops are 621 m and 398, respectively. Increasing k to 10 changes these metrics to 811 m and 305, respectively. However, fewer clusters result in shorter travel distances but higher energy depletion. Therefore, the preference depends on the relative importance of the considered criteria for a given scenario, as illustrated in Fig. 3.

Fig. 3

WSN clustering with different k (a) k = 5 ,(b) k = 10.

The OCNTMS approach aims to minimize both tour path length and energy consumption by defining the cost function $c{s}_{k}$, which represents the cost of dividing sensors into k clusters. The cost function encompasses metrics related to energy depletion and data collection delay. The energy consumption rate ${EN}_{k}$ for $k$ clusters is calculated using Eq. (20).

$${EN}_{k}={\sum }_{i=1}^{N}{E}_{i}$$

(20)

where the ${E}_{i}$ represents the energy consumption of node ${n}_{i}$, and the $N$ is the total number of nodes.

To address weight disparity among clusters, the sum of weights for all clusters is normalized using the min–max normalization process, as defined in Eq. (21).

$${Wc}_{j,norm}=\frac{{Wc}_{j}-{Wc}_{min}}{{Wc}_{max}-{Wc}_{min}}$$

(21)

where the ${Wc}_{j,norm}$ is the normalized weight sum of cluster $j$, the ${Wc}_{j}$ is the sum of weights in cluster $j$, the ${Wc}_{min}$ is the minimum weight sum among all clusters, and the ${Wc}_{max}$ is the maximum weight sum among all clusters. Subsequently, the standard deviation ${\sigma }_{W,norm}$ of the normalized weight sums is calculated using Eq. (22).

$${\sigma }_{W,norm}=\sqrt{\frac{1}{k}{\sum }_{j=1}^{k}{\left({Wc}_{j,norm}-\frac{1}{k}{\sum }_{j=1}^{k}{Wc}_{j,norm}\right)}^{2}}$$

(22)

The lower ${\sigma }_{W,norm}$ indicates that the weight sums are more consistent among clusters, implying a balanced distribution. While the higher ${\sigma }_{W,norm}$ indicates that some clusters have much higher or lower weight sums than others. The cost function ${cs}_{k}$ for data collection is formulated as Eq. (22). It denotes the cost of dividing sensors into $k$ clusters.

$${cs}_{k}={\omega }_{1}\left(\frac{{TL}_{k}}{L+H}\right)+{\omega }_{2}\frac{{EN}_{k}}{{er}_{init}\left|N\right|}+(1-{\omega }_{1}-{\omega }_{2}){\sigma }_{W}$$

(23)

where the ${TL}_{k}$ represents the total tour length for $k$ clusters, the $L$ and $H$ are the dimensions of the sensor field, the ${EN}_{k}$ is the total energy consumption rate for $k$ clusters, the ${er}_{init}$ is the initial energy of the nodes, the $\left|N\right|$ is the total number of nodes, and the ${\sigma }_{W}$ is the standard deviation of the normalized weight sums. The coefficients ${\omega }_{1}$ and ${\omega }_{2}$ are set to 0.2 and 0.4, respectively, representing the importance of tour length and network energy consumption. Each term in the cost function is normalized to ensure that they are on the same scale.

After obtaining the cost function ${cs}_{k}$, the cost function-driven optimal clustering algorithm is executed, as shown in Algorithm 2. The optimal cluster number k is determined through several iterations. In each iteration, the weight-balanced k-medoids clustering algorithm is used to cluster the nodes for a given k. To evaluate the resulting clustering, the initial link set is constructed to determine the data transmission path from each sensor to its corresponding CHs. Additionally, the ACO algorithm is used to construct the mobile path of the MS. Combining the weight differences between clusters, the $c{s}_{k}$ can be calculated. If the $c{s}_{k}$ is less than the current optimal $cs$, the final cluster number is set to k. This process continues until the termination condition is met.

Algorithm 2

Cost function-driven optimal clustering.

Network topology optimization stage

Cluster link construction based on LB-OFNS

To effectively manage energy consumption and data transmission paths in WSNs, the LB-OFNS method is proposed. This method not only reduces the network’s total energy consumption but also balances the load across the entire network, thereby extending its lifetime. Additionally, with a dynamic scoring system and level-aware selection mechanism, this method can flexibly adapt to various network operating conditions, ensuring the stability and efficiency of data transmission.

Cluster initialization

The cluster initialization phase forms the foundation for building an efficient sensor network. During this phase, nodes within the entire cluster are orderly organized into multiple levels based on their physical distance from the cluster head node $C{H}_{j}$. This process mainly involves the following steps:

Step 1: The $C{H}_{j}$ first sends out a SETUP message. This message contains important information, such as the cluster head node’s ID, location coordinates, synchronization time information, and transmission power information.

Step 2: After receiving the SETUP message from $C{H}_{j}$, each node ${n}_{i}$ will calculate its distance from the $C{H}_{j}$ using the Euclidean distance. It helps each node determine its network level and form a multi-layer network structure: The first layer is a circular area centered on the MS with a radius of TR. Each subsequent layer is also centered on the MS, with an outer radius of TR × N and an inner radius of TR × (N-1), until the entire sensing field is covered.

The multi-layer network structure supports efficient multi-hop transmission, allowing data to be transmitted through multiple nodes layer by layer to the cluster head. This not only reduces the energy consumption of individual nodes but also helps balance the load across the network.

Step 3: Within each network level, the node clustering is performed. This step aims at optimizing network management and data transmission paths by identifying spatially dense groups of nodes. The clustering process within each network level includes the following:

Setting parameters: Set a neighborhood size and a minimum sample number. The neighborhood size determines the distance threshold between nodes, with nodes closer than this threshold considered neighbors. The minimum sample number specifies the number of neighboring nodes required for a node to be considered part of the core.

Identifying core points: Identify core points as nodes with a sufficient number of neighboring nodes, marking high-density areas.

Identifying edge and noise points: Identify edge points as nodes directly connected to core points, and noise points as isolated nodes that cannot connect to any core points.

Forming clusters: Form clusters based on the identified core and edge points. Each cluster consists of core points and their connected edge points, while noise points are not clustered and handled separately.

Optimal forwarding node selection

When selecting the optimal forwarding nodes, the traversal order of nodes is based on the density of their clusters. The system starts from the outermost nodes and moves inward, beginning with the highest-density clusters and gradually transitioning to lower-density clusters, finally handling nodes marked as noise. To precisely select the optimal forwarding nodes in each cluster, a dynamic scoring mechanism is designed in LB-OFNS.

The process of selecting the optimal forwarding nodes begins by calculating a comprehensive score for each potential forwarding node. The score is based on the node’s remaining energy, its distance advantage to the target node, and its current load status. This ensures that the selected node has enough energy to support subsequent operations and is in the most advantageous position for data transmission. The scoring formula is defined by Eq. (24).

$$\begin{array}{*{20}c} {S_{i} = \varphi \cdot \left( {\frac{{e_{i} }}{{er_{init} }}} \right) + \left( {1 - \varphi } \right) \cdot \left( {\frac{1}{{d_{inner,i} }}} \right)} \\ \end{array}$$

(24)

where the ${S}_{i}$ is the score of node ${n}_{i}$, the $\varphi$ is a parameter that adjusts the importance of energy and distance factors to suit different network requirements and strategies. It is set to 0.45 throughout the simulations. The ${e}_{i}$ represents the remaining energy of node ${n}_{i}$, the $e{r}_{init}$ is the initial energy of the nodes, and the ${d}_{inner,i}$ denotes the distance from node ${n}_{i}$ to the inner layer. This score reflects the node’s forwarding capability in an ideal state without any additional burden. The load-aware dynamic weight is calculated using Eq. (25).

$$L{D}_{i}=1-\frac{cn{t}_{i}}{{cnt}_{max}}$$

(25)

where the $L{D}_{i}$ is the load-aware dynamic weight of node ${n}_{i}$, the $cn{t}_{i}$ represents the current load count of node ${n}_{i}$, and the ${cnt}_{max}$ is the maximum load count across all nodes. Each node maintains a dynamic counter that records the number of tasks processed by the node. This dynamic adjustment helps avoid overuse of highly loaded nodes, preventing over-reliance on a single node, balancing the load across the network, and extending node lifespan.

The final score $F{S}_{i}$ of node ${n}_{i}$ is determined by combining the basic score ${S}_{i}$ and the load adjustment factor $L{D}_{i}$, as shown in Eq. (26).

$$\begin{array}{*{20}c} {FS_{i} = S_{i} \cdot LD_{i} } \\ \end{array}$$

(26)

The $F{S}_{i}$ is used to identify the optimal forwarding node, ensuring efficient and balanced data transmission within the network. Each node maintains a level counter that indicates its position in the network hierarchy, which is crucial for executing the node selection strategy. When selecting the optimal forwarding node, two main strategies are employed:

1. Cross-level relay selection: If the direct next-level forwarding node is unavailable, the system implements a cross-level relay selection strategy. This strategy prioritizes nodes from the same level but closer to the inner layers as temporary relays, bridging to the inner-layer nodes. This strategy relies on the nodes’ level counters to ensure that only the current level or more inner-level nodes are selected as relays.

2. Sequential level verification: The chosen optimal forwarding node must have at least one node from the next lower level within its transmission range. This condition ensures the continuity and reliability of data transmission. If none of the candidate nodes for a given node meet this condition, the system reevaluates candidates with lower scores. For nodes in the innermost layer of the network, since they can directly establish links with the cluster head node, the highest-scoring node is directly selected as the optimal forwarding node.

The design of LB-OFNS

The Algorithm 3 shows the pseudocode of LB-OFNS algorithm. It first performs network layering and inter-layer clustering through cluster initialization. Then, it selects the optimal forwarding nodes using a comprehensive scoring and level-aware selection mechanism. Finally, data aggregation is performed before data forwarding, where inner layer nodes collect and aggregate data from the same layer or outer layer nodes. This aggregation process effectively compresses the data, reduces information redundancy, and transforms the large amounts of raw data collected from various sensor nodes into a more informative and manageable format. Figure 4 shows the link set structure of a single cluster in the network using load-balanced optimal forwarding node selection, with the hierarchical structure and inter-node link relationships labeled.

Fig. 4

Link set structure of a single cluster using load-balanced optimal forwarding node selection.

Algorithm 3

LB-OFNS algorithm

MS tour construction based on GA-MARL

After determining the optimal cluster number k, the MS tour among the cluster head nodes is optimized using the GA-MARL algorithm ¹². At this stage, the priority shifts from computational speed to achieving the most optimal path to maximize data collection efficiency and minimize energy consumption.

The GA-MARL method was initially introduced by Alipour et al. ¹² to address the Traveling Salesman Problem. It combines the global optimization capabilities of genetic algorithms (GA) with the adaptive learning strengths of multi-agent reinforcement learning (MARL), providing an effective solution for dynamic path planning in complex network environments. GA-MARL offers the advantage of incorporating multi-agent learning, which aligns well with the dynamic and distributed nature of WSNs. This makes it more suitable for optimizing the MS paths in scenarios involving non-uniform data generation.

Compared to ACO, GA-MARL effectively explores the solution space and is designed to avoid local optima, resulting in shorter MS tour lengths. Although GA-MARL is computationally more intensive and requires longer convergence times, this is acceptable since the MS path planning occurs once after the optimal cluster number k has been determined. The enhanced optimization capabilities of GA-MARL make it particularly suitable for final path planning. Therefore, GA-MARL is adopted to optimize the MS path under non-uniform data generation scenarios. The specific steps are as follows:

Initial solution generation: The MARL is used to generate an initial set of feasible solutions (paths) for the MS. Each agent represents a potential path. Through interactions with the network environment, agents learn and improve their paths to minimize travel time and energy consumption.

Solution optimization: The initial paths generated by MARL serve as the initial population for the GA. Through GA operations such as selection, crossover, and mutation, the population evolves over generations, refining the MS path to achieve optimal data collection efficiency.

The GA-MARL approach dynamically adjusts the MS path in response to network changes, significantly enhancing network performance and energy efficiency.

Performance evaluation

In this section, the performance of OCNTMS is evaluated by comparing it with existing algorithms such as ACO-MSPD³⁰, EAPC³⁷, and HPDMS³⁸. Under the scenario where sensor nodes generate non-uniform data, these algorithms are analyzed based on two key metrics: network energy consumption and network lifetime. Additionally, the performance of OCNTMS in both uniform and non-uniform data generation scenarios is compared. Finally, the network topology optimization process of a WSN using OCNTMS is presented.

Simulation environment

In this paper, each simulation scenario was independently run 30 times to account for the stochastic nature of the metaheuristic algorithms and the non-uniform data generation model. The average results and error ranges were calculated to reflect variability.

The simulations were carried out in a sensor field measuring 250 m by 250 m, with 200 to 400 sensor nodes randomly distributed. Each sensor node had a transmission range of 40 m and an initial energy of 2 Joules. A MS with unlimited energy and unrestricted mobility was employed for data collection.

In the node non-uniform data generation model, the base data generation rate ($\lambda$) was set to 1 packet per minute, and the maximum deviation proportion ($\Delta$) was 0.5, meaning that the random variable ${r}_{i}$ ranged from − 0.5 to 0.5. The data generation interval ($T$) was 10 min, and the data packet size ($B$) was 500 bits. For detailed simulation parameters, including those related to the energy model and algorithms such as the weight-balanced k-medoids clustering, cost function-driven optimal clustering, ACO, LB-OFNS, and GA-MARL, refer to Table 1.

Table 1 Simulation parameters.

Analysis of results

Analysis of OCNTMS performance

The OCNTMS has designed two primary objective functions to optimize WSN performance: minimizing network energy consumption and maximizing network lifetime.

Network energy consumption

The energy consumed by all sensor nodes in the network until the first node depletes its energy.

The objective function for network energy consumption is formulated to minimize this value, thereby enhancing the overall energy efficiency of the network. Detailed statistical results for network energy consumption of OCNTMS under varying node counts are presented in Table 2. These results include the best, worst, mean, median, standard deviation (Std), and variance (Var) values derived from 30 independent simulation runs for each node count. While Fig. 5 illustrates the box plot of network energy consumption across 30 independent runs for each node count. It provides a visual representation of the variability and consistency of energy consumption performance. Combing Table 2 with Fig. 5 shows that as the number of nodes increases, the network energy consumption for OCNTMS rises. The relatively low standard deviation and variance values suggest that the OCNTMS maintains stable and consistent performance across different simulation runs.

Table 2 Network energy consumption ($J$) for OCNTMS.

Fig. 5

Network energy consumption box plot for OCNTMS.

To further evaluate the performance of OCNTMS, its network energy consumption is compared with other algorithms, as shown in Fig. 6. As the number of nodes increases, the energy consumption of all algorithms rises. However, the proposed OCNTMS exhibits a lower rate of energy consumption growth in all cases. Specifically, compared to the EPAC, ACO-MSPD, and HPDMS algorithms, the energy consumption is reduced by 28.8%, 19.7%, and 9.3%, respectively. Furthermore, under the constraint of non-uniform data generation, the OCNTMS maintains a relatively stable energy consumption growth curve across different scenarios with varying node counts. This performance difference highlights the high optimization of OCNTMS in terms of energy efficiency.

Fig. 6

Comparison of energy consumption by varying the number of sensor nodes.

Additionally, Fig. 7 compares the energy consumption of OCNTMS in both uniform ($\Delta =0$) and non-uniform data generation scenarios as the number of nodes increases. In both uniform and non-uniform data generation scenarios, network energy consumption increases with the number of nodes. However, the difference in energy consumption growth under different data generation modes demonstrates the OCNTMS’s efficiency in handling non-uniform data generation. Specifically, from 200 to 400 nodes, the energy consumption growth in the non-uniform data scenario is about 93.3%. While it is about 76.7% in the uniform data scenario. The OCNTMS requires more energy to handle scenarios where nodes generate non-uniform data constraints.

Fig. 7

Comparison of network energy consumption in non-uniform and uniform data scenarios.

Network lifetime

The duration from the start of network operation until the first node depletes its energy, typically measured in rounds.

The objective function for network lifetime is formulated to maximize this value, thereby extending the operational longevity of the network. Detailed statistical results for network lifetime are presented in Table 3, encompassing best, worst, mean, median, Std, and Var values derived from 30 independent simulation runs for each node count. While Fig. 8 showcases the box plot of network lifetime across 30 independent runs for each node count. It provides a visual representation of the variability and consistency of network longevity performance. Combing Table 3 with Fig. 8 indicates that as the number of nodes increases, network lifetime decreases, which is due to higher energy demands. The low standard deviation and variance values further confirm the reliability and stability of OCNTMS across multiple simulation runs.

Table 3 Network Lifetime (Rounds) for OCNTMS.

Fig. 8

Network lifetime box plot for OCNTMS.

To further evaluate the effectiveness of OCNTMS, its network lifetime is compared with other existing algorithms, as depicted in Fig. 9. According to the results, the OCNTMS significantly outperforms the other three algorithms in terms of network lifetime. Although all algorithms show a decrease in network lifetime as the number of nodes increases, the OCNTMS consistently exhibits the longest network lifetime in all cases, potentially increasing network lifetime by up to 40%. This improvement is due to the OCNTMS algorithm’s balanced clustering optimization based on weight equilibrium and network topology optimization based on load balancing, which evenly distributes energy consumption across all nodes. This not only reduces network operational costs but also enhances network stability and reliability, making it suitable for long-term applications in WSNs under non-uniform data environments.

Fig. 9

Comparison of network lifetime by varying the number of sensor nodes.

Figure 10 shows the comparison of network lifetime for OCNTMS in scenarios with uniform ($\Delta =0$) and non-uniform data generation as the number of nodes increases. The network lifetime curves in both uniform and non-uniform data environments are close, decreasing from approximately 500 rounds to 300 rounds, maintaining stable network operation. The OCNTMS demonstrates similar and stable performance in both uniform and non-uniform data environments, and its performance in both environments is comparable.

Fig. 10

Comparison of network lifetime in non-uniform and uniform data scenarios.

Network topology optimization of OCNTMS

This section demonstrates how the OCNTMS algorithm is applied in a WSN scenario under non-uniform data constraints. First, 250 nodes are randomly deployed in a 250 m × 250 m area, as shown in Fig. 11.

Fig. 11

250 nodes are randomly deployed in a 250 m × 250 m.

Initially, each node is assigned a weight based on its residual energy and data generation rate. The next step is the optimal cluster selection stage in OCNTMS. During this stage, weight-balanced k-medoids clustering is performed on the network for different values of k. Then it uses the BFS and ACO algorithms for lightweight construction to calculate the energy consumption of the network under the current number of clusters, which is used for cost function calculation. The clustering strategy optimizes the number and structure of clusters by considering path length, energy consumption rate, and weight differences between clusters.

Through iterative optimization, the optimal energy efficiency and network stability in a non-uniform data environment are achieved, resulting in the current optimal cluster number for the WSN being k = 6, as shown in Fig. 12. The Fig. 13 illustrates the clusters and cluster head nodes when the optimal cluster number is 6.

Fig. 12

Variations of cs against k for the WSN scenario of Fig. 9

Fig. 13

The optimal number of clusters and the positions of the cluster head nodes for the given example in Fig. 11.

Finally, the network topology optimization stage of OCNTMS is entered, constructing a load-balanced set of links within each cluster and the optimal path for the MS to collect information from all cluster head nodes, as shown in Fig. 14. When constructing links within each cluster, a hierarchical strategy establishes efficient multi-hop transmission. The best relay nodes are selected based on residual energy, distance advantage, and dynamic load adjustment. It avoids excessive reliance and overuse of a single node, helping to balance the network load and extend the lifetime of individual nodes.

Fig. 14

Optimal network construction for the WSN scenario of Fig. 13.

Conclusion

This study proposes an efficient data collection approach for MS-based WSNs in the environment with non-uniform data generation, named OCNTMS. Through innovative methods such as weight-balanced clustering, cost function optimization, load-balanced link construction, efficient node forwarding selection, and GA-MARL algorithms for planning the MS path, OCNTMS aims to improve network energy efficiency, enhance data transmission, and extend network lifetime. Simulation results demonstrate that OCNTMS has significant advantages over existing approaches in terms of network energy consumption and lifetime, proving its potential value and practicality in real-world WSN applications. However, the OCNTMS assumes a static network topology during each data collection cycle, which limits its ability to quickly adapt to dynamic conditions, such as unexpected node failures due to high energy consumption or heavy load. Thus, future work will focus on enhancing OCNTMS’s adaptability, enabling quicker responses to node failures and improving overall network resilience.

In addition, given the large number of devices, node heterogeneity, and non-uniform data generation in IoT environment, OCNTMS can help optimize data collection efficiency and energy consumption. Specifically, its weight-balanced clustering and load-balancing strategies can enhance network stability and scalability when handling large-scale and dynamically changing topologies. It is crucial for the long-term operation of resource-constrained IoT devices. Thus, future work will consider extending OCNTMS to IoT applications while taking into account practical factors (such as node heterogeneity, security, and mobility) to further improve IoT reliability and performance.