Introduction

Bitumen is a viscoelastic material; it melts at elevated temperatures but is typically solid at room temperature. Maltenes (a combination of saturates, aromatics, and resins), asphaltenes, and other components make up the bitumen that is refined from crude oil1,2,3,4. Wherein, comparison to the other components, asphaltenes have the greatest molecular weights and are the most polar5. Bitumen’s elasticity is determined by its asphaltene concentration, whereas its viscosity is absorbed by maltenes from rubbers and polymers6,7. However, in recent years, the need for a better highway system in a variety of climatic settings has grown significantly due to rising traffic volume and axle weights. The two main types of distress in HMA pavements are moisture damage, fatigue cracking, and permanent deformation8. The major processes of moisture degradation in bituminous pavements include loss of bitumen film cohesiveness and stiffness as well as the collapse of the adhesive connection between bitumen and aggregate which increases the overall cost of highways due to regular maintenance and rehabilitation9.

Fatigue cracking is the most common form of bitumen cracking, which occurs because of the constant wear and tear of vehicles10. In HMA pavements, fatigue cracking occurs primarily because of the structure’s inability to withstand repeated loads, and this is the most significant source of pavement distress11,12. Due to a decrease in their tensile strength, pavements are more susceptible to cracking when they are subjected to increased loads or temperature fluctuations13. HMA fatigue cracking is related to the binder percentage and the asphalt’s stiffness. The higher the asphalt percentage in a mix, the more likely it is to deform (i.e., be more flexible) instead of fracture under repetitive stress14. Fatigue cracking induces tensile stresses at the bottom of asphalt layers, which causes cracks that propagate toward the surface of the HMA. The growth of these cracks depends on the strain level applied by fatigue stresses at the bottom of HMA. Strain levels are dependent on many factors, including the stiffness of the material, dimensions, and other properties. HMA pavement has this healing potential up to a certain limit of strain. If the strain level falls below this limit, then damage accumulation is very minimal, and damage can be repaired by chemical healing15. Researchers have adopted various approaches to address the distresses countered by bituminous mixes due to a number of reasons.

According to an experimental investigation by Khodaii et al.,16, adding coarse and dense graded mixes may drastically alter mechanical characteristics, notably permanent deformation of asphalt mixtures with and without SBS-modified mixtures. It was found that 5% Styrene Butadiene Styrene SBS content suggests a suitable impact on permanent deformation in the range of 4% and 6% SBS content. Acording to Kalyoncuoglu et al.,17 the performance of HMA was enhanced by using (2%, 3.5%,5% and 6%) SBS polymers which by performing wheel tracking and dynamic creep tests under different loads and temperatures. Additionally, it was shown via indirect tensile testing that modified asphalt mixes had higher strengths than controlled samples, meaning that SBS modified samples are more resistant to the development of fissures. SBS showed extraordinary performance in improving the mechanical performance of the flexible pavements. However, in-depth research is needed to explore the effect of SBS on the rheological properties of bitumen and the resistance of hot mix asphalt to mechanical failures. This study explores the application of SBS to overcome the chances of permanent deformation in flexible pavements by evaluating the dynamic modulus and phase angle (Ø) of SBS-modified mixes. The dynamic modulus indicates the stiffness of asphalt, with higher values showing better resistance to deformation, which helps prevent issues like rutting and fatigue cracking. A low modulus suggests the pavement may be too flexible, making it prone to damage under heavy traffic loads. On the other hand, the phase angle measures the viscoelastic behavior of the material, with higher values indicating more viscous (permanent) deformation and lower values showing more elastic (recoverable) behavior. A high phase angle means more energy is dissipated as heat, leading to greater fatigue damage over time.

Literature review

The Pakistan National Highway and Motorway Road network is over 260,000 km long and accounts for approximately 80% of Pakistan’s traffic. Approximately 2.5 trillion Pakistani rupees is the value of these assets. The irony is that the condition of this asset is constantly deteriorating because of poor pavement design, poor design mix, and vice versa. Repeated loads at high temperatures are typical distresses that cause rutting in asphalt pavements18. In-wheel paths occurred because of the alliance of densification and shear deformation that appear in longitudinal depressions19. In Pakistan, the majority of the highways and motorways do not show resistance to rutting in the early life of the pavement. Several hot mix asphalt factors contribute to deformation in flexible pavements, such as binder properties, gradation class (how coarse or fine), types of particles, and lastly, the amount of compaction effort applied. Furthermore, factors related to loading patterns include vehicle types, tire types and pressures, vehicle speeds, and axle loads. Environmental factors, including climate and pavement temperature, also affect the type and intensity of rutting20. Rutting also causes safety concerns when vehicles travel at high-speed maneuvers from one lane to the other and also leads to higher maintenance and reduction in the service life of the pavement21. This observation is supported by the fact that the accident rate increases as the rut of pavement increases22,23,24.

According to Hrabalova et al.,25 research, adding sulfur to SBS improves asphalt’s elastic recovery. Al-Hadidy26 discovered a similar result, although SBS and starch (ST) modified mixes improved the aforementioned attributes, combining the two avoids moisture damage and temperature impacts. Khan et al.,27 claimed that adding nano silica and SBS to bituminous mixes improve rutting resistance and resistance to moisture damage by 56% and 18% respectively. Veeraragavan28, conducted studies that demonstrated the dynamic mechanical behavior of asphalt mixtures that included crumb rubber and the SBS polymer. Performance testing was done on the blended products, including dynamic modulus, and static and dynamic creep tests at various temperatures. This research found that the dynamic modulus had higher values and a lesser rate of deformation upon exposure to a higher temperature. Frequency, temperature, and binder showed a significant impact on the dynamic mechanical behavior of asphalt by statistical analysis, specifically the multi-level factorial analysis of variance. By use of polymer modifiers in the superpave’s mix design and assessment, processes are expected to provide HMAs with improved resistance to fatigue cracking, fatigue rutting mitigation at intermediate temperatures, and fatigue mitigation at low service temperatures29.

The existence and quantity of the copolymer’s structure were used by J-S Chen30 to analyze the appearance of the SBS-modified binders. As the amount of polymer in the asphalt binder increases, the scattered polymer particles inflate to create local SBS networks, drastically improving the binder’s mechanical characteristics (viscosity, softening point, toughness, dynamic modulus, etc.). SBS concentrations between 5% and 6% were shown to be optimal for the formation of a continuous polymer framework, however, the precise minimum percentage depends more on the underlying asphalt than on the polymer itself. It seems that the critical network between asphalt and polymer, which is somewhat greater than the phase inversion content, is what defines the appropriate SBS content.

Yu et al.,31 studied the effects of UV aging duration and intensity equivalent conversion on the behavior of the asphalt mixture using thirteen samples that were prepared and molded with an appropriate dose of 5% SBS by weight of the binder. Testing the bending modulus, dynamic modulus, and scanning electron microscopy (SEM) were used to assess the dynamic mechanical qualities and micro-structure morphological features of aged asphalt mortar. The results showed that when both the UV dose and the aging period increased, the SBS-modified asphalt mortar exhibited a higher bending modulus. The storage modulus and dynamic modulus both increased steadily as the aging process progressed. Cong32, evaluated the impacts of RAP and rejuvenating agents on the performance of recovered SBS modified asphalt. At low temperature, anti-cracking performance, fatigue life, moisture cracking susceptibility, and other properties were examined. Reclaimed SBS modified asphalt mixtures including a rejuvenating agent and a binder concentration of 5% exhibited enhanced anti-cracking performance, rutting resistance moisture susceptibility, dynamic modulus, low-temperature, and fatigue resistance. As a result, the rejuvenating agent will assist in the preparation of longer-lasting RAP-containing asphalt pavement.

Zhang33 found that adding an SBS modifier boosted asphalt binder viscosity at high temperatures while also lowering its temperature sensitivity and improving high-temperature performance. SBS-modified asphalt has a higher melting point than regular asphalt. Bitumen modification by 3%, 5%, and 7% Styrene butadiene styrene (SBS) was investigated by Sing34, , and the findings were compared to those of mixes made with unmodified VG 30 HMA. The results reveal that the strength characteristics, rutting resistance, and moisture susceptibility of the SBS-modified mixtures are greatly enhanced. When it comes to bonding with ordinary bitumen, aggregates with higher calcium (Ca) content are preferable to those with higher silica (Si) content. Siliceous aggregates show a larger percentage improvement in strength and moisture susceptibility when treated with modified bitumen, in contrast to calcareous aggregates. Zhang et al.,35 conducted dynamic modulus and temperature sensitivity tests and found that by contrasting the actions of RTFO-aged and unaged SBS modified asphalt, we may learn how the oxidation degree of bitumen affects the aging features of bitumen with SBS copolymer. Bitumen matrix aging effects are larger than SBS copolymers’ aging effects in determining the low-temperature ductility, viscosity, and dynamic modulus of a short-term aged SBS sample.

Li36, compared the performance of SBS, Base Asphalt (BA), and Carbon Black (CB) modified asphalt mixtures and found that the temperature dependence of dynamic modulus of all asphalt mixtures tends to become less obvious with increasing loading frequency. While both SBS and CB may reduce asphalt’s susceptibility to temperature changes, the SBS MA combination is the least temperature-sensitive of the three, followed by the CBMA and the BA. Furthermore, CB and SBS are both capable of visibly enhancing the anti-deformation performance of the pavement structure by increasing the dynamic modulus of the BA mixture, and the improvement impact of CB is almost identical to that of SBS. Using a neural network trained on data from simulated bitumen.

Multi expression programming

MEP (Multi-Expression Programming) is an advanced linear-based technique within Genetic Programming (GP). Unlike traditional GP methods, MEP employs linear chromosomes to represent potential solutions. While it shares core operational principles with Gene Expression Programming (GEP), MEP uniquely encodes multiple software solutions within a single chromosome. Despite being a newer branch of GP, MEP has demonstrated considerable power by storing numerous expressions in one chromosome, which facilitates more diverse and effective problem-solving. Each chromosome in the MEP population represents a potential solution. The fitness values of these chromosomes are evaluated and compared, with the best chromosome selected to contribute to the final solution37,38. This ability to encode various software solutions or programs in a single chromosome is one of MEP’s unique features39. Oltean et al.40 highlighted that in a binary environment, this process results in the separation of two offspring, forming the basis for parent selection. This procedure is reiterated based on predetermined termination criteria until the optimal program is achieved. During this iterative process, offspring undergo mutations41. The MEP model offers similar flexibility to modify different parameters for optimal performance, akin to the GEP model. These parameters include the function set, crossover probability, subpopulation size, and code length. MEP’s performance depends on several factors, including the number and size of subpopulations, algorithm/code length, crossover probability, and the array of functions41. When dealing with large population sizes and multiple programs, the quantity and size of subpopulations affect evaluation complexity and computation time. Additionally, code length significantly influences the complexity of the resulting mathematical expressions.

Materials and methods

The current study evaluated the effect of SBS application in bituminous mixes. A total of 7 different combinations of SBS were evaluated by assessing the dynamic modulus and phase angle of the mixes using SPT and measuring the consistency properties of control and modified bitumen. Researchers42,43 reported the best performance of SBS-modified mixes with SBS around up to 6% by weight this is why this study evaluated 7 different combinations of SBS including (0% 2%, 3%, 4%, 5%, 6%, and 7%). The overall flow of different activities of this study can be seen in Fig. 1.

Fig. 1
figure 1

Methodological flowchart.

Full size image

Materials

Babozai quarry located in Katlang Tehsil of district Mardan, Pakistan provided the coarse and fine aggregates which were used according to NHA Class B gradation and Attock refinery limited (ARL) in Rawalpindi provided penetration grade 60/70 bitumen for fabrication of Asphalt Samples. For this study, grade 60/70 was chosen since it is mostly used in practice in Pakistan and is suitable for climatic zones with a colder to milder environment fulfilling the criteria of NHA specifications. The properties of aggregates and binder used in this study are shown in Tables 1 and 2.

Table 1 Aggregate properties.
Full size table
Table 2 Binder properties.
Full size table

Styrene-butadiene-styrene

Styrene-butadiene-styrene triblock copolymer (SBS) is a material that has both plastic and rubber properties51,52 and is made up of polystyrene and polybutadiene53 shown in Fig. 2. According to Aguirre et al.54 and Airey et al.,55, polystyrene enhances the durability of SBS at high temperatures, whereas polybutadiene increases its flexibility at room temperature. Nowadays, the use of SBS modified asphalt in pavement construction is widespread in China56,57,58. Previous study has found a wide range of SBS glass transition temperatures59,60. Meanwhile, SBS-modified asphalt possesses excellent permanent deformation resistance61. Furthermore, SBS without C double bonds may improve the asphalt mixture’s resistance to fatigue and crack damage53. Surprisingly, SBS might operate well with various polymer modifiers such as crumb rubber, EVA, and so on62. As a result, SBS has the potential to improve the low-temperature characteristics of LDPE/EVA compound-modified asphalt. SBS modifier (YH-791H) used in this study was imported from “Shijiazhuang Tuya Technology Co. Ltd, Shijiazhuang City, China”. Properties of SBS used in this study has been shown in Table 3.

Fig. 2
figure 2

Sample styrene-butadiene-styrene.

Full size image
Table 3 SBS (YH -791) properties.
Full size table

Asphalt mixture design

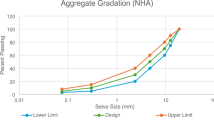
Marshall Mix Design was used to determine optimum bitumen content (OBC) and Mix volumetrics. 4.2% OBC was selected at 4% air voids. It is evident from Fig. 3; Table 4 that NHA Class B Aggregate gradation and all volumetric properties, stability, and flow meet the required NHA specifications criteria.

Table 4 Volumetric properties of mix at optimum bitumen content.
Full size table
Fig. 3
figure 3

Aggregate gradation of mix design.

Full size image

Consistency testing

Virgin bitumen samples were modified by adding varying proportions of SBS to see its impact on the consistency of the bitumen. The current study evaluated the effect of SBS on the consistency of bituminous mixes by comparing the softening point, penetration, and ductility of modified bitumen with control samples. A total of 7 different samples such as 0%, 2%, 3%, 4%, 5%, 6%, and 7% were tested for the above-mentioned tests. The effect of varying percentages of SBS with respect to the total weight of bitumen was evaluated for three consistency measuring tests.

Dynamic modulus and phase angle calculation

Sample preparation

The bitumen and aggregates were heated up to 180 °C, SBS at the rate of 500 g/min was added and mixed with the help of a high shear mixture at 500 rpm for the first 30 min. Then, every mix is followed by blending for 2 h at a speed greater than 1500 rpm. The temperature was maintained at 180 °C during the whole mixing process and after proper uniform mixing the modified bitumen was kept in the oven for 2 h to retain the obtained morphology. SBS (in 7 different proportions i.e. 0% 2%, 3%, 4%, 5%, 6%, and 7%) was added into the high-shear mixer once the morphology of the blend was obtained. According to AASHTO TP 62-07, the combined binder and aggregates were blended and compacted using superpave gyratory compactor (SGC). However, these specimens were not of the desired size, this is why they were cored and cut to create a cylindrical specimen with a 150 mm height and 100 mm diameter. The mixing procedure is shown in Fig. 4.

Fig. 4
figure 4

SBS and bitumen mixing procedure.

Full size image

Sample performance test

Dynamic modulus and phase angle were determined for varying SBS percentages at different temperatures and frequencies. Samples were tested at four different temperatures i.e. 4.4, 21.1, 37.8, and 54.4 °C and six different frequencies i.e. 25, 10, 5, 1, 0.5. and 0.1 Hz using AMPT as shown in Fig. 5. AMPT comprises a trail axial cell, a hydraulic actuator with a pump, a temperature-controlled environmental chamber for specimen placement, refrigeration for temperature reduction, heating units for temperature increase, and a computer system for controlling and collecting data. It enables the performance evaluation of asphalt mixtures under various loading and temperature conditions.

Fig. 5
figure 5

Asphalt mixture performance tester.

Full size image

The dynamic modulus of HMA might be made to look like the mixture’s dynamic stress state, which is a crucial feature for use in designing asphalt pavement constructions63. Uniaxial compression dynamic moduli of asphalt mixes are used in the design process of asphalt pavement across the globe because they add to more accurate structural design64. The absolute value of the dynamic modulus (E*), which quantifies the HMA’s stiffness in the face of sinusoidal loading. The dynamic modulus (E*) describes the connection between stress and strain for linear viscoelastic materials subjected to a sinusoidal load. The real component of the dynamic modulus is a complex number and quantifies the inner damping or viscosity, and the imaginary component indicates the elastic stiffness. Hence, Eq. (1) may be used to express the real and imaginary parts of the dynamic modulus (E*).

$${\text{{E}}}^{*}={\text{{E}}}^{{\prime\:}}+\mathfrak{i}\text{{E}}^{\prime\prime}$$
(1)

where ί = √− 1, E″ = loss or viscous modulus, E′ = storage or elastic Modulus.

E* corresponds to the elastic component for any material with elasticity. When expressed mathematically, the dynamic modulus is equal to the product of the maximum applied stress and Elastic materials have an E” value of 0, so the elastic component equals E*. The dynamic modulus is defined by Eq. (2) as the product of the maximum recoverable axial strain and dynamic pressure stress.

$$\:{\text{{E}}}^{*\:}=\frac{{\sigma\:}_{o}}{{\text{{E}}}_{o}}$$
(2)

In addition, master E* curves were created for each combination based on the average E* values measured during dynamic modulus tests conducted over a range of temperatures and frequencies. To have a common point of reference, the E* values were normalized to 21.1 °C. To ascertain the impact and interactions of various factors that influence dynamic modulus and phase angle (Ø), a two-level factorial design has been used. The elements considered include temperature, loading frequency, and SBS. To determine the major and insignificant effects on dynamic modulus and Ø, factorial plots were designed, including cumulative standardized, pareto chart, and cube plot. Both SBS-modified and unmodified mixtures are produced using the dynamic modulus predictive models. Their statistics are also shown in tabular form, and the accuracy of the model’s prediction is examined by computing the mean absolute percentage error (MAPE) and comparing the fitted and observed data using a plot. Additionally, sensitivity analysis is performed on the findings of the dynamic modulus test. Isochronal curves are plots where the panel variable is the frequency, and all temperatures are shown in a single panel as opposed to isothermal curves where the panel variable is temperature.

Regression modeling

The effectiveness of the pavement is evaluated under several conditions, including those involving temperature, loading, and weather. Predicting pavement performance throughout the design phase is essential for a lengthy pavement life. In this instance, the performance indicator dynamic modulus is dependent upon the volumetric characteristics of the mix, the loading frequency, and the test temperature. For the creation of the model for the dynamic modulus finding, the data from laboratory tests are employed. Cobb-Douglas’ general form as shown in Eq. (3) was used in cost-based empirical investigations to illustrate the effect of two or more inputs with various functional forms. Researchers have adopted sigmoid model to fit the dynamic modulus of asphalt mixture65,66. However, this study adopted Cobb-Douglas form due to its key advantages over sigmoid model. The Cobb-Douglas form is valued for its simplicity, interpretability, and flexibility in modeling material behavior. Each exponent in the equation represents the elasticity of the dependent variable, making it easy to see how factors like temperature, frequency, and strain affect outcomes such as the dynamic modulus. A key benefit is that it can be linearized for easier estimation using regression techniques67. Unlike models with fixed bounds, Cobb-Douglas has no inherent upper or lower limits for E∗E^*E∗, allowing it to describe the behavior of asphalt mixtures across a wide range of conditions. This makes it a useful alternative to the more complex sigmoid model offering clearer insights into the relative contribution of different variables68.

$$\:{\text{{E}}}^{*}=\:\alpha\:{T}^{{\beta\:}_{1}}\times\:{F}^{{\beta\:}_{2}}\times\:{S}^{{\beta\:}_{3}}$$
(3)

where: α, β1, β2, β3 = Regression Coefficients, T = Temperature, F = Frequency, S = SBS.

Model validation measures the regression model’s ability to predict observed data. Measures are used to evaluate the predictive power of regression models. For model validation, 20% of the data has been selected. The difference between the observed and estimated data values is divided by the observed value, resulting in a mean absolute percentage error (MAPE) and R2 as shown in Eqs. (4) and (5). By multiplying the mean absolute error by 100, the error can be calculated as a percentage.

$$\:MAPE=\frac{100\%}{n}{\sum\:}_{i=1}^{n}\frac{|At-Ft|}{At}$$
(4)
$$\:{R}^{2}=\:1-\:\frac{{\sum\:}_{i=1}^{n}\left({\widehat{Y}}_{i-}\stackrel{-}{Y}\right)}{{\sum\:}_{i=1}^{n}\left({y}_{i-}\stackrel{-}{y}\right)}$$
(5)

where: Ft = fitted value, At = actual value. \(\:{y}_{i},\:\:\widehat{{Y}_{i}}\) = actual and predicted output. \(\:\stackrel{-}{y},\:\:\stackrel{-}{Y}\:\)= mean values of actual and predicted outputs and.

Multi expression programming

A Genetic Programming technique called MEP employs a linear depiction of chromosomes. MEP individuals are collections of genes that encode sophisticated computer programmes. Expressions encoded by MEP people are represented similarly to how compilers convert °C or Pascal expressions into machine code. The capacity of MEP to store many answers to an issue in a particular nucleotide is a special property. For a fitness task, the best option is often picked. When addressing issues involving symbolic regression or categorization. One parsing of the chromosome is sufficient to evaluate the expressions encoded into an MEP person. Crossover and mutation offspring are always MEP individuals with the proper syntax (computer programs). Therefore, no further processing is required to mend recently acquired persons. Speeding up the use of SBS in the construction industry requires the application of cutting-edge machine learning techniques and MEP to predict the dynamic modulus at different temperatures and the SBS content. The unique encoding property of the MEP allows for the encapsulation of several equations (chromosomes) in a single programme. The final replication of the issue is picked from among the finest of the chosen chromosomes. In contrast to other machine learning techniques, MEP does not need to know the final equation in advance. After the MEP has evolved, any mathematical mistakes in the final phrase are checked for and fixed. When compared to other soft computing systems, MEP’s decoding process is straightforward. Even though MEP has several significant benefits over many other algorithms, its application to civil engineering is limited.

The basic arithmetical processes of multiplication, division, addition, and subtraction were considered to build an optimum equation that is simple and easy. How accurate the model is before the process is ended depends on how many generations were utilized to construct it. Table 5 presents the overall parameter setting for MEP modeling for SBS modified HMA mixes.

Table 5 MEP hyper-parameter for SBS modified HMA.
Full size table

Sensitivity analysis

Sensitivity analysis is used to explain how various independent variables (Inputs) affect the dependent variable (Output) under a predetermined set of circumstances. Sensitivity analysis indicates how sensitive the output is to certain input variables or changes in the input parameters. The results of the tests show that when the temperature is increased, the dynamic modulus decreases, and vice versa. The opposite phenomenon is seen when frequency falls, which lowers the dynamic modulus values. Testing at higher temperatures necessitates great care and the samples must be maintained to condition for such required period at equilibrium, as evidenced by the significant variation in dynamic modulus results. This implies that the test is highly sensitive to and prone to errors at higher temperatures. Once the proper temperature has been maintained for the necessary amount of time, the test should be performed. Using isothermal and isochronal curves, we can see whether the average value of dynamic modulus has risen or fallen as a function of testing temperature and loading frequency. As shown in Fig. 15, the value of dynamic modulus decreases as temperature rises while rising as frequency rises. Due to strain’s temperature sensitivity, the proportion of stress to peak recoverable strain increases with decreasing temperature, making objects stiffer at lower temperatures and more flexible at higher temperatures., dynamic modulus, is greater at temperatures lower than at other temperatures. Since the mix was stiffer and less likely to deform under stress, it had a greater dynamic modulus of 6% SBS.

Results and discussion

Consistency testing

SBS in six different combinations i.e. 2%, 3%, 4%, 5%, 6%, and 7% was added into bitumen and compared with the original bitumen. The addition of SBS into bitumen increased the softening point of the bitumen. The softening point recorded for all the combinations of the SBS modified samples was higher than the control sample. The addition of 2% SBS resulted in increasing the softening point from 49 to 50.9 °C. Similarly, 5% addition resulted in increasing the softening point from 49 to 71 °C. The maximum increase of 31 °C in softening point was observed as a result of the addition of 7% of SBS as shown in Fig. 6. From the figure, it can be observed that the impact of the addition of SBS on the softening point was more severe for the addition of SBS of 4% and above.

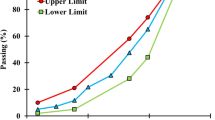
Figure 7 shows the effect of SBS on the penetration of the bitumen with references to control samples. From the figure, it can be seen that the penetration of the bitumen decreases with an increase in the SBS percentage. The reduction in penetration at 4% and above SBS shows somewhat flatter behavior as compared to lower percentages. The maximum reduction in penetration was observed as a result of the addition of 7% SBS into the mix where the penetration dropped from 66 to 55 mm while the maximum penetration drop between two consecutive mixes was observed as a result of the addition of 3% SBS. The difference between penetration of 0% and 2% SBS was 3 mm while the difference between penetration for 2% and 3% SBS was 8 mm. Detailed results can be seen in Fig. 7. Figure 8 presents the effect of SBS on ductility where it can be seen that the ductility of bitumen reduces with the increase in SBS in the bitumen. The ductility reduced from 100 to 64 cm as a result of 7% addition of SBS. The reduction in ductility as a result of SBS addition showed somewhat symmetrical behavior on both sides of 4% SBS. Overall, for the consistency analysis of SBS modified bitumen, it can be concluded that the addition of SBS increases the stiffness and rigidity of the bitumen. This is why it is recommended to add SBS into higher penetration grades when they are intended to be used in low-temperature conditions.

Fig. 6
figure 6

Measured softening point of SBS modified asphalt.

Full size image
Fig. 7
figure 7

Measured penetration of SBS modified asphalt.

Full size image
Fig. 8
figure 8

Measured ductility of SBS modified asphalt.

Full size image

Dynamic modulus test

Master curves development

To assist in pavement structural response design, the test findings were used to develop master curves. Testing the dynamic modulus of an asphalt mixture under severe stress circumstances, such as very high and low-frequency loads, is challenging due to the constraints of test instrumentation or time69. Since the dynamic modulus of AC exhibits time-temperature dependence characteristics, a dynamic modulus master curve of asphalt mixture can be made based on the time-temperature equivalence principle, which can accurately characterize this behavior and contribute greatly to the structural design and mechanical analysis of asphalt pavement70. Utilizing the time superposition principle, a smooth, uniform curve that shifts each temperature to the reference temperature was used triplicate specimens were tested at each temperature, and the desired frequencies at 21 °C as a reference temperature, and an average of those values were used to produce Master curves. The MS Excel solver add-in tool is used to decrease the sum of squared errors to fit the curve. In addition, a low frequency, such as (0.1 Hz), represents traffic moving at a slow pace, and a high frequency, such as (25 Hz), represents traffic moving at a fast rate. Figure 9 demonstrates that at both low (4.4 °C) and high (54.4% °C) temperatures, 6% SBS has the best possible dynamic modulus for slow and fast traffic, respectively. All seven mixes’ master curves show that lower frequencies separate them more than higher frequencies.

Fig. 9
figure 9

Master Curves for dynamic modulus dynamic modulus for all mixtures.

Full size image

Figure 10 presents the effect of frequency and temperature for every combination of SBS on dynamic modulus of the mixes. From the figure, it can be seen that in terms of temperature, the highest dynamic modulus was observed in the case of 4.4 °C for all the combinations of SBS, while on the other hand, increasing the frequency results in the increase of dynamic modulus while keeping the temperature and SBS percentage constant. Overall, the figure shows that the maximum dynamic modulus was observed as a result of 6% of SBS at 4.4 °C and 25 Hz frequency. Detailed results can be observed in Fig. 10.

Fig. 10
figure 10

Effect of SBS on dynamic modulus.

Full size image

Dynamic modulus for two-level factorial design

To examine how different variables interact with one another and with the dynamic modulus, a two-level factorial design approach is utilized. Low and high levels of design approaches were taken into consideration as shown in Table 6.

Table 6 Factors considered in the study for two factorial design process.
Full size table

Due to the factorial design, the main and interaction impacts are shown in Table 7. SBS and frequency have a greater impact on dynamic modulus values since a positive sign indicates a direct relation and Temperature is represented by a negative sign that is, it is inversely related to dynamic modulus. The analysis was done at a 0.05 level of significance. The factors with a p-value of 0.05 or less are thus considered significant. SBS, temperature, and frequency given that their p-values are less than 0.05, the two-way interactions between temperature and frequency, temperature and SBS, and temperature, frequency, and SBS and three-way interaction were found to be significant.

Table 7 Dynamic modulus main and interaction effect estimate.
Full size table

The Analysis of Variance (ANOVA) for the measured data of dynamic modulus up to three-way interaction effects is shown in Table 8. It denotes that there are three variables explaining the major impact Temperature, Frequency, and SBS, meaning that there are three degrees of freedom for the main effect. The significance of a factor may be determined by examining the relationship between the p-value (typically less than 0.05) as well as the value of F (typically more than 10). Therefore, the main effect, two-way interaction, and three-way interaction are all regarded as significant since they have a large impact on dynamic modulus.

Table 8 ANOVA for dynamic modulus.
Full size table

The cumulative normal probability plot for the standardized main and interaction effects with a 95% confidence interval is shown in Fig. 11. The probability plot offers a clear view of the importance of many parameters. Dots in red and black indicate significant variables and those that are not. The negative slope of the curve for temperature suggests an inverse connection with dynamic modulus, whereas the positive slope for frequency and SBS implies a direct link with dynamic modulus. This indicates that temperature and frequency together as well as temperature and SBS have a significant impact on dynamic modulus.

Fig. 11
figure 11

Cumulative normal plot for dynamic modulus.

Full size image

Dynamic Modulus signifies when one element fails to have the same impact on responses at varying levels of some other component, as seen in the Fig. 12. When one variable is changed, the influence of the other changes, which is when two variables interact. The importance of the interaction effect between the factors has been shown by non-parallel lines, which signifies that negligible factor interactions generate comparable patterns in the response at different levels of a different factor and vice versa. The intensity of the interaction, in this example temperature, is expressed by the steepness of the line slope. Because there is no parallel line in Fig. 12, there is a strong interaction between the parameters of temperature and SBS and frequency and temperature. As a result, dynamic modulus is significantly affected by these three factors.

Fig. 12
figure 12

Plot of dynamic modulus interaction effects.

Full size image

Using a Pareto chart, Fig. 13 illustrates the importance of the factor effect and the interaction effect. For a 95% confidence interval, the bars in this graph exceed the t-critical value showing that temperature, frequency, and SBS are important characteristics that influence the value of dynamic modulus. A Pareto chart may be used to understand the importance of each component as well as how they relate to one another. Additionally, it shows the relative importance of the component impact, also known as the standardized effect. In this case, to show that lines in the plot that cross the reference line are significant whereas lines that do not cross the reference line are not, a T-critical reference line is drawn. As their bars also cross the reference line, temperature, frequency, temperature and SBS, and other factors all significantly affect the value of dynamic modulus.

Fig. 13
figure 13

Dynamic modulus pareto chart.

Full size image

Phase angle

The phase angle is the angle at which compressive stress lags the axial strain. The phase angle is 0◦ for an entirely elastic material and an entirely viscous material phase angle is 90◦. The value of the phase angle for the material ranges from 0 to 90 degrees and is shown in Eq. (6).

$$\:\:\varnothing\:=\frac{{t}_{i}}{{t}_{p}}\times\:360$$
(6)

where, ti = time lag between a cycle of stress and strain, tp = time for a stress cycle.

Phase angle initially rises with temperature and falls with frequency. On the other hand, the phase angle exhibits opposite behavior and starts to decline with a temperature rise and drops with a reduction in frequency; yet this appears to be judged fit until temperature surpasses 37.8 °C. From the Fig. 14, it is obvious that the phase angle first rises with temperature but then begins to decline. The fact that phase angle increases dynamic modulus at lower temperatures shows that most of the energy is due to HMA’s viscoelastic nature. The binder has the most impact on the phase angle of asphalt mixes. As a result, it adheres to the binder’s phase angle trend. The phase angle for asphalt mixes, however, falls with decreasing frequency or rising temperature due to the aggregate impact, and more energy is lost in viscoelasticity since the aggregate mostly influences the phase angle at low frequency and high temperatures.

Fig. 14
figure 14

Variation of dynamic modulus with phase angle.

Full size image

Phase angle for two-level factorial design

SBS, frequency, and temperature all have substantial effects on phase angle, as shown in Table 9. The temperature has an arithmetic sign that is directly proportional to the phase angle, but frequency and SBS have a negative sign that is inversely proportional to the phase angle. There is also no significance in the two-way interaction of temperature & SBS, temperature & frequency, and frequency & SBS, since their p-value is more than 0.05, and the three-way interactions are likewise significant because their p-value is lower than 0.05.

Table 9 Phase angle main and interaction effect estimate.
Full size table

Figure 15 presents the effect of frequency and temperature for every combination of SBS on the phase angle of the mixes. From the figure, it can be seen that in terms of temperature, the lowest phase angle was observed in the case of 4.4 °C for all the combinations of SBS, while on the other hand, increasing the frequency results in a decrease in phase angle while keeping the temperature and SBS percentage constant. Overall, the figure shows that the least phase angle was observed as a result of 6% of SBS at 4.4 °C and 25 Hz of frequency. Detailed results can be observed in Fig. 15.

Fig. 15
figure 15

Effect of SBS on phase angle.

Full size image

Table 10 displays the results of the phase angle’s analysis of variance (ANOVA). The table shows that the main effect and the two-way interaction are significant while three-way interactions are insignificant as shown by a greater value of F than 10 and a lower value of P, respectively. Three elements (Temp, Freq, and SBS) are influencing the phase angle response, which has a degree of freedom of three.

Table 10 ANOVA for phase angle.
Full size table

Figure 16 depicts the primary impacts of the variables affecting the phase angle graphically. A considerable influence on the response, i.e., phase angle, can be seen in the distance from the normal line for all three components, i.e., temperature, frequency, and SBS. The phase angle is more dependent on that component that is far from the normal line. The red dots on the graph represent the significant and inverse relationship between temperature and phase angle, whereas the blue dots indicate the significant and direct relationship between frequency and phase angle. Two-way interaction is also significant while three-way interaction is insignificant.

Fig. 16
figure 16

Phase angle normal plot.

Full size image

Figure 17 shows the interaction plot, the phase angle is affected by temperature, SBS, and frequency as shown by the non-parallel lines. Therefore, all the interactions are significant. Figure 18 shows the Pareto chart for phase angle, which indicates the significance of variables. It is clear from the figure that; temperature, SBS, and frequency bar cross the reference line individually, and all are significant. On the other hand, SBS, frequency and temperature jointly do not influence the phase angle since the bar does not cross the reference line and conforms to the primary effect plot in this experiment. When the temperature and frequency bars cross the reference line in a two-way interplay, they have a considerable influence on the phase angle.

Fig. 17
figure 17

Interaction plot for phase angle.

Full size image
Fig. 18
figure 18

Phase angle pareto chart.

Full size image

Regression modelling

The model for the SBS unmodified and modified mixes utilized in the research is developed using a non-linear regression analysis technique. The overall model was created using SPSS software and nonlinear regression. Table 11 displays the model’s statistics and parameters. If the R2 is larger than 0.7, the model is good and approved since it captures 79% of the variance in dynamic modulus. All independent variables have a significant critical value of t-stat at a 95% confidence interval, i.e., 2.3808. The final version of the SBS modified model can be written as shown in Eq. (7).

$$\:{\text{{E}}}^{*}=37963.633\times\:{T}^{-0.691}\times\:{F}^{0.122}\times\:{SBS}^{0.222}$$
(7)
Table 11 Model for non-linear regression summary.
Full size table

The MAPE of the model employed in this study was recorded to be 8.29%, which means the regression model was excellent as MAPE was less than 10, and similarly, R2 (coefficient of Determination) was 0.91, the depicted model is great for forecasting dynamic modulus using temperature, frequency, and SBS. Figure 19 depicts the model’s validation plot. Larger data around the 45° line indicate great predictive performance, as would be expected from a model of this kind.

Fig. 19
figure 19

Regression model validation for SBS modified HMA.

Full size image

Multi expression programming (MEP)

In material engineering settings, for example, where a little change in an asphalt pavements variable might have a large effect on Hot Mix Asphalt stiffness and dynamic modulus, MEP is useful since the uncertainty in the target equation isn’t immediately apparent. Numerous solutions exist for a linear chromosome in MEP, allowing the software to make an educated guess by considering a wider range of possible locations. To kick off the MEP modelling for the SBS Modified HMA, the researcher settled on a subpopulation size of 500.

$$\begin{aligned}{\text{{E}}}^{*}&=\left(\left(\left(\frac{64-F}{\surd\:T}\:\right)+\left(\frac{4096}{2 F}\right)+\frac{64}{F}+S\right)+\left(64ST+\left(\frac{{8192 S}^{2}{T}^{2}-32768{S}^{2}T}{{F}^{2}}\right)\right) \right.\nonumber\\&\left.\quad+\left(16384+4{F}^{2}-512F+\left(\frac{4096 S}{{F}^{2}}\right)\right)+\left(64-F*\left(\frac{64}{F}\:+S-2T-4-\left(\frac{64-F}{\surd\:T}\right)\right)\right)\right)\end{aligned}$$
(8)
$${\text{{E}}}^{*}=\frac{64+63F- {F}^{2}}{\sqrt{T}}+\frac{4096S+T{S}^{2}\left(8192T-32768\right)}{{F}^{2}}+F\left(2T-508\right)+64ST-FS+S+16,384$$
(9)

where, T = Temperature, F = Frequency, S = SBS, E*= Dynamic Modulus.

A programme with more generations would result in better results with less error. Utilizing cross-over and mutation rates, it is also feasible to determine the probability that children may experience genetic functions. The combination that produced the best outcomes out of many combinations was selected. It’s important to remember that a model’s accuracy is influenced by how long it takes to develop. The model’s development never ends as new variables are included in the setup. Contrarily, this research hypothesizes that 500 generations mark the end of starting to change or the threshold at which the fitness function alters by less than 5%. Equation (8) refers to the final MEP model for calculating the dynamic modulus of SBS Modified HMA which has been simplified and presented in Eq. (9). MEP model validation for SBS modified HMA R2 is 96.67% as shown in Fig. 20.

Fig. 20
figure 20

MEP model validation for SBS modified HMA.

Full size image

Sensitivity analysis

The stress-strain relationship in Fig. 21 demonstrates that dynamic modulus increased with higher frequency or with an increase in frequency. At higher loading frequencies, decreased tire-to-pavement contact time/pressure results in a rise in dynamic modulus. The graphs reveal that SBS 6% has a greater dynamic modulus than 7%, which is also the optimal SBS percent advised in this research for a combination to attain a higher dynamic modulus. Higher temperatures have a lower dynamic modulus because they are more prone to errors and strain, both of which are adversely effected by temperature and flexibility. Figure 22 presents the Isochronal curves for dynamic modulus which shows that the lowest dynamic modulus was observed against 0% SBS. The dynamic modulus reduces with an increase in temperature. From the figure, it can be seen that the mix having the highest SBS content resulted in the highest dynamic modulus. While keeping the SBS constant, it can be observed that the overall dynamic modulus increased with the increases in frequency.

Fig. 21
figure 21

Isothermal curves for dynamic modulus.

Full size image
Fig. 22
figure 22

Isochronal curves for dynamic modulus.

Full size image

Isochronal and isothermal curves are the best representations of the relationship between phase angle, frequency, and temperature. At temperatures of 4.4 °C and 21.1 °C, the phase angle rises with decreasing frequency, but at 37.8 °C and 54.4 °C, the phase angle decreases significantly. Lower temperatures tend to favor the elastic component, whereas higher temperatures are more likely to favor the viscous component in blends. Figure 23 shows that 0% SBS mix has a larger phase angle at every temperature and frequency because they include more bitumen than other mixes, which results in a higher phase angle and less temperature decrease.

Figure 24 shows isochronal curves which show the variation of different temperatures at a single frequency 0% of SBS shows a higher phase angle at all frequencies and tends to decrease at a higher frequency. Overall, 0% SBS shows more phase angle due to the highest binder content than other mixes. The phase angle increases from 4.4 to 37.8 °C before decreasing at frequencies of 0.1 Hz, 0.5 Hz, and 1 Hz. However, at 5 Hz, 10 Hz, and 25 Hz it rises as the phase angle tends toward the elastic part at lower temperatures and the viscous part at the higher temperature.

Fig. 23
figure 23

Isothermal curves for phase angle.

Full size image
Fig. 24
figure 24

Isochronal curves for phase angle.

Full size image

Conclusions

The results of this study can be adopted across the globe with certain conditions. The developed relation can help researchers in cases where the properties of materials and environmental conditions match the properties and environmental conditions of the research presented in this article. However, the outcome can vary depending on the material properties and environment. Furthermore, based on the above consistency and performance testing, the following conclusions have been drawn from this research study:

  1. (a)

    When SBS content was raised to 7%, the modifier became the dominant matrix and formed an uninterrupted film around the droplets of the binder. This resulted in an increase in penetration value up to a critical concentration of 7%. Consequently, a dose of 6% SBS is recommended since the penetration value stabilizes as the SBS percentage rises. Overall, a 46% drop in penetration value is observed.

  2. (b)

    An increase in the proportion of SBS causes the softening point to rise. Bitumen’s softening point rises as its asphaltene concentration rises, making it more viscous. Polymer swelling and maltene absorption by the polymer phase led to a rise in asphaltene concentration and a stiffer mix because of the softening point rising from 49 °C to 80 °C and overall, 63% increase in softening point was observed.

  3. (c)

    Ductility decreased from 100 to 64 cm and a 56% drop is observed due to the addition of SBS, the mix becomes stiffer and a reduction in bitumen ductility occurs as it becomes brittle, However, 50 cm ductility value is acceptable for road works. This research recommends 6% SBS as the optimal proportion as 6% addition fulfills the strength and consistency properties of the mix.

  4. (d)

    Specimens with 6% SBS content showed higher dynamic modulus as compared to other mixes at frequencies 25, 10, 5, 1, 0.5 and 0.1 Hz on low and high temperatures. An increase of 2.10 times dynamic modulus was observed at 6% SBS at different frequencies as compared to the unmodified mix which is also the optimal SBS % recommended to use in the HMA mix.

  5. (e)

    According to the findings of a two-level factorial design study, dynamic modulus, and Ø is significantly affected by temperature, frequency, and SBS.

  6. (f)

    Phase angle initially increased with increasing temperature and then started decreasing after attaining a peak value at 37.8 °C at lower frequencies. This was owing to asphalt concrete’s reduced temperature dependence on the binder and greater temperature interaction with aggregate.

  7. (g)

    Master curves showed that higher dynamic modulus was observed at 6% SBS at lower and higher temperatures & frequencies. Hence 6% SBS dosage by weight of binder is recommended for use in HMA at any temperature in Pakistan.

  8. (h)

    Isothermal and Isochronal plots revealed that the 0% SBS mix is showing an increase in Phase angle and less drop is observed due to higher bitumen content as compared to other mixes.