Introduction

Background

With the increasing impact of climate change and the rise in extreme weather events globally, flood forecasting has become an essential requirement for many countries and regions@@@1,2,3. Effective flood forecasting not only allows for early predictions of flood timing, location, and intensity, thereby mitigating flood damage, but also improves flood management efficiency and optimises resource allocation@@@4. However, the changing global climate is shifting precipitation patterns, increasing extreme weather frequency, and altering the spatial and temporal distribution of floods@@@5, creating substantial challenges for traditional flood forecasting models. Research shows a marked increase in extreme rainfall events, complicating future predictive accuracy even further@@@6. As a result, existing flood forecasting models must adapt to these changes, including recalibrating model parameters related to input variables such as precipitation, river levels, and surface evaporation rates to account for the randomness and uncertainty brought about by climate change@@@7. Specifically, researchers should leverage the latest climate data and technologies, such as artificial intelligence and machine learning, to improve model adaptability and accuracy. Additionally, future flood forecasting systems should incorporate more climate drivers, such as changes in ocean-atmosphere circulation patterns, land use transitions, and the effects of urbanization on flood basins@@@8. For instance, urbanization may exacerbate flooding by increasing surface runoff due to hardened surfaces, which alters flood flow paths@@@9. Therefore, the focus of future research will be on developing more efficient and accurate flood forecasting models and methods to meet the challenges posed by climate change, providing more reliable support for flood prevention and mitigation.

Literature review

The origins of flood forecasting technology date back to the 1930s, primarily relying on simple empirical formulas and hydrological models. Methods such as the unit hydrograph for deriving rainfall-runoff and the Muskingum method for river flood calculation were introduced in the United States, alongside the estimation of the S-curve for rainfall-runoff@@@10,11. During this period, research mainly focused on the simple relationship between rainfall and runoff, making forecasting relatively straightforward.Since the late 1950s, with the application of computation and systems theory, scholars have proposed various conceptual methods for hydrological simulation. These methods include hydrological models based on watershed hydrological processes and river hydraulics, such as the Sacramento model in the United States@@@12, the Xin’anjiang model in China@@@13, and the TOPKAPI model in Italy@@@14. Hydrological modeling has evolved significantly over time. The SCS-CN model, developed in the 1950s, was one of the earliest approaches to quantify the rainfall-runoff relationship and remains widely used for its simplicity. However, despite its simplicity, the SCS-CN model often faces limitations in predictive accuracy. Several modifications have been proposed to enhance its predictive abilities. Later advancements in mathematics and computer science facilitated the development of more sophisticated distributed hydrological models, such as the MIKE SHE model@@@15,16. Distributed models emphasise the physical processes of precipitation, surface, and subsurface interactions, enhancing quantitative analysis of the rainfall-runoff relationship. While these models have the potential to improve computational accuracy in hydrological processes, their effectiveness hinges on factors like data quality, model calibration, and specific watershed characteristics. In cases where these conditions are suboptimal, distributed models may not yield higher accuracy. By the late 1980s, with advancements in computing, remote sensing, and information technology, integrating remote sensing with geographic information systems (GIS) flourished. Hydrologists began to consider coupled hydrological, hydraulic, and environmental processes, marking a major developmental shift@@@17. Such models have enabled effective optimisation of water resource management at larger scales, particularly for complex river basins that span broad geographical regions and include multiple sub-basins@@@18,19. These expansive river basins demand comprehensive management strategies due to varied hydrological conditions and the need for coordinated water resource management across regions@@@18,19. Since the early 21st century, rapid developments in artificial intelligence technologies, such as neural networks and support vector machines, have been applied to flood forecasting. Hydrologists now leverage extensive meteorological and hydrological data, employing deep learning to refine rainfall-runoff models@@@20,21,22. As illustrated in Fig. 1, machine learning has become central in flood forecasting research, with keywords like ‘flood forecasting,’ ‘precipitation,’ and ‘streamflow’ closely linked to ‘machine learning’. This emphasis underscores the growing reliance on machine learning models to address the complexity and nonlinearity inherent in hydrological processes. Notably, the figure highlights frequent applications of models like LSTM, ANN, and Random Forest, underscoring their importance in managing time-series data and large datasets, which are crucial for improving flood prediction accuracy. Hybrid models that combine conceptual hydrological models with deep learning have gained significant traction among hydrologists. For instance, the TdCNN model, which employs a two-dimensional hidden layer architecture to capture the spatiotemporal characteristics of hydrological data, has demonstrated improved adaptability and accuracy in flood forecasting across various lead times@@@23,24. The complexity and nonlinearity of rainfall-runoff formation over time scales are well-documented@@@1,2,3. Existing conceptual hydrological models and supervised deep learning approaches often encounter generalisation challenges, leading to significant simulation errors in flood modelling@@@25. However, unsupervised deep learning can effectively capture the complex characteristics of highly nonlinear processes like rainfall-runoff@@@26. Research indicates that commonly used deep learning models for hydrological forecasting, such as LSTM (Long Short-Term Memory)@@@27,28,29, TCN (Temporal Convolutional Network)@@@21,22,30, and Transformer@@@31,32,33, generally exhibit more advanced theoretical foundations and architectures than traditional artificial neural networks, particularly in handling complex, nonlinear processes over extended periods. These models have shown superior forecasting accuracy in multi-period flood predictions. Additionally, the MHAFFM model, which combines a multi-head attention mechanism with multiple linear regression, has yielded substantial improvements in flood forecasting accuracy and stability over benchmark models, especially in managing prediction result oscillations and maintaining interpretability@@@23,24.

Fig. 1
figure 1

Co-occurrence network diagram of high-frequency keywords on the topic of flood forecast and machine learning.

Full size image

Research gap and objective

As a relatively new application of time series prediction models in flood forecasting, the TCN has demonstrated promising potential@@@5,34. While TCN models have been effectively applied in other fields, their use in hydrology—particularly for flood prediction—remains in an exploratory phase. Wang et al.@@@5 developed a TCN-Attention model to predict daily average streamflow at the Huayuankou hydrological station, incorporating multiple influencing factors. Furthermore, Wang et al.@@@5 introduced dilated convolution to enhance high-order hydrological feature extraction, successfully applying the improved TCN model to the Lushui River Basin. Zhang et al.@@@35 coupled variational mode decomposition (VMD) with TCN to construct a VMD-TCN model, which was utilised to predict monthly runoff at the Xianyang and Huaxian hydrological stations in the Weihe River Basin. Most studies have focused on refining the TCN network structure to improve performance, yet have often overlooked the influence of hyperparameters on simulation accuracy@@@7. Hyperparameter selection not only affects simulation outcomes but also plays a critical role in the model’s overall processing speed. Currently, hyperparameter selection frequently depends on human experience and extensive experimentation, resulting in significant expenditures of manpower, time, and computational resources@@@36. Therefore, effective methods are needed to optimise the hyperparameters of machine learning models. To address this need, this study makes several key contributions: we propose a novel PSO–TCN flood forecasting model, which couples the TCN with the particle swarm optimization (PSO) algorithm to effectively optimize hyperparameters, thereby enhancing model accuracy and computational efficiency in flood prediction. Furthermore, we develop the PSO–TCN–Bootstrap hybrid model by incorporating the Bootstrap method to estimate the uncertainty of the model’s predictions, allowing for the generation of confidence intervals and providing a more robust flood risk assessment. The study applies the PSO–TCN model to the Tailan River Basin in Xinjiang for validation, comparing its performance against the traditional TCN model and demonstrating its potential to improve flood prediction accuracy and enable real-time responses to flood risks. Finally, we identify avenues for future research, including the application of the model in watersheds with varied hydrological characteristics and its potential for long-term flood risk analysis and water resource management.

Methods

Particle swarm optimization

PSO is a heuristic optimisation algorithm introduced by Eberhart and Kennedy in the late 20th century. This algorithm models the cooperative and competitive behaviour of individuals within a group by simulating the foraging behaviour of birds, effectively framing the problem as a group search for the optimal solution@@@37,38. In PSO, each candidate solution is referred to as a ‘particle’, with each particle characterised by position and velocity attributes. The algorithm iteratively optimises particle positions by updating velocity and position based on each particle’s own best-known position and the best-known position in its neighbourhood. Through these directional and distance adjustments, particles iteratively converge towards the optimal solution. PSO demonstrates robust global search capabilities and convergence properties, making it well-suited for continuous and discrete optimisation problems alike@@@39. The algorithm has been applied extensively across fields, including function optimisation, machine learning, and neural network training@@@36. The algorithm’s principle is outlined below@@@36.

Assuming that m particles in an N-dimensional space form a populationet, where \(x_{i} = \left[ {x_{i1} ,x_{i2} ,...,x_{iN} } \right]\), the feature of the i-th particle at time t is represented as follows:

$$X_{i} = (x_{i1}^{t} ,x_{i2}^{t} ,...,x_{iN}^{t} )^{T}$$
(1)
$$V_{i}^{t} = (v_{i1}^{t} ,v_{i2}^{t} ,...,v_{iN}^{t} )^{T}$$
(2)
$$P_{i}^{t} = (p_{i1}^{t} ,p_{i2}^{t} ,...,p_{iN}^{t} )^{T}$$
(3)
$$P_{g}^{t} = (p_{g1}^{t} ,p_{g2}^{t} ,...,p_{gN}^{t} )^{T}$$
(4)

In the equation, Xi and \(V_{i}^{t}\) represent the position and velocity of the particle, while \(P_{i}^{t}\) and \(P_{g}^{t}\) represent the individual best solution and the global best solution.

The updated position and velocity of the particle at time t+1 are given by:

$$V_{id}^{t + 1} = wV_{id}^{t} + c_{1} r_{1}^{t} (p_{id}^{t} - x_{id}^{t} ) + c_{2} r_{2}^{t} (p_{gd}^{t} - x_{id}^{t} )$$
(5)
$$x_{id}^{t + 1} = x_{id}^{t} + v_{id}^{t + 1}$$
(6)

In the equation, \(wV_{id}^{t}\) as the previous velocity of the particle, \(c_{1} r_{1}^{t} (p_{id}^{t} - x_{id}^{t} )\) as the cognitive component, which represents the particle’s own consideration, indicating the distance between the current position i and the local optimal position, \(c_{2} r_{2}^{t} (p_{gd}^{t} - x_{id}^{t} )\) as the “social” component, referring to information sharing and cooperation between particles, indicating the distance between the current position i and the global optimal position;\(V_{id}^{t + 1}\) as the d-dimensional component of the velocity vector for particle i in the t+1 iteration; w represents the inertia weight, c1 and c2 are learning factors within the range of [0, 2], and r1 and r2 are random numbers distributed between [0, 1]. The position and velocity of the particle are constrained within the range of [−Vmax, Vmax] and [−Xmax, Xmax] respectively.

Temporal convolutional networks

Temporal Convolutional Networks (TCNs) are a deep learning model designed for time series analysis@@@35. Unlike traditional Recurrent Neural Networks (RNNs) and Long Short-Term Memory networks (LSTMs), TCNs leverage convolutional operations to capture sequential dependencies, allowing them to process multiple data points in parallel, which enhances their capacity to handle larger datasets efficiently and reduces training time. By incorporating dilated convolutions and residual connections, TCNs effectively manage long-term dependencies, mitigating issues like vanishing and exploding gradients@@@5. The core of TCNs lies in building the model through stacking multiple convolutional layers, where each layer’s input derives from the output of the previous layer, thereby extracting features from the data via convolution operations. Unlike conventional Convolutional Neural Networks (CNNs), TCNs typically employ a kernel size of 1, focusing exclusively on the current timestep’s features. This approach allows the model to capture essential information for future predictions while avoiding the complexities associated with processing multiple timesteps simultaneously@@@36. TCNs integrate residual connections and dilated convolutions to enhance model performance. Residual connections allow a convolutional layer’s input to be directly added to its output, improving the model’s learning of input–output relationships. Meanwhile, dilated convolutions expand the receptive field of the convolutional layers, enabling the model to capture long-range temporal dependencies. In hydrological forecasting, TCNs have demonstrated significant potential. By extracting high-order features from time series data through convolutional layers, they provide accurate predictions of floods, runoff, and river water levels. For instance, TCN models surpass traditional Artificial Neural Networks (ANNs) and LSTM models in flood forecasting, offering higher predictive accuracy and faster convergence speeds. In runoff prediction, TCN models have shown strong performance in studies on California watersheds, accurately reflecting the physical relationships between input variables and runoff@@@40.

In TCN, causal convolutions in one-dimensional form are used to ensure that the output has the same length as the input. For an input sequence q, the calculation formula@@@36 of the causal convolution F(T) at time step T is as follows:

$$F(T) = (q * f)(T) = \sum\nolimits_{i = 0}^{k - 1} {f(i)} \cdot q_{s - i}$$
(7)

In the equation, T represents the T-th time step, q is the input one-dimensional sequence, f is the convolution kernel, k represents the size of the convolution kernel, s represents the current time step or index of the input sequence q. Specifically, s serves as the reference point for the convolution operation, starting from the current time step T and qs-i represents the value in the sequence on which the convolution kernel operates.

The formula for dilated convolution is as follows:

$$F(T) = (q *_{d} f)(T) = \sum\nolimits_{i = 0}^{k - 1} {f(i)} \cdot q_{s - d \cdot i}$$
(8)

In the equation, F(T) represents the dilated convolution operation on the sequence element s, q is the input one-dimensional sequence, d is the dilation factor, f is the filter, k represents the size of the filter, and s-d·i represents the past information direction.

From Fig. 2, it can be observed that the TCN network is composed of multiple residual blocks. Each residual block consists of two causal dilated convolutions, followed by weight normalization to accelerate the convergence speed of gradient descent. The calculation formula is as follows:

$$y = \varphi (w \cdot x + b)$$
(9)
$$w = \frac{g}{\left\| v \right\|}v$$
(10)
Fig. 2
figure 2

TCN network architecture.

Full size image

In the equation, w represents the weight size, v represents a multi-dimensional vector, and g represents a scalar. The rectified linear unit (ReLU) activation function is then applied to introduce non-linearity between layers. The calculation formula is as follows:

$${\text{Re}} LU(x) = \max (0,x)$$
(11)

Finally, dropout is added for regularization, randomly dropping neurons from the network with a certain probability to prevent overfitting. The calculation formula is as follows:

$$y = pf(wx)$$
(12)

In Eq. (12), pf represents a composite function, where p refers to a dropout regularization operation to prevent overfitting, and f refers to an activation function such as ReLU, applied after the linear transformation wx. This helps introduce non-linearity into the model and regularize the network.

There are several reasons for applying PSO to the hyperparameter optimization of TCN in deep learning.Global Optimization Capability: PSO effectively explores the entire search space, avoiding local optima, which is an advantage over traditional methods like grid search or random search. Fast Convergence: PSO can quickly find suitable hyperparameter combinations through group cooperation and information sharing, accelerating the optimization process.Strong Adaptability: PSO demonstrates good adaptability when dealing with high-dimensional and complex problems, flexibly responding to various types of hyperparameters.Reduced Human Intervention: Automated hyperparameter optimization lowers the subjectivity of parameter selection, enhancing model performance.Suitable for Dynamic Environments: PSO can update and optimize hyperparameters in real time, adapting to data changes in scenarios that require frequent parameter adjustments.

Bootstrap method

The Bootstrap method is a interval prediction method proposed by American statistics professor Efron, which can effectively overcome the limitation of traditional point displacement prediction that can only obtain deterministic predicted values@@@41. This method is easy to calculate and implement, and is widely used in quantifying uncertainty interval predictions related to given estimates. The basic principle of Bootstrap is to perform equally probable repeated sampling with replacement on the original sample. By estimating the parameters from each resampled dataset, we can infer the approximate form of the empirical distribution. In this context, the term “empirical distribution” refers to the distribution inferred from the repeated samples, which approximates the underlying population distribution based on the original dataset@@@42. Given a set of samples: X1, X2,...,Xn from an unknown distribution F, with observed values x1, x2,...,xn, and \(\theta\) is a random variable dependent on X and F. Now, randomly sample with replacement from X, that is, the probability of a certain sample being selected for each sampling is 1/N, repeat sampling B times, generate B mutually independent Bootstrap samples, which can be represented as X*1, X*2,…, X*B, and construct the empirical distribution \(\overline{F}^{1}\), \(\overline{F}^{2}\),…, \(\overline{F}^{B}\) based on this; for the random variable \(\theta\), calculate the estimated values of B groups of Bootstrap samples \(\overline{\theta }_{1}\), \(\overline{\theta }_{2}\),…, \(\overline{\theta }_{B}\), then the estimate value is:

$$\overline{\theta } = \frac{1}{B}\sum\limits_{{{\text{i}} = 1}}^{B} {\hat{\theta }_{i} }$$
(13)

The estimate value of the Bootstrap sample variance is:

$$\hat{\sigma }_{\theta }^{2} = \frac{1}{B - 1}\sum\limits_{i = 1}^{B} {\left( {\hat{\theta }_{{\text{i}}} - \overline{\theta } } \right)}$$
(14)

PSO–TCN–Bootstrap flood forecasting model.

The PSO–TCN–Bootstrap model involves three primary steps in the flood forecasting process, as illustrated in Fig. 3. The modelling steps are as follows: (1) Define the range for each hyperparameter, which includes six key parameters: the number of neurons, the number of hidden layers, the learning rate, block size, time step, and number of iterations. (2) Randomly initialise the position of each particle. Each particle’s position represents a multidimensional variable encompassing all hyperparameter dimensions. The NSE on the validation set serves as the objective function@@@43. At each iteration, update the particle positions until the maximum iteration count is reached to identify the optimal NSE of the TCN model. (3) Apply the Bootstrap-based uncertainty estimation method, coupling it with the output layer of the PSO-TCN model to form the second-layer output for flood forecasting. This step estimates the uncertainty in the model’s predictions by incorporating the Bootstrap method. By generating multiple resampled predictions, the Bootstrap method creates a distribution of predicted outcomes, which allows us to estimate prediction intervals and quantify the uncertainty in the flood forecasting results. This approach provides a probabilistic forecast rather than a single deterministic value, which helps to reflect the variability and uncertainty inherent in flood prediction.

Fig. 3
figure 3

PSO–TCN–Bootstrap model structure.

Full size image

Model evaluation indicator selection

We evaluate the forecasting performance of TCN and PSO-TCN models using the Nash-Sutcliffe efficiency coefficient (NSE), root mean squared error (RMSE), and relative error (RE) for the runoff process@@@44,45. NSE serves as a holistic reflection of the flood prediction effectiveness, making it suitable as the objective function for parameter calibration, which is supported by numerous references, RMSE represents the error of runoff process simulation, and RE represents the error of peak flow simulation. The mathematical representations are as follows:

$$NSE = 1 - \frac{{\sum\nolimits_{t = 1}^{n} {(Q_{t}^{S} - Q_{t}^{O} )^{2} } }}{{\sum\nolimits_{t = 1}^{n} {(Q_{t}^{S} - \overline{{Q^{O} }} )^{2} } }}$$
(15)
$$RMSE = \sqrt {\sum\nolimits_{t = 1}^{n} {\frac{{(Q_{t}^{O} - Q_{t}^{S} )^{2} }}{n}} }$$
(16)
$$RE = \left| {\frac{{Q_{t - \max }^{O} - Q_{t - \max }^{S} }}{{Q_{t - \max }^{O} }}} \right| \times 100\%$$
(17)

where \(Q_{{\text{ t}}}^{O}\) and \(Q_{t}^{S}\) represent the observed discharge and simulated discharge values, \(Q_{t - \max }^{O}\) and \(Q_{t - \max }^{S}\) represent the observed and forecasted peak floods, respectively. n represents the total number of hydrological sample data, and t represents the t-th time step. The NSE value ranges from (−∞, 1), with a higher value indicating higher prediction accuracy and the range of RMSE and RE is (0, +∞), and a smaller value closer to 0 indicates better prediction performance@@@46.

Case study

Study area

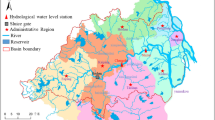
The Tailan River Basin is situated in Wensu County, Aksu region, Xinjiang, with geographic coordinates of 80° 21′ 44″~81° 10′ 14″ E and 40° 41′ 41″~42° 15′ 13″ N (Fig. 4). Originating from Tumur Peak in the southwestern Tianshan Mountains, the Tailan River has two main tributaries upstream: the Datailan River and the Xiaotailan River. These tributaries converge 8 km before the river exits the mountains, forming the main Tailan River. A hydrological station is positioned above the mountain pass, covering a watershed area of 1324 km2. The basin’s average annual temperature is 7.9 °C, with recorded extremes of 37.6 °C and −27.4 °C. The historical maximum annual precipitation reaches 336.7 mm, while the minimum is 18.7 mm, giving a rainfall extreme ratio of approximately 17@@@47. The Tailan River’s multi-year average runoff depth is 569.2 mm. Although annual runoff variability is minimal, its distribution across the year is highly uneven. The primary flood season spans June to August, with flooding events typically arising from a combination of rainfall and meltwater@@@48.

Fig. 4
figure 4

Geographical location of the study area and schematic diagram of rainfall stations distribution.

Full size image

Processing of rainfall-runoff data

Rainfall-runoff data from 1960 to 2014 were collected and compiled, including rainfall data from three rain gauge stations and runoff data from the hydrological station at the outlet section of the Tailan River Basin. A total of 50 flood events were recorded, with a time interval interpolation of 1 h. All the data were extracted from the “Hydrological Yearbook of the Tailan River Basin”. The model training and validation were conducted based on a ratio of 7:3 for flood events@@@1,2,3, with 35 flood events used for training and 15 flood events used for validation. The rainfall-runoff data were normalized using the “maximum–minimum” method@@@38 to accelerate the convergence speed of the machine learning model during computation. The rainfall and flow data corresponding to each flood event were processed into a time-series feature dataset that can be recognized by the deep learning model, as shown in Table 1. \(P_{t}^{(1)}\), \(P_{t}^{(2)}\),…, \(P_{t}^{(m)}\) represent the rainfall amounts at time t in the m-th rainfall station from the first grid.

Table 1 Time-step format of input data for the ML model.
Full size table

Model parameters setting

The hyperparameters of the TCN model include the number of neurons, number of hidden layers, learning rate, block size, time step, and number of iterations. In this study, the NSE was selected as the objective function, with the particle swarm optimisation algorithm applied to determine the optimal hyperparameter values for flood forecasting. Initial optimal ranges were referenced from previous literature@@@36, as follows: 16–256 (with intervals of 16) for the number of neurons, 1–5 (interval of 1) for hidden layers, 0.0001–0.1 (intervals of 0.0001, 0.001, 0.01, 0.1) for the learning rate, 16–160 (interval of 16) for block size, 4–8 (interval of 1) for time steps, and 150–350 (interval of 25) for the number of iterations. Seven lead times were set at 1 h, 2 h, 3 h, 4 h, 5 h, 6 h, and 7 h.

Lead time and model initialization settings

Parameter calibration revealed that the best predictions occur when the sliding window size is set to 6. Figure 5 illustrates the working mechanism of the TCN model with a sliding window input of 6 h and corresponding lead time settings, including 1 h, 2 h, 3 h, 4 h, 5 h, 6 h and 7 h. Q1 is predicted by \(P_{0}^{(m)}\), Q1 and \(P_{1}^{(m)}\) are then included in the new sliding window to predict Q2, and this process continues until the sliding prediction is completed.

Fig. 5
figure 5

Schematic diagram of lead time settings and Sliding window working mechanism.

Full size image

Results and discussion

Overall accuracy evaluation

The results in Table 2 and Fig. 6 clearly highlight the superior performance of the PSO–TCN model over the TCN model in all evaluation metrics for flood forecasting in the Tailan River basin. Specifically, the PSO–TCN model consistently achieves higher NSE values in both the training and validation periods, with the difference becoming more pronounced at shorter lead times (e.g., 1 h, 2 h) and further widening as lead time increases. For instance, at a 1-h lead time, the NSE for the PSO–TCN model is 0.93, compared to 0.87 for the TCN model. Furthermore, the PSO–TCN model demonstrates significantly lower RE and RMSE values, reflecting its superior accuracy and lower error rates. At a 1-h lead time, the PSO-TCN model achieves an RE of 2.11%, markedly lower than the 5.66% observed for the TCN model, while the RMSE for PSO–TCN is 20.34 m3/s compared to 44.14 m3/s for TCN.

Table 2 Performance comparison of TCN and PSO–TCN models under different lead time conditions in the Tairan River Basin.
Full size table
Fig. 6
figure 6

Radar chart of evaluation indicators for flood forecasting results in the Tailan River Basin.

Full size image

The radar charts in Fig. 6 further strengthen this conclusion, offering a visual comparison between the models. Across all lead times, the PSO–TCN model (represented by the blue line) outperforms the TCN model (represented by the red line) in terms of NSE, RE, and RMSE during both the training and validation periods. This performance advantage is particularly evident at shorter lead times, though the PSO–TCN model maintains its superior performance even as lead times increase. These findings underscore the PSO–TCN model’s greater reliability and accuracy for flood forecasting in the Tailan River basin, especially when dealing with extended forecast periods.

Comparison results of typical flood events.

In order to further verify the forecasting performance of the model, a comparison analysis of the forecasting performance of the TCN model and the PSO–TCN model was conducted for a typical flood event with a large peak flow in the Tailan River basin (flood date: 19990714). Figure 7 and Table 3 show the evaluation metrics, including the NSE, RE, and RMSE, for the forecasted runoff process at different lead times. From the comprehensive perspective of Fig. 7 and Table 3, when the lead time is 1 h, the forecasted runoff process of the TCN and PSO–TCN models matches well with the observed runoff process, accurately reflecting the actual flood runoff process, and the accuracy of peak flow forecasting is also at a high level. The NSE is all greater than or equal to 0.85, and the RE is less than 10%. The advantage of the forecasting accuracy of the PSO–TCN model is not significant, but there is still a slight improvement. When the lead time is increased to 7 h, the forecast error of the TCN model significantly increases, especially underestimating the peak flow, with an NSE of 0.31, RE and RMSE reaching as high as 38.01% and 118.93 m3/s, respectively, while the corresponding values for the PSO–TCN model are 0.52, 24.76%, and 85.94 m3/s for these three indicators. Therefore, it is considered that the PSO–TCN model has better peak flow modeling capability, and the optimization algorithm can significantly improve the flood forecasting accuracy of the TCN model. From Fig. 7, it can be seen that the PSO-TCN model can fit the measured flow well in the 1–3 h lead time for land water basins, with the confidence intervals covering all measured flow points and narrow interval widths, indicating that the confidence intervals can effectively reflect the forecast uncertainty. The degree of fit between the forecasted and observed flood processes in the 4–7 h lead time has decreased, with significant fluctuations during the rising process. The confidence intervals gradually widen, indicating increasing forecast uncertainty, but the coverage rate still remains close to 95%.

Fig. 7
figure 7

Forecasting process of typical flood events in the verification period for TCN and PSO–TCN Models.

Full size image
Table 3 Statistical evaluation of forecasting results for typical flood events in the verification period for TCN and PSO–TCN models.
Full size table

Advantages and limitations of the PSO–TCN–Bootstrap model

This study constructed a PSO–TCN–Bootstrap flood forecasting model by coupling the particle swarm optimization algorithm, the TCN temporal convolutional neural network, and the Bootstrap probability model, which can significantly improve the accuracy of flood forecasting under specific conditions. In particular, this method shows improved performance in short-term forecasting scenarios (1–3 h), complex flood processes characterized by non-linear hydrological responses, and when sufficient data are available to fully train the model@@@49,50. The PSO–TCN–Bootstrap model can reduce the relative error of peak flow forecasting and the root mean square error of flood process forecasting, while further enhancing the robustness of machine learning models. Based on comprehensive weighted calculations of simulation accuracy during the training period and verification period, compared with the TCN model, the PSO–TCN–Bootstrap model improves the average NSE by 0.07–0.10 and reduces the RE and RMSE by 2.85–3.67% and 19.79–20.19 m3/s, respectively, when the lead time is 1–3 h. When the lead time is 4–7 h, the PSO-TCN-Bootstrap model improves the average NSE by 0.11–0.21 and reduces the RE and RMSE by 4.01–6.45% and 22.03–23.97 m3/s, respectively. In the model calculation process, the PSO–TCN–Bootstrap model can significantly improve the calculation efficiency during the verification process and promote the convergence speed of model training, which is an important improvement in promoting advanced flood prediction. However, this study still cannot overcome the problem of decreasing accuracy of flood forecasting as the lead time increases. Future research will aim to integrate mechanisms of flood generation and improve model interpretability to further enhance the generalization ability of machine learning models in flood forecasting applications@@@51,52. To enhance the performance of the PSO–TCN–Bootstrap model over longer lead times, future research will explore the integration of numerical weather prediction models. These models will provide forecasted rainfall data as inputs to hydrological models, thereby extending the forecast period and improving the accuracy of long-term flood predictions. Furthermore, the application of data assimilation techniques, such as Kalman filtering, will be investigated to continuously adjust and update model predictions in real-time. This approach aims to mitigate the decrease in accuracy that often occurs as the lead time increases. Together, these strategies are expected to enhance the generalization capability and robustness of the model in practical flood forecasting applications. Traditional deep learning models provide only point estimates, resulting in limited uncertainty (or risk) information for flood decision-making. By adding Bootstrap to the output layer of the TCN, we achieve probabilistic interval predictions for flood forecasting, which offers more uncertainty information for flood management decisions.

Furthermore, the Bootstrap method typically requires a large number of repeated samples, and each sampling necessitates model training or computation, which can lead to significant computational overhead, especially when dealing with large datasets or complex models. Each Bootstrap sample generates a new dataset, and if the sample size is large, it may consume a lot of memory, affecting computational efficiency. In some cases, the convergence speed of Bootstrap estimates can be slow, particularly when the sample size is small or the feature dimension is high, requiring more sampling iterations to obtain reliable results. These are objective limitations of this study that need further refinement in future research.

Conclusion

This paper constructed a flood forecasting model for the Tailan River Basin by coupling particle swarm hyperparameter optimization algorithm, time-convolved Bootstrap probability sampling neural network. The model was verified based on 50 historical flood events, and the brief conclusions are as follows:

  1. (1)

    The overall accuracy of the PSO–TCN-Bootstrap flood forecasting model is better than that of the TCN model in the Tailan River Basin, and the peak error and root mean square error of the flood process are lower than those of the TCN model. The PSO–TCN–Bootstrap flood forecasting model has better applicability in the Tailan River Basin. PSO performs exceptionally well in handling high-dimensional and complex search spaces, effectively avoiding the local optimum issues that traditional gradient descent methods may encounter. Additionally, the parallel computing characteristics of PSO allow it to efficiently manage a large number of hyperparameters while reducing computational costs and time, significantly enhancing the model’s performance and training efficiency.

  2. (2)

    As the lead time increases, the flood simulation accuracy of the TCN and PSO–TCN–Bootstrap models will both decrease, but the TCN model shows a significant downward trend, while the PSO–TCN–Bootstrap model shows a slow downward trend. The PSO–TCN–Bootstrap model has better robustness than the TCN model. This study enhances flood forecasting by incorporating Bootstrap into the output layer of the TCN, enabling probabilistic interval predictions. This approach provides additional uncertainty information for flood prevention decisions, increasing the scientific basis and reliability of those decisions. However, the Bootstrap method typically requires a large number of repeated samples, with model training or computation performed after each sampling, which affects the overall computational efficiency.

  3. (3)

    When the lead time is 1–3 h, compared with the TCN model, the PSO–TCN–Bootstrap forecasting accuracy slightly improves; when the lead time is 4–7 h, the PSO–TCN–Bootstrap forecasting accuracy will significantly improve. However, when the lead time exceeds 5 h, the PSO-TCN-Bootstrap model’s RE will still exceed 20%. In the future, it is expected to integrate the mechanism of flood process occurrence and further improve the generalization ability of machine learning models in flood forecasting applications.

  4. (4)

    Future research can focus on parameter optimization algorithms and explore the application of flood process probability forecasting in scheduling, as well as study the impact of basin lag time and forecast horizon length on prediction accuracy. Additionally, it may be worthwhile to investigate the incorporation of extra constraints into the loss function of deep learning models to ensure that the performance of probability forecasts balances reliability and concentration.