Introduction

The study of entropy optimization is a significant research topic in fluids. This phenomena varies with varying characteristics of fundamental fluids and dispersion of nanoparticles, alloys, carbides or other nanomaterials. Entropy of the fluid is depend on the irreversibility of the fluidic system and it recognize as influential motive in thermal science and mechanical engineering etc. In the past few decades, the researchers concentrated on the entropy performance of various fluids with additional physical effects. In 2022, Berrehal et al.1 discussed a model for hybrid nanofluid with the key emphasize on entropy analysis. They considered warmly accelerating wedge in the presence of surface convection, spherical and non-spherical hybrid nanoparticles. An addition of MHD phenomena in the momentum equation highly alter the entropy and thermal behaviour of the system. Hence, Zeeshan et al.2 discussed the results for \(\:Nt,\:Nb\) and \(\:Le\) in the range of \(\:0.1\) to \(\:1.0\) and found the system solutions using RSM (response surface methodology).

The solar thermal radiations and activation energy significantly contribute in the dynamics of fluidic system. Acting radiations on the system enhance the internal energy of the molecules which increase the overall performance of the physical setup. Thus, keeping in mind the significance of these phenomenon, Acharya et al.3 proposed a model for nanofluid through wedge shaped physical setup. The authors upgraded the existing model using solar radiations and activation energy aspects and then examined significant contributions with special focus on thermodynamic optimization of the system. Further, the irreversibility of the system studied due to thermal transfer and fluid frictional aspects. In 2021, Yu et al.4 reported entropy modelling for transient Maxwell nanofluid flow under bi-diffusional effects. They performed the modelling for elastic wedge under Cattaneo Christov thermal flux effects. They also accommodated the convective wedge surface condition and analyzed its contribution in the temperature performance. Recently, Ashraf et al.5 and Khan et al.6 discussed the models for energy and entropy augmentation in conventional hybrid nanofluids. Along with characteristics of (GO/MoS2) and (H2O)/(CH2OH)2, the authors added the effects of solar radiations, MHD and viscous dissipation. The studies were reported for incompressible nanofluids in the laminar flow ranges and obtained beneficial results for the heat and entropy augmentations.

The presence of pores at the wedge surface disturb the heat, mass and entropy generation. Thus, Goud and Reddy7 addressed the effects of permeability of the surface using thermal radiations and dissipation phenomena. The accuracy of the results provided by comparing them with published data. In 2024, Rafique et al.8 investigated that tendency of entropy generation enhanced for higher Hartmann and \(\:Br\) values while it reduced for \(\:\alpha\:\). Further, the Bejan number values boosted with increasing \(\:\alpha\:\) but drops for \(\:{\varphi\:}_{2},\:Br\) and \(\:M\). Sen et al.9 introduced a model for (Diamond/Co3O4)/EG hybrid nanoliquid for nonlinearly radiated magnetized fluid and conducted the analysis for entropy optimization. From the study, they deduced that the heat transport tendency in simple nanofluid is less then hybrid nanofluid10. Hence, they recommended that use of hybrid type fluid is good to optimize the heat transfer and entropy. In 2024, Waseem et al.11 discussed the importance of Cu and TiO2 nanoparticles on entropy in magnetized and dissipative fluid. They concluded that higher dissipation and Prandtl effects deprecated the temperature while entropy enhanced for larger magnetic effects. The nonlinear radiative effects on entropy and thermal performance of hybrid nanofluid through a wedge type physical setup have been demonstrated by Mabood et al.12.

Recently, Zainal et al.13 made efforts towards the stability treatment of the nanofluid model termed as Falkner Skan Flow model (FSFM). The problem formulated for unsteady case and achieved estimations for shear drag, heat transfer rate due to varying surface convection. Mahmood et al.14 predicted that Brinkman number augments entropy rate in the existence of nanoparticles clustering. It is noticed that the shear drag enhanced from 3.35 to 7.18% for both resistive and assisting flow cases while uniform declines in the thermal efficiency is observed from 7.27 to 10.24% against the higher Eckert number values. In 2021, Saeed et al.15 determined the dynamics of nanofluid flowing towards stagnant point. The results studied via fractional approach and examined that the drifting velocity uphill in the presence of electrical field. Occurrence of homogenous/heterogeneous reactions and hall current in a fluidic system affect the rate of thermal transport and momentum. In this regard, Hamid et al.16 reported a study for (GO-MoS2)/(C2H6O2)H2O through magnetized surface. The results revealed that the surface convection boosts the temperature.

The normally acting magnetic field and resistive heating effects are interesting physical aspects. Abbas et al.17 pointed the influences of these effects under combined convection for ternary nanofluid. Further, they observed that shear drag on the surface can be maximized against stronger mixed convective effects. Recently, Khadija et al.18 analyzed entropy phenomena using the effects of MHD and surface elasticity. The results were estimated for Bejan number which is the ratio of entropy caused by heat transfer to the total entropy of the system. Further, it is reported that the heat transfer rate augmented 10.55% in comparison with regular fluid. Madhukesh et al.19 examined that thermophoretic particles deposition and heating species inside the fluid alter the heat and mass transport characteristics. They found that the Schmidt number favors the mass while thermophoretic number resist it.

Aluminum alloys are have versatile applications because of their excellent thermophysical characteristics, light weight, corrosion resistance and strength. These characteristics make them more effective than other metals. The alloys are good conductors and playing significant role in the heat transfer applications. The thermal properties of common fluids can be improved using aluminum alloys. Many studies have been accessible in the literature for nanofluids using the influence of single type of nanomaterials. Hence, the current study focuses on the Thermal transport efficiency using ternary alloys and their comparison with the nano and hybrid alloys based nanofluids. Further, the model extended for significant physical controls like dissipation energy, nonlinear solar radiations, convective condition, and concentration of ternary alloys. To validate the study, the comparative results will be plotted for ternary, nano and hybrid nanofluids which will reflect the efficiency and validity of the problem.

Model development

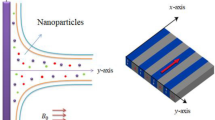
The streamlined flow of (AA7072/AA7075/Ti6AI4V)/(C2H6O2/H2O) 50:50% ternary nanofluid is taken in this study. The flow configuration is consider for a physical setup termed as Riga wedge which is formed by alternating arrangement of magnets. The \(\:x\)-coordinate is designated parallel to the surface while \(\:y\)-coordinate is normal to the wedge surface. Moreover, the surface is subject to convective heat condition and \(\:{T}_{\infty\:},\:{T}_{w}\) are the temperature of the fluid layers at ambient location and adjacent to the surface. The velocities of fluid’s layers are taken as \(\:{u}_{e}={x}^{m}{U}_{\infty\:}\) and \(\:{u}_{w}={x}^{m}{U}_{w}\) (\(\:0.0\le\:m\le\:1\) and \(\:{U}_{w},\:{U}_{\infty\:}\) are constants) at free stream and at the surface, respectively. Further, the angel between the wedge sides is taken \(\:\alpha\:\pi\:\) in which \(\:\alpha\:\) denotes the effects of Hartree pressure. The physics laws which administrates the present situation are described in Eqs. (1–3) along appropriate physical conditions and similarity rules in Eqs. (4–5), respectively.

$$\:{u}_{x}=-{v}_{y}$$
(1)
$$\:{u}_{x}u+{u}_{y}v={u}_{e}{u}_{e}^{{\prime\:}}+\frac{{\mu\:}_{alloysnanof}}{{\rho\:}_{alloysnanof}}{u}_{yy}+\frac{{M}_{o}{J}_{o}\pi\:}{8{\rho\:}_{alloysnanof}}{e}^{(-\frac{\pi\:}{a}y)}$$
(2)
$$\:{T}_{x}u+{T}_{y}v=\frac{{k}_{alloysnanof}}{{\left(\rho\:{c}_{p}\right)}_{alloysnanof}}{T}_{yy}-\frac{1}{{\left(\rho\:{c}_{p}\right)}_{alloysnanof}}{\left({q}_{r}\right)}_{y}+\frac{{\mu\:}_{alloysnanof}}{{\left(\rho\:{c}_{p}\right)}_{alloysnanof}}{\left({u}_{y}\right)}^{2}$$
(3)
$$\:u=0,\:-{k}_{alloysnanof}{T}_{y}-{h}_{f}\left({T}_{f}-T\right)=0,\:v=0\:when\:y=0$$
(4)
$$\:u-{u}_{e}=0,\:T-{T}_{\infty\:}=0\:when\:y\to\:\infty\:$$
(5)
$$\:\chi\:={\left(\frac{2x{u}_{e}\left(x\right){\nu\:}_{f}}{m+1}\right)}^{0.5}F\left(\eta\:\right),\:\eta\:={\left(\frac{{u}_{e}\left(x\right)\left(m+1\right)}{2x{\nu\:}_{f}}\right)}^{0.5}y,\:\beta\:\left(\eta\:\right)=\frac{T-{T}_{\infty\:}}{{T}_{w}-{T}_{\infty\:}},\:$$
(6)

The current ternary nanofluid problem is only valid for laminar boundary layer flow. The alloys nanomaterial uniformly saturated in base fluid. Moreover, it is essential that the fluid in incompressible and viscous. The model is not applicable beyond these limitations. The velocity components \(\:u\) and \(\:v\) calculated from the stream function \(\:\chi\:\) defined in Eq. (6) by using the rule \(\:u={\chi\:}_{y}\) and \(\:v=-{\chi\:}_{x}\) so that it satisfies the continuity equation. The radiative flux in the energy equation is expanded using \(\:{q}_{r}=-\frac{16{\sigma\:}^{*}}{3{k}^{*}}{T}_{\infty\:}^{3}{T}_{y}\). Further, the important quantities for shear drag and Nusselt number are calculated from the following formulas.

$$\:{C}_{f}=\frac{{\mu\:}_{alloysnanof}}{{u}_{e}^{2}{\rho\:}_{f}}{u}_{y}\:when\:y=0$$
(7)
$$\:Nu=-x\left[\frac{{k}_{alloysnanof}+{q}_{y}}{{k}_{f}\left({T}_{w}-{T}_{\infty\:}\right)}\right]{T}_{y}\:when\:y=0$$
(8)

In order to modify the basic model, thermophysical properties of ternary nanofluid20 given in Table 1 (see Refs21,22,23). are used. Further, \(\:{\widehat{\mathfrak{H}}}_{3}={\varphi\:}_{3},\:{\widehat{\mathfrak{H}}}_{1}={\varphi\:}_{1}\) and \(\:{\widehat{\mathfrak{H}}}_{2}={\varphi\:}_{2}\) representing the concentration of alloys in the (C2H6O2/H2O)50:50%. The particular values of AA7072, AA7075, Ti6AI4V and (C2H6O2/H2O)50:50% which used in the present analysis are given in Fig. 1 while Fig. 2 demonstrating the changes in thermophysical properties of ternary nanofluid at different values of alloys concentration.

Table 1 Thermophysical properties of (AA7072/AA7075/Ti6AI4V)/(C2H6O2/H2O) 50:50% ternary nanofluid.
Full size table
Fig. 1
figure 1

The properties of AA7072, AA7075, Ti6AI4V and (C2H6O2/H2O) 50:50%.

Full size image
Fig. 2
figure 2

Changes in the properties of (AA7072/AA7075/Ti6AI4V)/(C2H6O2/H2O) 50:50%.

Full size image

Finally, the subsequent (AA7072/AA7075/Ti6AI4V)/(C2H6O2/H2O) 50:50% ternary model is obtained after using the above information.

$$\frac{{\frac{{\mu _{{alloysnanof}} }}{{\mu _{f} }}}}{{\frac{{\rho _{{alloysnanof}} }}{{\rho _{f} }}}}F^{\prime\prime\prime} + FF^{\prime\prime} + 2m\left( {m - 1} \right)^{{ - 1}} \left( {1 - F^{{'2}} } \right) + \frac{{\sigma _{{alloysnanof}} }}{{\sigma _{f} }}Me^{{ - \alpha \eta }} = 0$$
(9)
$$\:{\beta\:}^{{\prime\:}{\prime\:}}+\frac{\frac{{\left(\rho\:{c}_{p}\right)}_{alloysnanof}}{{\left(\rho\:{c}_{p}\right)}_{f}}}{\frac{{k}_{alloysnanof}}{{k}_{f}}}PrF{\beta\:}^{{\prime\:}}+\frac{\frac{{\mu\:}_{alloysnanof}}{{\mu\:}_{f}}}{\frac{{k}_{alloysnanof}}{{k}_{f}}}PrEc{F}^{{\prime\:}{\prime\:}2}+\frac{4Rd}{3\frac{{k}_{alloysnanof}}{{k}_{f}}}\left[\begin{array}{c}\left(1+{\theta\:}_{w}-1\right){\beta\:}^{3}\\\:+\left(1+\left({\theta\:}_{w}-1\right){\beta\:}^{2}\right)*\\\:\left({\theta\:}_{w}-1\right){\beta\:}^{{\prime\:}2}\end{array}\right]=0$$
(10)

The appropriate model conditions are given in Eq. (11).

$$\:F\left(0\right)=0,\:{F}^{{\prime\:}}\left(0\right)=0,{F}^{{\prime\:}}\left(\infty\:\right)=1,\:{\beta\:}^{{\prime\:}}\left(0\right)=-{B}_{i}\left(1-\beta\:\left(0\right)\right),\:\beta\:\left(\infty\:\right)\to\:0$$
(11)

Further, reduced form of shear drag and Nusselt number formulas are given in Eq. (12), respectively.

$$\:{C}_{f}{R}_{ex}^{0.5}=\frac{{\mu\:}_{alloysnanof}}{{\mu\:}_{f}}{F}^{{\prime\:}{\prime\:}}\left(0\right)\:and\:{N}_{u}{R}_{ex}^{-0.5}=-\frac{{k}_{alloysnanof}}{{k}_{f}}\beta\:{\prime\:}\left(0\right)$$
(12)

Entropy of the fluidic system highly depend on the heat transfer and frictional forces. Hence, entropy formula for the current problem is defined as.

$$\:{\stackrel{\sim}{S}}_{entropy}=\frac{{k}_{alloynanof}}{{T}_{\infty\:}^{2}}\left[{T}_{y}^{2}+\frac{16{\sigma\:}^{*}{T}_{\infty\:}^{3}}{3{k}_{f}{k}^{*}}{T}_{y}^{2}\right]+\frac{{\mu\:}_{alloysnanof}}{{T}_{\infty\:}}{u}_{y}^{2}$$
(13)

By defining, characteristic entropy as \(\:{S}_{{g}_{0}}=\frac{{k}_{f}\varDelta\:{\text{T}}^{2}}{{x}^{2}{T}_{\infty\:}^{2}}\) and \(\:\frac{{T}_{\infty\:}}{\varDelta\:T}={{\Omega\:}}^{-1}\) and using in Eq. (13), we obtained the subsequent expression.

$$\:{N}_{g}=\frac{{\stackrel{\sim}{S}}_{entropy}}{{S}_{{g}_{0}}}={R}_{ex}\left[\frac{m+1}{2}\right]\left[\frac{{k}_{alloysnanof}}{{k}_{f}}\left(1+\frac{4}{3}Rd\right){\beta\:}^{{\prime\:}2}+\frac{{B}_{r}{\mu\:}_{alloysnanof}}{{\mu\:}_{f}}{F}^{{\prime\:}{\prime\:}2}\right]$$
(14)

Further, the parameters appeared in the model are \(\:{R}_{d}=\frac{16}{3}\frac{{\sigma\:}^{*}{T}_{\infty\:}^{3}}{{k}_{f}{k}^{*}}\) (thermal radiation number), \(\:{P}_{r}=\frac{{\mu\:}_{f}{\left({c}_{p}\right)}_{f}}{{k}_{f}}\) (Prandtl number), \(\:{R}_{ex}=\frac{{u}_{e}x}{{\nu\:}_{f}}\) (local Reynolds number), and \(\:{\theta\:}_{w}=\frac{{T}_{w}}{{T}_{\infty\:}}\) (temperature ratio number), \(\:Br=PrEc\) (Brinkman number) and \(\:M={\left(\frac{{\sigma\:}_{f}}{{\mu\:}_{f}}\right)}^{0.5}BL\) denotes the Hartmann number.

Mathematical analysis

The present ternary nanofluid problem is nonlinear24 and contained the physical constraints appeared due to directed solar radiations, dissipation and convective heat condition etc. Under such situation, it is reliable to analyze the problem numerically. Hence, the model solved using RKF-4525, using MATHEMATICA 13.0 version. It is fact that this scheme is easy to use for IVP26 which obtained from the higher order nanofluid model. For initiation of the scheme, it is essential to transform the model using feasible transformative functions in the view of differential order. In this research, the third and second system is achieved for the velocity and temperature equations. Thus, appropriate transformations are made and acquired desired suitable IVP27. After, that the proposed scheme applied and furnished the physical results in the subsequent section. The scheme is easy to adopt and accuracy is kept as \(\:{10}^{-6}\).

The working procedure of the model is given below.

The transformations for the problem are defined as below and rearrange the equations as in Eqs. (18, 20).

$$\:{y}_{1}=F,\:{y}_{2}={F}^{{\prime\:}},\:{y}_{3}={F}^{{\prime\:}{\prime\:}},\:{y}_{3}^{{\prime\:}}=F{\prime\:}{\prime\:}{\prime\:}$$
(15)
$$\:{y}_{4}=\beta\:,\:{y}_{5}={\beta\:}^{{\prime\:}},\:{y}_{5}^{{\prime\:}}=\beta\:{\prime\:}{\prime\:}$$
(16)
$$\frac{{\frac{{\mu _{{alloysnanof}} }}{{\mu _{f} }}}}{{\frac{{\rho _{{alloysnanof}} }}{{\rho _{f} }}}}F^{\prime\prime\prime} = - FF^{\prime\prime} - 2m\left( {m - 1} \right)^{{ - 1}} \left( {1 - F^{{'2}} } \right) - \frac{{\sigma _{{alloysnanof}} }}{{\sigma _{f} }}Me^{{ - \alpha \eta }}$$
(17)
$$y_{3} ' = \frac{{\frac{{\mu _{{alloysnanof}} }}{{\mu _{f} }}}}{{\frac{{\rho _{{alloysnanof}} }}{{\rho _{f} }}}}\left[ { - y_{1} y_{3} - 2m\left( {m - 1} \right)^{{ - 1}} \left( {1 - \left( {y_{2} } \right)^{2} } \right) - \frac{{\sigma _{{alloysnanof}} }}{{\sigma _{f} }}Me^{{ - \alpha \eta }} } \right]$$
(18)
$$\:{\beta\:}^{{\prime\:}{\prime\:}}=-\left[\frac{\frac{{\left(\rho\:{c}_{p}\right)}_{alloysnanof}}{{\left(\rho\:{c}_{p}\right)}_{f}}}{\frac{{k}_{alloysnanof}}{{k}_{f}}}PrF{\beta\:}^{{\prime\:}}+\frac{\frac{{\mu\:}_{alloysnanof}}{{\mu\:}_{f}}}{\frac{{k}_{alloysnanof}}{{k}_{f}}}PrEc{F}^{{\prime\:}{\prime\:}2}+\frac{4Rd}{3\frac{{k}_{alloysnanof}}{{k}_{f}}}\left[\begin{array}{c}\left(1+{\theta\:}_{w}-1\right){\beta\:}^{3}\\\:+\left(1+\left({\theta\:}_{w}-1\right){\beta\:}^{2}\right)*\\\:\left({\theta\:}_{w}-1\right){\beta\:}^{{\prime\:}2}\end{array}\right]\right]$$
(19)
$$\:{y}_{5}^{{\prime\:}}=-\left[\frac{\frac{{\left(\rho\:{c}_{p}\right)}_{alloysnanof}}{{\left(\rho\:{c}_{p}\right)}_{f}}}{\frac{{k}_{alloysnanof}}{{k}_{f}}}Pr{y}_{1}{y}_{5}+\frac{\frac{{\mu\:}_{alloysnanof}}{{\mu\:}_{f}}}{\frac{{k}_{alloysnanof}}{{k}_{f}}}PrEc{\left({y}_{3}\right)}^{2}+\frac{4Rd}{3\frac{{k}_{alloysnanof}}{{k}_{f}}}\left[\begin{array}{c}\left(1+{\theta\:}_{w}-1\right){{y}_{4}}^{3}\\\:+\left(1+\left({\theta\:}_{w}-1\right){{y}_{4}}^{2}\right)*\\\:\left({\theta\:}_{w}-1\right){{y}_{5}}^{2}\end{array}\right]\right]$$
(20)

The initial and boundary conditions are arranged in the following manner in the Matlab software. The subscript “\(\:a\)” indicates the initial while “\(\:b\)” indicates the use of boundary conditions in the code.

$$\:\left.\begin{array}{c}{y}_{a}\left(1\right)\\\:{y}_{a}\left(2\right)\\\:{y}_{a}\left(4\right)\\\:{y}_{b}\left(2\right)-1\\\:{y}_{b}\left(4\right)\end{array}\right\}$$
(21)

After that, calling the functions \(\:{y}_{2}\) and \(\:{y}_{4}\) the results obtained. The validity and convergence of the results is clear from (Figs. 3, 4). The study is compared with Rehman et al.28 in Fig. 3. The studies are aligned with each other under the restriction as mentioned in (Fig. 3). This provide the reliability and compatibility of the analysis.

Fig. 3
figure 3

The validity of the study with previous literature result.

Full size image

Results interpretation

This section designates to analyze the impact of physical constraints on the performance of temperature, entropy optimization, numerical estimations for shear drag and Nusselt number. The results furnished and discussed comprehensively.

Figure 4a–f demonstrating the comparative temperature performance for varying ranges of Eckert number, magnetic, thermal radiations, temperature ratio and Biot number, respectively. It is inspected that presence of high energy dissipation elevates the temperature of nanofluids. However, optimum changes in the temperature are obvious for ternary nanofluid followed by hybrid and mono nanofluids. Physically, the energy dissipates quickly due to increasing ranges of \(\:Ec\) from \(\:0.1\) to \(\:0.4\). As, the dissipation effects increases, it produces maximum heat in the fluid which transfer to neighboring particles. As a consequence whole temperature of the fluidic system enhanced. The temperature for all type of nanofluids controlled by strengthening the magnetic effects. Physically, increase in magnetic field affects the Brownian motion and convection process inside the fluid. Hence, the nanoparticles Brownian movement become slow down and the convection process reduces against the strong magnetic field. Due to this, the heat transfer declines over the region. The optimum depreciation is examined near the surface due to dominant magnetic strength. Further, the temperature in nanofluid reduces rapidly than that of ternary and hybrid nanofluids. Physically, mono nanofluid has weak thermal conductivity due to dispersion of single type of nanoparticle while hybrid and ternary types have stronger capacity to store heat. This happens due to addition of two and three types of nanoparticles in the base (C2H6O2-H2O) 505:50% hybrid base liquid.

Influence of radiation number, \(\:{\theta\:}_{w},\:\alpha\:\) and \(\:{B}_{i}\) are demonstrated in Fig. 4c–f, respectively. All these physical constraints have crucial contribution in the temperature performance of nanofluids. However, significant contribution of \(\:{\theta\:}_{w}\) and \(\:{B}_{i}\) is observed in the working domain. Physically, firstly conduction and then convection take place in the surrounding of the surface due to convective heat condition. The molecules placed at the surface gain energy due to which their density decreases and these escape to the top and particles with high density settled down at the bottom. This process continued as a result the temperature augmented. Further, the most dominant variations are examined for ternary nanofluid in which cumulative thermal conductivity of ternary alloys have important contribution. Moreover, the thermal boundary layer region is obvious almost beyond \(\:\eta\:=1.0\) in all the cases.

Fig. 4
figure 4

The temperature performance for varying model parameters.

Full size image

Entropy is one of the significant concept in the study of nanofluids and greatly changed due to dispersion of nanoparticles at different concentration in the basic solvent. Physically, the entropy tells that how much the energy is unavailable to do work in the fluidic system and produces due to irreversibility of the system. Hence, Fig. 5a–f organized to analyze the disorder of the fluidic system using different ranges of the parameters.

It is investigated that entropy of the system for \(\:{B}_{r}\) and \(\:M\) augmented and illustrated in Fig. 5a,b, respectively. In both the cases, optimum energy disorder is examined for conventional fluid followed by hybrid, simple and ternary nanofluids. Smaller changes in the entropy are noticed for ternary nanofluid. Physically, strong thermal conductivity of ternary nanofluid makes them more efficient which controls the system disorder. Maximum energy in the system can be utilized to do work while this disorder increases for other fluids. Hence, ternary nanofluid under \(\:{B}_{r}=\text{0.1,0.2,0.3,0.4}\) and \(\:M=\text{0.1,0.2,0.3,0.4}\) has less disorder and the fluid is more effective. Further, it approaches to asymptotic region as the range of \(\:\eta\:\) increases.

In Fig. 5c,d, it is analyzed that entropy reduced with increase in \(\:{\Omega\:}\) and radiative effects. However, rapid decrease in entropy is examined for conventional fluid for \(\:{\Omega\:}=\text{0.1,0.2,0.3,0.4}\) and \(\:{R}_{d}=\text{0.1,0.2,0.3,0.4}\). As, more energy is available in conventional fluid which is unable to take part in the performance of fluidic system. Hence, the rapid decrement is obvious while slow depreciation is noticed for other three types of nanofluids. Insertion of nonlinear solar radiations and convective thermal condition also favor the entropy. The ternary nanofluid possesses slow changes in entropy due to their higher efficiency. These influential effects are demonstrated in (Fig. 5e,f).

Fig. 5
figure 5

The entropy performance for varying model parameters.

Full size image

The heatlines and streamlines are greatly influenced by the influential model parameters. Therefore, to investigate these patterns, Figs. 6a–f and 7a–d are organized in the presence of physical parameters. The heatlines are plotted for \(\:{B}_{i}=03,\:0.8,\:1.3,\:1.8,\:2.2,\:3.0\) in Fig. 7a–d while all other parameters are fixed. It is obvious that the heatlines intensity increases near the surface under higher convection effects. Physically, when convection phenomena become rapid the fluid layers near to it gain maximum energy as a consequence the heatlines intensity augments in this region. Away from the surface, the intensity reduces as it can be seen from the plotted results. The streamlines pattern for \(\:M=0.0,\:\text{0.3,0.8,1.1}\) are furnished in Fig. 7a–d. It is observed that when the magnets effects increases the streamlines pattern become dense.

Fig. 6
figure 6

The heatlines intensity under different parametric values.

Full size image
Fig. 7
figure 7

The streamlines intensity due to different values of the parameters.

Full size image

Different physical constraints like magnetic effects, thermal radiations, temperature ratio number, Eckert and Biot numbers highly influenced the shear drag and heat transfer rate in nanofluids. Hence, Tables 2 and 3 presenting the estimations for these quantities under increasing values. The estimations performed for ternary, hybrid, nano and simple fluids as mentioned in the tabulated results.

It is examined that increasing the magnetic strength, the shear drag enhanced in all the cases. It augmented from \(\:0.839261\) to \(\:1.184730\) for ternary, \(\:0.912421\) to \(\:1.305360\) for hybrid, \(\:1.036800\) to \(\:1.501480\) for nano and \(\:1.006430\) to \(\:1.478690\) for conventional fluids. It indicates that the shear drag at the surface can be maximized by employing high strength magnetic effects on the fluidic system. Hence, it is a good tool for enlargement of skin friction coefficient. These estimations are given in (Table 2). Impacts of model quantities on the heat transfer performance of three fluidic systems are estimated in (Table 3). In this case, reverse role of magnetic effects is noted that the heat transfer rate reduced when the strength of magnetic increases. However, dominant variations are observed for ternary nanofluid case. Similarly, implementing convective heat conditions favors the rate of heat transfer in the current models. Hence, variations in Biot number are good to enhance the performance.

Table 2 Estimations for shear drag for different parametric values.
Full size table
Table 3 Estimations for heat transfer rate for different parametric values.
Full size table

Conclusions

The model analysis for hydrocarbon based fluid saturated by ternary alloys is presented in this research. The problem formulated for Riga type geometry under influential effects of nonlinear solar radiations, dissipation and surface convection. The resultant nanofluid model investigated numerically and examined that:

  • Increasing the viscous dissipation from \(\:10\%\) to \(\:40\%\) and temperature ratio number \(\:{\theta\:}_{w}\) from \(\:10\%\) to \(\:70\%\) enhances the ternary nanofluid temperature thermal boundary layer reduces for stronger Eckert number.

  • The thermal radiations significantly enhances the temperature of ternary nanofluid while for hybrid and nano this increase is slow due to weak thermal conductivity.

  • The magnetic number strength in the range of \(\:10\%\) to \(\:40\%\) reduces the thermal transport because it declines the Brownian movement of nanoparticles and convection process.

  • The entropy of conventional fluid is observed very high than rest of the types for \(\:Br=M=10\%,20\%,30\%,40\%\), and it deprecates for \(\:{\Omega\:}=Rd=10\%,20\%,30\%,40\%\). However, the entropy vanishes towards the free stream position.

  • The shear drag improved from \(\:0.839261\) to \(\:1.184730\:\)(for ternary), \(\:0.912421\) to \(\:1.305360\) (hybrid), \(\:1.036800\:\)to \(\:1.501480\) (nano) and \(\:1.006430\) to \(\:1.478690\) when \(\:M\) varies from \(\:20\%\) to \(\:70\%\).