Exploring nonlinear chaotic systems with applications in stochastic processes

Abstract

This manuscript explores the stability theory of several stochastic/random models. It delves into analyzing the stability of equilibrium states in systems influenced by standard Brownian motion and exhibit random variable coefficients. By constructing appropriate Lyapunov functions, various types of stability are identified, each associated with distinct stability conditions. The manuscript establishes the necessary criteria for asymptotic mean-square stability, stability in probability, and stochastic global exponential stability for the equilibrium points within these models. Building upon this comprehensive stability investigation, the manuscript delves into two distinct fields. Firstly, it examines the dynamics of HIV/AIDS disease persistence, particularly emphasizing the stochastic global exponential stability of the endemic equilibrium point denoted as $E^*$, where the underlying basic reproductive number is greater than one ($R_0 > 1$). Secondly, the paper shifts its focus to finance, deriving sufficient conditions for both the stochastic market model and the random Ornstein–Uhlenbeck model. To enhance the validity of the theoretical findings, a series of numerical examples showcasing stability regions, alongside computer simulations that provide practical insights into the discussed concepts are provided.

Introduction

Random and stochastic systems are becoming widely used as realistic models of physical phenomena than deterministic systems. Furthermore, the solution of the deterministic system is itself a mean of the stochastic solution of the model. Nowadays, stochastic and random differential equations are drawing a lot of attention because of their evolution in systems of our daily life. Therefore, involving randomness in the formulation of the differential equations provides an attractive study of the phenomena of interest¹. Stochastic differential equations (SDEs) now describe applications in many disciplines including engineering, finance, economics, physics, population dynamics, biology, and medicine^{2,3,4,5,6,7,8,9}.

Chaotic is commonly used to describe a state of disorder, unpredictability, or lack of control. In various contexts, it can refer to a system, situation, or environment characterized by randomness and complexity. Chaos theory, a branch of mathematics and physics, explores the behavior of dynamic systems that are highly sensitive to initial conditions, leading to seemingly random and unpredictable outcomes. In everyday language, chaos is often employed to depict a disorganized or tumultuous situation, where events unfold in a manner that is difficult to anticipate or manage. The concept of chaos extends beyond its mathematical origins and is frequently invoked to describe the complex and intricate nature of systems ranging from weather patterns and traffic flow to social dynamics and personal experiences. Embracing chaos can sometimes be a catalyst for creativity, innovation, and adaptation, as it challenges traditional order and opens up new possibilities^10,11.

The main contributions of this paper lie in its innovative approach to stability analysis of differential models involving stochastic processes and other models involving uncertainty through random coefficients and their interdisciplinary applications. Unlike traditional methods, this study leverages random variable coefficients, which are not commonly used in existing literature, see^12,13,14. This innovative approach provides deeper insights into the models and their results, as the random variables can follow various distributions, offering a more comprehensive understanding of the system’s behavior. To the best of our knowledge, no prior works have applied this methodology, making our findings both unique and groundbreaking. This novel perspective enhances the robustness and applicability of the stability criteria established in this paper, setting it apart from previous research^7,8,9.

Unlike previous works, this study constructs novel Lyapunov functions to identify various types of stability, including asymptotic mean-square stability, stability in probability, and stochastic global exponential stability in the sense of the mean-square. The paper uniquely applies these theoretical findings to both epidemiology and finance, providing new insights into the stochastic global exponential stability of the endemic equilibrium point in HIV/AIDS dynamics and deriving sufficient conditions for stability in financial models such as the stochastic market model and the random Ornstein–Uhlenbeck model. Additionally, numerical examples and computer simulations validate the theoretical results and offer practical insights, making the findings more accessible and applicable to real-world scenarios. This dual focus and practical validation distinguish this work from existing literature.

HIV/AIDS epidemic model and some financial market models can be represented by the nonlinear stochastic differential equation (SDE) in the form:

$$\begin{aligned} \left\{ \begin{array}{cc} \begin{aligned} & dx(t) = \mu (t,x(t)) dt + \sigma (t,x(t))dW(t) \quad t_0 \le t \le T, \, x \in \mathbb {R} \\ & x(t_{0}) = x_{0} \end{aligned} \end{array}\right. \end{aligned}$$

(1)

Firstly, our study of stability focuses on this general equation. A white noise, W(t), the time derivative of the Wiener process, disturbs the right side. By introducing new principles that are different from those of classical calculus, a new type of calculus tackles the fact that even Brownian motion is not differentiable anywhere^1,15,16. Authors in^16,17 have examined the existence and uniqueness theorems for the solution of (1). Now we address some necessary conditions on this system:

• 1. A stochastic process $\{x(t),t \in T\}$ defined on the probability space $(\Omega ,\mathcal {F},\mathbb {P})$ is called a second-order stochastic process endowed with the norm if $\left\| x \right\| ^{2}_{2} = \mathbb {E}[x^{2}(t)] < \infty$, i.e., $\mathbb {E}\left[ \int _{0}^{T} \left| x^{2}\right| dt\right] < +\infty ,$ and square-integrable process if $\int _{0}^{\infty } \mathbb {E}\left[ x^{2}(t)\right] dt < +\infty$, where $\mathbb {E} \, [ \, \cdot \, ]$ denotes the expectation value operator.

• 2. Assume that there is a unique global solution $x(t,t_{0},x_{0})$ for each $x_{0}$ and for positive constants $M_{1}, M_{2}$ such that $t \in [t_{0},\infty )$ and $x_{1}, x_{2}$ are in $\mathbb {R}_{+} \times \mathbb {R}$, then

  $$\begin{aligned} \begin{aligned}&\left| \mu (t,x_{1}) - \mu (t,x_{2}) \right| \le M_{1}\left| x_{1} - x_{2} \right| , \\&\left| \sigma (t,X_{1}) - \sigma (t,x_{2}) \right| \le M_{2} \left| x_{1} - x_{2} \right| . \end{aligned} \end{aligned}$$

  (2)

• 3. Assume that the system admits the trivial solution $x(t) = 0$, i.e., $\mu (t,0) = \sigma (t,0) = 0$.

• 4. The process’s initial state, $x_{0}$, is described in (1) as a second-order $\mathbb {R}$-valued random variable such that $\mathbb {E}\vert x_{0}\vert ^2 < \infty$.

• 5. The following processes are both Borel measurable: $\mu :[t_{0},\infty ) \times \mathbb {R} \rightarrow \mathbb {R}, \, \sigma :[t_{0},\infty ) \times \mathbb {R} \rightarrow \mathbb {R}$. It is expected that the coefficients $\mu$ and $\sigma$ will satisfy the Lipschitz condition 2, and be continuous with regard to t¹⁸.

• 6. Assume that $\mathcal {K}$ be the family of all continuous non-decreasing functions $\upsilon : \mathbb {R}_{+} \rightarrow \mathbb {R}_{+}$ such that $\upsilon (0) = 0$ and $\upsilon (x) > 0$ for $x > 0$. Let us define the set $Q_{h}$ as follows,

  $$Q_{h} = \left\{ h>0, x\in \mathbb {R}, t \ge t_{0}: \Vert x(t)\Vert _2<h\right\} .$$

Numerous issues about the stability of equilibrium states in nonlinear stochastic systems can be simplified to the study of the zero solution of the associated linear system, as mentioned in¹⁹. According to (1), the linear stochastic system is:

$$\begin{aligned} dx(t) = F(t) x(t) dt + G(t) x(t) dW(t). \end{aligned}$$

(3)

Theorem 1.1

In a sufficiently small neighborhood of $x = 0$ such that

$$\begin{aligned} \left| \mu (t,x) - F \cdot x \right| + \left| \sigma (t,x) - G \cdot x \right| < \delta \left| x \right| , \end{aligned}$$

(4)

and if the zero solution of (3) is asymptotically mean-square stable, then the solution of (1) is stochastically stable.

There is still considerable scope for the application of our study of stability

• 1. The mathematical HIV/AIDS model

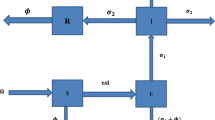
  $$\begin{aligned} \begin{aligned}&\dot{S}(t) = \Lambda - \beta S(t)I(t) - \Lambda S(t),\\&\dot{I}(t) = \beta S(t)I(t) - \Lambda I(t) - \delta I(t),\\&\dot{A}(t) = \delta I(t) - \Lambda A(t) - d A(t),\\&S(t_{0}) = S_{0}, \, \, \, I(t_{0}) = I_{0}, \, \, \, A(t_{0}) = A_{0}. \, \, \, \\ \end{aligned} \end{aligned}$$

  (5)

  The three compartments S, I, and A are the fractions of the susceptible population, infected and AIDS individuals, respectively. All the parameters involved in the model are non-negative and are described in Table 1.

  Table 1 The physical meaning for model parameters.

  $R_{0} = \dfrac{\beta }{\delta + \Lambda },$ is the average new infections produced by one infected individual and it is called the basic reproduction number. $E^0 = (1,0,0)$ is the disease-free equilibrium. For the global stability of this equilibrium for $R_0 \le 1$, see Theorem 10 in⁶. Many recent works on HIV/AIDS mathematical models are mentioned in¹². We focus on the point at which the disease will persist $E^*$, the endemic equilibrium

  $$E^{*} = (S^*, I^*, A^*) = \left( \dfrac{\delta + \Lambda }{\beta },\dfrac{(\beta - \delta - \Lambda )\Lambda }{\beta (\delta + \Lambda )},\dfrac{\delta \Lambda (\beta - \delta - \Lambda )}{\beta (d+\Lambda )(\delta + \Lambda )}\right) .$$

• 2. Stock prices can be described by the Black–Scholes pricing model, which was developed by²⁰. The Black–Scholes model was given an analytical solution by the authors in²¹, and this model was numerically handled by the authors in^22,23. The stability of the Ornstein–Uhlenbeck model with random variable inputs is also covered in the study.

Our main results begin with the study of the stability of the zero solution of the stochastic and random system rigorously. This is followed by the study of the mechanisms of the stochastic HIV/AIDS persistence, the stochastic Black–Scholes market model, and the random Ornstein–Uhlenbeck model. The second section of this paper introduces the rigorous study of the stability of the stochastic and random nonlinear general system. The main case studies are presented in the third section. Some illustrating numerical examples with regions of stability and numerical simulations are shown in Section 4. To close the paper, the conclusion and further directions are presented in Section 5.

Stability analysis of random and stochastic systems

We will examine different forms of stability of the system’s trivial equilibrium (1) in this section. For both $\mu , \, \sigma$ being Borel measurable functions and stochastic processes, the following stability measures are examined: asymptotic mean-square, exponential mean-square, global exponential mean-square, and stochastic stability. Global stability of an equilibrium point may be described as the inevitable fate of the processes regardless of its setting situation and size of perturbation (random inputs and/or stochastic terms). Regardless of the initial states of the system, global exponential stability makes any trajectory tends to the attractor and the resulting oscillations will decay in an exponential rate. Our theoretical study of stability can be extended to cover many applications in biology, ecology, finance, etc.

We have the following results.

Theorem 2.1

The zero solution of (1) is stochastically stable, i.e., stable in probability if the chosen Lyapunov function satisfies

• 1. $\mathbb {E}\mathcal {V}(t,x) \ge c_{1} \mathbb {E}\left| x(t)\right| ^{2}$.

• 2. $\mathbb {E}\mathcal {V}(t_{0},x_{0}) \le c_{2} \vert x_{0}\vert ^{2}$.

• 3. $\mathbb {E}\left[ \mathcal {V}(t,x) - \mathcal {V}(t_{0},x_{0})\right] \le 0$.

Theorem 2.2

The zero solution of (1) is asymptotically mean-square stable if the chosen Lyapunov function satisfies

• 1. $\mathbb {E}\mathcal {V}(t,x) \ge c_{1} \mathbb {E}\left| x(t)\right| ^{2}$.

• 2. $\mathbb {E}\mathcal {V}(t_{0},x_{0}) \le c_{2}\vert x_{0} \vert ^{2}$.

• 3. $\mathbb {E}\left[ \mathcal {V}(t,x) - \mathcal {V}(t_{0},x_{0})\right] \le - c_{3} \int _{t_{0}}^{t} \mathbb {E}\left| x(s)\right| ^{2} ds$.

Theorem 2.3

(1) has a zero solution that is exponentially mean-square stable globally if the chosen Lyapunov function satisfies

• 1. $\mathbb {E}\mathcal {V}(t,x) \ge c_{1} e^{\lambda t}\mathbb {E}\left| x(t)\right| ^{2}$.

• 2. $\mathbb {E}\mathcal {V}(t_{0},x_{0}) \le c_{2} \vert x_{0} \vert ^{2}$.

• 3. $\mathbb {E}\textrm{L}\mathcal {V}(t,x) \le 0$.

Proofs of Theorems 2.1 to 2.3 are presented in Appendix A. These theorems establish the stability of the system under the influence of a stochastic process (Wiener process), taking into account all imposed conditions and assumptions. Furthermore, under certain conditions satisfied by the Lyapunov function, we achieve global stability in the mean-square sense.

The uncertainty can be considered via the outcome $\omega$ of an experiment. Consider the stochastic differential equation (SDE) with random coefficients:

$$\begin{aligned} \left\{ \begin{aligned} dx(t,\omega )&= a(\omega )f(t,\omega )dt + b(\omega )g(t,\omega )dW(t), \\ x(t_{0})&= x_{0}. \end{aligned} \right. \end{aligned}$$

(6)

Here, $a(\omega )$ and $b(\omega )$ are random variables that obey certain conditions, W(t) is a one-dimensional Brownian motion, and $x(t):= x(t,\omega )$, $f(t,\omega )$, and $g(t,\omega )$ are stochastic processes.

Theorem 2.4

(6) has a zero solution that is asymptotically mean square stable if

• 1. $a(\omega ),b(\omega )$ are random variables of 4th order.

• 2. $f(t,\omega ),g(t,\omega )$ are 4th order stochastic processes.

The proof of Theorem 2.4, presented in Appendix A, establishes the stability of the system under the influence of random coefficients and stochastic processes. This is achieved using an appropriate Lyapunov function that satisfies specific conditions. The stability of the system is obtained through certain conditions that must be met by the random coefficients and stochastic processes. This provides valuable insights into the distributions that the random variables can follow.

Applications

Persistence of the stochastic HIV/AIDS model

We perturb the deterministic system (5) by the Brownian motion which is proportional to the deviation of the current state of the system from the endemic equilibrium $E^*$. Therefore, the stochastic HIV/AIDS model will be in the form

$$\begin{aligned} \begin{aligned}&dS(t) = \left( \Lambda - \beta S(t)I(t) - \Lambda S(t) \right) dt + \sigma _1 (S(t) - S^*) dW_{1}(t),\\&dI(t) = \left( \beta S(t)I(t) - \Lambda I(t) - \delta I(t)\right) dt + \sigma _2 (I(t) - I^*) dW_{2}(t),\\&dA(t) = \left( \delta I(t) - \Lambda A(t) - d A(t)\right) dt + \sigma _3 (A(t) - A^*) dW_{3}(t).\\ \end{aligned} \end{aligned}$$

(7)

The environmental noise is included in the model by considering the standard Brownian motion $W_{i}(t)$ for $i = 1,2,3$ and $\sigma _1, \sigma _2$ and $\sigma _3$ are the corresponding intensities. Based on Theorems 2.1, 2.2 and 2.3, we shall prove the stochastic stability and stochastic global exponential stability of the nonlinear model (7) through the study of mean-square stability and global exponential mean-square stability of its corresponding linear system. Using the transformation

$$\begin{aligned} \left\{ \begin{array}{cc} \begin{aligned} & x_{1}(t) = S(t) - S^*, \\ & x_{2}(t) = I(t) - I^*, \\ & x_{3}(t) = A(t) - A^*,\\ \end{aligned} \end{array}\right. \end{aligned}$$

we center the system (7) on the equilibrium $E^*$ and linearize, we get

$$\begin{aligned} \begin{aligned}&dx_{1}(t) = \left( -(\Lambda + \beta I^*)x_{1}(t) - \beta S^*x_{2}(t) \right) dt + \sigma _1 x_{1}(t) dW_{1}(t),\\&dx_{2}(t) = \left( \beta I^*x_{1}(t) + (\beta S^*- \Lambda - \delta ) x_{2}(t) \right) dt + \sigma _2 x_{2}(t) dW_{2}(t),\\&dx_{3}(t) = \left( \delta x_{2}(t) - (\Lambda + d) x_{3}(t) \right) dt + \sigma _3 x_{3}(t) dW_{3}(t).\\ \end{aligned} \end{aligned}$$

(8)

Proposition 3.1

Given $R_{0} > 1$, if the following conditions

$$\begin{aligned} \begin{aligned}&\beta (S^*- I^*) \le 2 \Lambda - \sigma _{1}^{2} \\&\beta (3 S^*+ I^*) \le 2 \Lambda + \delta - \sigma _{2}^{2}, \\&\sigma _{3}^{2} \le 2 (\Lambda + d) - \delta . \end{aligned} \end{aligned}$$

(9)

are satisfied, then $E^*$ of (7) is stochastically stable.

The next proposition investigates the conditions of stochastic global exponential stability for the persistence of the HIV/AIDS disease inspiring by the results obtained by Theorem 2.3 on the general system (1).

Proposition 3.2

Given $R_{0} > 1$, if the following conditions

$$\begin{aligned} \begin{aligned}&\sigma _{1}^{2} + \dfrac{1}{R_{0}} + \varepsilon \le 2 \Lambda + \beta (I^*- S^*), \\&\sigma _{2}^{2} + \dfrac{1}{R_{0}} + \varepsilon + \beta (3S^*+ I^*) \le 2\Lambda + \delta , \\&\sigma _{3}^{2} + \dfrac{1}{R_{0}} + \varepsilon + \delta \le 2 (\Lambda + d), \end{aligned} \end{aligned}$$

(10)

are satisfied, then the endemic equilibrium of (7) is stochastically globally exponentially stable.

The proofs of Propositions 3.1 and 3.2 are given in Appendix B. These two propositions demonstrate that the dynamics of the HIV/AIDS epidemic model are entirely governed by the basic reproduction number.

The Black–Scholes market (B-SM) stochastic model

The risk-neutral probability metric governs the process of stock pricing since, the following linear SDE for $\mathbb {P}$

$$\begin{aligned} \left\{ \begin{array}{cc} \begin{aligned} & dx(t) = r x(t)dt + \sigma x(t) dW(t), \\ & x(t_{0}) = x_{0} > 0. \end{aligned} \end{array}\right. \end{aligned}$$

(11)

The solution stochastic process x(t), the initial state $x_{0}$, and the arbitrary constant r are all described in (11), the term $\sigma x(t) dW(t)$ provides a suitable explanation of the uncertainty of the stock prices process. As such, the stochastic process’s probabilistic behavior is limited to a certain pattern, such as the Gaussian distribution²⁴. The amount of the stock price’s random swings is controlled by the volatility $\sigma > 0$. In order to verify the stability of this model, we will now introduce some appropriate stochastic Lyapunov functions. Consider the model:

$$\begin{aligned} \left\{ \begin{array}{cc} \begin{aligned} dx(t) & = r x(t)dt + \sigma \sin (x(t)) dW(t), \\ x(t_{0}) & = x_{0} > 0. \end{aligned} \end{array}\right. \end{aligned}$$

(12)

Proposition 3.3

Equation (12) is

• 1. Stable in probability if $2r - \lambda \sigma < 0$.

• 2. Mean square exponentially stable if $\sigma ^{2} + 2r - \lambda \sigma < 0$.

• 3. Mean square stable if $\sigma ^{2} + 2 r < 0$.

The random Ornstein–Uhlenbeck model

The Ornstein–Uhlenbeck process driven by random variable inputs

$$\begin{aligned} \dot{S}(t,\omega ) = - A(\omega ) S(t,\omega ) + \sigma S(t,\omega ) C(\omega ), \end{aligned}$$

(13)

is a random model of volatility in finance of the process of asset prices. The process $\lbrace S(t), t \ge 0\rbrace$ is the price of a stock with a nonnegative random variable drift $A(\omega )$ , the volatility $\sigma > 0$ and a random variable $C(\omega )$.

Proposition 3.4

Equation (13) is

• 1. Mean square exponentially stable if $\Vert A(\omega ) \Vert _{4} + 2 \sigma \Vert C(\omega ) \Vert _{2} < \lambda \sigma - 1$, $\lambda > 0$.

• 2. Mean square stable if $\sigma \Vert C(\omega ) \Vert _{2} < \Vert A(\omega ) \Vert _{2}$.

• 3. Stochastically stable if only $A(\omega )$ is a nonnegative random variable.

The proofs for the Propositions 3.3 and 3.4 are detailed in Appendix B. These proofs explore the stability of the systems under specific conditions related to the parameters and random coefficients. By analyzing these conditions, we can determine the stability characteristics of the Black–Scholes model and the Ornstein–Uhlenbeck process.

Verification

In this section, we introduce some illustrative examples which include one and two-dimensional stochastic and random systems. Necessary and sufficient conditions are investigated. Areas of stability and many numerical simulations of the solutions are shown. The solution of (1), x(t) can be considered in the integral form

$$\begin{aligned} x(t) = x_{0} + \int _{t_{0}}^{t} \mu (s,x(s)) ds + \int _{t_{0}}^{t} \sigma (s,x(s))dW(s), \end{aligned}$$

(14)

where the last integral is understood as an Itô stochastic integral.

We employ the Euler–Maruyama numerical approach for the numerical simulation²⁵. This method does a better job with tiny values of the step size $\Delta t$. According to (14), the integrals can be approximated as follows

$$\begin{aligned} \int _{t_{n}}^{t_{n+1}} \mu (s,x) ds \approx \mu (t_{n},x_{n})\Delta t \, \, \, \, \, \, \, \, \, \, \, \text {and} \, \, \, \, \, \int _{t_{n}}^{t_{n+1}} \sigma (s,x) dW(s) \approx \sigma (t_{n},x_{n})\Delta W_{n}. \end{aligned}$$

Then Euler–Maruyama scheme takes the form

$$\begin{aligned} x_{n+1} = x_{n} + \mu (t_{n},x_{n}) \Delta t + \sigma (t_{n},x_{n})\Delta W_{n}. \end{aligned}$$

(15)

This scheme is strongly convergent with order 0.5. It is computationally costly (error and time) to take $\Delta t$ very small. Therefore, choosing small enough values of $\Delta t$ is recommended.

Example 1

Consider the nonlinear stochastic scalar differential equation

$$\begin{aligned} dx(t) = -a x(t)dt + b \sin (x(t)) dW(t). \end{aligned}$$

(16)

According to Theorem. 2.2, the Lyapunov function $\mathcal {V}(t,x) = x^{2}(t)$ gives an asymptotic mean-square stability condition for the zero solution of (16) in the form

$$\begin{aligned} b^{2} - 2 a < 0. \end{aligned}$$

(17)

The region of mean-square stability is shown by condition (17) in Fig. 1a in (a, b)-space of parameters. Using the fundamental Euler–Maruyama scheme (15), numerical simulations of the solution of (16) with $x(t) = 0$ are shown in Fig. 4. At the point (1, 1) in the stability region, Fig. 4a shows 50 blue stable trajectories that converge to zero. At the point (1, 2), Fig. 4b shows 50 red unbounded trajectories.

Fig. 1

Mean square stability regions.

Example 2

Consider the analog nonlinear stochastic scalar differential equation to Example 1 with random coefficients $A(\omega )$, $C(\omega )$, and W(t) is the one-dimensional Brownian process:

$$\begin{aligned} dx(t,\omega ) = -A(\omega ) x(t,\omega )dt +C(\omega ) \sin (x(t,\omega )) dW(t). \end{aligned}$$

(18)

According to Theorems. 2.2 and 2.4, the asymptotic mean-square stability condition for (18) is:

$$\begin{aligned} \Vert C(\omega ) \Vert _{4}^{2} < 2 \Vert A(\omega ) \Vert _{2}. \end{aligned}$$

(19)

If $x(t,\omega )$ is independent of $A(\omega )$ and $C(\omega )$, then $\Vert C(\omega )\Vert ^{2}_{2} < 2 \Vert A(\omega )\Vert$ is the mean-square stability condition. Numerical simulations of the solution of (18) with $x(t) = 0$ show the stability of 100 trajectories in Fig. 6a–d. In these figures, $A(\omega )$, $C(\omega )$ can follow any random probability distribution under condition (19). We conclude that $A(\omega )$ cannot follow an unbounded distribution (e.g., Gaussian) for stability. Figure 6e shows a numerical simulation of 100 unstable (red) trajectories for specific parameters of the distributions of $A(\omega )$ and $C(\omega )$. The presence of these coefficients as random variables allows for a wider type of probability distributions such as Binomial, Beta, Gaussian, etc., and this provides greater flexibility and makes very attractive differential equations with random coefficient variables in dealing with real applications.

Example 3

Consider the two-dimensional system of stochastic differential equation

$$\begin{aligned} \left\{ \begin{array}{cc} \begin{aligned} & dx_{1}(t) = \left( - a x_{1}(t) + x_{2}(t)\right) dt + x_{1}(t)dW_{1}(t), \\ & dx_{2}(t) = - b x_{2}(t)dt + x_{2}(t)dW_{2}(t). \end{aligned} \end{array}\right. \end{aligned}$$

(20)

$W(t) = \left( W_{1}(t), W_{2}(t) \right) ^{T}$ is a standard Wiener process, $x(t) = \left( x_{1}(t), x_{2}(t) \right) ^{T}$ is a two-dimensional vector function where T is the transposition. The system in matrix form

$$\begin{aligned} \begin{pmatrix} dx_{1}(t) \\ dx_{2}(t) \end{pmatrix} = \begin{pmatrix} - a x_{1}(t) + x_{2}(t) \\ - b x_{2}(t) \end{pmatrix} dt + \begin{pmatrix} x_{1}(t)dW_{1}(t) \\ x_{2}(t)dW_{2}(t) \end{pmatrix}. \end{aligned}$$

Introducing a Lyapunov function $\mathcal {V}(t,x) = x_{1}^{2}(t) + x_{2}^{2}(t)$ implies

$$\begin{aligned} \textrm{L}\mathcal {V}(t,x(t)) = - 2 a x_{1}^{2}(t) + 2 x_{1}(t)x_{2}(t) - 2 b x_{2}^{2}(t) + x_{1}^{2}(t) + x_{2}^{2}(t). \end{aligned}$$

$$\begin{aligned} \mathbb {E}\textrm{L}\mathcal {V}(t,x(t)) \le (2-2a) \mathbb {E} \left[ x_{1}^{2}(t)\right] + (2-2b) \mathbb {E} \left[ x_{2}^{2}(t)\right] . \end{aligned}$$

Hence, according to Theorem. 2.2, the zero solution of (20) is asymptotically mean-square stable if $a > 1$ and $b > 1$ for arbitrary constants a, b. Figure 1b gives the mean square stability region in (a, b)-space of parameters. 50 stable trajectories $x_{1}(t)$ (blue) and $x_{2}(t)$ (green) are simulated with $x(t) = 0$ at the point (1.2, 1.5) in Fig. 5a and 50 unbounded trajectories at the point (0.01, 0.02) as shown in Fig. 5b.

Example 4

Consider the two-dimensional random system with random variables $B(\omega )$, $C(\omega )$, and a nonnegative random variable $A(\omega )$. W(t) is a Wiener process:

$$\begin{aligned} \begin{pmatrix} dx_{1}(t,\omega ) \\ dx_{2}(t,\omega ) \end{pmatrix} = \begin{pmatrix} a x_{1}(t,\omega ) + A(\omega ) x_{2}(t,\omega ) \\ - b x_{2}(t,\omega ) \end{pmatrix} dt + \begin{pmatrix} B(\omega ) x_{1}(t,\omega ) dW_{1}(t) \\ C(\omega ) x_{2}(t,\omega )dW_{2}(t) \end{pmatrix}, \end{aligned}$$

(21)

The zero solution of (21) is asymptotically mean-square stable if:

$$\begin{aligned} \begin{aligned} 2 a + \Vert A(\omega ) \Vert _{2} + \Vert B(\omega ) \Vert _{4}^{2}&< 0, \\ - 2 b + \Vert A(\omega ) \Vert _{2} + 2 \Vert C(\omega ) \Vert _{4}^{2}&< 0. \end{aligned} \end{aligned}$$

(22)

Under these conditions and according to Theorem, 2.3, Fig. 7a–d show the numerical simulation of stable solutions for different probability distributions, and Fig. 7e shows unstable (unbounded) solutions for specific values of the parameters of the probability distributions.

Example 5

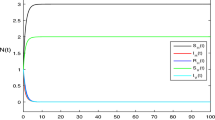
Consider the stochastic nonlinear HIV/AIDS model (7), for $R_0 > 1$ and conditions of stochastic global exponential stability of $E^*$ (10), the disease persists for different values of the parameters involved in the system. Figure 8 shows the persistence of the HIV/AIDS epidemic through the stability of $E^*$. The basic reproduction number $R_0$ is sensitive to the change in the transmission rate of the disease $\beta$, increasing in $\beta$ implies an increase in $R_0$. The parameter of transmission can be decreased by choosing less risky sexual behaviors, getting tested and treated for STDs, etc.

Example 6

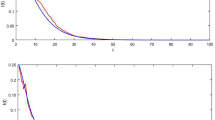
We consider the nonlinear stochastic Black–Scholes market model (12). Under the investigated conditions of Proposition 3.3, the stochastic stability regions for (12) given by the condition imposed on the parameters are shown in Fig. 2 for different values of the parameter $\lambda$ in $(r,\sigma )$-space of parameters. Figure 3 shows the mean-square exponential stability regions. Increasing $\lambda$ gives better stability regions. Figure 1c shows the mean-square stability region. The numerical simulations of the solution of (12) with $x(t) = 0$ are shown in Fig. 9. At the point $(-1,1)$, 50 blue stable trajectories are simulated in Fig. 9a and 50 red unbounded trajectories in Fig. 9b at the point (1, 1).

Fig. 2

Stochastic stability regions of (12).

Fig. 3

Mean square exponential stability regions of (12).

Example 7

We consider the random Ornstein–Uhlenbeck model (13). The numerical simulations of the solution of (13) with $x(t) = 0$ are shown in Fig. 10 for different values of parameters of the probability distributions with $\lambda = 3$ in the light of conditions obtained by Proposition 3.4.

Discussion

We deal with nonlinear stochastic differential equations and analyze the stability of solutions based on mean-square stability conditions. Therefore, A differential equation shows stability at point (1,1) and instability at point (1,2), illustrated with Figs. 1, 2, 3 and 4 of stable and unstable trajectories. A similar stochastic equation with random coefficients $A(\omega )$ and $C(\omega )$ is analyzed, showing stability and instability through various probability distributions of the coefficients as in Figs. 5, 6 and 7. The Black–Scholes model is examined with stability regions for different values of the parameter $\lambda$, with plots demonstrating stable and unstable solutions at different points as in Figs. 8, 9. The Ornstein–Uhlenbeck model with random parameters is studied, with plots showing solution stability under different parameter values as in Fig. 10.

Fig. 4

Trajectories of solution of (16) with $x_{0} = 1.5$.

Fig. 5

Trajectories of solution of (20) with $x_{1}(0) = 1.0$ and $x_{2}(0) = -1.0$.

Fig. 6

Trajectories of solution of (18) with $x_{0} = 0.5$.

Fig. 7

Trajectories of solution of (21) with $x_{1}(0) = 1.0$, $x_{2}(0) = -1.0$ and $a = -2, \, \, b =2$.

Fig. 8

Numerical simulation of the path (S, I, A) of (7) with $(S(0),I(0),A(0)) = (0.3,0.6,0.55), \varepsilon = 0.02,$ and $\Delta t = 0.013$.

Fig. 9

Trajectories of solution of (12) with $x_{0} = 0.5$.

Fig. 10

Trajectories of solution of (13) with $x_{0} = 0.1$.

Stability in the mean-square sense is crucial when analyzing stochastic systems like the Black–Scholes model and the Ornstein–Uhlenbeck process. This type of stability ensures that the expected value of the square of the system’s state remains bounded over time, which is essential for predicting long-term behavior. In financial models, such as the Black–Scholes, mean-square stability helps understand how sensitive the option prices are to fluctuations in market parameters like volatility and interest rates. For the Ornstein–Uhlenbeck process, which models mean-reverting behavior, mean-square stability guarantees that the process will consistently return to its mean, preventing divergence and ensuring reliable long-term predictions.

Similarly, in our dynamics of the HIV/AIDS model, mean-square stability is vital for understanding the progression of the disease under various treatment strategies and random perturbations. This stability ensures that the expected value of the square of the infected population remains bounded, providing insights into the effectiveness of interventions and the long-term behavior of the epidemic. By ensuring mean square stability, we can develop more robust and reliable models that aid in decision-making and policy formulation for controlling the spread of HIV/AIDS.

Conclusion

In our comprehensive study, we have delved into the stochastic stability, mean-square stability, and stochastic global exponential stability of the trivial equilibrium in both linear and nonlinear stochastic systems. Our findings, as presented in⁶, highlight the mechanisms that could potentially lead to eradicating the disease. This investigation has allowed us to explore the dynamics of the persistence of the HIV/AIDS epidemic. Moreover, we have examined the dynamics of the random Ornstein–Uhlenbeck model, which plays a crucial role in modeling various physical and financial phenomena. Additionally, we have analyzed the stochastic Black–Scholes market model, which is essential for the pricing of financial derivatives and understanding market risks.