A decision-making model for blasting risk assessment in mines using FBWM and GRA methods

Abstract

Due to the extensive use of explosives, the failure to identify hazards and assess risks in blasting may lead to catastrophic consequences. However, classical risk assessment approaches are limited in their ability to address ambiguity and uncertainty, as well as in assigning weights to the criteria involved in the risk assessment process. This study employs a multi-criteria decision-making system to address these limitations and assess the risks associated with blasting. The proposed model integrates Grey Relational Analysis (GRA) to prioritize risks and the Fuzzy Best-Worst Method (FBWM) to assign weights to the criteria critical to the risk assessment process. The findings indicated that “not using personal anti-static protection devices during blasting (R12)”, “placing the explosive fuse near explosive materials (R15)”, and “bringing explosive materials to the explosion site before completing drilling and blasting operations (R23)” were the most significant blasting risks, respectively. These risks stem from operational processes, human factors, and the working environment, thus requiring special attention. The weighting of the study criteria, including Consequence (C), Probability (P), and Exposure (E), revealed that the C criterion, with a final weight of 0.538, was the most influential in the risk assessment process. The P and E criteria, with weights of 0.294 and 0.167, respectively, ranked second and third in importance among the assessment criteria. To ensure the applicability and accuracy of the proposed method, a validation study comprising two distinct parts—sensitivity analysis and comparative analysis—was conducted. The results of these evaluations highlighted the appropriate and reliable performance of the proposed approach. This approach can assist decision-makers, managers, and risk analysts in more accurately identifying and assessing risks by addressing some of the limitations inherent in classical risk assessment methods.

Introduction

The mining industry is one of the oldest human activity sectors, encompassing of coal, metal, and non-metallic mineral mines¹. Mines play a vital role in supplying the raw materials for various industries².

Due to disregard for safety principles and lack of familiarity with equipment and methods, working in mines has resulted in individual health issues, decreased production, and the wastage of substantial assets, as well as environmental degradation including soil, air, and water pollution, land subsidence, and noise pollution. Additionally, this situation undermines the credibility of the mining sector^3,4. The occurrence of these hazards not only affects the miners, and mine owners, but also has a detrimental impact on policymakers, governments, and local communities.

Despite these hazards, the growth of the mining industry is regarded as inevitable due to its significant contribution to the economies of numerous countries and the employment of many individuals within this sector. In spite of intensive efforts to improve mine safety standards, accidents continue to pose a serious risk in this field. According to prior research, the incidence of mining accidents remains relatively high⁵.

In recent years, the fatality rate in underground mines has exceeded six times that of all other sectors combined⁶. Additionally, the high number of accidents and injuries among mine workers results in a significant loss of working days⁷. The substantial costs associated with these accidents adversely affect personnel, mining companies, and governments alike. In their study, Arango et al. estimated that a fatal accident and loss of equipment could cost a mining company over $3.8 million⁸. Among other mine operations, blaster vocations, contribute significantly to mining accidents due to the inherent risks associated with their work. Because of working with enormous amounts of explosives, even minor mistake can have catastrophic consequences. In this profession, the most severe potential outcome is the death of a blaster⁹. Consequently, identifying, analyzing, and managing hazards can provide essential guidance for effectively performing tasks in this field¹⁰.

There are various limitations when utilizing classical methods for risk assessment, such as HAZOP, JSA, FMEA, and similar techniques. For example, in classical methods, there is no weight assignment to criteria that involved in risk assessment¹¹. Consequently, the main criterion for risk assessment may vary based on the type of task and could be overlooked. Moreover, in classical methods, due to the reliance on pre-determined data and tables in risk calculation and prioritization, two different risks may have the same risk priority number¹². This situation can be problematic, especially in industries where it is financially impractical to eliminate or mitigate all risks. Furthermore, during classical risk assessment, the existence of uncertainty is possible due to diverse experiences, knowledge, and personal differences among experts.

According to the above, conducting risk assessments using techniques with higher degrees of sensitivity and accuracy is becoming increasingly essential. Many research has been conducted with the aim of developing classical risk assessment techniques.

Soltani integrated the ARAS and Shannon entropy methodologies to evaluate and prioritize the risks associated with explosive warehouses. The results showed that the combination these two methods facilitates precise risk assessment¹³. Additionally, the effectiveness of using combined risk assessment methods in GUL, TANG, and WANG studies has also been proven^14,15,16. To our knowledge, so far, no study has been conducted to identify and assess the risks associated with blasting using the combined Fine–Kinney-FBWM-GRA technique. To achieve this objective and propose a method for risk assessment with enhanced sensitivity, this research was undertaken.

The following are the main developments in this study. (1) Application of fuzzy sets aims to address ambiguities in human judgment and evaluations during the decision-making process. (2) Using the FBWM method to assign weights to the criteria of the Fine–Kinney method and improve this risk assessment approach. Overall, employing the FBWM method can yields decisions with greater accuracy in situations where data are ambiguous compared to the BWM method. (3) The implementation of the GRA method for prioritizing risks can effectively and practically establish the order of risk priorities. (4) The adoption of linguistic terms instead of crisp numbers in determining the values of C, P, and E can help mitigate uncertainty.

Literature review

To date, numerous studies have sought to employ the Fine–Kinney method for assessing workplace risks, primarily focusing on addressing various limitations inherent to this approach. In this context, a novel integrated methodology was developed by Gul et al. to prioritize control measures in the liquid fuel tank area of petrol stations, combining the Fine–Kinney, BBWM, and fuzzy VIKOR methods. The proposed approach in this study proved to be precise, sensitive, and practical¹⁷. Fang et al., in their research, concentrated on risk assessment in construction operations utilizing the Fine–Kinney method. They implemented the GLDS (Gained and Lost Dominance Score) and CRITIC methods to overcome the limitations of the classical Fine–Kinney approach. findings of their study demonstrated that employing these methods alongside fuzzy sets can effectively rank potential risks with a high degree of reliability¹⁸.

Dogan et al. developed an innovative model for risk assessment of hazards occurring in a medium-sized gas filling facility by integrating the Fine–Kinney, TOPSIS, and AHP methods. The results of their study indicated that the proposed model not only addressed the limitations of the classical Fine–Kinney method but also demonstrated satisfactory efficiency¹⁹.

Gul et al., in their study, presented a developed model using the Fine–Kinney, FAHP, and VIKOR methods to identify risks associated with construction and operation of wind turbines. In their analysis, VIKOR was employed to prioritize various risks, while FAHP was used to determine the weights of the risk assessment criteria. Their study effectively identified the most important hazards for both the operation and construction phases of the wind turbine²⁰.

In a study by Tang et al. aimed at assessing the risk of ballast tanks, a hybrid approach was employed that integrated the interval type-2 fuzzy set, BWM, and TODIM methods to address the limitations of the classical Fine–Kinney method. The effectiveness of this hybrid approach was evaluated through sensitivity analysis, which demonstrated that the method possesses adequate reliability¹⁶.

Based on our review and knowledge, no study to date has examined and assessed the risk of blasting hazards using the GRA prioritization method and FBWM weighting in a fuzzy environment. Unlike existing literature, the present study was conducted with this aim.

Materials and methods

This section, introduces a novel risk assessment approach that combines the FBWM weighting technique and the GRA prioritization method, specifically utilizing the Fine–Kinney criteria. To ensure that the proposed method was effective and applicable, it was used to analyze blasting risks.

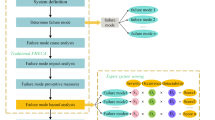
The hazards of this activity were identified and compiled through a combination of literature sources and expert interviews. Following this, criteria were weighted, and risk prioritization was performed using the integrated approach. The visual overview of the proposed fuzzy-based risk model is shown in Fig. 1.

Fig. 1

The proposed methodology.

Fine–Kinney method

The Fine–Kinney method, introduced by Kinney et al. in 1976, is widely used to assess occupational hazards in work environments²¹. This method determines the Risk Priority Number (RPN) by multiplying three key risk criteria: consequence, probability, and exposure. Table 1 presents the scales for each of these parameters, while Table 2 explains the interpretation of the resulting RPN values¹².

Table 1 Scales of Fine–Kinney risk assessment method.

Table 2 The RPN explanation.

Fuzzy sets

Professor Lotfi introduced the theory of fuzzy sets in 1965²². Unlike classical set theory, fuzzy sets are highly effective at handling ambiguity and uncertainty within human decision-making process. By using linguistic terms, it is possible to solve many problems in human decision-making that are not accurate due to poorly defined limitations. In uncertain conditions, By converting linguistic terms into fuzzy numbers, the views, knowledge, and experiences of an individual or a group of decision-makers are analyzed^14,23. The triangular fuzzy number (TFN) is expressed as F = (L M U). In this set, L, M, and U represent low, medium, and high fuzzy values, respectively. TFN membership degree is displayed as below¹⁴:

$$\:\mu\:{\bar A}=\left\{\begin{array}{c}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}x<l\\\:(x-l)/(m-l)\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}l\le\:x\le\:m\\\:(u-x)/(u-m)\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}m\le\:x\le\:u\\\:0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}x\ge\:u\end{array}\right.$$

(1)

TFN has good computational efficiency, and the reason is the ease of their mathematical operations. The calculations of fuzzy numbers such as ${\bar A_1}\:$and ${\bar A_2}$are as follows¹²:

The addition operation:

$${\bar A_1} + {\bar A_2} = \left( {{l_1} + {l_2}.\:{m_1} + {m_2}.\:{u_1} + {u_2}} \right)$$

(2)

The subtraction operation:

$${\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftharpoonup$}} \over A} _1} - {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftharpoonup$}} \over A} _2} = \left( {{l_1} - {u_{2.}}\:{m_1} - {m_{2.}}\:{u_1} - {l_2}} \right)$$

(3)

The multiplication operation:

$${\mathop A\limits^\prime _1}x{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftharpoonup$}} \over A} _2} = \left( {{l_1}x{l_{2.}}\:{m_1}x{m_{2.}}\:{u_1}x{u_2}} \right)$$

(4)

In this study, the following relationship was used to convert fuzzy numbers into definite numbers.

$$\:R\left({\bar A}_{i}\right)=\frac{{l}_{i}+4{m}_{i}+{u}_{i}}{6}\:$$

(5)

FBWM method

The Best Worst Method (BWM), introduced by Rezaei in 2015²⁴, s a recent multi-criteria decision-making approach based on pairwise comparisons. This method is particularly suited for deterministic environments. In this approach, the weighting of criteria begins by determining the priority of the most important criterion relative to other criteria and continues by identifying the priority of the least important criterion relative to the rest of the criteria. Choosing the best and worst criteria in this method minimizes the number of comparisons and enhancing the efficiency of the model. In the BWM method, a 9-point scale is used for prioritizing criteria. In 2017, Guo et al. investigated the BWM model in a fuzzy environment²⁵.

According to their study, human qualitative judgments have ambiguity and uncertainty. To solve this limitation, the Fuzzy Best Worst Method (FBWM) technique was presented by them. FBWM steps are presented below.

Step 1: Creating a multi-criteria decision-making system (criteria selection).

In this step, decision criteria for evaluating the available options are selected.

Step 2: Selection of the best (most important) and worst (least important) criteria by experts.

In this stage, experts determine the most and least important criteria among those selected in the previous step. The most important criterion is displayed as ${\bar C}$and the least important criterion is labeled as ${\bar C}_{w}$.

Step 3: Fuzzy comparisons of the most important criterion ${\bar C}_{b}\:$with other criteria.

At this stage, the fuzzy preferences of the best criterion compared to the other criteria are established using the linguistic terms provided by the decision-makers (see Table 3). These linguistic terms are then converted into triangular fuzzy numbers (TFNs) based on the rules in Table 3. The fuzzy vector representing the comparison of the best criterion with the other criteria is shown in Eq. (6).

Table 3 Transformation rules of linguistic variables of decision-makers.

$${\tilde A_B} = \left( {{{\tilde a}_{B1}},{{\tilde a}_{B2}}, \ldots ,{{\tilde a}_{Bn}}} \right)$$

(6)

where ${\tilde A}_{B}$ displays the fuzzy Best-to-Others vector; ${\tilde a}_{Bj}$ represents the fuzzy preference of the most important criterion ${\tilde C}_{b}\:$ over criterion j, j = 1, 2, ···, n. It can be known that ${\tilde a}_{BB}$ = (1, 1, 1).

Step 4: Fuzzy comparison of all criteria with the least important criterion ${\tilde C}_{w}$.

At this stage, the fuzzy preferences of each criterion are determined relative to the least important criterion, using the linguistic terms provided in Table 3. These linguistic terms are then converted into triangular fuzzy numbers (TFNs) according to the rules in Table 3. The fuzzy vector representing the comparison of all criteria with the least important criterion is shown in Eq. (7).

$${\tilde A}_{w}=\left({\tilde a}_{1w},{\tilde a}_{2w},\ldots\:,{\tilde a}_{nw}\right)$$

(7)

where ${\tilde A}_{w}$ shows the fuzzy others-to-worst vector; ${\tilde a}_{iw}$ represents the fuzzy preference of the least importance criterion ${\tilde C}_{w}\:$ over criterion i, i = 1, 2, ···, n. It can be known that ${\tilde a}_{ww}$ = (1, 1, 1).

Step 5: Determining the fuzzy weights of criteria.

Using the nonlinear optimization problem (Eq. 8), the fuzzy weight $\:\left({\tilde w}_{1}^{*},{\tilde w}_{2}^{*},\ldots\:,{\tilde w}_{n}^{*}\right)\:$of different criteria is calculated. The graded mean integration representation (GMIR) (Eq. 5) method is used to convert fuzzy numbers into crisp values.

$$\:\begin{array}{c}\text{min}{\stackrel{\sim}{\xi\:}}^{*}\\\:\\\:\text{\:}\text{s}\text{.}\text{t}\text{.}\text{\:}\left\{\begin{array}{c}\left|\frac{\left({l}_{B}^{w},{m}_{B}^{w},{u}_{B}^{w}\right)}{\left({l}_{j}^{w},{m}_{j}^{w},{u}_{j}^{w}\right)}-\left({l}_{Bj},{m}_{Bj},{u}_{Bj}\right)\right|\le\:\left({k}^{*},{k}^{*},{k}^{*}\right)\\\:\left|\frac{\left({l}_{j}^{w},{m}_{j}^{w},{u}_{j}^{w}\right)}{\left({l}_{W}^{w},{m}_{W}^{w},{u}_{W}^{w}\right)}-\left({l}_{jW},{m}_{jW},{u}_{jW}\right)\right|\le\:\left({k}^{*},{k}^{*},{k}^{*}\right)\\\:\sum\:_{j=1}^{n}\:R\left({\stackrel{\sim}{w}}_{j}\right)=1\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:{l}_{j}^{w}\le\:{m}_{j}^{w}\le\:{u}_{j}^{w}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:{l}_{j}^{w}\ge\:0\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:j=\text{1,2},\cdots\:,n\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\end{array}\right.\end{array}$$

(8)

Step 6: Consistency ratio calculation for fuzzy BWM.

In the FBWM method, the consistency ratio (CR) is used to evaluate the reliability of the calculated weights. The CR value ranges from 0 to 1, with 0 indicating fully consistent and reliable weights, while a value closer to 1 suggests higher inconsistency and reduced reliability in the pairwise comparisons. A pairwise comparison is considered consistent if${\tilde a}_{Bj}\times\:{\tilde a}_{jW}={\tilde a}_{BW}$; otherwise, it is deemed inconsistent²⁶. Consequently, maximum inconsistency occurs if ${\tilde a}_{Bj}\:$ and ${\tilde a}_{jW}$ are equal ${\tilde a}_{BW}$. Before calculating CR, the value of consistency index CI must be known. The CI is calculated using Eq. (9).

$$\:(CI{)}^{2}-\left(1+2{u}_{BW}\right)\times\:CI+\left({u}_{BW}^{2}-{u}_{BW}\right)=0$$

(9)

In this equation, $\:{u}_{BW}$ represents the upper bound of ${\tilde a}_{BW}=\left({l}_{BW},{m}_{BW},{u}_{BW}\right)$, which is used in pairwise comparisons. The CI values for various fuzzy numbers are reported in Table 3. Finally, the CR value can be calculated using Eq. (10)²⁵.

$$\:\text{C}\text{R}=\frac{{\xi\:}^{*}}{\text{C}\text{I}}$$

(10)

In this equation, $\:{\xi\:}^{\text{*}}\:$is the crisp value of ${\tilde \xi ^{{*}}} = \left( {{k^{{*}}},{k^{{*}}},{k^{{*}}}} \right)$, which is calculated by solving Eq. (8). Detailed information about how to calculate the weights of the criteria using the FBWM method is given in Table A1 in Appendix A.

GRA method

The Grey Relational Analysis (GRA) approach examines system behavior through relational analysis and model creation²⁷. This method was initially developed by Deng in 1989²⁸. The steps of the GRA method are described below²⁹.

Step 1: Create a gray relationship.

The meaning of creating a gray relationship in the GRA method is to build a decision matrix. The decision matrix with m options and n criteria will be as follows.

$$\:\text{Y}=\left[\begin{array}{c}{y}_{11}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{y}_{12}\cdots\:\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{y}_{1n}\\\:{y}_{21}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{y}_{22}\cdots\:\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{y}_{2n}\\\:⋮\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}⋮\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}⋮\\\:{y}_{m1}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{y}_{m2}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{y}_{mn}\end{array}\right]$$

(11)

Step 2: Normalization.

Normalization is necessary for multi-criteria decision-making (MCDM) solutions due to the potential for varying criteria. According to the concept of normalization, each $\:{Y}_{i}$ is converted into a comparative series of $\:{X}_{i}$.$\:\:{X}_{i}=\left({x}_{i1},{x}_{i2},\dots\:,{x}_{ij},\dots\:,{x}_{in}\right)$

To convert any $\:{Y}_{ij}$ to $\:{X}_{ij}$, one of the following relations is used.

$$\:\text{T}\text{h}\text{e}\:\text{b}\text{i}\text{g}\text{g}\text{e}\text{r},\:\text{t}\text{h}\text{e}\:\text{b}\text{e}\text{t}\text{t}\text{e}\text{r}\::\:{x}_{ij}=\frac{{y}_{ij}-min\left({y}_{ij}\right)}{max\left({y}_{ij}\right)-min\left({y}_{ij}\right)}$$

(12)

$$\:\text{T}\text{h}\text{e}\:\text{s}\text{m}\text{a}\text{l}\text{l}\text{e}\text{r},\:\text{t}\text{h}\text{e}\:\text{b}\text{e}\text{t}\text{t}\text{e}\text{r}:\:{x}_{ij}=\frac{max\left({y}_{ij}\right)-{y}_{ij}}{max\left({y}_{ij}\right)-min\left({y}_{ij}\right)}$$

(13)

$$\:{\text{T}\text{h}\text{e}\:\text{c}\text{l}\text{o}\text{s}\text{e}\text{r}\:\text{t}\text{o}\:\text{t}\text{h}\text{e}\:\text{d}\text{e}\text{s}\text{i}\text{r}\text{e}\text{d}\:\text{v}\text{a}\text{l}\text{u}\text{e}\:y}^{*},\:\text{t}\text{h}\text{e}\:\text{b}\text{e}\text{t}\text{t}\text{e}\text{r}:\:{x}_{ij}=\frac{\left|{y}_{ij}-{y}^{*}\right|}{max\left\{max\left({y}_{ij}\right)-{y}^{*},{y}^{*}-min\left({y}_{ij}\right)\right\}}$$

(14)

Step 3: Reference Sequence Definition.

After creating the gray relations using the above equations, all the values will be between zero and one, as when the concept of normalization is used. The closer$\:\:{x}_{ij}$ is to one, the more desirable it is. Consequently, the comparison series in which all options are equal to 1 will be the optimal choice. The reference sequence, defined as a series where all functional values are equal to 1, is formulated as follows:

$$\:{X}_{0}=\left({x}_{01},{x}_{02},\dots\:,{x}_{0j},\dots\:,{x}_{0n}\right)\:=\:(\text{1,1},\dots\:,1,\dots\:,1)$$

(15)

Step 4: Determination of Gray Relational Coefficient.

Using the gray relation coefficient, the proximity of each $\:{x}_{ij}$ to $\:{X}_{0j}$ is measured. If the gray relation coefficient is larger, it indicates greater proximity. This value is calculated using the following relationship.

$$\:{\upgamma\:}({X}_{0j},{x}_{ij})=\frac{{\Delta\:}\text{m}\text{i}\text{n}-\text{r}{\Delta\:}max}{{\Delta\:}\text{i}\text{j}-\text{r}{\Delta\:}max}$$

(16)

$\:{\Delta\:}\text{i}\text{j}$ must be calculated to perform the above calculations ($\:{\Delta\:}\text{i}\text{j}={X}_{0j}-{x}_{ij}$). $\:{\Delta\:}\text{m}\text{i}\text{n}$ and $\:{\Delta\:}max$ are the smallest and largest values of $\:{\Delta\:}\text{i}\text{j}$, respectively. In this equation, r is the distinguishing coefficient. The value of r is between 0 and 1. Based on the results of the sensitivity analysis of Lin et al.‘s study, an r value equal to 0.5 has good stability³⁰.

Step 5: Determining the Gray Relational Grade.

Gray Relational Grade is calculated with the following formula. In this regard, W is the weight of the criteria, which is calculated by weight determination methods (in this paper, using the FBWM). The option that has the highest value of Gray Relational Grade is selected as the best option. How to rank the risks for R1, for example, is presented in Appendix A and Table A2 to facilitate a better understanding of this section. 

$$\:{\Gamma\:}\left({X}_{0j},{x}_{ij}\right)=\sum\:\:\text{W}\text{j}\:{\upgamma\:}({X}_{0j},{x}_{ij})$$

(17)

Case study

To evaluate the effectiveness of the proposed method, its application was tested in a real-world setting. Specifically, this decision-making tool was applied to assess blasting-related risks, an essential step in minimizing financial and physical hazards for workers in this field. The following steps were taken to prioritize the risks and check the effectiveness of the suggested method.

Determination of blasting hazards

Initially, a list of fire risks was compiled from various sources, including interviews with experts and reviews of previous studies. The number of 24 critical risks was determined. These risks are listed in Table 4, while Table 5 provides details about the experts involved in the study. In this study, an expert is defined as an individual who meets the following conditions: (1) holds at least a master’s degree (2) possesses knowledge of the blasting process (3) is familiar with the Fine–Kinney risk assessment method (4) has an understanding of fuzzy sets and multi-criteria decision-making systems.

Table 4 Identifying the risks of the blasting.

Table 5 Characteristics of experts.

Determination of risk assessment criteria

Fine–Kinney criteria were used in this study. These criteria included consequence (C), probability (P), and Exposure (E)^14,16.

Validation study

This section aims to validate the results of the risk prioritization conducted in this study. To achieve this, a two-step approach was utilized, which includes a sensitivity analysis followed by a comparative analysis. In the first step, sensitivity analysis was conducted to assess the stability of the model and evaluate how changes in one variable affect others. Specifically, this analysis aimed to evaluate the influence of changes in criterion weights on the risk ranking results. To achieve this, four different weight combinations were designed, and the effect of altering the weights on the risk prioritization was analyzed. Table 6 presents a detailed overview of the weight vectors used for the criteria in this study.

Table 6 The weight vectors created for the sensitivity analysis.

In the second part of the validation process, a comparative analysis was conducted. At this stage, the risk ranking results obtained from the proposed method were compared with five widely-used multi-criteria decision-making methods in risk assessment, including VIKOR, TOPSIS, EDAS, ARAS, and CoCoSo. To assess the accuracy and consistency of the results, correlation coefficients between the proposed model and these methods were calculated. For all methods, the criteria weights determined using the FBWM method were employed to ensure direct and coherent comparisons between the results. The findings of the comparative analysis are presented in Table 16, which highlights both the similarities and minor differences observed across the methods.

Results

Qualitative determination of risk scores and forming the initial matrix

At this stage, experts qualitatively determined the values for C, P, and E to identified risks using the linguistic terms in Table 7. These values were then used to create the initial qualitative risk matrix, as shown in Table 8. According to the information in Table 7, each qualitative value is equivalent to a TFN. Therefore, the fuzzy values were first converted to TFNs, and following their defuzzification, a numerical matrix was generated, presented in Table 9.

Table 7 Average triangular fuzzy numbers range of 7 degree.

Table 8 Qualitative risk values determined by experts.

Table 9 Initial matrix.

Determining the weight of the criteria

The FBWM method was used to establish the weights of the criteria for the proposed approach. This process began by forming a panel of experts who identified the best and worst criteria among the selected options. The experts then assessed the importance of these criteria relative to one another through pairwise comparisons, using linguistic terms as outlined in Table 3. The outcomes of these pairwise comparisons are summarized in Table 10. Utilizing Eq. (6) in conjunction with the data presented in Table 10, the fuzzy best-to-others vector was determined as follows:

Table 10 Fuzzy preferences criteria.

$${\tilde A_B} = [\left( {{\rm{1,1}},1} \right),(3/2,2,5/2),(5/2,3,7/2)].$$

Similarly, using Eq. (7) and Table 10, the fuzzy others-to-worst vector was identified as:

$${\tilde A}_{w}=\left[\right(5/2,3,7/2),(3/2,2,5/2),(\text{1,1},1\left)\right]$$

Based on the provided explanations, to determine the optimal weights of the various criteria and the value of $\:{\xi\:}^{\text{*}},$ a nonlinearly constrained optimization problem was formulated using Eq. (8), which is detailed below:

$$\:\begin{array}{c}s.t.\left\{\begin{array}{c}min{\stackrel{\sim}{\xi\:}}^{*}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:\:\\\:\left|\frac{\left({l}_{1}^{w},{m}_{1}^{w},{u}_{1}^{w}\right)}{\left({l}_{1}^{w},{m}_{1}^{w},{u}_{1}^{w}\right)}-\left({l}_{11},{m}_{11},{u}_{11}\right)\right|\le\:\left({k}^{*},{k}^{*},{k}^{*}\right)\\\:\left|\frac{\left({l}_{1}^{w},{m}_{1}^{w},{u}_{1}^{w}\right)}{\left({l}_{2}^{w},{m}_{2}^{w},{u}_{2}^{w}\right)}-\left({l}_{12},{m}_{12},{u}_{12}\right)\right|\le\:\left({k}^{*},{k}^{*},{k}^{*}\right)\\\:\left|\frac{\left({l}_{1}^{w},{m}_{1}^{w},{u}_{1}^{w}\right)}{\left({l}_{3}^{w},{m}_{3}^{w},{u}_{3}^{w}\right)}-\left({l}_{13},{m}_{13},{u}_{13}\right)\right|\le\:\left({k}^{*},{k}^{*},{k}^{*}\right)\\\:\left|\frac{\left({l}_{1}^{w},{m}_{1}^{w},{u}_{1}^{w}\right)}{\left({l}_{3}^{w},{m}_{3}^{w},{u}_{3}^{w}\right)}-\left({l}_{13},{m}_{13},{u}_{13}\right)\right|\le\:\left({k}^{*},{k}^{*},{k}^{*}\right)\\\:\left|\frac{\left({l}_{2}^{w},{m}_{2}^{w},{u}_{2}^{w}\right)}{\left({l}_{3}^{w},{m}_{3}^{w},{u}_{3}^{w}\right)}-\left({l}_{23},{m}_{23},{u}_{23}\right)\right|\le\:\left({k}^{*},{k}^{*},{k}^{*}\right)\\\:\left|\frac{\left({l}_{3}^{w},{m}_{3}^{w},{u}_{3}^{w}\right)}{\left({l}_{3}^{w},{m}_{3}^{w},{u}_{3}^{w}\right)}-\left({l}_{33},{m}_{33},{u}_{33}\right)\right|\le\:\left({k}^{*},{k}^{*},{k}^{*}\right)\\\:\:\\\:\sum\:_{j=1}^{3}\:R\left({\stackrel{\sim}{w}}_{j}\right)=1\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:{l}_{j}^{w}\le\:{m}_{j}^{w}\le\:{u}_{j}^{w}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:{l}_{j}^{w}\ge\:0\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:j=\text{1,2},3\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\end{array}\right.\end{array}$$

(18)

Then, the following constrained nonlinear optimization problem can be obtained, represented by concrete number:

$$\:\begin{array}{c}min{k}^{*}\\\:\text{\:}\text{s}\text{.}\text{t}\text{.}\text{\:}\left\{\begin{array}{c}{l}_{1}-1.5*{u}_{2}\le\:k*{u}_{2};{l}_{1}-1.5*{u}_{2}\ge\:-k*{u}_{2};\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:{m}_{1}-2*{m}_{2}\le\:k*{m}_{2};{m}_{1}-2*{m}_{2}\ge\:-k*{m}_{2};\:\:\:\:\:\:\:\:\:\:\:\:\\\:{u}_{1}-2.5*{l}_{2}\le\:k*{l}_{2};{u}_{1}-1.5*{l}_{2}\ge\:-k*{l}_{2};\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:{l}_{1}-2.5*{u}_{3}\le\:k*{u}_{3};{l}_{1}-2.5*{u}_{3}\ge\:-k*{u}_{3};\:\:\:\:\:\:\:\:\:\:\:\:\\\:{m}_{1}-3*{m}_{3}\le\:k*{m}_{3};{m}_{1}-3*{m}_{3}\ge\:-k*{m}_{3};\:\:\:\:\:\:\:\:\:\:\\\:{u}_{1}-3.5*{l}_{3}\le\:k*{l}_{3};{u}_{3}-3.5*{l}_{3}\ge\:-k*{l}_{3};\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:{l}_{2}-1.5*{u}_{3}\le\:k*{u}_{3};{l}_{2}-1.5*{u}_{3}\ge\:-k*{u}_{3};\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:{m}_{2}-2*{m}_{3}\le\:k*{m}_{3};{m}_{2}-2*{m}_{3}\ge\:-k*{m}_{3};\:\:\:\:\:\:\:\:\:\:\\\:{u}_{2}-2.5*{l}_{3}\le\:k*{l}_{3};{u}_{2}-2.5*{l}_{3}\ge\:-k*{l}_{3};\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:\frac{1}{6}*{l}_{1}+\frac{1}{6}*4*{m}_{1}+\frac{1}{6}*{u}_{1}+\frac{1}{6}*{l}_{2}+\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:\frac{1}{6}*4*{m}_{2}+\frac{1}{6}*{u}_{2}+\frac{1}{6}*{l}_{3}+\frac{1}{6}*4*{m}_{3}+\frac{1}{6}*{u}_{3}=1\:\:\\\:{l}_{1}\le\:{m}_{1}\le\:{u}_{1};\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:{l}_{2}\le\:{m}_{2}\le\:{u}_{2};\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:{l}_{3}\le\:{m}_{3}\le\:{u}_{3};\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:{l}_{1}>0;{l}_{2}>0;{l}_{3}>0\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:k\ge\:0\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\end{array}\right.\end{array}$$

(19)

By solving this equation, the fuzzy weights for all three criteria and the value of $\:{\xi\:}^{\text{*}}\:$were obtained. Subsequently, the crisp weights of the criteria calculated using Eq. (5). The fuzzy and crisp weights of the criteria, along with the value of$\:\:{\xi\:}^{\text{*}}$, are presented in Table 11. Given that $\:{a}_{BW}={a}_{13}=(5/2,3,7/2),$ the CI for this case is 6.69. The CR is calculated as 0.273/6.69 = 0.0408, indicating a high level of consistency due to its proximity to zero.

Table 11 Final weights of the criteria.

Prioritizing blasting risks

The GRA method was used to determine the prioritization of blasting process risks. The first step involved forming initial risk matrix which is presented in Table 9. The values in this matrix were normalized using Formulas (12)–(14), as detailed in Table 12. Following normalization the reference sequence was defined using Eq. (15). Utilizing this reference sequence, the gray relation coefficient was calculated according to Eq. (16), as shown in Table 13. Finally, the prioritization of blasting risks was established using Eq. (17). Risk prioritization is shown in Table 14; Fig. 2.

Table 12 Normalized decision matrix.

Table 13 The gray relation coefficient values.

Table 14 Results of GRA.

Fig. 2

Ranking of hazards.

Validation study

In this part, the results of validation performed by sensitivity analysis and comparative analysis are presented. The ranking order of 24 different risks according to 4 weight vectors can be seen in Table 15; Fig. 3. These results provide insights into the validity of the proposed model. Furthermore, the comparative analysis between the proposed method and widely-used multi-criteria decision-making methods in risk assessment is detailed in Table 16. This table also includes the correlation coefficients between the GRA method and the other methods. Based on the data provided, a satisfactory correlation is observed between the developed method and these methods.

Table 15 Changes in risk rankings with variations in criteria weights.

Table 16 Comparison model with MCDM methodologies.

Fig. 3

The line chart of parameters’ sensitivity analysis.

Discussion

Mining environments inherently carry a high potential for accidents, prompting experts to develop effective methods for assessing and preventing these risks. Blasting, in particular, stands out among mining activities due to its sensitivity and the use of large quantities of explosives, which exposes operators to unique hazards. The prediction and assessment of these specific risks are crucial for adopting appropriate mitigation strategies. To address this need, the present study was conducted with the aim of providing a novel approach for prioritizing blasting-related risks. Additionally, this method seeks to overcome limitations commonly associated with classical risk assessment methods, providing a more comprehensive framework for evaluating these hazards.

One limitations of classical risk assessment methods such as Fine–Kinney is their inability to assign specific weights to influential criteria in risk assessment¹². To address this, the FBWM method was employed in the present study to weight the criteria (C, P, and E). The FBWM method was chosen over the classical BWM approach to reduce uncertainty and enhance accuracy in evaluation²⁵. Due to these advantages, FBWM has been widely applied in risk assessment across various studies³¹. As shown in Tables 11 and 12, after identifying the most important criterion (C) and the least important criterion (E), qualitative prioritization was established, enabling the calculation of each criterion’s weight. The resulting fuzzy weights for C, P, and E were (0.530, 0.530, 0.612), (0.261, 0.285, 0.380), and (0.163, 0.163, 0.201), respectively with the crisp weights calculated as 0.538, 0.294, and 0.167. Thus, criterion C has a higher weight and importance than P and E, highlighting its critical role in the assessment framework.

Since the C criterion holds the highest weight, it necessitates implementing more robust control measures, as it indicates that the risk event could lead to severe consequences. This weight reflects the potential for significant damage not only to personnel and equipment but also to the organization’s reputation and productivity. Similar findings have been observed in other studies that aimed to assign weights to criteria in classical risk assessment methods. In Akbari et al.‘s study, which prioritized risks in the molybdenum operation process, criterion C was found to carry a higher fuzzy weight than other criteria³². Likewise, in research by Fatih et al. on risk assessment in the textile production industry, criterion C was identified as more impactful compared to the other criteria³³.

One of the key challenges in applying MCDM methods is to assign criterion weights in a way that ensures logical consistency and alignment across the comparisons. Inconsistencies in these comparisons can significantly impact the final results, potentially compromising their reliability³⁴. To address this, the present study calculated the Consistency Ratio (CR). CR serves as an indicator of the consistency level of decision-makers’ judgments in the weighting process³⁵. As shown in Table 11, the CR value in this study is 0.0408, which is very close to zero, indicating a high level of consistency in the pairwise comparisons and confirming the reliability of the calculated weights³⁶. In other words, a low CR value reflects a strong alignment in the evaluations and criterion weights with minimal inconsistencies. This high level of consistency assures decision-makers of the model’s accuracy and supports the trustworthiness of the results³⁷.

This study also provides insights into the prioritization of blasting risks using the GRA method. Unlike classical risk assessment methods, the GRA approach enables managers and decision-makers to make more informed and rational decisions, even in situations with ambiguous or uncertain data^38,39. The key advantages of the GRA method include its simplicity, comprehensiveness, and high level of predictability, making it an effective tool for assessing and prioritizing risks.

As shown in Table 14, “not using personal anti-static protection devices during blasting” (R12) was identified as the most significant risk in the blasting process. Following that, “placing the explosive fuse near explosives materials” (R15) and “bringing explosive materials before completing drilling and blasting operations to the explosion site” (R23) were ranked as the second and third most significant risks in this process, respectively. Conversely, the assessment results indicated that risks such as, “using explosives more than necessary” (R1), “not blowing the warning light before the explosion” (R5), and “presence of domestic and wild animals in the vicinity of the blasting operation area” (R24) were of comparatively lower importance among the identified blasting risks.

The absence of personal anti-static protection devices during blasting operations significantly increases the risk of unintentional explosions or sparks, posing severe dangers to individuals involved. Given the high-risk nature of blasting, the consistent use of anti-static protection equipment is crucial for safeguarding worker health and safety.

Managers, employers, and workers must prioritize the correct use of these devices and actively promote workplace safety. Similar findings are highlighted in Karimi et al.‘s study, which underscores the role of personal protective equipment in mitigating blasting-related risks⁴⁰. To further reduce blasting hazards, it is essential to implement strategies such as comprehensive employee training, providing standard-compliant protective gear, conducting regular supervision and inspections, following established safety guidelines, and fostering a strong safety culture within the workplace.

To assess the applicability and reliability of the proposed model, a validation study was conducted in two stages. In the first stage, four different weighting combinations were created to assess their effects on risk prioritization. The selection of these weights was such that the impact of each criterion on risk prioritization could be examined separately.

As shown in Table 15, altering the weighting combinations led to changes in the risk rankings. For example, when Criterion C received a higher weight, risks with severe consequences ranked higher, whereas emphasizing Criteria P or E led to different prioritization outcomes. These findings highlight the model’s strong validity and its adaptability to changing criterion weights. This adaptability enhances the model’s precision, supporting more effective and tailored managerial decision-making⁴¹.

In the second stage of the validation study, the risk prioritization results from the proposed method were evaluated by comparing them with those derived from other widely used multi-criteria decision-making methods in risk assessment. Table 16 provides a comparative analysis of three high-priority and three low-priority risks across these methods. The findings indicate that the proposed model demonstrates significant alignment with these methods and the main risks are almost in the similar positions. However, minor differences in rankings were observed, which can be attributed to structural variations in how each method analyzes relationships and prioritizes options. Previous studies have shown that when such differences are minimal, they do not substantially impact the decision-making process¹².

Another key finding from the validation study was the strong correlation between the proposed model and several established risk assessment methods. Specifically, the correlation coefficients with the VIKOR, TOPSIS, ARAS, EDAS, and CoCoSo methods were 0.95, 0.98, 0.99, 0.86, and 0.99, respectively. This high level of consistency underscores the alignment of the proposed method with these well-established approaches, highlighting its reliability in risk assessment. Overall, this comparative analysis confirms that the proposed model provides a high degree of accuracy and robustness in prioritizing risks across different contexts, even when minor ranking differences are present. These findings further validate the credibility and effectiveness of the proposed approach, demonstrating its viability alongside other scientifically recognized methods.

Conclusion

Risk assessment in blasting, which is one of the most hazardous activities in mining due to the handling of explosives, is highly essential. Given the limitations encountered with conventional methods, conducting further research to propose more precise and sensitive approaches can improve the risk assessment process. The present study was conducted with this objective. The results of this research underscore the proposed method’s capacity to provide a more adaptable, reliable framework for risk assessment, particularly in high-risk environments where conventional methods may fall short. This study demonstrated that by integrating the FBWM and GRA methods, the proposed model allows for weighting of criteria and the prioritization of various risks with high sensitivity, effectively addressing uncertainties. Consequently, the accuracy and efficiency of risk assessment are significantly improved. The findings confirm that this method substantially enhances the assessment of blasting risks and offers a structured, adaptable framework that is more aligned with the complexities of real-world scenarios. This model holds potential for broader applications in diverse industrial units. Future studies are encouraged to explore the application of this model in other high-risk activities and industries, as well as to incorporate additional criteria for a more comprehensive risk assessment.