Kinetic alfven-acoustic waves at relativistic and ultra-relativistic Fermi energies

Abstract

The study of dense degenerate plasmas at extreme temperatures and densities motivates the investigation of relativistic and ultrarelativistic regimes. In this paper, we are presenting a comprehensive study of the linear and nonlinear propagation characteristics for kinetic Alfven acoustic waves (KAAW) at relativistic and ultra relativistic Fermi energies with small temperature corrections. The linear wave propagation of fast and slow modes for relativistic KAAW are studied and a comparative analysis of both the modes is plotted for relativistic, ultrarelativistic and nonrelativistic regimes. It has been investigated that for constant magnetic fields, the phase velocity of these waves decreases due to an increase in both the specific heat and thermal pressure at low plasma beta values and KAAW propagate more efficiently in outer regions with lower specific heat than in denser inner regions of neutron stars. Various theoretical approaches like Sagdeev pseudopotential approach, dynamical analysis, and finite amplitude expansion method are employed to analyse the nonlinear relativistic and ultrarelativistic KAAW. Phase space trajectories have been plotted to study the nonlinear structures corresponding to arbitrary amplitude perturbations. The existence regions of solitary kinetic Alfven acoustic waves (SKAAW) and the physical reasons for their dependence on different parameters have also been shown. Possible applications are envisaged in the intense laser-matter interactions, plasma photonics, dense astrophysical objects like the interior state of terrestrial planets, neutron stars, and white dwarfs where relativistic effects dominate the microscopic scale and may have macroscopic consequences.

Introduction

Degenerate quantum plasma is a mature, yet dynamic, field of investigation. This captivating form of matter is ubiquitously studied on a microscale^1,2. Interestingly, even while studying such exotic states^3,4on an astrophysical scale^5,6, its quantum effects are found to be significant and non-negligible. Quantum plasmas occur naturally in dense astrophysical environments like, active galactic nuclei, neutron stars⁷, white dwarfs⁸, and the inner region of black hole’s accretion disks. But it must be noted that due to their distance from the Earth, it becomes very difficult to collect their data, apart from a spectroscopic approach. Nevertheless, scientists have gathered substantial information by observations from space telescopes like Hubble^{9,10,11,12,13,14}, James Webb^15,16,17and X-ray observatories^18,19,20, about black holes, neutron stars, and white dwarfs. However, there is still much more left to be discovered about these compact celestials as no in-situ data can be collected using the present-day technology. Therefore to study them in detail, they must be observed in laboratories^21,22, where they are reported to exist in quantum dots, carbon nanotubes, micro-electronics, nanophononics²³and intense laser-plasma interactions²⁴. Such plasmas are characterized by extremely high densities and relatively low temperatures ($\:T\ll\:{T}_{F}$)²⁵. Due to the recent advancements in technology, dense plasma layer of micrometer order depth has been generated in the laboratory, with the average density of $\:{10}^{29}{m}^{-3}$and the electron temperatures at 2–4 keV²³. This work has been verified at a virtual laser plasma laboratory²⁶ by the usage of X-ray spectra and particle-in-cell (PIC) simulation, where all the formation phases were observed. This was done by the irradiation of femtosecond laser pulses of relativistic intensities on Au and Ni nanowires. Using PIC simulations, it was also predicted that this density can increase by one more order at $\:{10}^{30}{m}^{-3}$, if the nanowires are made of Uranium, rather than Au or Ni. This tabletop laser plasma is eerily reminiscent to the dense astrophysical environments, and hence allows a closer peek at these celestial objects.

Degenerate plasma exhibits relativistic effects when the Fermi energy becomes comparable to the rest mass energy ($\:{\epsilon\:}_{F}\:\sim\:{{m}_{o}c}^{2}$), which happens due to an increase in mean energy of matter as a result of compression²⁷. However, relativistic effects and their observations have always remained spellbinding for researchers²⁸, in both astrophysical and laboratory environments. Nevertheless, intense plasma interactions are providing new avenues for research and development in the relativistic regimes²⁹. This not only has direct applications in inertially confined fusion plasmas, but also for the study of ultra-high energy cosmic rays in astrophysics³⁰. Needless to say, relativistic effects in plasmas are not limited to degeneracy only and can appear in other forms too. For instance, highly intense short laser pulses have been used to observe relativistic plasma waves^31,32, aiding in the acceleration of the particles to relativistic energies. In astrophysical landscapes, relativistic and ultrarelativistic effects²⁷plays a crucial role in shaping the dynamics of neutron stars, white dwarfs and swirling accretion disks of black holes, which comes about due to the extreme conditions of density, temperature¹⁹and magnetic fields³³. It is imperative to note that thermonuclear fusion ceases to exist in a white dwarf and the star’s structure is held by a balance between the electron degeneracy pressure and the immense force due to gravity³⁴. In these compressed states, relativistic degenerate electrons are surrounded by bare nuclei of carbon and other heavier elements due to which they can be modelled as a one component plasma³⁵. Whereas neutron stars are held together by a balance between neutron degeneracy pressure and gravity³⁶. Lenzen et al.³⁷ have expressed the total number density of electrons from the nuclei density of condensed magnetic matter. The surface electron density at neutron star is proportional to $\:{B}^{6/5}$, for example, $\:{n}_{e}\approx\:{10}^{34}{m}^{-3}$ for $\:B\approx\:{10}^{8}\:Tesla$³⁷.

Astrophysical environments are rich in various phenomena such as instabilities, anisotropies, high energy interaction, relativistic effects and X-ray bursts from stars etc. The existence of MHD waves in the surface layer of neutron stars are justified^38,39. Hence it becomes crucial to deal with wave dispersions and nonlinearities to study plasma in such domains. In recent decades, substantial research has been conducted to investigate the aforementioned phenomena. Tsintsadze N. L. et al.⁴⁰ showed that high frequency electrical fields in the transverse direction are not “steady” in a relativistic plasma. Using such instabilities, the existence of strong cosmic radiation can be explained. Flacco et al.⁴¹suggested strong cosmic magnetization is the consequence of ultra-high energy particles and studied magnetic fields driven by relativistic electrons in plasma. For an ultrarelativistic degenerate electron positron gas, the nonlinear screening effects have been investigated and it was observed that screening length was reduced due to strong spatial fluctuations in the potential field⁴². Due to the prevailing nonlinearities in the MHD equations, the presence of solitary structures becomes possible. Solitary structures are observed throughout nature^43,44,45and are also present in Fermionic superfluids⁴⁶. The particle nature of solitons has been verified experimentally⁴⁶ and their existence is supported by theoretical models and experimental studies. Roy et al.⁴⁷carried out the stability analysis of electromagnetic (EM) solitons and studied their dependence on degeneracy parameters for a dense relativistic laser plasma. Modulational instabilities of EM waves in partially degenerate relativistic plasma have also been carried out for nonlinear solitary structures⁴⁸. El-Labany et al.⁴⁹have shown simulation results of oblique interactions of solitons in a relativistic dense plasma. Trapped electron distribution^50,51,52interestingly changes the order of nonlinearities in a plasma system, and this verified phenomenon^53,54,55,56has also compelling implications in both the relativistic and ultrarelativistic regimes⁵⁷. Following the work by Shah et al.⁵⁷, Iqbal et al.⁵⁸ investigated the effect of quantizing magnetic field on nonlinear ion acoustic waves and examined the solitary profiles by varying density, magnetic field, and Mach number.

Investigation of kinetic Alfven-acoustic waves (KAAW) in a partially degenerate relativistic plasma can find applications in laser-solid density plasma interactions²³, superdense stars, and nano-scale photonics. Primarily, KAAW were theoretically studied for classical plasmas^59,60,61. In the laboratory, KAAW have been investigated in spontaneous fluctuations of temperature filament⁶²and in the experiments on magnetized helium plasmas⁶³. In space, the Kelvin-Helmholtz instability⁶⁴and 2D vortex structures in ionosphere observed by IC-B-1300 satellite⁶⁵are considered as an effective source of KAAW. In dense astrophysical objects, research on Alfven waves highlights various phenomena. Studies explore spin effects on KAW^66,67, SKAAW⁶⁸in nonrelativistic dense plasma and Alfven waves driven winds in proto-neutron stars⁶⁹. Observations on fast radio burst (FRBs) data from SGR 1935 + 2154 (SGR 1935 + 2154 is a galactic magnetar) consider these FRBs as a source of Alfven waves⁷⁰. Simulations show their role in explaining quasi-periodic oscillations⁷¹in neutron star cores and for the generation of plasmoids⁷². These plasmoids are closed magnetic loops that accelerate and drive blast waves into magnetar winds. Observations connect Alfven wave activity with X-ray and radio emissions from magnetars and soft gamma repeaters⁷³, providing insight into high-energy astrophysical events. Recently, Chen et al.⁷⁴ proposed that instabilities in the magnetospheres of neutron stars could generate relativistic Alfven waves and boost the electric currents along the curved magnetic field lines.

In this paper, relativistic and ultra relativistic regimes of degenerate plasmas are considered using two-potential theory⁷⁵. This approach is valid for low frequency ($\:{\omega\:}^{2}<<{{\omega\:}_{ci}}^{2}$) and low $\:\beta\:\left(=\:2{{c}_{s}}^{2}/{{v}_{A}}^{2}\right)$ plasmas $\:\left(1>\beta\:>\:{m}_{e}/{m}_{i}\right)$. At the outset in the following section, we furnish the set of MHD equations and present the linear dispersion relation of relativistic KAAW. We have also discussed the limiting cases for ultrarelativistic and nonrelativistic regimes. Next, in section III, we analyse the nonlinear dynamics of the relativistic KAAW by using Sagdeev pseudopotential approach, dynamical analysis, and finite amplitude expansion method in a stationary frame of reference and discussed different wave solutions. In section IV, the nonlinear analysis of ultrarelativistic KAAW is carried out to study the nonlinear structures. Finally, we consolidate our work and give the conclusions in section V.

Governing equations of magnetohydrodynamic (MHD) model

We study the propagation characteristics of KAAW for a dense plasma immersed in a uniform external magnetic field $\:{\mathbf{B}}_{\mathbf{o}}={\text{B}}_{\text{o}}\widehat{\text{z}}$, where $\:{\text{B}}_{\text{o}}$ is the magnetic field strength and $\:\widehat{\text{z}}$ is the unit vector along the z-direction. Relativistic degeneracy implies that the Fermi energy of the electrons is comparable to the rest mass energy of electrons. Due to the finite ion Larmour radius effect, we consider electrons to be inertialess in comparison to heavy ions ($\:{m}_{i}\gg\:{m}_{e}$), which can be modelled classically. We choose the propagation vector $\:\varvec{k}$ to lie in the x-z plane and apply the two-potential theory, such that, the gradients of the potentials $\:\varnothing\:$ and $\:\psi\:$ can be written as the components of electric field $\:\varvec{E}$⁷⁵ and as pointed out in the preceding section, the two potential approximation is applicable in low $\:\beta\:$ plasma. Most of the astrophysical plasmas are low $\:\beta\:$ plasma. Thus, we have

$$\:k=\left(Sin\theta\:\:,\:0\:,\:Cos\theta\:\right)\:,\:\:{E}_{x}=-\raisebox{1ex}{$\partial\:\varnothing\:$}\!\left/\:\!\raisebox{-1ex}{$\partial\:x$}\right.\:,\:\:{E}_{z}=-\raisebox{1ex}{$\partial\:\psi\:$}\!\left/\:\!\raisebox{-1ex}{$\partial\:z$}\right.\:,\:\:and\:\:\:\:{E}_{y}=0$$

(1)

The dynamics of low frequency KAAW⁷⁶ are governed by the ion equation of motion,

$$\:{m}_{i}\left({\partial\:}_{\varvec{t}}+{\varvec{v}}_{\varvec{i}}.\nabla\:\right){\varvec{v}}_{\varvec{i}}=e\left(\varvec{E}+{\varvec{v}}_{\varvec{i}}\times\:{\varvec{B}}_{0}\right)$$

(2)

The continuity equation and the low frequency approximation of Maxwell’s curl equations are given by

$$\:{\partial\:}_{\varvec{t}}{n}_{\varvec{q}}+\nabla\:.\left({n}_{\varvec{q}}\:{\varvec{v}}_{\varvec{q}}\right)=0$$

(3)

$$\:\nabla\:\times\:\left(\nabla\:\times\:\varvec{E}\right)=-{\mu\:}_{0}\:{\partial\:}_{\varvec{t}}\:\varvec{j}$$

(4)

Where $\:{n}_{\varvec{q}}$ and $\:{\varvec{v}}_{\varvec{q}}(q=i,\:e)$ respectively be the density and velocity of the species. $\:\varvec{j}(=\:e\left({n}_{i}{\varvec{v}}_{\varvec{i}}-\:{n}_{e}{\varvec{v}}_{\varvec{e}}\:\right))$is the current density and the electron density for partially degenerate relativistic plasma is described by the following distribution⁵⁷

$$\:{n}_{eR}={N}_{oR}\left[{{\left\{\left(1+\left.{{\Psi\:}}_{R}\right)\right.\right.}^{2}-\left.{\epsilon}_{0}^{2}\right\}}^{\frac{3}{2}}+\frac{{\pi\:}^{2}{T}_{R}^{2}}{2}\frac{\left\{2{\left(1+{{\Psi\:}}_{R}\right)}^{2}-{\epsilon}_{0}^{2}\right\}}{\sqrt{{\left(1+{{\Psi\:}}_{R}\right)}^{2}-{\epsilon}_{0}^{2}}}\right]$$

(5)

We note that the expression $\:\left(5\right)$ follows from the Fermi-Dirac distribution function and here $\:{N}_{oR}\left(={\mu\:}^{3}/3{\pi\:}^{2}{\left(\hslash\:c\right)}^{3}\right)$ is the relativistic background density, $\:{{\Psi\:}}_{R}\left(=e\:\psi\:/\mu\:\right)$ is the normalized potential, $\:{\epsilon}_{o}\left(={m}_{e\:}{c}^{2}/\mu\:\right)$ is the total normalized energy, $\:{T}_{R}\left(=T/\mu\:\right)$ is the normalized ambient temperature the presence of which indicates partial degeneracy, and $\:\mu\:\left(={\epsilon\:}_{Fo}+{m}_{e\:}{c}^{2}\right)$ is the chemical potential for a relativistic quantum plasma. The subscript R denotes relativistic case. The Fermi energy is given by $\:{\epsilon\:}_{Fo}=({\hslash\:}^{2}/2{m}_{e}){\left(3{\pi\:}^{2}{N}_{oR}\right)}^{2/3}$ and in the absence of perturbed potential the electron number density$\:{\:n}_{eoR}$ is defined as,

$$\:{n}_{eoR}={N}_{oR}\left[{\left(1-{\epsilon}_{0}^{2}\right)}^{\frac{3}{2}}+\frac{{\pi\:}^{2}{T}_{R}^{2}}{2}\frac{\left(2-{\epsilon}_{0}^{2}\right)}{\sqrt{1-{\epsilon}_{0}^{2}}}\:\right]$$

(6)

At a certain point in a plasma system both the relativistic and nonrelativistic situations cannot coexist. However, as we move towards the core, the density increases and system transits from nonrelativistic to a relativistic regime.

In the given geometry, we linearize Eqs. (1–4) for the low frequency KAAW waves $\:\left({\omega\:}^{2}<<{\varOmega\:}_{ci}^{2}\right)$ and obtain the components of momentum equation. The linearized ion and electron continuity equations come from quasi-neutrality condition $\:({n}_{eoR}\approx\:\:{n}_{ioR})$ and Eq. (4) is solved for two scalar potentials $\:\varnothing\:$ and $\:\psi\:$. The current density $\:{j}_{z}$ is obtained by using linearized electron continuity equation. Further, by eliminating the dimensionless potential $\:{\varPhi\:}_{R}\left(=e\:\varnothing\:/\mu\:\right)$, we obtain the linear dispersion relation given by,

$$\:\left(1-\frac{{v}_{AR}^{2}\:{\:k}_{z}^{2}\:}{{\omega\:}^{2}}\right)\left(1-\frac{\:{{C}_{sFR}^{2}\:k}_{z}^{2}\:}{{\omega\:}^{2}}\right)=\frac{{v}_{AR}^{2}\:{\:k}_{z}^{2}}{{\omega\:}^{2}}\:{\lambda\:}_{sFR}$$

(7)

The linear dispersion relation of KAAW is crucial for understanding wave propagation, which is influenced by both the Alfven velocity and ion thermal velocity. We note that the two factors on the left-hand side of Eq. (7), individually set to zero when $\:{\lambda\:}_{sFR}=0$ (i.e. when $\:{k}_{x}\to\:0$), give Alfven and ion acoustic wave dispersion equations for a relativistic quantum plasma. These two waves are coupled through the coupling parameter $\:{\lambda\:}_{sFR}\left(={\:k}_{x}^{2}\:{C}_{sFR}^{2}/{\omega\:}_{ci}^{2}\right)$. Here, $\:{C}_{sFR}\left(=\sqrt{\mu\:/{m}_{i}\:{A}_{R}}\right)$is the relativistic Fermi ion sound velocity⁵⁷, $\:{\omega\:}_{ci}\left(=e{B}_{0}/{m}_{i}\right)$ is the ion cyclotron frequency and $\:{v}_{AR}(={B}_{0}/{{\mu\:}_{o}\:n}_{eoR}\:{m}_{i})$ is the Alfven velocity for a relativistic quantum plasma. The factor $\:{A}_{R}$ carries both the relativistic and small temperature effects, defined as

$$\:{A}_{R}=\frac{\left[6{\left(1-{\epsilon}_{0}^{2}\right)}^{2}+{\pi\:}^{2}{T}_{R}^{2}\left(2-3{\epsilon}_{0}^{2}\right)\right]}{\left(1-{\epsilon}_{0}^{2}\right)\left[2{\left(1-{\epsilon}_{0}^{2}\right)}^{2}+{\pi\:}^{2}{T}_{R}^{2}\left(2-{\epsilon}_{0}^{2}\right)\:\right]}$$

(8)

We obtain the frequencies of both the fast and slow modes of KAAW from the dispersion relation in Eq. (7) as,

$$\:{\omega\:}_{\pm\:}^{2}=\frac{{k}_{z}^{2}\:}{2}\left[{C}_{sFR}^{2}+{v}_{AR}^{2}\left(1+{\lambda\:}_{sFR}\right)\pm\:\sqrt{{\left({C}_{sFR}^{2}+{v}_{AR}^{2}\left(1+{\lambda\:}_{sFR}\right)\right)}^{2}-4\:{C}_{sFR}^{2}{v}_{AR}^{2}\:}\:\right]$$

(9)

The $\:\pm\:$ sign corresponds to fast and slow modes respectively. Equation (9) shows that for perpendicular propagation i.e. at $\:\theta\:={90}^{o}$, $\:\omega\:/k\to\:\infty\:$ and there will be no wave momentum in the medium. Also, as $\:\omega\:={\omega\:}_{ci}$ the group velocity goes to zero and wave dispersion will disappear.

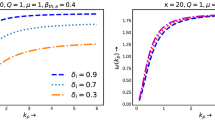
The fast and slow features of relativistic KAAW are shown in Fig. 1. Figure 1(a) is plotted for the normalized wave frequency $\:\left(\omega\:/{k\:v}_{AR}\right)$ against the normalized perpendicular wave number $\:\left({k}_{x}/k\right)$ with $\:k=\sqrt{{k}_{x}^{2}+{k}_{z}^{2}\:}$ and Fig. 1(b) is plotted for the normalized wave frequency $\:\left(\omega\:/{\omega\:}_{ci}\right)$ against the normalized wave number $\:\left(k/{k}_{o}\right)$, with $\:{k}_{o}$ a reference wave number, for angle of propagation $\:{85}^{o}$. It is observed that the wave frequencies are affected by the small temperature effects. At higher $\:{T}_{R}$, the ion thermal velocity increases and modifies the phase velocity of KAAW.

Fig. 1

Dispersion relation plots for slow and fast relativistic KAAW at $\:{\text{T}}_{R}=0$ and $\:{\text{T}}_{R}=0.5$. Other parameters are $\:{n}_{0}=1\times\:{10}^{36}\:{m}^{-3}$, $\:{B}_{0}=1\times\:{10}^{9}\text{T}$, and $\:\:\theta\:={85}^{^\circ\:}$ (a) Normalized wave frequency $\:\left(=\omega\:/{k\:v}_{AR}\right)$ against the normalized perpendicular wave number $\:\left(={k}_{x}/k\right)$, (b) Normalized wave frequency $\:\left(\omega\:/{\omega\:}_{ci}\right)$ against the normalized wave number $\:\left(=k/{k}_{o}\right)$ at $\:\theta\:={85}^{^\circ\:}$.

We now briefly consider the two limiting cases of ultrarelativistic and nonrelativistic regimes.

A. Ultrarelativistic case: In a superdense plasma, the Fermi energy becomes much greater than the rest mass energy of electrons, i.e. $\:{\epsilon\:}_{Fo}\gg\:{m}_{e}{c}^{2}$, and degenerate plasma is characterized in ultrarelativistic regime. In this regime $\:{\epsilon}_{o}\to\:0$ and Fermi energy is defined as $\:{\epsilon\:}_{Fo}={cp}_{F}={\left(3{\pi\:}^{2}{n}_{0}\right)}^{1/3}\hslash\:c$. Thus, the distribution given by Eq. (5) becomes

$$\:{n}_{eU}=\:{N}_{oU}\left(1+{{\Psi\:}}_{U}\right)\left[{\left(1+{{\Psi\:}}_{U}\right)}^{2}+{\pi\:}^{2}{T}_{U}^{2}\right]$$

(10)

Where $\:{N}_{oU}=\frac{{{\epsilon\:}_{Fo}}^{3}}{3{\pi\:}^{2}{\left(hc\right)}^{3}}$ is the ultrarelativistic background density and in the absence of perturbed potential the electron number density is $\:{n}_{eoU}={N}_{oU}\left[1+{\pi\:}^{2}{T}_{U}^{2}\right]$. Adopting the same procedure for $\:{n}_{eU}$, the set of Eqs. (1–4) finally gives the linear dispersion relation for ultrarelativistic degenerate plasma, as

$$\:\left(1-\frac{{V}_{AU}^{2}{k}_{z}^{2}}{{\omega\:}^{2}}\right)\left(1-\frac{{C}_{sFU}^{2}{k}_{z}^{2}}{{\omega\:}^{2}}\right)=\frac{{V}_{AU}^{2}{k}_{z}^{2}}{{\omega\:}^{2}}{\lambda\:}_{SFU}$$

(11)

Where $\:{\lambda\:}_{SFU}\left(={\:k}_{x}^{2}\:{C}_{sFU}^{2}/{\omega\:}_{ci}^{2}\right)$ is the coupling parameter, $\:{c}_{sFU}\left(=\sqrt{{\epsilon\:}_{Fo}/{m}_{i}\:{A}_{U}}\right)$ is the ultrarelativistic Fermi ion sound velocity, $\:{v}_{AU}(={B}_{0}/\sqrt{{{\mu\:}_{o}\:n}_{eoU}\:{m}_{i}})$ is the Alfven velocity for a relativistic quantum plasma, and $\:{A}_{U}$ is the ultrarelativistic factor for a partially degenerate plasma, defined as

$$\:{A}_{U}=\frac{\left(3+{\pi\:}^{2}{T}_{U}^{2}\right)}{\left(1+{\pi\:}^{2}{T}_{U}^{2}\right)}$$

(12)

B. Nonrelativistic case: In the nonrelativistic case, the Fermi energy is much less than the rest mass energy of electrons, i.e. $\:{\epsilon\:}_{Fo}\ll\:{m}_{e}{c}^{2}$ and we retrieve the results already presented by Sabeen et al. and Asam et al.^68,77.

It is clearly seen that the relativistic, ultrarelativistic and nonrelativistic KAAW show dispersion for both the slow and fast modes in a degenerate plasma as shown in Fig. (2). These waves can traverse through ultra-high densities and transfer energy, parallel to the strong ambient magnetic fields along with the trail of charged particles. It also shows that, in constant magnetic fields, as plasma shifts from nonrelativistic to ultrarelativistic regimes, the phase velocity of KAAW decreases due to an increase in both the specific heat and thermal pressure at low plasma beta $\:\left({\beta\:}_{FR}=\frac{2{{C}_{sFR}}^{2}}{{{v}_{AR}}^{2}}\right)\:$values i.e. $\:\frac{{m}_{e}}{{m}_{i}}<{\beta\:}_{FR}<1\:$. This intriguing result shows that KAAW propagate more efficiently in outer regions with lower specific heat than in denser inner regions of neutron stars.

Fig. 2

Dispersion relation plots for relativistic, ultrarelativistic and nonrelativistic regimes for fully degenerate case with $\:{n}_{0}=1\times\:{10}^{36}\:{m}^{-3}$, $\:{B}_{0}=1\times\:{10}^{9}\text{T}$, and $\:\:\theta\:={85}^{^\circ\:}$ (a) slow mode of KAAW (b) fast mode of KAAW.

Nonlinear analysis of relativistic KAAW

• A. Pseudopotential method.

We investigate the nonlinear spread of KAAW in a partially degenerate relativistic magnetoplasma by employing Sagdeev potential (pseudopotential) approach. In order to examine the existence conditions of nonlinear solitary profiles, we choose a normalized comoving frame of reference, such that $\:\xi\:={\:k}_{x}\:x+{\:k}_{z}\:z-M\:t$⁷⁸. $\:{\:k}_{x}$ and $\:{\:k}_{z}$ are the directional cosines and $\:M(=u/{C}_{sFR})$is the Mach number. In this one-dimensional frame, the wave propagates obliquely to the ambient magnetic field $\:{\varvec{B}}_{\varvec{o}}$ and will be stationary with respect to $\:\xi\:$. In this stationary frame, the particle number densities are normalized by their respective equilibrium densities, velocities by relativistic Fermi ion sound velocity $\:{C}_{sFR}$, scale length by ion gyroradius $\:(={C}_{sFR}/{\omega\:}_{ci})$, and time scale by $\:{\omega\:}_{ci}$. Thenceforth, the system of Eqs. (1–4) in the dimensionless frame $\:\xi\:$ is as follows,

$$\:-M\:{\partial\:}_{\xi\:}{v}_{z}+{v}_{x}{\:k}_{x}{\partial\:}_{\xi\:}{v}_{z}+{v}_{z}{\:k}_{z}{\partial\:}_{\xi\:}{v}_{z}=-{A}_{R}{\:k}_{z}{\partial\:}_{\xi\:}{{\Psi\:}}_{R}$$

(13)

$$\:{v}_{x}={\:k}_{x}\:M\:{A}_{R}\:{\partial\:}_{\xi\:}^{2}{\varPhi\:}_{R}$$

(14)

$$\:-M\:{\partial\:}_{\xi\:}{n}_{R}+{\:k}_{x}{\partial\:}_{\xi\:}\left({n}_{R}{v}_{x}\right)+{\:k}_{z}{\partial\:}_{\xi\:}\left({n}_{R}{v}_{z}\right)=0$$

(15)

$$\:2{A}_{R}{\:k}_{x}^{2}{\:k}_{z}^{2}{\partial\:}_{\xi\:}^{4}\left({\varPhi\:}_{R}-{{\Psi\:}}_{R}\right)={\beta\:}_{FR}\:\left[{M}^{2}{\:\partial\:}_{\xi\:}^{2}{n}_{R}-M{\:k}_{z}\:{\partial\:}_{\xi\:}^{2}{(n}_{R}{v}_{z})\right]$$

(16)

We integrate Eq. (15) by applying boundary conditions that as $\:\xi\:\to\:\infty\:$, the perturbed quantities $\:{v}_{x},{v}_{z},{{\Psi\:}}_{R}\to\:0$ and the number density $\:{n}_{R}\to\:{\alpha\:}_{R}$, yields

$$\:{\:k}_{x}{v}_{x}+{\:k}_{z}{v}_{z}=M\left(1-\frac{{\alpha\:}_{R}}{{n}_{R}}\right)$$

(17)

$$\:2{A}_{R}{\:k}_{x}^{2}{\:k}_{z}^{2}{\partial\:}_{\xi\:}^{2}\left({\varPhi\:}_{R}-{{\Psi\:}}_{R}\right)={\beta\:}_{FR}\:\left[{M}^{2}({n}_{R}-{\alpha\:}_{R})-M{\:k}_{z}{n}_{R}{v}_{z}\right]$$

(18)

Using Eqs. (5), (13) and (17), we get

$$\:{{\partial\:}_{\xi\:}v}_{z}=\frac{{A}_{R}{\:k}_{z}}{M\:{\alpha\:}_{R}}{\delta\:}_{1}^{-\frac{1}{2}}\left[{\delta\:}_{1}^{\:2}+{\delta\:}_{T}^{2}\:\left\{2{\left(1+{{\Psi\:}}_{R}\right)}^{2}-{\epsilon}_{0}^{2}\right\}\right]{\partial\:}_{\xi\:}{{\Psi\:}}_{R}$$

(19)

 $Here \;\:{n}_{R}=\left(\raisebox{1ex}{${n}_{eR}$}\!\left/\:\!\raisebox{-1ex}{${N}_{oR}$}\right.\right),\:\:{\alpha\:}_{R}={\delta\:}_{2}^{-\frac{1}{2}}\:\left[\:{\delta\:}_{2}^{\:\:2}+{\delta\:}_{T}^{2}\:\left(2-{\epsilon\:}_{0}^{2}\right)\right]\:,\:\:\:\:{\delta\:}_{T}=\frac{\pi\:\:\:{T}_{R}}{\sqrt{2}}\:\:\:,\:\:{\delta\:}_{1}={\left\{\left(1+\left.{{\Psi\:}}_{R}\right)\right.\right.}^{2}-\left.{\epsilon}_{0}^{2}\right\}$

$$\:{and\:\:\delta\:}_{2}=\left(1-{\epsilon}_{0}^{2}\right)$$

.

Integrating Eq. (19) and applying the boundary conditions $\:{{v}_{z},\:\psi\:}_{R}\to\:0$ as $\:\xi\:\to\:\infty\:$, we obtain an expression for the parallel ion velocity $\:{v}_{z}$

$$\:{v}_{z}=\frac{{A}_{R}\:{k}_{z}}{M\:{\alpha\:}_{R}}{\delta\:}_{1}^{\frac{1}{2}}\left[\frac{1}{5}{\delta\:}_{1}^{\:2}+{\delta\:}_{T}^{2}\left\{{\epsilon}_{0}^{2}+\:\frac{2}{3}{\delta\:}_{1}\right\}\right]+{C}_{1}$$

(20)

The constant of integration

$$\:{C}_{1}=-\frac{{A}_{R}{\:k}_{z}}{M\:{\alpha\:}_{R}}{\delta\:}_{2}^{\:\frac{1}{2}}\left[\:\frac{1}{5}{\delta\:}_{2}^{\:\:2}+{\delta\:}_{T}^{2}\:\left\{{\epsilon}_{0}^{2}+\frac{2}{3}{\delta\:}_{2}\right\}\right]$$

(21)

Solving Eqs. (14), (17) and (18) gives the following expression

$$\:{A}_{R}{\:k}_{x}^{2}\:{\partial\:}_{\xi\:}^{2}{{\Psi\:}}_{R}=1-\frac{{\alpha\:}_{R}}{{n}_{R}}-\frac{{\:k}_{z\:\:}{v}_{z}\:}{M}-\frac{{\beta\:}_{FR}\:{M}^{2}}{2\:{\:k}_{z}^{2}}\left({n}_{R}-{\alpha\:}_{R}\right)+\frac{{\beta\:}_{FR}\:M\:{n}_{R\:}{v}_{z}}{2\:{\:k}_{z\:\:}}$$

(22)

We insert Eqs. (5) and (20) in the above expression and expand the term $\:\raisebox{1ex}{${\alpha\:}_{R}$}\!\left/\:\!\raisebox{-1ex}{${n}_{R}$}\right.$ with respect to temperature. Here, we have ignored higher order terms and the terms containing $\:{T}_{R}^{4}$ (for a quantum plasma $\:{\text{T}}_{R}<1$). Moreover, Eq. (22) is integrated to express through Sagdeev potential⁷⁹ in the usual manner,

$$\:V\left({{\Psi\:}}_{R}\right)=\:-\frac{1}{2}\:{\left({\partial\:}_{\xi\:}{{\Psi\:}}_{R}\right)}^{2}$$

(23)

Therefore Eq. (22) yields,

$$\begin{aligned} V\left({{\Psi}}{R}\right)&=-\frac{1}{{A}{R}{k}{x}^{2}}\left[{{\Psi}}{R}+{\alpha}{R}{\delta}{1}^{-\frac{1}{2}}\left\{1-\frac{1}{5}{\delta}{T}^{2}{\delta}{1}^{-2}\left({\epsilon}{0}^{2}+\frac{10}{3}{\delta}{1}\right)\right\}-\frac{{k}{z}^{2}{A}{R}}{{M}^{2}{\alpha}{R}}\left\{\frac{1}{35}{\delta}{1}^{\frac{7}{2}}+\frac{{\delta}{T}^{2}}{3}{\delta}{1}^{\frac{3}{2}}\left({\epsilon}{0}^{2}+\frac{2}{5}{\delta}{1}\right)-{C}{1}{{\Psi}}{R}\right\} \right.\\ &\quad -\frac{{\beta}{FR}\:{M}^{2}}{2{k}{z}^{2}}\left\{\frac{1}{5}{\delta}{1}^{\frac{5}{2}}+{\delta}{T}^{2}{\delta}{1}^{\frac{1}{2}}\left({\epsilon}{0}^{2}+\frac{2}{3}{\delta}{1}\right)-{\alpha}{R}{{\Psi}}{R}\right\} \\ &\quad \left.+\frac{{\beta}{FR}{A}{R}}{2{\alpha}{R}}\left\{\frac{1}{50}{\delta}{1}^{5}-\frac{{C}{1}}{5}{\delta}{1}^{\frac{5}{2}}+{\delta}{T}^{2}{\delta}{1}^{\frac{1}{2}}\left({\epsilon}{0}^{2}+\frac{2}{3}{\delta}{1}\right)\left\{\frac{1}{5}{\delta}{1}^{\frac{5}{2}}-{C}{1}\right\}\right\}\right]+{C}{2}\end{aligned}$$

(24)

$\:{C}_{2}$ is the constant of integration and defined as,

$$\begin{aligned}\:{C}{2}&=\frac{1}{\:{A}{R}{k}{x}^{2}\:}\left[{\alpha\:}{R}\:{\delta\:}{2}^{-\frac{1}{2}}\left\{1-\frac{1}{5}{\delta\:}{T}^{2}{\:\delta\:}{2}^{\:-2}\left({\epsilon}{0}^{2}+\frac{10}{3}{\delta\:}{2}\right)\right\}\right.\\ &\quad -\frac{{k}{z}^{2}\:{A}{R}}{{M}^{2}{\alpha\:}{R}}\left\{\frac{1}{35}\:{\delta\:}{2}^{\frac{7}{2}}+\frac{{\delta\:}{T}^{2}}{3}{\delta\:}{2}^{\frac{3}{2}}\:\left({\epsilon}{0}^{2}+\frac{2}{5}{\delta\:}{2}\right)\right\}\\ &\quad -\frac{{\beta\:}{FR}\:{M}^{2}}{2{\:k}{z}^{2}}\left\{\frac{1}{5}\:{\delta\:}{2}^{\frac{5}{2}}+{\delta\:}{T}^{2}\:{\delta\:}{2}^{\frac{1}{2}}\left({\epsilon}{0}^{2}+\frac{2}{3}{\delta\:}{2}\right)\right\}\\ &\left.\quad +\frac{{\beta\:}{FR}\:{A}{R}}{2\:{\alpha\:}{R}}\left\{\frac{1}{50}{\delta\:}{2}^{5}-\frac{{C}{1}}{5}{\delta\:}{2}^{\frac{5}{2}}+{\delta\:}{T}^{2}{\:\delta\:}{2}^{\frac{1}{2}}\left({\epsilon}{0}^{2}+\frac{2}{3}{\delta\:}{2}\right)\left\{\frac{1}{5}\:{\delta\:}{2}^{\frac{5}{2}}-{C}{1}\right\}\right\}\right]\end{aligned}$$

(25)

The obtained expression of Sagdeev Pseudopotential $\:V\left({{\Psi\:}}_{R}\right)$ in Eq. (24) does not give solitary KAAW except for fully degenerate relativistic plasma, i.e. $\:{\text{T}}_{R}=0$ (see Figs. (3–5) in the next sub section). Therefore, for partially degenerate relativistic regime the nonlinear KAAW is further analysed by employing dynamical analysis.

• B. Autonomous Dynamical Analysis.

As seen in the previous subsection, the presence of fractional nonlinearities show that the Sagdeev potential approach does not yield solitary solution for KAAW and, therefore, it will be useful to perform a qualitative analysis of phase portraits in a dynamical system^80,81. Such a system enables the understanding of wave trajectories in a phase space to provide a better analysis from the numerical solution. Considering $\:Q={\partial\:}_{\xi\:}{{\Psi\:}}_{R}$, we get the following dynamical system

$$\:\left[\begin{array}{c}\dot{{{\Psi\:}}_{R}}={\partial\:}_{\xi\:}{{\Psi\:}}_{R}=W\\\:\dot{W}={\partial\:}_{\xi\:}W\end{array}\right.$$

(26)

$$\begin{aligned} \:{Where\:\:\:\:\partial\:}_{\xi\:}W&=\frac{1}{\:{A}_{R}{k}_{x}^{2}\:}\left[1-{{\alpha\:}_{R}\:\delta\:}_{1}^{-\frac{3}{2}}\left\{1-{\delta\:}_{T}^{2}\:{\delta\:}_{1}^{\:-2}\left(2{\left(1+{{\Psi\:}}_{R}\right)}^{2}-{\epsilon}_{0}^{2}\right)\right\}\right.\\ &\quad -\frac{{k}_{z}^{2}\:{A}_{R}}{{M}^{2}{\alpha\:}_{R}}\left\{\frac{1}{5}{\delta\:}_{1}^{\frac{5}{2}}+{\delta\:}_{T}^{2}\:{\delta\:}_{1}^{\frac{1}{2}}\left\{{\epsilon}_{0}^{2}+\:\frac{2}{3}{\delta\:}_{1}\right\}+\frac{1}{5}{\delta\:}_{2}^{\:\frac{5}{2}}+{\delta\:}_{T}^{2}\:{\delta\:}_{2}^{\:\frac{1}{2}}\left\{{\epsilon}_{0}^{2}+\frac{2}{3}{\delta\:}_{2}\right\}\right\}\\ &\quad -\frac{{\beta\:}_{FR}\:{M}^{2}}{2{\:k}_{z}^{2}}\left\{{\delta\:}_{1}^{\frac{3}{2}}+{\delta\:}_{T}^{2}{\:\delta\:}_{1}^{-\frac{1}{2}}\left\{2{\left(1+{{\Psi\:}}_{R}\right)}^{2}-{\epsilon}_{0}^{2}\right\}-{\alpha\:}_{R}\right\}\\ &\quad +\frac{{\beta\:}_{FR}{A}_{R}}{2\:{\alpha\:}_{R}}\left\{{\delta\:}_{1}^{\frac{3}{2}}+{\delta\:}_{T}^{2}\:{\delta\:}_{1}^{-\frac{1}{2}}\left\{2{\left(1+{{\Psi\:}}_{R}\right)}^{2}-{\epsilon}_{0}^{2}\right\}\right\}\left\{\frac{1}{5}\left\{{\delta\:}_{1}^{\frac{5}{2}}+{\delta\:}_{2}^{\:\frac{5}{2}}\right\}\right.\\ &\quad \left.\left.+{\delta\:}_{T}^{2}\:{\delta\:}_{1}^{\frac{1}{2}}\left\{{\epsilon}_{0}^{2}+\frac{2}{3}{\delta\:}_{1}\right\}+{\delta\:}_{T}^{2}\:{\delta\:}_{2}^{\:\frac{1}{2}}\left\{{\epsilon}_{0}^{2}+\frac{2}{3}{\delta\:}_{2}\right\}\right\}\right]\end{aligned}$$

(27)

The Hamiltonian for the system carries effective potential⁸², which in our case is $\:V\left({{\Psi\:}}_{R}\right)$. Here Hamiltonian function $\:H\left({{\Psi\:}}_{R},W\right)$ is defined as,

$$\:H\left({{\Psi\:}}_{R},W\right)=\frac{{W}^{2}}{2}+V\left({{\Psi\:}}_{R}\right)$$

(28)

The characteristics equation $\:det\left(J-\lambda\:\:I\right)=0$ along with Jacobian matrix $\:J=\left(\begin{array}{cc}0&\:1\\\:Q&\:0\end{array}\right)$ gives the required eigenvalues $\:{\:\lambda\:}_{\:\text{1,2}}$ as,

$$\:\left|\begin{array}{cc}-\lambda\:&\:1\\\:Q&\:-\lambda\:\end{array}\right|=0\:\:\:\:\:{\Rightarrow\:\:\:\:\lambda\:}_{\:\text{1,2}}=\pm\:\sqrt{Q}$$

(29)

Where “I” is the identity matrix and $\:Q={\partial\:}_{{{\Psi\:}}_{R}}\left({\partial\:}_{\xi\:}W\right)$. Here, for different parametric values, the fixed points and eigenvalues are obtained numerically due to the transcendental nature of the dynamical system. For $\:Q<0,$ the imaginary eigen values correspond to the centers and for $\:Q>0$, real eigen values correspond to saddle points⁸³.

The dynamical system in Eq. (26) has been analysed by phase space plots to study the wave solutions in Figs. (2–5) for relativistic KAAW in a dense plasma with the support of numerical computations. The physical parameters used for plotting phase portraits are taken from the precincts of white dwarfs and neutron stars. For studying relativistic and ultrarelativistic regimes, the number density ranges⁸ from $\:1\times\:{10}^{32}\:{m}^{-3}$ to $\:1\times\:{10}^{38}\:{m}^{-3}$. Here, we have taken the parameters $\:{N}_{o}=1\times\:{10}^{36}\:{m}^{-3}$ and magnetic field $\:{B}_{o}=1\times\:{10}^{9}\text{T}\:$ for the aforementioned dense stars. Mach number $\:M=0.6\:$is taken for the subsonic regime that means the phase velocity is less than the relativistic Fermi ion sound velocity is i.e. $\:(\omega\:/k)<{C}_{sFR}$. The angle of propagation $\:\theta\:$ is taken $\:{75}^{^\circ\:}$ because these KAAW propagate at large angles with respect to ambient magnetic field$\:{\:B}_{o}$.

Fig. 3

Dynamical plots with $\:{n}_{0}=1\times\:{10}^{36}\:{m}^{-3}$, $\:{B}_{0}=1\times\:{10}^{9}\text{T}$ ,$\:\:\theta\:={75}^{^\circ\:}$and $\:M=0.6$. (a) Phase portrait at $\:{\text{T}}_{R}=0.1$ (b) The corresponding nonlinear solitary pulses (c) The corresponding nonlinear periodic KAAW (d) The Effective potential.

In Fig. 3, we have plotted the phase portraits, effective potential and the corresponding nonlinear structures for partially degenerate relativistic KAAW. The phase portrait of dynamical system in Fig. 3(a) gives nonlinear homoclinic orbit (NHO) for $\:{\text{T}}_{R}=0.1$, which corresponds to the nonlinear solitary pulses in Fig. 3(b). The closed nonlinear periodic orbits (NPO) within the NHO corresponds to the nonlinear periodic kinetic Alfven acoustic wave (NPKAAW) in Fig. 3(c). Mostly conservative systems cause such trajectories. The outermost closed orbit, which encloses NHO, is the nonlinear super periodic orbit (NSPO). For these trajectories, we have numerically calculated the equilibrium points (fixed points) and the eigenvalues. Eigenvalues show that the fixed point $\:{\text{s}}_{o}$is the saddle point and the fixed points $\:{\text{s}}_{1},\:{\text{s}}_{2}$ are the centers. Figure 3(d) is the effective potential of the aforementioned nonlinear structures.

In case of a fully degenerate relativistic KAAW, the phase portraits, effective potential, and the corresponding nonlinear structures have been plotted in Fig. 4. It is observed in Fig. 4(a) that for a NHO, there exists a saddle point $\:{\text{s}}_{o}\left(\text{0,0}\right)$ at the origin at $\:{\text{T}}_{R}=0$. In the phase portrait this corresponds to the solitary waves. Figure 4(b) shows homoclinic orbits corresponding solitary kinetic Alfven acoustic waves (SKAAW). We have numerically obtained the range of Mach number at $\:{\text{T}}_{R}=0$ for which SKAAW are obtained, i.e. $\:0.316\le\:M\le\:1.4$. The range of Mach number confirms the existence of SKAAW for both the sub and supersonic regimes of a fully degenerate relativistic plasma. NPO enclosing the fixed point $\:{\text{s}}_{1\:}$corresponds to the NPKAAW is shown in Fig. 4(c). The eigenvalues have shown that the equilibrium point $\:{\text{s}}_{1}$ is the center and the effective potential of the nonlinear structures is shown in Fig. 4(d).

Fig. 4

Dynamical plots with $\:{n}_{0}=1\times\:{10}^{36}\:{m}^{-3}$, $\:{B}_{0}=1\times\:{10}^{9}\text{T}$ ,$\:\:\theta\:={75}^{^\circ\:}$and $\:M=0.6$. (a) Phase portrait at $\:{\text{T}}_{R}=0$ (b) The corresponding solitary KAAW (c) The corresponding nonlinear periodic KAAW (d) The effective potential.

Fig. 5

Sagdeev potential plots corresponding to solitary profiles at $\:{\text{T}}_{R}=0$ (a) effect of number density for $\:{B}_{o}=1\times\:{10}^{9}\text{T}$ ,$\:\:\theta\:={75}^{^\circ\:}$and $\:M=0.6$ (b) effect of magnetic field for $\:{n}_{o}=1\times\:{10}^{36}\:{m}^{-3}$ ,$\:\:\theta\:={75}^{^\circ\:}$and $\:M=0.6$ (c) effect of Mach number for $\:{n}_{o}=1\times\:{10}^{36}\:{m}^{-3}$, $\:{B}_{o}=1\times\:{10}^{9}\text{T}$ and $\:\theta\:={75}^{^\circ\:}\:$(d) effect of angle of propagation for $\:{n}_{o}=1\times\:{10}^{36}\:{m}^{-3}$, $\:{B}_{o}=1\times\:{10}^{9}\text{T}$ and $\:M=0.6$.

In Fig. 5(a), (c), and (d), the increase in $\:{n}_{o},\:M$ and $\:\theta\:$ decreases the width of the Sagdeev potential. This effective potential corresponds to the SKAAW, where both the amplitude and energy density decrease with increasing values of number density, Mach number, and angle of propagation. This occurs because these physical parameters enhance dispersive effects relative to the nonlinear effects. Furthermore, as the ambient magnetic field​ increases, the energy density and amplitude of SKAAW grow, as shown in Fig. 5(b). It is well known that $\:{B}_{o}$​ consistently contributes energy to KAAW, and a similar effect is observed for relativistic SKAAW.

It has been examined that above $\:{\text{T}}_{R}=0$, the nonlinear solitary pulses are obtained corresponding to homoclinic orbits, and we do not get solitary structures, as shown in Fig. 3. A further increase in temperature gives rise to nonlinear periodic orbits, as shown in Fig. 6. For $\:{\text{T}}_{R}=0.3$, the phase space trajectories show NPO, enclosing the fixed point $\:{\text{s}}_{1}$,i.e. center, corresponding to NPKAAW (Fig. 6(a)). The corresponding travelling wave solution is shown in Fig. 6(b).

Fig. 6

Dynamical plots with $\:{n}_{0}=1\times\:{10}^{36}\:{m}^{-3}$, $\:{B}_{0}=1\times\:{10}^{9}\text{T}$ ,$\:\:\theta\:={75}^{^\circ\:}$and $\:M=0.6$. (a) Phase portrait at $\:{\text{T}}_{R}=0.3$ (b) The corresponding nonlinear periodic KAAW.

• A. Finite amplitude solitary KAAW.

In order to get an exact solution of our nonlinear KAAW in a relativistic degenerate plasma, we use small amplitude perturbation expansion method, i.e. $\:{{\Psi\:}}_{R}<1$. So, Eq. (24) gets the form

$$\begin{aligned} &{A}_{R}{\:k}_{x}^{2}\:{\partial\:}_{\xi\:}^{2}{{\Psi\:}}_{R}-\left(1-\frac{{M}^{2}}{{k}_{z}^{2}}\right)\left[\left(\frac{3\:{\beta\:}_{FR}{\delta\:}_{2}^{\:\frac{1}{2}}}{2}-\frac{3\:{k}_{z}^{2}}{{\delta\:}_{2}{\:M}^{2}}\right)-\left\{\frac{4}{{\delta\:}_{2}^{\:3}}\frac{{k}_{z}^{2}}{{\:M}^{2}}-\frac{{\beta\:}_{FR}\left(2+3{\epsilon}_{0}^{2}\right)}{2{\:\delta\:}_{2}^{\:\frac{3}{2}}}\right\}{\delta\:}_{T}^{2}\right]{{\Psi\:}}_{R}\\ &\quad -\frac{3}{2{\:\delta\:}_{2}^{\:2}}\left[\frac{9{\beta\:}_{FR}{\delta\:}_{2}^{\:\frac{3}{2}}}{2}\left(1-\frac{\left(2-{\epsilon}_{0}^{2}\right){\:M}^{2}}{9\:{k}_{z}^{2}}\right)-\left(\left(4+{\epsilon}_{0}^{2}\right)+\frac{3\:{k}_{z}^{2}}{{M}^{2}}\right)\right.\\ &\quad \left.+\left\{\frac{4}{{\:\delta\:}_{2}^{\:2}}\left(\left(3+{\epsilon}_{0}^{2}\right)+\frac{2{k}_{z}^{2}}{{\:M}^{2}}\right)-\frac{3{\beta\:}_{FR}\:}{2\:{\delta\:}_{2}^{\:\frac{1}{2}}}\left(\left(2+3{\epsilon}_{0}^{2}\right)+\frac{{\epsilon}_{0}^{4}{\:M}^{2}}{3\:{k}_{z}^{2}}\right)\right\}{\delta\:}_{T}^{2}\right]{\:{\Psi\:}}_{R}^{2}=0 \end{aligned}$$

(30)

Here, we can get a localized stationary wave solution that describes the formation and spread of a nonlinear structure. The analytical form of the well-recognized soliton solution is given as

$$\:{{\Psi\:}}_{R}\left(\xi\:\right)={{\Psi\:}}_{0R}{\:Sech}^{2}\left({\varDelta\:}^{-1}\:\xi\:\right)$$

(31)

Where $\:\varDelta\:$ is the width and $\:{{\Psi\:}}_{0R}$ is amplitude of solitary structure and is expressed as

$$\:\varDelta\:=2{\left(\frac{1}{{A}_{R}{\:k}_{x}^{2}}\left(1-\frac{{M}^{2}}{{k}_{z}^{2}}\right)\left[\left(\frac{3\:{\beta\:}_{FR}{\delta\:}_{2}^{1/2}}{2}-\frac{3\:{k}_{z}^{2}}{{\delta\:}_{2}{\:M}^{2}}\right)-\left\{\frac{4}{{\delta\:}_{2}^{\:3}}\frac{{k}_{z}^{2}}{{\:M}^{2}}-\frac{{\beta\:}_{FR}\left(2-3{\epsilon}_{0}^{2}\right)}{2{\:\delta\:}_{2}^{\:\frac{3}{2}}}\right\}{\delta\:}_{T}^{2}\right]\right)}^{-1/2}$$

(32)

$$\:{{\Psi\:}}_{0R}=\:\frac{\left(1-\frac{{M}^{2}}{{k}_{z}^{2}}\right)\left[\left(\frac{3\:{\beta\:}_{FR}{\delta\:}_{2}^{\:3/2}}{2}-\frac{3\:{k}_{z}^{2}}{{\delta\:}_{2}{\:M}^{2}}\right)-\left\{\frac{4}{{\delta\:}_{2}^{\:3}}\frac{{k}_{z}^{2}}{{\:M}^{2}}\:-\:\frac{{\beta\:}_{FR}\left(2-3{\epsilon}_{0}^{2}\right)}{2{\:\delta\:}_{2}^{\:3/2}}\right\}{\delta\:}_{T}^{2}\right]}{\frac{1}{{\delta\:}_{2}^{\:2}}\left[\frac{9{\beta\:}_{FR}{\delta\:}_{2}^{3/2}}{2}\left(1-\frac{\left(2-{\epsilon}_{0}^{2}\right){M}^{2}}{9\:{k}_{z}^{2}}\right)-4+{\epsilon}_{0}^{2}+\frac{3{k}_{z}^{2}}{{M}^{2}}+\left\{\frac{4}{{\:\delta\:}_{2}^{2}}\left(3+{\epsilon}_{0}^{2}+\frac{2{k}_{z}^{2}}{{\:M}^{2}}\right)-\frac{3{\beta\:}_{FR}}{2{\delta\:}_{2}^{1/2}}\left(2+3{\epsilon}_{0}^{2}+\frac{{\epsilon}_{0}^{4}{M}^{2}}{3\:{k}_{z}^{2}}\right)\right\}{\delta\:}_{T}^{2}\right]}$$

(33)

We get analytic range of Mach number for the existance of finite amplitude SKAAW in a partially degenerate relativistic plasma as,

$$\:{k}_{z} < M<{k}_{z}{\delta\:}_{2}^{1/4}\:\sqrt{\left(2/{\beta\:}_{FR}\right)\left[(3\:{\delta\:}_{2}^{\:2}-4\:{\delta\:}_{T}^{2})/(3\:{\delta\:}_{2}^{\:4}+\left(2-{\epsilon}^{2}\left(7-{\epsilon}^{2}\left(8-{3\epsilon}^{2}\right)\right)\right){\delta\:}_{T}^{2})\right]}$$

(34)

$$0 < M<{k}_{z}$$

(35)

And in case of fully degenerate relativistic plasma the analytic range for SKAAW is given as,

$$\:{k}_{z}\le\:M\le\:{k}_{z}\:{\delta\:}_{2}^{-3/4}\sqrt{2/{\beta\:}_{FR}}$$

(36)

Fig. 7

At $\:{n}_{0}=1\times\:{10}^{36}\:{m}^{-3}$, $\:{B}_{0}=1\times\:{10}^{9}\text{T}$ (a) $\:{{\Psi\:}}_{0R}$vs. $\:M$ gives compressive regime at $\:{\text{T}}_{R}=0$ (b) $\:{\text{T}}_{R}$vs. $\:M$ gives the existence region for SKAAW (c) 3D plot showing hump and dip for partial degeneracy (d) The rarefactive SKAAW for $\:{\text{T}}_{R}=0.258$ .

Analytical ranges for nonlinear SKAAW, given in Eqs. (34–36), are in accordance with the linear dispersion relation in Eq. (9), that for $\:\theta\:={90}^{o}$, $\:{k}_{z}\to\:0$ and there will be no propagation of nonlinear structures in the medium. In Eq. (34), the upper limit depends on the angle of propagation, plasma beta, partial degeneracy and relativistic effects but the lower limit only depends on the angle of propagation. We have also shown these ranges of Mach number graphically to analyse the existence regions for SKAAW.

Fig. 8

$\:{\text{T}}_{R}$vs. $\:M$ (a, b) The existence regions and the ranges of Mach number at different angles of propagation. (c, d) The effect of magnetic field and density on the ranges of Mach number at constant angle of propagation.

For the relativistic regime, we get both the compressive and the rarefactive finite amplitude SKAAW. In the case of fully degenerate plasma, Fig. 7(a) is plotted against the amplitude and Mach number, gives the.

compressive SKAAW only for the complete range of Mach number. The shaded area in Fig. 7(b) accounts for the existence region of SKAAW for the fully and partially degenerate plasmas. Here it is worth noticing that for every value of normalized ambient temperature $\:{T}_{R}$ there is an upper limit of Mach number given by the boundary of shaded area. The increase in $\:{T}_{R}$ decreases the upper limit of Mach number but the lower limit remains fixed for the specific values of density, magnetic field and angle of propagation (see Eq. (34)). The existence regions of compressive and rarefactive SKAAW are also distinguished in Fig. 7(b). The humps and dips are due to the partial degeneracy, as shown in Fig. 7(c). After $\:{T}_{R}=0.258$, the range of Mach number changes (see Eq. (35)) and we only get rarefactive SKAAW, as shown in Fig. 7(d). In the partial degeneracy limits the rise in $\:{T}_{R}$ decreases the depth and increases the amplitude of SKAAW, which means that normalized ambient temperature lowers the energy density and increases the dispersive effects in comparison to the nonlinear effects.

It is observed that an increase in the angle of propagation for SKAAW decreases the upper and the lower range of Mach number at fixed value of $\:{T}_{R}\:$, and hence the existence region for SKAAW narrows down (see Fig. 8(a) and (b)). The increase in ambient magnetic field and density also decreases the upper range of Mach number (see Fig. 8(c) and (d)). The effect of varying density on the normalized ambient temperature $\:{T}_{R}\left(=T/\mu\:\right)$ is obvious and clear in Fig. 8(d). Therefore, at constant angle of propagation the increase in density can give SKAAW for the greater values of $\:{T}_{R}$ .

Fig. 9

Dynamical plots with $\:{n}_{0}=1\times\:{10}^{38}\:{m}^{-3}$, $\:{B}_{0}=2\times\:{10}^{10}\text{T}$ ,$\:\:\theta\:={85}^{^\circ\:}$and $\:M=0.6$. (a) Phase portrait at $\:{\text{T}}_{R}=0$ (b) The corresponding nonlinear solitary pulses (c) The corresponding nonlinear periodic KAAW (d) The Effective potential.

Nonlinear analysis of Ultrarelativistic KAAW

In the ultrarelativistic regime ($\:{\epsilon\:}_{Fo}\gg\:{m}_{e}{c}^{2}$) of nonlinear KAAW, we follow the steps of Sagdeev pseudopotential approach of the previous sub section and derive an expression of Sagdeev potential by using Eq. (10),

$$\begin{aligned} V\left({{\Psi\:}}_{U}\right)&=-\frac{1}{{A}_{U}\:{k}_{x}^{2}}\left[{{\Psi\:}}_{U}+\frac{{\alpha\:}_{U}}{2}\left\{{\left(1+{{\Psi\:}}_{U}\right)}^{-2}-\frac{{\:\pi\:}^{2}{T}_{U}^{2}}{2}{\left(1+{{\Psi\:}}_{U}\right)}^{-4}\right\}-\frac{{k}_{z}^{2}\:{A}_{U}}{{M}^{2}\:{\alpha\:}_{U}}\left\{\frac{1}{20}{\left(1+{{\Psi\:}}_{U}\right)}^{5}+\frac{{\:\pi\:}^{2}{T}_{U}^{2}}{6}{\left(1+{{\Psi\:}}_{U}\right)}^{3}-{C}_{3}{\psi\:}_{u}\right\}\right.\\ &\quad -\frac{\beta\:{M}^{2}}{2{k}_{z}^{2}}\left\{\frac{1}{4}{\left(1+{{\Psi\:}}_{U}\right)}^{4}+\frac{{\:\pi\:}^{2}{T}_{U}^{2}}{2}{\left(1+{{\Psi\:}}_{U}\right)}^{2}-{\alpha\:}_{U}{{\Psi\:}}_{U}\right\}\\ & \quad \left.+\frac{\beta\:\:{A}_{U}}{16\:{\alpha\:}_{U}\:}\left\{\frac{1}{4}{\left(1+{{\Psi\:}}_{U}\right)}^{8}+{\:\pi\:}^{2}{T}_{u}^{2}{\left(1+{{\Psi\:}}_{U}\right)}^{6}\right\}-{C}_{3}\left\{\frac{1}{4}{\left(1+{{\Psi\:}}_{U}\right)}^{4}+\frac{{\:\pi\:}^{2}{T}_{U}^{2}}{2}{\left(1+{{\Psi\:}}_{U}\right)}^{2}\right\}\right]+{C}_{4} \end{aligned}$$

(37)

Where $\:{C}_{3}$, $\:{C}_{4}$ and $\:{\alpha\:}_{U}$ are the constants of integration and carry the ultrarelativistic effects with partial degeneracy, defined as

$$\:{C}_{3}=-\frac{{A}_{U}{\:k}_{z}}{M\:{\alpha\:}_{U}}\:\left\{\frac{1}{4}+\frac{{\:\pi\:}^{2}{T}_{U}^{2}}{2}\right\}$$

(38)

$$\:{C}_{4}=\frac{1}{{A}_{U}\:{k}_{x}^{2}}\left[\frac{{\alpha\:}_{U}}{2}\left\{1-\frac{{\:\pi\:}^{2}{T}_{U}^{2}}{2}\right\}-\frac{{k}_{z}^{2}\:{A}_{U}}{{M}^{2}\:{\alpha\:}_{U}}\left\{\frac{1}{20}+\frac{{\:\pi\:}^{2}{T}_{U}^{2}}{6}\right\}-\frac{\beta\:{M}^{2}}{2{k}_{z}^{2}}\left\{\frac{1}{4}+\frac{{\:\pi\:}^{2}{T}_{U}^{2}}{2}\right\}+\frac{\beta\:{A}_{U}}{16{\alpha\:}_{U}\:}\left\{\frac{1}{4}+{\:\pi\:}^{2}{T}_{U}^{2}-{C}_{3}\left\{\frac{1}{4}+\frac{{\:\pi\:}^{2}{T}_{U}^{2}}{2}\right\}\right\}\right]$$

(39)

$$\:{\alpha\:}_{U}=1+{\:\pi\:}^{2}{T}_{U}^{2}$$

(40)

The Sagdeev Pseudopotential $\:V\left({{\Psi\:}}_{U}\right)$ for the ultrarelativistic regime is different from the relativistic regime and does not contain fractional nonlinearities. Equation (37) does not give solitary KAAW for both fully and partially degenerate ultrarelativistic plasmas (see Fig. (8)). As discussed in the previous section, for relativistic SKAAW, an increase in number density​ enhances wave dispersion, leading to a decrease in energy density. In the ultrarelativistic regime, a further rise in number density​ intensifies dispersive effects, disrupting the balance between dispersion and nonlinearity. This imbalance causes the system to transition from SKAAW to nonlinear periodic KAAW.

To analyze the nonlinear KAAW for ultrarelativistic regime, we follow the steps of dynamical analysis of the previous sub section to understand the wave trajectories in a phase space. We have taken the parameters $\:{N}_{o}=1\times\:{10}^{38}\:{m}^{-3}$, magnetic field $\:{B}_{0}=2\times\:{10}^{10}\text{T}\:$, and angle of propagation is $\:\theta\:={85}^{^\circ\:}$. Figure 9 comprises of the phase portraits, effective potential and the corresponding nonlinear structures. The phase portrait in Fig. 9(a) gives NHO for $\:{\text{T}}_{R}=0$, corresponding to the nonlinear solitary pulse in Fig. 9(b). The NPO within the NHO corresponds to the nonlinear periodic kinetic Alfven acoustic waves in ultrarelativistic regime (see Fig. 9(c)). For these phase portraits, we have numerically calculated two fixed points, a center and a saddle point. Figure 9(d) is the effective potential of the nonlinear structures.

The exact solution of the aforementioned system can also be obtained by following the finite amplitude perturbation expansion method of the previous sub section to analyse the nonlinear solitary KAAW in ultrarelativistic regime.

Conclusions

We have investigated the linear and nonlinear analysis of relativistic and ultrarelativistic KAAW for the wave propagation in dense magnetized degenerate plasmas. The frequencies of fast and slow modes have shown variation with small temperature corrections. Wave dispersion for relativistic, ultrarelativistic and nonrelativistic KAAW have shown that these waves propagate more effectively in outer regions with lower specific heat than in denser inner regions of a neutron stars. Nonlinear analysis of arbitrary amplitude perturbations has shown SKAAW for the fully degenerate case and nonlinear solitary pulses or NPO in the relativistic regime for partial degeneracy. It has been observed that for the existence of nonlinear solitary waves, the range of Mach number is strongly coupled with the normalized ambient temperature $\:{T}_{R}$. The range of Mach number has shown variation with magnetic field and density. The existence regions have been plotted for finite amplitude perturbations and it has been shown that the humps and dips in SKAAW are due to the small temperature corrections. Moreover, after a certain temperature, only rarefactive structures can propagate. It is due to the fact that the change in $\:{\text{T}}_{R}$ shifts the balance between nonlinearity and dispersion, which changes the sign of amplitude $\:\left(\:{{\Psi\:}}_{0R}\:\right)$[see Eq. (33)]. It has been found that for the ultrarelativistic case rise in number density​ increases dispersive effects, disrupting the balance between dispersion and nonlinearity, and the system transit from SKAAW to nonlinear periodic KAAW. These linear and nonlinear wave propagation for the relativistic and ultrarelativistic KAAW have never been investigated before. Analytical and graphical results have shown that these waves can transfer energy by propagate through the regions of ultra-high densities and temperatures and may have potential applications in astrophysics and ultrahigh energy physics like relativistic plasma nanophononics²³.