Exact breather waves solutions in a spatial symmetric nonlinear dispersive wave model in (2+1)-dimensions

Abstract

In this article, the spatial symmetric nonlinear dispersive wave model in (2+1)-dimensions is studied, which have many applications in wave phenomena and soliton interactions in a two-dimensional space with time. In this framework, the Hirota bilinear form is applied to acquire diverse types of breather wave solutions from the foresaid equation. Abundant breather wave solutions are presented by the Hirota bilinear form and a mixture of exponentials and trigonometric functions with the usage of symbolic computation. In addition, the symbolic computation and the applied method for governing model are investigated. The movement role of the waves is investigated and the theoretical analysis of the acquired solutions is discussed using the bilinear technique of all produced solutions with 2D, density and 3D plots with respective parameters. The computational difficulties and outcomes highlight the clarity, effectiveness, and simplicity of the approaches, suggesting that these schemes can be applied to a variety of dynamic and static nonlinear equations governing evolutionary phenomena in computational physics as well as to other real-world situations and a wide range of academic fields.

Introduction

Nonlinearity can be found everywhere due to the fact that nature is nonlinear in nature. In many physical problems such as fluid dynamics, plasma physics, nonlinear optics and quantum field theory, nonlinear partial differential equations (PDEs) are prevalent. Integrable nonlinear evolution equations, e.g., the shallow water wave model¹, the fractional generalized CBS-BK equation², the Biswas-Milovic equation³, the nonlinear Schrödinger equation (NLSE)⁴, the NLSE with dual form⁵ have many interesting features including traveling wave solutions, which normally take form of solitary waves, bilinear forms, the exact N-soliton solutions and bi-Hamiltonian structures, etc. Several physical applications, including deep water waves, stochastic systems, plasma physics, nonlinear optical fibers, magneto-static spin waves, and so forth, are made possible by NLSE, which is a significant physical model^6,7,8,9,10.

NLPDEs play a significant role in physics, mechanics, chemistry, biology, mathematics, and engineering by allowing researchers to formulate and solve problems involving functions of several variables^11,12,13,14 and multi-label feature selection algorithms¹⁵. They are particularly valuable in describing phenomena where linear approximations are insufficient, as they capture the intricate nonlinear relationships present in nature^{16,17,18,19,20}. The importance of NLPDEs lies in their ability to provide insights into the behavior of complex systems, offering a deeper understanding of the underlying physical processes including online distributed stochastic mirror descent algorithm²¹, the nonlinear generalized systems subject to nonlinear algebraic constraints²², the Hamilton-Jacobi-Issacs inequality²³, the function/multi-function system using interpolative Kannan operators²⁴ and real-time subsurface scattering method by extending the photon beam diffusion model²⁵. Exact solutions of NLPDEs are particularly valuable as they offer precise mathematical descriptions of these phenomena, aiding in the development of new mathematical models, numerical methods containing the fractional Ornstein-Uhlenbeck process with periodic mean function²⁶, an efficient adaptive transfer network²⁷, the virtual multiple quasi-notch-filters method²⁸, and analytical techniques^29,30. The authors investigated uniform finite-time stabilization, mean square uniform stabilization, and mean square uniform asymptotic/exponential stabilization of linear discrete time-varying stochastic systems³¹.

To identify the explicit and solitary wave solutions of nonlinear PDEs, the traveling wave solution approach is essential. Nonlinear PDEs have soliton solutions, which stand for a single traveling wave^32,33,34,35. More precisely, the balance of the dispersion and nonlinear components of nonlinear equations yields solutions for solitons, which has generated interest in solitary wave theory across a wide range of fields^36,37. Soliton exists in a stable form^{38,39,40,41,42}. It stays concentrated in one area and doesn’t spread. The principle of superposition is not followed by it. The idea of solitary waves in nonlinear media has attracted a lot of attention because of its many uses in very rapid communications. Scholars have conducted an in-depth analysis of nonlinear models’ well-posedness, concentrating on solitary and shallow water waves. Solitons propagate through monomode optical fibers, which are employed in long-distance communication systems and fiber optic-based ultra-fast pulse inspection equipment^43,44,45. High-bandwidth data transport across thousands of kilometers via huge erbium-doped fiber amplifiers using optical solitons looks to be technically feasible in the near future. Mastering soliton properties has also been effectively achieved through a periodic modification of the core diameter^46,47,48.

Several recent methodologies have yielded numerous numerical and analytical solutions. These estimation techniques scrutinize the evolving wave solutions of equations, a pivotal factor in production, and innovate new computational methods for evaluating the estimated equations. For example, of these methods, the Gaussian mixture model⁴⁹, the maximum power point tracking technique⁵⁰, the optimal deep learning method^51,52,53, the machine learning for image⁵⁴, the implementation of machine learning models⁵⁵, multiple rogue wave solutions^56,57. Researchers have developed several approaches for finding analytical solutions to NLPDEs. These approaches include the federated learning-based optimization method⁵⁸, method based on solving Riccati equation and Bode integral⁵⁹, the iterative learning control method⁶⁰, the finite difference method based on the fully coupled effective stress⁶¹ and a train arrival neural temporal point process⁶².

Several efficient techniques have been developed over the years to obtain the exact solutions including fluorescence correlation spectroscopy technique⁶³, spatial-temporal feature interaction fusion network⁶⁴, remote sensing image analysis technology⁶⁵, real-time subsurface scattering technique⁶⁶ and the classical a-Weyl theorem⁶⁷.

In physics, a breather is a nonlinear wave in which energy concentrates in a localized and oscillatory fashion. This contradicts with the expectations derived from the corresponding linear system for infinitesimal amplitudes, which tends towards an even distribution of initially localized energy.

Feng et al.⁶⁸ obtained the exact analytical solutions and novel interaction solutions by Hirota bilinear method and symbolic computation. Tan et al.⁶⁹ studied the effect of three wave mixing by the long wave limit approach. Ma et al.⁷⁰ obtained the localized interaction solutions based on a Hirota bilinear transformation.

In this paper, we will discuss the following spatial symmetric nonlinear dispersive wave (SSNDW) model in (2+1)-dimensions⁷¹

$$\begin{aligned} \left\{ \begin{array}{ll} \Xi (u)=\alpha \Xi _1(u)+\beta \Xi _2(u),\ \ \ \ \ \ \ \Xi _1(u)=3u_{xx}p_y+3u_xp_{xy}+3u_{xy}v+3u_yv_x+\\ u_{xxxy}+ u_{tx}-u_{yy}+ 3u_{yy}q_x+ 3u_yq_{xy}+3u_{xy}w+3u_xw_y+u_{xyyy}+ u_{ty}-u_{xx},\\ \Xi _2(u)=4uu_{xy}+5u_xu_y+u_{yy}v+u_{xx}w+v_xw_y+u+{xxyy}, \end{array} \right. \end{aligned}$$

(1)

with relations $v_y = u_x, w_x = u_y, p_x = v, q_y = w$, and we search the breather waves via the indicated ansatz using exponential and trigonometric functions.

The new optical soliton solutions to the spatially temporal (n+1)-dimensional nonlinear Schrödinger’s equation with anti-cubic nonlinearity were investigated in⁷². The optical solitons with Radhakrishnan-Kundu-Lakshmanan model in the presence of Kerr law media with the aid of the modified simple equation and $\exp (-\varphi (q))$ method were studeid⁷³. Also, new optical solitons for the Hirota-Maccari system were constructed in⁷⁴. New dual-mode nonlinear Schrödinger’s equations were studied with cubic and quadratic cubic nonlinearities⁷⁵.

The nonlinear two dimensional Zakharov-Kuznetsov modified equal width equation was investigated under the observation of extended modified rational expansion method and determined the multiple solitary wave solutions⁷⁶. The extended modified rational expansion method based on symbolic computation was used to find the multiple solitary wave solutions for nonlinear two-dimensional Jaulent-Miodek Hierarchy equation⁷⁷. The newly exact soliton solutions of the nonlinear fractional Kairat-II equation under extended simple equation method were obtained by Iqbal et al.⁷⁸. Computational approaches for nonlinear gravity dispersive long waves and multiple soliton solutions for coupled system nonlinear (2+1)-dimensional Broer-Kaup-Kupershmit dynamical equation were studied in⁷⁹. The dynamic characteristics of the generalized coupled Drinfeld-Sokolov-Wilson equation was considered⁸⁰.

The spatial symmetric nonlinear dispersive wave model holds significance due to its inclusion of integrable nonlinear equations in two spatial dimensions, including complex time, allowing the concept of complexifying time to be examined.

The structure of this paper is given as under: The breather wave solutions of SSNDW model is presented in the “Breather wave solutions of SSNDW model” section by plenty of the solutions by help of Hirota bilinear method. The result and discussion are investigated in “Result and discussion” section. Finally, we approach some kind of results and conclusion in “Conclusion” section.

Breather wave solutions of SSNDW model

By using the following variable transformation

$$\begin{aligned} u(x,y,t)=2\partial _{xy}(\ln (g)),\ \ \ v(x,y,t)=2\partial _{xx}(\ln (g)),\ \ \ w(x,y,t)=2\partial _{yy}(\ln (g)),\ \ \ \end{aligned}$$

(2)

$$p(x,y,t)=2\partial _{x}(\ln (g)),\ \ \ q(x,y,t)=2\partial _{y}(\ln (g)),$$

where g is a function of x, y, t. The spatial symmetric (2+1)-dimensional model (1) can be transformed into the following bilinear form

$$\begin{aligned} L(g)=\left[ s_1(D_x^3D_y+D_y^3D_x+D_tD_x+D_tD_y-D_x^2-D_y^2)+s_2 D_x^2D_y^2\right] g.g= \end{aligned}$$

(3)

$$2s_1(gg_{xxxy}-g_yg_{xxx}-3g_xg_{xxy}+3g_{xx}g_{xy}+gg_{tx}-g_xg_t+gg_{xyyy}-$$

$$g_xg_{yyy}- 3g_yg_{xyy}+3g_{yy}g_{xy}+ gg_{ty}-g_yg_t+g_x^2-gg_x+g_y^2-gg_y)+$$

$$2s_2\left( gg_{xxyy}-2g_yf_{xxy}-2g_xg_{xyy}+g_{xx}g_{yy}+2g_{xy}^2\right) =0,$$

in which D offers the bilinear Hirota operator given as

$$\begin{aligned} D_{X_1}^{s_1}...D_{X_n}^{s_n}F.G=(\partial _{X_1}-\partial _{X'_1})^{s_1}...(\partial _{X_n}-\partial _{X'_n})^{s_n}\,F(X_1,...,X_n)\times G(X_1,...,X_n)\left| \right. _{X'_1=X_1,...,X'_n=X_n}. \end{aligned}$$

(4)

By typical computation, a exact connection between the nonlinear demonstrate condition and the bilinear demonstrate condition can be investigated to be

$$\begin{aligned} F(u)=\left( \frac{L(g)}{g^2}\right) _{xy}, \end{aligned}$$

(5)

where the included functions u, v, w, p, q are determined through the logarithmic derivative transformations of g in (2).

Following the steps of this method, g(x, y, t) has a solution of the following form

$$\begin{aligned} g(x,y,t)=\exp (-l_1)+k_1\exp (l_1)+k_2\cos (l_2)+k_3\sin (l_3), \ \ \ l_i=\alpha _ix+\beta _iy+\lambda _it+\mu _i,\ \ \ i=1,2,3, \end{aligned}$$

(6)

where $\alpha _i,\beta _i,\lambda _i,\mu _i,i=1,2,3$ are constants to be determined later. The assumptions used in the “breather wave method” are special cases of Eq. (2). Substituting Eq. (6) into Eq. (4), a set of algebraic equations including eleven set of equations about $\alpha _i,\beta _i,\lambda _i,\mu _i,i=1,2,3$ are obtained. With the aid of Maple software, we have the following results:

Case (1):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _3=-\beta _3,\ \ k_2=0,\ \ \lambda _{{1}}=-\frac{1}{2}\,{\frac{A_{{2}}+A_{{3}}}{A_{{1}}}},\ \ \lambda _{{3}}={\frac{\beta _{{3}} \left( A_{{4}}+A_{{5}} \right) }{A_{ {1}}}},\ \ \\ s_{{2}}=-\frac{1}{2}\,{\frac{ \left( -4\,{\beta _{{3}}}^{4}{k_{{3}}}^{2}+{ \beta _{{3}}}^{2}{k_{{3}}}^{2}+2\,k_{{1}} \left( 3\,\beta _{{1}}{\alpha _ {{1}}}^{3}-3\,{\alpha _{{1}}}^{2}{\beta _{{3}}}^{2}+3\,\alpha _{{1}}{ \beta _{{1}}}^{3}+6\,\alpha _{{1}}\beta _{{1}}{\beta _{{3}}}^{2}-3\,{\beta _{{1}}}^{2}{\beta _{{3}}}^{2}+2\,{\beta _{{3}}}^{4}-2\,{\beta _{{3}}}^{2} \right) \right) s_{{1}}}{{\beta _{{3}}}^{4}{k_{{3}}}^{2}+k_{{1}} \left( 3\,{\alpha _{{1}}}^{2}{\beta _{{1}}}^{2}+{\alpha _{{1}}}^{2}{ \beta _{{3}}}^{2}-4\,\alpha _{{1}}\beta _{{1}}{\beta _{{3}}}^{2}+{\beta _{{ 1}}}^{2}{\beta _{{3}}}^{2}-{\beta _{{3}}}^{4} \right) }}, \\ A_{{1}}= \left( \alpha _{{1}}+\beta _{{1}} \right) \left( {\beta _{{3}}} ^{4}{k_{{3}}}^{2}+3\,{\alpha _{{1}}}^{2}{\beta _{{1}}}^{2}k_{{1}}+{ \alpha _{{1}}}^{2}{\beta _{{3}}}^{2}k_{{1}}-4\,\alpha _{{1}}\beta _{{1}}{ \beta _{{3}}}^{2}k_{{1}}+{\beta _{{1}}}^{2}{\beta _{{3}}}^{2}k_{{1}}-{ \beta _{{3}}}^{4}k_{{1}} \right) , \\ A_{{2}}=2\,k_{{1}} ( 4\,{\alpha _{{1}}}^{5}\beta _{{1}}{\beta _{{3}} }^{2}-4\,{\alpha _{{1}}}^{4}{\beta _{{1}}}^{2}{\beta _{{3}}}^{2}-16\,{ \alpha _{{1}}}^{3}{\beta _{{1}}}^{3}{\beta _{{3}}}^{2}-4\,{\alpha _{{1}}}^ {3}\beta _{{1}}{\beta _{{3}}}^{4}-4\,{\alpha _{{1}}}^{2}{\beta _{{1}}}^{4} {\beta _{{3}}}^{2}-8\,{\alpha _{{1}}}^{2}{\beta _{{1}}}^{2}{\beta _{{3}}}^ {4}+4\,\alpha _{{1}}{\beta _{{1}}}^{5}{\beta _{{3}}}^{2}- ,\\ 4\,\alpha _{{1}}{ \beta _{{1}}}^{3}{\beta _{{3}}}^{4}- 3\,{\alpha _{{1}}}^{4}{\beta _{{1}}}^{ 2}-{\alpha _{{1}}}^{4}{\beta _{{3}}}^{2}+ 4\,{\alpha _{{1}}}^{3}\beta _{{1} }{\beta _{{3}}}^{2}-3\,{\alpha _{{1}}}^{2}{\beta _{{1}}}^{4}+6\,{\alpha _{ {1}}}^{2}{\beta _{{1}}}^{2}{\beta _{{3}}}^{2}+{\alpha _{{1}}}^{2}{\beta _{ {3}}}^{4}+4\,\alpha _{{1}}{\beta _{{1}}}^{3}{\beta _{{3}}}^{2}-{\beta _{{1 }}}^{4}{\beta _{{3}}}^{2}+{\beta _{{1}}}^{2}{\beta _{{3}}}^{4} ), \\ A_{{3}}={\beta _{{3}}}^{2}{k_{{3}}}^{2} ( 2\,{\alpha _{{1}}}^{3} \beta _{{1}}{\beta _{{3}}}^{2}+4\,{\alpha _{{1}}}^{2}{\beta _{{1}}}^{2}{ \beta _{{3}}}^{2}+2\,{\alpha _{{1}}}^{2}{\beta _{{3}}}^{4}+2\,\alpha _{{1} }{\beta _{{1}}}^{3}{\beta _{{3}}}^{2}+4\,\alpha _{{1}}\beta _{{1}}{\beta _{ {3}}}^{4}+2\,{\beta _{{1}}}^{2}{\beta _{{3}}}^{4}- \\ {\alpha _{{1}}}^{2}{ \beta _{{1}}}^{2}-{\alpha _{{1}}}^{2}{\beta _{{3}}}^{2}-4\,\alpha _{{1}} \beta _{{1}}{\beta _{{3}}}^{2}-{\beta _{{1}}}^{2}{\beta _{{3}}}^{2}+3\,{ \beta _{{3}}}^{4} ), \\ A_{{4}}=k_{{1}} \left( \alpha _{{1}}-\beta _{{1}} \right) ( 3\,{ \alpha _{{1}}}^{4}{\beta _{{1}}}^{2}-{\alpha _{{1}}}^{4}{\beta _{{3}}}^{2} +6\,{\alpha _{{1}}}^{3}{\beta _{{1}}}^{3}+6\,{\alpha _{{1}}}^{3}\beta _{{1 }}{\beta _{{3}}}^{2}+3\,{\alpha _{{1}}}^{2}{\beta _{{1}}}^{4}+14\,{\alpha _{{1}}}^{2}{\beta _{{1}}}^{2}{\beta _{{3}}}^{2}-{\alpha _{{1}}}^{2}{\beta _{{3}}}^{4}+ \\ 6\,\alpha _{{1}}{\beta _{{1}}}^{3}{\beta _{{3}}}^{2}-2\, \alpha _{{1}}\beta _{{1}}{\beta _{{3}}}^{4}-{\beta _{{1}}}^{4}{\beta _{{3}} }^{2}-{\beta _{{1}}}^{2}{\beta _{{3}}}^{4}-6\,{\alpha _{{1}}}^{2}{\beta _{ {1}}}^{2}-2\,{\alpha _{{1}}}^{2}{\beta _{{3}}}^{2}+4\,\alpha _{{1}}\beta _ {{1}}{\beta _{{3}}}^{2}-2\,{\beta _{{1}}}^{2}{\beta _{{3}}}^{2}-2\,{\beta _{{3}}}^{4}), \\ A_{{5}}=-{\beta _{{3}}}^{2}{k_{{3}}}^{2} \left( \alpha _{{1}}-\beta _{{1} } \right) \left( {\alpha _{{1}}}^{2}{\beta _{{3}}}^{2}+2\,\alpha _{{1}} \beta _{{1}}{\beta _{{3}}}^{2}+{\beta _{{1}}}^{2}{\beta _{{3}}}^{2}-\beta _ {{1}}\alpha _{{1}}+{\beta _{{3}}}^{2} \right) . \end{array} \right. \end{aligned}$$

(7)

Then the exact breather wave solution will be as

$$\begin{aligned} u_1=2\frac{\partial ^2}{\partial x \partial y}\ln g_1,\ \ \ v_1=2\frac{\partial ^2}{\partial x^2}\ln g_1,\ \ \ w_1=2\frac{\partial ^2}{\partial y^2}\ln g_1,\ \ \ \end{aligned}$$

(8)

$$g_1=\exp (-l_1)+k_1\exp (l_1)+k_3\sin (l_3), \ \ \ l_i=\alpha _ix+\beta _iy+\lambda _it+\mu _i,\ \ \ i=1,2,3.$$

Case (2):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _{{1}}=i\alpha _{{3}}+i\beta _{{3}}-\beta _{{1}},\ \ k_2=0,\ \ \lambda _{{1}}={\frac{A_{{1}}+A_{{2}}}{A_{{3}}+A_{{4}}}},\ \ \lambda _{{3}}={\frac{A_{{5}}+A_{{6}}}{A_{{3}}+A_{{4}}}},\ \ \\ s_{{2}}=2\,{\frac{s_{{1}} \left( 4\,\alpha _{{1}}{\beta _{{1}}}^{3}\beta _{{3}}- 4\,\alpha _{{1}}\beta _{{1}}{\beta _{{3}}}^{3}-\alpha _{{3}}{\beta _{{1}}}^ {4}+6\,\alpha _{{3}}{\beta _{{1}}}^{2}{\beta _{{3}}}^{2}-\alpha _{{3}}{ \beta _{{3}}}^{4}+3\,{\beta _{{1}}}^{4}\beta _{{3}}+2\,{\beta _{{1}}}^{2}{ \beta _{{3}}}^{3}-{\beta _{{3}}}^{5}+2\,\alpha _{{1}}\beta _{{1}}\beta _{{3 }}-\alpha _{{3}}{\beta _{{1}}}^{2}+\alpha _{{3}}{\beta _{{3}}}^{2}+{\beta _ {{1}}}^{2}\beta _{{3}}+{\beta _{{3}}}^{3} \right) }{4\,\alpha _{{1}}{ \beta _{{1}}}^{3}\beta _{{3}}-4\,\alpha _{{1}}\beta _{{1}}{\beta _{{3}}}^{3 }-\alpha _{{3}}{\beta _{{1}}}^{4}+6\,\alpha _{{3}}{\beta _{{1}}}^{2}{\beta _{{3}}}^{2}-\alpha _{{3}}{\beta _{{3}}}^{4}+3\,{\beta _{{1}}}^{4}\beta _{{ 3}}+2\,{\beta _{{1}}}^{2}{\beta _{{3}}}^{3}-{\beta _{{3}}}^{5}}},\\ A_{{1}}=4\,k_{{1}} ( 16\,{\alpha _{{3}}}^{3}{\beta _{{1}}}^{4}\beta _{{3}}\alpha _{{1}}-16\,{\alpha _{{3}}}^{3}{\beta _{{1}}}^{2}{\beta _{{3}} }^{3}\alpha _{{1}}-4\,{\alpha _{{3}}}^{2}{\beta _{{1}}}^{6}\alpha _{{1}}+ 72\,{\alpha _{{3}}}^{2}{\beta _{{1}}}^{4}{\beta _{{3}}}^{2}\alpha _{{1}}- 52\,{\alpha _{{3}}}^{2}{\beta _{{1}}}^{2}{\beta _{{3}}}^{4}\alpha _{{1}}-8 \,\alpha _{{3}}{\beta _{{1}}}^{6}\beta _{{3}}\alpha _{{1}}+ \\ 96\,\alpha _{{3} }{\beta _{{1}}}^{4}{\beta _{{3}}}^{3}\alpha _{{1}}-56\,\alpha _{{3}}{\beta _{{1}}}^{2}{\beta _{{3}}}^{5}\alpha _{{1}}-4\,{\beta _{{1}}}^{6}{\beta _{{ 3}}}^{2}\alpha _{{1}}+40\,{\beta _{{1}}}^{4}{\beta _{{3}}}^{4}\alpha _{{1} }-20\,{\beta _{{1}}}^{2}{\beta _{{3}}}^{6}\alpha _{{1}}+7\,{\alpha _{{3}}} ^{2}{\beta _{{1}}}^{4}\alpha _{{1}}-2\,{\alpha _{{3}}}^{2}{\beta _{{1}}}^{ 2}{\beta _{{3}}}^{2}\alpha _{{1}}- \\ {\alpha _{{3}}}^{2}{\beta _{{3}}}^{4} \alpha _{{1}}+38\,\alpha _{{3}}{\beta _{{1}}}^{4}\beta _{{3}}\alpha _{{1}}+ 4\,\alpha _{{3}}{\beta _{{1}}}^{2}{\beta _{{3}}}^{3}\alpha _{{1}}-2\, \alpha _{{3}}{\beta _{{3}}}^{5}\alpha _{{1}}-6\,{\beta _{{1}}}^{6}\alpha _{ {1}}+27\,{\beta _{{1}}}^{4}{\beta _{{3}}}^{2}\alpha _{{1}}+8\,{\beta _{{1} }}^{2}{\beta _{{3}}}^{4}\alpha _{{1}}-{\beta _{{3}}}^{6}\alpha _{{1}}- \\ 4\,{ \alpha _{{3}}}^{4}{\beta _{{1}}}^{5}+24\,{\alpha _{{3}}}^{4}{\beta _{{1}}} ^{3}{\beta _{{3}}}^{2}-4\,{\alpha _{{3}}}^{4}\beta _{{1}}{\beta _{{3}}}^{4 }-16\,{\alpha _{{3}}}^{3}{\beta _{{1}}}^{5}\beta _{{3}}+96\,{\alpha _{{3}} }^{3}{\beta _{{1}}}^{3}{\beta _{{3}}}^{3}-16\,{\alpha _{{3}}}^{3}\beta _{{ 1}}{\beta _{{3}}}^{5}-4\,{\alpha _{{3}}}^{2}{\beta _{{1}}}^{7}+140\,{ \alpha _{{3}}}^{2}{\beta _{{1}}}^{3}{\beta _{{3}}}^{4}- \\ 24\,{\alpha _{{3}}} ^{2}\beta _{{1}}{\beta _{{3}}}^{6}-8\,\alpha _{{3}}{\beta _{{1}}}^{7}\beta _{{3}}+32\,\alpha _{{3}}{\beta _{{1}}}^{5}{\beta _{{3}}}^{3}+88\,\alpha _{ {3}}{\beta _{{1}}}^{3}{\beta _{{3}}}^{5}-16\,\alpha _{{3}}\beta _{{1}}{ \beta _{{3}}}^{7}-4\,{\beta _{{1}}}^{7}{\beta _{{3}}}^{2}+20\,{\beta _{{1} }}^{5}{\beta _{{3}}}^{4}+20\,{\beta _{{1}}}^{3}{\beta _{{3}}}^{6}-4\, \beta _{{1}}{\beta _{{3}}}^{8}+ \\ 12\,{\alpha _{{3}}}^{3}{\beta _{{1}}}^{3} \beta _{{3}}+4\,{\alpha _{{3}}}^{3}\beta _{{1}}{\beta _{{3}}}^{3}-7\,{ \alpha _{{3}}}^{2}{\beta _{{1}}}^{5}+38\,{\alpha _{{3}}}^{2}{\beta _{{1}}} ^{3}{\beta _{{3}}}^{2}+13\,{\alpha _{{3}}}^{2}\beta _{{1}}{\beta _{{3}}}^{ 4}+2\,\alpha _{{3}}{\beta _{{1}}}^{5}\beta _{{3}}+40\,\alpha _{{3}}{\beta _ {{1}}}^{3}{\beta _{{3}}}^{3}+14\,\alpha _{{3}}\beta _{{1}}{\beta _{{3}}}^{ 5}- \\ 6\,{\beta _{{1}}}^{7}+5\,{\beta _{{1}}}^{5}{\beta _{{3}}}^{2}+ 16\,{ \beta _{{1}}}^{3}{\beta _{{3}}}^{4}+5\,\beta _{{1}}{\beta _{{3}}}^{6}) , \\ A_{{2}}=-{k_{{3}}}^{2} ( 16\,{\alpha _{{3}}}^{3}{\beta _{{1}}}^{4} \beta _{{3}}\alpha _{{1}}-16\,{\alpha _{{3}}}^{3}{\beta _{{1}}}^{2}{\beta _ {{3}}}^{3}\alpha _{{1}}-2\,{\alpha _{{3}}}^{2}{\beta _{{1}}}^{6}\alpha _{{ 1}}+42\,{\alpha _{{3}}}^{2}{\beta _{{1}}}^{4}{\beta _{{3}}}^{2}\alpha _{{1 }}-22\,{\alpha _{{3}}}^{2}{\beta _{{1}}}^{2}{\beta _{{3}}}^{4}\alpha _{{1} }-2\,\alpha _{{1}}{\alpha _{{3}}}^{2}{\beta _{{3}}}^{6}- \\ 4\,\alpha _{{3}}{ \beta _{{1}}}^{6}\beta _{{3}}\alpha _{{1}}+36\,\alpha _{{3}}{\beta _{{1}}}^ {4}{\beta _{{3}}}^{3}\alpha _{{1}}+4\,\alpha _{{3}}{\beta _{{1}}}^{2}{ \beta _{{3}}}^{5}\alpha _{{1}}-4\,\alpha _{{1}}\alpha _{{3}}{\beta _{{3}}}^ {7}-2\,{\beta _{{1}}}^{6}{\beta _{{3}}}^{2}\alpha _{{1}}+10\,{\beta _{{1}} }^{4}{\beta _{{3}}}^{4}\alpha _{{1}}+10\,{\beta _{{1}}}^{2}{\beta _{{3}}}^ {6}\alpha _{{1}}-2\,\alpha _{{1}}{\beta _{{3}}}^{8}- \\ 4\,{\alpha _{{3}}}^{4} {\beta _{{1}}}^{5}+24\,{\alpha _{{3}}}^{4}{\beta _{{1}}}^{3}{\beta _{{3}}} ^{2}-4\,{\alpha _{{3}}}^{4}\beta _{{1}}{\beta _{{3}}}^{4}-4\,{\alpha _{{3} }}^{3}{\beta _{{1}}}^{5}\beta _{{3}}+56\,{\alpha _{{3}}}^{3}{\beta _{{1}}} ^{3}{\beta _{{3}}}^{3}-4\,{\alpha _{{3}}}^{3}\beta _{{1}}{\beta _{{3}}}^{5 }-2\,{\alpha _{{3}}}^{2}{\beta _{{1}}}^{7}+ 6\,{\alpha _{{3}}}^{2}{\beta _{ {1}}}^{5}{\beta _{{3}}}^{2}+ \\ 50\,{\alpha _{{3}}}^{2}{\beta _{{1}}}^{3}{ \beta _{{3}}}^{4}+10\,{\alpha _{{3}}}^{2}\beta _{{1}}{\beta _{{3}}}^{6}-4 \,\alpha _{{3}}{\beta _{{1}}}^{7}\beta _{{3}}+8\,\alpha _{{3}}{\beta _{{1}} }^{5}{\beta _{{3}}}^{3}+28\,\alpha _{{3}}{\beta _{{1}}}^{3}{\beta _{{3}}}^ {5}+16\,\alpha _{{3}}\beta _{{1}}{\beta _{{3}}}^{7}-2\,{\beta _{{1}}}^{7}{ \beta _{{3}}}^{2}+2\,{\beta _{{1}}}^{5}{\beta _{{3}}}^{4}+10\,{\beta _{{1} }}^{3}{\beta _{{3}}}^{6}+ \\ 6\,\beta _{{1}}{\beta _{{3}}}^{8}+ 3\,{\alpha _{{3 }}}^{2}{\beta _{{1}}}^{4}\alpha _{{1}}+22\,{\alpha _{{3}}}^{2}{\beta _{{1} }}^{2}{\beta _{{3}}}^{2}\alpha _{{1}}-5\,{\alpha _{{3}}}^{2}{\beta _{{3}}} ^{4}\alpha _{{1}}-6\,\alpha _{{3}}{\beta _{{1}}}^{4}\beta _{{3}}\alpha _{{1 }}+28\,\alpha _{{3}}{\beta _{{1}}}^{2}{\beta _{{3}}}^{3}\alpha _{{1}}+2\, \alpha _{{3}}{\beta _{{3}}}^{5}\alpha _{{1}}-7\,{\beta _{{1}}}^{4}{\beta _{ {3}}}^{2}\alpha _{{1}}+ \\ 2\,{\beta _{{1}}}^{2}{\beta _{{3}}}^{4}\alpha _{{1} }+ {\beta _{{3}}}^{6}\alpha _{{1}}- 4\,{\alpha _{{3}}}^{3}{\beta _{{1}}}^{3} \beta _{{3}}+20\,{\alpha _{{3}}}^{3}\beta _{{1}}{\beta _{{3}}}^{3}+{\alpha _{{3}}}^{2}{\beta _{{1}}}^{5}-10\,{\alpha _{{3}}}^{2}{\beta _{{1}}}^{3}{ \beta _{{3}}}^{2}+21\,{\alpha _{{3}}}^{2}\beta _{{1}}{\beta _{{3}}}^{4}-6 \,\alpha _{{3}}{\beta _{{1}}}^{5}\beta _{{3}}- \\ 8\,\alpha _{{3}}{\beta _{{1}} }^{3}{\beta _{{3}}}^{3}+6\,\alpha _{{3}}\beta _{{1}}{\beta _{{3}}}^{5}-5\, {\beta _{{1}}}^{5}{\beta _{{3}}}^{2}-6\,{\beta _{{1}}}^{3}{\beta _{{3}}}^{ 4}-\beta _{{1}}{\beta _{{3}}}^{6} ) , \\ A_{{3}}=4\,k_{{1}} \left( \alpha _{{3}}+\beta _{{3}} \right) \left( 4\, \alpha _{{1}}{\beta _{{1}}}^{3}\beta _{{3}}-4\,\alpha _{{1}}\beta _{{1}}{ \beta _{{3}}}^{3}-\alpha _{{3}}{\beta _{{1}}}^{4}+6\,\alpha _{{3}}{\beta _{ {1}}}^{2}{\beta _{{3}}}^{2}-\alpha _{{3}}{\beta _{{3}}}^{4}+3\,{\beta _{{1 }}}^{4}\beta _{{3}}+2\,{\beta _{{1}}}^{2}{\beta _{{3}}}^{3}-{\beta _{{3}}} ^{5} \right) , \\ A_{{4}}=-{k_{{3}}}^{2} \left( \alpha _{{3}}+\beta _{{3}} \right) \left( 4\,\alpha _{{1}}{\beta _{{1}}}^{3}\beta _{{3}}-4\,\alpha _{{1}} \beta _{{1}}{\beta _{{3}}}^{3}-\alpha _{{3}}{\beta _{{1}}}^{4}+6\,\alpha _{ {3}}{\beta _{{1}}}^{2}{\beta _{{3}}}^{2}-\alpha _{{3}}{\beta _{{3}}}^{4}+3 \,{\beta _{{1}}}^{4}\beta _{{3}}+2\,{\beta _{{1}}}^{2}{\beta _{{3}}}^{3}-{ \beta _{{3}}}^{5} \right) , \\ A_{{5}}=4\,k_{{1}} ( 16\,\alpha _{{1}}{\alpha _{{3}}}^{3}{\beta _{{1 }}}^{3}{\beta _{{3}}}^{2}-16\,\alpha _{{1}}{\alpha _{{3}}}^{3}\beta _{{1}} {\beta _{{3}}}^{4}-12\,\alpha _{{1}}{\alpha _{{3}}}^{2}{\beta _{{1}}}^{5} \beta _{{3}}+72\,\alpha _{{1}}{\alpha _{{3}}}^{2}{\beta _{{1}}}^{3}{\beta _ {{3}}}^{3}-44\,\alpha _{{1}}{\alpha _{{3}}}^{2}\beta _{{1}}{\beta _{{3}}}^ {5}- 24\,\alpha _{{1}}\alpha _{{3}}{\beta _{{1}}}^{5}{\beta _{{3}}}^{2}+ \\ 96 \,\alpha _{{1}}\alpha _{{3}}{\beta _{{1}}}^{3}{\beta _{{3}}}^{4}-40\, \alpha _{{1}}\alpha _{{3}}\beta _{{1}}{\beta _{{3}}}^{6}-12\,\alpha _{{1}}{ \beta _{{1}}}^{5}{\beta _{{3}}}^{3}+40\,\alpha _{{1}}{\beta _{{1}}}^{3}{ \beta _{{3}}}^{5}-12\,\alpha _{{1}}\beta _{{1}}{\beta _{{3}}}^{7}- 4\,{ \alpha _{{3}}}^{4}{\beta _{{1}}}^{4}\beta _{{3}}+ 24\,{\alpha _{{3}}}^{4}{ \beta _{{1}}}^{2}{\beta _{{3}}}^{3}-4\,{\alpha _{{3}}}^{4}{\beta _{{3}}}^{ 5}+ \\ 2\,{\alpha _{{3}}}^{3}{\beta _{{1}}}^{6}-26\,{\alpha _{{3}}}^{3}{\beta _{{1}}}^{4}{\beta _{{3}}}^{2}+86\,{\alpha _{{3}}}^{3}{\beta _{{1}}}^{2}{ \beta _{{3}}}^{4}-14\,{\alpha _{{3}}}^{3}{\beta _{{3}}}^{6}-6\,{\alpha _{{ 3}}}^{2}{\beta _{{1}}}^{6}\beta _{{3}}-30\,{\alpha _{{3}}}^{2}{\beta _{{1} }}^{4}{\beta _{{3}}}^{3}+118\,{\alpha _{{3}}}^{2}{\beta _{{1}}}^{2}{\beta _{{3}}}^{5}-18\,{\alpha _{{3}}}^{2}{\beta _{{3}}}^{7}- \\ 18\,\alpha _{{3}}{ \beta _{{1}}}^{6}{\beta _{{3}}}^{2}+2\,\alpha _{{3}}{\beta _{{1}}}^{4}{ \beta _{{3}}}^{4}+74\,\alpha _{{3}}{\beta _{{1}}}^{2}{\beta _{{3}}}^{6}-10 \,\alpha _{{3}}{\beta _{{3}}}^{8}-10\,{\beta _{{1}}}^{6}{\beta _{{3}}}^{3} +10\,{\beta _{{1}}}^{4}{\beta _{{3}}}^{5}+18\,{\beta _{{1}}}^{2}{\beta _{{ 3}}}^{7}-2\,{\beta _{{3}}}^{9}+20\,\alpha _{{1}}{\alpha _{{3}}}^{2}{\beta _{{1}}}^{3}\beta _{{3}}- \\ 4\,\alpha _{{1}}{\alpha _{{3}}}^{2}\beta _{{1}}{ \beta _{{3}}}^{3}- 12\,\alpha _{{1}}\alpha _{{3}}{\beta _{{1}}}^{5}+56\, \alpha _{{1}}\alpha _{{3}}{\beta _{{1}}}^{3}{\beta _{{3}}}^{2}+4\,\alpha _{ {1}}\alpha _{{3}}\beta _{{1}}{\beta _{{3}}}^{4}-24\,\alpha _{{1}}{\beta _{{ 1}}}^{5}\beta _{{3}}+20\,\alpha _{{1}}{\beta _{{1}}}^{3}{\beta _{{3}}}^{3} +4\,\alpha _{{1}}\beta _{{1}}{\beta _{{3}}}^{5}- \\ 5\,{\alpha _{{3}}}^{3}{ \beta _{{1}}}^{4}+22\,{\alpha _{{3}}}^{3}{\beta _{{1}}}^{2}{\beta _{{3}}}^ {2}+3\,{\alpha _{{3}}}^{3}{\beta _{{3}}}^{4}-29\,{\alpha _{{3}}}^{2}{ \beta _{{1}}}^{4}\beta _{{3}}+42\,{\alpha _{{3}}}^{2}{\beta _{{1}}}^{2}{ \beta _{{3}}}^{3}+7\,{\alpha _{{3}}}^{2}{\beta _{{3}}}^{5}-6\,\alpha _{{3} }{\beta _{{1}}}^{6}-23\,\alpha _{{3}}{\beta _{{1}}}^{4}{\beta _{{3}}}^{2}+ 28\,\alpha _{{3}}{\beta _{{1}}}^{2}{\beta _{{3}}}^{4}+ \\ 5\,\alpha _{{3}}{ \beta _{{3}}}^{6}-18\,{\beta _{{1}}}^{6}\beta _{{3}}-15\,{\beta _{{1}}}^{4 }{\beta _{{3}}}^{3}+4\,{\beta _{{1}}}^{2}{\beta _{{3}}}^{5}+{\beta _{{3}}} ^{7} ), \\ A_{{6}}=-{k_{{3}}}^{2} ( 16\,\alpha _{{1}}{\alpha _{{3}}}^{3}{\beta _{{1}}}^{3}{\beta _{{3}}}^{2}-16\,\alpha _{{1}}{\alpha _{{3}}}^{3}\beta _{ {1}}{\beta _{{3}}}^{4}+32\,\alpha _{{1}}{\alpha _{{3}}}^{2}{\beta _{{1}}}^ {3}{\beta _{{3}}}^{3}-32\,\alpha _{{1}}{\alpha _{{3}}}^{2}\beta _{{1}}{ \beta _{{3}}}^{5}+16\,\alpha _{{1}}\alpha _{{3}}{\beta _{{1}}}^{3}{\beta _{ {3}}}^{4}-16\,\alpha _{{1}}\alpha _{{3}}\beta _{{1}}{\beta _{{3}}}^{6}- \\ 4\, {\alpha _{{3}}}^{4}{\beta _{{1}}}^{4}\beta _{{3}}+24\,{\alpha _{{3}}}^{4}{ \beta _{{1}}}^{2}{\beta _{{3}}}^{3}-4\,{\alpha _{{3}}}^{4}{\beta _{{3}}}^{ 5}+4\,{\alpha _{{3}}}^{3}{\beta _{{1}}}^{4}{\beta _{{3}}}^{2}+56\,{\alpha _{{3}}}^{3}{\beta _{{1}}}^{2}{\beta _{{3}}}^{4}-12\,{\alpha _{{3}}}^{3}{ \beta _{{3}}}^{6}+20\,{\alpha _{{3}}}^{2}{\beta _{{1}}}^{4}{\beta _{{3}}}^ {3}+40\,{\alpha _{{3}}}^{2}{\beta _{{1}}}^{2}{\beta _{{3}}}^{5}- \\ 12\,{ \alpha _{{3}}}^{2}{\beta _{{3}}}^{7}+12\,\alpha _{{3}}{\beta _{{1}}}^{4}{ \beta _{{3}}}^{4}+8\,\alpha _{{3}}{\beta _{{1}}}^{2}{\beta _{{3}}}^{6}-4\, \alpha _{{3}}{\beta _{{3}}}^{8}+4\,\alpha _{{1}}{\alpha _{{3}}}^{2}{\beta _ {{1}}}^{3}\beta _{{3}}+12\,\alpha _{{1}}{\alpha _{{3}}}^{2}\beta _{{1}}{ \beta _{{3}}}^{3}+4\,\alpha _{{1}}{\beta _{{1}}}^{3}{\beta _{{3}}}^{3}-4\, \alpha _{{1}}\beta _{{1}}{\beta _{{3}}}^{5}- \\ {\alpha _{{3}}}^{3}{\beta _{{1} }}^{4}-2\,{\alpha _{{3}}}^{3}{\beta _{{1}}}^{2}{\beta _{{3}}}^{2}+7\,{ \alpha _{{3}}}^{3}{\beta _{{3}}}^{4}+3\,{\alpha _{{3}}}^{2}{\beta _{{1}}}^ {4}\beta _{{3}}+10\,{\alpha _{{3}}}^{2}{\beta _{{1}}}^{2}{\beta _{{3}}}^{3 }+7\,{\alpha _{{3}}}^{2}{\beta _{{3}}}^{5}-\alpha _{{3}}{\beta _{{1}}}^{4} {\beta _{{3}}}^{2}+6\,\alpha _{{3}}{\beta _{{1}}}^{2}{\beta _{{3}}}^{4}- \\ \alpha _{{3}}{\beta _{{3}}}^{6}+3\,{\beta _{{1}}}^{4}{\beta _{{3}}}^{3}+2 \,{\beta _{{1}}}^{2}{\beta _{{3}}}^{5}-{\beta _{{3}}}^{7}). \end{array} \right. \end{aligned}$$

(9)

Then the exact breather wave solution will be as

$$\begin{aligned} u_2=2\frac{\partial ^2}{\partial x \partial y}\ln g_1,\ \ \ v_2=2\frac{\partial ^2}{\partial x^2}\ln g_1,\ \ \ w_2=2\frac{\partial ^2}{\partial y^2}\ln g_1,\ \ \ \end{aligned}$$

(10)

$$g_2=\exp (-l_1)+k_1\exp (l_1)+k_3\sin (l_3), \ \ \ l_i=\alpha _ix+\beta _iy+\lambda _it+\mu _i,\ \ \ i=1,2,3.$$

Case (3):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _1=-i\alpha _3,\ \ \beta _1=-i\beta _3,\ \ k_1=-\frac{1}{4}k_3^2, \ \ k_2=0,\ \ s_1=0,\ \ \\ g(x,y,t)={\textrm{e}^{-t\lambda _{{1}}+ix\alpha _{{3}}-iy\beta _{{3}}-\mu _{{1}}}}-\frac{1}{4} \,{k_{{3}}}^{2}{\textrm{e}^{t\lambda _{{1}}-ix\alpha _{{3}}+iy\beta _{{3}}+ \mu _{{1}}}}+k_{{3}}\sin \left( t\lambda _{{3}}+x\alpha _{{3}}+y\beta _{{3 }}+\mu _{{3}} \right) ,\\ u_3=-32\,\alpha _{{3}}\beta _{{3}}{k_{{3}}}^{2}/\left( -8\,\sin \left( t\lambda _{{3}}+x\alpha _{{3}}+y \beta _{{3}}+\mu _{{3}} \right) k_{{3}} \left( {k_{{3}}}^{2}{\textrm{e}^{t \lambda _{{1}}-ix\alpha _{{3}}+iy\beta _{{3}}+\mu _{{1}}}}-4\,{\textrm{e}^{-t \lambda _{{1}}+ix\alpha _{{3}}-iy\beta _{{3}}-\mu _{{1}}}} \right) +\right. \\ \left. {\textrm{e}^{2\,t\lambda _{{1}}-2\,ix\alpha _{{3}}+2\,iy\beta _{{3}}+2\,\mu _ {{1}}}}{k_{{3}}}^{4}-16\, \left( \cos \left( t\lambda _{{3}}+x\alpha _{{3}}+y\beta _{{3}}+\mu _{{3} } \right) \right) ^{2}{k_{{3}}}^{2}+8\,{k_{{3}}}^{2}+16\,{\textrm{e}^{-2 \,t\lambda _{{1}}+2\,ix\alpha _{{3}}-2\,iy\beta _{{3}}-2\,\mu _{{1}}}} \right) ,\\ v_3=8\,{\alpha _{{3}}}^{2}k_{{3}} \left( -i{\textrm{e}^{t\lambda _{{1}}-ix \alpha _{{3}}+iy\beta _{{3}}+\mu _{{1}}}} \left( \cos \left( t\lambda _{{3 }}+x\alpha _{{3}}+y\beta _{{3}}+\mu _{{3}} \right) +i\sin \left( t\lambda _{{3}}+x\alpha _{{3}}+y\beta _{{3}}+\mu _{{3}} \right) \right) {k_{{3}}} ^{2}-\right. \\ \left. 4\,i{\textrm{e}^{-t\lambda _{{1}}+ix\alpha _{{3}}-iy\beta _{{3}}-\mu _{{ 1}}}} \left( \cos \left( t\lambda _{{3}}+x\alpha _{{3}}+y\beta _{{3}}+\mu _{{3}} \right) -i\sin \left( t\lambda _{{3}}+x\alpha _{{3}}+y\beta _{{3}} +\mu _{{3}} \right) \right) \right) /\\ {\textrm{e}^{2\,t\lambda _{{1}}-2\,ix\alpha _{{3}}+2\,iy\beta _{{3}}+2\,\mu _ {{1}}}}{k_{{3}}}^{4}-8\,\sin \left( t\lambda _{{3}}+x\alpha _{{3}}+y \beta _{{3}}+\mu _{{3}} \right) k_{{3}} \left( {k_{{3}}}^{2}{\textrm{e}^{t \lambda _{{1}}-ix\alpha _{{3}}+iy\beta _{{3}}+\mu _{{1}}}}-4\,{\textrm{e}^{-t \lambda _{{1}}+ix\alpha _{{3}}-iy\beta _{{3}}-\mu _{{1}}}} \right) -\\ 16\, \left( \cos \left( t\lambda _{{3}}+x\alpha _{{3}}+y\beta _{{3}}+\mu _{{3} } \right) \right) ^{2}{k_{{3}}}^{2}+8\,{k_{{3}}}^{2}+16\,{\textrm{e}^{-2 \,t\lambda _{{1}}+2\,ix\alpha _{{3}}-2\,iy\beta _{{3}}-2\,\mu _{{1}}}},\\ w_3=8\,{\beta _{{3}}}^{2}k_{{3}} \left( -i{\textrm{e}^{t\lambda _{{1}}-ix\alpha _{{3}}+iy\beta _{{3}}+\mu _{{1}}}} \left( i\sin \left( t\lambda _{{3}}+x \alpha _{{3}}+y\beta _{{3}}+\mu _{{3}} \right) -\cos \left( t\lambda _{{3} }+x\alpha _{{3}}+y\beta _{{3}}+\mu _{{3}} \right) \right) {k_{{3}}}^{2}+ \right. \\ \left. 4\,i{\textrm{e}^{-t\lambda _{{1}}+ix\alpha _{{3}}-iy\beta _{{3}}-\mu _{{1}}}} \left( \cos \left( t\lambda _{{3}}+x\alpha _{{3}}+y\beta _{{3}}+\mu _{{3} } \right) +i\sin \left( t\lambda _{{3}}+x\alpha _{{3}}+y\beta _{{3}}+\mu _ {{3}} \right) \right) \right) /\\ ({\textrm{e}^{2\,t\lambda _{{1}}-2\,ix\alpha _{{3}}+2\,iy\beta _{{3}}+2\,\mu _ {{1}}}}{k_{{3}}}^{4}-8\,\sin \left( t\lambda _{{3}}+x\alpha _{{3}}+y \beta _{{3}}+\mu _{{3}} \right) k_{{3}} \left( {k_{{3}}}^{2}{\textrm{e}^{t \lambda _{{1}}-ix\alpha _{{3}}+iy\beta _{{3}}+\mu _{{1}}}}-4\,{\textrm{e}^{-t \lambda _{{1}}+ix\alpha _{{3}}-iy\beta _{{3}}-\mu _{{1}}}} \right) -\\ 16\, \left( \cos \left( t\lambda _{{3}}+x\alpha _{{3}}+y\beta _{{3}}+\mu _{{3} } \right) \right) ^{2}{k_{{3}}}^{2}+8\,{k_{{3}}}^{2}+16\,{\textrm{e}^{-2 \,t\lambda _{{1}}+2\,ix\alpha _{{3}}-2\,iy\beta _{{3}}-2\,\mu _{{1}}}}). \end{array} \right. \end{aligned}$$

(11)

Case (4):

$$\begin{aligned} \left\{ \begin{array}{ll} R_{{2}}=\frac{1}{2}\,{\frac{ \sqrt{2} \sqrt{M_{{1}} \left( -M_{{2}}+ \sqrt{- 12\,M_{{1}}{\alpha _{{1}}}^{2}{\beta _{{1}}}^{2}+{M_{{2}}}^{2}} \right) }}{M_{{1}}}} ,\ \ M_{{1}}=2\,{\alpha _{{1}}}^{2}+4\,\beta _{{1}}\alpha _{{1}}+2\,{\beta _{{1 }}}^{2}+3,\\ M_{{2}}=-6\,\beta _{{1}}{\alpha _{{1}}}^{3}-12\,{\alpha _{{1}}}^{2}{\beta _{{1}}}^{2}-6\,\alpha _{{1}}{\beta _{{1}}}^{3}+{\alpha _{{1}}}^{2}-4\, \beta _{{1}}\alpha _{{1}}+{\beta _{{1}}}^{2},\ \ \alpha _3=-R_2,\ \ \beta _3=R_2,\\ k_{{1}}=-\frac{1}{2}\,{\frac{{k_{{3}}}^{2} \left( 6\,{\alpha _{{1}}}^{3}\beta _ {{1}}{R_{{2}}}^{2}+12\,{\alpha _{{1}}}^{2}{\beta _{{1}}}^{2}{R_{{2}}}^{2 }+6\,\alpha _{{1}}{\beta _{{1}}}^{3}{R_{{2}}}^{2}-{\alpha _{{1}}}^{2}{R_{ {2}}}^{2}+4\,\alpha _{{1}}\beta _{{1}}{R_{{2}}}^{2}-{\beta _{{1}}}^{2}{R_ {{2}}}^{2}-3\,{\alpha _{{1}}}^{2}{\beta _{{1}}}^{2} \right) }{{R_{{2}}}^ {2} \left( {\alpha _{{1}}}^{4}-5\,\beta _{{1}}{\alpha _{{1}}}^{3}-12\,{ \alpha _{{1}}}^{2}{\beta _{{1}}}^{2}-5\,\alpha _{{1}}{\beta _{{1}}}^{3}+{ \beta _{{1}}}^{4}+2\,{\alpha _{{1}}}^{2}-8\,\beta _{{1}}\alpha _{{1}}+2\,{ \beta _{{1}}}^{2} \right) +3\,{\alpha _{{1}}}^{2}{\beta _{{1}}}^{2} \left( {\alpha _{{1}}}^{2}+2\,\beta _{{1}}\alpha _{{1}}+{\beta _{{1}}}^{2 }+2 \right) }} , \\ k_2=0,\ \ s_{{2}}=1/2\,{\frac{s_{{1}} \left( R_{{2}} \left( \alpha _{{1}}-\beta _ {{1}} \right) \left( 4\,{R_{{2}}}^{2}-{\alpha _{{1}}}^{2}+2\,\beta _{{1 }}\alpha _{{1}}-{\beta _{{1}}}^{2}-2 \right) -\alpha _{{1}}\lambda _{{3}}- \beta _{{1}}\lambda _{{3}} \right) }{R_{{2}} \left( \alpha _{{1}}-\beta _{ {1}} \right) \left( {R_{{2}}}^{2}+\beta _{{1}}\alpha _{{1}} \right) }} ,\\ \lambda _{{1}}=-{\frac{A_{{1}}}{ \left( {R_{{2}}}^{2}+\beta _{{1}} \alpha _{{1}} \right) \left( \alpha _{{1}}-\beta _{{1}} \right) R_{{2}} \left( 2\,{\alpha _{{1}}}^{2}+4\,\beta _{{1}}\alpha _{{1}}+2\,{\beta _{{1 }}}^{2}+3 \right) }},\ \ \ A_{{1}}={R_{{2}}}^{3} \left( \alpha _{{1}}+\beta _{{1}} \right) \left( \alpha _{{1}}-\beta _{{1}} \right) \left( {\alpha _{{1}}}^{4}+5\,\beta _{ {1}}{\alpha _{{1}}}^{3}+\right. \\ \left. 8\,{\alpha _{{1}}}^{2}{\beta _{{1}}}^{2}+5\, \alpha _{{1}}{\beta _{{1}}}^{3}+{\beta _{{1}}}^{4}+{\alpha _{{1}}}^{2}+4\, \beta _{{1}}\alpha _{{1}}+{\beta _{{1}}}^{2}-1 \right) +{R_{{2}}}^{2} \lambda _{{3}} \left( {\alpha _{{1}}}^{4}-5\,\beta _{{1}}{\alpha _{{1}}}^{ 3}-12\,{\alpha _{{1}}}^{2}{\beta _{{1}}}^{2}-5\,\alpha _{{1}}{\beta _{{1}} }^{3}+{\beta _{{1}}}^{4}+\right. \\ \left. 2\,{\alpha _{{1}}}^{2}-8\,\beta _{{1}}\alpha _{{1 }}+2\,{\beta _{{1}}}^{2} \right) + R_{{2}}\alpha _{{1}}\beta _{{1}} \left( \alpha _{{1}}-\beta _{{1}} \right) \left( \alpha _{{1}}+\beta _{{ 1}} \right) \left( \beta _{{1}}{\alpha _{{1}}}^{3}+2\,{\alpha _{{1}}}^{2 }{\beta _{{1}}}^{2}+\alpha _{{1}}{\beta _{{1}}}^{3}-2\,{\alpha _{{1}}}^{2} -2\,\beta _{{1}}\alpha _{{1}}-2\,{\beta _{{1}}}^{2}-3 \right) \\ -{\alpha _{{ 1}}}^{2}{\beta _{{1}}}^{2}\lambda _{{3}} \left( \alpha _{{1}}+\beta _{{1}} \right) ^{2}. \end{array} \right. \end{aligned}$$

(12)

Then, the exact breather wave solution will be as

$$\begin{aligned} u_4=2\frac{\partial ^2}{\partial x \partial y}\ln g_4,\ \ \ v_4=2\frac{\partial ^2}{\partial x^2}\ln g_4,\ \ \ w_4=2\frac{\partial ^2}{\partial y^2}\ln g_4,\ \ \ \end{aligned}$$

(13)

$$g_4=-\frac{1}{2}\,{\frac{{k_{{3}}}^{2} \exp (l_1)\left( 6\,{\alpha _{{1}}}^{3}\beta _ {{1}}{R_{{2}}}^{2}+12\,{\alpha _{{1}}}^{2}{\beta _{{1}}}^{2}{R_{{2}}}^{2 }+6\,\alpha _{{1}}{\beta _{{1}}}^{3}{R_{{2}}}^{2}-{\alpha _{{1}}}^{2}{R_{ {2}}}^{2}+4\,\alpha _{{1}}\beta _{{1}}{R_{{2}}}^{2}-{\beta _{{1}}}^{2}{R_ {{2}}}^{2}-3\,{\alpha _{{1}}}^{2}{\beta _{{1}}}^{2} \right) }{{R_{{2}}}^ {2} \left( {\alpha _{{1}}}^{4}-5\,\beta _{{1}}{\alpha _{{1}}}^{3}-12\,{ \alpha _{{1}}}^{2}{\beta _{{1}}}^{2}-5\,\alpha _{{1}}{\beta _{{1}}}^{3}+{ \beta _{{1}}}^{4}+2\,{\alpha _{{1}}}^{2}-8\,\beta _{{1}}\alpha _{{1}}+2\,{ \beta _{{1}}}^{2} \right) +3\,{\alpha _{{1}}}^{2}{\beta _{{1}}}^{2} \left( {\alpha _{{1}}}^{2}+2\,\beta _{{1}}\alpha _{{1}}+{\beta _{{1}}}^{2 }+2 \right) }}$$

$$+ \exp (-l_1)+k_3\sin (l_3), \ \ \ l_i=\alpha _ix+\beta _iy+\lambda _it+\mu _i,\ \ \ i=1,2,3, \ \ \ R_{{2}}=\frac{1}{2}\,{\frac{ \sqrt{2M_{{1}} \left( -M_{{2}}+ \sqrt{- 12\,M_{{1}}{\alpha _{{1}}}^{2}{\beta _{{1}}}^{2}+{M_{{2}}}^{2}} \right) }}{M_{{1}}}},$$

so that $M_{{1}} \left( -M_{{2}}+ \sqrt{-12\,M_{{1}}{\alpha _{{1}}}^{2}{\beta _{{ 1}}}^{2}+{M_{{2}}}^{2}} \right) >0$ and $-12\,M_{{1}}{\alpha _{{1}}}^{2}{\beta _{{1}}}^{2}+{M_{{2}}}^{2}>0$.

Case (5):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _1=-i\beta _3,\ \ \alpha _3=-\beta _3,\ \ \beta _1=i\beta _3,\ \ k_1=k_1, \ \ k_2=0,\ \ s_{{2}}=\frac{1}{2}\,{\frac{s_{{1}} \left( 4\,{\beta _{{3}}}^{2}-1 \right) }{{ \beta _{{3}}}^{2}}} ,\ \ \\ g_5(x,y,t)={\textrm{e}^{-t\lambda _{{1}}+ix\beta _{{3}}-iy\beta _{{3}}-\mu _{{1}}}}+k_1{\textrm{e}^{t\lambda _{{1}}-ix\beta _{{3}}+iy\beta _{{3}}+ \mu _{{1}}}}+k_{{3}}\sin \left( t\lambda _{{3}}-x\beta _{{3}}+y\beta _{{3 }}+\mu _{{3}} \right) ,\\ \end{array} \right. \end{aligned}$$

(14)

Then the exact breather wave solution will be as

$$\begin{aligned} u_5=2\frac{\partial ^2}{\partial x \partial y}\ln g_5,\ \ \ v_5=2\frac{\partial ^2}{\partial x^2}\ln g_5,\ \ \ w_5=2\frac{\partial ^2}{\partial y^2}\ln g_5. \end{aligned}$$

(15)

Case (6):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _{{1}}=-{\frac{{\beta _{{3}}}^{2}}{\beta _{{1}}}},\ \ \alpha _3=-\beta _3,\ \ \beta _1=i\beta _3,\ \ k_2=0, \\ \lambda _{{1}}=\frac{1}{2}\,{\frac{2\,k_{{1}} \left( 4\,{\beta _{{1}}}^{8}{ \beta _{{3}}}^{2}-8\,{\beta _{{1}}}^{4}{\beta _{{3}}}^{6}+4\,{\beta _{{3}} }^{10}+{\beta _{{1}}}^{8}+6\,{\beta _{{1}}}^{6}{\beta _{{3}}}^{2}-6\,{ \beta _{{1}}}^{4}{\beta _{{3}}}^{4}+6\,{\beta _{{1}}}^{2}{\beta _{{3}}}^{6 }+{\beta _{{3}}}^{8} \right) +{\beta _{{1}}}^{6}{\beta _{{3}}}^{2}{k_{{3} }}^{2}-6\,{\beta _{{1}}}^{4}{\beta _{{3}}}^{4}{k_{{3}}}^{2}+{\beta _{{1}} }^{2}{\beta _{{3}}}^{6}{k_{{3}}}^{2}}{ \left( {\beta _{{1}}}^{2}{\beta _{ {3}}}^{2}{k_{{3}}}^{2}+{\beta _{{1}}}^{4}k_{{1}}+6\,{\beta _{{1}}}^{2}{ \beta _{{3}}}^{2}k_{{1}}+{\beta _{{3}}}^{4}k_{{1}} \right) \beta _{{1}} \left( \beta _{{1}}-\beta _{{3}} \right) \left( \beta _{{1}}+\beta _{{3} } \right) }} ,\\ \lambda _{{3}}={\frac{\beta _{{3}} \left( {\beta _{{1}}}^{6}-{\beta _{{1} }}^{4}{\beta _{{3}}}^{2}-{\beta _{{1}}}^{2}{\beta _{{3}}}^{4}+{\beta _{{3} }}^{6}+2\,{\beta _{{1}}}^{4}+2\,{\beta _{{1}}}^{2}{\beta _{{3}}}^{2} \right) }{{\beta _{{1}}}^{2} \left( \beta _{{1}}-\beta _{{3}} \right) \left( \beta _{{1}}+\beta _{{3}} \right) }},\\ s_{{2}}=\frac{1}{2}\,{\frac{s_{{1}} \left( 4\,{\beta _{{1}}}^{2}{\beta _{{3}}}^ {2}{k_{{3}}}^{2}+12\,{\beta _{{1}}}^{4}k_{{1}}+8\,{\beta _{{1}}}^{2}{ \beta _{{3}}}^{2}k_{{1}}+12\,{\beta _{{3}}}^{4}k_{{1}}-{\beta _{{1}}}^{2} {k_{{3}}}^{2}+4\,{\beta _{{1}}}^{2}k_{{1}} \right) }{{\beta _{{1}}}^{2}{ \beta _{{3}}}^{2}{k_{{3}}}^{2}+{\beta _{{1}}}^{4}k_{{1}}+6\,{\beta _{{1}} }^{2}{\beta _{{3}}}^{2}k_{{1}}+{\beta _{{3}}}^{4}k_{{1}}}}. \end{array} \right. \end{aligned}$$

(16)

Then the exact breather wave solution will be as

$$\begin{aligned} u_6=2\frac{\partial ^2}{\partial x \partial y}\ln g_6,\ \ \ v_6=2\frac{\partial ^2}{\partial x^2}\ln g_6,\ \ \ w_6=2\frac{\partial ^2}{\partial y^2}\ln g_6, \end{aligned}$$

(17)

$$g_6(x,y,t)={\textrm{e}^{-t\lambda _{{1}}+{\frac{x{\beta _{{3}}}^{2}}{\beta _{{1}}}}-y \beta _{{1}}-\mu _{{1}}}}+k_{{1}}{\textrm{e}^{t\lambda _{{1}}-{\frac{x{ \beta _{{3}}}^{2}}{\beta _{{1}}}}+y\beta _{{1}}+\mu _{{1}}}}+$$

$$k_{{3}}\sin \left( {\frac{t\beta _{{3}} \left( {\beta _{{1}}}^{6}-{\beta _{{1}}}^{4 }{\beta _{{3}}}^{2}-{\beta _{{1}}}^{2}{\beta _{{3}}}^{4}+{\beta _{{3}}}^{6 }+2\,{\beta _{{1}}}^{4}+2\,{\beta _{{1}}}^{2}{\beta _{{3}}}^{2} \right) }{{\beta _{{1}}}^{2} \left( \beta _{{1}}-\beta _{{3}} \right) \left( \beta _{{1}}+\beta _{{3}} \right) }}-x\beta _{{3}}+y\beta _{{3}}+\mu _{{3}} \right) .$$

Case (7):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _{{1}}=-\frac{1}{2}\,{\frac{{R_{{3}}}^{2}+{\beta _{{1}}}^{2}}{\beta _{{1} }}} ,\ \ \beta _{{3}}=\lambda _3= \sqrt{2\,\beta _{{1}} \sqrt{{\beta _{{1}}}^{2}-2}+{\beta _{{ 1}}}^{2}},\ \ \alpha _3=k_1=k_2=0, \\ \lambda _{{1}}=\frac{1}{2}\,{\frac{4\,{\beta _{{1}}}^{4}s_{{1}}-4\,{\beta _{{1}} }^{4}s_{{2}}+4\,{\beta _{{1}}}^{2}{\beta _{{3}}}^{2}s_{{1}}-4\,{\beta _{{ 1}}}^{2}{\beta _{{3}}}^{2}s_{{2}}+{\beta _{{1}}}^{2}s_{{1}}+8\,{\beta _{{ 1}}}^{2}s_{{2}}-{\beta _{{3}}}^{2}s_{{1}}}{\beta _{{1}}s_{{1}}}}. \end{array} \right. \end{aligned}$$

(18)

Then the exact breather wave solution will be as

$$\begin{aligned} u_7=2\frac{\partial ^2}{\partial x \partial y}\ln g_7,\ \ \ v_7=2\frac{\partial ^2}{\partial x^2}\ln g_7,\ \ \ w_7=2\frac{\partial ^2}{\partial y^2}\ln g_7, \end{aligned}$$

(19)

$$g_7(x,y,t)={\textrm{e}^{-1/2\,{\frac{t \left( 4\,{\beta _{{1}}}^{4}s_{{1}}-4\,{\beta _{{1}}}^{4}s_{{2}}+4\,{\beta _{{1}}}^{2}{\beta _{{3}}}^{2}s_{{1}}-4\,{ \beta _{{1}}}^{2}{\beta _{{3}}}^{2}s_{{2}}+{\beta _{{1}}}^{2}s_{{1}}+8\,{ \beta _{{1}}}^{2}s_{{2}}-{\beta _{{3}}}^{2}s_{{1}} \right) }{\beta _{{1}} s_{{1}}}}+1/2\,{\frac{x \left( {\beta _{{1}}}^{2}+{\beta _{{3}}}^{2} \right) }{\beta _{{1}}}}-y\beta _{{1}}-\mu _{{1}}}}+k_{{3}}\sin \left( t \beta _{{3}}+y\beta _{{3}}+\mu _{{3}} \right) ,$$

so that $2\,\beta _{{1}} \sqrt{{\beta _{{1}}}^{2}-2}+{\beta _{{1}}}^{2}>0$.

Case (8):

$$\begin{aligned} \left\{ \begin{array}{ll} R_{{4}}= \sqrt{2\,\alpha _{{1}} \sqrt{{\alpha _{{1}}}^{2}-2}+{\alpha _{{1 }}}^{2}},\ \ \alpha _{{3}}=\lambda _3=R_4,\ \ \beta _{{1}}=-\frac{1}{2}\,{\frac{{R_{{4}}}^{2}+{\alpha _{{1}}}^{2}}{\alpha _{{1 }}}},\ \ \beta _3=k_1=k_2=0, \\ \lambda _{{1}}=1/2\,{\frac{4\,{R_{{4}}}^{2}{\alpha _{{1}}}^{2}s_{{1}}-4 \,{R_{{4}}}^{2}{\alpha _{{1}}}^{2}s_{{2}}+4\,{\alpha _{{1}}}^{4}s_{{1}}- 4\,{\alpha _{{1}}}^{4}s_{{2}}-{R_{{4}}}^{2}s_{{1}}+{\alpha _{{1}}}^{2}s_ {{1}}+8\,{\alpha _{{1}}}^{2}s_{{2}}}{\alpha _{{1}}s_{{1}}}} . \end{array} \right. \end{aligned}$$

(20)

Then the exact breather wave solution will be as

$$\begin{aligned} u_8=2\frac{\partial ^2}{\partial x \partial y}\ln g_8,\ \ \ v_8=2\frac{\partial ^2}{\partial x^2}\ln g_8,\ \ \ w_8=2\frac{\partial ^2}{\partial y^2}\ln g_8, \end{aligned}$$

(21)

$$g_8(x,y,t)={\textrm{e}^{-1/2\,{\frac{t \left( 4\,{R_{{4}}}^{2}{\alpha _{{1}}}^{2}s_{ {1}}-4\,{R_{{4}}}^{2}{\alpha _{{1}}}^{2}s_{{2}}+4\,{\alpha _{{1}}}^{4}s_ {{1}}-4\,{\alpha _{{1}}}^{4}s_{{2}}-{R_{{4}}}^{2}s_{{1}}+{\alpha _{{1}}} ^{2}s_{{1}}+8\,{\alpha _{{1}}}^{2}s_{{2}} \right) }{\alpha _{{1}}s_{{1}} }}-x\alpha _{{1}}+1/2\,{\frac{y \left( {R_{{4}}}^{2}+{\alpha _{{1}}}^{2 } \right) }{\alpha _{{1}}}}-\mu _{{1}}}}+k_{{3}}\sin \left( tR_{{4}}+xR_ {{4}}+\mu _{{3}} \right) ,$$

so that $2\,\alpha _{{1}} \sqrt{{\alpha _{{1}}}^{2}-2}+{\alpha _{{1}}}^{2}>0$.

Case (9):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _{{1}}={\frac{\alpha _{{3}}\beta _{{1}}}{\beta _{{3}}}},\ \ k_{{1}}=-\frac{1}{4}\,{\frac{{\beta _{{3}}}^{2}{k_{{3}}}^{2}}{{\beta _{{1}}}^{2 }}},\ \ k_2=0,\\ \lambda _{{1}}=-{\frac{ \left( {\alpha _{{3}}}^{3}{\beta _{{1}}}^{2}s_{{ 1}}-3\,{\alpha _{{3}}}^{3}{\beta _{{3}}}^{2}s_{{1}}+{\alpha _{{3}}}^{2}{ \beta _{{1}}}^{2}\beta _{{3}}s_{{2}}-3\,{\alpha _{{3}}}^{2}{\beta _{{3}}}^ {3}s_{{2}}+\alpha _{{3}}{\beta _{{1}}}^{2}{\beta _{{3}}}^{2}s_{{1}}-3\, \alpha _{{3}}{\beta _{{3}}}^{4}s_{{1}}-{\alpha _{{3}}}^{2}s_{{1}}\beta _{{ 3}}-{\beta _{{3}}}^{3}s_{{1}} \right) \beta _{{1}}}{s_{{1}}{\beta _{{3}}} ^{2} \left( \alpha _{{3}}+\beta _{{3}} \right) }}, \\ \lambda _{{3}}=-{\frac{3\,{\alpha _{{3}}}^{3}{\beta _{{1}}}^{2}s_{{1}}-{ \alpha _{{3}}}^{3}{\beta _{{3}}}^{2}s_{{1}}+3\,{\alpha _{{3}}}^{2}{\beta _ {{1}}}^{2}\beta _{{3}}s_{{2}}-{\alpha _{{3}}}^{2}{\beta _{{3}}}^{3}s_{{2} }+3\,\alpha _{{3}}{\beta _{{1}}}^{2}{\beta _{{3}}}^{2}s_{{1}}-\alpha _{{3} }{\beta _{{3}}}^{4}s_{{1}}-{\alpha _{{3}}}^{2}s_{{1}}\beta _{{3}}-{\beta _ {{3}}}^{3}s_{{1}}}{\beta _{{3}} \left( \alpha _{{3}}+\beta _{{3}} \right) s_{{1}}}}. \end{array} \right. \end{aligned}$$

(22)

Then the exact breather wave solution will be as

$$\begin{aligned} u_9=2\frac{\partial ^2}{\partial x \partial y}\ln g_9,\ \ \ v_9=2\frac{\partial ^2}{\partial x^2}\ln g_9,\ \ \ w_9=2\frac{\partial ^2}{\partial y^2}\ln g_9, \end{aligned}$$

(23)

$$g_9(x,y,t)={\textrm{e}^{t\lambda _{{1}}-{\frac{x\alpha _{{3}}\beta _{{1}}}{\beta _{{3}} }}-y\beta _{{1}}-\mu _{{1}}}}-1/4\,{\frac{{\beta _{{3}}}^{2}{k_{{3}}}^{2 }}{{\beta _{{1}}}^{2}}{\textrm{e}^{-t\lambda _{{1}}+{\frac{x\alpha _{{3}} \beta _{{1}}}{\beta _{{3}}}}+y\beta _{{1}}+\mu _{{1}}}}}+k_{{3}}\sin \left( -t\lambda _{{3}}+x\alpha _{{3}}+y\beta _{{3}}+\mu _{{3}} \right) .$$

Case (10):

$$\begin{aligned} \left\{ \begin{array}{ll} R_{{4}}=\frac{1}{3}\,{\frac{ \sqrt{3} \sqrt{ \left( 8\,{\beta _{{3}}}^{2}-1 \right) \left( 4\,{\beta _{{3}}}^{2}+2\, \sqrt{4\,{\beta _{{3}}}^{4}+ 16\,{\beta _{{3}}}^{2}-2}-1 \right) }}{8\,{\beta _{{3}}}^{2}-1}} ,\ \ \alpha _{{1}}=R_4\beta _3,\ \ \alpha _3=-\beta _3,\ \ \beta _{{1}}=R_4\beta _3,\\ k_{{1}}=\frac{1}{4}\,{\frac{ \left( 8\,{\beta _{{3}}}^{2}-1 \right) {k_{{3}}}^ {2}}{2\,{R_{{4}}}^{2}{\beta _{{3}}}^{2}+2\,{\beta _{{3}}}^{2}-1}},\ \ k_2=0,\ \ \lambda _3=0,\\ \lambda _{{1}}=\frac{1}{3}\,{\frac{R_{{4}}\beta _{{3}} \left( 24\,{R_{{4}}}^{2} {\beta _{{3}}}^{4}s_{{1}}-12\,{R_{{4}}}^{2}{\beta _{{3}}}^{4}s_{{2}}-30 \,{R_{{4}}}^{2}{\beta _{{3}}}^{2}s_{{1}}-8\,{\beta _{{3}}}^{4}s_{{1}}+4 \,{\beta _{{3}}}^{4}s_{{2}}+3\,{R_{{4}}}^{2}s_{{1}}+10\,{\beta _{{3}}}^{ 2}s_{{1}}-4\,{\beta _{{3}}}^{2}s_{{2}}+s_{{1}} \right) }{s_{{1}}}}. \end{array} \right. \end{aligned}$$

(24)

Then the exact breather wave solution will be as

$$\begin{aligned} u_{10}=2\frac{\partial ^2}{\partial x \partial y}\ln g_{10},\ \ \ v_{10}=2\frac{\partial ^2}{\partial x^2}\ln g_{10},\ \ \ w_{10}=2\frac{\partial ^2}{\partial y^2}\ln g_{10}, \end{aligned}$$

(25)

$$g_{10}(x,y,t)={\textrm{e}^{-xR_{{4}}\beta _{{3}}-yR_{{4}}\beta _{{3}}-\lambda _{{1}}t-\mu _ {{1}}}}+\frac{1}{4}\,{\frac{ \left( 8\,{\beta _{{3}}}^{2}-1 \right) {k_{{3}}}^ {2}{\textrm{e}^{xR_{{4}}\beta _{{3}}+yR_{{4}}\beta _{{3}}+\lambda _{{1}}t+ \mu _{{1}}}}}{2\,{R_{{4}}}^{2}{\beta _{{3}}}^{2}+2\,{\beta _{{3}}}^{2}-1} }+k_{{3}}\sin \left( -x\beta _{{3}}+y\beta _{{3}}+\mu _{{3}} \right) ,$$

so that $\left( 8\,{\beta _{{3}}}^{2}-1 \right) \left( 4\,{\beta _{{3}}}^{2}+2 \, \sqrt{4\,{\beta _{{3}}}^{4}+16\,{\beta _{{3}}}^{2}-2}-1 \right) >0$.

Case (11):

$$\begin{aligned} \left\{ \begin{array}{ll} R_{{5}}={\frac{ \sqrt{ \left( 8\,{\beta _{{3}}}^{2}+1 \right) \left( 8\,{\beta _{{3}}}^{2}+2\, \sqrt{-24\,{\beta _{{3}}}^{2}+6}-5 \right) }}{ 8\,{\beta _{{3}}}^{2}+1}} ,\ \ \alpha _{{1}}={\frac{R_{{5}}\beta _{{3}} \left( 8\,{R_{{5}}}^{2}{\beta _ {{3}}}^{2}+{R_{{5}}}^{2}-16\,{\beta _{{3}}}^{2}+10 \right) }{8\,{\beta _ {{3}}}^{2}+1}},\\ \alpha _3=-\beta _3,\ \ \beta _{{1}}=R_5\beta _3,\\ k_{{1}}=-1/4\,{\frac{{k_{{3}}}^{2} \left( 8\,{\beta _{{3}}}^{2}+1 \right) }{16\,{\beta _{{3}}}^{2}-1}},\ \ k_2=0,\ \ \lambda _{{1}}=-4\,{\frac{\beta _{{3}} \left( 16\,{\beta _{{3}}}^{4}s_{{ 1}}-8\,{\beta _{{3}}}^{4}s_{{2}}-4\,{\beta _{{3}}}^{2}s_{{1}}+2\,{\beta _ {{3}}}^{2}s_{{2}}+3\,s_{{1}} \right) R_{{5}}}{ \left( 8\,{\beta _{{3}}} ^{2}+1 \right) s_{{1}} \left( {R_{{5}}}^{2}-1 \right) }} ,\\ \lambda _{{3}}=2\,{\frac{\beta _{{3}} \left( 48\,{R_{{5}}}^{2}{\beta _{{ 3}}}^{4}+6\,{R_{{5}}}^{2}{\beta _{{3}}}^{2}-16\,{\beta _{{3}}}^{4}-9\,{R _{{5}}}^{2}-10\,{\beta _{{3}}}^{2}-1 \right) }{ \left( 8\,{\beta _{{3}}} ^{2}+1 \right) \left( 8\,{R_{{5}}}^{2}{\beta _{{3}}}^{2}-11\,{R_{{5}}} ^{2}-8\,{\beta _{{3}}}^{2}-1 \right) }} . \end{array} \right. \end{aligned}$$

(26)

Then the exact breather wave solution will be as

$$\begin{aligned} u_{11}=2\frac{\partial ^2}{\partial x \partial y}\ln g_{11},\ \ \ v_{11}=2\frac{\partial ^2}{\partial x^2}\ln g_{11},\ \ \ w_{11}=2\frac{\partial ^2}{\partial y^2}\ln g_{11}, \end{aligned}$$

(27)

$$g_{11}(x,y,t)={\textrm{e}^{-\lambda _{{1}}t-{\frac{xR_{{5}}\beta _{{3}} \left( 8\,{R_{{5 }}}^{2}{\beta _{{3}}}^{2}+{R_{{5}}}^{2}-16\,{\beta _{{3}}}^{2}+10 \right) }{8\,{\beta _{{3}}}^{2}+1}}-yR_{{5}}\beta _{{3}}-\mu _{{1}}}}- \frac{1}{4}\,{\frac{{k_{{3}}}^{2} \left( 8\,{\beta _{{3}}}^{2}+1 \right) }{16\,{ \beta _{{3}}}^{2}-1}{\textrm{e}^{\lambda _{{1}}t+{\frac{xR_{{5}}\beta _{{3} } \left( 8\,{R_{{5}}}^{2}{\beta _{{3}}}^{2}+{R_{{5}}}^{2}-16\,{\beta _{{ 3}}}^{2}+10 \right) }{8\,{\beta _{{3}}}^{2}+1}}+yR_{{5}}\beta _{{3}}+\mu _{{1}}}}}$$

$$+ k_{{3}}\sin \left( 2\,{\frac{t\beta _{{3}} \left( 48\,{R_{{5 }}}^{2}{\beta _{{3}}}^{4}+6\,{R_{{5}}}^{2}{\beta _{{3}}}^{2}-16\,{\beta _ {{3}}}^{4}-9\,{R_{{5}}}^{2}-10\,{\beta _{{3}}}^{2}-1 \right) }{ \left( 8\,{\beta _{{3}}}^{2}+1 \right) \left( 8\,{R_{{5}}}^{2}{\beta _{{3}}}^{ 2}-11\,{R_{{5}}}^{2}-8\,{\beta _{{3}}}^{2}-1 \right) }}-x\beta _{{3}}+y \beta _{{3}}+\mu _{{3}} \right) ,$$

so that $\left( 8\,{\beta _{{3}}}^{2}+1 \right) \left( 8\,{\beta _{{3}}}^{2}+2 \, \sqrt{-24\,{\beta _{{3}}}^{2}+6}-5 \right) >0$.

Case (12):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _{{1}}=-i\alpha _2,\ \ \beta _{{1}}=i\beta _2,\\ k_{{1}}=-\frac{1}{4}k_2^2,\ \ k_3=0,\ \ \ s_1=0. \end{array} \right. \end{aligned}$$

(28)

Then the exact breather wave solution will be as

$$\begin{aligned} u_{12}=2\frac{\partial ^2}{\partial x \partial y}\ln g_{12},\ \ \ v_{12}=2\frac{\partial ^2}{\partial x^2}\ln g_{12},\ \ \ w_{12}=2\frac{\partial ^2}{\partial y^2}\ln g_{12}, \end{aligned}$$

(29)

$$g_{12}(x,y,t)={\textrm{e}^{-\lambda _{{1}}t+ix\alpha _{{2}}-iy\beta _{{2}}-\mu _{{1}}}}-1/4 \,{k_{{2}}}^{2}{\textrm{e}^{\lambda _{{1}}t-ix\alpha _{{2}}+iy\beta _{{2}}+ \mu _{{1}}}}+k_{{2}}\cos \left( t\lambda _{{2}}+x\alpha _{{2}}+y\beta _{{2 }}+\mu _{{2}} \right) .$$

Case (13):

$$\begin{aligned} \left\{ \begin{array}{ll} R_{{2}}=\frac{1}{2}\,{\frac{ \sqrt{2} \sqrt{M_{{1}} \left( -M_{{2}}+ \sqrt{- 12\,M_{{1}}{\alpha _{{1}}}^{2}{\beta _{{1}}}^{2}+{M_{{2}}}^{2}} \right) }}{M_{{1}}}} ,\ \ M_{{1}}=2\,{\alpha _{{1}}}^{2}+4\,\beta _{{1}}\alpha _{{1}}+2\,{\beta _{{1 }}}^{2}+3,\\ M_{{2}}=-6\,\beta _{{1}}{\alpha _{{1}}}^{3}-12\,{\alpha _{{1}}}^{2}{\beta _{{1}}}^{2}-6\,\alpha _{{1}}{\beta _{{1}}}^{3}+{\alpha _{{1}}}^{2}-4\, \beta _{{1}}\alpha _{{1}}+{\beta _{{1}}}^{2},\ \ \alpha _2=-R_2,\ \ \beta _2=R_2, \ \ k_3=0,\\ k_{{1}}=-\frac{1}{2}\,{\frac{{k_{{2}}}^{2} \left( {R_{{2}}}^{2} \left( 6\,{ \alpha _{{1}}}^{3}\beta _{{1}}+12\,{\alpha _{{1}}}^{2}{\beta _{{1}}}^{2}+6 \,\alpha _{{1}}{\beta _{{1}}}^{3}-{\alpha _{{1}}}^{2}+4\,\alpha _{{1}} \beta _{{1}}-{\beta _{{1}}}^{2} \right) -3\,{\alpha _{{1}}}^{2}{\beta _{{1 }}}^{2} \right) }{{R_{{2}}}^{2} \left( {\alpha _{{1}}}^{4}-5\,{\alpha _{ {1}}}^{3}\beta _{{1}}-12\,{\alpha _{{1}}}^{2}{\beta _{{1}}}^{2}-5\,\alpha _{{1}}{\beta _{{1}}}^{3}+{\beta _{{1}}}^{4}+2\,{\alpha _{{1}}}^{2}-8\, \alpha _{{1}}\beta _{{1}}+2\,{\beta _{{1}}}^{2} \right) +3\,{\alpha _{{1}} }^{2}{\beta _{{1}}}^{2} \left( {\alpha _{{1}}}^{2}+2\,\alpha _{{1}}\beta _ {{1}}+{\beta _{{1}}}^{2}+2 \right) }},\\ s_{{2}}=\frac{1}{2}\,{\frac{s_{{1}} \left( 4\,{R_{{2}}}^{3}\alpha _{{1}}-4\,{R _{{2}}}^{3}\beta _{{1}}-R_{{2}} \left( \alpha _{{1}}-\beta _{{1}} \right) \left( {\alpha _{{1}}}^{2}-2\,\alpha _{{1}}\beta _{{1}}+{\beta _ {{1}}}^{2}+2 \right) -\alpha _{{1}}\lambda _{{2}}-\beta _{{1}}\lambda _{{2 }} \right) }{R_{{2}} \left( \alpha _{{1}}-\beta _{{1}} \right) \left( { R_{{2}}}^{2}+\alpha _{{1}}\beta _{{1}} \right) }}, \end{array} \right. \end{aligned}$$

(30)

Then, the exact breather wave solution will be as

$$\begin{aligned} u_{13}=2\frac{\partial ^2}{\partial x \partial y}\ln g_{13},\ \ \ v_{13}=2\frac{\partial ^2}{\partial x^2}\ln g_{13},\ \ \ w_{13}=2\frac{\partial ^2}{\partial y^2}\ln g_{13}, \end{aligned}$$

(31)

$$g_{13}(x,y,t)={\textrm{e}^{{\frac{t \left( A_{{1}}+A_{{2}}+A_{{3}} \right) }{ \left( { R_{{2}}}^{2}+\alpha _{{1}}\beta _{{1}} \right) \left( \alpha _{{1}}- \beta _{{1}} \right) R_{{2}} \left( 2\,{\alpha _{{1}}}^{2}+4\,\alpha _{{1 }}\beta _{{1}}+2\,{\beta _{{1}}}^{2}+3 \right) }}-x\alpha _{{1}}-y\beta _{ {1}}-\mu _{{1}}}}+k_{{2 }}\cos \left( t\lambda _{{2}}-xR_{{2}}+yR_{{2}}+\mu _{{2}} \right) -$$

$$\frac{1}{2}\,{\frac{{k_{{2}}}^{2} \left( {R_{{2}}}^{2} \left( 6\,{\alpha _{{1}}}^{3}\beta _{{1}}+12\,{\alpha _{{1}}}^{2}{\beta _ {{1}}}^{2}+6\,\alpha _{{1}}{\beta _{{1}}}^{3}-{\alpha _{{1}}}^{2}+4\, \alpha _{{1}}\beta _{{1}}-{\beta _{{1}}}^{2} \right) -3\,{\alpha _{{1}}}^{ 2}{\beta _{{1}}}^{2} \right) }{{R_{{2}}}^{2} \left( {\alpha _{{1}}}^{4}- 5\,{\alpha _{{1}}}^{3}\beta _{{1}}-12\,{\alpha _{{1}}}^{2}{\beta _{{1}}}^{ 2}-5\,\alpha _{{1}}{\beta _{{1}}}^{3}+{\beta _{{1}}}^{4}+2\,{\alpha _{{1}} }^{2}-8\,\alpha _{{1}}\beta _{{1}}+2\,{\beta _{{1}}}^{2} \right) +3\,{ \alpha _{{1}}}^{2}{\beta _{{1}}}^{2} \left( {\alpha _{{1}}}^{2}+2\,\alpha _{{1}}\beta _{{1}}+{\beta _{{1}}}^{2}+2 \right) }}$$

$$\times {\textrm{e}^{-{\frac{t \left( A_{{1}}+A_{{2}}+A_{{3}} \right) }{ \left( {R_{{2}}}^{2}+\alpha _{{1}}\beta _{{1}} \right) \left( \alpha _{{1}}-\beta _{{1}} \right) R_{ {2}} \left( 2\,{\alpha _{{1}}}^{2}+4\,\alpha _{{1}}\beta _{{1}}+2\,{\beta _{{1}}}^{2}+3 \right) }}+x\alpha _{{1}}+y\beta _{{1}}+\mu _{{1}}}},$$

so that $M_{{1}} \left( -M_{{2}}+ \sqrt{-12\,M_{{1}}{\alpha _{{1}}}^{2}{\beta _{{ 1}}}^{2}+{M_{{2}}}^{2}} \right) >0$ and $-12\,M_{{1}}{\alpha _{{1}}}^{2}{\beta _{{1}}}^{2}+{M_{{2}}}^{2}>0$.

Case (14):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _{{1}}=-{\frac{{\beta _{{2}}}^{2}}{\beta _{{1}}}},\ \ \ \alpha _2=-\beta _2,\ \ \ k_3=0,\\ \lambda _{{1}}=\frac{1}{2}\,{\frac{2\,k_{{1}} \left( 4\,{\beta _{{1}}}^{8}{ \beta _{{2}}}^{2}-8\,{\beta _{{1}}}^{4}{\beta _{{2}}}^{6}+4\,{\beta _{{2}} }^{10}+{\beta _{{1}}}^{8}+6\,{\beta _{{1}}}^{6}{\beta _{{2}}}^{2}-6\,{ \beta _{{1}}}^{4}{\beta _{{2}}}^{4}+6\,{\beta _{{1}}}^{2}{\beta _{{2}}}^{6 }+{\beta _{{2}}}^{8} \right) +{\beta _{{1}}}^{6}{\beta _{{2}}}^{2}{k_{{2} }}^{2}-6\,{\beta _{{1}}}^{4}{\beta _{{2}}}^{4}{k_{{2}}}^{2}+{\beta _{{1}} }^{2}{\beta _{{2}}}^{6}{k_{{2}}}^{2}}{ \left( {\beta _{{1}}}^{2}{\beta _{ {2}}}^{2}{k_{{2}}}^{2}+{\beta _{{1}}}^{4}k_{{1}}+6\,{\beta _{{1}}}^{2}{ \beta _{{2}}}^{2}k_{{1}}+{\beta _{{2}}}^{4}k_{{1}} \right) \beta _{{1}} \left( \beta _{{1}}-\beta _{{2}} \right) \left( \beta _{{1}}+\beta _{{2} } \right) }} ,\\ \lambda _{{2}}={\frac{\beta _{{2}} \left( {\beta _{{1}}}^{6}-{\beta _{{1} }}^{4}{\beta _{{2}}}^{2}-{\beta _{{1}}}^{2}{\beta _{{2}}}^{4}+{\beta _{{2} }}^{6}+2\,{\beta _{{1}}}^{4}+2\,{\beta _{{1}}}^{2}{\beta _{{2}}}^{2} \right) }{{\beta _{{1}}}^{2} \left( \beta _{{1}}-\beta _{{2}} \right) \left( \beta _{{1}}+\beta _{{2}} \right) }} ,\\ s_{{2}}=1/2\,{\frac{s_{{1}} \left( 4\,{\beta _{{1}}}^{2}{\beta _{{2}}}^ {2}{k_{{2}}}^{2}+12\,{\beta _{{1}}}^{4}k_{{1}}+8\,{\beta _{{1}}}^{2}{ \beta _{{2}}}^{2}k_{{1}}+12\,{\beta _{{2}}}^{4}k_{{1}}-{\beta _{{1}}}^{2} {k_{{2}}}^{2}+4\,{\beta _{{1}}}^{2}k_{{1}} \right) }{{\beta _{{1}}}^{2}{ \beta _{{2}}}^{2}{k_{{2}}}^{2}+{\beta _{{1}}}^{4}k_{{1}}+6\,{\beta _{{1}} }^{2}{\beta _{{2}}}^{2}k_{{1}}+{\beta _{{2}}}^{4}k_{{1}}}}. \end{array} \right. \end{aligned}$$

(32)

Then, the exact breather wave solution will be as

$$\begin{aligned} u_{14}=2\frac{\partial ^2}{\partial x \partial y}\ln g_{14},\ \ \ v_{14}=2\frac{\partial ^2}{\partial x^2}\ln g_{14},\ \ \ w_{14}=2\frac{\partial ^2}{\partial y^2}\ln g_{14}, \end{aligned}$$

(33)

$$g_{14}(x,y,t)={\textrm{e}^{-\lambda _{{1}}t+{\frac{x{\beta _{{2}}}^{2}}{\beta _{{1}}}}-y \beta _{{1}}-\mu _{{1}}}}+k_{{1}}{\textrm{e}^{\lambda _{{1}}t-{\frac{x{ \beta _{{2}}}^{2}}{\beta _{{1}}}}+y\beta _{{1}}+\mu _{{1}}}}+$$

$$k_{{2}}\cos \left( {\frac{t\beta _{{2}} \left( {\beta _{{1}}}^{6}-{\beta _{{1}}}^{4 }{\beta _{{2}}}^{2}-{\beta _{{1}}}^{2}{\beta _{{2}}}^{4}+{\beta _{{2}}}^{6 }+2\,{\beta _{{1}}}^{4}+2\,{\beta _{{1}}}^{2}{\beta _{{2}}}^{2} \right) }{{\beta _{{1}}}^{2} \left( \beta _{{1}}-\beta _{{2}} \right) \left( \beta _{{1}}+\beta _{{2}} \right) }}-x\beta _{{2}}+y\beta _{{2}}+\mu _{{2}} \right) .$$

Case (15):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _{{1}}={\frac{\alpha _{{2}}\beta _{{1}}}{\beta _{{2}}}},\ \ \ k_{{1}}=-1/4\,{\frac{{\beta _{{2}}}^{2}{k_{{2}}}^{2}}{{\beta _{{1}}}^{2 }}} ,\ \ \ k_3=0,\\ \lambda _{{1}}=-{\frac{ \left( {\alpha _{{2}}}^{3}{\beta _{{1}}}^{2}s_{{ 1}}-3\,{\alpha _{{2}}}^{3}{\beta _{{2}}}^{2}s_{{1}}+{\alpha _{{2}}}^{2}{ \beta _{{1}}}^{2}\beta _{{2}}s_{{2}}-3\,{\alpha _{{2}}}^{2}{\beta _{{2}}}^ {3}s_{{2}}+\alpha _{{2}}{\beta _{{1}}}^{2}{\beta _{{2}}}^{2}s_{{1}}-3\, \alpha _{{2}}{\beta _{{2}}}^{4}s_{{1}}-{\alpha _{{2}}}^{2}\beta _{{2}}s_{{ 1}}-{\beta _{{2}}}^{3}s_{{1}} \right) \beta _{{1}}}{s_{{1}}{\beta _{{2}}} ^{2} \left( \alpha _{{2}}+\beta _{{2}} \right) }} ,\\ \lambda _{{2}}=-{\frac{3\,{\alpha _{{2}}}^{3}{\beta _{{1}}}^{2}s_{{1}}-{ \alpha _{{2}}}^{3}{\beta _{{2}}}^{2}s_{{1}}+3\,{\alpha _{{2}}}^{2}{\beta _ {{1}}}^{2}\beta _{{2}}s_{{2}}-{\alpha _{{2}}}^{2}{\beta _{{2}}}^{3}s_{{2} }+3\,\alpha _{{2}}{\beta _{{1}}}^{2}{\beta _{{2}}}^{2}s_{{1}}-\alpha _{{2} }{\beta _{{2}}}^{4}s_{{1}}-{\alpha _{{2}}}^{2}\beta _{{2}}s_{{1}}-{\beta _ {{2}}}^{3}s_{{1}}}{\beta _{{2}} \left( \alpha _{{2}}+\beta _{{2}} \right) s_{{1}}}} . \end{array} \right. \end{aligned}$$

(34)

Then, the exact breather wave solution will be as

$$\begin{aligned} u_{15}=2\frac{\partial ^2}{\partial x \partial y}\ln g_{15},\ \ \ v_{15}=2\frac{\partial ^2}{\partial x^2}\ln g_{15},\ \ \ w_{15}=2\frac{\partial ^2}{\partial y^2}\ln g_{15}, \end{aligned}$$

(35)

$$g_{15}(x,y,t)={\textrm{e}^{\lambda _{{1}}t-{\frac{x\alpha _{{2}}\beta _{{1}}}{\beta _{{2}} }}-y\beta _{{1}}-\mu _{{1}}}}-1/4\,{\frac{{\beta _{{2}}}^{2}{k_{{2}}}^{2 }}{{\beta _{{1}}}^{2}}{\textrm{e}^{-\lambda _{{1}}t+{\frac{x\alpha _{{2}} \beta _{{1}}}{\beta _{{2}}}}+y\beta _{{1}}+\mu _{{1}}}}}+$$

$$k_{{2}}\cos \left( -{\frac{t \left( s_{{1}} \left( {\alpha _{{2}}}^{2} +{\beta _{{2}}}^{2} \right) \left( 3\,\alpha _{{2}}{\beta _{{1}}}^{2}- \alpha _{{2}}{\beta _{{2}}}^{2}-\beta _{{2}} \right) +3\,{\alpha _{{2}}}^{ 2}{\beta _{{1}}}^{2}\beta _{{2}}s_{{2}}-{\alpha _{{2}}}^{2}{\beta _{{2}}}^ {3}s_{{2}} \right) }{\beta _{{2}} \left( \alpha _{{2}}+\beta _{{2}} \right) s_{{1}}}}+x\alpha _{{2}}+y\beta _{{2}}+\mu _{{2}} \right) .$$

Case (16):

$$\begin{aligned} \left\{ \begin{array}{ll} R_{{6}}=\frac{1}{3}\,{\frac{ \sqrt{ 3\left( 8\,{\beta _{{2}}}^{2}-1 \right) \left( 4\,{\beta _{{2}}}^{2}+2\, \sqrt{4\,{\beta _{{2}}}^{4}+ 16\,{\beta _{{2}}}^{2}-2}-1 \right) }}{8\,{\beta _{{2}}}^{2}-1}} ,\ \ \ \alpha _1=R_6\beta _2,\ \ \alpha _2=-\beta _2,\ \ \beta _1=R_6\beta _2,\\ k_{{1}}=\frac{1}{4}\,{\frac{ \left( 8\,{\beta _{{2}}}^{2}-1 \right) {k_{{2}}}^ {2}}{2\,{R_{{6}}}^{2}{\beta _{{2}}}^{2}+2\,{\beta _{{2}}}^{2}-1}} ,\ \ \ k_3=\lambda _2=0,\\ \lambda _{{1}}=\frac{1}{3}\,{\frac{R_{{6}}\beta _{{2}} \left( 24\,{R_{{6}}}^{2} {\beta _{{2}}}^{4}s_{{1}}-12\,{R_{{6}}}^{2}{\beta _{{2}}}^{4}s_{{2}}-30 \,{R_{{6}}}^{2}{\beta _{{2}}}^{2}s_{{1}}-8\,{\beta _{{2}}}^{4}s_{{1}}+4 \,{\beta _{{2}}}^{4}s_{{2}}+3\,{R_{{6}}}^{2}s_{{1}}+10\,{\beta _{{2}}}^{ 2}s_{{1}}-4\,{\beta _{{2}}}^{2}s_{{2}}+s_{{1}} \right) }{s_{{1}}}} . \end{array} \right. \end{aligned}$$

(36)

Then, the exact breather wave solution will be as

$$\begin{aligned} u_{16}=2\frac{\partial ^2}{\partial x \partial y}\ln g_{16},\ \ \ v_{16}=2\frac{\partial ^2}{\partial x^2}\ln g_{16},\ \ \ w_{16}=2\frac{\partial ^2}{\partial y^2}\ln g_{16}, \end{aligned}$$

(37)

$$g_{16}(x,y,t)={\textrm{e}^{-xR_{{6}}\beta _{{2}}-yR_{{6}}\beta _{{2}}-\lambda _{{1}}t-\mu _ {{1}}}}+\frac{1}{4}\,{\frac{ \left( 8\,{\beta _{{2}}}^{2}-1 \right) {k_{{2}}}^ {2}{\textrm{e}^{xR_{{6}}\beta _{{2}}+yR_{{6}}\beta _{{2}}+\lambda _{{1}}t+ \mu _{{1}}}}}{2\,{R_{{6}}}^{2}{\beta _{{2}}}^{2}+2\,{\beta _{{2}}}^{2}-1} }+k_{{2}}\cos \left( -x\beta _{{2}}+y\beta _{{2}}+\mu _{{2}} \right) ,$$

so that $\left( 8\,{\beta _{{2}}}^{2}-1 \right) \left( 4\,{\beta _{{2}}}^{2}+2 \, \sqrt{4\,{\beta _{{2}}}^{4}+16\,{\beta _{{2}}}^{2}-2}-1 \right) >0$.

Case (17):

$$\begin{aligned} \left\{ \begin{array}{ll} R_{{7}}={\frac{ \sqrt{ \left( 8\,{\beta _{{2}}}^{2}+1 \right) \left( 8\,{\beta _{{2}}}^{2}+2\, \sqrt{-24\,{\beta _{{2}}}^{2}+6}-5 \right) }}{ 8\,{\beta _{{2}}}^{2}+1}} ,\ \ \alpha _{{1}}={\frac{R_{{7}}\beta _{{2}} \left( 8\,{R_{{7}}}^{2}{\beta _ {{2}}}^{2}+{R_{{7}}}^{2}-16\,{\beta _{{2}}}^{2}+10 \right) }{8\,{\beta _ {{2}}}^{2}+1}} ,\ \ \ \alpha _2=-\beta _2,\ \ \beta _1=R_7\beta _2,\\ k_{{1}}=-\frac{1}{4}\,{\frac{{k_{{2}}}^{2} \left( 8\,{\beta _{{2}}}^{2}+1 \right) }{16\,{\beta _{{2}}}^{2}-1}} ,\ \ \ k_3=0,\ \ \lambda _{{1}}=-4\,{\frac{\beta _{{2}} \left( 16\,{\beta _{{2}}}^{4}s_{{ 1}}-8\,{\beta _{{2}}}^{4}s_{{2}}-4\,{\beta _{{2}}}^{2}s_{{1}}+2\,{\beta _ {{2}}}^{2}s_{{2}}+3\,s_{{1}} \right) R_{{7}}}{ \left( 8\,{\beta _{{2}}} ^{2}+1 \right) s_{{1}} \left( {R_{{7}}}^{2}-1 \right) }},\\ \lambda _{{2}}=2\,{\frac{\beta _{{2}} \left( 48\,{R_{{7}}}^{2}{\beta _{{ 2}}}^{4}+6\,{R_{{7}}}^{2}{\beta _{{2}}}^{2}-16\,{\beta _{{2}}}^{4}-9\,{R _{{7}}}^{2}-10\,{\beta _{{2}}}^{2}-1 \right) }{ \left( 8\,{\beta _{{2}}} ^{2}+1 \right) \left( 8\,{R_{{7}}}^{2}{\beta _{{2}}}^{2}-11\,{R_{{7}}} ^{2}-8\,{\beta _{{2}}}^{2}-1 \right) }}. \end{array} \right. \end{aligned}$$

(38)

Then, the exact breather wave solution will be as

$$\begin{aligned} u_{17}=2\frac{\partial ^2}{\partial x \partial y}\ln g_{17},\ \ \ v_{17}=2\frac{\partial ^2}{\partial x^2}\ln g_{17},\ \ \ w_{17}=2\frac{\partial ^2}{\partial y^2}\ln g_{17}, \end{aligned}$$

(39)

$$g_{17}(x,y,t)={\textrm{e}^{4\,{\frac{t\beta _{{2}} \left( 16\,{\beta _{{2}}}^{4}s_{{1}}- 8\,{\beta _{{2}}}^{4}s_{{2}}-4\,{\beta _{{2}}}^{2}s_{{1}}+2\,{\beta _{{2} }}^{2}s_{{2}}+3\,s_{{1}} \right) R_{{7}}}{ \left( 8\,{\beta _{{2}}}^{2} +1 \right) s_{{1}} \left( {R_{{7}}}^{2}-1 \right) }}-{\frac{xR_{{7}} \beta _{{2}} \left( 8\,{R_{{7}}}^{2}{\beta _{{2}}}^{2}+{R_{{7}}}^{2}-16 \,{\beta _{{2}}}^{2}+10 \right) }{8\,{\beta _{{2}}}^{2}+1}}-yR_{{7}} \beta _{{2}}-\mu _{{1}}}}-$$

$$\frac{1}{4}\,{\frac{{k_{{2}}}^{2} \left( 8\,{\beta _{{ 2}}}^{2}+1 \right) }{16\,{\beta _{{2}}}^{2}-1}{\textrm{e}^{-4\,{\frac{t \beta _{{2}} \left( 16\,{\beta _{{2}}}^{4}s_{{1}}-8\,{\beta _{{2}}}^{4}s_ {{2}}-4\,{\beta _{{2}}}^{2}s_{{1}}+2\,{\beta _{{2}}}^{2}s_{{2}}+3\,s_{{1 }} \right) R_{{7}}}{ \left( 8\,{\beta _{{2}}}^{2}+1 \right) s_{{1}} \left( {R_{{7}}}^{2}-1 \right) }}+{\frac{xR_{{7}}\beta _{{2}} \left( 8\,{R_{{7}}}^{2}{\beta _{{2}}}^{2}+{R_{{7}}}^{2}-16\,{\beta _{{2}}}^{2}+ 10 \right) }{8\,{\beta _{{2}}}^{2}+1}}+yR_{{7}}\beta _{{2}}+\mu _{{1}}}}} +$$

$$k_{{2}}\cos \left( 2\,{\frac{t\beta _{{2}} \left( 48\,{R_{{7}}}^{2}{ \beta _{{2}}}^{4}+6\,{R_{{7}}}^{2}{\beta _{{2}}}^{2}-16\,{\beta _{{2}}}^{ 4}-9\,{R_{{7}}}^{2}-10\,{\beta _{{2}}}^{2}-1 \right) }{ \left( 8\,{ \beta _{{2}}}^{2}+1 \right) \left( 8\,{R_{{7}}}^{2}{\beta _{{2}}}^{2}- 11\,{R_{{7}}}^{2}-8\,{\beta _{{2}}}^{2}-1 \right) }}-x\beta _{{2}}+y \beta _{{2}}+\mu _{{2}} \right) ,$$

so that $\left( 8\,{\beta _{{2}}}^{2}+1 \right) \left( 8\,{\beta _{{2}}}^{2}+2 \, \sqrt{-24\,{\beta _{{2}}}^{2}+6}-5 \right) >0$.

Case (18):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _2=R_{{4}}, \ \ \beta _{{1}}=-\frac{1}{2}\,{\frac{{R_{{4}}}^{2}+{\alpha _{{1}}}^{2}}{\alpha _{{1 }}}} ,\ \ \beta _2=k_1=k_3=0,\ \ \lambda _2=R_4,\\ \lambda _{{1}}=\frac{1}{2}\,{\frac{4\,{R_{{4}}}^{2}{\alpha _{{1}}}^{2}s_{{1}}-4 \,{R_{{4}}}^{2}{\alpha _{{1}}}^{2}s_{{2}}+4\,{\alpha _{{1}}}^{4}s_{{1}}- 4\,{\alpha _{{1}}}^{4}s_{{2}}-{R_{{4}}}^{2}s_{{1}}+{\alpha _{{1}}}^{2}s_ {{1}}+8\,{\alpha _{{1}}}^{2}s_{{2}}}{\alpha _{{1}}s_{{1}}}} . \end{array} \right. \end{aligned}$$

(40)

Then, the exact breather wave solution will be as

$$\begin{aligned} u_{18}=2\frac{\partial ^2}{\partial x \partial y}\ln g_{18},\ \ \ v_{18}=2\frac{\partial ^2}{\partial x^2}\ln g_{18},\ \ \ w_{18}=2\frac{\partial ^2}{\partial y^2}\ln g_{18}, \end{aligned}$$

(41)

$$g_{18}(x,y,t)={\textrm{e}^{-{\frac{t \left( 4\,{R_{{4}}}^{2}{\alpha _{{1}}}^{2}s_{ {1}}-4\,{R_{{4}}}^{2}{\alpha _{{1}}}^{2}s_{{2}}+4\,{\alpha _{{1}}}^{4}s_ {{1}}-4\,{\alpha _{{1}}}^{4}s_{{2}}-{R_{{4}}}^{2}s_{{1}}+{\alpha _{{1}}} ^{2}s_{{1}}+8\,{\alpha _{{1}}}^{2}s_{{2}} \right) }{2\alpha _{{1}}s_{{1}} }}-x\alpha _{{1}}+{\frac{y \left( {R_{{4}}}^{2}+{\alpha _{{1}}}^{2 } \right) }{2\alpha _{{1}}}}-\mu _{{1}}}}+k_{{2}}\cos \left( tR_{{4}}+xR_ {{4}}+\mu _{{2}} \right) .$$

Case (19):

$$\begin{aligned} \left\{ \begin{array}{ll} \alpha _{{1}}={\frac{\alpha _{{3}}\beta _{{1}}}{\beta _{{3}}}}, \ \ \alpha _2=\alpha _3,\ \ \beta _2=\beta _3,\ \ \lambda _{{1}}={\frac{ \left( {\alpha _{{3}}}^{2}+{\beta _{{3}}}^{2} \right) \beta _{{1}}}{\beta _{{3}} \left( \alpha _{{3}}+\beta _{{3}} \right) }},\ \ \lambda _{{2}}={\frac{{\alpha _{{3}}}^{2}+{\beta _{{3}}}^{2}}{\alpha _{{3 }}+\beta _{{3}}}} ,\\ \lambda _{{3}}={\frac{{\alpha _{{3}}}^{2}+{\beta _{{3}}}^{2}}{\alpha _{{3 }}+\beta _{{3}}}},\ \ s_{{2}}=-{\frac{ \left( {\alpha _{{3}}}^{2}+{\beta _{{3}}}^{2} \right) s_{{1}}}{\beta _{{3}}\alpha _{{3}}}}. \end{array} \right. \end{aligned}$$

(42)

Then, the exact breather wave solution will be as

$$\begin{aligned} u_{19}=2\frac{\partial ^2}{\partial x \partial y}\ln g_{19},\ \ \ v_{19}=2\frac{\partial ^2}{\partial x^2}\ln g_{19},\ \ \ w_{19}=2\frac{\partial ^2}{\partial y^2}\ln g_{19}, \end{aligned}$$

(43)

$$g_{19}(x,y,t)={\textrm{e}^{-{\frac{t \left( {\alpha _{{3}}}^{2}+{\beta _{{3}}}^{2} \right) \beta _{{1}}}{\beta _{{3}} \left( \alpha _{{3}}+\beta _{{3}} \right) }}-{\frac{x\alpha _{{3}}\beta _{{1}}}{\beta _{{3}}}}-y\beta _{{1 }}-\mu _{{1}}}}+k_{{1}}{\textrm{e}^{{\frac{t \left( {\alpha _{{3}}}^{2}+{ \beta _{{3}}}^{2} \right) \beta _{{1}}}{\beta _{{3}} \left( \alpha _{{3}}+ \beta _{{3}} \right) }}+{\frac{x\alpha _{{3}}\beta _{{1}}}{\beta _{{3}}}} +y\beta _{{1}}+\mu _{{1}}}}+$$

$$k_{{2}}\cos \left( {\frac{t \left( {\alpha _ {{3}}}^{2}+{\beta _{{3}}}^{2} \right) }{\alpha _{{3}}+\beta _{{3}}}}+x \alpha _{{3}}+y\beta _{{3}}+\mu _{{2}} \right) +k_{{3}}\sin \left( { \frac{t \left( {\alpha _{{3}}}^{2}+{\beta _{{3}}}^{2} \right) }{\alpha _ {{3}}+\beta _{{3}}}}+x\alpha _{{3}}+y\beta _{{3}}+\mu _{{3}} \right) .$$

Result and discussion

This portion compares the arrangements to the spatial symmetric nonlinear dispersive wave model in (2+1)-dimensions arising in wave phenomena and soliton interactions in a two-dimensional space with time inferred from the expository wave arrangements in this article and those found within the writing. Numerous analysts have examined to analyze the SSNLDW arising with diverse procedures. Alternately, the nonlinear differential administrator has been utilized to produce numerous wave arrangements for the specified equation as shown in the related section.

Furthermore, an analysis based on the Hirota bilinear scheme is made on arrangements advertised in this original copy as well as we found by breather wave solutions. In spite of employing a assortment of strategies, nineteen cases including each one three breather solutions have been effectively completed including breather-wave form solutions to the spatial symmetric nonlinear dispersive wave model.

For Case (1), we have plotted behaviour of breather wave solutions of (8) by substituting the values for parameters $\alpha _1 = 1, \alpha _3 = 2, \beta _1 = 2, \beta _3 = 1, k_1 = 1, k_3 = 2, s_1 = 3, \mu _1 = 1, \mu _2 = 1, \mu _3 = 2$ into Eq. (8), $u_1$, $v_1$ and $w_1$. Without loss of generality, to facilitate the investigation of the dynamic behavior of interactions of breather can be obtained, which is

$$\begin{aligned} \left\{ \begin{array}{ll} u_1(x,y,t)=2\,{\frac{2\,{\textrm{e}^{-l_{{1}}}}+2\,{\textrm{e}^{l_{{1}}}}-2\,\sin \left( l_{{2}} \right) }{{\textrm{e}^{-l_{{1}}}}+{\textrm{e}^{l_{{1}}}}-2\, \sin \left( l_{{2}} \right) }}-2\,{\frac{ \left( -{\textrm{e}^{-l_{{1}}} }+{\textrm{e}^{l_{{1}}}}-2\,\cos \left( l_{{2}} \right) \right) \left( -2\,{\textrm{e}^{-l_{{1}}}}+2\,{\textrm{e}^{l_{{1}}}}+2\,\cos \left( l_{{2}} \right) \right) }{ \left( {\textrm{e}^{-l_{{1}}}}+{\textrm{e}^{l_{{1}}}}-2 \,\sin \left( l_{{2}} \right) \right) ^{2}}},\\ v_1(x,y,t)=2\,{\frac{{\textrm{e}^{-l_{{1}}}}+{\textrm{e}^{l_{{1}}}}+2\,\sin \left( l_{ {2}} \right) }{{\textrm{e}^{-l_{{1}}}}+{\textrm{e}^{l_{{1}}}}-2\,\sin \left( l_{{2}} \right) }}-2\,{\frac{ \left( -{\textrm{e}^{-l_{{1}}}}+{ \textrm{e}^{l_{{1}}}}-2\,\cos \left( l_{{2}} \right) \right) ^{2}}{ \left( {\textrm{e}^{-l_{{1}}}}+{\textrm{e}^{l_{{1}}}}-2\,\sin \left( l_{{2} } \right) \right) ^{2}}},\\ w_1(x,y,t)=2\,{\frac{4\,{\textrm{e}^{-l_{{1}}}}+4\,{\textrm{e}^{l_{{1}}}}+2\,\sin \left( l_{{2}} \right) }{{\textrm{e}^{-l_{{1}}}}+{\textrm{e}^{l_{{1}}}}-2\, \sin \left( l_{{2}} \right) }}-2\,{\frac{ \left( -2\,{\textrm{e}^{-l_{{1 }}}}+2\,{\textrm{e}^{l_{{1}}}}+2\,\cos \left( l_{{2}} \right) \right) ^{ 2}}{ \left( {\textrm{e}^{-l_{{1}}}}+{\textrm{e}^{l_{{1}}}}-2\,\sin \left( l_ {{2}} \right) \right) ^{2}}} ,\\ l_1=2t+x+2y+1,\ \ l_2=(23/6)t+x-y-2. \end{array} \right. \end{aligned}$$

(44)

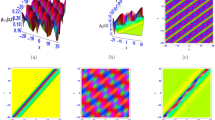
Figures 1, 2, 3, 4, 5 and 6 illustrate the breathe waves which contains 3D dimensional, density and 2D dimensional plots. In order to explore the dynamic behavior of the breather waves to the spatial symmetric nonlinear dispersive wave model are discussed. Unfortunately, it is very difficult to directly solve the extreme points of the equation, so we consider the case of $|t|\rightarrow \infty$. Figures (1) and (2) for $u_1$, (3) and (4) for $v_1$ and (5) and (6) for $v_1$ present the breather wave position along with periodic movement on the track $y=-x$. In addition, Fig. 2 presents properties lump periodic along $y=-x$. All properties are offered in three-dimensional, contour, density and two-dimensional plots.

Fig. 1

Lump solution $u_1$ (44) with different parameters $\alpha _1 = 1, \alpha _3 = 2, \beta _1 = 2, \beta _3 = 1, k_1 = 1, k_3 = 2, s_1 = 3, \mu _1 = 1, \mu _2 = 1, \mu _3 = 2$, f1($t=1$), f2($y=1$), f3($x=1$), f4($t=2$), f5($y=2$) and f6($x=2$).

Fig. 2

2D plots of Breather wave solution $u_1$ (44) f1($t=1$), f2($y=1$), f3($x=1$), f4($t=2$), f5($y=2$) and f6($x=2$).

Fig. 3

Lump solution $v_1$ (44) with different parameters $\alpha _1 = 1, \alpha _3 = 2, \beta _1 = 2, \beta _3 = 1, k_1 = 1, k_3 = 2, s_1 = 3, \mu _1 = 1, \mu _2 = 1, \mu _3 = 2$, f1($t=1$), f2($y=1$), f3($x=1$), f4($t=2$), f5($y=2$) and f6($x=2$).

Fig. 4

2D plots of Breather wave solution $v_1$ (44) f1($t=1$), f2($y=1$), f3($x=1$), f4($t=2$), f5($y=2$) and f6($x=2$).

Fig. 5

Breather wave solution $w_1$ (44) with different parameters $\alpha _1 = 1, \alpha _3 = 2, \beta _1 = 2, \beta _3 = 1, k_1 = 1, k_3 = 2, s_1 = 3, \mu _1 = 1, \mu _2 = 1, \mu _3 = 2$, f1($t=1$), f2($y=1$), f3($x=1$), f4($t=2$), f5($y=2$) and f6($x=2$).

Fig. 6

2D plots of Breather wave solution $w_1$ (44) f1($t=1$), f2($y=1$), f3($x=1$), f4($t=2$), f5($y=2$) and f6($x=2$).

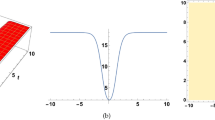
For Case (14), we have plotted behaviour of breather wave solutions of (33) by substituting the values for parameters $\alpha _3 = 1, \beta _1 = 1, \beta _2 = 1/2, k_1 = 1, k_2 = 2, s_1 = 3, \mu _1 = 1, \mu _2 = 1, \mu _3 = 2$ into Eq. (33), $u_1$. Without loss of generality, to facilitate the investigation of the dynamic behavior of interactions of breather can be obtained, which is

$$\begin{aligned} \left\{ \begin{array}{ll} u_{14}(x,y,t)=2\,{\frac{-1/4\,{\textrm{e}^{-l_{{1}}}}-1/4\,{\textrm{e}^{l_{{1}}}}+1/2\, \cos \left( l_{{2}} \right) }{{\textrm{e}^{-l_{{1}}}}+{\textrm{e}^{l_{{1}}}} +2\,\cos \left( l_{{2}} \right) }}-2\,{\frac{ \left( 1/4\,{\textrm{e}^{- l_{{1}}}}-1/4\,{\textrm{e}^{l_{{1}}}}+\sin \left( l_{{2}} \right) \right) \left( -{\textrm{e}^{-l_{{1}}}}+{\textrm{e}^{l_{{1}}}}-\sin \left( l_{{2}} \right) \right) }{ \left( {\textrm{e}^{-l_{{1}}}}+{ \textrm{e}^{l_{{1}}}}+2\,\cos \left( l_{{2}} \right) \right) ^{2}}} ,\\ v_{14}(x,y,t)=2\,{\frac{1/16\,{\textrm{e}^{-l_{{1}}}}+1/16\,{\textrm{e}^{l_{{1}}}}-1/2\, \cos \left( l_{{2}} \right) }{{\textrm{e}^{-l_{{1}}}}+{\textrm{e}^{l_{{1}}}} +2\,\cos \left( l_{{2}} \right) }}-2\,{\frac{ \left( 1/4\,{\textrm{e}^{- l_{{1}}}}-1/4\,{\textrm{e}^{l_{{1}}}}+\sin \left( l_{{2}} \right) \right) ^{2}}{ \left( {\textrm{e}^{-l_{{1}}}}+{\textrm{e}^{l_{{1}}}}+2\, \cos \left( l_{{2}} \right) \right) ^{2}}} ,\\ w_{14}(x,y,t)=2\,{\frac{{\textrm{e}^{-l_{{1}}}}+{\textrm{e}^{l_{{1}}}}-1/2\,\cos \left( l _{{2}} \right) }{{\textrm{e}^{-l_{{1}}}}+{\textrm{e}^{l_{{1}}}}+2\,\cos \left( l_{{2}} \right) }}-2\,{\frac{ \left( -{\textrm{e}^{-l_{{1}}}}+{ \textrm{e}^{l_{{1}}}}-\sin \left( l_{{2}} \right) \right) ^{2}}{ \left( {\textrm{e}^{-l_{{1}}}}+{\textrm{e}^{l_{{1}}}}+2\,\cos \left( l_{{2}} \right) \right) ^{2}}} ,\\ l_1=(41/38)t-(1/4)x+y+1,\ \ l_2=(205/96)t-(1/2)x+(1/2)y+1. \end{array} \right. \end{aligned}$$

(45)

Figures 7 and 8 illustrate the breathe waves which contains 3D dimensional, density and 2D dimensional plots. In order to explore the dynamic behavior of the breather waves to the spatial symmetric nonlinear dispersive wave model are discussed. Unfortunately, it is very difficult to directly solve the extreme points of the equation, so we consider the case of $|t|\rightarrow \infty$. Figures (7) and (8) for $u_{14}$ present the breather wave position along with periodic movement on the track $y=-x$. In addition, Fig. 8 presents properties breather periodic along $y=-x$. All properties are offered in three-dimensional, contour, density and two-dimensional plots.

Fig. 7

Breather wave solution $u_{14}$ (45) with different parameters $\alpha _3 = 1, \beta _1 = 1, \beta _2 = 1/2, k_1 = 1, k_2 = 2, s_1 = 3, \mu _1 = 1, \mu _2 = 1, \mu _3 = 2$, f1($t=1$), f2($y=1$), f3($x=1$), f4($t=2$), f5($y=2$) and f6($x=2$).

Fig. 8

2D plots of Breather wave solution $u_{14}$ (45) f1($t=1$), f2($y=1$), f3($x=1$), f4($t=2$), f5($y=2$) and f6($x=2$).

For Case (19), we have plotted behaviour of breather wave solutions of (43) by substituting the values for parameters $\alpha _3 = 1/2, \beta _1 = 1/3, \beta _3 = 1/2, k_1 = 1, k_2 = 2, k_3=3, s_1 = 3, \mu _1 = 1, \mu _2 = 1, \mu _3 = 2$ into Eq. (43), $u_{19}$. Without loss of generality, to facilitate the investigation of the dynamic behavior of interactions of breather can be obtained, which is

$$\begin{aligned} \left\{ \begin{array}{ll} u_{19}(x,y,t)=2\,{\frac{1/9\,{\textrm{e}^{-l_{{1}}}}+1/18\,{\textrm{e}^{l_{{1}}}}-1/2\, \cos \left( l_{{2}} \right) -3/4\,\sin \left( t/2+x/2+y/2+2 \right) }{ {\textrm{e}^{-l_{{1}}}}+1/2\,{\textrm{e}^{l_{{1}}}}+2\,\cos \left( l_{{2}} \right) +3\,\sin \left( t/2+x/2+y/2+2 \right) }}-2\,{\frac{ \left( - 1/3\,{\textrm{e}^{-l_{{1}}}}+1/6\,{\textrm{e}^{l_{{1}}}}-\sin \left( l_{{2}} \right) +3/2\,\cos \left( t/2+x/2+y/2+2 \right) \right) ^{2}}{ \left( {\textrm{e}^{-l_{{1}}}}+1/2\,{\textrm{e}^{l_{{1}}}}+2\,\cos \left( l _{{2}} \right) +3\,\sin \left( t/2+x/2+y/2+2 \right) \right) ^{2}}} ,\\ v_{19}(x,y,t)=2\,{\frac{1/9\,{\textrm{e}^{-l_{{1}}}}+1/18\,{\textrm{e}^{l_{{1}}}}-1/2\, \cos \left( l_{{2}} \right) -3/4\,\sin \left( t/2+x/2+y/2+2 \right) }{ {\textrm{e}^{-l_{{1}}}}+1/2\,{\textrm{e}^{l_{{1}}}}+2\,\cos \left( l_{{2}} \right) +3\,\sin \left( t/2+x/2+y/2+2 \right) }}-2\,{\frac{ \left( - 1/3\,{\textrm{e}^{-l_{{1}}}}+1/6\,{\textrm{e}^{l_{{1}}}}-\sin \left( l_{{2}} \right) +3/2\,\cos \left( t/2+x/2+y/2+2 \right) \right) ^{2}}{ \left( {\textrm{e}^{-l_{{1}}}}+1/2\,{\textrm{e}^{l_{{1}}}}+2\,\cos \left( l _{{2}} \right) +3\,\sin \left( t/2+x/2+y/2+2 \right) \right) ^{2}}} ,\\ w_{19}(x,y,t)=2\,{\frac{1/9\,{\textrm{e}^{-l_{{1}}}}+1/18\,{\textrm{e}^{l_{{1}}}}-1/2\, \cos \left( l_{{2}} \right) -3/4\,\sin \left( t/2+x/2+y/2+2 \right) }{ {\textrm{e}^{-l_{{1}}}}+1/2\,{\textrm{e}^{l_{{1}}}}+2\,\cos \left( l_{{2}} \right) +3\,\sin \left( t/2+x/2+y/2+2 \right) }}-2\,{\frac{ \left( - 1/3\,{\textrm{e}^{-l_{{1}}}}+1/6\,{\textrm{e}^{l_{{1}}}}-\sin \left( l_{{2}} \right) +3/2\,\cos \left( t/2+x/2+y/2+2 \right) \right) ^{2}}{ \left( {\textrm{e}^{-l_{{1}}}}+1/2\,{\textrm{e}^{l_{{1}}}}+2\,\cos \left( l _{{2}} \right) +3\,\sin \left( t/2+x/2+y/2+2 \right) \right) ^{2}}} ,\\ l_1=(41/38)t-(1/4)x+y+1,\ \ l_2=(205/96)t-(1/2)x+(1/2)y+1. \end{array} \right. \end{aligned}$$

(46)

Figures 9 and 10 illustrate the breathe waves which contains 3D dimensional, density and 2D dimensional plots. In order to explore the dynamic behavior of the breather waves to the spatial symmetric nonlinear dispersive wave model are discussed. Unfortunately, it is very difficult to directly solve the extreme points of the equation, so we consider the case of $|t|\rightarrow \infty$. Figures (9) and (10) for $u_{14}$ present the breather wave position along with periodic movement on the track $y=-x$. In addition, Figs. 9 and 10 present properties two lines along $y=-x$. All properties are offered in three-dimensional, contour, density and two-dimensional plots.

Fig. 9

Breather wave solution $u_{19}$ (46) with different parameters $\alpha _3 = 1/2, \beta _1 = 1/3, \beta _3 = 1/2, k_1 = 1, k_2 = 2, k_3=3, s_1 = 3, \mu _1 = 1, \mu _2 = 1, \mu _3 = 2$, f1($t=1$), f2($y=1$), f3($x=1$), f4($t=2$), f5($y=2$) and f6($x=2$).

Fig. 10

2D plots of Breather wave solution $u_{19}$ (46) f1($t=1$), f2($y=1$), f3($x=1$), f4($t=2$), f5($y=2$) and f6($x=2$).

Conclusion

This paper included the Hirota bilinear technique to resolve the spatial symmetric nonlinear dispersive wave model. As a resultant, numerous breather waves are created, counting combination of exponential and trigonometric function solutions. It is important to note that test function method is one of the most useful methods for solving nonlinear partial differential equations. The accuracy of the results was tested using Maple software by substituting the obtained results into the original equation. For the above results, we use Maple software to get the two-dimensional, three-dimensional plots and density plots. There is no doubt that the significance of this study, at the same time, nonlinear partial differential equations are also worthy of further research and exploration. After that, we will also devote ourselves to new research work, and sincerely hope that we and other researchers can explore other interesting results. We will study N-soliton for m of solutions in future work.