Introduction

Over recent years, substantial research has intensified around healthcare, particularly following the Covid-19 pandemic’s impact. The World Health Organization (WHO)1 identifies heart diseases as some of the deadliest conditions worldwide, responsible for the largest number of fatalities. Heart disease encompasses a broad spectrum of conditions impairing cardiac function. Data from the WHO underscores that cardiovascular diseases currently stand as the predominant global cause of death, leading to approximately 17.9 million deaths annually. Additionally, life is claimed by heart disease every 34 s globally. Often undetected until acute events such as heart attacks occur, heart disease presents diagnostic challenges due to its vast range of influencing factors, as illustrated by the abnormal heart rhythm in Fig. 1. Diagnosing heart disease is inherently complex, as numerous risk factors contribute to its onset. Risk elements such as tobacco use, excessive alcohol consumption, obesity, physical inactivity, mental health disorders, advanced age, sex, inadequate sleep, and several others intensify vulnerability. Harmful lifestyle choices like poor dietary habits lead to high cholesterol, elevated triglycerides, obesity, and hypertension significantly heighten the probability of cardiovascular ailments2. Symptoms recognized by the American College of Cardiology encompass sleep disturbances, erratic heartbeat (irregular rhythm), limb swelling, and occasionally rapid weight gain (around 2–3 kg per day). These manifestations overlap with symptoms of various other conditions, particularly those affecting the elderly, complicating accurate diagnosis and heightening the risk of fatal outcomes. As time progresses, an expanding pool of research and clinical data is emerging, offering valuable insights. Numerous public databases now provide extensive patient information, facilitating studies on how technological advancements can be harnessed to improve diagnostic precision and detect diseases before reaching fatal stages. The primary catalyst for heart disease, often termed coronary heart disease, is frequently due to the narrowing of coronary arteries that supply blood to the heart. Although procedures like angioplasty are effective for diagnosing heart conditions, they are costly and can provoke adverse physical responses in some patients. Consequently, these methods are less feasible for extensive application, particularly in nations with significant low-income populations.

Fig. 1
figure 1

Pathological heart rhythm.

Full size image

Developing healthcare solutions that ensure both high-quality outcomes and cost-effectiveness is essential, especially as healthcare institutions increasingly seek affordable, non-invasive testing methods3. To address these needs for widespread, accessible diagnostics, a computer-assisted decision-making system could be constructed to aid in identifying various medical conditions. The rapid advancement of artificial intelligence (AI), machine learning (ML), and deep learning models has greatly benefited fields such as healthcare, where extensive datasets from medical diagnostics facilitate robust algorithm training4,5,6,7,8. These models support clinical systems that enhance diagnostic accuracy. Optimizing models are particularly promising in regression and classification tasks, while medical systems can provide an initial diagnostic assessment, signaling potential health issues9. Developing highly diagnostics for pulmonary nodules demands precise feature selection, critical for establishing effective Content-Based Image Retrieval (CBIR) and Computer-Aided Diagnosis (CAD) systems10. CAD typically involves two phases: feature extraction and classification. CBIR systems often require a robust set of visual attributes such as texture, shape, and granularity to construct a comprehensive search index11. Building optimal ML architectures, a skillful configuration of hyperparameters to maximize classification performance and accuracy. Given the complexity of combinatorial optimizations, manual methods often fall short; thus, meta-heuristic algorithms, inspired by natural processes, offer an effective solution12. These algorithms, using global and local search techniques with randomization, excel at finding highly optimized solutions with minimal computational costs, making them invaluable across fields such as engineering and healthcare. Metaheuristic algorithms have proven their effectiveness in solving complex optimization problems for various domains. For instance, the Multiobjective Brown Bear Optimization (MOBBO) algorithm and the Multiobjective Harris Hawks Optimization (MOHO) algorithm have been successfully applied to constrained structural optimization and optimal truss design, demonstrating their ability to balance exploration and exploitation in search spaces13,14. Also, metaheuristic techniques have been employed for system identification in UAV applications, showcasing their fairness and robustness15. Optimization techniques are useful for solving complex nonconvex problems across various domains. Recent advancements, such as the meta learning-based alternating minimization algorithm have demonstrated significant potential in enhancing the performance of these techniques16. Also, machine learning methods have played an important role in advancing healthcare applications employing bioinformatics and machine learning for colon cancer diagnosis and staging classification17. Heart disease remains a leading cause of mortality worldwide driven by complex pathophysiological mechanisms. Among these, the activation of cardiac fibroblasts plays an important role in cardiac remodeling and fibrosis, processes central to heart disease progression. Xanthohumol is a natural compound, effectively inhibits TGF-β1-induced cardiac fibroblast activation by modulating the PTEN/Akt/mTOR signaling pathway, offering valuable insights into potential therapeutic targets18. The cellular process of mitophagy has been shown to have a dual role in myocardial ischemia/reperfusion injury19. This underscores the complexity of balancing protective and detrimental processes during heart disease progression. Building on these biological insights, this study integrates such mechanisms into a predictive modeling framework, aiming to enhance diagnostic accuracy and therapeutic guidance in heart disease. This study employs meta-heuristic methodologies to navigate the intricate challenges of feature extraction and classification in heart disease diagnosis. These techniques iteratively refine candidate solutions, facilitating the identification of pivotal features while optimizing classifier performance. Among the explored algorithms, the Greylag Goose Optimization (GGO) algorithm emerged as particularly effective, excelling in feature selection and parameter tuning tasks. GGO’s proven efficacy across diverse domains, including healthcare, finance, and engineering, underscores its suitability for this research. The primary aim of integrating machine learning with a meta-heuristic framework like GGO is to elevate diagnostic precision, especially in detecting heart disease. This synergy enhances the model’s capability to discern complex patterns, enabling more accurate evaluations and prompt clinical interventions. The research combines GGO with Long Short-Term Memory (LSTM) networks to optimize hyperparameter tuning, thereby enhancing the model’s ability to classify intricate heart disease patterns. To ensure robust classification accuracy, rigorous preprocessing steps were undertaken, including scaling, normalization, and imputation of missing values. Following preprocessing, GGO was applied in its binary variant to extract the most influential features contributing to classification performance. Several classifiers were evaluated, encompassing Support Vector Classification (SVC), Stochastic Gradient Descent (SGD), Naive Bayes (NB), K-Nearest Neighbors (KNN), Decision Tree (DT), Random Forest (RF), and LSTM. Among these, LSTM demonstrated superior efficacy, delivering the most accurate classification outcomes. Subsequently, GGO was deployed for fine-tuning the LSTM model’s hyperparameters, and its performance was benchmarked against six alternative optimization algorithms: Al-Biruni Earth Radius (BER), Dipper Throated Optimization (DTO), Particle Swarm Optimization (PSO), Whale Optimization Algorithm (WOA), Grey Wolf Optimizer (GWO), and Falcon Optimization Algorithm (FOA). The GGO-LSTM configuration outperformed its counterparts, achieving the highest classification accuracy and establishing itself as the most effective approach for heart disease prediction.

The paper’s structure unfolds as follows: Sect. “Related work” provides an extensive review of contemporary literature, Sect. "Materials and methods" delineates the proposed methodology, Sect. "The proposed framework" presents a comprehensive analysis of experimental results, and Sect. “Experimental results” concludes with key findings and prospective research directions.

Related work

Due to the potential for increased survival rates, researchers are primarily focused on developing novel methods for the automated identification and diagnosis of significant heart disease, as early detection is crucial in the case of heart disease. This section presents research findings on heart disease classification based on ML/DL and textural/image analysis. Harshit Jindal et al.20 combined three machine learning techniques: Random Forest, Logistic Regression, and KNN. The accuracy of their combined model was 87.5%. They concluded that their excellent precision was primarily attributable to the utilization of more medical features. Heart rate, getting older, cholesterol, fasting sugar, pain in the chest, sexuality, and other factors were among the thirteen characteristics they utilized. There were 304 items in the dataset overall. Otoom et al.21 devised a method for analysis and monitoring. The suggested system detects and tracks coronary artery disease. The UCI is where Cleveland Heart statistics are obtained. There are 76 attributes/features and 303 cases in this collection. Of the 76 functionalities, 13 are currently in use. For detection, two tests using three different algorithms—Bayes Naive, SVM, and Function Trees FT—are run. For detection, the WEKA tool is employed. Using the SVM approach, the 88.3% accuracy is attained following the Holdout test. In the cross-validation examination the accuracy of SVM and Bayes net is 83.8%. The use of FT results in an accuracy of 81.5%. The most efficient First selection algorithm is used to choose the top seven attributes. Cross-validation examines are used for validation. Using the seven best features that were chosen for the test, Bayes Naive obtained 84.5% accuracy, SVM yielded 85.1% accuracy, and FT accurately classified 84.5% of the features. Following extensive testing with a wide range of algorithms, Apurb Rajdhan et al.22 concluded that the technique of Random Forests proved exceptionally accurate, having a predictive accuracy of 90.16% in predicting cardiac illnesses. They selected 14 features out of the 76 features in the UCI Cleveland cardiovascular disease dataset. These characteristics include the patient’s maximum heartbeat, age, sex, and the intensity of their chest discomfort. They also experimented with Naive Bayes, Decision trees, and Logistic Regression in addition to Random Forest, with outcomes of 85.25%, 85.25%, and 81.97%, correspondingly. The Cleveland Heart Disease dataset was used by Amin Ul Haq et al.23 to test seven different algorithms: KNN, SVM, Logistic Regression, Decision Tree, Random Forest, Naïve Bayes, and Neural Networks. To determine which characteristics in the dataset were most crucial, they employed Lasso. The most noteworthy numbers were 88%, 87%, and 86% for the Support Vector Machine, Logistic Regression, and Neural Networks at g = 0.0001 and c = 100, respectively. Notably, at fold cross-validation of 10, Logistic Regression outperformed, with 89% accuracy. Nine algorithms were investigated by Rahul Katarya et al.24: Multilayer Perception, Decision Tree, Naïve Bayes, K Nearest Neighbor, SVM, Random Forest, ANN, Deep Neural Networks, as well as Logistic Regression. After obtaining the database from the UCI repository, they selected 14 features out of the 76 features, normalized them, and used the Python module NAN to fill in any missing data. Age, sex, cholesterol, kind of chest discomfort, sugar, sitting arterial pressure, blood fasting, and other factors were among the selected characteristics. The three algorithms with the best accuracy, Random Forest, Logistic Regression, Artificial Neural Networks, and Support Vector Machines, were 95.6%, 93.4%, and 92.3%, respectively. According to Youness Khourdifi et al.25, every algorithm performed better under conditions. With the dataset they utilized, Random Forest, K-Nearest Neighbor, and Neural Networks were the algorithms that performed the best. Additionally, their findings demonstrated that the hybrid optimization strategy greatly improved predictions in healthcare records. Additionally, they recommended Particle Swarm Optimization (PSO) and Ant Colony Optimization (ACO), two techniques for dataset optimization. They created a hybrid of the two approaches and applied it to Random Forest, yielding an accuracy of 99.6%, and K-Nearest Neighbor, which produced a 99.65% accuracy. Their dataset was obtained from an automated learning library at UCI.

As shown in Table 1, several researchers have employed different combinations of machine learning algorithms and datasets to classify heart diseases. For instance, Harshit Jindal et al. utilized a combination of Random Forest, Logistic Regression, and KNN, achieving an accuracy of 87.50% using a dataset with 304 items and 13 features. Otoom et al. applied Bayes Naive, SVM, and Function Trees (FT) on the Cleveland Heart Disease dataset, with SVM yielding the highest accuracy at 88.3%. Similarly, Apurb Rajdhan et al. found Random Forest to be the most accurate at 90.16% among the algorithms they tested. Amin Ul Haq et al. reported notable results with SVM and Logistic Regression, achieving accuracies of 88% and 89%, respectively, through cross-validation. Rahul Katarya et al. demonstrated the superior performance of Random Forest, Logistic Regression, and ANN, with accuracy rates as high as 99.6% when optimized with PSO and KNN. Finally, Youness Khourdifi et al. highlighted the effectiveness of hybrid optimization strategies, with Random Forest combined with ACO and KNN combined with ACO achieving accuracies of 99.6% and 99.65%, respectively.

Table 1 Summary of related work on heart disease classification.
Full size table

This summary table illustrates the diverse methodologies and their respective accuracies, demonstrating the advancements in heart disease classification research. Researchers have significantly improved the predictive accuracy of heart disease diagnoses by leveraging a combination of optimization algorithms and machine learning techniques. These studies provide a solid foundation for further exploration and development of more sophisticated models and techniques in the field.

Materials and methods

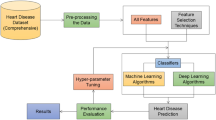
This section articulates the methodological framework and resource allocation underpinning the study, which seeks to enhance heart disease classification by synergistically leveraging the Greylag Goose Optimization (GGO) algorithm and Long Short-Term Memory (LSTM) networks. The proposed architecture is structured into pivotal stages, encompassing meticulous data preprocessing, feature extraction executed via the binary encoding mechanism of the GGO algorithm, and the strategic deployment of an array of classifiers to achieve elevated levels of classification precision.

Greylag goose optimization (GGO) algorithm

The Greylag Goose Optimization (GGO) algorithm begins by assembling a randomized population of candidate solutions, each represented as \(\:{Y}_{i}\)(i = 1, 2,…, n). This collection constitutes the GGO swarm. A target function, Fn, is applied to assess every individual, guiding the search toward the optimal solution Z, which emerges through evaluating Fn ​ across the entire population. The GGO algorithm segments the population into two distinct groups: an exploitative group \(\:{n}_{2}\) and an exploratory group \(\:{n}_{1}\), dynamically adjusting the ratio between them according to the optimal solution identified thus far. At the outset, efforts are evenly allocated, with 50% directed toward exploration and 50% toward exploitation. However, if the optimal solution remains stagnant over three consecutive iterations, the algorithm expands the exploratory group to circumvent entrapment in local optima. The exploration phase uncovers promising zones within the search space, preventing stagnation by advancing toward the current best solution. The geese explorers assess potential choices within their vicinity, selecting the optimal one based on fitness evaluation. GGO then updates individual vectors, refining positions in alignment with the best solution found. In the exploitation phase, this subset refines existing solutions, progressing towards the optimal solution with guidance from three sentinel agents who direct the other members. To ensure robust exploitation and avoid convergence on local optima, the algorithm employs the triangle inequality and the law of large numbers principles. At the end of each iteration, GGO alters the positions within the search space and randomizes individual roles to transition members between exploration and exploitation. The GGO algorithm dynamically refines individual positions within each group through iterative adjustments and random shuffling, preserving population diversity. This process persists until convergence on the optimal solution, as outlined in Algorithm 1.

Algorithm 1
figure a

GGO Algorithm.

Full size image

Binary GGO optimization algorithm

The GGO optimization algorithm presents a robust approach to enhancing feature selection for LSTM parameters. In this method, GGO adopts a binary encoding format tailored to the feature selection process, which operates within a constrained search space limited to binary values, 0 and 1. The aim is to evaluate the relevance of specific features; thus, GGO values are translated into a binary [0, 1] scheme within the binary GGO framework proposed in this section. This process, articulated through Eq. 1 and Eq. 2, utilizes the Sigmoid function to transform continuous data into binary form, aligning with the requirements of feature selection.

$$\:{Bi}_{t}^{*}=\:\left\{\begin{array}{c}1\:\:\:\:\:\:\:\:\:if\:sigmoid\:\left({Bi}_{t}^{*}\right)\ge\:0.5\\\:0\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:otherwise\:\:\:\:\:\:\:\:\end{array}\right.$$
(1)
$$\:Sigmoid\left({Bi}_{t}^{*}\right)=\frac{1}{1+{e}^{-10\left({Bi}_{*}^{i}-0.5\right)}}$$
(2)

where \(\:{Bi}_{t}^{*}\:\) denotes the optimal solution at a given iteration \(\:t\). Algorithm 2 outlines the stages of the proposed binary GGO (bGGO) method, which is employed to select the most relevant feature subset, thereby improving the classification accuracy for caries cases.

Algorithm 2
figure b

bGGO Algorithm.

Full size image

The long short-term memory (LSTM)

Long Short-Term Memory (LSTM) networks are a specialized form of recurrent neural networks (RNNs) designed to overcome certain limitations inherent in traditional RNN architectures. In the training process of an RNN, sequential data is propagated through the network, moving from the input vector to the output neurons, while errors are computed and sent backward to adjust the network parameters. These networks incorporate feedback loops within their hidden layers, allowing information to circulate bidirectionally, thereby enabling the hidden state to retain knowledge from previous time steps. As a result, the model’s output is influenced by earlier predictions. However, traditional RNNs struggle to capture long-term dependencies, primarily due to the issue of vanishing gradients, where the influence of earlier information diminishes as it propagates through more time steps. This phenomenon leads to the network primarily encoding short-term dependencies, with information from earlier steps fading over time. The gradient of the loss function approaches zero as more layers with activation functions are added, exacerbating this issue. LSTM networks, or LSTM-ANNs, address this challenge by introducing memory units and gating mechanisms that enable the model to capture long-term dependencies. The inclusion of cell states and three distinct gates allows LSTMs to selectively retain or discard information, making them capable of learning dependencies across thousands of time steps. Thus, LSTM networks are adept at remembering and forgetting critical information, allowing them to model long-term temporal relationships with far greater effectiveness than conventional RNNs26.

The proposed framework

This paper methodological framework commences with an initial phase dedicated to comprehensive data preprocessing, encompassing the removal of null entries, normalization, and scaling to ensure standardized and well-prepared input data for subsequent analytical stages. Central to this phase is the adoption of feature selection methodologies, wherein seven binary-form optimization techniques are employed: Greylag Goose Optimization (GGO), Al-Biruni Earth Radius (BER)27, Dipper Throated Optimization (DTO)28, Particle Swarm Optimizer (PSO)29, Whale Optimization Algorithm (WOA)30, Grey Wolf Optimizer (GWO)31, and Falcon Optimization Algorithm (FOA)32. In the subsequent phase, the study employs the proposed feature selection mechanism, leveraging the binary encoding of GGO (bGGO) to isolate the most relevant features. This stage is pivotal in identifying optimal attributes, enhancing classification precision by discarding superfluous or irrelevant data points. The refined dataset is then utilized for classification via a suite of machine learning models, with feature selection outcomes informing the choice of classifiers. The ensemble of classifiers explored in this study comprises Support Vector Classifier (SVC)33, Stochastic Gradient Descent (SGD)34, Random Forest Classifier (RFC)35, K-Nearest Neighbors (KNN)36, Gaussian Naïve Bayes (NB), Decision Tree (DT), and Long Short-Term Memory (LSTM)37. To ensure peak performance, LSTM hyperparameters are fine-tuned using the proposed optimization strategy. The optimization process begins by generating a population of candidate solutions, each representing a distinct parameter configuration. Each candidate, symbolizing a Greylag Goose, is evaluated against a fitness function based on its classification performance on a validation dataset. Guided by fitness-weighted vectors, individuals in the population traverse the search space, iteratively converging toward optimal configurations. Through systematic adjustments, the algorithm incrementally refines the population, culminating in the identification of the most effective LSTM parameterization. Termination occurs once the predefined convergence threshold or maximum iteration count is reached, with the optimal solution defined by the highest fitness score. A visual representation of this sequential process is provided in Fig. 2, illustrating the robustness of the framework. By integrating GGO for both feature selection and hyperparameter optimization, followed by LSTM-based classification, the methodology demonstrates its efficacy. Further elaboration on the LSTM architecture and the motivations for selecting GGO would enrich the discussion. Details of the LSTM’s hyperparameter configuration are summarized in Table 2.

Table 2 Hyperparameters of the LSTM model.
Full size table

The rationale for choosing GGO is that GGO effectively balances exploration and exploitation, which is critical in avoiding local optima. The algorithm dynamically adjusts the search behavior based on the progress of iterations, ensuring efficient convergence. GGO is compared to other algorithms such as PSO and GWO are widely used, GGO demonstrated superior performance in terms of feature selection and optimization. GGO computational cost is competitive with other metaheuristics algorithms, making it suitable for the relatively high-dimensional heart disease dataset used in this study.

Fig. 2
figure 2

The proposed heart disease classification framework.

Full size image

This research explores how GGO can enhance the tuning of LSTM parameters. Optimizing LSTM parameters is essential for maximizing performance and achieving the highest classification accuracy. Before using GGO to adjust the values in LSTM, it is crucial to determine the parameters that require optimization.

Experimental results

This section elaborates on the evaluation of the proposed algorithm under diverse experimental scenarios. The experiments utilized established mathematical functions as benchmarks to determine their minimum values within specified search domains. These functions are widely recognized in the literature for assessing the efficacy of optimization techniques, serving as a consistent metric for comparison. To highlight the superior performance and efficacy of the proposed algorithm, termed Greylag Goose Optimization (GGO), a comparative analysis was conducted against seven prominent optimization methodologies. The selected algorithms are GGO, BER, DTO, PSO, WAO, GWO, and FOA and were chosen for their substantial recognition and established relevance in practical applications, underscoring their utility as robust baselines for performance evaluation.

Dataset description

This dataset offers a valuable resource for machine learning and data science professionals to develop predictive models for diagnosing heart disease, explore the impact of various disease-related factors, and create algorithms that enhance heart disease treatment and prevention strategies. The study utilizes the “Heart Failure Dataset,” which was collected and made publicly available on Kaggle. The effectiveness of heart disease classification and prediction systems enables individuals to assess their risk of heart disease at a low cost, while also empowering healthcare providers to make data-driven decisions based on the patient’s risk profile. The data is sourced from an online heart disease prediction system hosted on Kaggle, accessible at: https://www.kaggle.com/datasets/fedesoriano/heart-failure-prediction?%20resource=download. The dataset includes key input features such as Age, Resting Blood Pressure (RestingBP), Cholesterol levels, Fasting Blood Sugar (FastingBS), Maximum Heart Rate (MaxHR), OldPeak, and the presence of heart disease. These features are utilized to classify the outcome variable of heart disease. Figure 3 illustrates a histogram that visually represents the correlation between the input features and the output variable in the heart disease dataset.

Fig. 3
figure 3

Histogram plot for each feature in the dataset.

Full size image

Figure 4 presents the correlation matrix, a fundamental statistical tool for analyzing the relationships between variables within a dataset. Typically, this matrix provides a detailed display of pairwise correlations across all variables, with values ranging from − 1 to + 1 that indicate the strength and direction of these relationships. By leveraging the correlation matrix, we can uncover significant patterns, assess the direction of associations, and identify potential predictors within the data. This insight is vital for predictive modeling, as it assists in selecting relevant features, reducing dimensionality, and addressing issues related to multicollinearity, ultimately refining the model’s efficiency and accuracy38.

Fig. 4
figure 4

Correlation matrix between features in the dataset.

Full size image

Feature selection results

This research utilized advanced feature selection methodologies to implement seven distinct optimization algorithms in their binary variants: GGO, BER, DTO, PSO, WOA, GWO, and FOA39,40,41,42,43,44. The comparative performance of these techniques is systematically analyzed in Table 3, which delineates the results obtained through each approach. Notably, the findings underscore the superior efficacy of the proposed binary Greylag Goose Optimization (bGGO) method, which consistently outperforms its counterparts across key performance metrics, as evidenced by its dominance over other binary feature selection algorithms45.

Table 3 Evaluation of the suggested feature selection technique (bGGO) in comparison to other competitive techniques.
Full size table

Figure 5 presents a comparative analysis of the average error rates across ten distinct feature selection methodologies, including the proposed bGGO approach. The graphical representation highlights the pronounced efficacy of the bGGO technique, as evidenced by its minimal average error, thereby underscoring its resilience and superior performance relative to competing strategies.

Fig. 5
figure 5

The average error of the results acquired using bGGO, the proposed feature selection technique.

Full size image

Figure 6 encapsulates a multifaceted depiction of the outcomes obtained through the proposed feature selection technique, utilizing an array of analytical visualizations, including residual plots, quartile–quartile (QQ) plots, homoscedasticity assessments, and heatmaps. These visual tools collectively highlight the robustness and dependability of the methodology, offering nuanced insights into its efficacy across diverse evaluation metrics.

Fig. 6
figure 6

Analysis plots of the obtained outcomes based on bGGO, the proposed feature selection technique.

Full size image

The results presented in the QQ plot exhibit a pronounced alignment with a linear trend, affirming the reliability of the selected features in accurately diagnosing heart disease. Complementing these findings, the outcomes depicted in the homoscedasticity and residual plots reinforce the focus on robust performance metrics. Additionally, the heatmap validates the effectiveness of the bGGO methodology, demonstrating its capacity to achieve optimal outcomes when benchmarked against alternative feature selection approaches. Table 4 further substantiates the exceptional efficacy of the proposed bGGO technique, highlighting its superior performance across a diverse array of evaluative metrics relative to prior strategies. Statistical analysis involving p-value computations for algorithmic pairwise comparisons revealed that the bGGO approach exhibits statistically significant advantages. The study rigorously tests the primary hypotheses, encompassing both null and alternative scenarios, to draw definitive conclusions about the proposed technique’s dominance.

Table 4 The Wilcoxon signed-rank test for evaluating the effectiveness of the proposed feature selection technique (bGGO) in comparison to existing binary optimization techniques.
Full size table

The statistical preeminence of the proposed technique over existing methodologies is evidenced by its notably lower p-value (p < 0.005). To further substantiate these findings, a one-way analysis of variance (ANOVA) was conducted to determine the presence of statistically significant discrepancies between the performance of the proposed bGGO approach and other binary optimization techniques. The detailed outcomes of this ANOVA analysis are encapsulated in Table 5, which unequivocally affirms the proposed technique’s superiority, statistical significance, and robust efficacy in feature selection tasks.

Table 5 The analysis-of-variance (ANOVA) test for assessing the proposed bGGO technique.
Full size table

Classification results

The experiment was conducted to underscore the impact of the feature selection methodology on classification outcomes. Machine learning classifiers were utilized to categorize the input data, leveraging the attributes identified through the bGGO framework. This technique significantly enhanced the feature space and optimized overall classifier performance. The classification results for various machine learning algorithms, post-feature selection, are summarized in Table 6. The classifiers evaluated include SVC, SGD, Gaussian NB, K-Nearest Neighbors Classifier (KNC), Decision Tree (DT), Random Forest (RF), and LSTM. Among these, the LSTM model emerged as the most proficient, achieving remarkable metrics of 0.917949, 0.907336, 0.9263804, 0.90733591, 0.92638, and 0.907336 for accuracy, sensitivity, specificity, p-value, n-value, and F-score, respectively. Serving as the fitness function, the LSTM model was further refined through optimization using the GGO algorithm alongside six other optimization strategies, demonstrating its capability to achieve superior classification results.

Table 6 Various classifiers for the categorization of heart disease.
Full size table

The classification results for the seven optimization algorithms, utilizing the LSTM model as the fitness function, are presented in Table 7. The performance of the GGO-LSTM combination is compared against other LSTM-enhanced optimization techniques, such as BER, DTO, PSO, GWO, WAO, and FOA, highlighting the superior effectiveness of the GGO-LSTM approach46,47,48,49,50. The GGO-LSTM method demonstrated exceptional performance, achieving impressive values of 0.995763 for accuracy, 0.996086 for sensitivity, 0.995516 for specificity, 0.994141 for p-value, 0.997006 for n-value, and 0.995112 for F-score. Multiple optimizers were utilized to fine-tune the LSTM parameters, and their respective outcomes were thoroughly evaluated. The data presented in this table clearly illustrates that the proposed GGO-LSTM approach outperforms all other optimization strategies. These results unequivocally emphasize the critical role of feature selection in enhancing classification accuracy.

Table 7 Findings of optimization methods LSTM Model for the classifying heart disease.
Full size table

Figure 7 provides a comprehensive evaluation of the accuracy achieved by the GGO + LSTM hybrid approach in comparison to other optimization algorithms applied to the LSTM model, with a focus on the objective function. This analysis assesses the efficiency of the GGO + LSTM method in optimizing the objective function for heart disease classification, comparing its performance against various other optimization strategies. The presented results serve to enhance understanding of the relative effectiveness of these techniques, establishing a benchmark for their practical application. Through this visual representation, researchers and practitioners are equipped to discern the distinctive strengths and limitations of each optimization algorithm, enabling them to select the most suitable method for refining heart disease classification models.

Fig. 7
figure 7

Assessing the accuracy of the GGO + LSTM approach and optimization algorithms using the LSTM model, considering the objective function.

Full size image

Figure 8 showcases histograms that depict the distribution of accuracy results for the GGO + LSTM hybrid approach in comparison to alternative optimization techniques used with LSTM models. These histograms visually represent the variability and dispersion of accuracy scores across different optimization methods, providing valuable insights into their performance. By analyzing these graphical representations, researchers can gain a deeper understanding of how the results are distributed, enabling the identification of patterns, outliers, and potential areas for optimization across the methods. The histograms presented in Fig. 8 facilitate drawing meaningful conclusions regarding the effectiveness of various optimization strategies when integrated with LSTM models for heart disease classification tasks.

Fig. 8
figure 8

Histograms of the accuracy results achieved by the GGO + LSTM approach, as well as alternative combinations of optimization techniques with LSTM models.

Full size image

Table 8 displays the ANOVA results for the proposed GGO + LSTM approach, highlighting its ability to achieve outstanding performance through the effective application of search space exploration techniques. To maximize the technique’s potential, it is essential to strike a balanced equilibrium between exploration and exploitation within the search domain. Additionally, it is critical to begin the exploitation phase early in each iteration and progressively increase the number of participants in the exploitation group as the process unfolds. This strategic approach ensures optimal utilization of the search space, leading to superior outcomes.

Table 8 The outcomes of the ANOVA of the proposed GGO algorithm with LSTM model for heart disease classification.
Full size table

Figure 9 presents a series of visualizations, including the heatmap, QQ plot, residual plot, and heteroscedasticity plot, to illustrate the performance of the proposed GGO + LSTM technique. The use of homoscedasticity, quartile-quartile (QQ) plots, and residual plots emphasizes the robustness and effectiveness of the approach. The QQ plot reveals a close alignment with a linear trend, further validating the suitability of the selected features for heart disease classification. Additional validation of these results is provided through the insights gained from the homoscedasticity and residual plots, reinforcing the accuracy and reliability of the findings.

Fig. 9
figure 9

Analysis plots of the results of the proposed GGO + LSTM and other algorithms.

Full size image

Table 9 presents the results of the Wilcoxon rank-sum test, which is utilized to assess whether there are statistically significant differences in the outcomes produced by the various algorithms. A p-value below 0.05 signifies a statistically significant advantage. The findings from this analysis demonstrate that the GGO + LSTM approach outperforms the other techniques, establishing its superiority and confirming the statistical significance of its performance.

Table 9 The Wilcoxon signed-rank test findings of the proposed approach (GGO + LSTM), with various configurations of other optimization algorithms with the LSTM model for heart disease classification.
Full size table

Classification results analysis

In the analysis of classification results, an in-depth evaluation is conducted to assess the performance of various algorithms, including the novel GGO + LSTM approach, in predicting heart disease. This comprehensive evaluation involves scrutinizing several key metrics—such as accuracy, precision, recall, F1 score, sensitivity, and specificity—which provide valuable insights into the strengths and weaknesses of each algorithm’s predictive capabilities. By carefully analyzing these metrics, we gain a holistic understanding of how each algorithm performs in identifying heart disease instances. This critical step not only highlights the advantages and limitations of different methods but also aids in determining the most effective algorithm for heart disease prediction51,52,53,54,55.

Fig. 10
figure 10

Regression plot: accuracy vs. F-score for the proposed GGO + LSTM approach and other algorithms.

Full size image

Figure 10 illustrates a regression plot that depicts the correlation between accuracy and F-score for the proposed GGO + LSTM approach and several competing algorithms. This graphical representation enables a clear understanding of the interaction between these two crucial performance metrics, with each algorithm represented as a data point. The regression line fitted to these points offers insights into the general relationship between accuracy and F-score, highlighting whether a consistent pattern exists. Variations from the regression line reveal the distinct trade-offs between accuracy and F-score for each algorithm, reflecting their individual capabilities. This visualization serves as a powerful tool for researchers to compare the performance of the GGO + LSTM approach against other algorithms, identifying which methods balance high accuracy with a strong F-score in heart disease prediction.

Fig. 11
figure 11

KDE plot of accuracy for the proposed GGO + LSTM approach and other algorithms.

Full size image

Figure 11 presents a Kernel Density Estimation (KDE) plot, which illustrates the distribution of accuracy scores for both the GGO + LSTM approach and several reference algorithms. This plot offers a detailed kernel density estimate, providing a more nuanced understanding of the variability and spread of accuracy scores across the different algorithms. Each algorithm is represented by a probability density curve, with higher peaks signifying regions of greater concentration, where accuracy scores are more densely clustered. The KDE plot allows researchers to discern any underlying patterns in the distribution and compare the accuracy performance of the GGO + LSTM approach against other methods. This visualization serves as a comprehensive tool for evaluating the overall predictive power and comparative effectiveness of each algorithm in the context of heart disease classification.

Fig. 12
figure 12

Sensitivity (TRP) by model for the proposed GGO + LSTM approach and other algorithms.

Full size image

Figure 12 displays the sensitivity, or True Positive Rate (TPR), for both the proposed GGO + LSTM approach and several other algorithms. Sensitivity is a vital metric in binary classification tasks, such as heart disease prediction, as it indicates the model’s ability to correctly identify positive instances (i.e., heart disease cases). Each model is represented by a data point or bar reflecting its corresponding sensitivity value. By evaluating the sensitivity of the GGO + LSTM approach against other algorithms, researchers can assess how effectively each model detects actual positive cases. This comparison highlights the algorithms with higher sensitivity, demonstrating their proficiency in accurately identifying heart disease cases. Ultimately, this analysis allows for a deeper understanding of the GGO + LSTM approach’s effectiveness in heart disease classification relative to other methods.

Fig. 13
figure 13

Specificity (TNP) by model for the proposed GGO + LSTM approach and other algorithms.

Full size image

Figure 13 illustrates the specificity, or True Negative Rate (TNR), for the proposed GGO + LSTM approach alongside other models. Specificity is an essential metric in binary classification tasks, such as heart disease prediction, as it reflects the model’s capability to correctly identify true negatives (i.e., instances where heart disease is absent). Each model is represented by a data point or bar corresponding to its specific value. By comparing the specificity values across different models, we can gauge the success of each algorithm in minimizing false positives. This visual representation highlights the algorithms that excel in identifying cases without heart disease, providing insight into their effectiveness. Analyzing specificity across various models offers a comprehensive understanding of the GGO + LSTM approach’s relative performance and its potential contribution to heart disease classification.

Fig. 14
figure 14

Boxplots for model metrics for the proposed GGO + LSTM approach and other algorithms.

Full size image

Figure 14 presents boxplots comparing the performance metrics of the GGO + LSTM approach with other models. These boxplots provide a clear, graphical representation of key performance indicators, such as accuracy, F1 score, sensitivity, and specificity, allowing for a detailed comparative analysis of their distributions across different algorithms. Each metric is displayed in its own boxplot, where the median value is marked by a line in the center of the box, the interquartile range (IQR) is represented by the edges of the box, and the whiskers extend to the minimum and maximum values within 1.5 times the IQR. Outliers are highlighted as individual data points beyond this range. A careful examination of these boxplots enables researchers to assess the central tendency, spread, and variability of each metric for the GGO + LSTM approach and the other models. This visualization aids in identifying performance differences between the algorithms, providing insights into the relative strengths and weaknesses of each method in heart disease prediction.

Fig. 15
figure 15

Pairplot with regression lines for the proposed GGO + LSTM approach and other algorithms.

Full size image

Figure 15 showcases a pair plot complete with regression lines, offering a comprehensive visualization of the interrelationships among different performance metrics for both the GGO + LSTM approach and other algorithms. This plot enables the exploration of the associations between various metrics such as accuracy, F1 score, sensitivity, and specificity, presented in pairs. Each pair of metrics is displayed using scatter plots, with a corresponding regression line that indicates the direction and strength of their correlation. These regression lines are particularly useful for identifying trends or patterns within the data, highlighting potential correlations across different performance measures. By examining this pair plot, researchers can gain valuable insights into how the metrics interact with one another across different algorithms. Additionally, comparing the regression lines for the GGO + LSTM approach with those of the other algorithms offers a relative performance evaluation, pinpointing areas of strength and opportunities for improvement in the heart disease classification task. Table 10 demonstrates a comprehensive comparison with existing state-of-the-art methods between the proposed model and prior studies for heart disease classification.

Table 10 Comprehensive comparison between the proposed model and several studies for heart disease classification.
Full size table

Conclusion and future work

This research introduces the Greylag Goose Optimization (GGO) algorithm with the goal of enhancing the accuracy of heart disease classification. Initially, essential data preprocessing steps such as scaling, normalization, and the removal of missing values are conducted. Feature selection is then performed using the binary format of GGO (bGGO), which is specifically designed to identify the most optimal feature set that improves classification accuracy. This binary version of GGO is benchmarked against six other binary optimization algorithms, namely, BER, DTO, PSO, WAO, GWO, and FOA. For the classification phase, multiple machines learning classifiers, including SVC, SGD, Naïve Bayes (NB), KNN, Decision Tree (DT), Random Forest (RF), and LSTM, are employed. Among these, the LSTM model demonstrates superior performance, achieving an accuracy of 91.79%. Further optimization of the LSTM’s hyperparameters is conducted using GGO, yielding the highest accuracy of 99.578%. Statistical evaluations are performed using ANOVA and Wilcoxon signed-rank tests to assess the significance of feature selection and classification results. Additionally, several graphical representations are created to demonstrate the robustness and efficiency of the proposed methodology. The findings clearly indicate that the proposed approach outperforms alternative methods, with the effective selection of disease-related features and dimensionality reduction significantly enhancing predictive accuracy and mitigating overfitting in heart disease analysis. Looking ahead, improving early prediction rates for heart disease could be achieved by collecting and analyzing sensor data, followed by the application of optimal methods. This study highlights the efficacy of the GGO algorithm for feature selection and hyperparameter tuning. Future research will explore the use of other optimization algorithms, such as Genetic Algorithms (GA), Differential Evolution (DE), and Adaptive Particle Swarm Optimization (APSO), along with the implementation of transfer learning using pre-trained models on larger, more diverse datasets. These efforts aim to further enhance model performance, reduce training time, and address challenges related to limited labeled data, ultimately contributing to the development of practical diagnostic tools for heart disease classification.