Combined compression and encryption of linear wireless sensor network data using autoencoders

Abstract

In a linear wireless sensor network (LWSN), sensor nodes are deployed in a linear fashion to monitor and gather data along a linear path or route. Generally, the base station collects the data from the contiguously placed nodes in the same order. When the sensors are deployed closely and with a gradual variation of sensor data along the route, a high degree of correlation exists among the sensed data. The sensed data sequence can be compressed with very low loss in such a situation. In this paper, a joint compression and encryption method for LWSN data is presented. The method is based on the dimension reduction property of an autoencoder at the bottleneck section. The Encoder part of the trained Autoencoder, housed at the Base Station (BS), reduces the number of data samples at the encoded output. Hence, the data gets compressed at the output of the Encoder. The output of the Encoder is encrypted using an asymmetric encryption that provides immunity to the Chosen Plaintext Attack. Thus, both data compression and encryption are achieved together at the BS. Therefore, the procedure at the BS is denoted as joint compression and encryption. The encrypted data is sent to the Cloud Server for secured storage and further distribution to the End User, where it is decrypted and subsequently decompressed by the Decoder part of the trained Autoencoder. The decompressed data sequence is very nearly equal to the original data sequence. The proposed lossy compression has a mean square reconstruction error of less than 0.5 for compression ratios in the range of 5 to 10. The compression time taken is short even though the Autoencoder training process, which occurs once in a while, takes a relatively long time.

Introduction

A linear wireless sensor network (LWSN) is a particular type of wireless network where sensor nodes are deployed along a narrow-width path like railway lines, mountain highways, pipelines, river banks, bridges etc., to continuously monitor their current status. A simple LWSN topological deployment with n sensor nodes is shown in Fig. 1. The sensor nodes are placed sequentially and identified by their sequence numbers according to the placement order. The sensed data from the sensor nodes are collected periodically in the same physical placement order by the Base Station (BS). Due to their narrow spread, data sequences from LWSNs have higher spatiotemporal correlation than those from general wireless sensor networks (WSNs), which are widely spread. Hence, the compression of LWSN data is more efficient (less lossy) than WSN data. Therefore, in this work, LWSNs are chosen for low-loss compression.

Fig. 1

Linear wireless sensor network with n nodes.

Data Compression (DC)^{1,2,3,4,5,6,7,8} reduces the size of the sensor data while maintaining its essential characteristic features. DC is advantageous in applications with limited memory space and communication bandwidth while the original data size is substantially large. DC can be lossy or lossless. In practical lossy compression, the reconstructed (expanded or decompressed) output data marginally differs from the original data. In many applications, this difference does not affect the overall performance, and it is acceptable. In such cases, the lossy compression offers a higher Compression Ratio (CR). In our proposed scheme, we develop a lossy compression scheme for LWSN data, based on Autoencoders, that provides a relatively large CR with acceptable data loss.

Fig. 2

Encoder and decoder sections of AE.

An Autoencoder (AE)⁹ is a kind of deep learning network. A schematic diagram of an AE is shown in Fig. 2.

An AE can undergo supervised or unsupervised learning. In this work, supervised learning is employed. The AE has two sections, namely the Encoder (AEE) and the Decoder (AED), with the Latent Space (LS) in between, as shown in Fig. 2. In the LS, the data dimension is the lowest and holds the compressed data. Thus, the Encoder provides the requisite compression. The Decoder section reconstructs the compressed data, and the reconstructed source data is available at the output of the decoder. The detailed working of the AE is described in “Overall layout” section.

Most of the WSN data are stored in public Cloud Servers (CS) for low-cost economy and flexible distribution. When the data to be stored are sensitive, it is essential to encrypt them and then forward the cipher data to the CS for privacy and security. In the existing literature, security and privacy aspects are not effectively addressed during the ‘compress-transmit-store at CS process. To mitigate this, in this work, data encryption and decryption are carried out in the LS of the AE, as the data size is minimal in the LS. Thus, encryption and decryption take place in the LS region of the AE, as shown in Fig. 3. Hence, the encryption/decryption keyspace and ciphertext size are much lower than that of direct encryption without the AE.

In this work, to take care of secured storage at CS, an Autoencoder Compression scheme together with an encryption/decryption mechanism is presented. This method is denoted as ‘Joint Compression and Encryption for LWSN data’ and is abbreviated by CCE. The main contributions of CCE are:

• Design of AE for adequate compression and low-loss reconstruction.

• Secure asymmetric encryption/decryption scheme using matrix keys in the LS region of the AE.

The novelty of CCE is that the insertion of the Encrypter and Decrypter, as in Fig. 3, does not affect the performance of the trained/tested AE in the reconstruction of the original data.

Fig. 3

Encrypter and decrypter in the latent-space of AE.

The remainder of this paper is organized as follows: “Related work” section gives the related work. “Overall layout” section describes the architecture of AE, its training and testing details, the working of the Key Generation Center (KGC), encryption, and decryption units. “CCE algorithm” section contains the CCE algorithm and related discussions. “Experimental results and comparative evaluation” section records experimental results and evaluates the comparative performance using appropriate metrics. “Conclusion” section holds the conclusion and the future scope.

Related work

Several DC techniques^1,2,3 are available for the lossy compression of the data generated from large WSNs with hundreds of sensor nodes. In the Transform-based approaches^4,5, the DCT (Discrete Cosine Transform) and different versions of Discrete Wavelet Transforms (DWT’s) are used for the lossy compression of sensor data. In⁴, the DCT is applied block-wise, and the regions of higher-order coefficients are discarded after the transformation of data blocks. Then, the inverse DCT is applied to get the lossy compressed data back. In⁵, the DC technique is applied to the data from the Wireless Body Sensor Networks (WBSNs). Here, the authors have used DWT with the extended lifting scheme to get an almost lossless compression. In Compressed Sensing^6,7,8, the sparsity of sensor data is exploited to achieve efficient compression. Here, fewer samples than the Nyquist rate are used to reduce the amount of data transmission. Compressive Sensing techniques are adopted when the data redundancy is relatively high.

In⁶, the authors present a multi-hop routing algorithm for Wireless Sensor Networks (WSNs) that leverages compressive sensing and a multi-objective genetic algorithm to minimize energy consumption while maximizing data accuracy and network lifetime which improves routing efficiency.

In⁷, a power-efficient Compressive Sensing (CS) approach for the continuous monitoring of ECG (electrocardiogram) and PPG (photoplethysmogram) signals in wearable systems is presented. CS minimizes the amount of data that needs to be transmitted, effectively reducing power consumption.

In⁸, the proposed Decentralized Compressed Sensing (DCS) algorithm enables each sensor node to locally process and compress its data before transmission, eliminating the need for a central processing hub for the WSN. The DCS algorithm improves the scalability and resilience to faults.

In our work, we use a deep-learning network for data compression. Therefore, we briefly discuss the existing works where Deep Learning (DL) methods are employed for data compression. Several authors have used Deep Learning (DL) based techniques for the compression of data from wireless transmitters, digital images, and WSNs. Here, the feature extraction capabilities of the DL networks are utilized for data size reduction.

In⁹, a comprehensive review of AEs, their types, characteristics, and applications are presented. The authors have analyzed several improved versions of AEs and discussed their relative merits and demerits. A taxonomy of autoencoders based on their structures and principles are described in detail. Additionally, future research directions are suggested, such as improving training efficiency, handling large-scale data, and exploring novel architectures.

In¹⁰, the authors used Neural Networks to process the physical layer operations of a point-to-point communication system. Here, a well-trained Autoencoder models a stochastic noisy communication channel. The data entering the channel is compressed, and then the channel-impaired data is decompressed at the receiver. During this process, it was found that the passage of the signal through the Autoencoder (AE) reduces the noise and distortion caused by the channel. However, the major limitation of this scheme is the physical channel, and the simulated channel used for model training may not match perfectly for different communication contexts.

In¹¹, the AE acts as the wireless communication interface between the transmitter and the receiver in the physical layer. In this scheme, the end-to-end communication process is jointly optimized at the transmitter section of the encoder and the decoder in the receiver section. The AE is driven by one-hot vectors corresponding to the input data. Additionally, the authors used a CNN-based deep learning technique where the in-phase and the quadrature components of the modulated signal were used to train the AE. The main concept is to model the transmitter, the physical channel, and the receiver as a single unit that takes care of channel noise and distortion. However, the design here is oriented more toward reliability than data compression.

In¹², the scheme uses AEs for the design of a multi-colored visual light communication system. The authors have shown that the signal recovery can be optimized by the proper choice of hyperparameters during the Training of AEs. However, this can be used only for short distances and along the line of sight.

In¹³, an Autoencoder-based end-to-end communication is realized where the algorithm alternates between the reinforced learning at the transmitter and simple supervised learning at the receiver end. Here, identical training sequences are used to train the transmitter and the receiver. This is accomplished by setting the same seed for the random number generators on either side. Using the identical training sequences for this staggered supervised learning minimizes the effect of channel noise and Rayleigh fading on the received signal.

In¹⁴, the authors presented a smart management system based on AEs that addresses data compression and anomaly detection in BG5 (Beyond G5) system. Here, the digital twin (virtual representation of physical objects or systems) of telemetry sensor data is created, which requires higher compression ratios and accurate reconstruction provided by pools of AEs. The AEs for compression are selected based on the density and diversity of the input data. Accurate and fast anomaly detection is demonstrated on single-sensor (SS-AD) and multiple-sensor (MS-AGD) scenarios. However, the overall computational load due to multiple AEs is very high.

In¹⁵, a stacked Restricted Boltzmann Machine (RBM) Auto-Encoder (SRBM-AE) network with a non-linear training model is used for the compression and decompression of WSN data. The encoder part provides compression while the decoder part decompresses. ‘Contrastive Divergence’ learning has been adopted to train the RBM’s. The main limitation of this method is that the input and the output of different layers have to be binary. This involves data conversion pre-processing, which incurs a high computational overhead.

The techniques used in^{10,11,12,13,14,15} can be refined further and adopted for the compressed transmission of wireless sensor data. However, the methods used in^{10,11,12,13,14,15} do not provide any cryptographic security with key-based encryption and decryption for LWSN data.

Overall layout

The overall layout of CCE, including the LWSN and other associated units, is shown in Fig. 4. The LWSN consists of n sensor nodes closely spaced for better spatiotemporal correlation. For straight identification, the j^th sensor node is identified by s(j) for j = 1 to n. Thus, the collection of sensor nodes is represented as,

${\text{SN }}={\text{ }}[{\text{s}}\left( {\text{1}} \right),{\text{ s}}\left( {\text{2}} \right), \ldots ,{\text{ s}}\left( j \right), \ldots ,{\text{ s }}\left( n \right)]$

The BS periodically collects the data from these sensors using TDMA through a Gateway which acts as a bridge between the LSWN and the BS.

Fig. 4

CCEwith the LWSN and other associated units.

Each sensor node is allocated a specific ‘time slot’ within a TDMA frame to transmit its data to the BS. This ensures that nodes do not interfere with each other while transmitting, reducing collisions and improving reliability. (Here, single-hop transmission is assumed for simplicity in explanation). The allocation arrangement of time slots for s(j)’s is shown in Table 1, for two TDMA frames. Here GP = Guard Period.

Table 1 Allocation of time slots for sensor nodes.

For a given frame, data sent from s(j) is denoted by x(j) for j = 1 to n. These x(j)’s form vector X as,

$$X=[{\text{x}}\left( {\text{1}} \right),{\text{ x}}\left( {\text{2}} \right), \ldots ,{\text{ x}}\left( {\text{j}} \right), \ldots ,{\text{ x}}\left( {\text{n}} \right)]$$

(1)

Fig. 5

Encoder (AEE) and decoder (AED) sections of autoencoder.

Row vector X is the input to the AE-Encoder (AEE) that acts as the data compressor, as shown in Fig. 5.

Various layers of AE

The various layers of the AE¹⁶ are shown in Fig. 5, which is an expanded view of Fig. 2. The input layer, the first layer of AEE, with n neurons, accepts the input X of size 1× n, and forwards it to the next layer, which is the first dense layer¹⁷ of AEE. A dense layer is a fully connected layer. That is, the neurons of a dense layer are connected to every neuron of the preceding layer, and the weights and biases are controlled by backpropagation. The dimension of the first dense layer, with linear activation, is kept the same as n to improve the accuracy of the AE. The second dense layer, with linear activation, has m neurons with m < n. Hence, this layer reduces the data dimension from m to n.

In AEE and AED, unlike the Rectified linear unit (Relu), linear activation¹⁸ is used to keep both the positive and negative values of its input, which is found to give good results in the encryption process that follows AEE (as shown in Fig. 3). Batch Normalization [19] normalizes the activation outputs of a hidden layer by scaling and shifting during each training iteration (epoch) so that the mean is zero and the standard deviation is one. The output of the Batch Normalization Layer is denoted as D, which is also the input to the AED.

In AED, the first dense layer, with linear activation, upsamples the dimension from m to n. With linear activation, the AED’s second dense layer provides better accuracy without changing the dimension and gives the reconstructed output Y, almost equal to the input X. Different layers and the corresponding changes in dimensions are shown in Table 2.

Table 2 Different layers of the AE.

Generation of data samples for training, validating, and testing

Training signals (data) are synthetically generated using Bessel functions and sinusoids so that the samples are closely correlated and slowly varying. The data sample from the jth sensor node in the ith TDMA frame Fm(i) is represented by x(i, j) for j = 1 to n and for i = 1 to Q where n is the number of sensor nodes, and Q is the number of TDMA frames. The data set is shown in Table 3. Here, the id of the j^th sensor node is s(j). The ith TDMA frame is denoted by Fm(i). (In Table 3, Matlab-like notations are used to represent the rows, columns, and elements of the data samples.)

Table 3 Training/validating/testing data samples.

For example, 100 data samples from x(1,1) to x(1,100) at time slot ts(i), represented by X(1), a row vector, is shown in Fig. 4. We can observe the close spatial correlation among the samples. In Table 3, The i^th row vector X(i) is formed for i = 1 to R as,

$$\:\varvec{X}\left(i\right)=\left[x\left(i,1\right),\:x\left(i,2\right),\dots\:,x(i,j),\dots\:,x(i,n)\right]$$

(2)

Samples of a row vector are shown in Fig. 6, where n = 100. The sample values could be environmental parameters like temperature, air pollution, etc., with appropriate scale factors.

Fig. 6

Data samples from 100 contiguous sensors at time slot ts(1).

In CCE, we have Q number of row vectors of size 1×n as our synthesized data set. Out of this, the training set, the validation set, and the testing set are formed, as shown in Table 4.

Table 4 Dataset break up.

In Table 3, the first T row vectors are used for training, the next V for validation, and the remaining S for testing where T + Val + TS = Q.

Training with validation of AE

In CCE, training and testing of the AE is conducted without encryption/decryption (ED) units, as in Fig. 5. The ED units are inserted after thorough training and testing of the AE, as shown in Fig. 3. This insertion of ED units between AEE and AED does not change the data value D, the output of AEE, which is exactly the input to AED. In Fig. 3, the Encrypter converts data D to E and, subsequently, the Decrypter converts E back to D. Thus, CCE inserts ED units without altering the basic characteristic of the AE that uses supervised learning. This is the novelty of CCE.

The AE is trained with SGD (Stochastic Gradient Descent) optimizer and MSE (Mean Square Error) loss function. The training is carried out using the Keras function autoencoder.fit(…) as,

history   =   autoencoder.fit(data, data, epochs   =   1000,batch_size   =   300,

validation_data=(val_data, val_data))

Here, the initial batch is size set to 300 while the number of epochs to 1000. The model’s metrics during training are obtained from the history²⁰. The variations of training or model accuracy and training loss versus epochs are shown in Fig. 7(a) and (b). In Fig. 7(a), the final value of training accuracy is found to be greater than 0.8 but less than 0.9. The accuracy can be improved using more training samples and epochs as well as proper regularization. Model loss, as plotted in Fig. 7(b), measures how well the autoencoder has learned to compress and reconstruct input data. Model loss is the the means squared difference between the input data and its reconstruction with reference to training and testing data values.

Fig. 7

Training accuracy and loss versus epochs.

If the size of the training dataset is relatively small and the situation permits, the real-time training data from the WSN nodes can be collected over the desired number of time slots by the BS and can be used for training the AE.

Testing the AE

After successful training with high accuracy, the trained AE is ready for testing. During testing, the test set XTest (see Table 4) is applied as the input to the successfully trained AE. Then, its output, denoted by YTest is predicted and compared with XTest to get the test error denoted by TError, as shown in Fig. 8.

Fig. 8

Testing of the trained AE.

TError is obtained as,

$${\varvec{T}}{\varvec{E}}{\varvec{r}}{\varvec{r}}{\varvec{o}}{\varvec{r}}\,=\,{\varvec{X}}{\varvec{T}}{\varvec{e}}{\varvec{s}}{\varvec{t}}-{\varvec{Y}}{\varvec{T}}{\varvec{e}}{\varvec{s}}{\varvec{t}}$$

(3)

Here, the sizes of XTest, YTest, and TError are all equal to TS×n (uncompressed). Ideally, when the AE is perfectly trained, the output YTest is exactly equal to the input XTest. Then, TError will be zero. But in practice, there is a small error. The Test Mean Square Error (Tmse) is given by,

$$Tmse\,=\,mse({\varvec{T}}{\varvec{E}}{\varvec{r}}{\varvec{r}}{\varvec{o}}{\varvec{r}})$$

(4)

The acceptance level of Tmse depends on the application and context. If Tmse is above the acceptance limit, the hyperparameters of the AE are adjusted, and the layers are redesigned until the error goes below the acceptance limit.

Key generation center

The KGC is housed at the BS and generates the decryption keys H₁, H_2,H_3, and the encryption keys G₁, G_2,G₃ as follows. A random integer unimodular matrix U is initially generated using the Nathan Brixius algorithm²¹.

$${\varvec{U}}\,=\,{\text{rand}}\_{\text{unimod}}\left( L \right)$$

(5)

where the size of U is L×L. The size parameter L is selected as,

$$L\,=\,m\,+\,{\text{2}}*k$$

(6)

where m is the data length of the row vector D, which is the output of the Batch Normalization Layer of AEE as shown in Fig. 5. Now, let the matrix inverse of U, denoted by V, be calculated as,

$${\varvec{V}}\,=\,{\text{inv}}\left( {\varvec{U}} \right)$$

(7)

Since U is unimodular, its determinant is ± 1. Hence, the matrix inverse V of U exists, and the elements of V are integers. From (7),

$$\:{\varvec{V}}_{L\times\:L}*{\varvec{U}}_{L\times\:L}={\varvec{I}}_{L\times\:L}$$

(8)

where, $\:{\varvec{I}}_{L\times\:L}$ represents the identity matrix of size L×L.

Key generation for encryption and decryption

To get encryption and decryption keys, matrices V and U are partitioned as,

$$\:\varvec{V}=\left[\begin{array}{c}{\varvec{G}}_{1,\:\:(\varvec{m}\times\:\varvec{L})}\\\:{\varvec{G}}_{2,(\varvec{k}\times\:\varvec{L})}\\\:{\varvec{G}}_{3,(\varvec{k}\times\:\varvec{L})}\end{array}\right],\:\:\:\:\:\:\:\:\:\:\varvec{U}=\left[{\varvec{H}}_{1,\:(\varvec{L}\times\:\varvec{m})},\:\:{\varvec{H}}_{2,\:(\varvec{L}\times\:\varvec{k})},{\varvec{H}}_{3,\:(\varvec{L}\times\:\varvec{k})},\right]$$

(9)

The sizes of the sub-matrices G₁, G₂, G₃ are (m×L), (k×L), (k×L) respectively and H₁, H₂, H₃ are (L×m), (L×k), (L×k) as given in the respective subscripts of (9). Now, the RHS of (8) is also partitioned as,

$$\:{\varvec{I}}_{\varvec{L}\times\:\varvec{L}}=\left[\begin{array}{ccc}{\varvec{I}}_{\varvec{m}\times\:\varvec{m}}&\:{0}_{m\times\:\varvec{k}}&\:{0}_{m\times\:\varvec{k}}\\\:{0}_{k\times\:\varvec{m}}&\:{\varvec{I}}_{\varvec{k}\times\:\varvec{k}}&\:{0}_{\varvec{k}\times\:\varvec{k}}\\\:{0}_{k\times\:\varvec{m}}&\:{0}_{k\times\:\varvec{k}}&\:{\varvec{I}}_{\varvec{k}\times\:\varvec{k}}\end{array}\right]$$

(10)

Equations (9) and (10) are substituted in (8) to get,

$$\:\left[\begin{array}{c}{\varvec{G}}_{1}\\\:{\varvec{G}}_{2}\\\:{\varvec{G}}_{3}\end{array}\right]*\left[{\varvec{H}}_{1},\:\:{\varvec{H}}_{2},{\:\varvec{H}}_{3}\right]=\left[\begin{array}{ccc}{\varvec{I}}_{\varvec{m}\times\:\varvec{m}}&\:{0}_{m\times\:\varvec{k}}&\:{0}_{m\times\:\varvec{k}}\\\:{0}_{k\times\:\varvec{m}}&\:{\varvec{I}}_{\varvec{k}\times\:\varvec{k}}&\:{0}_{\varvec{k}\times\:\varvec{k}}\\\:{0}_{k\times\:\varvec{m}}&\:{0}_{k\times\:\varvec{k}}&\:{\varvec{I}}_{\varvec{k}\times\:\varvec{k}}\end{array}\right]$$

(11)

In (11) size indicating subscript information is deleted for simpler representation.

From (11),

$$\:\left[\begin{array}{ccc}{\varvec{G}}_{1}*{\varvec{H}}_{1}&\:{\varvec{G}}_{1}*{\varvec{H}}_{2}&\:{\varvec{G}}_{1}*{\varvec{H}}_{3}\\\:{\varvec{G}}_{2}*{\varvec{H}}_{1}&\:{\varvec{G}}_{2}*{\varvec{H}}_{2}&\:{\varvec{G}}_{2}*{\varvec{H}}_{3}\\\:{\varvec{G}}_{3}*{\varvec{H}}_{1}&\:{\varvec{G}}_{3}*{\varvec{H}}_{2}&\:{\varvec{G}}_{3}*{\varvec{H}}_{3}\end{array}\right]=\left[\begin{array}{ccc}{\varvec{I}}_{\varvec{m}\times\:\varvec{m}}&\:{0}_{m\times\:\varvec{k}}&\:{0}_{m\times\:\varvec{k}}\\\:{0}_{k\times\:\varvec{m}}&\:{\varvec{I}}_{\varvec{k}\times\:\varvec{k}}&\:{0}_{\varvec{k}\times\:\varvec{k}}\\\:{0}_{k\times\:\varvec{m}}&\:{0}_{k\times\:\varvec{k}}&\:{\varvec{I}}_{\varvec{k}\times\:\varvec{k}}\end{array}\right]$$

(12)

Equating the matching product matrices of the LHS with those of the RHS side of (12), we get,

$$\:\left.\begin{array}{c}{\varvec{G}}_{1}*{\varvec{H}}_{1}={\varvec{I}}_{\varvec{m}\times\:\varvec{m}}\\\:{\varvec{G}}_{2}*{\varvec{H}}_{2}={\varvec{G}}_{3}*{\varvec{H}}_{3}={\varvec{I}}_{\varvec{k}\times\:\varvec{k}}\\\:{\varvec{G}}_{2}*{\varvec{H}}_{1}={\varvec{G}}_{3}*{\varvec{H}}_{1}={0}_{k\times\:\varvec{m}}\\\:{\varvec{G}}_{1}*{\varvec{H}}_{2}={\varvec{G}}_{1}*{\varvec{H}}_{3}={0}_{m\times\:\varvec{k}}\\\:{\varvec{G}}_{2}*{\varvec{H}}_{3}={\varvec{G}}_{3}*{\varvec{H}}_{2}={0}_{\varvec{k}\times\:\varvec{k}}\end{array}\right\}\:$$

(13)

The sizes of G₁, G₂, G₃, and H₁, H₂, H₃ are given in (9). In CCE, integer matrices G₁, G₂, G₃ are the Encryption Keys, and H₁, H₂, H₃ are the Decryption Keys. At the beginning of a session, the decryption keys H₁, H₂, H₃, which do not change from encryption to the next encryption, are sent to the End User through a secured channel by the KGC. These keys are used to decrypt the encrypted data from the Cloud Server.

Example 1

Example 1 illustrates the generation of integer matrix keys. Here m = 3, k = 3, and L = m + 3*k = 9. The unimodular matrix U, generated using (5), and its inverse V are shown in Tables 5 and 6. In Table 5, matrix partitions G₁, G₂, G₃ are shown in distinct background colors. Similarly, in Table 6, H₁, H₂, and H₃ are shown in matching colors. From the numerical values of Tables 5 and 6, the equality constraint of (13) can be verified.

Table 5 Matrix U with submatrices G₁, G₂, G₃.

Table 6 Matrix V with submatrices H₁, H₂, H₃.

Encryption and decryption in CCE

In CCE, after the successful training of the AE, the Encoder Section AEE, and the Decoder Section AED are separated. Then, the Encrypter and Decrypter units are inserted, with CS in between, as shown in Fig. 9. The input D to the Encrypter is from the output of AEE, and the output of the Decrypter, which is the same as D, is the input to the AED (see Fig. 3).

Fig. 9

The working arrangement of Encrypter, CS, and Deccrypter.

Encryption of D

At the start of every encryption operation, a random vector R of size 1×m is generated as,

$$R\,=\,{\mathbf{randi}}\left( {\left[ {LB,UB} \right],{\text{ }}{\mathbf{1}},K} \right)$$

(14)

The input vector D of size 1×m is encrypted using matrices G₁, G₂, and G₃, with sizes as given by (9), to get,

$$\:\varvec{E}=\varvec{D}*{\varvec{G}}_{1}+\varvec{R}\varvec{*}{\varvec{G}}_{2}+\varvec{R}\varvec{*}{\varvec{G}}_{3}$$

(15)

In (15), the size of $\:\varvec{D}*{\varvec{G}}_{1}$ is (1×m) ×(m×L) = 1×L, those of $\:\left(\varvec{R}\varvec{*}{\varvec{G}}_{2}\right)$ and $\:\left(\varvec{R}\varvec{*}{\varvec{G}}_{3}\right)$ are (1×k) ×(k×L) = 1×L. Therefore, the encrypted vector E has a size of 1×L. In (15), the random vector R acts as the digital signature, and R also prevents CPA (Chosen Plaintext Attack) as will be explained later while discussing the security aspects of Encryption. The random vector R is changed over successive encryptions and thus, randomized encryption is provided. Vector E is the output of the Encrypter, which is stored in the CS for subsequent decryption by the End User.

Authentication and decryption of E

On receiving vector E, the End User checks the integrity of E from the CS, by decrypting the signature verification matrices P and Q as,

$$\:\varvec{P}=\varvec{E}*{\varvec{H}}_{2}$$

(16)

$$\:\varvec{Q}=\varvec{E}*{\varvec{H}}_{3}$$

(17)

On substituting for E from (15) into (16), we get,

$$\:\varvec{P}=\left(\varvec{D}*{\varvec{G}}_{1}+\varvec{R}\varvec{*}{\varvec{G}}_{2}+\varvec{R}\varvec{*}{\varvec{G}}_{3}\right)*{\varvec{H}}_{2}=\varvec{D}\varvec{*}{\varvec{G}}_{1}\varvec{*}{\varvec{H}}_{2}+\varvec{R}\varvec{*}{\varvec{G}}_{2}\varvec{*}{\varvec{H}}_{2}+\varvec{R}\varvec{*}{\varvec{G}}_{3}\varvec{*}{\varvec{H}}_{2}$$

(18)

From (18), and (13), we have,

$$\:\varvec{P}=\varvec{R}$$

(19)

Similarly, from (15), (17), and (13), we get,

$$\:\varvec{Q}=\varvec{R}$$

(20)

In (19) and (20), the matrix R embedded in E is the digital signature. From (19) and (20),

$$\:\varvec{P}=\varvec{Q}$$

(21)

If there is no error in E, then the equality condition $\:\varvec{P}=\varvec{Q}$ is satisfied. Otherwise, $\:\varvec{P}\ne\:\varvec{Q}$ means the encrypted E received by the End User has been corrupted or tampered with by an attacker. Then, the received E is discarded. Thus, the authentication of the message as well as the source is provided by the digital signature.

When the signature verification is correct, the End User decrypts it using the matrix Key is carried out as,

$$\:\widehat{\varvec{D}}\:=\:\varvec{E}\varvec{*}{\varvec{H}}_{1}$$

(22)

The correctness of decryption is proved by substituting E in (22) from (15) to get,

$$\:\widehat{\varvec{D}}\:=(\varvec{D}*{\varvec{G}}_{1}+\varvec{R}\varvec{*}{\varvec{G}}_{2}+\varvec{R}\varvec{*}{\varvec{G}}_{3})\:\varvec{*}{\varvec{H}}_{1}$$

(23)

This is expanded as,

$$\:\:\:\:\:\widehat{\varvec{D}}\:=\varvec{D}\varvec{*}{\varvec{G}}_{1}\varvec{*}{\varvec{H}}_{1}+\varvec{R}\varvec{*}{\varvec{G}}_{2}\varvec{*}{\varvec{H}}_{1}+\varvec{R}\varvec{*}{\varvec{G}}_{3}\varvec{*}{\varvec{H}}_{1}$$

(24)

From (13) it can be seen that,$\:\:{\varvec{G}}_{1}\varvec{*}{\varvec{H}}_{1}={\varvec{I}}_{\varvec{m}\times\:\varvec{m}},$ and $\:{\varvec{G}}_{2}\varvec{*}{\varvec{H}}_{1}={\varvec{G}}_{3}\varvec{*}{\varvec{H}}_{1}={0}_{k\times\:\varvec{m}}.$ Hence

$$\:\widehat{\varvec{D}}\:=\:\varvec{D}$$

(25)

Thus, the correctness of the decryption process is proved.

Ciphertext expansion ratio

The ciphertext expansion ratio (CER) is a measure of the increase in size between the ciphertext and plaintext. The higher the CER, the greater the related computational and communication cost. In CCE, the plaintext D and the ciphertext E have sizes (1×m) and (1×L) respectively. Therefore, in the light of Eqs. (6),

$$\:CER\left(\text{i}\text{n}\:\text{t}\text{e}\text{r}\text{m}\text{s}\:\text{o}\text{f}\:\text{e}\text{l}\text{e}\text{m}\text{e}\text{n}\text{t}\text{s}\right)=\frac{\text{L}\text{e}\text{n}\text{g}\text{t}\text{h}\:\text{o}\text{f}\:\varvec{E}}{\text{L}\text{e}\text{n}\text{g}\text{t}\text{h}\:\text{o}\text{f}\:\varvec{D}}=\frac{L}{m}=\frac{m+2*k}{m}=1+\:\frac{2*k}{m}$$

(26)

When m > > 2*k, CER is very nearly equal to one. Thus, CCE has an excellent CER.

Computational cost of encryption and decryption

The encryption process, as given by (15), can be rewritten as, $\:\varvec{E}=\varvec{D}*{\varvec{G}}_{1}+\varvec{R}\varvec{*}\left({\varvec{G}}_{2}+{\varvec{G}}_{3}\right).$ This involves the product of matrices $\:\varvec{D}\varvec{*}{\varvec{G}}_{1}$ of sizes (1×m) and (m×L). Therefore, with D as type ‘float’, the number of floating point multiplications (FPMs) required is (m*L). Similarly, the matrix product $\:\varvec{R}\varvec{*}\left({\varvec{G}}_{2}+{\varvec{G}}_{3}\right)$ with sizes (1×k) and (k×L) needs (k*L) FPMs. Cost of matrix addition $\:\left({\varvec{G}}_{2}+{\varvec{G}}_{3}\right)$ is ignored. Hence, the total number of FPMs is (m*L)+ (k*L) = (m+k) *L. On substituting for L from (6), the total number of FPMs is (m+k) *(m+2*k). Since m is generally greater than k (which is normally set at 2 or 3 to keep the CER low), the overall computational cost is O(m²). Similarly, it can be shown that the computational cost of decryption is O(m²).

Security of encryption

Immunity against CPA is provided by randomizing the encryption operation as given by (15) by choosing different R’s for consecutive encryptions.

Exhaustive search attack

The size of the encryption key G₁ is (m×L). Taking the mean size of an element in a key as two decimal digits, the chance of correctly determining a single element is 10^‒2. Therefore, the probability of correctly determining all the elements of G₁ out of (m×L) digits, represented by p, is 10^‒2*(m×L), which is insignificantly small. Thus, the Exhaustive Search Attack is infeasible. In CCE, L = m + 2*k. By increasing k, the value of p can be reduced further. However, an increase in k increases the CER, as indicated by (26).

Immunity against the chosen ciphertext attack (CCA)

The encryption process given by (15), can be rewritten as,

$$\:\varvec{E}=\left[\begin{array}{cc}\varvec{D}&\:\varvec{R}\end{array}\right]*\left[\begin{array}{c}{\varvec{G}}_{1}\\\:\left({\varvec{G}}_{2}+{\varvec{G}}_{3}\right)\end{array}\right]$$

(27)

From (27), we see that the data vector D is concatenated with a random vector R before encryption. Therefore, the CCA hacker, knowing D’s and E’s cannot determine R’s as R’s are random and change over successive encryptions, where identical plaintexts do not encrypt to the same ciphertext. Thus the CCA is prevented, as the attacker cannot distinguish whether the plaintexts are the same or distinct.

Working of the CCE

Once the successful training and testing are over, AE is ready to be deployed in the actual field of the WSN. The Encoder section (AEE) with Encrypter is at the BS, while the Decoder section(AED) with Decrypter is at the End User. and the secret key is transferred to the end user through a secured channel. Now the BS periodically collects real-world data samples from all the sensors at the specified time slots. In a given TDMA frame, let the data samples collected from all the n sensors at their time slot be assembled into the data vector X as given by (1). The size of X is 1×n. The AEE at the BS compresses X (length n) to D(length m) with a reduction of data size from n to m. The Encrypter at BS increases the length to L, which is equal to m + 2*k. Therefore the Compression Ratio (CR) is given by CR = n/L = n/(m + 2*k)$\:.$ When m is relatively large compared to 2*k (k is normally set to 2 or 3), CR is approximately given by,

$$\:CR\:\approx\:\:\frac{n}{m}$$

(27)

The Encrypter at the BS transmits E to the CS for storage and distribution. When the End User needs the data, they get E from the CS. Then, the Decrypter at the End User decrypts and decompresses E to reconstruct Y, which is very nearly equal to X. This operation repeats for all the data collected by the BS in the succeeding time frames. The change in dimensionality is shown in Table 1 without enrypter/decrypter units.

CCE algorithm

The task carried out by CCE can be summarized in the CCE Algorithm.

CCE algorithm.

The performance of the compression/decompression can be improved using more layers with multiple steps instead of a single-step change as implemented in CCE.

Benefits of using the encrypter in the latent domain of the autoencoder

Efficient encryption

The latent domain represents a compressed version of the input data. This reduces computational costs and the time required for encryption and decryption compared to encrypting the full data directly.

Preventing model inversion attacks

Encrypting the latent domain makes it harder for adversaries to perform model inversion attacks, where they have to invert both the Encoder part of the AE and the encrypter block to reconstruct the original input data from the model’s compressed and encrypted output.

Experimental results and comparative evaluation

All the experiments are carried out using the synthetic data generated using algebraic functions. The dataset is generated with good diversity but with good correlation. It is also assumed that the spatial and temporal sensor data variations are slow and moderately smooth.

Evaluation of the training process

Experiment 1

The AE is designed and constructed as in Fig. 2. The parameters chosen are n = 60 and m = 30. The encryption Sizes of the training and validation set are 800 and 100 (see Table 4). The batch size = 300, the number of epochs = 800, Learning rate = 0.001 with Stochastic Gradient Descent optimization. Other required parameters are set by default. The training is carried out using the Autoencoder.fit(…) function. The variations of mse’s for train and validation, and mae’s (mean absolute error) for training and validation are plotted in Fig. 10. The first 199 values are relatively high, and if included, the y-scaling of the plots would have hidden the finer details in the remaining epochs. Here, it is found that increasing the epochs beyond 800 does not reduce the errors further.

Fig. 10

Model loss during training with validation.

Figure 10 shows that the errors are slightly higher due to a lesser degree of correlation among the training data. (Including more dense layers in the construction of AE and increasing the number of training data sets could reduce the reconstruction losses.)

Testing performance of AE

Testing is carried out after successful training.

Experiment 2

The AE setup is n = 60 and m = 30. Two test vectors, XTest¹ and XTest², each of size 1×n, are applied to the Encoder input, and the corresponding error vectors TError¹ and TError² are obtained. These values are plotted in Fig. 11 (a) and (b). From the error plots, we see that the errors range between − 0.15 to + 0.15. In this experiment, the Tmse’s of TError¹ and TError² are found to be 0.00740293 and 0.00879383, respectively.

Fig. 11

(a) Two Test input vectors XTest[1] and XTest[2]. (b) Two Error vectors TError[1] and TError[2].

Reconstruction error vs. compression ratio

The reconstruction error and CR are adversely related in the sense that if CR is improved, the error performance deteriorates. That is, if CR is increased, the error also increases. In Experiment 3, the Tmse versus CR performance of AE is visualized.

Experiment 3

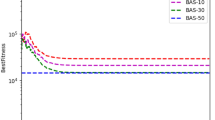
The AE setup is setup with n = 60 and m = 30, 20, 15, 12, 10, which gives the CR ratios of 2, 3, 4, 5, 6. After the training, the test input Xtest¹ is applied to the AE and the corresponding TError¹ is calculated. Then, the Tmse values are calculated using these m’s for the number of epochs set to 500, 600, and 700. Low epoch values are chosen to increase the error for dominant visibility. The resulting plots are shown in Fig. 12. From Fig. 12, it can be inferred that Tmse increases non-linearly as the CR increases.

Fig. 12

Reconstruction error vs. compression ratio.

Comparison with other methods

The Coefficient of Determination (CoD) measures the correlation between the original and reconstructed data. It is defined as²²,

$$\:CoD=1-\frac{{SS}_{res}}{{SS}_{tot}}\:\:\:\:\:$$

(28)

where, $\:{SS}_{res}$ is the residual sum of squares given by,

$$\:{SS}_{res}=\sum\:{\left({y}_{true}-{y}_{predict}\right)}^{2}$$

$$\:{SS}_{tot}=\sum\:{\left({y}_{true}-{mean(y}_{true})\right)}^{2}$$

CoD lies between 0 and 1. Under ideal conditions, $\:{y}_{predict}$ is equal to $\:{y}_{true}$ and CoD(ideal) = 1. The higher the CoD, the better is the performance. In Experiment 4, we compare the CoD values of CCE with LIU method [15] and SAYED method¹⁴.

Experiment 4

The AE setup is the same as in Example 3, except that the number of epochs is set at 500. The value of m is varied from 10 to 20. The CoD values are calculated using the CCE, LIU [15], and SAYED¹⁴ methods, and the results are plotted in Fig. 13. From Fig. 13, it can be observed that CCE performs better compare to the othe two methods. However, the CoD performance very much depends on the characteristics of the data samples and spatial correlation among them.

Fig. 13

Coefficient of determination versus compression ratio.

Conclusion

A new method of joint compression and embedded encryption of sequential data from a linear Wireless sensor Network has been presented. The method uses a custom-built Autoencoder integrated with the encrypt-decrypt layers. Thus, both compression and encryption are jointly realized with matching decryption and decompression. The reconstruction error is between 2 and 5%. The encrypter-decrypter units combined with The encoding-decoding units of the Autoencoder provide higher security at the Cloud Server. The performance can be improved by cascading more hidden layers and fine-tuning hyperparameters of the Autoencoder deep learning network.