The influence of Nusselt number on dropwise condensation heat transfer for a single droplet on inclined and grooved surfaces

Abstract

Dropwise condensation (DWC) is a widely studied vapor–liquid phase-change process that has attracted significant research attention due to its exceptional energy transfer efficiency. Therefore, it is highly important to predict the heat transfer rate during DWC and the factors that affect it. This study presents a computational fluid dynamics (CFD) investigation on DWC heat transfer under diverse circumstances for a single droplet on inclined and rough surfaces with Wenzel structure. Drop’s shape simulation was done utilizing the Surface Evolver (SE) software and the governing equations were solved based on the finite volume method. Moreover, for different Nusselt numbers ($Nu$), the average heat flux was calculated by considering the effect of different inclination angles, contact angles, and saturation temperatures. Validation was performed by comparing the outcomes with the available data in the literature, and a satisfactory agreement was achieved. The study revealed that the average heat flux for a water droplet with the saturation temperature ${T}_{sat}$ = 313 K on an inclined surface with an inclination angle of β  =  90° increases by 151.79% when the Nu is increased from 510 to 740. Similarly, for a droplet on a rough surface with a roughness index of ${r}_{i}$ = 0.6, the increase in heat flux is 152%. Moreover, an increase in saturation temperature results in a higher heat flux for both inclined and rough surfaces. The augmentation follows a specific trend for each of the surfaces.

Introduction

The process of condensation occurs when vapor transforms into liquid on a solid surface, caused by the surface being cooler than its adjacent vapor^1,2. There are various industrial applications for condensation, such as power generation³, air conditioning⁴, thermal desalination⁵, refrigeration cycles⁶ and water harvesting⁷. In this regard, there are two main types of condensation processes: Filmwise condensation (FWC) and Dropwise condensation (DWC)^8,9. FWC occurs when the vapor condenses on the surface in the form of liquid films, while DWC happens when the vapor condenses in the shape of liquid droplets^10,11. Although it should be noted that typically a combination of both types occurs during the process.

The latter type (DWC) has attracted more attention to itself since Schmidt et al.¹² asserted that the heat transfer rate in this type is exceptionally higher compared to FWC. Ever since, researchers have been trying to create a condition in which DWC gets a better chance of occurring on the solid surface. There are multiple factors that can affect the process of condensation and the type that can take place on the surface. Decreasing the surface energy can highly increase the chance of DWC to happen^13,14,15. The inclined and grooved surfaces possess lower surface energy. The groove nanostructures can be categorized in two types. If the liquid droplet fills in the roughness, the type would be called Wenzel structure and if the droplet stays on top of the roughness and does not fill it, it would be called Cassie structure^16,17.

Regarding the heat transfer rate in condensation, there are other factors such as the contact angle of the droplet on the surface, the angle of inclination of the surface and also the structure of the solid surface also the physical and chemical properties of the liquid which can affect the rate of heat transfer. In an experimental work, Tancon et al.¹⁸ explored the impact of surface inclination on DWC for three different angles and reported that the heat transfer coefficient (HTC) of the liquid droplet was 40% higher for a droplet on a vertical surface compared to a horizontal one and 10% higher compared to a surface with an inclination angle of 45°. Sikarwar et al.¹⁹ studied DWC of metal vapors underneath inclined surfaces for three metal vapors and compared the results with the ones from water. They reported that among all the studied cases, Sodium has the lowest HTC and an inclined surface yields a higher heat transfer compared to horizontal. Baghel et al.²⁰ considered all the thermal resistances inside a single droplet and studied the influence of different parameters on heat transfer for a single liquid droplet underneath a solid surface. Their results imply that the heat transferring a deformed and a spherical cap droplet is equal.

Regarding grooved surfaces and their impact on heat transfer during DWC, numerous studies has been done. Farhat et al.²¹ simulated the behavior of liquid droplets on horizontal and microgrooved surfaces, numerically. In their research study, they benefited from SE software to simulate the geometry of the droplets in Cassie state and the results were in reasonable agreement with the experimental works. Mohammadpour et al.²² examined the impact of roughness indexes for a Wenzel structure on the heat transfer rate while taking Marangoni convection into account. They reported that increasing the roughness index would result in a lower heat transfer rate and Marangoni convection causes a higher heat transfer during the process of DWC. Peng et al.²³ conducted experimental research to study the influence of microgroove orientation on the dynamics of condensed droplets and the condensation heat transfer performance on both horizontal and vertical surfaces. They reported that the heat flux for vertical surfaces was 20–64% higher than that of horizontal surfaces.

Investigating the influence of diverse dimensionless numbers on heat transfer during DWC has attracted enormous attention to itself specifically during the past several years. Phadnis and Rykaczewski²⁴ theoretically studied the effect of Marangoni convection on heat transfer in DWC for liquid droplets. They used a finite element method to carry out the simulation and reported with the presence of Marangoni convection, the heat transfer rate is higher under special conditions. Besides, they indicated that these results cannot be accurate for droplets with the radius below 100 μm. In a 3D numerical investigation, Sikarwar et al.²⁵ studied fluid flow and temperature distribution inside a pendant droplet. They took the Reynolds number (100–1000) into consideration for a droplet with the Prandtl number ($Pr$) of 5.8. Their findings indicated that at higher Reynolds numbers, the temperature variation is approximately uniform and wall pressure increases with the increase of Reynolds number. So far in most available works, only conductive heat transfer has been considered in DWC while in many practical cases convective heat transfer cannot be neglected. Nusselt number (Nu) provides a good indicator for studying these two types of heat transfer when the process is taking place.

Pang et al.²⁶ correlated heat transfer for a condensate droplet and asserted that the previous research is only predicting heat transfer rate accurately when the Biot number ($Bi$) is too small and hence, they suggested a more precise model to calculate the heat transfer rate. Chavan et al.²⁷ studied the conduction thermal resistance for a 2D modal and presented an expression to calculate heat transfer in a single droplet considering $Nu$, $Bi$ numbers and contact angle of the droplet. In another work, Sikarwar et al.²⁸ scrutinized the influence of drop shape on heat transfer for an obtained shape from two-circle approximation method and SE software. They presented the relation between $Nu$ with respect to temperature difference and found out that the heat transfer rate in the two-circle approximation method is slightly more than the SE method.

By reviewing the available works, it is realized that a limited number of studies have investigated the influence of Nu number on the heat transfer rate in DWC considering inclined and grooved surfaces. Thereby, in the current research work, a computational fluid dynamics study carried out in order to investigate the effect of Nu number on heat transfer for a single droplet on an inclined surface with diverse inclination angles and also on a grooved surface with Wenzel structure. For simulating the drop shapes in the desired conditions, SE, an open-source software is used. The obtained geometries are transferred to a CFD solver to carry out the aforementioned objective of this study. Furthermore, different parameters such as the droplet height, the contact angle, the saturation temperature and the roughness index are also scrutinized.

Model description

Geometry

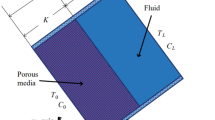
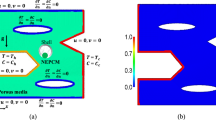
In the present study, both inclined and grooved surfaces are simulated. A suitable tool for simulating liquid droplets on a solid surface is SE software²⁹. This software is an interactive program for the study of surfaces shaped by surface tension and other energies, and subjected to various constraints. The SE evolves the surface toward minimal energy by a gradient descent approach. The main intention is to find a minimal energy surface³⁰. For the inclined surface, a 20 µl liquid droplet with the contact angle of 110° on a solid substrate, which has been coated to ease the process of condensation, has been simulated in seven different inclination angles. The thermo-physical properties of liquid droplet, solid substrate and the coating layer has been provided in Tables 1 and 2, respectively. In Fig. 1, a liquid droplet can be seen on an inclined surface with an inclination angle of 90°. The simulation of the liquid droplet on the rough surface with the Wenzel structure has also been done in SE software. Ibrahim et al.³¹ pointed out that on a sinusoidal structure the chance of DWC to occur is quite high and hence, this structure has been chosen for purpose of the simulation in this study where a 4 µl liquid droplet in three different contact angles has been studied on a coated solid surface. Figure 2 demonstrates a liquid droplet on a Wenzel structure. As it can be seen in Fig. 2, the roughness index (${r}_{i}$) has been defined in order to simulate structures with diverse roughness levels.

Fig. 1

Schematic of a simulated liquid droplet on a solid surface in SE software considering $\theta$ = 110°; $\beta$ = 90°; $V$ = 20 µl; ${\rho }_{l}$ = 992.1 kg/m³.

Fig. 2

Schematics of the generated grid for a liquid water droplet on a grooved surface (Wenzel structure) at r_i = 0.4 designed by SE software at $\theta$ = 160°; $V$ = 4 µl; ρ_l  =  992.1 kg/m³.

Table 1 Liquid droplets thermo-physical characteristics^6,32.

Table 2 Thermo-physical properties of the coating layer and the condensing surface^6,33.

Mathematical formulation

The working fluid in this research was considered an incompressible fluid and the effect of viscous dissipation was assumed to be negligible. The governing equations for the domains are mass, momentum and energy equations. These equations have been solved in Cartesian coordinates by employing of finite volume method. The simplified version of these equations is presented in Eqs. (1) to (3):

$$\frac{\partial {u}_{j}}{\partial {x}_{j}} = 0$$

(1)

$$\frac{\partial {u}_{i}}{\partial t}+{u}_{j}\frac{\partial {u}_{i}}{\partial {x}_{j}} = -\frac{1}{\rho }\frac{\partial P}{\partial {x}_{i}}+\frac{\mu }{\rho }\frac{{\partial }^{2}{u}_{i}}{\partial {x}_{j}^{2}}+{g}_{i}$$

(2)

$$\frac{\partial T}{\partial t}+{u}_{j}\frac{\partial T}{\partial {x}_{j}} = \alpha \frac{{\partial }^{2}T}{\partial {x}_{j}^{2}}$$

(3)

where ${u}_{i}$ and ${g}_{i}$ are the fluid velocity and the gravitational acceleration in ${x}_{i}$-direction, $P$ is the pressure and $T$ stands for the temperature.

In Table 1 the saturated temperature of the surrounding vapor (${T}_{sat}$) has been provided. By employing this temperature and also Eq. (5), it would possible to calculate the capillary temperature (T_cap). Additionally, heat transfer coefficient (h) has been calculated utilizing Eq. (1).

$${T}_{cap} = {T}_{sat}\left(1-\frac{2\sigma }{r{h}_{lv}\rho }\right)$$

(4)

In Eq. (4), σ (N/m), r (m), $h$_lv (J/kg) and $\rho$ (kg/m³) represent surface tension, droplet radius, the latent heat of vaporization, and liquid density, respectively.

Also, the dimensionless number of Nusselt implies the ratio of convective heat transfer to conductive heat transfer within a fluid.

$$Nu = \frac{hd}{K}$$

(5)

In Eq. (5), h is the heat transfer coefficient (W/m² K), d is the height of the droplet (m) and K is the thermal conductivity of the fluid (W/m K).

Boundary conditions

In this study, unsteady, 3D, coupled Navier-Stokes and energy equations are solved. Also, on the solid surface, the Dirichlet boundary condition (${T = T}_{w}$) has been considered. In addition, the Robin boundary condition (HTC = h_i) and $T = {T}_{cap}$ have been applied in the droplet interface with the surrounding. In Figs. 3 and 4, the applied boundary conditions for the liquid droplet on the inclined and rough surface can be seen, respectively.

Fig. 3

The selected boundary conditions for a droplet on surface with inclination angle of $\beta$.

Fig. 4

The selected boundary conditions for a droplet on a grooved surface.

Numerical model

For solving the governing equations, the second-order upwind method in a pressure-based CFD solver was utilized. Additionally, the semi-implicit method for pressure‐linked equations (SIMPLE) algorithm was considered in order to couple pressure and velocity fields.

Grid analysis

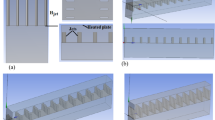
Generating a proper mesh structure for a studied domain can be quite significant since it can influence the spent time and the final results. Thus, mesh generation was well applied in this research. The blockMesh utility was utilized for creating the most suitable mesh in this study. The generated grids for the liquid droplet on a solid surface with an inclination angle and a rough surface, are given in Figs. 5 and 6, respectively from different perspectives. The grids are unstructured and generated with tetrahedral elements.

Fig. 5

The generated grid for a liquid droplet on an inclined surface with β  =  30° at diverse views, (A) X–Z plane (Y  =  0), (B) X–Y plane (Z  =  0).

Fig. 6

The generated grid for a liquid droplet on a grooved surface with r_i = 0.4 at diverse views, (A) X–Z plane (Y  =  0), (B) X–Y plane (Z  =  0).

A key portion of the simulation approach is the grid generation, since it influences the solution, convergence and time. As it is depicted in Fig. 7, the mesh independency was carried out for the internal temperature of the liquid droplet on an inclined solid surface against its height. Based on the results, a mesh of 1.2 million elements was chosen to continue the research for the droplet on the inclined surface due to a lower computational cost that it causes. Also, Fig. 8 exhibits the mesh independency for the internal temperature of the liquid droplet on a rough surface. According to Figs. 8 and 80 thousand elements have been utilized.

Fig. 7

Temperature profile in the midline of the droplet (X–Y plane, Z  =  0) against the droplet height for various mesh sizes ranging from 1.2 to 2.4 million elements for contact angle (θ)  =  110°, V  =  20 µl, ${T}_{sat}$ = 313 K, $\varDelta T$ = 10 K, $\widehat{\sigma }$ = 0.04, δ_w  =  1 mm, δ_c  =  10 μm, ${K}_{c}$ = 0.2 W/m K and ${K}_{w}$ = 180 W/m K.

Fig. 8

Temperature profile against droplet height in the midline of the droplet (X–Y plane; Z  =  0) for disparate grid sizes and for $V = 4 {\upmu }\,\text{l}$, $Pr = 4.32$, ${T}_{sat} = 313 \,\text{K}$, $\varDelta T = 10 \,\text{K}$, ${r}_{i} = 0.6$ and $\theta = 160^\circ$.

Model validation

The validation of this work has been done by comparison of the obtained outcomes from SE software to an empirical work, as well as the results from the CFD solver with both theoretical and experimental works. For validating the obtained simulated droplet shape achieved from the SE software, the shape of a droplet in an experimental work investigated by Annapragada et al.³⁴ has been compared with the derived droplet shape in the present research. As shown in Fig. 9, the results of the comparisons are quite satisfactory.

Fig. 9

The comparison of the obtained simulated droplet shape from SE software with an experimental work for a liquid water droplet with β  =  15°, $V$ = 10 µl and ${T}_{sat}$ = 313 K.

In order to evaluate the average heat flux through a single droplet, Baghel et al.²⁰ in a numerical investigation simulated a liquid droplet with V  =  3.59 µl at different contact angles. The present study has considered a droplet under the same conditions using SE software, as shown in Fig. 10 (A). The compared results of the two works demonstrate a good agreement. To ensure accuracy, the CFD results were also compared with Rajkumar et al.’s experimental work³⁵. Their study focused on the effect of subcooling degree on the heat transfer coefficient for a single droplet. The results showed that the HTC decreases with an increase in the subcooling degree. This research simulated the same droplet under the same conditions and compared it to Rajkumar’s work. As depicted in Fig. 10 (B), the results of these two works are in acceptable agreement.

Fig. 10

Validation of the present study with the available data of (A) Baghel et al.²⁰ at $V = 3.59 {\upmu }\,\text{l}$, ${T}_{sat} = 313\,\text{K}$, $\varDelta T = 10 \,\text{K}$, $\widehat{\sigma } = 0.04$, $\beta$ = 0°and ${r}_{i} = 0$, (B) Rajkumar et al.³⁵ at $V = 10 {\upmu }\,\text{l}$, $\beta$ = 0°and ${r}_{i} = 0$.

Result and discussion

In the current research, the influence of Nusselt number on the heat transfer rate as well as temperature distribution inside a single liquid droplet on both an inclined surface with different inclination angle and a rough surface with different roughness index has been investigated. The impact of other variable including contact angle, saturation temperature and Pr number have also been studied.

The influences of Nusselt number on average heat flux for a single droplet on an inclined surface

Nusselt number is a non-dimensional number which is determined as the ratio of convective to conductive heat transfer. A higher Nu number yields a higher HTC (Eq. (1)). In this part the Nu number effect on the average heat flux for a droplet on an inclined surface at four diverse Nu numbers has been studied. As it is depicted in Fig. 11A, by increasing the Nu number from 510 to 740 for the water droplet at β  =  90°, the average heat flux increases by 151.79%. This result implies that when the connective heat transfer is dominant at the interface of the liquid and the solid surface, the average heat flux gets more influenced by it compared to conductive heat transfer. Another important point that can be noticed in Fig. 11A, is that increasing the Nu number does not cause the impact of the angle of inclination to become significant as for Nu  =  740, the average heat flux increases by 4.29% from β  =  0° to β  =  90°. This number for Nu numbers equal to 660, 580 and 510 is 4.28%, 4.22% and 5.91% respectively. In Fig. 11B the effect of Nu number average heat flux for an Ethylene Glycol droplet on an inclined surface has been studied. For this fluid it is realized that the Nu number has a greater impact on the average heat flux as the average heat flux increases by 8.73% from β  =  0° to β  =  90° which for Nu numbers equal to 660, 580 and 510 it is 8.67%, 8.64% and 8.58% respectively. Additionally, by comparing Fig. 11A with Fig. 11B it can be noticed that increasing the Pr number would result in decreasing the average heat flux where as an example at Nu  =  740 and β  =  90°, the average heat flux for water is 123.45% greater than the one for Ethylene Glycol. The impact of inclination angle on average heat flux at diverse Nu numbers for Ethylene Glycol is also more noticeable than water.

Fig. 11

Average heat flux versus angle of inclination at different Nu numbers at θ  =  110°, V  =  20 µl, $\widehat{\sigma }$ = 0.04, δ_w  =  1 mm, δ_c  =  10 μm, ${K}_{c}$ = 0.2 W/m K and ${K}_{w}$ = 180 W/m K, (A) Water (${T}_{sat}$ = 313 K) and (B) Ethylene Glycol (${T}_{sat}$ = 295 K).

The influences of Nusselt number on average heat flux for a single droplet on a rough surface

As it was mentioned previously, a rough surface can improve the chance of DWC to occur. In this section the effect of Nu number on a single droplet on a rough surface for different roughness indexes (${r}_{i}$) and contact angles has been investigated. Figure 12 presents variations of average heat flux against contact angle at diverse Nu numbers. As it can be inferred in Fig. 12, increasing the Nu number in all roughness indexes results in increasing the average heat flux. An important point that can be derived from Fig. 12 is that when the roughness index increases, the impact of Nu number on the average heat flux virtually stays the same. To be more specific, by increasing Nu  =  510 to Nu  =  740 at θ  =  160°, in all three roughness indexes, the average heat flux increases by almost 152%. It is worth noting that when examining each of the cases separately, in the scenario where ${r}_{i}$ is equal to 0 and the angle rises from θ  =  90° to θ  =  160°, the average heat flux increases by approximately 35.7%. For ${r}_{i}$ values of 0.4 and 0.6, the corresponding increase in average heat flux is 29.25% and 22.8%, respectively. This result indicates that by making a surface rougher, even though the chance of DWC increase but the impact of the Nu number on the average heat flux decreases and no significant improvement should be expected.

Fig. 12

Variation of average heat flux against contact angle at diverse Nu numbers at V  =  4 µl, $\widehat{\sigma }$ = 0.04, δ_c  =  10 μm, ${K}_{c}$ = 0.2 W/m K, β  =  0° and ${T}_{sat}$ = 313 K, (A) ${r}_{i}$ = 0, (B) ${r}_{i}$ = 0.4 and (C) ${r}_{i}$ = 0.6.

The effect of saturation temperatures on average heat flux for a water droplet on an inclined surface

Discovering how saturation temperature can influence the average heat flux for a water droplet on an inclined surface at different Nu numbers is the subject of this section. Five different saturation temperature have been studied and the achieved results have been compared and analyzed. Figure 13 shows the change in the average heat flux at different saturation temperatures. As it can be noticed, the augmentation of the saturation temperature leads to an augmentation in the average heat flux at all $Nu$ numbers. Even though increasing the $Nu$ number has resulted in higher average heat flux but it is important to understand that at any particular Nu number, the average heat flux increase with an almost constant trend. To be more clear, taking ${T}_{sat}$ = 313 K into consideration, at all four different Nu numbers the average heat flux increases by 4.3% from β  =  0° to β  =  90°. This trend is accurate and almost the same for all the other four saturation temperatures. At a constant Nu number, $Nu$ = 740 as an instance, average heat flux increases by 4.7% from ${T}_{sat}$ = 290 K to ${T}_{sat}$ = 313 K at any specific inclination angle.

Fig. 13

Average heat flux against angle of inclination for diverse saturation temperatures at $\theta = 110^\circ$, $V$ = 20 µl,${\delta }_{c}$ = 10 μm, $\widehat{\sigma }$ = 0.04, ${\delta }_{w}$ = 1 mm, ${K}_{c}$ = 0.2 W/m K and ${K}_{w}$ = 180 W/m K (A) $Nu$ = 740, (B) $Nu$ = 660, (C)$Nu$ = 580 and (D) $Nu$ = 510.

The effect of saturation temperatures on average heat flux for a water droplet on a rough surface

In this section the effect of saturation temperature on the average heat flux for a water droplet on a rough surface with the roughness indexes of 0, 0.4 and 0.6 while considering four different Nu numbers, has been investigated. As it is depicted in Fig. 14, increasing the contact angle, as well as the $Nu$ number results in increasing the average heat flux. By comparing the four presented charts in Fig. 14 it can be concluded that enhancing the Nu number from 510 to 580, 660 and 740, will cause the average heat flux to improve by 51%, 101% and 151%, respectively. Another point that Fig. 14 presents is that the highest value of the average heat flux at a particular Nu number is still lower than the lowest value at its proceeding Nu number which implies that a slight improvement in the $Nu$ number can increase the heat transfer rate inside the liquid droplet on a grooved surface.

Fig. 14

Variations of average heat flux against contact angle for diverse saturation temperatures at $V$ = 4 µl, $\widehat{\sigma }$ = 0.04, δ_c  =  10 μm, ${K}_{c}$ = 0.2 W/m K, β  =  0°and ${r}_{i}$ = 0.6, (A) $Nu$ = 740, (B) $Nu$ = 660, (C) $Nu$ = 580 and (D) $Nu$ = 510.

The impact of saturation temperatures on temperature distribution for a water droplet on an inclined surface

Temperature variation inside the liquid droplet can present valuable information regarding the point that if the temperature distribution is uniform or not which can be useful in assessing the heat transfer rate inside the droplet. In the following sections the change in temperature profile against droplet height will be studied at different Nu numbers and for both inclined and rough cases. In Fig. 15, it can be seen that the temperature does not increase with a virtually steady rate towards the interface of the liquid with the vapor surrounding it. This basically implies that the temperature profile cannot be considered uniform and thus, there will be heat transferring inside the droplet which its value gets influenced by the difference between the saturation temperature and the solid surface temperature. Consequently, when the Nu number decreases the temperature distribution gets more uniform which results in a less amount the average heat flux. Regarding to the visible trend in Fig. 15, it can be asserted that for a liquid droplet with its unique conditions there will be a particular Nu number which for values less than that number the heat transfer is neglectable²⁸.

Fig. 15

Variation of temperature versus droplet height for diverse saturation temperatures at $\theta$ = 110°, β  =  90°, $V$ = 20 µl, $\hat {\sigma }$ = 0.04, δ_w  =  1 mm, δ_c  =  10 μm, ${K}_{c}$ = 0.2 W/m K and ${K}_{w}$ = 180 W/m K (A) $Nu$ = 740, (B) $Nu$ = 660, (C) $Nu$ = 580 and (D) $Nu$ = 510.

The impact of saturation temperatures on temperature distribution for a water droplet on a rough surface

Figure 16 illustrates that for the considered saturation temperatures, the temperature increases until almost half of the droplet height and then becomes steady towards the interface of the droplet. This suggests that the effect of the released heat during the DWC process diminishes moving from the droplet’s interface with the vapor towards its interface with the solid surface. By comparing the four presenting charts in Fig. 16, it would be obvious that by increasing the Nu number the heat transfer rate increases as well, which eventually results in a higher average heat flux.

Fig. 16

Variation of temperature against droplet height for different saturation temperatures at $\theta = 160^\circ$, $V$ = 4 µl, $\widehat{\sigma }$ = 0.04, δ_c  =  10 μm, ${K}_{c}$ = 0.2 W/m K, β  =  0° and ${r}_{i}$ = 0.6 (A) $Nu$ = 740, (B) $Nu$ = 660, (C) $Nu$ = 580 and (D) $Nu$ = 510.

Conclusions

In this work a computational fluid dynamics study has been investigated to scrutinize the impact of the Nusselt number on the average heat flux for a liquid droplet on an inclined and rough surface. For simulating the geometry of the droplet on the surface, Surface Evolver software and a CFD solver were employed. Different variables including surface inclination angle, contact angle, saturation temperature and roughness index were studied along with the Nu number to evaluate the heat transfer passing through the droplet. The obtained results indicated that by raising the Nu number the average heat flux increases for a droplet on both the inclined and rough surfaces. On the inclined surface for Nu < 740, the impact of angle of inclination on the average heat flux is not quite considerable (less than 4.29% for a water droplet). On the contrary, for a droplet on the rough surface the influence of contact angle on the average heat flux noticeably increases while the Nu number improves. For a droplet on the inclined surface at any particular Nu number, the increase of the saturation temperature has a similar trend on the average heat flux in which from β  =  0° to β  =  45° the average heat flux remains virtually constant but from β  =  45° to β  =  90° the increase in the average heat flux becomes significant. This trend for a droplet on a grooved surface is in the way that from θ  =  90° to $\theta$ = 125°, the average heat flux increases while from $\theta$ = 125° to $\theta$ = 160°, the average heat flux does not change remarkably. Besides, studying the temperature profiles for both the inclined and rough cases showed that when the Nu number increases the temperature profile becomes less uniform suggesting a higher heat transfer rate passing the droplet and thus, a larger value for the average heat flux.