Introduction

Neutron techniques have become attractive and essential for various applications. Cold and thermal neutrons are widely used in neutron scattering, diffraction, imaging, and activation analysis1,2,3,4, while fast neutrons are of particular interest in several scientific and technological applications such as radiotherapy, nuclear safeguards, radiation protection, astrophysics, and underground physics5,6,7,8,9. One of the key factors for using fast neutrons is the knowledge of neutron spectrum and flux. However, measuring fast neutron spectrum and flux has been quite challenging because neutrons are neutral particles not directly measured by radiation detectors. The Time of Flight (ToF) technique is one approach that can measure neutron energy straightforwardly but it requires complex experimental setups and exhibits low efficiency. Another typical approach is applying unfolding techniques to convert a spectrum of neutron-induced secondary particles to the incident neutron spectrum with a prior understanding of the detector response.

Neutron spectrum unfolding is usually a sophisticated technique. Many research groups have been studying unfolding algorithms and achieved imperfect but encouraging results. Some groups worked with simulation data10,11, while others dealt with actual measured spectra12,13,14. The unfolding of actual measured spectra requires a more comprehensive effort, combining experimental measurements, calibration, simulation, mathematical algorithms, and validation. For example, gamma background rejection is necessary to avoid false classification between neutron and gamma events, while energy calibration is critical for accurate measurements.

We made one attempt to unfold neutron spectra observed by a state-of-the-art solution-grown trans-stilbene detector and obtained results that were close to the standard spectra15. Trans-stilbene is very attractive for neutron detection applications in mixed gamma-neutron fields since it has an excellent Pulse Shape Discrimination (PSD) capability for neutron-gamma separation. Moreover, high-quality stilbene single crystals have recently been successfully grown by the solution technique, which improves the crystal optical transparency, light output, and PSD16. However, we observed the light yield nonproportionality of the stilbene and the Photomultiplier Tube (PMT) nonlinearity effect in the previous study, which could affect the energy calibration. The current study reports the measurement and correction of these effects to improve our unfolding results. One another dificulty of using a stilbene detector to unfold neutron spectra is about its Proton Response Function (PRF), which may show a complex dependence on (i) the geometry of the scintillator; (ii) the specific scintillator-photomultiplier combination; (iii) the signal processing method; (iv) the total charge integration window, and particularly (v) the angle-dependent anisotropy of stilbene17,18,19,20,21. To find out a PRF for our unfolding procedure, we characterized the PRF of our stilbene scintillator by proton beam test experiments and a ToF measurement. The direction of the proton beam and the head-on recoiled protons of the ToF measurement was designed to be parallel to the scintillator axis. The PRF was then used for neutron spectrum unfolding using the iterative Bayesian method, which provides a natural approach based on the probability theory. The same unfolding procedure was applied for both Cf-252 and AmBe neutron sources without any constraints, smoothness or assumption of prior knowledge of original spectra.

Instrumentation and methods

Stilbene and data acquisition system (DAQ)

The solution-grown stilbene crystal (Φ3.81 × 3.81 cm) was purchased from Inrad Optics. The experimental setups for AmBe and Cf-252 neutron spectrum measurement and unfolding were described in detail in our previous paper15. The data acquisition system (DAQ) included the following equipment: an R6233-100 PMT, a 500 Mega samples per second (MSPS) sampling rate Flash Analog to Digital Converter (FADC500, Notice company, Korea), and a control computer with a custom acquisition software. The computer was operated in linux system with a ROOT package22. The same DAQ was used for the R6233-100 PMT nonlinearity characterization and proton beam test experiment. H7195 PMTs, due to their fast timing characteristics and good linearity response, were used in the ToF experiment instead of the R6233-100 PMTs. A total integration window of 400 ns was applied for all PMT waveforms of gamma and neutron in relevant experiments. The PMTs were operated at negative supply voltages. The PSD ratio for particle identification was defined as a ratio between the delay charge and the total charge. Depending on the DAQ setup, the delayed integration gate was optimized at 16 ns, 24 ns, and 36 ns for the ToF experiment, the neutron spectrum measurement, and the proton beam test experiment, respectively.

PMT nonlinearity characterization

The nonlinearity response of the R6233-100 PMT was measured using an LED, which emits photons of 450 nm wavelengths. The LED was coupled with an integrating sphere, and emitted photons were transferred to the PMT through an optical fiber. The LED was operated in pulse mode provided by a 33250A Agilent waveform generator. The pulse width was kept at a constant of 15 ns, and the edge time was 5 ns to emulate radiation signals. The LED optical power was varied by changing its supply voltage and monitored by a PM400 projected capacitive touchscreen optical power and energy meter. PMT signals caused by the LED were then compared to the monitored values to investigate its nonlinear behavior quantitatively.

Proton beam test

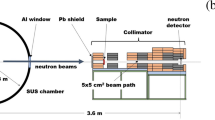
The measurement of the proton response of the 1.5-inch trans-stilbene scintillator in the high energy region between 10 and 25 MeV was performed at the Korea Institute of Radiological and Medical Sciences (KIRAMS) using a 45 MeV proton beam. The beam current was 1 nA. A 0.5 mm diameter pinhole was used to reduce the number of incident protons, avoiding a high pile-up rate in the measurement. Several Al degraders with different thicknesses from 1.5 to 3.5 mm were used to vary proton energy (Ep). In each configuration, the FADC500 was working in a fast mode, saving a total of about 100,000 pulses of 2 µs window length each pulse in less than 0.5 s without dead time. In the later off-line analysis, the integration window of 400 ns was used and a filter algorithm was applied to partially reject pile-up pulses. The energy deposited by protons into the stilbene detector was obtained by simulation. The PMT was operated in low gain mode with a supply voltage of 540 V to avoid saturation.

ToF experiment

Figure 1 presents the ToF experiment, which was performed at a dedicated neutron irradiation room of the Korea Research Institute of Standards and Science (KRISS)23. To reduce the effects of scattered neutrons from the wall, root, and floor, an AmBe source with an emission rate of 6.6 × 105 n/s was placed at the center of the radiation room, 8.0 × 6.6 × 6.4 m3. The stilbene was placed 200 cm in front of the source. Besides, two PbWO4 crystals (6 × 2 × 2 cm3) were put 6 cm behind the source to detect gamma coincidence events. PbWO4 was selected because of its high gamma detection efficiency and fast decay time. The two PbWO4 crystals were coupled to an H7195 PMT, and the stilbene was coupled to another H7195 PMT. PbWO4 is sensitive to gamma, while stilbene is sensitive to both gammas and neutrons. Therefore, we can observe not only photon-neutron but also photon-photon coincidence. The photon-photon coincidence was used for photon-neutron coincidence timing calibration.

Fig. 1
figure 1

ToF experimental setup at KRISS.

Full size image

Simulation and unfolding

The simulation model, Compton edge fitting, and spectrum unfolding were similar to our previous work15. The idea for Compton edge fitting was from Arneodo et al.24, and the unfolding technique was based on the iterative Bayesian method25. The general schema of the unfolding procedure is illustrated in Fig. 2. A small update in this work is that we investigated and applied a stop condition for the unfolding iteration, as will be discussed later in Section "Unfolding results". We used PHITS and MCNP simulation programs26,27 to support our study in this work instead of the Geant4 toolkit28, which was used in the previous study, because of a slight improvement observed in Compton edge fitting. PHITS and MCNP programs generated almost identical results in gamma and proton simulation. In the final step, only MCNP was used to simulate neutron spectra, which was considered time-consuming.

Fig. 2
figure 2

General schema of the iterative Bayesian unfolding method.

Full size image

Results and discussion

PMT nonlinearity characterization

The dependence of LED optical power on supply voltage is presented in Fig. 3a. It is obvious that the optical power increases with the increase of the supply voltage, but they do not follow a linear relationship. Therefore, only optical power, not supply voltage, was valid for characterizing PMT nonlinearity. In addition, PMT signals caused by LED were compared with those produced by stilbene under gamma and neutron excitations in Fig. 3 (b). Their rising and falling edges around the peak intensity were almost identical, indicating that the nonlinearity response of the PMT to the LED signals may also represent the nonlinearity response of the PMT to stilbene scintillation signals.

Fig. 3
figure 3

(a) Dependence of LED optical power on supply voltage and (b) LED waveform in comparison with gamma and neutron waveforms.

Full size image

Figure 4a illustrates the nonlinearity response of the R6233-100 PMT at different supply voltages. The measured ADC channel, representing the PMT output charge, was proportional to the LED optical power at supply voltage levels where the optical power was lower than a critical threshold. In these regions, each data set was fitted with a linear function \(y=ax\), which represents an expected linear relationship. The ADC channels dropped from the corresponding fitting lines when the optical power increased. The higher the optical power, the more deviation from linear was observed. The nonlinearity also depends on supply voltage, or in other words, the PMT gain, as shown in Fig. 4b. The variation is negative, meaning that the measured ADC channel is less than the expected ADC channel. This effect is well-known as the charge density effect during the electron multiplicating process inside a PMT. We used an empirical fitting function to make corrections to this effect as follows: \(y=exp\left[a{(x-b)}^{c}\right]\), where \(x\) represents the measured ADC channel, \(y\) represents the correction factor (\(y\) = Expected ADC Channel/Measured ADC Channel), and \(a\), \(b\) and \(c\) are fitting parameters. When \(x\le b\), the correction factor is set to 1, and nonlinearity becomes negligible. The fittings agreed well with the experimental data, as shown in Fig. 5, and were used for PMT nonlinearity correction. However, it was used for interpolation but not extrapolation to avoid any overestimation or underestimation. The consistency in stilbene nonproportionality in section "Stilbene nonproportionality and energy calibration" provided evidence to validate the PMT nonlinearity correction procedure.

Fig. 4
figure 4

PMT nonlinearity observed at different supply voltages. (a) Measured ADC channels deviated from expected (black solid lines) linear relationship. (b) Variation = (Measured ADC Channel—Expected ADC Channel)/Expected ADC Channel was plotted versus the Measured ADC Channel.

Full size image
Fig. 5
figure 5

Fitting for PMT nonlinearity correction factors.

Full size image

Stilbene nonproportionality and energy calibration

The nonproportionality of the detector system before and after PMT nonlinearity correction is shown in Fig. 6a,b, respectively. The nonproportionality in Fig. 6a combines two sources, including PMT nonlinearity and stilbene nonproportionality. After PMT nonlinearity correction, as described in section "PMT nonlinearity characterization", the results in Fig. 6b represent only stilbene nonproportionality. The consistency was observed in stilbene nonproportionality measured at different voltages. The result from the H7195 PMT was included without any correction. The H7195 PMT was working at 1180 V, which is much lower than its typical and maximum supply voltages of 2000 V and 2700 V, respectively. Consequently, the anode nonlinearity effect was observed as negligible for the H7195 PMT in this energy range. Our data was in excellent agreement with reported data by S. A. Payne et al. up to 0.662 MeVee29. However, we also observed the falling of the nonproportionality curve at the high energy tail, provided by the data around 1 MeVee (from Zn-65 and Na-22) and 4 MeVee (from the AmBe source). Nonproportionality of electron light production in organic scintillators is usually observed significant at low energy (< 662 keVee), while nonproportionality at higher energies is typically due to the PMT response. The reason for the downtrend observed by the H7195 PMT is suggested to be the nonlinearity of cathode response at low supply voltages and large currents. Meanwhile, the downtrend of the 700 V corrected data is supposed to be caused the extrapolation of the expected linear curves. To compensate for this downtrend, a second-order polynomial in log scale of energy was used for fitting, as suggested by Jaffe et al.30. The fitting agreed well with the experimental data, where the difference between them did not exceed 2%, as shown in Fig. 6b.

Fig. 6
figure 6

Nonproportionality (a) before and (b) after PMT nonlinearity correction. The nonproportionality at 0.662 MeVee was normalized to 100%. Connection lines in (a) are shown for visualization. Data at 1180 V in (b) is from an H7195 PMT.

Full size image

Because of the nonproportionality of the scintillator, using a simple linear function for energy calibration may result in a bias30, particularly in the high-energy region. Therefore, we examined several functions for the energy calibration and used the nonproportionality fitting curve above to evaluate its performance as illustrated in Fig. 7. Four functions to be examined were (i) \(y=ax+b\) (linear), (ii) \(y=a{x}^{2}+bx+c\) (poly2), (iii) \(y=x\left[a{log(x)}^{2}+blog(x)+c\right]\) (log), and (iv) \(y=\sqrt{a{x}^{3}+b{x}^{2}+cx+d}\) (root). As can be seen, none of the functions can describe the nonproportionality in a wide energy range from tens keVee to tens MeVee. However, all of them can be used in a specific energy range without any remarkable difference, for example, between 0.4 MeVee and 6 MeVee in the case of 700 V and between 0.05 MeVee and 1 MeVee in the case of 1100 V. In the case of 700 V, there was one crucial concern when extrapolating to a high energy value: the linear calibration was broken out at around 7 MeVee. In contrast, the others followed the general trend of the fitting curve. In this case, we used the root function, which showed the best agreement to the nonproportionality fitting curve. It is noted that there could be a bias of around -10% at 20 MeVee if the linear function was used in this energy calibration.

Fig. 7
figure 7

Energy calibration functions and corresponding nonproportionality behavior at 700 V and 1100 V. Nonproportionality at 700 V and 1100 V was fixed at 0.662 (conventional) and 0.200 (a selected experimental data point) MeVee, respectively.

Full size image

Proton beam test

Figure 8a presents the PSD diagram of the beam test experiment using a 2.5 mm thick degrader. The proton events were observed with a PSD ratio of around 0.19, while the band of background gamma was located lower at a PSD ratio of 0.11. The proton peaks were clearly seen between 10 and 12 MeVee, accompanied by pile-up events. A PSD ratio between 0.16 and 0.22 was applied to partially reject background gamma and pile-up. The proton peak was then obtained and fitted with a Gaussian peak and an exponential function, accounting for the low energy tail in the spectrum. The procedure was repeated for the data of different degrader thicknesses, as shown in Fig. 8b. Applying thicker degraders resulted in the lowering of proton peak energy and the broadening of the peak due to the straggling effect. The lowest energy of 6.5 MeVee was observed under the 3.5 mm thick degrader. We also made attempts with thicker degraders, but proton peaks were not clearly seen. Meanwhile, the highest energy peak of 15.0 MeVee was observed under 1.5 mm thick degradation, but it was unexpectedly broader than the others. The reason was unknown and may be from a fluctuation in the proton beam energy.

Fig. 8
figure 8

(a) PSD diagram of proton beam measurement using 2.5 mm degrader and (b) Proton peaks observed under various degrader thicknesses.

Full size image

On the other hand, the proton energy deposited into the scintillator volume was investigated by simulation. The simulation schema and results are shown in Fig. 9. The attenuators that decrease the proton energy are listed as follows: Al beam exit window (0.2 mm), dry air (230 cm), Al degrader (1.5–3.5 mm), Al detector housing (3.0 mm) and Teflon reflector (0.4 mm). In the simulation, only straggling during the transport of protons was considered for the smearing effect. The energy peaks were between 10 and 25 MeV. Finally, the high-energy proton response was obtained as a combination of the simulated deposited energy and the measured equivalent energy (Eee). The energy peaks and their Full Widths at Half Maximum (FWHMs) are show in Table 1. Even though the values of the FWHMs are similar between the simulation and experiment (except for the case of the 1.5 mm degrader thickness as described above in this Section), the FWHMs are presented in different units (MeV and MeVee). If we assume a local linear relationship between Ep and Eee, the estimated FWHMs in term of MeVee will be less than the observed FWHMs. For example, the 1.9 MeV FWHM will correspond to 1.1 MeVee, which is less than the observed FWHM of 2.0 MeVee. This can be explained by the simplification in the simulation model, which did not account for the divergence of the proton beam energy and the finite detector resolution. However, as stated above, this is only a rough estimation using a linear relationship between Ep and Eee. The actual relationship between Ep and Eee will derived later in Section "Proton response function".

Fig. 9
figure 9

Simulation schema and results for energy proton deposited into the scintillator volume.

Full size image
Table 1 Proton beam test results.
Full size table

ToF

The FADC500 has a 500 MHz sampling rate (2 ns per sample), which is not fine enough for the timing resolution required in this ToF experiment, particularly for high-energy neutrons. For example, a 6 MeV neutron travels a 200 cm distance in 59.0 ns, while the time required for a 7 MeV neutron to travel the same distance is 54.7 ns. Therefore, we applied a new approach to improve the timing resolution of the ToF experiment, as presented in Fig. 10. First, the rising edge of each waveform and a few sampling points of its falling edge were detected and fitted with a Gaussian function. A timing point of the waveform was defined in the Gaussian curve by a timing factor, which is a relative height to the maximum of the Gaussian peak, see Fig. 10a. Each time difference (TD) spectrum was extracted for each timing factor, ranging from 0.1 to 0.9, and the corresponding FWHM of the photon-photon coincidence peak was evaluated. As shown in Fig. 10b, the best timing resolution was observed at 0.3 timing factor, where FWHM was 1.3 ns. The TD spectrum under the optimized timing factor is presented in Fig. 10c, where the photon-photon coincidence peak was found at 37.3 ns.

Fig. 10
figure 10

Timing scheme of the ToF experiment. (a) Definition of the time difference between the waveforms, (b) optimization of timing resolution upon timing factor, and (c) Timing spectrum under the optimized timing factor of 0.3.

Full size image

Consequently, the ToF of a neutron was calculated as follows:

$${\text{ToF }} = {\text{ T}}_{{1}} - {\text{T}}_{0} = \left( {{\text{T}}_{{1}} - {\text{T}}_{{2}} } \right) + \left( {{\text{T}}_{{2}} - {\text{T}}_{0} } \right)$$

where T0 is the starting time, and T1 and T2 are the time a neutron or gamma reaches the stilbene detector after traveling a distance of 200 cm, respectively. T2 − T0 is a constant of 6.7 ns, while the (T1 − T2) is measurable by comparing the TD of scintillation signals:

$$\begin{gathered} {\text{T}}_{{1}} - {\text{T}}_{{3}} + {\text{offset}} = {\text{TD}}_{{{\text{neutron}}}} \hfill \\ {\text{T}}_{{2}} - {\text{T}}_{{3}} + {\text{offset}} = {\text{TD}}_{{{\text{gamma}}}} = { 37}.{\text{3 ns}} \hfill \\ \end{gathered}$$

where T3 is the time a coincident gamma reaches the PbWO4 detector, and offset represents any differences between the PbWO4 and stilbene detectors due to cable length, electronics, and PMT transition time.

We finally derived the following equation:

$${\text{ToF}} = {\text{TD}}_{{{\text{neutron}}}} {-}{ 3}0.{\text{6 ns}}$$

The ToF was used to derive the energy of the incident neutrons and construct a correlation diagram between the neutron energy and measured equivalent energy, as shown in Fig. 11a.

Fig. 11
figure 11

(a) Correlation diagram between neutron energy and equivalent energy with an estimated separation edge, and (b) PSD diagram observed by Stilbene detector and cutting conditions to reject gamma events.

Full size image

The PSD diagram for the stilbene detector in Fig. 11b was used to reject gamma events by setting a low PSD ratio limit of 0.35 and 0.31 for events with energy higher and lower than 0.5 MeVee, respectively. The false identification of neutron and gamma at low energy was unavoidable but considered negligibly. However, a nonnegligible effect may lead to a wrong calculation of the incident neutron energy. It can be seen in Fig. 11a that most of the events between 2.5 and 3.0 MeVee were observed for incident neutrons below 5 MeV but not above 6 MeV by the general trend. The possible reason is that the real coincidence gammas of these neutrons were missed, and the detected gammas were actually emitted from the previous reactions. The reasons for missing a real coincidence gamma in the gamma detector could be as follows: (i) the gamma was not directed to the detector, (ii) the gamma passed through the detector without any interaction, or (iii) a gamma-less reaction emitted neutron (> 6.6 MeV). This explanation also applied to all events observed below the separation edge in Fig. 11a. We considered this phenomenon for quasi-monoenergy neutron spectra of neutrons less than 4 MeV, where we used a linear background function to minimize its effect.

The smoothed quasi-monoenergy neutron spectra and corresponding recoil edge fittings are presented in Fig. 12. We fitted only the recoil falling edge but not the whole spectrum structure, and uniform distribution spectra of quasi-monoenergy incident neutron were used in the simulation. The fitting procedure was similar to those used in the gamma Compton edge fitting, where two parameters of spectrum scaling and broadening were scanned for optimum fitting performance. The simulated deposited energy and the measured equivalent energy around the fitting regions were used to investigate the proton response function in Section "Proton response function".

Fig. 12
figure 12

Extracted quasi-monoenergy neutron spectra and corresponding recoil edge fitting.

Full size image

Proton response function

The results collected from the proton beam test and ToF experiments are presented and compared with the data available in the literature in Fig. 13. Our ToF measurement was inspired by Tony H. Shin’s study19, and both data generally showed a good agreement with each other. However, it is worth noting that there were differences between the two measurements in the integration window (150 ns in Tony H. Shin’s work and 400 ns in this work) and the energy calibration procedure (light output relative to Cs-137 Compton edge without nonproportionality correction in Tony H. Shin’s work and electron equivalent energy in this work). On the other hand, our data at high energy were significantly larger compared with W. Hansen’s evaluation20. This could be an improvement due to the detailed investigations of nonproportionality and energy calibration. The reason may also be from the different properties of the stilbene crystals grown by different techniques. The combination of the ToF and beam test data was fitted by the following equation20:

$$y={p}_{1}{x}^{3}+{p}_{2}{x}^{2}+{p}_{3}x+{p}_{4}$$

where \(y\) =ln(Eee) and \(x\) =ln(Ep). Fitting results are \({p}_{1}\)= –0.0253, \({p}_{2}\)=0.0247, \({p}_{3}\)=1.67 and \({p}_{4}\)= –1.98. The fitting curve also agreed well with Tony H. Shin’s low energy data down to 0.8 MeV. On the high energy side, the fitting curve presents an almost simple linear relationship when proton energy is above 10 MeV. This curve was then used in the simulation to generate the detector response matrix for neutron spectrum unfolding. The detector response matrix also included the information of detection efficiency as well as energy resolution.

Fig. 13
figure 13

Proton response of stilbene.

Full size image

Unfolding results

Figure 14 presents the AmBe and Cf-252 neutron spectra measured by the stilbene detector in the equivalent energy scale. The spectra showed a small shift in the high energy region compared to the spectra in our previous study due to the new energy calibration procedure15. The spectra presented in Fig. 14 were used as inputs for the neutron spectrum unfolding.

Fig. 14
figure 14

AmBe and Cf-252 spectra in equivalent energy obtained by stilbene.

Full size image

The iteration of the unfolding procedure for the Cf-252 and AmBe neutron spectra is shown in Fig. 15. Both iterations started with a flat spectrum as prior, and the same stop condition was applied in both cases. The stop condition was selected based on our understanding of the statistical fluctuation of measured spectra, errors related to energy and timing calibration, and convergence power of the unfolding algorithm. First, every unfolded spectrum after the i-th steps was smeared by the detector response matrix and compared with the measured one. Then, the following two testing parameters for every data point were monitored:

Fig. 15
figure 15

Unfolding procedure for AmBe and Cf-252 neutron spectra.

Full size image
$$Ratio=\left|\frac{Smeared-Measured}{Measured}\right|$$
$$Deviation=\left|\frac{Smeared -Measured}{\sqrt{Smeared}+\sqrt{Measured}}\right|$$

Each measured data point was considered to pass the test if \(Ratio\) < 4% or \(Deviation\) < 1. The iteration stopped when at least 96% of all data points passed the test, meaning that 4% of unpassed data points could be considered outliers. The unfolding of the Cf-252 spectrum rapidly converged after 14 steps, while those of the AmBe spectrum converged after 123 steps. This is understandable because the AmBe neutron spectrum structure is more complicated than those of the Cf-252 fission spectrum. Consequently, more iterations were required to construct neutron peaks of the AmBe source and its relative intensities.

Figure 16 compares our unfolding results and standard spectra of Cf-252 and ISO 8529-2 recommended AmBe neutron sources31,32. Our previous results and some of the best unfolding efforts by A. Sharghi Ido et al. and Y. Chen et al. are also presented13,14,15. In the case of Cf-252, our current unfolded spectrum was very similar to those from A. Sharghi Ido et al. Both spectra agreed well with the standard spectrum between 2 and 4 MeV. This good agreement was an improvement compared to our previous report. A deviation of around 10% to 30% from the standard spectrum was observed in all unfolded spectra from 4 to 10 MeV, but it did not change the general structure of the unfolded spectra. On the other hand, the noticeable deviation was in the low energy between 1 and 2 MeV because it changed the smooth Watt fission spectrum to a step-like curve.

Fig. 16
figure 16

Comparison of (a) Cf-252 and (b) AmBe spectrum unfolding results and standard spectra. Unfolded AmBe spectrum in this work was normalized to the standard spectrum by area above 1.2 MeV, others were normalized by their maximum.

Full size image

The deviation was also found in the unfolded AmBe spectrum at low energy. This can be explained by the low PSD performance, the experimental errors in spectrum acquisition, the positive feedback of the unfolding, and particularly the uncertainty in PRF, as observed in our previous study. This behavior may also link to the presence of 12C(n,α) reactions, which produce alpha with a reaction threshold around 6–7 MeV neutrons. The anisotropy also grows significantly at low energies, producing a large uncertainty in the relationship between light produces and neutron energy. As a result, the one-to-one relationship between light and energy represented by a single PRF becomes incorrect. In general, the discrepancy at low energy remains a common challenge in almost all fast neutron spectrum unfolding efforts. We suggest that a high-precision measurement of PRF below 2 MeV and an alpha rejection method may be helpful to overcome this problem. Apart from the low energy region, our current AmBe unfolded spectrum matched the standard spectrum in peak position and relative intensity. This shows a significant upgrade compared to the previous results for the intensities of neutron peaks of 4.9, 6.7, and 7.9 MeV. One of the best unfolding efforts for the AmBe neutron spectrum was made by Chen et al.13, as presented in Fig. 16. However, the peak between 6 and 7 MeV was not observed in their work, and all peaks were slightly broader than expected. Overall, our study proved a better unfolding performance, achieving results that were closer to the standard spectrum.

Conclusion

Herein, the PRF of solution-grown trans-stilbene in the energy range 1–25 MeV was measured and reported using a monoenergy proton beam and recoil protons from neutron scattering reactions. This study also investigated the PMT nonlinearity and the solution-grown trans-stilbene light yield nonproportionality. Semi-empirical fitting functions were proposed for the first time to correct these effects. A 1.3 ns FWHM timing resolution was achieved in the ToF experiment by applying a Gaussian fitting to the rising edge of the PMT output scintillation waveform. The measured PRF was applied to unfold neutron spectra of the Cf-252 and AmBe sources using the iterative Bayesian unfolding method. The unfolded spectra agreed well with standard spectra in overall spectrum structure, peak position, and relative intensities. It is understandable that the protons recoiled from neutron scattering are not isotropic. Therefore, using a single calibration PRF curve is generally not enough to describe the response of stilbene to neutrons. However, the discrepancy of the anisotropy could be limited, which can explain why our results remain close to the standard spectra. Overal, this study proposed one of the reliable unfolding approaches in recent years, which is promising for fast neutron spectroscopy.