Leveraging multi-source data and teleconnection indices for enhanced runoff prediction using coupled deep learning models

Abstract

Accurate medium- to long-term runoff forecasting is crucial for flood control, drought resilience, water resources development, and ecological improvement. Traditional statistical methods struggle to utilize multifaceted variable information, leading to lower prediction accuracy. This study introduces two innovative coupled models—SRA-SVR and SRA-MLPR—to enhance runoff prediction by leveraging the strengths of statistical and deep learning approaches. Stepwise Regression Analysis (SRA) was employed to effectively handle high-dimensional data and multicollinearity, ensuring that only the most influential predictive variables were retained. Support Vector Regression (SVR) and Multi-Layer Perceptron Regression (MLPR) were chosen due to their strong adaptability in capturing nonlinear relationships and extracting latent hydrological patterns. The integration of these methods significantly improves prediction accuracy and model stability. By integrating 80 atmospheric circulation indices as teleconnection variables, the models tackle critical challenges such as high-dimensional data, multicollinearity, and nonlinear hydrological dynamics. The Yalong River Basin, characterized by complex hydrological processes and diverse climatic influences, serves as the case study for model validation. The results show that: (1) Compared to baseline single models, the SRA-MLPR model reduced RMSE (from 798.47 to 594.45) by 26% and MAPE (from 34.79 to 22.90%) by 34%, while achieving an NSE (from 0.67 to 0.76) improvement of 13%, particularly excelling in extreme runoff scenarios. (2) The inclusion of teleconnection indices not only enriched the predictive feature set but also improved model stability, with the SRA-MLPR demonstrating enhanced capability in capturing latent nonlinear relationships. (3) A one-month lag in atmospheric circulation indices was identified as the optimal predictor for basin-scale runoff, providing actionable insights into temporal runoff dynamics. (4) To enhance model interpretability, SHAP (SHapley Additive exPlanations) analysis was employed to quantify the contribution of atmospheric circulation indices to runoff predictions, revealing the dominant climate drivers and their nonlinear interactions. The results indicate that the Northern Hemisphere Polar Vortex and the East Asian Trough exert significant control over runoff dynamics, with their influence modulated by large-scale climate oscillations such as the North Atlantic Oscillation (NAO) and Pacific Decadal Oscillation (PDO). (5) The models’ scalability is validated through their modular design, allowing seamless adaptation to diverse hydrological contexts. Applications include improved flood forecasting, optimized reservoir operations, and adaptive water resource planning. Furthermore, the study demonstrates the potential of coupled models as generalizable tools for hydrological forecasting in basins with varying climatic and geographic conditions. This study highlights the potential of coupled models as robust and generalizable tools for hydrological forecasting across diverse climatic and geographic conditions. By integrating atmospheric circulation indices, the proposed models enhance runoff prediction accuracy and stability while offering valuable insights for flood prevention, drought mitigation, and adaptive water resource management. These methodological advancements bridge the gap between statistical and deep learning approaches, providing a scalable framework for accurate and interpretable hydrological, climatological, and environmental predictions. Given the escalating challenges brought about by climate change, the findings of this study make contributions to sustainable water management, interpretable decision-making support, and disaster preparedness at a global level.

Introduction

Accurate and stable medium- to long-term runoff predictions are of great significance for flood management, drought scheduling, water resource optimization, and ecological sustainability¹. However, runoff formation is a highly complex process influenced significantly by climatic systems, such as atmospheric circulation and oceanic oscillations, as well as basin topography and human activities. These factors impart nonlinearity and nonstationarity to runoff processes². Traditional statistical methods are limited in handling multi-source, high-dimensional data, especially in capturing complex relationships between variables, thereby restricting their predictive accuracy and model stability^3,4.

In recent years, advances in observation technologies and improved data availability have made it possible to enhance runoff prediction accuracy through the incorporation of multi-source data. Teleconnection indices, such as El Niño-Southern Oscillation (ENSO) and Pacific Decadal Oscillation (PDO), have emerged as critical variables reflecting global climate system dynamics and are widely applied in hydrological predictions^5,6,7,8,9. These indices offer valuable insights into the temporal and spatial impacts of atmospheric processes on hydrological phenomena, enriching the description of hydrological processes from multiple dimensions^{10,11,12,13,14,15,16}. Studies reveal that teleconnection events can significantly influence basin runoff formation and evolution by impacting precipitation and evaporation processes^17,18. Unlike meteorological variables, which primarily reflect the aftermath of climate-driven changes, atmospheric circulation indices serve as leading indicators of climate variability. Since meteorological variables are directly influenced by atmospheric circulation patterns, their variability is often implicitly embedded within teleconnection indices. This predictive advantage makes atmospheric circulation indices particularly valuable for medium- to long-term runoff forecasting, as they capture large-scale climate dynamics before their effects manifest in local meteorological conditions¹⁹. Studies have demonstrated that teleconnection patterns can influence precipitation and runoff formation weeks to months ahead, with their impact propagating through ocean-atmosphere interactions, planetary wave adjustments, and large-scale circulation shifts. This extended predictive capability highlights the importance of incorporating atmospheric circulation indices into hydrological forecasting frameworks, offering a more comprehensive approach beyond conventional meteorological predictors²⁰. For example, Fan et al. (2020) highlighted that precipitation teleconnections with large-scale ocean-atmosphere systems provide valuable insights for water resource management²¹. Similarly, Zhou et al. (2020) demonstrated that Madden-Julian Oscillation exerts a profound influence on mid-latitude circulation, altering weather patterns through the excitation of Rossby waves²². Additionally, Redolat et al. (2019) demonstrated that the inclusion of teleconnection factors, such as the Atlantic Multidecadal Oscillation index (AMOi) and the Upper-Level Mediterranean Oscillation index (ULMOi), significantly enhances the accuracy of annual temperature predictions for the Mediterranean region²³.

Although the integration of teleconnection indices has enriched the dimensionality of hydrological models, it has also introduced challenges such as high dimensionality, multicollinearity, and redundant variables. If left unaddressed, these issues can impair computational efficiency and reduce prediction accuracy²⁴. To address these challenges, researchers have explored variable selection and dimensionality reduction techniques, such as stepwise regression analysis (SRA)²⁵ and wavelet analysis²⁶, to improve computational efficiency and prediction accuracy. Furthermore, machine learning (ML) and deep learning (DL) offer new pathways for hydrological predictions due to their strengths in extracting implicit features from data and addressing complex nonlinear relationships^7,8,27. Among these, Support Vector Regression (SVR) has gained attention for its adaptability to nonlinear data, while Multi-Layer Perceptron Regression (MLPR) excels in capturing latent patterns and modeling complex, high-dimensional datasets^28,29.

Despite advancements in these individual models, their fixed structures and limited parameter selection ranges pose challenges in adapting to diverse basin characteristics³⁰. Coupled models, which integrate the strengths of multiple methodologies, have demonstrated enhanced prediction accuracy and robustness by considering the interactions and feedback mechanisms among variables^31,32. For instance, Nikpouret al. (2022) reported the superiority of a wavelet-artificial neural network coupled model for precipitation forecasting, while Zhang et al. (2021) proposed a coupled WA-ARMA-BP model for groundwater depth prediction, achieving notable accuracy improvements³³. Numerous studies have shown that coupled models are effective tools for significantly enhancing the accuracy and stability of forecasts in hydrology, climate, environmental science, and other fields^{34,35,36,37,38}.

Based on the aforementioned background, this study proposes two novel coupled models (SRA-SVR and SRA-MLPR) for medium- to long-term runoff prediction. Specifically, the coupled models first employ Stepwise Regression Analysis (SRA) to select key feature variables from multidimensional datasets, eliminating redundant information and multicollinearity issues, and generating multiple subsets of feature variables. This step ensures that only the most influential predictive factors are considered in the subsequent modeling process. Next, the selected feature variables are input into either the Support Vector Regression (SVR) or Multilayer Perceptron Regression (MLPR) models, where high-precision runoff predictions are achieved through hyperparameter optimization and iterative training. Using the Yalong River Basin as a study area, this paper explores the effectiveness and robustness of the coupled models in improving runoff prediction accuracy and validates their advantages in capturing the complex relationships between atmospheric circulation and runoff variability. This study provides a robust and scalable approach to improving hydrological forecasting, which holds significant implications for water resource management and environmental science. The main contributions of this study are as follows:

• 1. Development of two high-precision coupled models (SRA-SVR and SRA-MLPR) based on machine learning and deep learning, capable of comprehensively considering multiple variables and automatically extracting key features to improve prediction accuracy;

• 2. Expansion of the variable set for medium- to long-term runoff prediction by incorporating teleconnection indices and other atmospheric circulation variables, thereby enhancing the predictive power and applicability of the models;

• 3. Systematically exploring the lag effect of atmospheric circulation on basin runoff provides a critical basis for accurate runoff simulation and prediction;

• 4. Identification of key atmospheric circulation variables that significantly influence runoff variability, providing theoretical support for optimized basin water resource management;

• 5. Validation of the coupled models’ advantages over benchmark single models, particularly in terms of stability and accuracy under complex basin conditions.

Research methods and materials

Study area and data source

Study area

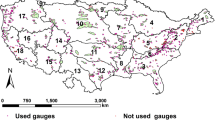
The Yalong River is located in the southwestern region of China and originates from the Kunlun Mountains within the Yushu Tibetan Autonomous Prefecture of Qinghai Province. The basin spans an area between 96°52′ and 102°48′ east longitude and 26°32′ to 33°58′ north latitude, flowing through parts of Sichuan Province, Yunnan Province, and the Tibet Autonomous Region before finally merging into the Jinsha River in Panzhihua city. Renowned for its diverse natural landscapes and rich ecological resources, the YaLong River Basin (YLRB) serves as a vital water resource for the urban water supply, agricultural irrigation, and hydroelectric power industries. It plays a crucial role in the economic prosperity and energy supply of the provinces along its route. The Yalong River has a total length of 1571 km, with a total decrease of 3830 m from the source to the mouth and a basin area of 136,000 square kilometers. Influenced by high-altitude westerly atmospheric circulation and southwestern monsoons, the basin exhibits significant variations in terrain elevation and latitudinal differences, resulting in pronounced horizontal and vertical climate changes. This creates highly complex meteorological conditions within the basin, featuring a dry and cold continental climate in the northern plateau areas, while the central and southern parts experience a distinct subtropical climate with pronounced dry and wet seasons. Moreover, there are evident climate variations along the vertical axis; mountainous areas within the same region are typically humid and rainy with lower temperatures, whereas valley areas are often sunny with less rainfall and relatively higher temperatures. The YLRB comprises numerous short tributaries, which exhibit a feather-like distribution in its water system. Figure 1 shows the specific location of the YLRB.

Fig. 1

Location of the YLRB and distribution of 4 hydrological stations. (The data used to create this figure were obtained from the National Catalogue Service for Geographic Information (www.webmap.cn), and the figure was generated using ArcGIS software (version 10.8, https://www.arcgis.com/).

In recent years, frequent occurrences of extreme weather events, such as extreme high temperatures and heavy rainfall, have led to intermittent flooding disasters in the YLRB, significantly impacting the human living environment. Therefore, conducting research on runoff prediction in the YLRB holds significant importance in safeguarding flood control and drought resistance scheduling, scientifically planning water resources, comprehensively and orderly utilizing water resources, and protecting the ecological environment in the region.

Data source

In this study, four primary hydrological stations in the YLRB, Lianghekou, Jinping, Guandi, and Ertan, were selected, and an in-depth analysis of monthly runoff data was conducted from 1953 to 2011. The distribution of these four stations is detailed in Fig. 1. We utilized the monthly average runoff values as data records and constructed graphs depicting the monthly runoff variations observed at these four stations (Fig. 2). For model training, a 10-fold cross-validation method was employed. Regarding dataset partitioning, 85% of the original runoff sequence was used as the shared dataset for training and validation, while the remaining 15% served as the test dataset.

The atmospheric circulation index data used in this paper were obtained from the China National Climate Centre (http://cmdp.ncc-cma.net/cn/monitoring.htm), providing 88 atmospheric circulation indices. Eighty out of the 88 atmospheric circulation indices were selected for experimentation in this study. The remaining eight indices were excluded for reasons such as columns with more than 80% missing values, zero values accounting for more than 80%, or 999/-999 values making up more than 80%. These indices were deemed to have no practical significance for the learning algorithm. Therefore, these abnormal and meaningless columns were removed from the analysis. Throughout the subsequent experiments and analyses, we used a refined dataset comprising 80 meaningful atmospheric circulation indices and monthly average runoff data from the four hydrological stations in the YLRB for an in-depth investigation.

Fig. 2

Monthly runoff observation values and variations at 4 hydrological stations in the YLRB. Monthly runoff observation values and variations at 4 hydrological stations in the YLRB. The asterisk ^* in the figure is used solely as an example for validation dataset verification. In the subsequent algorithm training process, the selection of the validation dataset was performed through random sampling following the K-fold cross-validation method.

Research methods

Data preprocessing

Data preprocessing is a crucial preliminary step in machine learning and deep learning and is vital for accurately and reliably extracting useful information from data. It refers to operations such as cleaning, transforming, integrating, and standardizing raw data before analysis and modeling to enhance data quality and applicability. The quality of data preprocessing directly impacts the accuracy and generalization performance of models³⁹. In the process of data analysis, data preprocessing plays a pivotal role in improving data quality, enhancing analytical results, and reducing model computation time.

Due to the substantial differences in the numerical ranges of various atmospheric circulation indices involved in this study, the min–max scaling preprocessing method was employed to uniformly express each atmospheric circulation index. This method is detailed in Formula 1.

$${x_{new}}=\frac{{x - {x_{min}}}}{{{x_{max}} - {x_{min}}}}$$

(1)

Spatiotemporal correlation coefficient

The spatiotemporal correlation coefficient is a statistical measure used to assess the correlation between variables in spatiotemporal data. It combines both temporal and spatial correlation analyses and can be employed to evaluate the degree of correlation between two variables at different times and locations. The value of the spatiotemporal correlation coefficient typically ranges from − 1 to 1, where 1 indicates complete positive correlation, -1 indicates complete negative correlation, and 0 indicates no linear correlation.

The calculation formula for the spatiotemporal correlation is as follows:

$$\rho = \frac{{\frac{1}{N}\sum\limits_{{i = 1}}^{n} {\sum\limits_{{j = 1}}^{m} {\left( {X_{{ij}} - \mu _{X} } \right)\left( {Y_{{ij}}^{{}} - \mu _{Y} } \right)} } }}{{\sigma _{X} \sigma _{Y} }}$$

(2)

Where.

X_i and Y_i are the corresponding sample observed values; $\bar {X}$and$\bar {Y}$are the respective means of the variable sequences; n and m are the length of the sequences; and $\sum$represents the summation operation.

Stepwise regression analysis

Stepwise regression (SRA), a widely-used statistical technique, plays a crucial role in resolving multicollinearity and variable redundancy within regression models. This method systematically iterates through the process of adding or removing independent variables, basing these decisions on their statistical significance in predicting the target variable. By doing so, it precisely identifies the most impactful predictors, thereby substantially enhancing the model’s predictive accuracy and robustness, as demonstrated in reference²⁵. This technique is particularly effective in evaluating the relative importance of each predictor, offering distinct advantages in handling high-dimensional feature selection and collinearity issues. Its effectiveness in these areas empowers researchers to build more parsimonious and accurate models, which is of utmost significance for the advancement of hydrological research and related applications.

The key steps in conducting feature dimension reduction using stepwise regression analysis for high-dimensional data are as follows: Initially, introduce independent variables one by one; after introducing each explanatory variable, conduct an F test to assess its significance. Next, t tests were performed on the selected explanatory variables to check for stability. If previously selected explanatory variables become insignificant due to the introduction of new explanatory variables, they are removed. This process is repeated until no significant explanatory variables are included in the regression equation, and no insignificant explanatory variables remain in the equation. This method ensures that the final set of explanatory variables is optimal and free from serious multicollinearity issues. The algorithmic structure is depicted in Fig. 3.

Fig. 3

Basic operational steps of the stepwise regression analysis method.

Grid search cross validation

Grid Search Cross Validation (GridSearchCV) is an essential tool in machine learning for hyperparameter optimization and model selection⁴⁰. It is a module within the scikit-learn library designed to automate the search for the best combination of hyperparameters within a specified grid and evaluate the model’s performance. GridSearchCV systematically explores all possible parameter combinations within a given parameter space and evaluates and compares the performance of each combination, ultimately identifying the optimal parameter set. When using this function, by specifying the parameter space, evaluation metric, number of cross-validation folds, and estimator, and adjusting and optimizing according to the specific context, one can obtain the best-performing model within the given parameter space. GridSearchCV aids in efficiently discovering the optimal parameter combination, reducing reliance on individual training and testing datasets, thereby enhancing the model’s performance and accuracy.

In this study, GridSearchCV is utilized for optimizing the hyperparameters during the training stages of various models.

Support vector regression

Support Vector Regression (SVR), a highly robust machine - learning technique, is celebrated for its remarkable ability to model intricate nonlinear relationships by leveraging kernel functions. This unique feature enables SVR to exhibit strong generalization capabilities even when dealing with relatively small datasets, as validated in reference⁴¹. SVR has been extensively and effectively applied in solving regression problems, especially when handling non - linear and high - dimensional data. By incorporating parameters such as the kernel function, penalty term (also referred to as the regularization parameter), gamma parameter, and tolerance deviation epsilon, SVR maps the feature variables into a high - dimensional space. It then constructs a set of hyperplane functions, F(X), with the aim of minimizing the sum of distances from all sample points to a particular function hyperplane within F(X). This specific hyperplane represents the optimal hyperplane that is sought after, as vividly depicted in Fig. 4. The utilization of SVR in our study allows for a more accurate capture of the complex relationships in hydrological data, contributing to more precise runoff predictions and a deeper understanding of hydrological processes.

Fig. 4

Schematic diagram of the basic principles of SVR.

Parameter optimization is a pivotal issue during SVR modeling training. In this paper, GridSearchCV is employed for parameter tuning in the SVR modeling process. The structure of the SVR algorithm optimized by the GridSearchCV algorithm used in this paper is depicted in Fig. 5A.

The optimization problem of SVR can be represented by Eq. (3):

$$\mathop {\min }\limits_{{\omega ,b}} \frac{1}{2}\omega ^{2} + C\sum\limits_{{i = 1}}^{l} {\left( {\xi _{i} + \xi _{i}^{*} } \right)}$$

(3)

s. t. $\left\{ {\begin{array}{*{20}l} {y_{i} - \omega \varphi \left( x \right) - b \le \varepsilon + \xi _{i} } \hfill & {i = 1,2, \cdots ,l} \hfill \\ { - y_{i} + \omega \varphi \left( x \right) + b \le \varepsilon + \xi _{i}^{*} } \hfill & {i = 1,2, \cdots ,l} \hfill \\ {\xi _{i}^{*} ,\xi _{i} \ge 0} \hfill & {i = 1,2, \cdots ,l} \hfill \\ \end{array} } \right.$

In Eq. (3), C is the penalty parameter; ${\xi _i}$ and $\xi _{i}^{ * }$ are slack variables; and $\:\epsilon\:$ is the tolerance deviation parameter.

To solve the optimization problem presented in Eq. (3), one can introduce the Lagrange multiplier and obtain the following:

$$f(x) = \sum\limits_{{i = 1}}^{l} {\left( {\alpha _{i}^{*} - \alpha _{i} } \right)} K\left( {x_{i} ,x} \right) + b$$

(4)

In Formula (4), both ${\alpha _i}$ and $\alpha _{i}^{ * }$represent Lagrange multiplier operators; $K\left( {{x_i},x} \right)$= $\phi {\left( {{x_i}} \right)^{\text{T}}} \cdot \phi (x)$ signifies the kernel function. Here, $\phi ( \cdot )$ denotes the mapping function from a low-dimensional feature space to a high-dimensional feature space, while $\phi {\left( {{x_i}} \right)^{\text{T}}} \cdot \phi (x)$ denotes the inner product after mapping to the higher-dimensional space.

Multi-layer perceptron regressor

Multi-Layer Perceptron Regression (MLPR), a regression model grounded in the Multi-Layer Perceptron (MLP) neural network, which is a key category of Multilayer Artificial Neural Network (ANN), exhibits remarkable capabilities. The fundamental structure of the MLPR consists of multiple layers of neurons form a multilayered neural network. Each neuron possesses an input and an output, and the connection weights between them can be adjusted through training. MLPR efficiently handles large-scale high-dimensional data, automatically extracts features, and deeply explores and fits implicit non-linear relationships between independent and target variables, offering significant advantages in solving regression problems^26,42. By identifying the latent non - linear mapping relationship between input features and output values, MLPR can accurately predict continuous target variables. Consequently, it makes a significant contribution to the progress of runoff prediction research and the improvement of the accuracy of hydrological forecasting.

By combining multiple layers of neurons, each layer in the MLPR is fully connected to the adjacent layers of neurons. It utilizes activation functions (such as Sigmoid, Tanh, and ReLU) to introduce non-linear mapping capabilities. MLPR operates through forward propagation, using activation functions to generate predicted output values. Backpropagation and gradient descent algorithms are also used to update the model’s weights and biases, thereby enhancing its fitting capability and generalization performance. The selection and optimization of parameters required by the MLPR method are crucial for ensuring model performance. These parameters may include the number of hidden layers, the number of neurons per layer, the learning rate, the activation function, the loss function, the batch size, the number of iterations, and whether dropout is necessary. In this study, the process of selecting and optimizing the necessary hyperparameters for MLPR will be conducted using the GridSearchCV method introduced in Sect. 2.2.4 for hyperparameter tuning.

If an MLPR has a network structure with only three layers, including one hidden layer, its computational process can be described using the following mathematical formula (5):

$$\begin{array}{*{20}{c}} {{\varvec{O}}={\varvec{H}}{{\varvec{W}}^{(2)}}+{{\varvec{b}}^{(1)}}} \\ {{\varvec{H}}=\sigma \left( {{\varvec{X}}{{\varvec{W}}^{(1)}}+{{\varvec{b}}^{(1)}}} \right)} \end{array}$$

(5)

In Formula (5), H represents the output of the first layer, which is also the input tensor for the first hidden layer; O denotes the output layer result; σ represents the activation function; and b signifies the bias for different network layers. X represents the input vector matrix. The σ activation function could be ReLU (formula (6)), sigmoid (formula (7)), or tanh (formula (8)), among other non-linear functions.

$$ReLU(x)=\hbox{max} (0,x)$$

(6)

$$Sigmoid(x)=\frac{1}{{1+{{\text{e}}^{ - x}}}}$$

(7)

$$Tanh(x)=\frac{{1 - {{\text{e}}^{ - 2x}}}}{{1+{{\text{e}}^{ - 2x}}}}$$

(8)

The algorithmic flowchart of MLPR combined with GridSearchCV optimization is shown in Fig. 5B.

Fig. 5

Flowchart of the MLPR algorithm optimized by GridSearchCV.

SHAP (SHapley additive exPlanations)

SHAP (SHapley Additive exPlanations) is a machine learning interpretability method based on cooperative game theory, first proposed by Lundberg and Lee⁴³. This approach utilizes Shapley value theory to quantitatively assess the contribution of each input feature to the model’s predictions, integrating concepts from cooperative game theory and local interpretability methods to form an additive attribution framework.

SHAP calculates the SHAP values for each feature by considering all possible feature combinations and their contributions to the prediction outcome. This enables a fair and rational distribution of contributions, providing an effective measure of feature importance and its impact on model output. SHAP is model-agnostic, meaning it can be applied to various types of machine learning models, including linear models, tree-based models, and neural networks, demonstrating strong generalizability.

Moreover, SHAP can provide both local and global interpretability. At the local level, it explains the contribution of each feature to a specific prediction instance. At the global level, it aggregates SHAP values across multiple instances to illustrate the average impact of each feature on model predictions across the entire dataset. The computed SHAP values have clear physical significance: positive values indicate that a feature tends to increase the prediction output, while negative values suggest a decreasing effect. The absolute magnitude of the SHAP value reflects the strength of the feature’s influence, offering an intuitive representation of the relationship between features and model predictions, thus enhancing interpretability.

In this study, we employ the SHAP interpretability method to provide an in-depth explanation of the constructed prediction model, aiming to improve transparency in model operations and deepen the understanding of atmospheric circulation indices that significantly affect runoff. By leveraging SHAP, we quantify the contribution of each input feature to the model’s predictions, thereby uncovering the intrinsic relationships between features and predictive outcomes, offering strong support for model interpretability.

The calculation formula for SHAP values is as follows:

$$\phi _{i} = \sum\limits_{{S \subseteq N\backslash \left\{ i \right\}}} {\frac{{\left| S \right|!\left( {n - \left| S \right| - 1} \right)!}}{{n!}}\left[ {f_{{S \cup \{ i\} }} \left( {x_{{S \cup \{ i\} }} } \right) - f_{S} \left( {x_{S} } \right)} \right]}$$

(9)

Among them, N represents the complete set of features, $S \subseteq N \setminus \{ i\}$ represents any feature subset after excluding feature i, ${f_S}\left( {{x_S}} \right)$ denotes the expected value of the model output given the features within subset S, and ${f_{S \cup \{ i\} }}\left( {{x_{S \cup \{ i\} }}} \right)$ represents the expected value of the model output after adding feature i. The coefficient $\frac{{\left| S \right|!\left( {n - \left| S \right| - 1} \right)!}}{{n!}}$ represents the weighting coefficient of the combined feature subset to ensure that all feature combination scenarios are taken into account during the calculation process.

Model evaluation metrics

To comprehensively evaluate the fitting and generalization capabilities of the models in this study, five metrics were selected: Nash - Sutcliffe efficiency coefficient (NSE), Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE), and Mean Squared Logarithmic Error (MSLE). NSE, which ranges from 0 to 1, evaluates regression model fit by integrating predicted - observed value differences and observed data variability, with values closer to 1 indicating a better fit. RMSE, measuring predictive model performance through the square root of average squared errors between predicted and observed values, is better when lower, as it implies higher accuracy. MAE, gauging predictive model accuracy as the average of absolute variances between predicted and actual values, shows that smaller values represent superior accuracy. MAPE, assessing predictive model accuracy by measuring the percentage difference between predicted and actual values, is more accurate when its value is smaller. MSLE, computing the average logarithmic discrepancies between predicted and observed values and effectively handling outliers, is preferred with lower values, as they signal enhanced predictive precision.

The calculation formulas for the five aforementioned metrics are presented as follows:

$$NSE = 1 - \frac{{\sum\limits_{{i = 1}}^{n} {\left( {y_{i} - \hat{y}_{i} } \right)^{2} } }}{{\sum\limits_{{i = 1}}^{n} {\left( {y_{i} - \bar{y}} \right)^{2} } }}$$

(10)

$$RMSE(y,\hat{y}) = \sqrt {\frac{{\sum\limits_{{i = 1}}^{n} {\left( {y_{i} - \hat{y}_{i} } \right)^{2} } }}{n}}$$

(11)

$$MAE(y,\hat{y}) = \frac{{\sum\limits_{{i = 1}}^{n} {\left| {y_{i} - \hat{y}_{i} } \right|} }}{n}$$

(12)

$$MAPE\left( {y,\hat{y}} \right) = \frac{{100\% }}{n}\sum\limits_{{i = 1}}^{n} {\left| {\frac{{y_{i} - \hat{y}_{i} }}{{y_{i} }}} \right|}$$

(13)

$$MSLE(y,\hat{y}) = \frac{1}{n}\sum\limits_{{i = 1}}^{n} {\left( {\log \left( {1 + y_{i} } \right) - \log \left( {1 + \hat{y}_{i} } \right)} \right)^{2} }$$

(14)

In the above five formulas, ${y_i}$ represents the i-th actual observed value. ${\hat {y}_i}$ represents the corresponding model-predicted value, $\:\stackrel{-}{y}$ represents the mean of the actual observed values, and n represents the number of samples used by the model.

Methodological framework

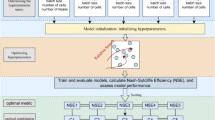
The methodological framework developed for this study is presented in Fig. 6 and comprises five key stages:

Multi-source data fusion and preprocessing

Firstly, runoff observation data from four hydrological stations in the YLRB and 88 atmospheric circulation indices (from 1952 to 2011) were fused. Subsequently, preprocessing steps were conducted on the merged data, which include but are not limited to: removing invalid columns, handling missing values, scaling transformations, and input normalization.

Exploration of temporal and spatial relationships

To explore the spatiotemporal relationship between runoff observational data and preprocessed atmospheric circulation index data, in order to determine the lag duration of atmospheric circulation indices affecting the runoff at watershed hydrological stations.

Data alignment and feature selection

The atmospheric circulation indices were aligned with runoff data from the four hydrological stations based on the lag duration determined in the previous step. The SRA component of the coupled model conducts feature selection for the 88 atmospheric circulation indices, identifying those significantly impacting the runoff. Considering issues such as multicollinearity, non-stationarity, and non-linear relationships, redundant and multicollinear variables are eliminated. Finally, based on preset feature selection criteria, four distinct optimized variable datasets are obtained (each corresponding to one hydrological station).

Model training, optimization, and evaluation

Defining a reasonable initial hyperparameter space for two coupled models (SRA-SVR and SRA-MLPR). Each of the four datasets is randomly divided into training, validation, and test sets. The GridSearchCV hyperparameter tuning tool is employed iteratively to optimize the models until the specified stopping conditions are met. This process yields the final eight selected coupled prediction models (each hydrological station corresponding to its SRA-SVR and SRA-MLPR models).

Model prediction

The test datasets for the four hydrological stations are input into the trained models from step 4 to obtain the models’ monthly runoff predictions for each station. The evaluation metrics shown in the bottom-right part of Fig. 6 are then used to assess the results.

Results and discussion

Analysis of spatiotemporal correlation between atmospheric circulation indices and runoff

Spatial variation analysis of the correlation between atmospheric circulation indices and runoff

Climate change is directly influenced by atmospheric circulation, and the spatiotemporal propagation and evolution characteristics of atmospheric circulation determine climate behavior. The runoff process in a basin is influenced primarily by factors such as precipitation, evaporation, and underlying surface conditions. When the underlying surface conditions in a basin are relatively stable, precipitation and evaporation become the main influencing factors of the runoff process, with atmospheric circulation being the direct limiting factor for precipitation and evaporation. Therefore, analyzing the correlation between atmospheric circulation indices and basin runoff is crucial for predicting changes in runoff.

Fig. 6

Flowchart of the integrated framework developed for runoff prediction.

We selected four major control section hydrological stations in the YLRB: the Lianghekou (LHK), Jinping (JP), Guandi (GD), and Ertan (ET) stations. The monthly average runoff of these four hydrological stations was chosen along with the 80 preprocessed atmospheric circulation indices for Spatiotemporal correlation analysis.

To facilitate the analysis of the spatiotemporal correlation between each hydrological station and various atmospheric circulation indices, we computed the spatiotemporal correlation coefficients based on Eq. 2. We then plotted a line graph as shown in Fig. 7, with the atmospheric circulation indices on the x-axis.

Figure 7 clearly shows a distinct spatial distribution pattern between runoff in the Yalong River Basin (YLRB) and atmospheric circulation indices. The graph illustrates stronger correlations between runoff in the upstream section and atmospheric circulation indices compared to the downstream sections, where correlations appear relatively weaker. Specifically, the monthly average runoff at the upstream LHK hydrological station in the YLRB demonstrated the highest correlation with various atmospheric circulation indices, with correlations greater than 0.7 on multiple atmospheric circulation indices and exceeding 0.8 at the highest point. Subsequently, the JP, GD, and ET hydrological stations downstream exhibited sequentially decreasing correlations with the atmospheric circulation indices. Among these stations, the monthly average runoff at ET, situated farthest downstream, demonstrated the lowest correlation with the atmospheric circulation indices. Overall, moving from upstream to downstream, the correlations gradually decrease.

Considering the geographical distribution of the hydrological stations in the YLRB, several reasons can explain these observations:

• 1. The upstream area of the basin is situated in the plateau region of the Kunlun Mountains, where the evolution of river runoff tends to be more natural, with relatively simple and stable runoff generation relationships. Studies have shown that high-altitude basins often exhibit relatively stable hydrological behaviors, primarily driven by natural climatic cycles with minimal anthropogenic disruptions⁴⁴.

• 2. The distribution of water systems in the upstream area is relatively concentrated without excessive branching or convergence, leading to simpler topological relationships within the water system⁴⁵. Consequently, the evolution patterns of river runoff in this region are relatively straightforward and stable.

• 3. The upstream area of the basin is less disturbed by human interference, and there is no large-scale urbanization or human development project. Hydrological processes within the basin are influenced primarily by natural conditions such as terrain, soil, precipitation, and evaporation⁴⁶. This also contributed to the relatively simple and stable evolution patterns of runoff in the upstream region.

Temporal variation analysis of the correlation between atmospheric circulation indices and runoff

In the preceding section of our research, we observed the most significant correlation between atmospheric circulation indices and the monthly average runoff at the LHK hydrological station among the four stations in the YLRB. Based on these findings, we considered selecting the monthly average runoff at LHK station to explore the temporal relationship between runoff and atmospheric circulation indices in the YLRB to be highly feasible.

For monthly runoff prediction, the complete hydrological cycle spans 12 months. Due to the lagged effect of atmospheric circulation indices on runoff and to analyze this phenomenon comprehensively, we conducted Pearson correlation analysis between the current month’s runoff at LHK station and the 80 atmospheric circulation indices from the previous 1 to 12 months. After calculating the correlation coefficients, we generated a correlation heatmap (Fig. 8). In the heatmap, darker colors represent stronger positive correlations, lighter colors indicate stronger negative correlations, and the middle transition zone depicts smaller absolute correlation values. The numerical labels on the left side of Fig. 8 correspond sequentially to the atmospheric circulation indices displayed on the horizontal axis of Fig. 7, in a one-to-one matching order.

Fig. 7

The correlation coefficients between the runoff at four hydrological stations in the YLRB and the atmospheric circulation indices.

Figure 8 clearly shows that the correlation between the monthly average runoff at LHK station and the atmospheric circulation index from the previous month (with a lag period of 1 month) is notably significant, while the correlations with other monthly indices are relatively smaller. Specifically, the correlation peaks at a lag period of 1 month and gradually decreases with increasing lag period, reaching its minimum at lag periods of 6 and 7 months. Subsequently, as the lag period extends to 12 months, the correlation gradually increases again. This trend is vividly depicted in Fig. 8. Analyzing this in relation to temporal and meteorological aspects, the reasons behind this are as follows:

• 1. The runoff process exhibits a cyclic nature, roughly corresponding to one revolution of the Earth around the sun (approximately 12 months).

• 2. A lag period of 12 months in the atmospheric circulation index corresponds to the previous year’s January runoff. Considering the cyclic nature of runoff, the 12th-month atmospheric circulation index corresponds to the runoff in January of the previous cycle. Therefore, as described in reason 1, the impact is most pronounced, and the correlation is greatest with a lag period of one month.

The results and analysis suggest that for medium- to long-term runoff forecasting in the YLRB, choosing a lag period of 1 month for atmospheric circulation indices is the most suitable option. Atmospheric circulation indices preceding this period have a relatively smaller impact on the current month’s runoff.

Based on the experimental results from the previous section, we lagged the atmospheric circulation index data by one month and chronologically aligned it with the runoff data from the four stations in the YLRB. Subsequently, by employing the screening and computation process through the SRA component of the coupled model on these aligned datasets, four sets of optimized feature variables were ultimately obtained. The results are presented in Table 1.

Fig. 8

Correlation heatmap displaying different lag periods between atmospheric circulation indices and the monthly average runoff at LHK station.

The screening results of atmospheric circulation indices by the SRA component of the coupled model

Table 1 illustrates the outcomes derived from the SRA component of the coupled model after the selection of atmospheric circulation indices concerning runoff at four hydrological stations within the YLRB. The obtained atmospheric circulation indices are identified by the model as factors significantly impacting the runoff at each respective hydrological station. All factors presented in Table 1 have undergone statistical significance tests (P < 0.05) with a confidence level of 95%. Additionally, their Variance Inflation Factor (VIF) values are all below 10, indicating no issues of multicollinearity.

Table 1 Results of SRA component screening factors.

Table 1 clearly shows that the coupled model has a significant overlap among the selected atmospheric circulation indices for the four hydrological stations. This indirectly reflects the spatial consistency of these four hydrological stations (the order of corresponding factors within the table for each station is related only to the randomness of the algorithm selection process and is unrelated to other aspects).

The conclusions drawn from Table 1 are as follows:

• (1) At a cumulative confidence level of 95%, the LHK station covers 18 atmospheric circulation indices, the JP station covers 15, the GD station covers 15, and the ET station covers 15. The overlap among the atmospheric circulation indices covered by each station indicates spatial consistency among these four stations.

• (2) Upon analyzing the required number of atmospheric circulation indices for each station, it was observed that the LHK (LHK) hydrological station requires the largest quantity of atmospheric circulation indices to achieve a 95% confidence level. This observation highlights a greater influence of natural conditions on upstream stations compared to middle and downstream stations. Specifically, as the initial hydrological station in the upstream basin, LHK is impacted by a larger number of atmospheric circulation indices. As stations progress downstream, human activities gradually intensify, resulting in increased impacts on downstream stations attributed to factors influenced by human activities. This cumulative effect diminishes the influence of natural conditions, including atmospheric circulation, from upstream to downstream to a certain extent.

Setting of model hyperparameters

The accuracy, generalizability, and convergence of machine learning or deep learning models strongly depend on the setting of hyperparameters. Therefore, setting these parameters is crucial for enhancing the overall performance of the model. Hyperparameters are pivotal in determining the convergence speed, performance, and generalization capability of algorithmic models. To select appropriate and superior hyperparameters, we selected multiple suitable candidate options for each parameter of the SRA-SVR and SRA-MLPR coupling models. Based on these candidate options, we utilized the GridSearchCV method introduced in Sect. 2.2.4 to conduct hyperparameter tuning. GridSearchCV is a hyperparameter tuning method that systematically explores the hyperparameter space of a model using cross-validation and the evaluation criteria set by the user to identify the best combination of hyperparameters. In the training phase of both coupling models in this study, 85% of the original runoff data sequences were used as a shared training and validation set (using 10-fold cross-validation), while the remaining 15% served as an independent test set.

Table 2 presents the hyperparameter settings used during the training and validation phases of the SRA-SVR model, along with the finalized optimal parameter values determined by the model. In terms of the choice of the feature mapping kernel function, the SRA-SVR model, through the GridSearchCV method, selects the widely adaptable radial basis function (RBF) kernel function, which better handles non-linear relationships and data distributions. In the selection of the Gamma function, the Scale function was used for consistent data scaling and simplification of the hyperparameter selection process, thereby accelerating the model’s convergence speed. The variations in the numerical values of the regularization parameter C and tolerance deviation Epsilon across the four hydrological stations show consistent dimensional tolerances among these stations, indicating certain commonalities among them. Furthermore, the required number of iterations for each station to achieve the final model result varies, which indirectly reflects the unique characteristics of each station.

Table 2 Hyperparameter tuning for the SRA-SVR model.

Like Tables 2 and 3 presents the hyperparameter settings used during the fitting and prediction processes of the SRA-MLPR model, along with the finalized optimal parameter values (as the nature of the SRA-SVR and SRA-MLPR models differ, their parameter items vary). Observing the numerical values in the table, concerning the choice of the activation function, the model employed the ReLU function. This function demonstrates strong non-linear expression capability and efficient computational performance, effectively addressing the issue of vanishing gradients.

Considering the distinct characteristics of the runoff data and predictor variables at four hydrological stations, namely, the LHK, JP, GD, and ET stations, the model included 6, 5, 7, and 7 layers, respectively.

Concerning the selection of the neural network optimization algorithm, the model chose the limited-memory Broyden–Fletcher–Goldfarb–Shanno (L-BFGS) algorithm due to its low memory footprint, rapid convergence, and suitability for handling large-scale data. This algorithm efficiently addresses optimization problems in non-linear contexts and is especially suitable for enhancing and optimizing target variables under the influence of multiple factors.

Additionally, the iteration count was set to the default value of 15,000, and the tolerance was configured as 1*10^− 7.

Table 3 Hyperparameter configuration for the SRA-MLPR mode.

Prediction results and analysis of the coupled model

The monthly runoff at the four hydrological stations in the YLRB, as illustrated in Fig. 2 earlier, demonstrated noticeable fluctuations. Their trend revealed a gradual increase in runoff from upstream to downstream hydrological stations. Additionally, all the hydrological stations under study exhibited distinct fluctuating patterns. This fluctuation poses a significant challenge not only during the model construction and fitting processes but also as a rigorous test of the model’s predictive performance.

Analysis of the runoff prediction results for the LHK and JP hydrological stations

Figure 9 depicts subplots A and B, which present the results of the machine learning coupled model SRA-SVR’s predictions on the runoff datasets of the LHK and JP hydrological stations after training with the training dataset’s predictors. Subplots C and D display the predictions of runoff volume for the two hydrological stations using the SRA-MLPR model based on deep learnings. In each subplot, the blue line corresponds to the observed runoff values at the hydrological station, while the orange line represents the model’s predictions. Upon observing subplots A and C, it is evident that for the predictions at the LHK hydrological station, the SRA-MLPR model outperforms the SRA-SVR model. This is manifested in the graphs where the orange prediction line in subplot C is closer to the actual runoff observations represented by the blue line than is the orange line in subplot A. Especially at the challenging peaks of runoff values that are hard to predict, the runoff values predicted by the SRA-MLPR align more accurately with the actual observed runoff values. Similar prediction results are also observed in subplots B and D, representing the predictions for the JP hydrological station.

Fig. 9

The prediction results for the full dataset of the LHK and JP hydrological stations by the coupled models SRA-SVR and SRA-MLPR are shown in Figure. Subplots A and C depict the prediction results of the two coupled models at the LHK hydrological station, while subplots B and D represent the prediction results of the two coupled models at the JP hydrological station.

Figure 10 shows the plots of the prediction results for the test dataset of the LHK and JP hydrological stations obtained by the SRA-SVR and SRA-MLPR coupled models. The x-axis represents the actual observed monthly runoff values for the respective hydrological stations, while the y-axis denotes the corresponding model-predicted monthly runoff values. A detailed analysis of the four subplots suggested that the monthly runoff values predicted by the SRA-MLPR model were closer to the actual observed runoff values. This is demonstrated in subplot D, which appears more evenly distributed around the line and lacks significant outliers in the prediction of larger values compared to subplot B. Subplots A and C exhibit similar tendencies.

Fig. 10

The plots of prediction results for the SRA-SVR and SRA-MLPR models on the test dataset from the LHK and JP hydrological stations. Subplots A and C illustrate the prediction results of the two coupled models at the LHK hydrological station, while subplots B and D display the prediction results at the JP hydrological station.

Runoff prediction analysis results at GD and ET hydrological stations

Figure 11 shows the numerical results of the monthly runoff predictions obtained by SRA-SVR and SRA-MLPR for the test dataset from the GD and ET hydrological stations. Like in Fig. 9, the blue line in the figure represents the actual observed monthly runoff at each hydrological station, while the orange line represents the corresponding model’s predicted values.

Figure 11 shows that, in subplot C, the orange line representing the predicted values is closer to the actual observed values at the hydrological station. Specifically, for several runoff peak values in the graph, the predicted results of the SRA-MLPR model represented by the orange line in subplot C closely align with the actual observed runoff values compared to those of the SRA-SVR model. Subplots B and D display the prediction results of SRA-SVR and SRA-MLPR at the ET hydrological station. Compared to the SRA-SVR model, the SRA-MLPR model demonstrates enhanced accuracy in predicting the majority of peak flow events. This is particularly evident in Subfigure D, which illustrates the peak flow predictions. The SRA-MLPR model exhibits superior performance in capturing both the common peak flows ranging from 3000 to 3500 m³/s and the less frequent, yet challenging extreme peak flows within the 4500 to 6000 m³/s range. The predicted runoff values by the SRA-MLPR align more closely with the actual observed runoff, with the forecasted fluctuations closely mirroring the observed ones, whereas the SRA-SVR model exhibits noticeable deviations. These findings underscore the SRA-MLPR model’s exceptional capability in handling complex runoff dynamics and accurately simulating extreme runoff conditions, highlighting its potential utility and advantages in hydrological forecasting.

Figure 12 shows the plots of the prediction results obtained by the SRA-SVR and SRA-MLPR models for the test dataset from the GD and ET hydrological stations. The horizontal axis represents the actual observed runoff values, while the vertical axis represents the model-predicted runoff values. Observations clearly reveal that the values predicted by the SRA-MLPR model closely align with the actual observed runoff values, and the predictive accuracy of the SRA-MLPR model is significantly better than that of the SRA-SVR model. In Fig. 12, the data points in subplot C are denser than those in subplot A and are more concentrated on both sides of the line, indicating greater consistency between the actual observed values and the predictions of the SRA-MLPR model. Further observation of the distribution of data points in subplots D and B emphasizes the superiority of the SRA-MLPR model over the SRA-SVR model in terms of high precision and generalizability.

Fig. 11

The prediction results for the full dataset of the SRA-SVR and SRA-MLPR coupled models at the GD and ET hydrological stations are depicted in the figure. Subplots A and C illustrate the prediction results of the two coupled models at the GD hydrological station, while subplots B and D illustrate the prediction results at the ET hydrological station.

Fig. 12

The plots of the prediction results for the test dataset of the SRA-SVR and SRA-MLPR coupled models at the GD and ET hydrological stations are presented. Subplots A and C depict the prediction results of the two coupled models at the GD hydrological station, while subplots B and D illustrate the results at the ET hydrological station.

Ablation study and analysis of model evaluation metrics

The ablation study refers to a systematic experimental method in scientific research to evaluate the extent of the impact of different components of a model on its overall performance. This method aims to assess the influence of certain components on the predictive capability or overall performance of the model by progressively removing, disabling, or modifying them.

To further understand the robustness, effectiveness, and accuracy of the coupled models constructed in this study, an ablation experiment was designed in this section. Five metrics, namely NSE, RMSE, MAE, MAPE, and MSLE, were selected for quantitative evaluation and comparative analysis of the overall coupled models and their constituent modules. To comprehensively compare the actual performance of each module, the comparative models established in this ablation study were SVR, SRA-SVR, MLPR, and SRA-MLPR. Corresponding models in the ablation study were experimentally verified under identical hyperparameter settings (see Sect. 3.3), the same dataset divisions, and identical experimental conditions. The introduction of all evaluation metrics has been detailed in Sect. 2.4. The experimental results, shown in Tables 4 and 5, display the values of these metrics, which were obtained by conducting 10-fold cross-validation for each model, and the averages are then calculated.

NSE is an effective indicator used to measure the goodness of fit and generalization performance of models. It finds extensive applications in prediction models across hydrological, climatic, and environmental domains. Tables 4 and 5 present the evaluation metric results of various models in the ablation study for the four hydrological stations on the testing dataset. Observations indicate that concerning the LHK hydrological station, SRA-SVR exhibits an approximate 2.5% improvement in the NSE goodness of fit metric compared to SVR. In the evaluation results of JP, GD, and ET hydrological stations, the NSE metric increased by 3.6%, 5.7%, and 2.9%, respectively. Similarly, at the LHK hydrological station, SRA-MLPR improved by 5% in NSE compared to MLPR. For JP, GD, and ET hydrological stations, SRA-MLPR exhibited improvements of about 2.7%, 5.9%, and 5.2%, respectively, over MLPR. The enhancement in goodness-of-fit NSE suggests that the SRA module in the constructed coupled models effectively removed multicollinearity and redundant variables from the original dataset. It accurately selects the significant feature variables that affect the target hydrological stations, thereby enhancing the accuracy of predictions.

Continuing the analysis of Tables 4 and 5, it becomes evident that the predictive performance of the coupled models surpasses significantly that of the individual models across all four hydrological stations. This phenomenon is most prominent at the JP station. By observing the MSLE error metric results for the JP station in Table 4, it is noticeable that SRA-MLPR exhibits a decrease of 27% compared to MLPR, while SRA-SVR shows a reduction of 36% compared to SVR. These outcomes indicate that the coupled models effectively enhance the accuracy of model predictions. This finding is consistent with the conclusion reported in reference^36,47.

Table 4 The ablation study compares the coupled model and the baseline model using the same evaluation metrics at the LHK and JP hydrological stations in the testing dataset.

To provide a clearer visualization of the prediction errors of each model at the four hydrological stations, we employ radar charts for visual representation. These charts are used to compare the performances of prediction error metrics such as the RMSE, MAPE, and MAE (refer to Fig. 13).

Fig. 13

Radar charts displaying various evaluation metrics for the SRA-SVR and SRA-MLPR coupled models at four hydrological stations in the YLRB.

Based on the observations from Fig. 13, it is evident that the performance of the coupled models (SRA-SVR and SRA-MLPR) significantly outperforms that of the single models across the three evaluation metrics. As illustrated in the graph, the coupled model consistently demonstrates smaller error metric values in each dimension assessing the model’s performance (RMSE, MAE, and MAPE), indicating more reliable, stable, and superior predictive outcomes. In particular, the superiority of the SRA-SVR and SRA-MLPR models is particularly evident at the LHK and ET stations. The error metric values represented by the yellow and orange lines consistently exhibit smaller magnitudes compared to those of the other single models, thereby highlighting the superior performance of the coupled models. Consequently, it can be inferred that the coupled models demonstrate enhanced precision and stability in comparison to the individual models.

Performance comparison between coupled models

In the previous section, we delved into the significant advantages of coupled models over single models in terms of error evaluation metrics. To further validate and compare the effectiveness of different coupling strategies, this section will compare two advanced coupled models and continue to analyze their performance in the application scenarios of the four main hydrological stations in the Yalong River basin.

Observing Tables 4 and 5, it can be noted that at the LHK station, compared to the SRA-SVR model, the generalization performance of the SRA-MLPR model has improved by approximately 6% in terms of the NSE index. Similarly, at the JP, GD, and ET hydrological stations, there are increases of about 4.3%, 4%, and 4%, respectively. These findings suggest that, compared to the SRA-SVR model, the SRA-MLPR coupled model based on deep learning exhibits superior fitting capability and generalization performance.

Table 5 The ablation study presents the comparison of the coupled model and the baseline model in terms of the same evaluation metrics at the GD and ET hydrological stations in the testing dataset.

The RMSE, MAE, MAPE, and MSLE are commonly used metrics for assessing the errors between predicted values and actual values in prediction models. Smaller values of these metrics indicate stronger predictive capabilities of the model. From Tables 4 and 5, it’s evident that across these four evaluation metrics, the SRA-MLPR model outperforms the SRA-SVR model in the predictions at each hydrological station. It’s also noticeable that both coupled models (SRA-MLPR and SRA-SVR) perform better than the individual models (SVR and MLPR). Specifically, at the LHK hydrological station, compared to the SRA-SVR model, the SRA-MLPR model exhibits a significant decrease in all four error metrics. Notably, there is a reduction of approximately 15.9% in MAPE and 23% in MSLE. Similar performance gaps between these two coupled models are observed in the four evaluation metrics at the other three hydrological stations. Moreover, there’s a significant disparity in performance between the coupled and individual models across all four hydrological stations. For instance, at the JP hydrological station, the SRA-SVR model, in comparison to the SVR model, shows a reduction of 20% in MAPE and 36% in MSLE, along with improvements in other metrics. Similarly, the SRA-MLPR model, compared to the MLPR model, demonstrates decreases of 11% in MAPE and 27% in MSLE, with varying degrees of reduction in RMSE and MAE. This trend is also validated in the evaluation metric results at the other hydrological stations.

To provide a more intuitive representation of the evaluation metrics for the predicted values of the two coupled models at each hydrological station, we analyze and visualize the error metrics for these prediction results (see Figs. 14, 15).

Figure 14 illustrates that in both RMSE and MAE evaluation metrics, the two coupled models outperform the individual models across the four hydrological stations in the studied basin. This indicates that coupled models, leveraging synergies between different modules, can effectively extract implicit information from the data, enhancing the overall model accuracy. Additionally, the results of the SRA-MLPR model across the four hydrological stations significantly outperform those of the SRA-SVR model. This suggests that the MLPR based on deep learning can tap into the latent information within the data more profoundly than the SVR based on machine learning, further enhancing the stability and accuracy of the overall model.

The noteworthy observation is the ascending trend in the values of these two error evaluation metrics across the four hydrological stations. Specifically, the RMSE and MAE values at the upper LHK station are relatively smaller compared to the three downstream stations, displaying a similar trend among these downstream stations. This indicates that as the water flow extends from the upper to the lower reaches, both natural factors and human activities gradually accumulate influences on the downstream discharge. This cumulative effect becomes more pronounced in the model evaluation results, notably reflected in the RMSE and MAE metrics of the predicted values.

Fig. 14

The RMSE and MAE evaluation values for the predictions at the four major hydrological stations in the Yalong River basin by the two coupled models and their corresponding single models.

Figure 15 displays the measurement results of different models on two error evaluation metrics, MAPE and MSLE. Upon observation, it’s apparent that the accuracy of predictions by SRA-MLPR outperforms that of the SRA-SVR model across all four hydrological stations. Specifically, concerning the MAPE and MSLE metrics at the LHK hydrological station, the SRA-MLPR model demonstrates approximately 19% and 30% lower error rates, respectively, compared to the SRA-SVR model. Similar tendencies of lower error metrics for the SRA-MLPR model compared to the SRA-SVR model are observed in the error metrics of the other three hydrological stations. Consequently, it can be concluded that the SRA-MLPR model based on deep learning demonstrates superior performance and generalization capabilities compared to the SRA-SVR model based on machine learning. The conclusion that the performance of deep neural network models is superior to machine learning models is also reported in references^28,29.

Fig. 15

The MAPE and MSLE evaluation values for the predictions at the four major hydrological stations in the Yalong River basin by the two coupled models and their corresponding single models.

In summary, the coupled runoff prediction models, SRA-MLPR and SRA-SVR, proposed in this paper leverage the collaborative nature of multiple modules to effectively utilize the advantages of feature selection, elimination of redundant and collinear variables, ultimately achieving the goal of stable and high-precision runoff prediction. These models provide scientific basis and technical support for hydrological forecasting, water resources management, and environmental science. In comparison, the SRA-MLPR model demonstrates greater accuracy and more stable generalization performance because of the unique ability of the MLPR component to extract deep information and explore potential non-linear relationships between independent and target variables. Across the five evaluation metrics (NSE, RMSE, MAE, MAPE, and MSLE), the SRA-MLPR model consistently outperforms the SRA-SVR model, demonstrating significantly enhanced predictive accuracy. Particularly in simulating and forecasting monthly runoff peaks, troughs, and variations influenced by multiple factors, the SRA-MLPR can more accurately capture latent information within the data. The experimental results provide a solid scientific basis and practical foundation for the implementation of the coupled models in practical applications, which have significant practical and reference value for research in the fields of water resources management, hydrological forecasting, climate prediction, and environmental science.

SHAP-based interpretability analysis of model predictions

To enhance the interpretability of our runoff prediction model, we employed SHAP (SHapley Additive exPlanations) analysis to quantify the contribution of individual atmospheric circulation indices to the model’s output. The Guandi hydrological station was selected as a representative study site for this analysis. The results provide key insights into the dominant climate factors driving runoff variations and reveal complex nonlinear interactions among different teleconnection patterns. The analysis is structured as follows: (1) feature importance ranking, (2) impact directionality of key features, and (3) interactions among major predictors.

Fig. 16

The feature importance plot of the model prediction results.

Feature importance analysis

Figure 16 illustrates the relative contributions of various atmospheric circulation indices in the runoff prediction model, with feature importance measured by the mean SHAP values. The results indicate that the Northern Hemisphere Polar Vortex Central Intensity Index exerts a significantly greater influence than other features, with an average SHAP value reaching 609.46, far exceeding that of other variables. This suggests that this index plays a dominant role in the model’s predictions and is likely a crucial teleconnection factor affecting runoff in the basin. This may be related to the strong regulatory effect of polar vortex variations on cold air transport in high-latitude regions. When the polar vortex strengthens, cold air in high latitudes remains concentrated near the poles, leading to reduced precipitation in mid-latitude regions and subsequently impacting the runoff process in the basin. Conversely, when the polar vortex weakens or undergoes morphological changes (e.g., vortex breakdown), enhanced southward movement of cold air may result in extreme precipitation events, thereby altering the runoff pattern in the basin⁴⁸.

The East Asian Trough Intensity Index ranks second in SHAP value (308.25), indicating that this factor also has a significant impact on runoff prediction in the basin. This aligns with climatological research findings that the depth of the East Asian trough directly affects the distribution and intensity of precipitation in East Asia. When the trough deepens, cold air from high latitudes more easily interacts with warm, moist air from the south, leading to increased precipitation and subsequently higher runoff in the basin⁴⁹.

Other circulation indices, such as the Asia Polar Vortex Area Index, the Asian Zonal Circulation Index, and the North Atlantic Oscillation (NAO) Index, also exhibit significant influences, suggesting that teleconnection climate factors impact basin runoff through mechanisms such as wave train transmission and planetary wave modulation⁵⁰.

Overall, the SHAP analysis reveals the critical role of atmospheric circulation systems—including polar vortex activity, trough intensity, zonal circulation, and oscillations—in basin runoff prediction, providing a valuable basis for developing hydrological forecasting models based on teleconnection indices.

Fig. 17

Beeswarm plot of the influence of features on the model prediction results.

Feature impact directionality on prediction

Figure 17 further reveals the positive and negative impacts of different atmospheric circulation indices on runoff prediction, as indicated by the direction of SHAP values. Specifically:

• Northern Hemisphere Polar Vortex Central Intensity Index: The SHAP value distribution shows that higher values of this index are generally associated with increased runoff, whereas lower vortex intensity tends to result in reduced runoff. This suggests that changes in polar vortex intensity may influence precipitation distribution and runoff processes by adjusting atmospheric circulation patterns in the Northern Hemisphere. For example, when the polar vortex is strong, cold air remains trapped in high-latitude regions, leading to decreased precipitation in mid-latitudes and, consequently, reduced runoff. Conversely, when the polar vortex weakens or breaks down, cold air intrudes into mid-latitude regions, increasing the frequency of extreme precipitation events⁴⁸, which in turn leads to higher runoff.

• East Asian Trough Intensity Index: The SHAP value distribution exhibits a distinct nonlinear pattern. That is, within certain ranges, a deepened East Asian trough may lead to increased runoff, whereas under specific conditions (such as trough displacement or morphological changes), it may instead contribute to runoff reduction. This complex relationship suggests that the influence of the East Asian trough may depend on the synergistic effects of other climatic factors, such as the Pacific Decadal Oscillation (PDO) or El Niño-Southern Oscillation (ENSO)⁵¹.

• North Atlantic Oscillation (NAO) Index: The SHAP value distribution indicates a degree of uncertainty in the influence of this index on runoff prediction. This may be related to phase shifts in the NAO (positive vs. negative phase). For example, during a positive NAO phase, westerly winds in the North Atlantic strengthen, leading to intensified high-pressure systems over Europe and Siberia, which may suppress the southward movement of cold air in East Asia, thereby reducing precipitation and runoff. In contrast, during a negative NAO phase, weakened westerlies increase the likelihood of cold air intrusion into the Asian continent, potentially enhancing precipitation and increasing runoff⁵².

This result indicates that the impacts of different atmospheric circulation indices on runoff prediction do not exhibit a simple linear relationship; instead, they are modulated by more intricate hydrological-meteorological interactions.

Fig. 18

The influence of feature interactions on the model prediction results.

Feature interaction and nonlinear effects

Figure 18 illustrates the impact of interactions between different atmospheric circulation indices on runoff prediction. This figure reveals significant dependencies between key atmospheric indices, shedding light on complex teleconnection mechanisms. The main findings include:

• Interaction between the Northern Hemisphere Polar Vortex Intensity Index and the East Asian Trough Intensity Index: The results indicate that when the polar vortex strengthens and the East Asian trough deepens, the magnitude of runoff prediction fluctuations increases significantly. This may be related to the influence of the polar vortex on East Asian atmospheric circulation. Variations in polar vortex intensity can lead to adjustments in the westerly jet stream, which in turn affects the position and strength of the East Asian trough, ultimately impacting precipitation and runoff⁵³.

• Interaction between the North Atlantic Oscillation (NAO) Index and the Asia Polar Vortex Area Index: Although this interaction exhibits some uncertainty, a discernible trend is observed. Specifically, when the NAO is in a negative phase and the Asia Polar Vortex Area is relatively large, the variability in runoff predictions increases. This may suggest that under a negative NAO phase, polar air mass intrusions become more active, while changes in the Asia Polar Vortex Area may enhance or weaken this effect. NAO variations may indirectly influence East Asian hydroclimate through mechanisms such as planetary wave propagation or stratosphere-troposphere coupling⁵⁰.

• Interaction between the East Asian Trough Intensity Index and Mid-Latitude Circulation Factors: The results show that the impact of the East Asian trough may be modulated by zonal circulation patterns. For example, when both the East Asian trough intensity and the Asian Zonal Circulation Index are high, the range of variation in runoff predictions increases accordingly. This suggests that the depth of the trough and the configuration of the zonal circulation jointly determine moisture transport and precipitation patterns, thereby influencing runoff⁵⁴.

The SHAP interaction analysis provides deeper insights into the complex synergistic effects among atmospheric teleconnection indices, offering a novel perspective on how different climate factors collectively influence hydrological processes. Moreover, this analysis highlights that the impact of individual variables alone is insufficient to fully explain the model’s predictive mechanisms, and that interactions between atmospheric indices may play a crucial role in runoff evolution.

Conclusions and prospects

Conclusions

To enhance the precision of medium- and long-term runoff forecasting, this study developed and validated two advanced coupled models—SRA-SVR and SRA-MLPR—for runoff prediction, integrating statistical and machine learning methods. By leveraging multi-source data, including teleconnection indices, and optimizing feature selection through Stepwise Regression Analysis (SRA), the models demonstrated superior predictive accuracy and robustness in the Yalong River Basin compared to the baseline model.

By incorporating SHAP-based interpretability analysis, this study establishes a transparent and interpretable modeling framework aimed at precisely assessing the specific contributions of atmospheric circulation indices to runoff prediction. The research provides critical insights into the spatiotemporal correlations between atmospheric circulation and hydrological processes, as well as the lag effects of climate variables on basin-scale runoff dynamics. SHAP analysis further elucidates the nonlinear interactions among these variables, offering insights into how climate change governs extreme hydrological events.

This enhanced interpretability not only strengthens confidence in model predictions but also provides valuable scientific support for policymakers and water resource managers in formulating climate-resilient hydrological strategies. Moreover, the application of SHAP underscores the potential of integrating machine learning with interpretable artificial intelligence techniques to advance hydrological science, bridging the gap between predictive accuracy and decision-making utility.

The key findings are as follows:

• (1) The two coupled models proposed in this study performed remarkably well on the testing sets at multiple sites in the basin, significantly surpassing single baseline models like SVR and MLPR. In terms of the NSE metric, the SRA-MLPR coupled model achieved a maximum accuracy improvement of 13% compared to single baseline models; on the RMSE and MSLE metrics, the SRA-MLPR reduced errors by 26% and 37% respectively. This result validates the synergistic advantage of coupled models in integrating learning modules, enabling in-depth exploration of information within multi-source, high-dimensional variable data, and significantly enhancing the accuracy of runoff predictions.

• (2) This study introduced atmospheric circulation indices as teleconnection factors for predicting runoff, providing a richer dimension for describing runoff. Atmospheric circulation indices, as a natural and objective variable unaffected by human factors, enhance the credibility of model input variables and prediction results.

• (3) The study found that the effective lag time of atmospheric circulation indices impacting the study basin is approximately one month. Exploring the impact of lag periods of atmospheric circulation indices on basin runoff is of significant practical importance. It not only helps optimize basin water resources management proactively, enhancing flood control and disaster reduction capabilities, but also maximizes the comprehensive benefits of basin reservoirs.

• (4) The coupled models effectively identified key circulation indices within multidimensional atmospheric circulation indices that influence runoff, effectively addressing the challenge of large hydrological data volumes with sparse effective information. In a high-dimensional data environment, the model achieved robust feature selection, thereby improving accuracy in prediction tasks and obtaining more accurate forecast results. It also achieved robust feature selection in high-dimensional data, thus obtaining higher accuracy in prediction tasks.

• (5) Noteworthy is that in the evaluation of multiple site testing sets, the coupled deep learning model SRA-MLPR demonstrated significant advantages over the coupled machine learning model SRA-SVR across all evaluation metrics. Specifically, in terms of the accuracy metric NSE, the SRA-MLPR showed an accuracy improvement of approximately 6% compared to SRA-SVR. Regarding error metrics RMSE and MSLE, SRA-MLPR achieved error reduction rates of up to 20% and 29% respectively. This comparative result strongly highlights the outstanding potential of the coupled deep learning model in deep mining potential patterns in high-dimensional datasets, particularly in accurately capturing complex nonlinear correlations and addressing extreme runoff events, providing a more effective approach and method for solving complex issues in hydrological forecasting.

• (6) SHAP-based interpretability enhances understanding of atmospheric circulation influences on runoff prediction. The incorporation of SHAP (SHapley Additive exPlanations) analysis in this study provided crucial insights into the contribution and interactions of atmospheric circulation indices in runoff forecasting. Through SHAP-based feature attribution, it was determined that the Northern Hemisphere Polar Vortex Intensity Index and the East Asian Trough Intensity Index were the most influential climate drivers, significantly affecting runoff variability. Additionally, the interaction between these key indices and large-scale oscillations such as the North Atlantic Oscillation (NAO) and the Pacific Decadal Oscillation (PDO) revealed intricate nonlinear dependencies, reinforcing the necessity of considering multi-factor influences in hydrological modeling. Importantly, SHAP analysis identified that certain atmospheric circulation indices had asymmetric influences on runoff, meaning their impact varied depending on extreme versus normal runoff conditions. This not only enhances confidence in model predictions by improving interpretability but also provides valuable physical insights into hydroclimatic teleconnections, enabling water resource managers to better anticipate and mitigate runoff fluctuations. The successful integration of explainable AI techniques in hydrological forecasting underscores the potential of merging machine learning methodologies with domain-specific physical insights to drive more robust and actionable predictive modeling in hydroclimatic sciences.

The findings of this study not only advance runoff forecasting methodologies but also provide valuable insights into the interactions between atmospheric circulation patterns and hydrological processes. The incorporation of teleconnection indices and SHAP interpretability methods enhances the interpretability of predictive models, rendering them more applicable in climate change impact assessments and adaptive water management strategies. Moreover, the demonstrated superiority of deep learning-based coupled models highlights the increasingly significant role of artificial intelligence in hydrology, paving the way for future research on intelligent, data-driven water resource planning and disaster prevention on a global scale.

Limitations and prospects

The research findings undoubtedly provide crucial decision-making references for runoff prediction, flood and drought control, and comprehensive water resources utilization in the Yalong River basin. Simultaneously, they offer practical methodological insights and significant references for hydrology, meteorology, climatology, and environmental forecasting in other river basins.

However, there are still some limitations, which can be summarized into two aspects:

• (1) While the proposed coupled models (SRA-SVR and SRA-MLPR) demonstrate strong predictive performance and enhanced interpretability through SHAP analysis, their generalizability across different climatic and hydrological regimes warrants further investigation.

• (2) The models primarily focus on natural climatic and hydrological drivers, with limited consideration of human activities such as land-use changes, urbanization, or water extraction. These anthropogenic factors can significantly alter runoff dynamics, especially in highly developed or densely populated basins.

Future research will focus on developing data-driven algorithmic models that integrate self-interpretability to address the aforementioned challenges.