Magnetic targets positioning method based on multi-strategy improved Grey Wolf optimizer

Abstract

Magnetic target state estimation is a widely applied technology, but it also faces many challenges in practical applications. One of the most critical challenges is the issue of estimation accuracy. The Grey Wolf Optimizer (GWO) is one of the more successful swarm intelligence algorithms in recent years, but its shortcomings have also been exposed when facing increasingly complex problems. Therefore, a Multi-Strategy Improved Grey Wolf Optimizer (MSIGWO) algorithm has been proposed to enhance the accuracy of magnetic target state estimation. In the initialization phase, Tent chaos mapping is introduced to enhance population diversity, prevent falling into local optima, and improve convergence speed. Multi-population fusion evolution strategies enhance population diversity, convergence accuracy, and global search ability. Nonlinear convergence factors better balance exploration and exploitation behaviors. Dynamic weight strategies increase the diversity of search samples and reduce the likelihood of falling into local optima. Adaptive dimensional learning better balances local and global searches, enhancing population diversity. Adaptive Levy flight enhances the ability to jump out of local optima and ensures convergence speed. In the CEC2018 benchmark function set of 29 benchmark function problems and magnetic target state estimation problems, the proposed MSIGWO was tested, and statistical indicators and Friedman test results show that compared with GWO and its advanced variants, the MSIGWO algorithm has superior performance. The application of this algorithm in magnetic target state estimation problems has proven its effectiveness and applicability.

Introduction

Magnetic target state estimation refers to the process of modeling magnetic targets as equivalent magnetic source models such as magnetic dipoles, rotating ellipsoids, arrays of magnetic dipoles¹, and hybrid models of magnetic dipoles and ellipsoids. Based on the magnetic signals that these models generate as disturbances in the background geomagnetic field over time and space, an analytical inversion is performed to ultimately obtain the motion state and magnetic moment parameters of the target. The magnetic dipole model has few unknown parameters and requires less computation, making it suitable for far-field conditions, but it cannot accurately simulate the target’s magnetic field in the near field. Ellipsoidal models and hybrid models have high precision in simulating the target’s magnetic field and are suitable for near-field conditions, but they have many unknown parameters and require substantial computation. The array model of magnetic dipoles can simulate the target’s magnetic field well, with fewer unknown parameters and less computation, which is conducive to realizing target state estimation. The main methods for magnetic target state estimation include the magnetic gradient tensor analytical method², nonlinear filtering method³, parameter optimization-based inversion method⁴, and machine learning-based state estimation techniques⁵. For mobile magnetic targets that can be equivalent to a magnetic dipole model, based on the static magnetic field measured by three 3-axis orthogonal magnetic induction coil arrays, the target function of the magnetic field and magnetic target parameters is established according to the law of electromagnetic induction. The trajectory is estimated using the least squares method, and Luo et al. used polynomial fitting to estimate velocity and magnetic moments⁶. The 3 × 3 receiving coil sensor array can overcome to some extent the increased errors under low signal-to-noise ratio conditions and the overlap of multi-target responses. This array uses an improved magnetic gradient tensor for precise target localization⁷. Zhang et al. proposed a real-time magnetic moment inversion method based on a high-speed mobile platform, which can estimate the magnetic moments of underwater magnetic targets through high-precision scalar magnetic field measurement data from the high-speed mobile platform, but this method has weak anti-interference capabilities⁸. McGinnity et al. proposed a clustering detection method for unexploded ordnance, including signal preprocessing, filtering, clustering, and hierarchical inversion, with the advantages of fast inversion and strong noise resistance, but such methods are highly dependent on the dataset⁹. You et al. proposed a magnetic target localization method based on total field and its spatial gradient measurements, derived an approximate formula for the target azimuth vector represented by the total field and its gradient, and proposed an iterative method to improve the accuracy of magnetic target localization. Simulation experiments verified the performance of this method¹⁰. Miao et al. proposed a method for quickly locating unknown magnets using data from magnetic sensor arrays, obtained the three-dimensional approximate positions of multiple targets based on normalized source intensity and magnetic gradient tensor inversion, and used the trust region reflection algorithm for precise inversion of magnetic moments and positions¹¹. Liu proposed three simplified planar magnetic gradient tensor measurement structures and provided differential measurement matrices¹². Wahlstrom et al., based on the magnetic dipole array model, constructed the chi-square distribution of magnetic field observation residuals to complete the test of target model matching¹³. Li et al. significantly improved the computational efficiency of magnetic field analysis of SPM motors while maintaining high accuracy through an innovative multi-current parallel resolution method. The core value lies in breaking through the bottleneck of traditional models relying on repetitive calculations, and providing an efficient tool for the rapid optimisation and design of complex permanent magnet motors¹⁴. In terms of positioning, there are technical applications in various fields^15,16,17,18. Cheng et al. significantly improved RTK positioning availability and accuracy in urban environments through three-frequency signal level-by-level parsing and RANSAC anomaly detection, providing a reliable instantaneous centimeter-level solution for highly dynamic scenarios¹⁹. Sun et al. proposed a breadth-first search (BFS)-based Service Function Chain Deployment Optimization (SFCDO) algorithm. The algorithm first finds the shortest path between the source and destination nodes using a BFS-based algorithm. Then, based on the shortest path, the path with the least number of hops is prioritized to perform SFCF, and finally the performance of greedy and simulated annealing (G-SA) algorithms is compared²⁰. Guo et al. significantly improved the extrication capability of planetary probes in loose terrain by combining a novel sweep-rotation gait with a Bayesian optimization algorithm, and experimentally verified its effectiveness and trajectory accuracy. The method provides an innovative solution to address the key challenges in planetary exploration²¹. Yang et al. proposed a segmentation analysis method for the effect of ambient light in the time/space dimension, which provides a new perspective for VLP noise research, and RatioVLP calculates the distance ratio by RSS ratio, and then the LM algorithm optimizes the positioning²². Lei et al. combined MSE (mean square error) and SSIM (structural similarity) loss and balanced pixel-level error with overall structural similarity, constructed a hybrid loss function, introduced L2-TV least squares optimization to remove the noise interference, RefineNet network significantly improved the quality of the GPR profiles, and TV-RTM imaging algorithm to achieve high-precision positioning²³. Lu et al. proposed a stochastic link transmission model to significantly improve computational efficiency while maintaining accuracy by simplifying the state tracking dimension, solving the core bottleneck problem of large-scale traffic network optimization and providing an efficient theoretical tool for urban traffic management²⁴. Ma et al. achieved navigation in GPS-free environments through fully embedded sensing with wider applicability²⁵. However, the above methods have more or less problems.

Magnetic gradient tensor analytical methods require multiple magnetic sensors to work together, which presents issues with sensor compensation and calibration. Nonlinear filtering methods suffer from unknown initial states and difficulties in estimating noise. Machine learning-based state estimation techniques face issues with incomplete data set collection. Parameter optimization-based inversion methods can overcome the aforementioned problems, enabling state estimation of magnetic targets based on a single sensor²⁶. These methods rely on the magnetic field model of the target to minimize the difference between the measured and calculated magnetic fields using optimization algorithms, with the key lying in the design of the optimization algorithm². Optimization problems involve finding a set of decision variables to maximize or minimize an objective function under certain constraints, and metaheuristic algorithms have shown good performance in handling such complex problems²⁷.

Metaheuristic algorithms are divided into swarm intelligence algorithms, physics-based algorithms, evolutionary algorithms, and human-based algorithms²⁸. Swarm intelligence algorithms are the most representative metaheuristics, solving problems by simulating collective behaviors in nature, such as Particle Swarm Optimization (PSO)²⁹, Ant Colony Optimization (ACO)³⁰, and Moth-Flame Optimization (MFO)³¹. Various new metaheuristic algorithms have emerged since 2025. HawkFish Optimization Algorithm (HFOA) is inspired by the sex change behavior of hawkfish. The algorithm effectively balances the exploration and exploitation of the search space, avoids the trapping of local optimal solutions, and improves the optimization efficiency and the quality of the solution by introducing mechanisms such as double fitness function, dynamic clustering and visual range adjustment. The algorithm performs well in solving complex optimization problems and outperforms other traditional optimization algorithms³². The Dream Optimization Algorithm (DOA) is inspired by human dreams. The algorithm combines a basic memory strategy, a forgetting and replenishment strategy to balance exploration and exploitation. The advantages of DOA are efficient exploration-exploitation balance, multi-stage dynamic strategy, low parameter dependence, and strong robustness, and the disadvantages are high consumption of computational resources, insufficient theoretical analyses, limited adaptation to dynamic environments, and local search accuracy to be improved³³. Tornado optimizer with Coriolis force (TOC) is inspired by the cyclic process of tornadoes and the natural inspiration of thunderstorms and storms evolving into Coriolis force tornadoes. Its advantages include innovative nature-inspired mechanism, high success rate and robustness, and multi-stage dynamic optimization capability, but it has the disadvantages of high parameter sensitivity, high consumption of computational resources, and limited adaptability to specific scenarios³⁴. The Artificial Lemming Algorithm (ALA) is inspired by the understanding of four different behaviors of lemmings in nature: long-distance migration, digging holes, foraging for food and avoiding predators. ALA excels in complex optimization problems, but parameter sensitivity and computational efficiency need to be further addressed³⁵. In terms of hybrid optimization algorithms, Cui et al. proposed an improved snow ablation optimization algorithm (MESAO) by introducing a level-based selection pressure mechanism, a covariance matrix learning strategy, a boundary adjustment strategy based on the history position and a random centroid inverse learning strategy in snow ablation optimization (SAO)³⁶. In response to the problems that the vulture search algorithm is prone to fall into local optimum and has low convergence accuracy, Wang et al. a multi-strategy modified vulture search algorithm (MSBES) to solve these problems. Adaptive control factors are used to replace the key control parameters, play the adaptive characteristics in the algorithm search process, enrich the search mechanism, and effectively balance the algorithm utilization and exploration ability. The Levy flight and adaptive weight fusion strategy are introduced to update the position equation, expand the search range, avoid too much population assimilation at the end of iteration, and enhance the premature resistance of the algorithm. Finally, adaptive variance probability is employed to enhance the exploration ability, the ability to get rid of local extremes and the ability to maintain population diversity³⁷.In order to solve the problems of slow convergence and difficulty in avoiding local optima in Golden Jackal Optimization algorithm (GJO), Yang et al. proposed Multi-Strategy Golden Jackal Optimization algorithm (MSGJO), which employs the set of good points, quasi-inverse learning strategy, and Chaotic Circle Perturbation strategy to enhance the original GJO³⁸. Batis et al. proposed ACGRIME, an improved version of the RIME optimization algorithm, which integrates chaos theory, adaptive weighting and Gaussian mutation to address these limitations in order to enhance exploration, balance exploration and exploitation, and improve the quality of the solution³⁹.

The Grey Wolf Optimizer (GWO) is a swarm intelligence-based metaheuristic optimization algorithm inspired by the leadership hierarchy and hunting behavior of grey wolves, with advantages such as simple structure, few control parameters, clear concept, low computational complexity, and ease of implementation⁴⁰. However, compared to other algorithms, GWO also has certain limitations, such as insufficient global search capability, low precision, and low population diversity when solving high-dimensional optimization problems^41,42. Kohli et al. designed a Chaotic Grey Wolf Optimizer (CGWO), introducing chaotic strategies to adjust global optimization parameters and improve convergence speed⁴³. To address the lack of population diversity, imbalance between exploitation and exploration, and premature convergence in GWO, Mohammad et al. proposed an Improved Grey Wolf Optimizer (IGWO), designing a Dimension Learning-based Hunting (DLH) search strategy, where DLH constructs a neighborhood for each wolf, sharing neighborhood information among the wolf pack, and dimension learning balances local and global searches, enhancing population diversity⁴⁴. Ahmed et al. proposed a GWO with a repository, evolutionary operators, random local search, and linearly decreasing population size; the repository saves local optimal information, evolutionary operators increase the algorithm’s exploration capability and population diversity, random local search improves the algorithm’s exploitation ability, and the linearly decreasing population size technique reduces the population scale at each iteration⁴⁵. Tsai et al. studied the inherent flaws of GWO and proposed three correction strategies, including eliminating the coefficient vector C, removing the absolute sign of factor D, and introducing a current-prey method⁴⁶. Yu et al. designed an Adaptive Learning Grey Wolf Optimizer (ALGWO), using a dynamic asymmetric search dynamic reverse learning strategy to improve search capability and adaptive dimension learning to enhance population diversity⁴⁷. Wang et al. proposed a Hybrid Contact List Subpopulation Mixed Evolution Grey Wolf Optimizer (CSELGWO), where the contact list mechanism is used to obtain high-quality local optimal information in the search space, and the hybrid contact list subpopulation generation mechanism uses information from the contact list to assist subpopulation updates, enhancing population diversity and convergence accuracy, with an archive and activation mechanism for Levy flight to avoid falling into local optima⁴⁸.

The aforementioned literature indicates that no single optimization algorithm can solve all optimization problems. Therefore, a Multi-Strategy Improved Grey Wolf Optimizer (MSIGWO) has been proposed, which incorporates Tent chaos mapping initialization, multi-population fusion evolution, non-linear convergence factors, dynamic weight strategies, adaptive dimensional learning, and adaptive Levy flight. The Tent chaos mapping is introduced in the initialization phase to enhance population diversity, prevent falling into local optima, and improve convergence speed. The multi-population fusion evolution strategy enhances population diversity, convergence accuracy, and overall optimization capabilities. The non-linear convergence factor better balances exploration and exploitation behaviors. The dynamic weight strategy increases the diversity of search samples, reducing the likelihood of falling into local optima. Adaptive dimensional learning better balances local and global searches, enhancing population diversity. Adaptive Levy flight enhances the ability to escape from local optima and ensures convergence speed. The proposed MSIGWO was tested on the CEC2018 benchmark function set, which includes 29 standard functions, as well as magnetic target state estimation problems. Statistical indicators and Friedman test results show that the algorithm outperforms GWO⁴⁰, IGWO⁴⁴, MELGWO⁴⁵, MGWO⁴⁶, ALGWO⁴⁷ and CSELGWO⁴⁸ algorithms.

The structure of the remainder of this paper is as follows: Sect. 2 provides a detailed introduction to the magnetic target state estimation problem model and the objective function. Section 3 introduces the Grey Wolf Optimizer (GWO) algorithm. Section 4 describes in detail the proposed Multi-Strategy Improved Grey Wolf Optimizer (MSIGWO) algorithm. Section 5 validates the performance of the proposed algorithm through numerical experiments. Section 6 provides a detailed analysis of the results from the magnetic target state estimation simulation experiments. Section 7 discusses the proposed algorithm. Finally, Sect. 8 summarizes the research findings and provides an outlook on future work.

Magnetic target state estimation method

Magnetic target state estimation involves estimating the system state based on a set of observed magnetic field data, which includes parameters such as position, velocity, heading, length, and magnetic moment. The process is divided into data collection, target signal detection and extraction, and state optimization with magnetic moment inversion, as shown in the flowchart of Fig. 1.

Fig. 1

Magnetic target state estimation method flowchart.

Target signal detection and extraction

Due to the interference from environmental magnetic fields and sensor noise, the measured signals are susceptible to distortion when extracting the target signals. Therefore, a dynamic threshold-based target signal extraction method is designed below⁴⁹. After the target signals are extracted, a decimation strategy is employed to reduce the computational complexity.

The magnitude of the magnetic field after subtracting the magnetic field baseline is

$${B_k}=\sqrt {{{\left( {{B_{x,k}} - {b_{x,k}}} \right)}^2}+{{\left( {{B_{y,k}} - {b_{y,k}}} \right)}^2}+{{\left( {{B_{z,k}} - {b_{z,k}}} \right)}^2}}$$

(1)

Where, B_x,k, B_y,k, and B_z,k represent the magnetic field measurements from the sensor at time instance k, while b_x,k, b_y,k, and b_z,k represent the baseline magnetic fields along the three axes at time instance k.

The dynamic threshold is

$${D_{{\text{T,}}k}}=\left( {1+\tau } \right){B_{{\text{base,}}k}}$$

(2)

Where, τ is a coefficient. The baseline magnetic field B_base,k at time k is

$${B_{{\text{base,}}k}}=\left\{ {\begin{array}{*{20}{c}} {\left( {1 - \sigma } \right){B_{{\text{base,}}k - 1}}+\sigma {B_k},}&{{B_k}<{D_{{\text{T,}}k}}} \\ {{B_{{\text{base,}}k - 1}},}&{{B_k} \geqslant {D_{{\text{T,}}k}}} \end{array}} \right.$$

(3)

Where, σ is a coefficient.

The size of the real-time magnetic field B_k and the dynamic threshold D_T,k are compared to determine whether the target enters or leaves the sensor detection range.

$$Flag=\left\{ {\begin{array}{*{20}{c}} {1,}&{{B_k} \geqslant {D_{{\text{T,}}k}}} \\ {0,}&{{B_k}<{D_{{\text{T,}}k}}} \end{array}} \right.$$

(4)

Where, Flag = 1, indicating that the target enters the sensor detection range, otherwise, indicating that the target leaves the sensor detection range.

When the sensor detects the target signal, it is divided into five states: initial state S₀, no target S₁, target close to S₂, target signal S₃, and target away from S₄. The state transition relationship is shown in Fig. 2. The state transition can be described as:

Fig. 2

State transfer relationship diagram.

• (1) S₀→S₁: if the initialization is completed, it is transferred to a non-target state.

• (2) S₁→S₁: if the magnetic field modulus is less than the dynamic threshold, there is no target.

• (3) S₁→S₂: if the magnetic field modulus ≥ dynamic threshold, the counter C₁ = C₁ + 1, indicating that the target is entering.

• (4) S₂→S₂: if the magnetic field modulus ≥ dynamic threshold, the counter C₁ = C₁ + 1, and C₁ < N₁, indicating that the target is entering.

• (5) S₂→S₃: if the magnetic field modulus ≥ dynamic threshold, and C₁ ≥ N₁, it is the target signal.

• (6) S₃→S₃: if the magnetic field modulus ≥ dynamic threshold, it is the target signal.

• (7) S₃→S₄: if the magnetic field modulus < dynamic threshold, then the counter C₂ = C₂ + 1, indicating that the target is leaving.

• (8) S₄→S₄: if the magnetic field modulus is less than the dynamic threshold, the counter C₂ = C₂ + 1, and C₂ < N₂, indicating that the target is leaving.

• (9) S₄→S₃: if the magnetic field modulus ≥ dynamic threshold, and C₂ < N₂, it is the target signal.

• (10) S₄→S₁: if the magnetic field modulus < dynamic threshold, and C₂ ≥ N₂, there is no target.

Thus, the target signal can be effectively detected and extracted through the above state transition steps.

System state space model

The magnetic dipole array model has the advantages of strong expansibility, high precision of magnetic field fitting and low computational time complexity. Therefore, the magnetic dipole array model is used as the recognition model. The carrier {b} coordinate system is established with the magnetic target as the center, and the sensor {s} coordinate system is established with the magnetic sensor as the center. The magnetic dipole array is arranged vertically on the central axis of the target, as shown in Fig. 3.

Fig. 3

Magnetic dipole array model.

The magnetic field model of magnetic dipole array is

$$\left[ {\begin{array}{*{20}{c}} {{B_x}} \\ {{B_y}} \\ {{B_z}} \end{array}} \right]=\sum\limits_{{i=1}}^{M} {\left[ {\begin{array}{*{20}{c}} {a_{x}^{i}}&{a_{y}^{i}}&{a_{z}^{i}} \\ {b_{x}^{i}}&{b_{y}^{i}}&{b_{z}^{i}} \\ {c_{x}^{i}}&{c_{y}^{i}}&{c_{z}^{i}} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {m_{x}^{i}} \\ {m_{y}^{i}} \\ {m_{z}^{i}} \end{array}} \right]}$$

(5)

Where, ${\mathbf{B}}={\left[ {\begin{array}{*{20}{c}} {{B_x}}&{{B_y}}&{{B_z}} \end{array}} \right]^{\text{T}}}$ is the magnetic field in the {b} system, $m_{j}^{i}\left( {i=1,2, \cdots ,M;j=x,y,z} \right)$ is the magnetic moment of the j-axis of the i^th magnetic dipole in the {b} system, and the coefficients of the coefficient matrix are

$$\left\{ {\begin{array}{*{20}{c}} {a_{x}^{i}={{{\mu _0}\left( {3x{{_{{}}^{i}}^2} - {{\left\| {{{\varvec{r}}^i}} \right\|}^2}} \right)} \mathord{\left/ {\vphantom {{{\mu _0}\left( {3x{{_{{}}^{i}}^2} - {{\left\| {{{\varvec{r}}^i}} \right\|}^2}} \right)} {\left( {4\pi {{\left\| {{{\varvec{r}}^i}} \right\|}^5}} \right)}}} \right. \kern-0pt} {\left( {4\pi {{\left\| {{{\varvec{r}}^i}} \right\|}^5}} \right)}}}&{a_{y}^{i}={{3{\mu _0}{x^i}{y^i}} \mathord{\left/ {\vphantom {{3{\mu _0}{x^i}{y^i}} {\left( {4\pi {{\left\| {{{\varvec{r}}^i}} \right\|}^5}} \right)}}} \right. \kern-0pt} {\left( {4\pi {{\left\| {{{\varvec{r}}^i}} \right\|}^5}} \right)}}}&{a_{z}^{i}={{3{\mu _0}{x^i}{z^i}} \mathord{\left/ {\vphantom {{3{\mu _0}{x^i}{z^i}} {\left( {4\pi {{\left\| {{{\varvec{r}}^i}} \right\|}^5}} \right)}}} \right. \kern-0pt} {\left( {4\pi {{\left\| {{{\varvec{r}}^i}} \right\|}^5}} \right)}}} \\ {b_{x}^{i}=a_{y}^{i}}&{b_{y}^{i}={{{\mu _0}\left( {3y{{_{{}}^{i}}^2} - {{\left\| {{{\varvec{r}}^i}} \right\|}^2}} \right)} \mathord{\left/ {\vphantom {{{\mu _0}\left( {3y{{_{{}}^{i}}^2} - {{\left\| {{{\varvec{r}}^i}} \right\|}^2}} \right)} {\left( {4\pi {{\left\| {{{\varvec{r}}^i}} \right\|}^5}} \right)}}} \right. \kern-0pt} {\left( {4\pi {{\left\| {{{\varvec{r}}^i}} \right\|}^5}} \right)}}}&{b_{z}^{i}={{3{\mu _0}{y^i}{z^i}} \mathord{\left/ {\vphantom {{3{\mu _0}{y^i}{z^i}} {\left( {4\pi {{\left\| {{{\varvec{r}}^i}} \right\|}^5}} \right)}}} \right. \kern-0pt} {\left( {4\pi {{\left\| {{{\varvec{r}}^i}} \right\|}^5}} \right)}}} \\ {c_{x}^{i}=a_{z}^{i}}&{c_{y}^{i}=b_{z}^{i}}&{c_{z}^{i}={{{\mu _0}\left( {3{z^i}^{2} - {{\left\| {{{\varvec{r}}^i}} \right\|}^2}} \right)} \mathord{\left/ {\vphantom {{{\mu _0}\left( {3{z^i}^{2} - {{\left\| {{{\varvec{r}}^i}} \right\|}^2}} \right)} {\left( {4\pi {{\left\| {{{\varvec{r}}^i}} \right\|}^5}} \right)}}} \right. \kern-0pt} {\left( {4\pi {{\left\| {{{\varvec{r}}^i}} \right\|}^5}} \right)}}} \end{array}} \right.$$

(6)

${\mu _0}=4\pi \times {10^{ - 7}}{H \mathord{\left/ {\vphantom {H m}} \right. \kern-0pt} m}$ is the vacuum permeability, ${\varvec{r}}_{{}}^{i}={\varvec{r}} - {\varvec{r}}_{{\text{d}}}^{i}$ is the coordinate of the magnetic sensor relative to the i^th magnetic dipole in the {b} system, ${\varvec{r}}={\left[ {\begin{array}{*{20}{c}} x&y&z \end{array}} \right]^{\text{T}}}$ is the coordinate of the magnetic sensor in the {b} system, ${\varvec{r}}_{{\text{d}}}^{i}={\left[ {\begin{array}{*{20}{c}} {\left( {i - {{\left( {M+1} \right)} \mathord{\left/ {\vphantom {{\left( {M+1} \right)} 2}} \right. \kern-0pt} 2}} \right)\Delta L}&0&0 \end{array}} \right]^{\text{T}}}$ is the coordinate of the i^th magnetic dipole, and $\Delta L={L \mathord{\left/ {\vphantom {L {\left( {M - 1} \right)}}} \right. \kern-0pt} {\left( {M - 1} \right)}}$ is the magnetic dipole spacing.

The magnetic target with fixed depth and low dynamic motion is modeled as CV model^50,51.

$${{\mathbf{r}}_k}=\left[ {\begin{array}{*{20}{c}} {{x_k}} \\ {{y_k}} \\ {{z_k}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} {{x_{k - 1}} - v{T_{\text{s}}}} \\ {{y_{k - 1}}} \\ {{z_{k - 1}}} \end{array}} \right]$$

(7)

Where, ${{\mathbf{r}}_k}={\left[ {\begin{array}{*{20}{c}} {{x_k}}&{{y_k}}&{{z_k}} \end{array}} \right]^{\text{T}}}$ is the coordinate of the magnetic sensor in the {b} system at time k, v is the target velocity modulus, and T_s is the sampling interval. The transformation matrix from {b} to {s} is

$${\varvec{C}}_{{\text{b}}}^{{\text{s}}}=\left[ {\begin{array}{*{20}{c}} {\cos \left( \theta \right)}&{\sin \left( \theta \right)}&0 \\ { - \sin \left( \theta \right)}&{\cos \left( \theta \right)}&0 \\ 0&0&1 \end{array}} \right]$$

(8)

θ is the angle(heading) between the x-direction of {b} and the x-direction of {s}, $\theta \in \left[ {0,2\pi } \right)$.

From formulas (5), (7) and (8), the magnetic field observation model in the {s} system can be obtained.

$$\left[ {\begin{array}{*{20}{c}} {{{\tilde {B}}_x}\cos \left( \theta \right) - {{\tilde {B}}_y}\sin \left( \theta \right)} \\ {{{\tilde {B}}_x}\sin \left( \theta \right)+{{\tilde {B}}_y}\cos \left( \theta \right)} \\ {{{\tilde {B}}_z}} \end{array}} \right]=\sum\limits_{{i=1}}^{M} {\left[ {\begin{array}{*{20}{c}} {a_{x}^{i}}&{a_{y}^{i}}&{a_{z}^{i}} \\ {b_{x}^{i}}&{b_{y}^{i}}&{b_{z}^{i}} \\ {c_{x}^{i}}&{c_{y}^{i}}&{c_{z}^{i}} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {m_{x}^{i}} \\ {m_{y}^{i}} \\ {m_{z}^{i}} \end{array}} \right]}$$

(9)

Where, ${\mathbf{\tilde {B}}}={\left[ {\begin{array}{*{20}{c}} {{{\tilde {B}}_x}}&{{{\tilde {B}}_y}}&{{{\tilde {B}}_z}} \end{array}} \right]^{\text{T}}}$ is the magnetic field in the {s} system.

State optimization and magnetic moment inversion

The magnetic field observation model (9) is transformed into

$${\mathbf{B}}={\mathbf{Fm}}$$

(10)

Where, B, F and m are the measured magnetic field, magnetic moment and coefficient matrix in the {b} system, respectively, expressed as

$${\mathbf{B}}={\left[ {\begin{array}{*{20}{c}} {B_{{x1}}^{{}}}& \cdots &{B_{{xN}}^{{}}}&{B_{{y1}}^{{}}}& \cdots &{B_{{yN}}^{{}}}&{B_{{z1}}^{{}}}& \cdots &{B_{{zN}}^{{}}} \end{array}} \right]^{\text{T}}} \in {{\mathbb{R}}^{3N}}$$

(11)

$${\mathbf{F}}=\left[ {\begin{array}{*{20}{c}} {a_{{x1}}^{1}}&{a_{{y1}}^{1}}&{a_{{z1}}^{1}}& \cdots &{a_{{x1}}^{M}}&{a_{{y1}}^{M}}&{a_{{z1}}^{M}} \\ \vdots & \vdots & \vdots & \cdots & \vdots & \vdots & \vdots \\ {a_{{xN}}^{{\text{1}}}}&{a_{{yN}}^{{\text{1}}}}&{a_{{zN}}^{{\text{1}}}}& \cdots &{a_{{xN}}^{M}}&{a_{{yN}}^{M}}&{a_{{zN}}^{M}} \\ {b_{{x1}}^{1}}&{b_{{y1}}^{1}}&{b_{{z1}}^{1}}& \cdots &{b_{{x1}}^{M}}&{b_{{y1}}^{M}}&{b_{{z1}}^{M}} \\ \vdots & \vdots & \vdots & \cdots & \vdots & \vdots & \vdots \\ {b_{{xN}}^{{\text{1}}}}&{b_{{yN}}^{{\text{1}}}}&{b_{{zN}}^{{\text{1}}}}& \cdots &{b_{{xN}}^{M}}&{b_{{yN}}^{M}}&{b_{{zN}}^{M}} \\ {c_{{x1}}^{1}}&{c_{{y1}}^{1}}&{c_{{z1}}^{1}}& \cdots &{c_{{x1}}^{M}}&{c_{{y1}}^{M}}&{c_{{z1}}^{M}} \\ \vdots & \vdots & \vdots & \cdots & \vdots & \vdots & \vdots \\ {c_{{xN}}^{{\text{1}}}}&{c_{{yN}}^{{\text{1}}}}&{c_{{zN}}^{{\text{1}}}}& \cdots &{c_{{xN}}^{M}}&{c_{{yN}}^{M}}&{c_{{zN}}^{M}} \end{array}} \right] \in {{\mathbb{R}}^{3N \times 3M}}$$

(12)

$${\mathbf{m}}={\left[ {\begin{array}{*{20}{c}} {m_{x}^{1}}&{m_{y}^{1}}&{m_{z}^{1}}& \cdots &{m_{x}^{M}}&{m_{y}^{M}}&{m_{z}^{M}} \end{array}} \right]^{\text{T}}} \in {{\mathbb{R}}^{3M}}$$

(13)

The unknown state vector of Eq. (10) is

$${\mathbf{x}}={\left[ {\begin{array}{*{20}{c}} x&y&v&\theta &{\Delta L}&{m_{x}^{1}}&{m_{y}^{1}}&{m_{z}^{1}}& \cdots &{m_{x}^{M}}&{m_{y}^{M}}&{m_{z}^{M}} \end{array}} \right]^{\text{T}}} \in {{\mathbb{R}}^{5+3M}}$$

(14)

The condition for the existence of solutions is N ≥ 2 + M.

The magnetic target state estimation problem is equivalent to solving the following optimization problem.

$${\mathbf{\hat {x}}}=\mathop {\arg \hbox{min} }\limits_{{\mathbf{x}}} J\left( {\mathbf{x}} \right)=\mathop {\arg \hbox{min} }\limits_{{\mathbf{x}}} \frac{{{{\left( {{\mathbf{B}} - {\mathbf{Fm}}} \right)}^{\text{T}}}\left( {{\mathbf{B}} - {\mathbf{Fm}}} \right)}}{{{{\mathbf{B}}^{\text{T}}}{\mathbf{B}}}}$$

(15)

Where, ${\mathbf{\hat {x}}}$ is the estimated state, the fitness function J(x) depends on B, F, m, and F depends on ${\mathbf{\tilde {x}}}={\left[ {\begin{array}{*{20}{c}} x&y&v&\theta &{\Delta L} \end{array}} \right]^{\text{T}}}$.

The steps of state optimization and magnetic moment inversion are:

• (1) The intelligent optimization algorithm initializes ${\mathbf{\tilde {x}}}={\left[ {\begin{array}{*{20}{c}} x&y&v&\theta &{\Delta L} \end{array}} \right]^{\text{T}}}$ and substitutes it into Eq. (10). The magnetic moment ${\mathbf{\hat {m}}}$ is calculated by the magnetic moment solution method.

• (2) Substituting the magnetic moment ${\mathbf{\hat {m}}}$ into the Eq. (15), the fitness function becomes.

$$J\left( {{\mathbf{\tilde {x}}}} \right)=\frac{{{{\left( {{\mathbf{B}} - {\mathbf{F\hat {m}}}} \right)}^{\text{T}}}\left( {{\mathbf{B}} - {\mathbf{F\hat {m}}}} \right)}}{{{{\mathbf{B}}^{\text{T}}}{\mathbf{B}}}}$$

(16)

Taking $J\left( {{\mathbf{\tilde {x}}}} \right)$ as the fitness function, the intelligent optimization algorithm is used to solve ${\mathbf{\tilde {x}}}$.

• (3) Repeat step (1) until the stopping condition is satisfied. Finally, the estimated state is obtained.

Evaluation

To evaluate the state estimation accuracy, the Root Mean Square Error (RMSE) or Relative Root Mean Square Error (RRMSE) of each component of the state vector is defined as

$$RMS{E_{\mathbf{r}}}=\sqrt {\frac{1}{{{M_C}}}\sum\limits_{{i=1}}^{{{M_C}}} {\left\| {{{{\mathbf{\hat {r}}}}_i} - {{\mathbf{r}}_i}} \right\|_{{}}^{2}} }$$

(17)

$$RMS{E_v}=\sqrt {\frac{1}{{{M_C}}}\sum\limits_{{i=1}}^{{{M_C}}} {{{\left| {{{\hat {v}}_i} - {v_i}} \right|}^2}} }$$

(18)

$$RMS{E_\theta }=\sqrt {\frac{1}{{{M_C}}}\sum\limits_{{i=1}}^{{{M_C}}} {{{\left| {{{\hat {\theta }}_i} - {\theta _i}} \right|}^2}} }$$

(19)

$$RMS{E_L}=\sqrt {\frac{1}{{{M_C}}}\sum\limits_{{i=1}}^{{{M_C}}} {{{\left| {{{\hat {L}}_i} - {L_i}} \right|}^2}} }$$

(20)

$$RRMS{E_{\mathbf{m}}}=\sqrt {\frac{1}{{{M_C}}}\sum\limits_{{i=1}}^{{{M_C}}} {\frac{{{{\left\| {{{{\mathbf{\hat {m}}}}_i} - {{\mathbf{m}}_i}} \right\|}^2}}}{{{{\left\| {{{\mathbf{m}}_i}} \right\|}^2}}}} }$$

(21)

Where M_C is the number of Monte-Carlo trials. ${{\mathbf{\hat {r}}}_i}$, ${\hat {v}_i}$, ${\hat {\theta }_i}$, ${\hat {L}_i}$ are the estimated values of position, speed, heading, length, and magnetic moment in the i^th trial, respectively; ${{\mathbf{r}}_i}$, ${v_i}$, ${\theta _i}$, ${L_i}$, ${{\mathbf{m}}_i}$ are the true values of position, speed, heading, length, and magnetic moment in the i^th trial, respectively.

Grey Wolf optimizer

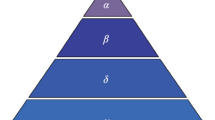
The structure of GWO is simple, and the parameter setting only needs to set the population size and the number of iterations. The local search level is high, which can better balance the exploration and development, and has a faster convergence speed⁵². GWO mimics the social hierarchy and hunting techniques of grey wolves. The social hierarchy is divided into α, β, δ and ω from high to low. α is the first optimal solution, β is the second optimal solution and is led by α, δ is the third optimal solution and is led by α and β, ω is an ordinary wolf and is led by α, β and δ. Hunting behavior is modeled as: search, track and approach prey, chase and encircle prey, attack and capture prey.

(1) Search, track and approach prey.

The process of searching, tracking and approaching prey is the algorithm initialization and initial iteration stage. The initialization process is

$$\begin{array}{*{20}{c}} {{X_{ij}}={l_j}+rand \cdot \left( {{u_j} - {l_j}} \right),}&{i \in \left[ {1,{N_{\text{p}}}} \right],}&{j \in \left[ {1,D} \right]} \end{array}$$

(22)

Where, $\left[ {{l_j},{u_j}} \right]$ is the search space, N_pop is the population size, and D is the population dimension.

(2) Pursuing and encircling prey.

The mathematical model of encirclement is

$${\mathbf{X}}\left( {t+1} \right)={{\mathbf{X}}_{\text{p}}}\left( t \right) - {\mathbf{AD}}$$

(23)

$${\mathbf{D}}\left( t \right)=\left| {{\mathbf{C}}{{\mathbf{X}}_{\text{p}}}\left( t \right) - {\mathbf{X}}\left( t \right)} \right|$$

(24)

Where, t is the current iteration number, X is the gray wolf position vector, X_p is the prey position vector, and D is the distance vector. The coefficients A and C are

$${\mathbf{A}}=2{\mathbf{a}}{{\mathbf{r}}_1} - {\mathbf{a}}$$

(25)

$${\mathbf{C}}=2{{\mathbf{r}}_2}$$

(26)

$${\mathbf{a}}=2 - 2\frac{t}{T}$$

(27)

Where, r₁ and r₂ are uniformly distributed random vectors in [0,1], a is the convergence factor, and T is the maximum number of iterations.

(3) Attack and capture prey.

The mathematical model of attack capture is

$$\left\{ \begin{gathered} {{\mathbf{X}}_1}\left( t \right)={{\mathbf{X}}_\alpha }\left( t \right) - {{\mathbf{A}}_1}{{\mathbf{D}}_\alpha }\left( t \right) \\ {{\mathbf{X}}_2}\left( t \right)={{\mathbf{X}}_\beta }\left( t \right) - {{\mathbf{A}}_2}{{\mathbf{D}}_\beta }\left( t \right) \\ {{\mathbf{X}}_3}\left( t \right)={{\mathbf{X}}_\delta }\left( t \right) - {{\mathbf{A}}_3}{{\mathbf{D}}_\delta }\left( t \right) \\ \end{gathered} \right.$$

(28)

$$\left\{ \begin{gathered} {{\mathbf{D}}_\alpha }\left( t \right)=\left| {{{\mathbf{C}}_1}{{\mathbf{X}}_\alpha }\left( t \right) - {\mathbf{X}}\left( t \right)} \right| \\ {{\mathbf{D}}_\beta }\left( t \right)=\left| {{{\mathbf{C}}_2}{{\mathbf{X}}_\beta }\left( t \right) - {\mathbf{X}}\left( t \right)} \right| \\ {{\mathbf{D}}_\delta }\left( t \right)=\left| {{{\mathbf{C}}_3}{{\mathbf{X}}_\delta }\left( t \right) - {\mathbf{X}}\left( t \right)} \right| \\ \end{gathered} \right.$$

(29)

$${\mathbf{X}}\left( {t+1} \right)=\frac{{{{\mathbf{X}}_1}\left( t \right)+{{\mathbf{X}}_2}\left( t \right)+{{\mathbf{X}}_3}\left( t \right)}}{3}$$

(30)

Where, X₁, X₂, X₃ are the transfer vectors used to update the gray wolf position, X_α, X_β, X_δ are the first three best solutions of the current iteration, A₁, A₂, A₃ are calculated by Eq. (25), C₁, C₂, C₃ are calculated by Eq. (26), D_α, D_β, D_δ are calculated by Eq. (29), X(t + 1) is the gray wolf update position.

When the prey stops moving, the hunting process ends and the wolves begin to attack. Controlled by parameters a and A, the first half of the GWO iteration time is used to explore and find the global solution, and the second half of the iteration time is used to develop and find the exact solution.

The GWO flow chart is shown in Fig. 4. The GWO pseudocode is shown in Algorithm 1.

Fig. 4

The flowchart of GWO.

Algorithm 1

The pseudo-code of GWO.

Multi-strategy improved grey Wolf optimizer

GWO has problems such as low population diversity, premature convergence, and easy to fall into local optimum⁴⁷. In the later stage of iteration, the algorithm is easy to fall into local optimum because of the decrease of convergence factor a and the decrease of exploration ability. If α, β and δ fall into local optimum, it is difficult to escape from local optimum in a short time. Therefore, design improvement measures to improve the performance of the algorithm.

Initialization of tent chaotic map

In the GWO initialization stage, the wolves are randomly initialized, and there are problems such as uneven distribution of wolves, too close or sparse between each other, which easily leads to the algorithm falling into local optimum. Chaotic maps such as Tent map, Chebyshev map, Sine map and Logistic map can produce a variety of sequences⁵³. Among them, Logistic chaotic map has the problems of small range of chaotic parameters and small mapping interval. Sine map has the phenomenon of boundary aggregation, while Tent chaotic map has the advantages of uniform distribution and low computational complexity, so as to avoid the algorithm falling into local optimum. The mapping iteration formula is⁵³:

$${\varsigma _{n+1}}=\left\{ {\begin{array}{*{20}{c}} {\frac{{{\varsigma _n}}}{\kappa },}&{0 \leqslant {\varsigma _n}<\kappa } \\ {\frac{{1 - {\varsigma _n}}}{{1 - \kappa }},}&{\kappa \leqslant {\varsigma _n} \leqslant 1} \end{array}} \right.$$

(31)

Where, n is the number of chaotic iterations, ${\varsigma _n} \in \left[ {0,1} \right]$, and the chaotic factor $\kappa =0.7$.

Thus, the initialization process becomes

$$\begin{array}{*{20}{c}} {{X_{ij}}={l_j}+{\varsigma _i}\left( {{u_j} - {l_j}} \right),}&{i \in \left[ {1,{N_{\text{p}}}} \right],}&{j \in \left[ {1,D} \right]} \end{array}$$

(32)

Let the chaotic initial state ${\varsigma _0}=rand\left[ {0,1} \right]$, the number of chaotic map iterations ${N_{\text{p}}}=1000$, Tent chaotic map and random iteration results are shown in Fig. 5. It can be seen from Fig. 5 that the Tent chaotic map is more evenly distributed.

Fig. 5

The value of the chaotic sequence.

Multi-population fusion evolution

The population evolution of GWO is completed only by the positional update of α, β, and δ wolves, while the information of α, β, and δ wolves has limitation, which will lead to the decrease of population diversity. Therefore, multiple population mechanisms based on contact lists are introduced to enhance the global optimization search capability⁴⁸.

The order of individuals in the original population was disturbed and they were equally distributed into sub-populations, and then contact lists were constructed for the individuals in the sub-populations separately and the sub-populations were updated. A random selection method was used to generate the sub-populations⁴⁸

$${{\mathbf{X}}_{sub}}={{\mathbf{X}}_{best}}+rand\left( {{\mathbf{S}} - {\mathbf{C}}} \right)$$

(33)

Where, ${{\mathbf{X}}_{sub}}$ is the subpopulation location, ${{\mathbf{X}}_{best}}$ is the optimal solution for each subpopulation, ${\mathbf{S}}$ is a random individual of the subpopulation, and ${\mathbf{C}}$ is a high-quality individual in the contact list that can provide information about the local optimum.

In order to enhance subpopulation diversity, an iterative recombination mechanism is introduced to enable information exchange between subpopulations, with an iterative recombination interval of

$${D_r}=\left\lceil {{d_{\hbox{max} }} - \left( {{d_{\hbox{max} }} - {d_{\hbox{min} }}} \right)\frac{t}{T}} \right\rceil$$

(34)

Where, ${d_{\hbox{max} }}$ and ${d_{\hbox{min} }}$ are the upper and lower limits of recombination time, respectively. At the beginning of the iteration, the frequency of recombination is low due to the high diversity of subpopulations; at the end of the iteration, the frequency of recombination is high and is used to improve the diversity. After extensive testing, d_max=30 and d_min=5.

Drawing on the idea that DE algorithm generates the next-generation populations through the differences between different individuals, it takes advantage of the high diversity of sub-populations to deeply interact the different information between the main population and each sub-population in order to improve the exploration efficiency. The information interaction formula is⁴⁸.

$$\left\{ {\begin{array}{*{20}{c}} {{\mathbf{V}}\left( {t+1} \right)={{\mathbf{X}}_{rand}}+F\left( t \right)\left( {{{\mathbf{X}}_{sub1}} - {{\mathbf{X}}_{sub2}}} \right),}&{if rand<R} \\ {{\mathbf{V}}\left( {t+1} \right)={{\mathbf{X}}_{rand}}+F\left( t \right)\left( {{{\mathbf{X}}_{sub3}} - {{\mathbf{X}}_{sub4}}} \right),}&{if rand>R} \end{array}} \right.$$

(35)

$$F\left( t \right)=1 - \left| {rand\left[ {\frac{{{N_{\text{p}}}\arctan \left( t \right)}}{T},0.01} \right] - 0.5} \right|$$

(36)

Where, ${{\mathbf{X}}_{rand}}$ is a randomly selected individual in the main population and ${{\mathbf{X}}_{sub}}$ is an individual in a sub-population. R = 0.5 is the population that changes the scale factor to control the information exchange through rand and R. $rand\left[ {{{{N_{\text{p}}}\arctan \left( t \right)} \mathord{\left/ {\vphantom {{{N_{\text{p}}}\arctan \left( t \right)} T}} \right. \kern-0pt} T},0.01} \right]$ denotes the generation of uniformly distributed random numbers within $\left[ {{{{N_{\text{p}}}\arctan \left( t \right)} \mathord{\left/ {\vphantom {{{N_{\text{p}}}\arctan \left( t \right)} T}} \right. \kern-0pt} T},0.01} \right]$. V is the newly generated population.

To generate further diverse populations, new populations are generated from ${X_j}\left( {t+1} \right)$ and ${V_j}\left( {t+1} \right)$ as

$$\left\{ {\begin{array}{*{20}{c}} {{U_j}\left( {t+1} \right)={V_j}\left( {t+1} \right),}&{if rand \leqslant CR,}&{j=1,2, \cdots ,D} \\ {{U_j}\left( {t+1} \right)={X_j}\left( {t+1} \right),}&{if rand>CR,}&{j=1,2, \cdots ,D} \end{array}} \right.$$

(37)

Where j = 1, 2, … D is the population dimension and CR = 0.9 is the scale factor.

Then, the fitness values of the new population U and the original population X generated by the information interaction are compared, and the dominant population is selected as the updated population

$$\left\{ {\begin{array}{*{20}{c}} {{X_j}\left( {t+1} \right)={U_j}\left( {t+1} \right),}&{if f\left( {{U_j}\left( {t+1} \right)} \right)<f\left( {{X_j}\left( {t+1} \right)} \right),}&{j=1,2, \cdots ,D} \\ {{X_j}\left( {t+1} \right)={X_j}\left( t \right),}&{if f\left( {{X_j}\left( t \right)} \right) \leqslant f\left( {{U_j}\left( {t+1} \right)} \right),}&{j=1,2, \cdots ,D} \end{array}} \right.$$

(38)

As a result, the evolution of population convergence and the enhancement of population diversity are achieved through the interaction of population information.

Nonlinear convergence factor

The algorithm must balance 2 modes of behavior, exploration and exploitation, during the iteration process. In the early iteration process, the algorithm should have strong global exploration capability and perform local exploitation, while in the late iteration it must have strong local exploitation capability to obtain more accurate information. The linear convergence factor of GWO cannot accurately balance the 2 phases of exploration and exploitation, so a more reasonable nonlinear convergence factor must be designed to balance exploration and exploitation. For this reason, a nonlinear convergence factor is introduced⁵⁴:

$$a=\left\{ {\begin{array}{*{20}{c}} {1+\cos {{\left[ {\pi \left( {\frac{{t - 1}}{{T - 1}}} \right)} \right]}^\eta },}&{if t \leqslant 0.5T} \\ {1 - {{\left| {\cos \left[ {\pi \left( {\frac{{t - 1}}{{T - 1}}} \right)} \right]} \right|}^\eta },}&{if t>0.5T} \end{array}} \right.$$

(39)

Where, the coefficient $\eta \in \left( {0,1} \right]$, which is taken as 0.7 in this paper.

In order to verify the validity of the above nonlinear convergence factors, they are compared with the convergence factors proposed in the literature^55,56, denoted by ${a_1}$, ${a_2}$, ${a_3}$ and ${a_4}$, respectively.

$${a_1}=\left\{ {\begin{array}{*{20}{c}} {1+\cos {{\left[ {\pi \left( {\frac{{t - 1}}{{T - 1}}} \right)} \right]}^\eta },}&{if t \leqslant 0.5T} \\ {1 - {{\left| {\cos \left[ {\pi \left( {\frac{{t - 1}}{{T - 1}}} \right)} \right]} \right|}^\eta },}&{if t>0.5T} \end{array}} \right.$$

(40)

$${a_2}=2 - 2\tan \left( {\frac{{\pi t}}{{4T}}} \right)$$

(41)

$${a_3}=2 - 2\sin \left( {\frac{{\pi {t^2}}}{{2{T^2}}}} \right)$$

(42)

$${a_4}=2 - \frac{{2t}}{T}$$

(43)

The a-values of the four factors change with iteration as shown in Fig. 6, with larger a-values at the beginning of the iteration making the coefficients $\left| {\mathbf{A}} \right|>1$ with strong global exploration capability, and smaller a-values at the end of the iteration making the coefficients $\left| {\mathbf{A}} \right|<1$ with strong local exploitation capability.

Fig. 6

Nonlinear convergence factor.

Dynamic weights

The equal weights used for the grey wolf ω position update in GWO will reduce the convergence speed of the algorithm, because the information held by the three species of wolves α, β and δ for the position update is different, and their contributions to the position update should also be different. For this reason, after introducing the dynamic weighting strategy, the optimal candidate solution ${{\mathbf{X}}_{i - {\text{GWO}}}}$ is

$${{\mathbf{X}}_{i - {\text{GWO}}}}\left( {t+1} \right)={w_1}{{\mathbf{X}}_1}\left( t \right)+{w_2}{{\mathbf{X}}_2}\left( t \right)+{w_3}{{\mathbf{X}}_3}\left( t \right)$$

(44)

$${w_1}=\frac{{f\left( {{{\mathbf{X}}_\alpha }} \right)}}{{f\left( {{{\mathbf{X}}_\alpha }} \right)+f\left( {{{\mathbf{X}}_\beta }} \right)+f\left( {{{\mathbf{X}}_\delta }} \right)}}$$

(45)

$${w_2}=\frac{{f\left( {{{\mathbf{X}}_\beta }} \right)}}{{f\left( {{{\mathbf{X}}_\alpha }} \right)+f\left( {{{\mathbf{X}}_\beta }} \right)+f\left( {{{\mathbf{X}}_\delta }} \right)}}$$

(46)

$${w_3}=\frac{{f\left( {{{\mathbf{X}}_\delta }} \right)}}{{f\left( {{{\mathbf{X}}_\alpha }} \right)+f\left( {{{\mathbf{X}}_\beta }} \right)+f\left( {{{\mathbf{X}}_\delta }} \right)}}$$

(47)

Where, X_α, X_β and X_δ are the first 3 best solutions of the current iteration, $f\left( \cdot \right)$ is the fitness function, and ${w_1}$, ${w_2}$, ${w_3}$ is the dynamic weight. In the implementation of minimum optimality search with ${w_1}<{w_2}<{w_3}$, the weights are δ, β, α in descending order, at the beginning of iteration α, β, δ are far away, the ordering of ${w_1}<{w_2}<{w_3}$ facilitates the global exploration, at the later stage of iteration α, β, δ become closer, the ordering of ${w_1}<{w_2}<{w_3}$ avoids the algorithm from precociousness, increases the diversity of searching samples, and decreases the possibility of falling into the local optimum.

Adaptive dimensional learning

In GWO, the optimal candidate solution ${{\mathbf{X}}_{i - {\text{GWO}}}}$ updated based on the positions of α, β, and δ without utilizing the positional information between individuals, and thus the population diversity may decrease. Adaptive dimensional learning is able to share the neighborhoods information between individuals to generate the second optimal candidate solutions ${{\mathbf{X}}_{i - {\text{ADL}}}}$, which improves the global exploration ability⁴⁷.

The neighbors of an individual ${{\mathbf{X}}_i}$ are represented as

$${{\mathbf{X}}_{i - {\text{N}}}}\left( t \right)=\left\{ {\left. {{{\mathbf{X}}_i}\left( t \right)} \right|\left\| {{{\mathbf{X}}_i}\left( t \right) - {{\mathbf{X}}_j}\left( t \right)} \right\| \leqslant ED{}_{i}\left( t \right),{{\mathbf{X}}_j}\left( t \right) \in {\mathbf{X}}} \right\}$$

(48)

$$ED{}_{i}\left( t \right)=\left\| {{{\mathbf{X}}_i}\left( t \right) - {{\mathbf{X}}_{i - {\text{GWO}}}}\left( {t+1} \right)} \right\|$$

(49)

Where, ${{\mathbf{X}}_{i - {\text{N}}}}$ is the neighbors, ${{\mathbf{X}}_j}$ is any individual in the current population X, ED_i is the Euclidean distance, and t is the current number of iterations.

In the dimension learning process, neither over-exploration nor over-exploitation is allowed; at the beginning of the iteration, individuals should learn as much as possible from their neighbors to enhance the population diversity, and at the later stage of the iteration, the second optimal candidate solution ${{\mathbf{X}}_{i - {\text{ADL}}}}$, needs to learn from the optimal leader wolf ${{\mathbf{X}}_\alpha }$, to obtain the global optimal solution. The above process is expressed as

$${X_{i - {\text{ADL,}}d}}\left( {t+1} \right)=\left\{ {\begin{array}{*{20}{c}} {{X_{i{\text{,}}d}}\left( t \right)+rand \cdot \left( {{X_{i - {\text{N}},d}}\left( t \right) - {X_{r1,d}}\left( t \right)} \right),}&{if rand<1 - \frac{t}{T}} \\ {{X_{\alpha {\text{,}}d}}\left( t \right)+rand \cdot \left( {{X_{r2,d}}\left( t \right) - {X_{r3,d}}\left( t \right)} \right),}&{if rand \geqslant 1 - \frac{t}{T}} \end{array}} \right.$$

(50)

Where, ${X_{i - {\text{N}},d}}\left( t \right)$ is the number on the d^th dimension of the neighbors X_i−N of a randomly chosen X_i, ${X_{\alpha {\text{,}}d}}\left( t \right)$ is the number on the d^th dimension of the optimal leader wolf ${{\mathbf{X}}_\alpha }$, and ${X_{r1,d}}$, ${X_{r2,d}}$, ${X_{r3,d}}$ is any randomly chosen individual from the current population X, respectively.

When the first optimal candidate solution ${{\mathbf{X}}_{i - {\text{GWO}}}}$ and the second optimal candidate solution ${{\mathbf{X}}_{i - {\text{ADL}}}}$ are obtained, the fitness of the two are compared, and the individual with smaller fitness is selected as the global optimal solution

$${{\mathbf{X}}_i}\left( {t+1} \right)=\left\{ {\begin{array}{*{20}{c}} {{{\mathbf{X}}_{i - {\text{GWO}}}}\left( {t+1} \right),}&{if f\left( {{{\mathbf{X}}_{i - {\text{GWO}}}}} \right)<f\left( {{{\mathbf{X}}_{i - {\text{ADL}}}}} \right)} \\ {{{\mathbf{X}}_{i - {\text{ADL}}}}\left( {t+1} \right),}&{if f\left( {{{\mathbf{X}}_{i - {\text{GWO}}}}} \right) \geqslant f\left( {{{\mathbf{X}}_{i - {\text{ADL}}}}} \right)} \end{array}} \right.$$

(51)

Adaptive levy flight

GWO has the problem of not being able to effectively jump out of the local optimum when it falls into the local optimum, and the randomization operation can alleviate the problem to a certain extent, but the jump range of the general randomization operation is small, which makes it difficult to jump out of the local optimum. On the other hand, the Levy flight has heavy-tailed distribution characteristics and longer step length, which can jump over a wide range and is more conducive to jumping out of the local optimum. However, unreasonable randomization can easily lead to the loss of the found optimal solution, destroying the original efficient search and affecting the convergence of the algorithm. A reasonable randomization operation should be able to jump out of the local optimum without interrupting the original favorable search situation. To this end, an adaptive Levy flight is introduced, i.e., the algorithm starts the Levy flight if the fitness satisfies the following conditions⁴⁸,

$$\xi \left( t \right)=\frac{{{f_{{\text{best}}}}\left( {t - 1} \right) - {f_\alpha }\left( t \right)}}{{\left| {{f_{{\text{average}}}}\left( t \right) - {f_\alpha }\left( t \right)} \right|}} \leqslant \varDelta \left( t \right)$$

(52)

Where, ${f_{{\text{best}}}}\left( t \right)$ is the optimal fitness of the t^th iteration, ${f_{{\text{average}}}}\left( t \right)$ is the average fitness of the previous iteration, ${f_\alpha }\left( t \right)$ is the current optimal fitness, and $\varDelta \left( t \right)$ is the flight threshold that varies with iteration. If the fitness does not continue to decrease after repeated iterations, the algorithm is in a stagnant state or reaches the global optimal solution. The more iterations the algorithm has, the smaller the fitness becomes, so the threshold $\varDelta$ must be adaptively adjusted according to the number of iterations.

The Levy flight is

$${{\mathbf{X}}_{i,{\text{Levy}}}}={{\mathbf{X}}_i}+s \cdot \left( {{{\mathbf{X}}_\alpha } - {{\mathbf{X}}_i}} \right)$$

(53)

Where, ${{\mathbf{X}}_{i,{\text{Levy}}}}$ is the updated individual after performing the Levy flight, ${{\mathbf{X}}_i}$ is the individual in the current population, ${{\mathbf{X}}_\alpha }$ is the optimal solution in the current population, and s is the Levy flight path.

The Levy flight path s is

$$s=\frac{u}{{{{\left| v \right|}^{\frac{1}{\beta }}}}}$$

(54)

$$\left\{ {\begin{array}{*{20}{c}} {{\sigma _u}={{\left\{ {\frac{{\sin \left( {\frac{{\pi \beta }}{2}} \right) \cdot \Gamma \left( {1+\beta } \right)}}{{{2^{\frac{{\beta - 1}}{2}}}\beta \cdot \Gamma \left( {\frac{{1+\beta }}{2}} \right)}}} \right\}}^{\frac{1}{\beta }}}} \\ {{\sigma _v}=1} \end{array}} \right.$$

(55)

Where, $\Gamma$ is the gamma function, u and v follow normal distribution with variance ${\sigma _u}$and ${\sigma _v}$, respectively, and parameter $\beta \in \left( {0,2} \right)$.

The flight threshold $\varDelta \left( t \right)$ that changes with iteration is

$$\Delta \left( t \right)=\frac{{t\left( {T - t+1} \right)}}{{{T^2}}}$$

(56)

If the algorithm initiates a Levy flight, the population is updated by comparing the fitness of the individuals obtained after the Levy flight to the fitness of the previous generation of the population, and replacing the individuals with greater fitness with those with less fitness. The ${{\mathbf{X}}_{i,{\text{best}}}}$ and ${{\mathbf{X}}_\alpha }$ are updated as

$${{\mathbf{X}}_{i,{\text{best}}}}\left( {t+1} \right)=\left\{ {\begin{array}{*{20}{c}} {{{\mathbf{X}}_{i,{\text{Levy}}}}\left( {t+1} \right),}&{if f\left( {{{\mathbf{X}}_{i,{\text{Levy}}}}} \right)<f\left( {{{\mathbf{X}}_{i,{\text{best}}}}} \right)} \\ {{{\mathbf{X}}_{i,{\text{best}}}}\left( t \right),}&{if f\left( {{{\mathbf{X}}_{i,{\text{Levy}}}}} \right) \geqslant f\left( {{{\mathbf{X}}_{i,{\text{best}}}}} \right)} \end{array}} \right.$$

(57)

$${{\mathbf{X}}_\alpha }\left( {t+1} \right)=\left\{ {\begin{array}{*{20}{c}} {{{\mathbf{X}}_{i,{\text{Levy}}}}\left( {t+1} \right),}&{if f\left( {{{\mathbf{X}}_{i,{\text{Levy}}}}} \right)<f\left( {{{\mathbf{X}}_\alpha }} \right)} \\ {{{\mathbf{X}}_\alpha }\left( t \right),}&{if f\left( {{{\mathbf{X}}_{i,{\text{Levy}}}}} \right) \geqslant f\left( {{{\mathbf{X}}_\alpha }} \right)} \end{array}} \right.$$

(58)

The fitness of ${{\mathbf{X}}_{i,{\text{best}}}}$ and ${{\mathbf{X}}_\alpha }$ are updated as

$$f\left[ {{{\mathbf{X}}_{i,{\text{best}}}}\left( {t+1} \right)} \right]=\left\{ {\begin{array}{*{20}{c}} {f\left[ {{{\mathbf{X}}_{i,{\text{Levy}}}}\left( {t+1} \right)} \right],}&{if f\left( {{{\mathbf{X}}_{i,{\text{Levy}}}}} \right)<f\left( {{{\mathbf{X}}_{i,{\text{best}}}}} \right)} \\ {f\left[ {{{\mathbf{X}}_{i,{\text{best}}}}\left( t \right)} \right],}&{if f\left( {{{\mathbf{X}}_{i,{\text{Levy}}}}} \right) \geqslant f\left( {{{\mathbf{X}}_{i,{\text{best}}}}} \right)} \end{array}} \right.$$

(59)

$$f\left[ {{{\mathbf{X}}_\alpha }\left( {t+1} \right)} \right]=\left\{ {\begin{array}{*{20}{c}} {f\left[ {{{\mathbf{X}}_{i,{\text{Levy}}}}\left( {t+1} \right)} \right],}&{if f\left( {{{\mathbf{X}}_{i,{\text{Levy}}}}} \right)<f\left( {{{\mathbf{X}}_\alpha }} \right)} \\ {f\left[ {{{\mathbf{X}}_\alpha }\left( t \right)} \right],}&{if f\left( {{{\mathbf{X}}_{i,{\text{Levy}}}}} \right) \geqslant f\left( {{{\mathbf{X}}_\alpha }} \right)} \end{array}} \right.$$

(60)

MSIGWO framework and computational complexity

The flowchart of MSIGWO is shown in Fig. 7. The pseudo-code of MSIGWO is shown in Algorithm 2. The computational complexity of MSIGWO mainly comes from 3 parts of the code such as population initialization, function module, and adaptation calculation. Let the population size be N_p, the optimization problem dimension be D, the maximum number of iterations be T, and the computational complexity be denoted as ‘O’, then the computational complexity of MSIGWO is:

Fig. 7

The flowchart of MSIGWO.

• (1) The Tent mapping is $O\left( {{N_{\text{p}}} \cdot D} \right)$, and the population is initialized as $O\left( {{N_{\text{p}}} \cdot D} \right)$, then the Tent mapping is initialized as$O\left( {{N_{\text{p}}} \cdot D} \right)$.

• (2) GWO trapping search process is $O\left( {{N_{\text{p}}} \cdot D} \right)$.

• (3) Information interaction is $O\left( {{N_{\text{p}}} \cdot D} \right)$, fitness calculation and population update are $O\left( {{N_{\text{p}}} \cdot D} \right)$, then population fusion evolution is $O\left( {{N_{\text{p}}} \cdot D} \right)$.

• (4) Adaptive dimensional learning is $O\left( {{N_{\text{p}}} \cdot D} \right)$.

• (5) Adaptive Levy flight is $O\left( {{N_{\text{p}}} \cdot D} \right)$.

Therefore, the computational complexity of one iteration of MSIGWO is $O\left( {{N_{\text{p}}} \cdot D} \right)$ and the computational complexity of T iterations is $O\left( {{N_{\text{p}}} \cdot D \cdot T} \right)$.

Algorithm 2

The pseudo-code of MSIGWO.

Numerical test evaluation and results

Numerical experiments are used to verify the performance of the MSIGWO algorithm.

Benchmarking function and test setup

The 29 benchmark functions in the CEC2018 test function set were utilized as test objects⁵⁷, and the test functions contained Unimodal, Multimodal, Hybrid, and Composition functions, with all the functions set to have dimensions of 10, 30, and 50, respectively, and all the functions were repeated independently for 30 runs. MSIGWO is compared with GWO⁴⁰, IGWO⁴⁴, MELGWO⁴⁵, MGWO⁴⁶, ALGWO⁴⁷ and CSELGWO⁴⁸ algorithms, and algorithm parameters are set as shown in Table 1. Wilcoxon signed rank test and Friedman test are used to analyze the differences and overall performance of the compared algorithms. The test computer processor is 11th Gen Intel(R) Core(TM) i5-1155G7 @ 2.50 GHz with 16.0GB of RAM using MATLAB 2021b platform.

Table 1 Parameter settings of the chosen competitors.

Exploration and exploitation evaluations

Unimodal functions are used to test the global optimization ability in the exploitation phase. Multimodal functions are used to test the exploration ability and the ability to discriminate the local optimum. The results are expressed as the difference of the fitness function, i.e., f − f_min, f is the optimality finding result, and f_min is the theoretical global optimum. The results of unimodal function and multimodal function tests are shown in Tables 2 and 3, respectively. Bolding is the best result, and ‘+/=/−’ indicates that the performance of the algorithm is better than, equal to or worse than the rest of the algorithms. From Table 2, it can be seen that MSIGWO has the strongest global optimality finding ability on Unimodal functions, especially in all dimensions of F3. From Table 3, MSIGWO has better optimization results in all dimensions from F4 to F9. For F10, MSIGWO has the best optimization result when the dimension is 10, and MSIGWO is second only to ALGWO when the dimension is 30 and 50, and the difference in values is not significant. This shows that MSIGWO has a strong exploration ability.

Table 2 Results of unimodal benchmark functions.

Table 3 Results of multimodal benchmark functions.

Evaluation of discriminant local optima

Hybrid and composite functions are used to test the algorithm’s ability to explore and jump out of the local optimum. The hybrid and composite function test results are shown in Tables 4 and 5 respectively, where bold is the best result. From Table 4, when the function is 10 dimensions, MSIGWO has the best performance on the three hybrid functions, second only to CSELGWO. When the function is 30 and 50 dimensions, MSIGWO has the best performance on 6 hybrid functions, surpassing all the remaining algorithms. From Table 5, when the function is 10 dimensional, MSIGWO has the best performance on 5 composite functions, outperforming all the rest of the algorithms. When the function is 30 and 50 dimensional, MSIGWO has the best performance on 6 composite functions over all the remaining algorithms. The results show that MSIGWO balances exploration and exploitation well and obtains a strong global optimization search capability.

Table 4 Results of hybrid benchmark functions.

Table 5 Results of composition benchmark functions.

Convergence analysis

The convergence of the algorithm is qualitatively analyzed using convergence curves. Figure 8 shows the convergence curves for some unimodal and multimodal functions, and Fig. 9 shows the convergence curves for some hybrid and combined functions. The function dimensions are 10, 30, and 50. the convergence curves are the average of the optimal solutions for 30 runs. As can be seen from the figure, MSIGWO fluctuates more at the beginning of the iteration and less at the end of the iteration. The downward trend of the convergence curves indicates that the wolves are finding the global optimal solution by updating their positions. Among all the convergence curves, MSIGWO has better convergence, indicating that MSIGWO achieves a balance between exploration and exploitation during the iteration process.

Fig. 8

The convergence curves of unimodal and multimodal functions with different dimensions.

Fig. 9

The convergence curves of hybrid and composition functions with different dimensions.

The convergence of the algorithm is quantitatively analyzed using the Overall Effectiveness (OE) evaluation metric, which is defined as⁴⁴

$$OE=100 \cdot \frac{{{N_{\text{t}}} - {N_{\text{l}}}}}{{{N_{\text{t}}}}}$$

(61)

Where, N_t is the total number of times the algorithm was tested and N_l is the number of times the algorithm performed poorly.

Table 6 shows the comparison of test performance results between MSIGWO and the rest of the algorithms, where bold is the best result. As can be seen from the table, MSIGWO has the largest OE, which is far more than the OE of the rest of the algorithms, indicating that MSIGWO has better convergence.

Table 6 Overall effectiveness of the MSIGWO and other algorithms.

Statistical analysis

To further validate the superiority of MSIGWO. Significant differences between MSIGWO and the rest of the algorithms were analyzed using Wilcoxon signed rank test analysis. Non-parametric Friedman test was used to rank the performance of all algorithms.

Wilcoxon signed rank test

A non-parametric Wilcoxon signed rank test was used to compare the performance of MSIGWO with the rest of the algorithms, with the significance level set at 0.05⁵⁸. The results of the Wilcoxon signed rank test are shown in Table 7, where ‘+/=/−’ indicates that MSIGWO performs significantly better, comparable or significantly worse than the rest of the algorithms. As can be seen from the table, the performance advantage of MSIGWO over the rest of the algorithms becomes more and more obvious as the dimensions increase. In all dimensions, MSIGWO has better performance compared to CSELGWO on 55 functions, equivalent performance on 18 functions, and worse performance on 14 functions. Compared to ALGWO, it has better performance on 52 functions, comparable performance on 30 functions and poor performance on 5 functions. Compared to MGWO, it has better performance on 85 functions, comparable performance on 2 functions and poor performance on 0 functions. Compared to MGWO, has better performance on 85 functions, comparable performance on 2 functions, and poor performance on 0 functions. Compared to MELGWO, it has better performance on 87 functions, comparable performance on 0 functions and poor performance on 0 functions. Compared to IGWO, it has better performance on 78 functions, comparable performance on 6 functions and poor performance on 3 functions. Compared to GWO, it has better performance on 84 functions, comparable performance on 3 functions and poor performance on 0 functions. Thus, MSIGWO has a clear advantage over the rest of the algorithms.

Table 7 Wilcoxon signed rank test results.

Non-parametric Friedman test

A non-parametric Friedman test was used to rank the performance of all algorithms. The statistical formula is⁵⁸

$${F_f}=\frac{{12n}}{{k\left( {k+1} \right)}}\left[ {\sum\limits_{j} {R_{j}^{2}} - \frac{{k{{\left( {k+1} \right)}^2}}}{4}} \right]$$

(62)

Where, k is the number of algorithms, n is the number of tests, and R_j is the average ranking of the j^th algorithm.

Table 8 shows the results of the Friedman test, where bold is the best result. The average ranking of each algorithm was calculated from the Friedman test and the p-value was calculated from the Hommel procedure with a significance level of 0.05⁵⁹. The results show that MSIGWO has the best performance in all dimensions.

Table 8 Friedman’s test results.

Sensitivity of parameters analysis

MSIGWO contains a variety of variable parameters, and parameter settings for multiple cluster convergence evolutionary stages can be found in the literature⁴⁸. Parameter sensitivity analyses were performed for η in the nonlinear convergence factor using all dimensions of CEC2018. The average ranking of each dimension was calculated, as shown in Table 9, where bold is the best result. From the experimental results, it can be seen that the overall results are best when η is 0.7 to 0.9. Therefore, η was set to 0.7.

Table 9 Parametric sensitivity analysis average ranking table.

Complexity analysis of MSIGWO

In order to verify whether MSIGWO can be used in low-power processing systems, the following computational complexity analysis is performed. The test functions are the 29 functions of CEC2018, all the algorithms are iterated 500 times, for each function repeat the test 30 times and take the average value as the computation time of the function, and finally take the average computation time of 29 functions as the computation time of the algorithms, as shown in Table 10, where the bolded is the best result. As can be seen from the table, MSIGWO has the longest computation time, which is due to the convergence of multiple strategies, which increases the computational steps of the algorithm. From the convergence analysis above, it can be seen that MSIGWO has good convergence and hence when applied in low power processing systems, the total number of iterations can be reduced to decrease the computation time.

Table 10 The average computation time (in seconds) on CEC2018.

Magnetic target state estimation simulation test

Simulation parameter settings

The following state estimation tests are performed on magnetic targets with different magnetic field equivalent models. The magnetic target parameters are shown in Table 11. target 1, target 2, and target 3 adopt the magnetic dipole array model with only uniaxial magnetic moment for representing the magnetic target with specific magnetic moment structure, and target 4 adopts the hybrid model of magnetic dipole array and ellipsoid for representing the ship target⁶⁰. The simulation working condition is shown in Table 12, and the target length is set to 112 m according to the length of medium and large ships. According to the magnitude of the magnetic field of the medium-large ship, the magnitude of the magnetic dipole magnetic moment ranges from − 1E6 ~ 1E6A·m² and the magnitude of the ellipsoid magnetic moment ranges from − 1E7 ~ 1E7A·m^{[2 61}. The simulation test condition is shown in Table 12, and y is set to -100 ~ 100 m and z is set to 0 ~ 100 m according to the effective range of the magnetic sensor. In order to verify the effectiveness of the target signal detection and extraction algorithm, x is set to -1000 ~ 1000 m. For ships with slow speed, v is set to 0 ~ 10 m/s. The attitude of the underwater magnetic sensor is unknown, and the 3-axis of the magnetic sensor may be at an arbitrary angle with the ship, θ is set to 0 ~ 2πrad. The ship’s static magnetic field is a low-frequency signal with a frequency < 1 Hz, so the sampling frequency F_s is set to 2Hz. Surface targets such as ships have a fixed depth relative to the magnetic sensors located on the seafloor, so the vertical velocity v_z is zero. Typically, the ship’s magnetic field signal has a large SNR, so the SNR is set to positive.

Table 11 The parameters of magnetic targets.

Table 12 Simulation test conditions.

Signal pre-processing

Some of the magnetic field waveforms of the 3 types of simulation targets are shown in Fig. 10. Figure 10(a), (c), (e), (g) shows the magnetic field waveforms of target 1, target 2, target 3, target 4 in {s}, respectively, and it can be seen from the figure that the magnetic field waveforms contain the complete magnetic field through characteristic curves of the complete magnetic target. Figure 10(b), (d), (f), and (h) show the magnetic field waveforms of target 1, target 2, target 3, and target 4 in {s}, respectively, and the five-pointed star in the figure is the position of the origin where the magnetic target is located, and the blue line is the motion trajectory of the sensor relative to the magnetic target in {b}. The parameters of the optimization algorithms are set as shown in Table 13, the state search space dimension D = 5, and the state optimization range is shown in Table 14². Each algorithm was repeated 100 times independently. In the signal preprocessing stage, in order to prevent the target magnetic field from distortion due to noise and other interference, the magnetic field waveform obtained after detection and extraction of the target magnetic field signal is shown in Fig. 11. In order to complete the identification of the target when the target passes near the magnetic sensor (i.e., before and after the arrival of the maximum value of the magnetic field modulus), and at the same time to ensure that the data is sufficiently informative, the first 2/3 of the magnetic field waveforms are taken, i.e., the waveform completeness I_m is 2/3². The resulting magnetic field waveform is shown in Fig. 11(c). Finally, down sampling is performed to obtain a magnetic field waveform with a data length _Nd of M + 2, as shown in Fig. 11(d).

Fig. 10

Magnetic field and the corresponding trajectory of targets (z = 30 m, y = 50 m, v = 6 m/s, SNR=+∞dB).

Fig. 11

Magnetic field of target 1 in {s} after pre-processing (z = 30 m, y = 50 m, v = 6 m/s, SNR=+∞dB).

Table 13 Parameter settings of the chosen competitors.

Table 14 State optimization scope.

Magnetic target state estimation

For Target 1, Target 2, and Target 3, the state estimation algorithm uses five magnetic dipole array models. The state estimation results for Target 1, Target 2, and Target 3 are shown in Tables 15 and 16, and Table 17, respectively. The results of the state estimation algorithm for Target 1, Target 2, and Target 3 are shown in Tables 18 and 19, and Table 20, respectively. Friedman test results for Target 1, Target 2, and Target 3, where bold is the best result. The average ranking of each algorithm is calculated from the Friedman test and the p-value is calculated from the Hommel procedure with a significance level of 0.05. The estimated magnetic moments of Target 1, Target 2, and Target 3 are shown in Fig. 12(a)(b)(c), respectively, and the magnetic moment estimation of MSIGWO has a high accuracy. Figure 13 is the convergence curve, which is the average of the optimal solutions of 100 runs, and MSIGWO is able to converge to the minimum value. Figure 12 shows the estimated magnetic field, and MSIGWO has high accuracy of magnetic field estimation. Figure 14 shows the estimated trajectory, and MSIGWO has high accuracy of trajectory estimation. Figure 15 shows the high accuracy of the estimation of magnetic moments by MSIGWO. From the table, it can be seen that under the case of model matching completely, although MSIGWO has the longest computation time, the computation time is < 13s, which can basically satisfy the state estimation of the low-speed target. MSIGWO has the best performance in position estimation, velocity estimation, heading estimation, length estimation, magnetic moment estimation, and magnetic field fitting error.

Fig. 12

Estimated magnetic field of MSIGWO (z = 30 m, y = 50 m, v = 6 m/s, SNR=+∞dB).

Fig. 13

The convergence curves of different targets.

Fig. 14

Estimated trajectory of MSIGWO (z = 30 m, y = 50 m, v = 6 m/s, SNR=+∞dB).

Fig. 15

Estimated magnetic moment of MSIGWO (z = 30 m, y = 50 m, v = 6 m/s, SNR=+∞dB).

Table 15 Estimated results of target 1 with different methods.

Table 16 Estimated results of target 2 with different methods.

Table 17 Estimated results of target 3 with different methods.

Table 18 Friedman’s test results of target 1.

Table 19 Friedman’s test results of target 2.

Table 20 Friedman’s test results of target 3.

Discussion

For the CEC2018 benchmark function test problems, the MSIGWO algorithm proposed in this paper has the following advantages:

• (1) In the 29 CEC2018 benchmark function test set, MSIGWO has 22 functions in the lead when the problem dimension is 10, and the performance advantage of MSIGWO becomes more and more obvious as the problem dimension increases.

• (2) In all dimensions of the 29 CEC2018 benchmark function test sets, MSIGWO has the smallest Friedman ranking, indicating that its optimization accuracy is the highest.

• (3) The convergence curve analysis shows that MSIGWO has a higher convergence speed compared to the other six algorithms.

• (4) The Wilcoxon test shows that there is a significant difference between MSIGWO and the other six algorithms, indicating that the improvement strategy is significantly effective.

For the magnetic target state estimation problem, the MSIGWO algorithm has the following advantages:

• (1) The state estimation accuracy of MSIGWO is significantly higher than the other six algorithms, with the position estimation error less than 3E-6 m and the velocity estimation error less than 2E-7 m/s. The state estimation accuracy of MSIGWO is significantly higher than that of the other six algorithms.

• (2) The magnetic target state estimation method proposed in this paper can accurately estimate the position, speed, heading, length, magnetic moment and other information of the magnetic target.

Conclusion

For the magnetic target state estimation problem, MSIGWO, which incorporates various strategies such as Tent chaotic mapping initialization, multiple swarm fusion evolution, nonlinear convergence factor, dynamic weighting strategy, adaptive dimension learning, and adaptive Levy flight, is proposed.

• (1) MSIGWO reduces the probability of falling into a local optimum, enhances population diversity, optimizes exploration and exploitation behaviors, and improves global convergence. Numerical simulation experiments show that MSIGWO has obvious advantages over algorithms such as GWO, IGWO, MELGWO, MGWO, ALGWO, and CSELGWO.

• (2) Under the conditions of high SNR and model matching, MSIGWO has the best performance in terms of position estimation, velocity estimation, heading estimation, length estimation, magnetic moment estimation, and magnetic field fitting error compared to algorithms such as GWO, IGWO, MELGWO, MGWO, ALGWO, CSELGWO, and so on.

• (3) Under the conditions of high SNR and incomplete model matching, MSIGWO does not have obvious advantages compared with algorithms such as GWO, IGWO, MELGWO, MGWO, ALGWO, and CSELGWO.

• (4) MSIGWO has large computational complexity and is suitable for low real-time scenarios or high-performance MCUs.

In future work, in addition to improving the performance of magnetic target state estimation accuracy, the issues of reducing the computational complexity and improving the applicability of the algorithm on MCU will be considered.