Introduction

The fossil fuels utilization major problem is the energy return and \(C{O_2}\) that are out of the green matter and energy cycle for thousand years over time1. This is released directly and the consequent GHGs increment the temperature of the Earth and produce unusual environment-related alterations like the storms, bipolar ice melting and rising oceans, droughts, floods, and the pests’ spread, infectious diseases and parasites2. At the same time, unintended and reckless utilization of them has increased environment-related pollution and problems3. Another problem that will lead to the use of fossil resources is that they are decreasing4. Therefore, according to the above explanations, the production of renewable energy and clean energy resources is a good idea for providing the energy with the least damage5. A good idea is to use the conversion technologies for this purpose6.

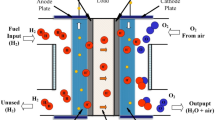
The main goal of new energy conversion technologies is to produce clean energy. In recent years, the fuel cell is presented as a new energy source with many benefits and a lot of research has been done to improve the structure and reduce its cost7. The fuel cell is considered as a renewable and clean energy resources, whose operating principles are similar to batteries but with a fundamental difference8. This energy source does not create pollution for the environment and due to its high efficiency, it is a suitable option for use in cars9. A fuel cell generates electrochemical power by converting the fuel’s chemical energy into electricity directly. At the anode of the fuel cell, an oxidation reaction takes place and the generated electron enters the external circuit and then enters the cathode10,11,12. The positive ion produced in the anode passes through the membrane (electrolyte) to the cathode side and in the presence of a catalyst with oxygen and electrons that enter the cathode side from the external circuit is converted to water13. The process of performing this chemical process is shown in Fig. 1.

Fig. 1
figure 1

The process of performing this chemical process.

Full size image

Based on regular operational conditions, a fuel cell can generate about 1.2 volts. For utilization in power generation structures that require rather high power, some cells should be combined together to produce more power14,15. However, the good sources of energy are Proton Exchange Membrane Fuel Cells (PEMFCs), they cannot respond well to changes in charge, which is mostly because of their low thermodynamic and electrochemical reaction. In connection with the discussion of optimizing the efficiency of fuel cells, different research works have been done, among which the following can be mentioned16.

Zhao et al.17 suggested an improved fuzzy-based control methodology for the fuel cell-based vehicle based on multi-island genetic algorithm (GA). In that study, a different technique was proposed for optimal a Fuel Cell Vehicle (FCV)’s Energy Management Strategy (EMS) to decrease the consuming of the fuel. In the presented method, Multi-island GA was utilized for membership function (MF) optimization. The simulations were done under driving cycles. The simulations indicated that the optimized fuzzy control EMS delivers reliable outputted power from the fuel cells by decreasing the \({H_2}\) consumption as much as possible. Derbeli et al.18 presented a well-organized technique for improving the PEMFC system efficiency based on a high step-up power converter. The idea was to adjust the duty cycle of the power converter based on forcing the PEMFC. Because of the nonlinear characteristic in the fuel cell dynamics, a sliding mode controller (SMC) was utilized. Although, the SMC delivers proper changes in the output power of the PEMFC. To resolve these issues, a reliable great order SMC was proposed by Twisting Optimizer. To confirm the effectiveness of the proposed technique, a hardware setup was performed on an actual PEM fuel cell stack. The results were simulated by dSPACE actual-time digital control platform to indicate the technique efficiency.

Kadri et al.19 suggested a technique for the simulation and controlling of a hybrid power system including fuel cell and a Doubly Fed wind turbine. To develop the energy system efficiency, they connected a super-capacitor storage system to a fuel cell. Simulations indicated the efficacy of the suggested control for energy management. They also performed the proposed mehod to dSpace 1104 board to real-time management of the system. Javaid et al.20 proposed another method based on sliding mode controllers (SMC) for a PEMFCs. They used particularly, the first-order and the second-order sliding mode controllers using super twisting optimizer. The real process was expressed based on the Pukurushpan’s ninth-order model. MATLAB/Simulink was utilized for simulation of the proposed method in terms of net power generated, oxygen excess ratio, compressor motor voltage, stack voltage/power produced. The results showed that the second-order sliding mode control results better efficiency for reject the disturbance and for set-point tracking.

Various studies have explored distinct control schemes optimized through different metaheuristic techniques. For instance, Çelik21 proposed a straightforward and effective method for estimating the excitation current of a synchronous motor aimed at power factor correction. The proposed adjustment of regression coefficients in the multiple linear regression models demonstrates superior estimation performance for synchronous motor excitation current compared to previous research. Chetty et al.22 presented a comprehensive strategy that integrates a 3-degrees of freedom PID-Acceleration (3-DOF-PIDA) controller with a disturbance observer-based control method. Their findings were validated through statistical and graphical analyses, considering time-varying step load fluctuations and diverse system parameter variations. Reference23 introduced an alternative approach utilizing the recently developed symbiotic organisms search (SOS) algorithm for tuning proportional-integral parameters. Lastly, Reference24 proposed a novel design methodology aimed at enhancing the performance of such controllers. To assess the effectiveness of the Stochastic Fractal Search, Particle Swarm Optimization was also employed in the case study.

In traditional PEM fuel cell systems that incorporate active hydrogen recovery, a notable decrease in output power is observed during the hydrogen purging process. Kun-Kuo and colleagues25 tackled this issue by implementing flow control strategies for oxygen and hydrogen, utilizing a proportional integral (PI) controller, a fuzzy PI controller, and an optimized fuzzy PI controller, respectively. Their research indicated that the hydrogen supply rate necessary to alleviate the power reduction during purging was highest when employing the optimized fuzzy PI controller, resulting in a 16.82% increase in the fuel cell system’s output power. This optimized controller was exclusively applied to the hydrogen side, leading to a reduction in the oxygen excess ratio from 32 to 29. Almousa and Rezk26 introduced an optimal design for a fuzzy logic control system aimed at maximizing power point tracking (MPPT) in PEMFCs. They also explored a novel application of the bald eagle search algorithm to determine the optimal parameters for adaptive fuzzy logic control. A thorough numerical analysis was performed to validate their proposed approach, revealing that the bald eagle search algorithm outperformed other optimization methods, achieving the best result of 1.7638, followed closely by a gradient-based optimizer at 1.7667, while the pelican optimization algorithm yielded the least favorable outcome of 1.7987. Korkmaz and colleagues27 compared various algorithms for modeling parameters of the H-1000XP PEMFC, finding that the Moth Flame Algorithm delivered the best performance among those evaluated. The Improved Grey Wolf Optimizer demonstrated the highest objective function efficiency at 98.60%. Conversely, the JAYA and Cuckoo Search algorithms were deemed unsuitable for parameter extraction from the fuel cell. Saidi et al.28 introduced a highly effective Dimension Learning-based Modified Grey Wolf Optimizer (DLHMGWO) aimed at estimating key parameters in PEMFC models. This approach successfully addressed the limitations associated with analytical, numerical, and hybrid methods. The efficacy of DLHMGWO was evaluated using experimental datasets from five different PEMFC technologies, and various assessment criteria demonstrated its superiority over 11 other studies. The implementation of DLHMGWO significantly enhanced the precision of PEMFC design and facilitated consistent control. In a separate study, Huang et al.29 developed an Improved Black Kite Algorithm. Utilizing a 30 kW PEMFC stack testing platform, they gathered four datasets under varying operating conditions and established a static model tailored for high-power PEMFCs. For traditional PEMFCs, the objective function values were recorded as 1.2558 for the NedStack PS6 dataset and 0.0119 for the BCS500W dataset.

  • Research gaps and contributions:

One of the main challenges lies in PEMFCs’ inability to efficiently adapt to changing load demands due to their nonlinear dynamics and low electrochemical and thermodynamic reactions. Although various fuel cell control strategies have been proposed, including fuzzy-based, sliding mode, or hybrid controllers, these models often exhibit limitations in terms of ripple reduction, system efficiency, and long-term durability improvements. Moreover, most traditional methods fail to integrate state-of-the-art metaheuristic optimization techniques to effectively handle the complexity of PEMFC systems. This study identifies the need for advanced optimization mechanisms to design optimal controllers to regulate PEMFC output voltage and minimize ripples, thus extending fuel cell longevity. To address the challenges associated with the dynamic behavior and ripple-prone output of PEMFCs, this study introduces a novel control strategy leveraging the ICOA. Unlike conventional optimization techniques, ICOA integrates self-adaptive and chaotic mechanisms to enhance solution quality, mitigate premature convergence, and ensure optimized performance across complex scenarios. By combining this improved optimization algorithm with a PID controller and incorporating a DC/DC converter, this research provides a holistic framework for stabilizing PEMFC output voltage, minimizing ripple interference, and improving system efficiency. Through comparative analyses and rigorous simulation, the proposed method demonstrates significant advancements in dynamic response, overshoot attenuation, and ripple reduction, laying the foundation for robust control strategies for PEMFC systems. Robust controller design demands validation across varying real-world conditions. Thus, beyond conventional step testing, this study incorporates dynamic load and disturbance scenarios to ensure comprehensive performance assessment.

System modeling

Statistical PEMFC design

In order to control the voltage level of fuel cells, it is first needed to consider the dynamic fuel cell design. In this study, the model mentioned in30 has been used. In this method, the fuel cell theory model with DC/DC converter has been presented. Figure 2 shows the circuit of this model.

Fig. 2
figure 2

Complete model of fuel cell with DC/DC converter.

Full size image

Due to electrons’ movement in the exterior circuit and the movement of protons in the membrane in fuel cells, a voltage cell unit is created at both ends, which is expressed by the following relation:

$${V_{FC}}={N_{cell}} \times \left( {{E_N} - {V_{\text{\varvec{\Omega}}}} - {V_C} - {V_A}} \right)$$
(1)

where, \({E_N}\) signifies the drop in thermodynamic potential of the PEMFC, \({N_{cell}}\) describes the cell numbers which are connected to deliver a satisfying output voltage, \({V_A}\) describes the activation voltage lost, \({V_{\text{\varvec{\Omega}}}}\) is the voltage lost due to the electrons transfer resistance between the electrodes and the protons movement between the membranes, and \({V_C}\). designates the voltage drop due to the addition of reactive concentrations close to the catalyst surfaces.

By considering Eq. (1), the thermodynamic potential voltage of the PEMFC is achieved as follows:

$$\begin{aligned} {E_N} & =1.229 - 8.5 \times {10^{ - 4}}\left( {{T_{FC}} - 298.15} \right)+4.31 \times {10^{ - 5}} \\ & \;\;\; \times {T_{FC}} \times \left( {ln\left( {{P_{{H_2}}}} \right)+0.5 \times ln\left( {{P_{{O_2}}}} \right)} \right) \\ \end{aligned}$$
(2)

where, \({T_{FC}}\) is the cell operation temperature (\(^\circ C\)), and \({P_{{H_2}}}~\)and\(~{P_{{O_2}}}\) describe the partial pressures of the \({H_2}\) and the \({O_2}\) (\(atm\)), respectively and are achieved by the following equation:

$${P_{{O_2}}}={R_{hc}} \times {P_{{H_2}O}}\left[ {\frac{1}{{\frac{{{R_{hc}} \times {P_{{H_2}O}}}}{{{P_c}}} \times {e^{\frac{{1.635{I_{FC}}/A}}{{T_{{FC}}^{{1.334}}{I_{FC}}}}}}}} - 1} \right]$$
(3)
$${P_{{H_2}}}=\frac{1}{2} \times {R_{ha}} \times {P_{{H_2}O}}\left[ {\frac{1}{{\frac{{{R_{ha}} \times {P_{{H_2}O}}}}{{{P_a}}} \times {e^{\frac{{1.635{I_{FC}}/A}}{{{T^{1.334}}{I_{FC}}}}}}}} - 1} \right]$$
(4)

where, \({I_{FC}}\) determines the fuel cell’s operational flow, A defines the membrane’s active section, \({R_{ha}}\) and \({R_{hc}}\) define the electrode’s relative humidity, and \({P_a}\) and \({P_c}\) describes the partial pressures provided by the positive and the negative sides, respectively31. Here, \({P_{{H_2}O}}\) describes the saturation vapor pressure of the PEMFC and is obtained by the following equation32:

$${P_{{H_2}O}}=\exp \left( { - 2.18+0.0295 \times \left( {{T_{FC}} - 273.15} \right) - 9.18 \times {{10}^{ - 5}}T_{c}^{2}+1.4 \times {{10}^{ - 7}}T_{c}^{3}} \right)$$
(5)

And the voltage drop due to the electrons’ transfer resistance between the electrodes and the protons’ transfer between the membranes is achieved as follows:

$${V_{\text{\varvec{\Omega}}}}=\left( {{R_m}+{R_c}} \right) \times {I_{FC}}$$
(6)

where,

$${R_m}=\frac{{{\rho _m}}}{S} \times l$$
(7)

where, S defines the membrane surface (\(c{m^2}\)), l describes the membrane thickness, \({R_c}\) and \({R_m}\) signifies the connection and the membrane resistances, respectively, and \({\rho _m}\) is the membrane resistivity and is achieved as follows:

$${\rho _m}=181.6 \times \frac{{\left( {1+0.03\left( {\frac{{{I_{FC}}}}{S}} \right)+0.062 \times {{\left( {\frac{{{I_{FC}}}}{S}} \right)}^{2.5}} \times {{\left( {\frac{{{T_{FC}}}}{{303}}} \right)}^2}} \right)}}{{\left( {\alpha - 0.063 - 3\left( {\frac{{{I_{FC}}}}{S}} \right)} \right)}} \times {e^{ - \frac{{{T_{FC}} - 303}}{{{T_{FC}}}}}}$$
(8)

where, \(\alpha\) describes an adaptable parameter.

Furthermore, the activation voltage loss has been achieved as follows:

$${V_A}= - \left( {{\gamma _1}+{\gamma _2} \times {T_{FC}}+{\gamma _3} \times {T_{FC}} \times \ln \left( {{C_{{O_2}}}} \right)+{\gamma _4} \times {T_{FC}} \times \ln \left( {{I_{FC}}} \right)} \right)$$
(9)

where, \({\gamma _i}\) signifies the experimental coefficients, where, \({\gamma _2}\) has been achieved by the following equation:

$${\gamma _2}=4.3 \times {10^{ - 5}}\ln \left( {{C_{{H_2}}}} \right)+2.1 \times {10^{ - 4}}\ln \left( A \right)+2.9 \times {10^{ - 3}}$$
(10)

where, \({C_{{H_2}}}\) and \({C_{{O_2}}}\) represent \({H_2}\) and \({O_2}\) saturations in the anode (\(mol/c{m^3}\)) and are achieved as follows:

$${C_{{H_2}}}=\frac{{{P_{{H_2}}}}}{{1.1 \times {{10}^6}}} \times {e^{\frac{{ - 77}}{{{T_{FC}}}}}}$$
(11)
$${C_{{O_2}}}=\frac{{{P_{{O_2}}}}}{{5.1 \times {{10}^6}}} \times {e^{\frac{{498}}{{{T_{FC}}}}}}$$
(12)

The last part of the equation is \({V_C}\), which is the focused voltage lost. This lost is mostly because of the addition of reactive concentrations close to the surfaces of catalyst33. This voltage lost is formulated as follows

$${V_C}= - \beta \times ln\left( {\frac{{J_{{max}}^{2} - J}}{{{J_{max}}}}} \right)$$
(13)

where, \(\beta\) defines a definite constant, and J and \({J_{max}}\) represent the standard flow density and the topmost flow density, respectively.

Dynamic design of the PEMFC

The fuel cell’s dynamic characteristics mostly depend on the effect of the loaded double layer. Although two different charged materials are connected, a charge accumulated on their surface exists or a charge move from a place to another one34. The charge layer on the surface of the electrolyte performs like reservoir of electrical energy and charge, act like a capacitor35. Changes in current cause a sudden delay in the ohmic voltage drop, which can be thought of as a 1st -order delay with activation and focus voltages. By considering delay with the time constant, we have:

$$\tau ={R_a} \times {C_{FC}}$$
(14)

where, \({C_{FC}}\) describes the equivalent capacitance, and \({R_a}\) is the equivalent resistance.

Resistance \({R_a}\) describes the activation voltage drop, outputted current, and the concentration voltage lost from the static design. In other words:

$${R_a}=\frac{{{V_A}+{V_C}}}{{{I_{FC}}}}$$
(15)

where, \({I_{FC}}\) signifies the instantaneous flow through the cell. The dynamic model of the PEMFC is indicated in Fig. 3.

Fig. 3
figure 3

The dynamic design of the PEM fuel cell.

Full size image

State space design

To achieve the of a fuel cell’s state space design, the formulas explaining the dynamic behavior of the circuit are shown in Fig. 3. The capacitor voltage of the cell model (\(V_{{FC}}^{C}\)) is achieved by the following equation:

$$\frac{{dV_{{FC}}^{C}}}{{dt}}=\frac{{{I_{FC}}}}{{{C_{FC}}}} \times \left( {1 - \frac{{V_{{FC}}^{C}}}{{{V_A}+{V_C}}}} \right)$$
(16)

For the voltage between the cathode and the anode of the cell, the following equation is given:

$${V_{OC}}={E_N} - V_{{FC}}^{C} - {V_{\text{\varvec{\Omega}}}}$$
(17)

For a stack with N cells, the voltage among their output is achieved by the following equation:

$${V_{OC}}={N_{cell}} \times \left( {{E_N} - V_{{FC}}^{C} - {V_{\text{\varvec{\Omega}}}}} \right)$$
(18)

The Eqs. (16–18) can be reformulated by the following formulation:

$$\dot {x}\left( t \right)=f\left( {x\left( t \right),u\left( t \right)} \right)y=g\left( {x\left( t \right),u\left( t \right)} \right)$$
(19)

\({\text{where}},{\text{~}}x=V_{{FC}}^{C},{\text{~}}u={I_{FC}},{\text{~and~}}y={V_{FC}}.\)

and, x defines the system state variable, u describes the system input.

The output of the voltage system is the two ends of the fuel cell terminals. Examining the fuel cell equations, we conclude that these equations are nonlinear35. In order to linearize, the small signal model, assuming a deviation from the variable operating point, can be defined as the decomposition of the sum of the constant amount and the deviation value as follows:

$$V_{{FC}}^{C}=v_{{FC}}^{C}+V_{{FC\delta }}^{C}{V_{FC}}={v_{FC}}+{V_{FC\delta }}{I_{FC}}={i_{FC}}+{I_{FC\delta }}$$
(20)

The working point \(\left( {x,~u} \right)=\left( {v_{{FC}}^{C},i_{{FC}}^{C}} \right)\). The model of the linear system mode is as follows:

$${\dot {x}_\delta }\left( t \right)={A_\delta }\left( U \right){x_\delta }\left( t \right)+{B_\delta }\left( U \right){u_\delta }{y_\delta }\left( t \right)={C_\delta }\left( U \right){x_\delta }\left( t \right)+{D_\delta }\left( U \right){u_\delta }$$
(21)

According to the following equation, conversion function of the fuel cell is achieved. This is the ratio of increasing voltage among the fuel cell outputs (\({V_{FC\delta }}\)) to additional current given by the fuel cell (\({I_{FC\delta }}\)) around the operating point, which is determined as follows.

$${G_{FC\delta }}\left( s \right)=\frac{{{V_{FC\delta }}\left( s \right)}}{{{I_{FC\delta }}\left( s \right)}}={C_{FC\delta }}{\left( {sI - A} \right)^{ - 1}}{B_{FC\delta }}+{D_{FC\delta }}$$
(22)

And in the general case (the case where the signal is small) we have:

$${G_{FC}}\left( s \right)=\frac{{{V_{FC}}\left( s \right)}}{{{I_{FC}}\left( s \right)}}={C_{FC}}{\left( {sI - A} \right)^{ - 1}}{B_{FC}}+{D_{FC}}$$
(23)

The fuel cell’s outputted voltage is not sufficient to reach the output voltage to supply the load. So, to solve this problem, we use a DC / DC converter. The output voltage reaches the desired voltage level during switching operations by power electronics. In this converter, the relationship between the distance when the switch is on (\({T_{ON}}\)) and the periodicity (T), is called the duty time (d) and is expressed by the following equation.

 

$$d={T_{ON}}/T$$
(24)

Assuming that the capacitor and inductor used in the DC / DC converter are ideal, the relationship between input voltage (\({V_i}\)) and input current (\({I_i}\)) to output voltage (\({V_o}\)( and output current (\({I_o}\)) are shown in Fig. 4.

Fig. 4
figure 4

The diagram of the DC/DC converter.

Full size image
$${V_O}=\frac{{{V_i}}}{{1 - d}}$$
(25)
$${I_O}={I_i} \times \left( {1 - d} \right)$$
(26)
$${V_O}={I_O} \times {R_O}$$
(27)

By combining the above equations, we have:

$${V_i}={I_i} \times {\left( {1 - d} \right)^2} \times {R_O}$$
(28)

Therefore, the fuel cell’s resistance is obtained as below:

$${R_i}=\frac{{{V_i}}}{{{I_i}}}={\left( {1 - d} \right)^2} \times {R_O}$$
(29)

In order to create a model that is as realistic as possible, the loss resistance for the inductor and capacitor (\({r_c},~{r_l}\)) is considered. This modified model of DC / DC converter is shown in Fig. 5.

Fig. 5
figure 5

The DC / DC diagram by considering the losses.

Full size image

After providing the state space equations for the circuit of Fig. 5, we have the transistor in both on and off states, i.e.,

$$\left[ {\begin{array}{*{20}{c}} {{{\dot {I}}_L}} \\ {{{\dot {V}}_c}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} { - \frac{{{r_l}}}{L} - \frac{{{r_c}}}{L}\left( {1 - d} \right)}&{ - \frac{1}{L}\left( {1 - d} \right)} \\ {\frac{1}{C}\left( {1 - d} \right)}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{I_L}} \\ {{V_c}} \end{array}} \right]+\left[ {\begin{array}{*{20}{c}} {\frac{{{r_c}}}{L}\left( {1 - d} \right)}&{\frac{1}{L}} \\ { - \frac{1}{C}}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{I_O}} \\ {{V_i}} \end{array}} \right]$$
(30)

To obtain the output equation if \({I_L}\) is considered as the output,

$${I_L}=\left[ {\begin{array}{*{20}{c}} 1&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{I_L}} \\ {{V_c}} \end{array}} \right]+\left[ {\begin{array}{*{20}{c}} 0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{I_O}} \\ {{V_i}} \end{array}} \right]$$
(31)

On the other hand, if the capacitor voltage is considered as an output variable, to get the output equation,

$${I_L}=\left[ {\begin{array}{*{20}{c}} 0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{I_L}} \\ {{V_c}} \end{array}} \right]+\left[ {\begin{array}{*{20}{c}} 0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{I_O}} \\ {{V_i}} \end{array}} \right]$$
(32)

In order to linearize, we use the small-signal model, such that: \({I_O}={i_O}+{I_{O\delta }}\), \({I_L}={i_L}+{I_{L\delta }}\), \({V_c}={v_c}+{V_{c\delta }}\), \({I_i}={v_i}+{V_{i\delta }}\), and \(d^{\prime}=D^{\prime}+d_{\delta }^{\prime }\). where, \(D^{\prime}=\left( {1 - D} \right)\). Therefore,

$$A = \left[ {\begin{array}{*{20}c} { - \frac{{r_{l} }}{L} - \frac{{r_{c} }}{L}d^{\prime } } & {\frac{{d^{\prime } }}{L}} \\ {\frac{1}{C}\left( {1 - d} \right)} & 0 \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} { - \frac{{r_{c} d_{\delta }^{\prime } }}{L}} & {\frac{{D_{\delta }^{\prime } }}{L}} \\ {\frac{{D_{\delta }^{'} }}{L}} & 0 \\ \end{array} } \right]$$
(33)

Therefore, the linearized model is represented as follows:

$$\left[ {\begin{array}{*{20}c} {\dot{I}_{L} } \\ {\dot{V}_{c} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \frac{{r_{l} }}{L} - \frac{{r_{c} }}{L}d^{\prime } } & { - \frac{{d^{\prime } }}{L}} \\ {\frac{{d'}}{C}} & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {I_{{L\delta }} } \\ {V_{{c\delta }} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\frac{{r_{c} }}{L}d^{\prime } } & {\frac{1}{L}} & {\frac{1}{L}\left( {r_{C} \left( {i_{o} - i_{L} } \right) - v_{C} } \right)} \\ { - \frac{1}{C}} & 0 & {\frac{{i_{L} }}{C}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {I_{O} } \\ {V_{i} } \\ \end{array} } \right]$$
(34)

which is equivalated by:

$$\left[ {\begin{array}{*{20}{c}} {{{\dot {I}}_L}} \\ {{{\dot {V}}_c}} \end{array}} \right]={A_{BC\delta }}\left[ {\begin{array}{*{20}{c}} {{I_{L\delta }}} \\ {{V_{c\delta }}} \end{array}} \right]+{B_{BC\delta }}\left[ {\begin{array}{*{20}{c}} {{I_O}} \\ {{V_i}} \end{array}} \right]$$
(35)

The primary objective of this study is to optimize the performance and longevity of Proton Exchange Membrane Fuel Cells (PEMFCs) by enhancing their control systems through the design and implementation of optimal controllers. PEMFCs, while offering clean and efficient energy, are characterized by dynamic challenges in managing voltage levels due to fluctuations in load demands and environmental conditions. To effectively regulate the output voltage of PEMFC stacks and ensure reliable operation, the integration of DC/DC converters becomes essential. The buck/boost DC/DC converter plays a crucial role in bridging the gap between the inherent limitations of PEMFC-generated voltage and the requirements of various connected loads. These converters enable efficient voltage regulation by compensating for dynamic changes in current and voltage levels, ensuring smooth and steady power delivery while minimizing ripples and overshoots harmful to the PEMFC’s longevity.

The scope of this research transitions seamlessly to the design of buck/boost controllers to focus on a comprehensive control system design. By integrating the PEMFC model with the DC/DC converter in a unified system, the optimization results gained through the ICOA are applied to both the controller and the converter. This ensures not only the effective operation of the PEMFC but also the voltage regulation through power electronics. Therefore, the introduced scope aligns with the study’s overarching motivation of improving PEMFC performance, ensuring voltage stability, reducing ripples, and increasing the stack lifetime.

DC/DC converter design

A fuel cell’s general diagram connected by a dc-dc converter is shown in Fig. 1. The system is generally modeled as a current source36,37. Given the small-signal equations for the fuel cell and dc-dc converter below, we obtain the state space formulas for the whole system.

$$\:{\dot{I}}_{CFC\delta\:}={A}_{FC\delta\:}{V}_{CFC\delta\:}+{B}_{FC\delta\:}{I}_{FC\delta\:}{\dot{V}}_{CFC\delta\:}={C}_{FC\delta\:}{V}_{CFC\delta\:}+{D}_{FC\delta\:}{I}_{FC\delta\:}$$
(36)

For the converter,

$$\:\left[\begin{array}{c}{\dot{I}}_{L\delta\:}\\\:{\dot{V}}_{c\delta\:}\end{array}\right]={A}_{BC\delta\:}\left[\begin{array}{c}{I}_{L\delta\:}\\\:{V}_{c\delta\:}\end{array}\right]+{B}_{BC\delta\:}\left[\begin{array}{c}{I}_{O\delta\:}\\\:{V}_{O\delta\:}\\\:{D}_{\delta\:}^{{\prime\:}}\end{array}\right]$$
(37)

Combining the above equations, the state space model is obtained as follows:

$$\begin{aligned} \left[ {\begin{array}{*{20}c} {\dot{I}_{{L\delta }} } \\ {\dot{V}_{{C\delta }} } \\ {\dot{V}_{{CFC\delta }} } \\ \end{array} } \right] & = \left[ {\begin{array}{*{20}c} { - \frac{{r_{l} }}{L} - \frac{{r_{c} }}{L}d^{\prime} + \frac{{d_{{FC\delta }} }}{L}} & { - \frac{{d^{\prime}}}{L}} & {\frac{{C_{{FC\delta }} }}{L}} \\ {\frac{{d^{\prime}}}{C}} & 0 & 0 \\ {B_{{FC\delta }} } & 0 & {A_{{FC\delta }} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {I_{{L\delta }} } \\ {V_{{C\delta }} } \\ {V_{{CFC\delta }} } \\ \end{array} } \right] \\ & \;\;\;\; + \left[ {\begin{array}{*{20}c} {\frac{{r_{c} }}{L}d^{\prime}} & {\frac{1}{L}\left( {r_{C} \left( {i_{o} - i_{L} } \right) - v_{C} } \right)} \\ { - \frac{1}{C}} & {\frac{{i_{L} }}{C}} \\ 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {I_{{O\delta }} } \\ {D^{\prime}_{\delta } } \\ \end{array} } \right] \\ \end{aligned}$$
(38)

The input state vectors are \({\left[ {\begin{array}{*{20}{c}} {{I_{O\delta }}}&{D_{\delta }^{\prime }} \end{array}} \right]^T}\) and \({\left[ {\begin{array}{*{20}{c}} {{I_{L\delta }}}&{{V_{C\delta }}}&{{V_{CFC\delta }}} \end{array}} \right]^T}\), respectively. To calculate the device conversion function, input variables, output variables and system output matrix must be defined. Therefore, if fuel cell outputted current control (\({I_L}\)) is needed, the output matrix of the system is \({C_{T\delta }}=\left[ {\begin{array}{*{20}{c}} 1&0&0 \end{array}} \right]\) by adjusting the duty time of the converter. However, when the control parameter is the output voltage of the converter, the output matrix of the system is\({C_{T\delta }}=\left[ {\begin{array}{*{20}{c}} 0&1&0 \end{array}} \right]\). In the first case where the control variable is the converter’s outputted voltage, the system conversion function with voltage output (\(y={V_C}\)) is as follows:

$${G_{T\delta }}\left( s \right)={C_{T\delta }}{\left( {sI - A} \right)^{ - 1}}{B_{T\delta }}+{D_{T\delta }}$$
(39)

Improved Coot Optimizer

Explanation

One of the members of the rail family are the coots. They are small water birds and are made of Fulica. Coots have big forehead shields, with colorful flier and red to dark red eyes. Below of the tail some of them are white. Reproduction, migratory behavior, habitat are examples of American coot conduct. To achieve a more efficient optimization method, the conduct of coot’s in water has been used. The conduct of coot in water involves three motions. A erratic motion of action and a synchronized motion. The coots also move sequentially in the water. Coots have dissimilar behaviors which are used for modeling the Coot Optimization Algorithm collective motion. All group move to the position of the goal and a number of coots move ahead of the group. So, four dissimilar motions of coots in the water are seen, these four motions are listed below.

  1. 1.

    Accident motion to different position.

  2. 2.

    Move in burst.

  3. 3.

    Make the same location as the front coots.

  4. 4.

    Guiding the group to reach optimal position.

Numerical pattern and algorithm

All optimization algorithms are modeled on a single basis. \(\vec {x}=\left[ {\overrightarrow {{x_1},} ~\overrightarrow {{x_2}} , \ldots \overrightarrow {{x_n}} } \right]\) is the beginning of the algorithm, and measured regularly. The object value is achieved as \(\left( {\vec {o}} \right)=\left\{ {{o_1}.{o_2}.~ \ldots {o_n}} \right\}\). It is also gotten better by a set of patterns which includes the center of the optimization method. The optimization methods which based on population search the optimum number of optimization subjects so there is no ensure of discovering a solution in one run, but chance of discovering the global optimal increase with enough amount of accidently solvent and repeat optimization. The population is created by the following formula (40):

$$CootPos\left( i \right)=rand\left( {1.n} \right)*\left( {ub - lb} \right)+lb$$
(40)

where, the coot location is indicated by \(CootPos\left( i \right)\),\(~lb\) and \(ub\) are the lower and upper bound of the research, respectively, which are shown according to formula (41), the amount of variables is denoted by n.

$$lb=\left[ {l{b_1}.l{b_2}.~ \ldots .~l{b_d}} \right].~ub=\left[ {u{b_1}.u{b_2}.~ \ldots .~u{b_d}} \right]$$
(41)

After determining the initial population and generating the location of each factor, the proportion of each solution must be measured using \({o_i}=f\left( {\vec {x}} \right)\). We randomly choose the group leader from among the coots (\(NL\)). So, the 4 motion of coots in water are enforced.

Random motion to this position and that position

In this research, we create accidently location through formula (42) and motion the coot to this location.

$$Q=rand\left( {1.n} \right). \times \left( {ub - lb} \right)+lb$$
(42)

Dissimilar parts of the research space are searched by this motion. The algorithm exits the local optimal if it grinds to a halt in the local optimal. Formula (43) shows coot’s new location.

$$Cootpos\left( i \right)=CootPos\left( i \right)+A \times R2 \times \left( {Q - CootPos\left( i \right)} \right)$$
(43)

where R2 is a random number limited in [0,1], A is measured according to formula (44).

$$A=1 - L \times \left( {\frac{1}{{Irer}}} \right)$$
(44)

where,\(~L\) and \(Iter\) are the flowing repetitions and the upper limit repetitions, respectively.

Move in a burst

To apply heat in a row, the middle location of two coots is used. The second way to apply the movement in a row is to measure the distance between two coots and motion the distance between the coots to another coot with a half-vector. In this research, the first one is used and formula (45) shows the new location of the coot.

$$CootPos\left( i \right)=0.5 \times \left( {CootPos\left( {i - 1} \right)+CootPos\left( i \right)} \right)$$
(45)

where, the second coot shown with \(CootPos\left( {i - 1} \right).\)

Set the location similar to the leader

Commonly the coots follow the groups head and determine their location similar to theirs. To know how each coot chooses its leader, we can conceive the mean location of the leaders as the coots change their location based on this mean location. To enforce this motion, we use formula (46) to choose the leaders.

$$F=1+\left( {iMOD~NL} \right)$$
(46)

The current coot index number is denoted by i, and the amount of leaders and the leader’s index number are denoted by \(NL\) and\(~F\), respectively.

The \(Coot\left( i \right)\) change its location similar to the leader’s F. The next location of the coots according to the chosen leader is expressed by formula (47).

$$CootPos\left( i \right)=LeaderPos\left( F \right)+2 \times R1 \times \cos \left( {2R{\text{\varvec{\Pi}}}} \right) \times \left( {LeaderPos\left( F \right) - CootPos\left( i \right)} \right)$$
(47)

where, R1 is a random number between [– 1,1], \(\pi\) is a fixed number equal to 3.14, R is a random number between [– 1,1], \(CootPos\left( i \right)\) is the current location of coot, \(LeaderPos\left( F \right)\) is selected leader location.

Guiding the group to reach optimal position (leader motion)

Leaders change their location to the optimal area to guide the group to the optimal area. Formula (48) is suggested to search for a better position around the current optimal point and to show the displacement of the leaders.

$$LeaderPos\left( i \right)=\left\{ {\begin{array}{*{20}{c}} {D \times R3 \times \cos \left( {2R\pi } \right) \times ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~R4<0.5} \\ {\left( {gBest - LeaderPos\left( i \right)} \right)+gBest~~~~~~~~~~~~~} \\ {D \times R3 \times \cos \left( {2R\pi } \right) \times ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~R4>=0.5} \\ {\left( {gBest - LeaderPos\left( i \right)} \right) - gBest} \end{array}} \right.$$
(48)

where, best position indicated by \(gBest\), R3, R4 are between [0,1], \(\pi\) is equal to 3.14, formula (49) indicate amount of D.

$$D=2 - L \times \left( {\frac{1}{{Iter}}} \right)$$
(49)

where, \(\:\:L\) and \(\:Iter\) are the flowing repetitions and the upper limit repetitions, respectively. In order for the algorithm not to get stuck in local optimum, \(\:2\times\:R3\) generates a larger random motion. \(\:\text{c}\text{o}\text{s}\left(2\text{R}{\Pi\:}\right)\) looks for around the best search factor.

We conceive all these motions randomly for save the random nature of the optimization algorithm. It can be concluded that the coot during the algorithm operation can move either randomly and in sequence or following the group leader.

Improved Coot Optimization algorithms

The Coot Optimization Algorithms is a newly presented bio-inspired technique in optimization that has te ability to be used in different optimization problems. Nevertheless, the Coot Optimization Algorithms designates good results for the problems, it sometimes needs some improvement to escape from local optimum and premature convergence. The present study proposed two improvement techniques for covering these issues. The first improvement mechanism is to provide self-adaptive weight. This helps more for resolving the convergence speed issues of the COA. As can be assessed the COA, the candidates should have promising values at the initial step, but in the next steps, the local search has been made. This is resolved by considering a weight to adjust approaching degree which can be achieved as follows:

$$LeaderPos\left( i \right)=\left\{ {\begin{array}{*{20}{c}} {D \times w \times \cos \left( {2R\pi } \right) \times ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~R4<0.5} \\ {\left( {gBest - LeaderPos\left( i \right)} \right)+gBest~~~~~~~~~~~~~} \\ {D \times w \times \cos \left( {2R\pi } \right) \times ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~R4>=0.5} \\ {\left( {gBest - LeaderPos\left( i \right)} \right) - gBest} \end{array}} \right.$$
(50)

The weight changes adaptively which rises gradually to reduce the difference between the best and worst solutions gradually. This action causes a good balance between the exploration and exploitation of the algorithm. The other improvement mechanism utilized in this study is chaotic mechanism. The chaotic mechanism is employed for adapting the best solution quality during the iterations.

Sometimes, the local value and global value provide equal result which delivers premature convergence for the problem. The chaotic mechanism van resolves this issue. This technique provides an ergodic results for regulating the solution quality38. Here, logistic map is employed for this purpose. With assuming this mechanism, the population updating is achieved by the following:

$$CootPos\left( i \right)={x_{m+1}} \times \left( {ub - lb} \right)+lb$$
(51)

where,

$${x_{m+1}}=4{x_m}\left( {1 - {x_m}} \right)$$
(52)

where, \({x_m}\) is the \({m^{th}}\) iteration value, m describes the iteration number, and \({x_0}\) defines an initial random value between 0 and 1. Figure 6 depicts the Pseudocode of the Improved Coot Optimizer algorithm.

Fig. 6
figure 6

The Pseudocode of the Improved Coot Optimizer algorithm.

Full size image

Algorithm verification

To formalize the AVOA, four varies benchmark operate have been used. The new IAVOA has been attained to four standard benchmark procedure result has been equated with another algorithm, consisting of Multi-verse optimize (MVO)39, the original COA40, Emperor penguin optimizer (EPO)41, and lion optimization algorithm (LOA)42 (Table 1).

Table 1 Parameter setting for various metaheuristic algorithms studied in this research.
Full size table

For benchmark functions (f1–f4), we report the best-achieved objective function values instead of RMSE to maintain consistency with standard optimization benchmarking practices. RMSE was only used in the PEMFC PID controller tuning problem as the engineering fitness function. The algorithm balance of 30 and the lower limit value for them is 0. The comparability analysis for the algorithm is based on lower limit value, upper limit value, fundamental value, the standard deviation value (\(std\))16 which is present in Table 2.

Table 2 The verification result of the studied algorithm.
Full size table

Table 2 presents the proposed improved coot optimization algorithm has lower mean value for all of the analyzed methods. Lower and upper values of this algorithm are less than the other optimization problems. The object of all four methods is to attain the lowest amount; the ICOA technique has the highest accuracy. We can conclude that our improved method has higher reliability and validness compared to other methods. Moreover, the results showed that the suggested technique has the lowest amount of the standard deviation value that indicates its better consistency toward the other methods.

The above results show that using the proposed improved coot optimization algorithm can be used as a proper optimized for solving the control problem in our purpose. Table 2 presents the final objective function values achieved by the Improved Coot Optimization Algorithm (ICOA) and three other state-of-the-art metaheuristic algorithms (COA, MVO, EPO, LOA) on four standard benchmark functions. The objective values represent the quality of the solutions found during optimization, where lower values indicate better performance. These results replace previously reported RMSE values, in response to reviewer feedback, ensuring standard benchmarking practices are followed. As observed, ICOA achieves the lowest values on all benchmark functions, demonstrating superior accuracy and convergence reliability.

To ensure a fair comparison of computational effort, all algorithms were tested under an equal budget of 6,000 fitness evaluations (iterations × population size). For ICOA (30 agents), this resulted in 200 iterations. Comparatively, MVO (50 agents) used 120 iterations, EPOA (40 agents) 150 iterations, and LOA (30 agents) 200 iterations. Convergence curves (Fig. 7) track the RMSE reduction over evaluations, with statistical significance confirmed via Wilcoxon signed-rank tests (p < 0.05). This validation method has also been confirmed in similar literature43,44,45. In this study, the proposed controller is validated not only through standard step responses but also under time-varying load profiles and disturbance rejection scenarios to emulate realistic operating conditions.

Fig. 7
figure 7

Convergence curves of ICOA and benchmark algorithms (MVO, EPOA, LOA) across four standard test functions (f1–f4). The function value is shown in logarithmic scale to clearly depict convergence behavior. ICOA (red trace) demonstrates superior convergence in all cases.

Full size image

Simulation results

As is explained in the previous sections, the main idea here is to model an optimal control structure for a PEMFC to provide the best efficiency of it in different terms like efficiency of using their power. Figure 8 shows the structure of the proposed PID controller-based system for optimal control of it.

Fig. 8
figure 8

The structure of the proposed PID-based system.

Full size image

This controller is a simple technique which is still considered as a proper method for control the objects in industries which is due to their easy to implement feature31. Therefore, in this study, we use a PID controller for adjusting the PEMFC system and providing the best efficiency of it46. Although PID controllers are widely seen as a foundational control approach and have historically been applied in various industrial applications due to their simplicity and ease of implementation, their effectiveness remains highly relevant when optimized with modern metaheuristic algorithms. In this study, the PID controller parameters (Kp, Ki, Kd) were rigorously optimized using the proposed ICOA to address key performance factors, such as minimizing overshoot, ripple, and settling time, which are critical for PEMFC systems. However, we acknowledge that modern alternatives, such as sliding mode controllers (SMCs), adaptive controllers, or fuzzy logic-based controllers, could provide further enhancements in dynamic performance and robustness under more complex operating conditions. Future research could explore such advanced control schemes in combination with optimization approaches like ICOA. For this study, the focus was on leveraging the ICOA’s potential to demonstrate significant performance improvements with the PID control strategy, which remains a practical and reliable choice for many real-world applications. The results obtained validate the approach by showcasing improved stability, reduced overshoot, and enhanced dynamic response for PEMFC systems.

Moreover, a steady-state error decreasing is delivered in addition to a dynamic response progressing by implementing the suggested control method. The study uses the Root Mean Square Error (RMSE) for optimizing the controller. The formulation for the RMSE is given below:

$$RMSE=\sqrt {\left( {\frac{1}{T}\mathop \smallint \limits_{0}^{T} {e^2}d{\text{{\rm T}}}} \right)}$$
(53)

The main idea of the optimization in this study is to provide an optimal feedback controller to minimize the fitness function (RMSE) based on the proposed improved Coot Optimization Algorithm. This will be achieved by selecting proper values for the decision variables, i.e., \({K_P}\), \({K_I}\), and \({K_D}\).

The RMSE was chosen as the cost function due to its ability to emphasize larger deviations, making it suitable for minimizing ripples and ensuring system stability in PEMFC voltage control. This quadratic nature of RMSE facilitates improved accuracy and dynamic response, particularly for high-efficiency applications like fuel cells. Compared to alternate functions like IAE or ISE, RMSE is superior in addressing ripple reduction and peak error sensitivity, aligning well with the study’s optimization objectives.

The simulations are performed to a 64-bit Matlab2017b software that is installed on a 8GB RAM-Core i7 Intel laptop with 2.00 GHz CPU, and 2.5 GHz frequency. The parameters related to the improved Coot Optimization Algorithm are as follows: Number of search agents is set 30 and Maximum number of iterations is set 200. The values used in the converter design are given in Table 347, and the specifications for the fuel cell are also given in Table 448.

Table 3 The parameter values used in the DC/DC converter47.
Full size table
Table 4 The parameter values used in the PEMFC48.
Full size table

We used the following system as a lab resulted system as the reference model49:

$$\dot {x}=Ax+Bu={10^3} \times \left[ {\begin{array}{*{20}{c}} { - 5}&{ - 6}&{ - 100} \\ {1.4}&0&0 \\ 0&0&{ - 0.03} \end{array}} \right]x+{10^3} \times \left[ {\begin{array}{*{20}{c}} {0.244}&{1032.4} \\ { - 2.56}&{117.6} \\ 0&0 \end{array}} \right]u$$
(54)

where, A is the stability matrix and A and A are selected so that the output of the reference model is 78.5 V. Now that we have the equations of state, we have the fuel cell conversion function, and in order to stabilize it, we series it with a PID controller and finally get feedback from the output. Therefore, Fig. 9 displays the system response in the non-optimized state. Note that, the tuning of controller parameters was achieved using both the mathematical formulations and MATLAB/Simulink modeling. A detailed Simulink model was constructed to emulate the dynamic behavior of the PEMFC system, integrated with the DC/DC converter, and the PID feedback loop. Simulink was employed to assess system transient responses, including rise time, settling time, and overshoot, thus validating the ICOA-tuned PID parameters in practical scenarios. The controller parameters were tuned by integrating the mathematical formulations with a dynamic simulation model built in MATLAB/Simulink. The Simulink environment provides a complete PEMFC system model, including DC/DC converter dynamics and PID feedback control, allowing the proposed ICOA to iteratively select optimal values for Kp, Ki, and Kd. This process ensures practical validation of the tuning results beyond theoretical derivations from Eq. (54), as Simulink simulations were used to analyze system responses under various operating conditions, including dynamic load changes and disturbances.

Fig. 9
figure 9

The system response in the non-optimized state.

Full size image

The time profile of the non-optimal system is as follows: 2.47% overshoot, 4.7 s settling time, and 2.73e-3 s rise time. As aforementioned, the main idea here is to provide an optimal PID controller for the system. To provide a proper analysis on the presented algorithm, its results were compared with Multiple-verse optimize (MVO)39, Emperor penguin optimization algorithm (EPOA)41, and lion optimization algorithm (LOA)42 from the literature. Table 5 tabulates the achieved control coefficients of the PID obtained from the COA and the comparative algorithms.

Table 5 The PID control coefficients obtained from the ICOA and comparative algorithms (MVO, EPO, LOA).
Full size table

The values of Kp and Ki obtained in Table 5 are relatively small, which can be attributed to the specific nature of the PEMFC system and the optimization approach used in this study. For PEMFC systems, precise control of output voltage with minimal overshoot and ripple requires high sensitivity to small deviations in the system’s dynamics. The ICOA effectively balances the proportional gain (Kp) and integral gain (Ki) to minimize these deviations while optimizing the system’s overall response. In this context, small values for Kp and Ki indicate that incremental adjustments in the controller’s response are sufficient to stabilize the system while avoiding excessive oscillations or instability. Similarly, the optimization process ensures that Kd remains at a suitable level to provide adequate damping and consistent dynamic performance. This is particularly advantageous for systems like PEMFCs, where the focus is on ripple reduction, steady-state accuracy, and maintaining relative stability. The results demonstrate that the optimized PID coefficients are not negligible but are carefully tuned to match the PEMFC system’s specific requirements, ensuring that the controller achieves robustness, minimal overshoot, fast settling time, and ripple reduction. Additionally, the comparative analysis highlights that the ICOA-provided coefficients outperform other techniques, confirming the effectiveness of the optimization approach.

In accordance with the benchmarking methodology suggested in Ref.50, all algorithms were executed under identical settings, including population size, stopping criteria, objective function, and boundary constraints. Table 6 summarizes the comparative results, highlighting the superior performance of ICOA in terms of best and average function values, convergence speed, and robustness (as indicated by standard deviation). Figure 10 illustrates the comparative performance of ICOA, MVO, EPO, and LOA in terms of best function value and output consistency (standard deviation). The results confirm the superiority of ICOA under uniform benchmarking conditions.

Table 6 Comparative performance of optimization algorithms under identical conditions.
Full size table

All algorithms were executed using the same initial population size, stopping criteria, and cost function. The results show that ICOA outperforms the other methods in terms of accuracy, convergence speed, and stability.

Fig. 10
figure 10

Comparative analysis of optimization algorithms in terms of best function value and result stability. All algorithms were evaluated under identical conditions.

Full size image

Given the random nature of this algorithm, one should not expect the same solution to be obtained every time. Therefore, all of the algorithms have been run 35 times independently and their best results are considered to the analysis. Figure 11 shows the comparison results of the step response for the PEM fuel cell system by various optimizers.

Fig. 11
figure 11

The comparison results of the step response for the PEMFC system based on different optimizers.

Full size image

Based on Fig. 11, the response of the optimal system by the proposed improved COA, Multiple-verse optimize (MVO)39, Emperor penguin optimization (EPO) algorithm41, and lion optimization algorithm (LOA)42, indicates the higher effectiveness of the suggested ICOA technique in optimizing the fuel cell outputted voltage51. From Fig. 11, the overshoot rate for the system designed by the proposed improved coot optimization algorithm is lower than the response obtained from other methods. Also, the speed of the system designed with this algorithm is higher than the system designed by other algorithms. The ratio by the ICOA is more satisfying than the non-optimal system shown in Fig. 9.

The system’s simulation achievements showed the best results for the suggested ICOA-based method which provides the following time characteristics: 0.75% overshoot, 3.76e−3 s settling time, and 1.26e−4 s rise time.

Therefore, as can be observed from the results, based on the profile of the ICOA, the amount of overshoot is significantly reduced, which significantly increases the relative stability of the system and ensures its overall stability. It is also observed that the settling time is reduced to an acceptable level, which ensures the improvement of speed and part of the relative stability of the system.

To provide more analysis on the proposed method, it is also performed to another case study from52. By considering to Fig. 12, the dc-dc converter’s loop gain is achieved as follows:

$$T\left( s \right)={G_c}\left( s \right){G_{PWM}}\left( s \right){G_{d{v_0}}}\left( s \right)H\left( s \right)$$
(55)

where, \({G_c}\left( s \right)\) is the controller transfer function and \(H\left( s \right)\) describes the feedback transfer function. The details of the system are as follows: \(Load=12{\text{\varvec{\Omega}}}\), \({f_s}=100\;{\text{kHz}}\), \(v_{{in}}^{ \wedge } = \left[ {16,~30} \right]\;{\text{V}}\), \(V_{{out}}^{ \wedge }=24\;{\text{V}}\), \({L_f}=10\;{\text{\varvec{\upmu}H}}\), and \({C_f}=100\;{\text{\varvec{\upmu}F}}\).

Fig. 12
figure 12

The closed loop configuration of the system.

Full size image

Finally, by considering the Boost mode (\(v_{{in}}^{ \wedge }=16~V\)), the final transfer function of the system with feedback can be defined as follows:

$$G\left( s \right)=\frac{{16 - \left( {5e - 5} \right)s}}{{\left( {1e - 9} \right){s^2}+\left( {8.33e - 7} \right)s+0.16}}$$
(56)

And by considering the Buck mode ((\(v_{{in}}^{ \wedge }=30~V\))), the final transfer function of the system with feedback can be defined follows:

$$G\left( s \right)=\frac{{30 - \left( {3.6e - 5} \right)s}}{{\left( {1e - 9} \right){s^2}+\left( {8.33e - 7} \right)s+0.3136}}$$
(57)

The bode diagram of the system before compensation for both Buck and Boost converters are shown in Fig. 1352.

Fig. 13
figure 13

The system’s “bode diagram” before compensation for both Buck and Boost converters.

Full size image

From Fig. 13, the efficiency of the Boost and Buck modes is too close. The results show a zero point at the right half side, a distortion on the frequency profile, and a low phase margin about 6.84◦ and 6.52◦, respectively. Moreover, large value is achieved by the phase margin slope in the neighborhood of the crossing frequency shows system’s weak anti-interference capability51,53. This shows a need for additional compensation to the system.

Based on52, and the proposed method, the final compensator after transforming to the transfer function mode is achieved as follows:

$$G\left( s \right)=\frac{{\left( {1+1.216e - 4s} \right)\left( {1+1.216e - 4s} \right)}}{{\left( {2.8e - 4s} \right)\left( {1+1.4e - 6s} \right)\left( {1+1.4e - 6s} \right)}}$$
(58)

and Fig. 14 depicts the final results for the bode diagram.

Fig. 14
figure 14

The “bode diagram” of the system after compensation by the proposed method.

Full size image

As can be inferred from Fig. 14, the phase margin and system gain have been enhanced after compensation that provides higher than about 15dB and 65◦, respectively which shows a satisfying anti-interference ability to the system. Bode diagram of the system with ICOA-tuned PID controller. A phase margin of 65° and gain margin of 15 dB confirm the system’s frequency-domain robustness.

  • Dynamic operating conditions.

To evaluate the robustness and adaptability of the proposed ICOA-PID controller, the PEMFC system was tested under dynamic operating conditions. A time-varying load profile was applied, including abrupt increases and decreases in demand. The voltage output response (Fig. 15) remained stable and well-regulated. Additionally, a disturbance signal was injected at the input of the DC/DC converter to test disturbance rejection (Fig. 15). In both scenarios, the controller maintained performance with minimal overshoot, fast recovery, and no steady-state error. Figure 15 illustrates the system’s response under a time-varying dynamic load current profile. The load undergoes two abrupt transitions (from 0.5 A to 1.2 A, and back to 0.8 A), simulating the effect of real-time user demand fluctuations. Despite these changes, the proposed ICOA-optimized PID controller maintains the output voltage within a tightly regulated range with negligible overshoot and rapid recovery. Further, Fig. 15 presents the system’s response to an external disturbance signal injected at the converter level. The disturbance is modeled as a short-duration input deviation, and the controller successfully rejects it with minimal impact on the voltage output, reaffirming the robustness and resilience of the control strategy.

Fig. 15
figure 15

Top: System voltage response under a time-varying load current profile. The controller effectively regulates output voltage despite abrupt increases and decreases in load (from 0.5 A to 1.2 A and back to 0.8 A), with minimal overshoot and fast settling. Bottom: Voltage response of the PEMFC system to an external disturbance injected at the converter input. The ICOA-optimized PID controller demonstrates strong disturbance rejection and maintains system stability with negligible deviation in Vout.

Full size image

Figure 15 further validate the controller’s robustness by demonstrating stable behavior under sudden load changes and external disturbances.

The verification of the proposed Improved Coot Optimization Algorithm (ICOA) already includes a direct comparison with the traditional Coot Optimization Algorithm (COA) under the same experimental conditions, as demonstrated in Table 2. Benchmark functions (f1–f4) were tested under an equal number of fitness evaluations (6,000 evaluations for all algorithms). This ensures a fair comparison of computational effort. The results show that ICOA consistently outperforms COA in all benchmark functions, achieving lower Mean Deviation (MD) and Standard Deviation (SD) values. Additionally, convergence curves presented for these functions (e.g., Fig. 7) illustrate faster and more stable convergence for ICOA compared to COA, attributed to the inclusion of self-adaptive weights (Eq. 50) and chaotic mechanisms (Eq. 51). These enhancements significantly improve the algorithm’s ability to escape local optima and ensure efficient exploitation. Nonetheless, to further strengthen the validation of ICOA’s superiority, additional case studies or practical controller optimization problems may be analyzed directly comparing COA and ICOA. This comparative analysis will help emphasize the enhanced accuracy, reliability, and convergence speed of ICOA for the specific application of PEMFC control. This can be one of the goals of future works.

  • Stability and robustness.

The research explicitly addresses the stability and robustness of the proposed control system through multiple validation methods. These include the improvement of the overshoot rate, settling time, and ripple reduction, which directly contribute to the stability and robustness of the PEMFC system. For example:

  1. (i)

    Dynamic system stability:

Through the use of the ICOA-optimized PID controller, the overshoot was reduced to 0.75% from the non-optimized system’s value of 2.47%. Similarly, the settling time was significantly improved, ensuring system behavior aligns with stability requirements during transient and steady-state stages.

  1. (ii)

    Frequency domain analysis:

The stability of the DC/DC converter was verified using Bode diagrams before and after compensation, demonstrating improved phase margin and system gain in both Boost and Buck modes. After compensation, the system achieved phase margins exceeding 65° and a gain of more than 15 dB, indicating robust performance under potential disturbances.

  1. (iii)

    Statistical robustness:

The effectiveness of ICOA was compared against other optimization techniques (MVO, EPO, LOA) through multiple benchmark functions under identical computational budgets. Statistical robustness was verified using SD and convergence results (Fig. 7). ICOA consistently provided lower SD values, affirming its reliability in avoiding local optima and maintaining consistent performance.

By analyzing both stability metrics and robustness indicators comprehensively, the study ensures that the PEMFC system operates reliably under varying conditions. Future work may further explore robustness tests under extreme environmental conditions or hardware-level noise impact if required, but the current results adequately validate the system’s stability and robustness.

The robustness of the ICOA-tuned PID controller was evaluated both in the time domain and frequency domain. In the time domain, two scenarios were simulated to reflect real-world disturbances: (i) dynamic load variations and (ii) external disturbance injection. Figure 15 demonstrates that the system maintains stable and regulated output under both conditions with negligible overshoot and fast settling. In the frequency domain, the Bode plot confirms a phase margin of approximately 65° and a gain margin of 15 dB, indicating strong robustness against system uncertainties and gain variations.

Conclusions

PEMFCs are increasingly recognized as promising clean energy sources due to their high efficiency, decentralized generation capability, and minimal environmental impact. However, optimizing their performance and ensuring longevity present several challenges, particularly in regulating output voltage and minimizing ripples under varying load demands. This study addressed these challenges by developing an advanced control framework utilizing a DC/DC converter coupled with a PID controller optimized through the ICOA. The research demonstrated the effectiveness of the ICOA in fine-tuning PID parameters to achieve significant enhancements in dynamic performance. Notable improvements include a reduction in voltage overshoot from 2.47 to 0.75% and a decrease in settling time from 4.7 s to substantially lower values. Ripple reduction and enhanced phase margins further validated the robustness of the proposed control method. Comparative analyses with other metaheuristic techniques—such as Multi-Verse Optimizer (MVO), Emperor Penguin Optimizer (EPO), and Lion Optimization Algorithm (LOA)—confirmed the superior performance of ICOA, as evidenced by benchmark functions and statistical evaluations.

The study also highlighted key mechanisms integrated into the ICOA, including adaptive weight adjustments and chaotic mapping, which facilitated efficient exploration and exploitation during optimization. These advancements enabled the algorithm to overcome the limitations of premature convergence and local optima, ensuring reliable performance across multimodal landscapes. Overall, the findings establish the ICOA-optimized PID control system as a practical and effective solution for stabilizing PEMFC output voltage while minimizing energy loss and improving system reliability. The achieved improvements in stability, efficiency, and robustness contribute significantly to the operational durability of PEMFCs under diverse conditions. The expanded simulation framework addresses both steady-state and dynamic operating conditions, reinforcing the controller’s practical viability and robustness. Further, the proposed control strategy demonstrates strong robustness against both parameter variations and external disturbances, verified through time-domain and frequency-domain analyses.

Future research directions could explore combining ICOA optimization with advanced control approaches such as sliding mode controllers or adaptive fuzzy logic systems to further enhance dynamic response and robustness under complex operating conditions. Additionally, hardware-level implementation under extreme environmental scenarios may provide deeper insights into the system’s practical viability.