Abstract
On August 21, 2021, a large earthquake occurred in the South Sandwich subduction zone, and the associated tsunami was widely observed. To robustly analyse the detailed seismic source process of this long-source duration (over 200 s) event occurring in a convexly shaped subduction zone, we applied the Potency Density Tensor Inversion with a non-rectangular and non-planar source surface to the broadband teleseismic P-waves. This method allows us to suitably reduce the effect of the time-increasing uncertainty of the Green’s function and the effect of modelling errors related to the fault geometry. We found the slip vectors of the 400 km long rupture area rotate clockwise to the south, corresponding to the clockwise rotation of the trench strike. Our results reveal that the rupture propagated up-dip to the shallow region, then propagated to the south-southeast along the trench, and stagnated for about 30 s at around 130 km south-southeast from the epicentre. After the stagnation of the rupture front, the moment-rate gradually increased with time, although a clear rupture area could not be identified for about 45 s. Afterwards the rupture re-propagated south-southwest along the trench from the stagnation area. The slow rupture growth following the stagnation of the fast rupture triggered a new fast rupture, which led to the 2021 South Sandwich Islands earthquake having the typical characteristics of a tsunami earthquake, with a long rupture duration and a slow average rupture front velocity.
Similar content being viewed by others
Introduction
Understanding the rupture process of tsunami-generating earthquakes is important for assessing the potential for future tsunami events. A “tsunami earthquake” is an event which has rupture characteristics that lead to the generation of tsunamis that are unusually large given the event’s magnitude1,2. It has been pointed out that tsunami earthquakes have a slow rupture front velocity and long rupture duration3,4. In the case of the 1992 Nicaragua earthquake, one of the typical tsunami earthquakes, the rupture front velocity and the rupture duration were reported to be 1.5 km/s, or less, and ~ 110 s, respectively2; it has been suggested that the slow slip along the plate interface occurred due to accumulated soft subducted sediments2. The mechanism of tsunami earthquakes is disputed in the scientific literature: variable frictional properties on the plate interface5, off-fault rupture6, accretionary prism rupture caused by rapid stress loading7, thermal pressurization8 and so on have been suggested being responsible for the heterogeneous rupture behaviour, typically characterized by a slow and long rupture process.
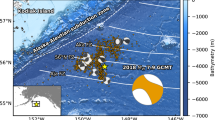
On August 12, 2021, the 2021 South Sandwich Islands (SSI) earthquake struck offshore the South Sandwich Islands, in the shallow part of the South Sandwich subduction zone9,10 classified as tectonic-erosion type11,12,13. In this subduction zone, the South American plate is subducting under the Sandwich plate at a rate of 70–78 mm/yr, in a west-southwest direction14 (Fig. 1). The South Sandwich trench curves convexly to the east15 (Fig. 1), and the South American plate is subducting obliquely in the southern region of this subduction zone. The bathymetric data on the South American plate16 shows several chains of seamounts extending in east-southeast to west-northwest directions. The aftershock distribution determined by the U.S. Geological Survey (USGS) extends from ~ 100 km north to ~ 300 km south of the mainshock epicentre along the South Sandwich trench17.
Summary of the study region. Three yellow stars are the epicentres of MW 7.5, MW 8.1 and mb 6.7 events reported by the USGS NEIC17, and two light blue beachballs are the moment tensors of MW 7.5 and MW 8.1 events. The grey square is the centroid location reported by the Global Centroid Moment Tensor (GCMT) project18,19, and the grey beachballs on the bottom right corner are the GCMT solution and the total moment tensor solution obtained in this study. The orange dots are the aftershocks from 2021-08-12 18:32:52 to 2021-8-15 18:32:52 (within three days after the MW 7.5 events) detected by the USGS NEIC. The vector shows the subduction velocity and azimuth of South American plate14. The white line indicates the plate boundary15, and the white front is the South Sandwich trench. The shaded background bathymetry is derived from SYNBATH16. The inset map shows the plates around the study region: Sandwich (SW), Scotia (SC), South American (SA), Antarctic (AN) and Africa (AF) plates15. The black lines are the plate boundaries15 and the box outlines the extent of this figure.
The USGS identified three independent events corresponding to the 2021 SSI earthquake (Fig. 1). At 18:32:52 (UTC), a moment magnitude (MW) 7.5 event occurred at 57.567° S, 25.032° W was followed 145 s later by an MW 8.1 event occurred about 90 km south of the epicentre of the first event; finally, 102 s later, a body-wave magnitude (mb) 6.7 event occurred about 280 km south-southeast (SSE) of the epicentre of the first event (Fig. 1). The Global Centroid Moment Tensor (GCMT) project18,19 reported only a MW 8.3 earthquake with a centroid at 59.48° S, 24.34° W (Fig. 1). Jia et al. (2022)9 applied the multiple point source inversion to the 2021 SSI earthquake using the low-frequency waveforms (0.002–0.05 Hz) and identified five sub-events: two thrust sub-events in the first 50 s, one long-period thrust sub-event for about 180 s with a centroid time of 90 s after the beginning of the rupture, and two thrust sub-events which occurred 3 min after the beginning of the rupture. Metz et al. (2022)10 carried out moment tensor inversion and finite fault inversion (FFI), and reported four sub-events. They also performed a teleseismic back-projection (BP) analysis and reported high-frequency (0.5–2 Hz) energy emitters migrating southward. Previous studies used long-period (20 s and longer) waveforms to perform source inversion and have shown that the 2021 SSI earthquake is composed of multiple sub-events9,10 and has the characteristics of a typical tsunami earthquake, with slow rupture front velocity and long rupture duration9. On the other hand, it also involves spatiotemporally complex high-frequency rupture inferred from the BP analysis10. To understand the rupture process of the 2011 SSI earthquake, which has the characteristics of a tsunami earthquake, it is essential to construct a detailed seismic source model that is able to explain the broadband teleseismic body waves.
In general, it is difficult to stably estimate the detailed seismic source process of an earthquake with complex fault geometries and a long rupture duration, such as the 2021 SSI earthquake. The influence of the uncertainty of the Green’s functions becomes dominant as the source duration gets longer20. A planar rectangle fault plane that is often adopted in the FFI may not necessarily be suitable for the actual curved and convex source fault, which can also increase the modelling uncertainty21,22. The recently proposed Potency Density Tensor Inversion (PDTI) has made it possible to estimate detailed source processes, including information on focal mechanism, by reducing the effects of the uncertainty of the Green’s functions21,23. In this study we apply the PDTI with a non-rectangular and non-planar source surface to the observed teleseismic waveforms of the 2021 SSI earthquake to estimate its source process, including spatiotemporal changes in fault geometry and slip vector. We discuss the complex rupture propagation during the 2021 SSI earthquake and propose the possibility of partial slip partitioning.
Method
In general, the earthquake source can be expressed by the volume density of the moment-rate tensor24. The moment-rate volume-density tensor is calculated by multiplying the potency-rate volume-density tensors by the rigidity. In the case of the fault dislocation, the potency-rate tensor is represented by a linear combination of five basis double-couple components21,25. Therefore, the teleseismic waveform of an earthquake observed at station \(\:j\) is given by:
where V is the 3-D source area, \(\:{\dot{P}}_{q}\) is a potency-rate volume-density function of \(\:q\)th basis double-couple component, \(\:{G}_{qj}\) is a true Green’s function of the \(\:q\)th basis double-couple component, \(\:\xi\:\) is the location in the V, \(\:{e}_{bj}\) is the background and instrumental noise and \(\:*\) denotes the convolution operator in the time domain.
In the FFI of seismic waveforms, the potency volume-density tensor is approximated by the fault slip vector (potency areal-density vector) on a pre-assumed fault plane26,27. The FFI method can resolve the spatiotemporal distribution of the potency density-rate (slip-rate) on the fixed fault plane, however it cannot identify fault ruptures with a different fault geometry.
In the multiple point source inversion, the moment volume-density tensor is approximated by a sum of the moment tensors at multiple point sources25,28,29. This approach makes no assumptions about the fault plane and thus allows discussion of the possibility of slip occurring on an unknown fault. However, the multiple point source inversion method is unable to estimate the detailed rupture process for each sub-event. In addition, only long-period waves can be analysed due to the effect of the modelling errors caused by the simplification of the source model.
In the PDTI method, the potency-rate volume-density tensor is approximated by the potency-rate areal-density tensor on a pre-assumed model surface21. Then, Eq. (1) becomes
where \(\:S\) is 2-D model surface and \(\:{\dot{P}{'}}_{q}\) is a potency-rate areal-density function. As a result, the ruptures occurring on various faults are projected onto the model surface as the potency-rate areal-density tensor. In the FFI method, the number of degrees of freedom of the potency tensor is reduced from five to two by specifying the fault plane26,27. However, in the PDTI method, the number of degrees of freedom of the potency tensor remains at five because the fault plane is never specified21. In other words, by increasing the degrees of freedom of the model, PDTI is capable of estimating a detailed seismic source process model including information on the fault geometry.
In general, a high degree of model freedom can lead to problems such as overfitting and unstable solutions. To avoid these problems, the PDTI method incorporates the modelling error derived from the uncertainty of the Green’s function into the data covariance matrix, as proposed by Yagi and Fukahata (2011)20, and applies Akaike’s Bayesian Information Criterion (ABIC)30,31,32 to reasonably evaluate the strength of the smoothing constraint. In this study, we use the latest version of PDTI, which introduces a time-adaptive smoothing constraint23 to avoid the problem of over-smoothing caused by fixing the smoothing strength.
For Eq. (2) to work successfully, it is necessary to reduce the modelling error by making the model surface \(\:S\) closer to the earthquake source faults. In this study, we analysed the source process by projecting the potency density tensor distribution onto a non-planar model created by referring to the slab geometry data in Slab2.033.
Data and model parameterization
For the PDTI, we used the vertical components of the teleseismic body P-waves from 47 stations at epicentral distances of 30°–100° downloaded from the SAGE Data Management Center (Fig. 2a). We selected stations, ensuring a high signal-to-noise ratio and better azimuthal coverage (Fig. 2a). We converted the observed waveforms to velocity waveforms by removing the instrument response and then decimated the signal by using a 1.2 s sampling. We calculated the theoretical Green’s functions using the method of Kikuchi and Kanamori25 with a sampling rate of 0.1 s. We used the 1-D averaged structure of the CRUST1.034 in the source region to calculate the theoretical Green’s function (see Supplementary Table S1). Other structure models, CRUST2.035 (see Supplementary Table S2) and ak135-F spherical average model36,37 (ak135-F) (see Supplementary Table S3), are also used to evaluate the robustness of the modelling (Fig. 3).
Summary of inversion results. (a) The station distribution used in the inversion, projected on the azimuthal equidistant map. The dotted circles show epicentral distances of 30° and 100°. (b) Moment rate function. The background grey colours show the time range of four episodes defined in this study. (c) Map projection of the potency density tensor distribution on the non-planar model. The star and black line indicate the epicenter17 and plate boundary15, respectively. (d) Potency-rate density evolution projected along strike. The contours of 0.04, 0.06, 0.08 and 0.10 m/s are shown as black lines. The vertical axis is distance from the epicentre. The large and small stars are the epicentres of the MW 8.1 and mb 6.7 events detected by the USGS17.
Summary of results from model sensitivity test. (a) The moment-rate functions when the Green’s function is calculated using two different structure models (CRUST2.035 and ak135-F36,37; see Supplementary Tables S2 and S3) and when the potency-rate density tensor distribution is projected onto a planar model with a strike of 190° and dip of 10°. (b, c) Potency-rate density evolution obtained with CRUST2.035 (see Supplementary Table S2) and ak135-F36,37 (see Supplementary Table S3) structure models for calculating the Green’s function, respectively. (d) Potency-rate density evolution obtained using the planar model. The large and small stars plotted in each figure are the epicentres of the MW 8.1 and mb 6.7 events, respectively detected by the USGS17.
According to the USGS aftershock distribution17, the 2021 SSI earthquake is assumed to have occurred near the subducted and curved slab surface. To cover the aftershock distribution within three days of the event (Fig. 1), we followed Yamashita et al. (2021)38 and set up a non-rectangular model plane with the strike and dip angles of 190° and 10°, respectively, with a maximum width of 150 km and length of 405 km, which is expanded using a bilinear B-spline with a knot spacing of 15 km in both the strike and dip directions. Then the depth of each knot is adjusted based on Slab2.033 to minimize the location error in the Green’s function. We adopted a hypocentre (initial rupture point) by using the USGS-determined epicentre17 of the first event (57.567° S, 25.032° W) and the corresponding depth of the Slab2.033 at 21.6 km. To enable fast rupture propagation immediately after an initial break and to reduce the number of model parameters, a hypothetical rupture initiation time was set for each spatial node. The hypocentre and the surrounding nodes were set to be able to rupture immediately after the initial break, and the other nodes were set to be able to rupture immediately after the hypothetical 2.0 km/s front had passed. Based on the reported long duration of the 2021 SSI earthquake9,10, the rupture duration at each knot is 180 s with a sampling interval of 1.2 s, and the total rupture duration is 280 s.
In general, the PDTI method adjusts the waveform length to mitigate the influence of the PP-waves on the inversion results. However, when this scheme is applied to an earthquake with a long rupture duration, such as the 2021 SSI earthquake, only a few observation points contribute to the results after 200 s from the origin time. The source time function of the 2021 SSI earthquake obtained using the empirical Green’s function39,40 shows that the peak value of the moment rate in the 80 s after the origin time is sufficiently smaller than the peak value in the 200 s after the origin time (see Supplementary Fig. S1). Therefore, in this study, the waveform from the arrival of the P-wave to 80 s after the arrival of the PP-wave was used for inversion to stabilize the solution after 200 s from the origin time.
Results
The spatial distribution of the potency density tensor, calculated by taking the temporal integration of potency-rate density functions at each knot, is dominated by thrust focal mechanisms that are similar to the total moment tensor (Figs. 1 and 2c). The source area spans about 400 km in length, with a maximum potency of 6.4 m at about 210 km south-southeast of the epicentre (Fig. 2c). The estimated total moment tensor solution, obtained by the spatiotemporal integration of the potency-rate density tensors, shows a thrust focal mechanism including a 25% non-double-couple component (Fig. 1). The total seismic moment is 6.47 × 1021 N m (MW 8.5). The slip vector of the nodal plane closest to the slab surface geometry shows a tendency to rotate clockwise to the south-southwest (SSW) (Fig. 4a). The moment rate function has ten or more spikes with the largest peak of 6.71 × 1019 N m/s at 201 s (Fig. 2b). The synthetic waveforms calculated from the obtained source process model well reproduce the observed waveforms, including the data points not used for the inversion (Supplementary Fig. S2). In this study, we define Episodes 1–4 based on the moment rate function (Fig. 2d) and snapshots (Supplementary Figs. S3, S4, S5).
Spatial variation of slip vectors. (a) The spatial variation of total slip vectors for each knot obtained by PDTI. The slip vectors are calculated for the preferred nodal plane. (b) The spatial variation of slip vectors for GCMT solutions18,19 of background events larger than MW 5.5. In both (a) and (b), the black solid line is the direction perpendicular to the strike of the subducting slab near the trench. The two black dashed lines indicate the direction of plate subduction14, the upper line and the lower line are corresponding to the most northerly and to the most southerly subduction vector azimuths denoted as arrows in Fig. 1, respectively. The vertical line indicates the initial rupture point.
In Episode 1, the thrust-type rupture propagated mainly on the up-dip side of the hypocentre and then reached the trench at 30 s after the origin time (OT) (Fig. 5, Supplementary Fig. S3). Figure 2d shows the time evolution of the rupture area projected along the strike of the model plane (190°). As shown in Fig. 2d, the thrust-type rupture also propagated asymmetrically in the SSW and north-northeast (NNE) directions until OT + 30 s. The rupture front velocity in the strike direction is about 2 km/s. The SSW rupture started at OT + 8 s, and the rupture front velocity in the strike direction is about 3 km/s.
In Episode 2, from OT + 30 s, the thrust-type rupture propagated unilaterally in southward direction along the trench, at the rupture front velocity in the strike direction of about 3 km/s from OT + 30 s to OT + 70 s and then the southward rupture propagation stagnated at around 130 km SSW from the epicentre (Figs. 2d and 5, Supplementary Fig. S3). Within this episode, a large fault slip event, with a peak along the trench at about 130 km SSE of the epicentre, begins at OT + 55 s and continues for about 35 s.
In Episode 3, the moment-rate function increases gradually from about OT + 100 s (Fig. 2d). This gradual increase continues for about 45 s. We note it is difficult to identify a clear rupture propagation during Episode 3 due to the relatively small potency-rate density (Fig. 2d, Supplementary Fig. S4).
Episode 4 begins with the rapid rise in the moment-rate function around OT + 145 s (Fig. 2d). This initiation coincides with the origin time of the secondary MW 8.1 event, as determined by the USGS (Fig. 2d). The thrust-type rupture propagated in the SW direction from around 100 km SSW of the epicentre and reached the southern end of the model area at about OT + 200 s (Fig. 2d, Supplementary Fig. S5). The maximum peak of the moment rate function equals 6.71 × 1019 N m/s, at 202 s (Fig. 2d).
Model sensitivity tests
In this study, we calculated the Green’s functions using the 1-D structure model that averaged the CRUST1.030 structure in the source region. In general, the longer the rupture duration, the more likely it is to be affected by the uncertainty of the Green’s functions20. The effect of the Green’s function uncertainty is introduced to the data covariance matrix according to Yagi and Fukahata (2011)20, but this approach cannot evaluate the effect of non-Gaussian errors originating from the model setting41. Although the effect of non-Gaussian errors originating from the setting of the structure model can be evaluated using a Bayesian multi-model estimation41,42,43, it is not practical to apply this approach to PDTI in terms of computational cost44. Therefore, we examined the behaviour of the solutions for two additional structure models: CRUST2.035 and ak135-F36,37. In addition to the structure sensitivity test, we also examined the behaviour of the solution when the model surface was set to a plane with a strike of 190° and dip of 10°, rather than the non-planar surface referenced in Slab2.033. In this test, a 1-D structure that averaged the CRUST1.0 model in the source region is used.
Figure 3 shows the variation in the solution when the structure or depth of the model surface is perturbed. The timing of the peaks of the moment-rate function, which can be seen in Episode 1, 2 and 4, is slightly perturbed depending on the model, but similar results are obtained for all models (Fig. 3a). This result is consistent with the results obtained by the model sensitivity test in previous research21. On the other hand, the amplitude of the moment-rate function is almost the same for all models in Episode 1, but the model dependence of amplitude increases after Episode 2 (Fig. 3a). This result suggests that the effect of model uncertainty increases over time. However, the key features of the moment-rate function, such as the gradual increase in the moment-rate during Episode 3 and the rapid increase in the moment-rate at the start of Episode 4, are reproduced in all models (Fig. 3a). The asymmetric bilateral rupture propagating in the NNE–SSW direction in Episode 1, the unidirectional rupture propagating in the SSW direction in Episode 2, the absence of a clear event in Episode 3, and the large slip event occurring 200 km SSW from the hypocentre in Episode 4 are all reproduced in the three alternative models (Fig. 3b, c, d). The rupture area at the start of Episode 4 differs depending on the model, but a relatively large potency-rate density region near the epicentre of the USGS’ secondary MW 8.1 event is commonly obtained in all three alternative models (Fig. 3b, c, d). The moment magnitudes are perturbed by the model setting, and the values range from MW 8.3–8.5 when using the different structural models and model geometries.
Discussion
We analysed the broadband teleseismic body P-waves from the 2021 SSI earthquake and found that the rupture process can be divided into four episodes (Fig. 2b, d). In Episode 1, the rupture propagated from the hypocentre to the shallow region while expanding in the NNE–SSW direction, reaching the South Sandwich trench (Supplementary Fig. S3). In Episode 2, the rupture propagated in the SSE direction along the trench, but after OT + 70 s, it remained stagnant around 130 km SSE of the epicentre (Supplementary Fig. S3). In Episode 3, a clear rupture area cannot be identified (Supplementary Fig. S4), but the moment-rate increases gradually with time (Fig. 2b). In Episode 4, the rupture propagated towards SSW, until OT + 200 s (Supplementary Fig. S5). Our seismic source model explains the broadband teleseismic body P-waveforms, and its characteristics are reproduced even when other three different model settings are used (Fig. 3). Evaluating the smoothing strength using ABIC30,31,32 prevents overfitting and makes it possible to estimate robust results. It is worth noting that the PDTI results are smoothed according to the amount of information in the data. In the following, we discuss a series of fast and slow rupture evolution in particular comparing with the previous BP analysis10, exhibiting the typical tsunami-earthquake characteristics but having a more heterogeneous rupture evolution. We also discuss a possibility of slip partitioning based on our finding of rotation of slip vector azimuths.
The PDTI method employed in this study reduces the effects of modelling errors by increasing the number of degrees of freedom of fault geometry and rupture front21,45,46, while the BP method resolves the rupture propagation process by tracking the wave radiation sources without requiring detailed model setting47,48,49. However, the BP that uses the standard formulation may not be capable of robustly estimating the source radiation, partly because (as revealed by Jia et al. (2022)9 and our PDTI result in this study) the 2021 SSI earthquake involves the focal mechanism change during the rupture process and it violates the implicit assumption of the standard BP formulation (e.g., a single radiation pattern throughout the rupture process). Moreover, careful selection of the regional arrays and travel-time calibration should be required to better perform the BP for this earthquake10, so here we compare our results with the BP result of Metz et al. (2022)10. The results of the BP method using high-frequency waveforms10 show that the rupture propagated in the SSE direction from the epicentre until OT + 100 s. The BP signal remained at a low level from OT + 100 to 160 s, while the strong BP signals are distributed about 250 km south of the epicentre after OT + 200 s10. Considering that the high-frequency waveforms are generally sensitive to disturbances of slip-rate and the rupture front propagation50,51, the results of this study can be compared with the BP result. The SSE rupture propagation until OT + 100 s obtained by the BP method corresponds to Episodes 1 and 2 of this study, the low-level BP signal from OT + 100 to OT + 145 s corresponds to Episode 3, and the strong BP signal from OT + 200 s corresponds to the large rupture event of Episode 4. After the start of Episode 4, the BP signal increases, but it is weaker than the other major BP signals10. This may suggest that the initial rupture of Episode 4 accelerated smoothly.
The averaged rupture front velocity of the 2021 SSI earthquake is about 1.5 km/s, estimated from the distance and time difference from the initial break and the major rupture event of Episode 4 (Fig. 2d), in agreement with previous research9,10. This slow rupture front velocity appears to reflect the characteristics of a tsunami earthquake2,52. However, our results also show that the rupture front propagated relatively fast in Episodes 1, 2 and 4. In Episode 1, the rupture front velocity in the strike direction is about 2–3 km/s (Fig. 2d). Considering that the rupture is not only propagating in the strike direction, but also towards the shallow region, the actual rupture front velocity may reach about 2.8–4.2 km/s. In Episode 2, the rupture front velocity in the strike direction is about 3 km/s (Fig. 2d). Adjusting for discrepancy between the strike direction and the actual rupture propagation direction, the rupture front velocity in Episode 2 is about 3.2 km/s. In the latter half of Episode 2, the rupture stagnates in the area around 59°S. During this stage, we observe the variation of the dip angle in our potency-rate density tensors; the higher dip angles, in particular, show variation in the shallow domain (down to ~ 10 km depth) (Fig. S7). A similar but shorter stagnation for about 10 s has been observed for the 2010 El Mayor-Cucapah earthquake, which is attributed to the geometric complexity of the fault53. Around the source region of the 2021 SSI earthquake, the convex structure that may be associated with subducting fracture zones and/or seamounts is observed on the oceanic plate near 59°S16, which can induce strength heterogeneity and affect rupture propagation. The smoothing strength increases over time because of the increase with time of the uncertainty of the Green’s function, thus it is difficult to trace the rupture front in Episode 4. If we take the USGS hypocentre of the MW 8.1 event as the starting point of Episode 4, the rupture velocity in Episode 4 is about 3.2 km/s (Fig. 2d). The rupture front velocity that can be identified separately for Episodes 1,2 and 4 is about 60–90% of the S-wave velocity, which is consistent with the rupture front velocity of regular earthquakes54,55.
In Episode 3, the moment-rate increases gradually for about 45 s, but a clear rupture area cannot be identified (Fig. 2b, d). On the other hand, the BP analysis results show that the source of the wave corresponding to Episode 3 is stagnating at a point about 110 km south-southeast of the hypocentre10. The BP analysis results suggest that the rupture area of Episode 3 is distributed around the rupture stagnation area of Episode 2 and the rupture initiation area of Episode 4. The gradual increase in the moment rate reflects the gradual increase in the rupture area and/or the gradual acceleration of fault slip-rate. Therefore, the shear stress loading due to the gradual expansion of the rupture area and/or the gradual acceleration of slip-rate may trigger the rupture of Episode 4. Notably, the long-period, slow rupture event has been reported by previous studies9,10; Jia et al.9 determined the long-period event with a peak at around 100 s in the shallow zone, based on analysis of the low-frequency components. We thus consider that the gradual increase of moment rate with less obvious rupture migration seen during Episode 3 (slow rupture growth) is relevant to the long-period event, and our source model is integrating those diverse source signatures obtained by previous studies (Supplementary Fig. S6).
In oblique subduction zones, slip partitioning often occurs between dip-slip interplate faults and strike-slip faults in the continental crust56,57. When slip partitioning occurs, the slip vector of the dip-slip fault can point in a direction between the relative plate subduction direction and the direction normal to the trench axis56,58,59. Figure 4a shows the spatial variation of the slip vector of the nodal plane closest to the slab surface geometry. The slip vectors obtained in this study show a tendency to rotate clockwise as the slip propagates south-southwest in response to the change in the trench strike. In the rupture region spanning the latitudes 57°S–58.4°S, the slip vector azimuth becomes larger towards the south, while at latitudes 58°S–58.4°S it becomes consistent with the trench-normal direction (Fig. 4a). Between latitudes 58.4°S–59.3°S, the slip vector azimuth is about 15° greater than the direction of plate subduction, and deviates from the trench-normal direction (Fig. 4a). From 59.3°S to 60.2°S, the slip vector azimuth becomes larger towards the south, and from 59.8°S–60.2°S it approaches the trench-normal direction again (Fig. 4a). A similar result can be observed using the background seismicity (earthquakes of MW > 5.5) from the GCMT solutions: the dip-slip vector azimuths seem to align with the trench-normal direction at latitudes 57°S–58°S, while the azimuths tend to orient between the trench-normal direction and subduction direction at latitudes 58°S–60°S (Fig. 4b). The spatial variation of the dip-slip vectors, including our results, suggests that slip partitioning56,58,59 may play a role in the convex South Sandwich subduction zone.
Conclusion
We estimated the spatiotemporal evolution of rupture propagation during the 2021 South Sandwich Islands earthquake by using the PDTI method. The results of the model sensitivity test using the three alternative models suggest that the rupture propagation process obtained in this study is stable. The rupture can be divided into four episodes. In Episode 1 (0–30 s), the fast rupture propagated in a shallow direction, in Episode 2 (35–100 s) the fast rupture propagated southeast along the trench and then stagnates, in Episode 3 (100–145 s) the rupture slowly expanded around the stagnant area, and in Episode 4 (145–280 s), the fast rupture propagated in a south-southwest direction along the trench. The results of this study demonstrate that the characteristics of tsunami earthquakes, such as long rupture duration and a slow average rupture front velocity, are observed in the case of the 2021 South Sandwich Islands earthquakes as a complex process: slow rupture growth after stagnation of the initial fast rupture and the triggering of a final fast rupture. The spatial variation of the slip vectors shows a tendency to rotate clockwise to the south, corresponding to the clockwise rotation of the strike of the convex South Sandwich trench to the south. Our detailed source model successfully explains the broadband tele-seismic P-waves and can provide a unified explanation of the previous back-projection result and the multiple point source inversion results of the long-period waveforms, shedding light on the highly heterogeneous rupture process of the 2021 South Sandwich Islands earthquake.
Data availability
All seismic data were downloaded from IRIS Wilber 3 system (https://ds.iris.edu/wilber3/) or IRIS Web Services (https://service.iris.edu/), including the following station networks: (1) Caribbean Network (CU; https://doi.org/10.7914/SN/CU); (2) GEOSCOPE (G; https://doi.org/10.18715/GEOSCOPE.G); (3) the Global Telemetered Seismograph Network (USAF/USGS) (GTSN) (GT; https://doi.org/10.7914/SN/GT); (4) the IRIS/IDA Seismic Network (II; https://doi.org/10.7914/SN/II) and (5) the Global Seismograph Network (IU; https://doi.org/10.7914/SN/IU). The moment tensor solutions of the Global Centroid Moment Tensor (GCMT) catalog are available through the website https://www.globalcmt.org/CMTsearch.html. The CRUST1.0, CRUST2.0 and ak135-F are available through the websites https://igppweb.ucsd.edu/~gabi/crust1.html, https://igppweb.ucsd.edu/~gabi/crust2.html and http://rses.anu.edu.au/seismology/ak135/ak135f.html, respectively. The Slab2 model is available at https://doi.org/10.5066/F7PV6 JNV. Plate motion data are obtained from Plate Motion Calculator (http://ofgs.aori.u-tokyo.ac.jp/~okino/platecalc_new.html). We used Generic Mapping Tools (v6.5.0) (https://docs.generic-mapping-tools.org/latest/index.html).
References
Kanamori, H. Mechanism of tsunami earthquakes. Phys. Earth Planet. Inter. 6, 346–359 (1972).
Kanamori, H. & Kikuchi, M. The 1992 Nicaragua earthquake: a slow tsunami earthquake associated with subducted sediments. Nature 361, 714–716 (1993).
Kikuchi, M. & Kanamori, H. Source characteristics of the 1992 Nicaragua tsunami earthquake inferred from teleseismic body waves. PAGEOPH 144, 441–453 (1995).
Sallarès, V. & Ranero, C. R. Upper-plate rigidity determines depth-varying rupture behaviour of megathrust earthquakes. Nature 576, 96–101 (2019).
Bilek, S. L. & Lay, T. Tsunami earthquakes possibly widespread manifestations of frictional conditional stability: VARIABILITY OF GREENLAND ACCUMULATION. Geophys. Res. Lett. 29 (1-), 18 (2002).
Fan, W., Bassett, D., Jiang, J., Shearer, P. M. & Ji, C. Rupture evolution of the 2006 Java tsunami earthquake and the possible role of splay faults. Tectonophysics 721, 143–150 (2017).
Fukao, Y. Tsunami earthquakes and subduction processes near deep-sea trenches. J. Geophys. Res. 84, 2303 (1979).
Mitsui, Y. & Yagi, Y. An interpretation of tsunami earthquake based on a simple dynamic model: failure of shallow megathrust earthquake: MEGAQUAKE AND TSUNAMI EARTHQUAKE. Geophys. Res. Lett. 40, 1523–1527 (2013).
Jia, Z., Zhan, Z. & Kanamori, H. The 2021 South sandwich Island M w 8.2 earthquake: A slow event sandwiched between regular ruptures. Geophys. Res. Lett. 49, e2021GL097104 (2022).
Metz, M. et al. Seismic and tsunamigenic characteristics of a multimodal rupture of rapid and slow stages: the example of the complex 12 August 2021 South sandwich earthquake. JGR Solid Earth 127, e2022JB024646 (2022).
Vanneste, L. E. & Larter, R. D. Sediment subduction, subduction erosion, and strain regime in the northern South Sandwich forearc: NORTHERN SOUTH SANDWICH FOREARC. J. Geophys. Res. 107, EPM 5-1-EPM 5–24 (2002).
Vanneste, L. E., Larter, R. D. & Smythe, D. K. Slice of intraoceanic Arc: insights from the first multichannel seismic reflection profile across the South sandwich Island Arc. Geology 30, 819–822 (2002).
Clift, P. & Vannucchi, P. Controls on tectonic accretion versus erosion in subduction zones: implications for the origin and recycling of the continental crust: SUBDUCTION TECTONICS. Rev. Geophys. 42, 2, 2003RG000127 (2004).
DeMets, C., Gordon, R. G. & Argus, D. F. Geologically current plate motions. Geophys. J. Int. 181, 1–80 (2010).
Bird, P. An updated digital model of plate boundaries: UPDATED MODEL OF PLATE BOUNDARIES. Geochem. Geophys. Geosyst. 4(3), 1027 (2003).
Sandwell, D. T. et al. Improved bathymetric prediction using geological information: SYNBATH. Earth Space Sci. 9, e2021EA002069 (2022).
U. S. Geological Survey. Advanced National Seismic System (ANSS) Comprehensive Catalog. (2017). https://doi.org/10.5066/F7MS3QZH
Dziewonski, A. M., Chou, T. A. & Woodhouse, J. H. Determination of earthquake source parameters from waveform data for studies of global and regional seismicity. J. Geophys. Res. 86, 2825–2852 (1981).
Ekström, G., Nettles, M. & Dziewoński, A. M. The global CMT project 2004–2010: Centroid-moment tensors for 13,017 earthquakes. Phys. Earth Planet. Inter. 200–201, 1–9 (2012).
Yagi, Y. & Fukahata, Y. Introduction of uncertainty of Green’s function into waveform inversion for seismic source processes: uncertainty of Green’s function in inversion. Geophys. J. Int. 186, 711–720 (2011).
Shimizu, K., Yagi, Y., Okuwaki, R. & Fukahata, Y. Development of an inversion method to extract information on fault geometry from teleseismic data. Geophys. J. Int. 220, 1055–1065 (2020).
Qiu, Q. & Barbot, S. Tsunami excitation in the outer wedge of global subduction zones. Earth Sci. Rev. 230, 104054 (2022).
Yamashita, S. et al. Potency density tensor inversion of complex body waveforms with time-adaptive smoothing constraint. Geophys. J. Int. ggac181 https://doi.org/10.1093/gji/ggac181 (2022).
Backus, G. & Mulcahy, M. Moment tensors and other phenomenological descriptions of seismic Sources–I. Continuous displacements. Geophys. J. Int. 46, 341–361 (1976).
Kikuchi, M. & Kanamori, H. Inversion of complex body waves—III. Bull. Seismol. Soc. Am. 81, 2335–2350 (1991).
Hartzell, S. H. & Heaton, T. H. Inversion of strong ground motion and teleseismic waveform data for the fault rupture history of the 1979 imperial Valley, California, earthquake. Bull. Seismol. Soc. Am. 73, 1553–1583 (1983).
Olson, A. H. & Apsel, R. J. Finite faults and inverse theory with applications to the 1979 imperial Valley earthquake. Bull. Seismol. Soc. Am. 72, 1969–2001 (1982).
Ross, Z. E. et al. Hierarchical interlocked orthogonal faulting in the 2019 Ridgecrest earthquake sequence. Science 366, 346–351 (2019).
Zhan, Z., Kanamori, H., Tsai, V. C., Helmberger, D. V. & Wei, S. Rupture complexity of the 1994 Bolivia and 2013 sea of Okhotsk deep earthquakes. Earth Planet. Sci. Lett. 385, 89–96 (2014).
Akaike, H. Likelihood and the Bayes procedure. Trabajos De Estadistica Y De Investigacion Operativa. 31, 143–166 (1980).
Yabuki, T. & Matsu’ura, M. Geodetic data inversion using a bayesian information criterion for Spatial distribution of fault slip. Geophys. J. Int. 109, 363–375 (1992).
Sato, D., Fukahata, Y. & Nozue, Y. Appropriate reduction of the posterior distribution in fully bayesian inversions. Geophys. J. Int. 231, 950–981 (2022).
Hayes, G. Slab2 - A comprehensive subduction zone geometry model. U S Geol. Surv. https://doi.org/10.5066/F7PV6JNV (2018).
Laske, G., Masters, G., Ma, Z. & Pasyanos, M. Update on CRUST1.0 - A 1-degree global model of Earth’s crust. EGU Gen. Assem. 15, 2658 (2013).
Bassin, C., Laske, G. & Masters, G. The current limits of resolution for surface wave tomography in North America. EOS Trans. AGU 81, F897 (2000).
Kennett, B. L. N., Engdahl, E. R. & Buland, R. Constraints on seismic velocities in the Earth from traveltimes. Geophys. J. Int. 122, 108–124 (1995).
Montagner, J. P. & Kennett, B. L. N. How to reconcile body-wave and normal-mode reference Earth models. Geophys. J. Int. 125, 229–248 (1996).
Yamashita, S. et al. Consecutive ruptures on a complex conjugate fault system during the 2018 Gulf of Alaska earthquake. Sci. Rep. 11, 5979 (2021).
Hartzell, S. H. Earthquake aftershocks as Green’s functions. Geophys. Res. Lett. 5, 1–4 (1978).
Dreger, D. S. Empirical Green’s function study of the January 17, 1994 Northridge, California earthquake. Geophys. Res. Lett. 21, 2633–2636 (1994).
Agata, R., Kasahara, A. & Yagi, Y. A bayesian inference framework for fault slip distributions based on ensemble modelling of the uncertainty of underground structure: with a focus on uncertain fault dip. Geophys. J. Int. 225, 1392–1411 (2021).
Raftery, A. E., Madigan, D. & Hoeting, J. A. Bayesian model averaging for linear regression models. J. Am. Stat. Assoc. 92, 179–191 (1997).
Tebaldi, C. & Knutti, R. The use of the multi-model ensemble in probabilistic climate projections. Phil Trans. R Soc. A. 365, 2053–2075 (2007).
Yagi, Y. et al. Barrier-Induced rupture front disturbances during the 2023 Morocco earthquake. Seismol. Res. Lett. 95, 1591–1598 (2024).
Hicks, S. P. et al. Back-propagating supershear rupture in the 2016 Mw 7.1 Romanche transform fault earthquake. Nat. Geosci. 13, 647–653 (2020).
Okuwaki, R., Hirano, S., Yagi, Y. & Shimizu, K. Inchworm-like source evolution through a geometrically complex fault fueled persistent supershear rupture during the 2018 palu Indonesia earthquake. Earth Planet. Sci. Lett. 547, 116449 (2020).
Yagi, Y., Nakao, A. & Kasahara, A. Smooth and rapid slip near the Japan trench during the 2011 Tohoku-oki earthquake revealed by a hybrid back-projection method. Earth Planet. Sci. Lett. 355–356, 94–101 (2012).
Okuwaki, R., Yagi, Y. & Hirano, S. Relationship between High-frequency radiation and asperity ruptures, revealed by hybrid Back-projection with a Non-planar fault model. Sci. Rep. 4, 7120 (2014).
Lay, T., Ye, L., Bai, Y., Cheung, K. F. & Kanamori, H. The 2018 M W 7.9 Gulf of Alaska Earthquake: Multiple Fault Rupture in the Pacific Plate. Geophys. Res. Lett. 45, 9542–9551 (2018).
Spudich, P. & Frazer, L. N. Use of ray theory to calculate high-frequency radiation from earthquake sources having spatially variable rupture velocity and stress drop. Bull. Seismol. Soc. Am. 74, 2061–2082 (1984).
Madariaga, R. High-frequency radiation from crack (stress drop) models of earthquake faulting. Geophys. J. Int. 51, 625–651 (1977).
Sallarès, V. et al. Large slip, long duration, and moderate shaking of the Nicaragua 1992 tsunami earthquake caused by low near-trench rock rigidity. Sci. Adv. 7, eabg8659 (2021).
Yamashita, S., Yagi, Y. & Okuwaki, R. Irregular rupture propagation and geometric fault complexities during the 2010 Mw 7.2 El Mayor-Cucapah earthquake. Sci. Rep. 12, 4575 (2022).
Caldeira, B., Bezzeghoud, M. & Borges, J. F. DIRDOP: a directivity approach to determining the seismic rupture velocity vector. J. Seismol. 14, 565–600 (2010).
Chounet, A., Vallée, M., Causse, M. & Courboulex, F. Global catalog of earthquake rupture velocities shows anticorrelation between stress drop and rupture velocity. Tectonophysics 733, 148–158 (2018).
Fitch, T. J. Plate convergence, transcurrent faults, and internal deformation adjacent to Southeast Asia and the Western Pacific. J. Geophys. Res. 77, 4432–4460 (1972).
Beck, M. E. On the mechanism of tectonic transport in zones of oblique subduction. Tectonophysics 93, 1–11 (1983).
McCaffrey, R. Oblique plate convergence, slip vectors, and forearc deformation. J. Geophys. Res. 97, 8905 (1992).
McClay, K. R., Whitehouse, P. S., Dooley, T. & Richards M. 3D evolution of fold and thrust belts formed by oblique convergence. Mar. Pet. Geol. 21, 857–877 (2004).
Wessel, P. et al. The generic mapping tools version 6. Geochem. Geophys. Geosyst. 20, 5556–5564 (2019).
Gasperini, P. & Vannucci, G. FPSPACK: a package of FORTRAN subroutines to manage earthquake focal mechanism data. Comput. Geosci. 29, 893–901 (2003).
Crotwell, H. P., Owens, T. J. & Ritsema, J. The TauP toolkit: flexible seismic Travel-time and Ray-path utilities. Seismol. Res. Lett. 70, 154–160 (1999).
Acknowledgements
We thank the editor Kazuki Koketsu and two anonymous reviewers for their thorough review and providing constructive suggestions and comments. This work was supported by JSPS Grant-in-Aid for Scientific Research (C) 22K03751. The facilities of IRIS Data Services and specifically the IRIS Data Management Center were used for access to waveforms, related metadata, and/or derived products used in this study. IRIS Data Services are funded through the Seismological Facilities for the Advancement of Geoscience (SAGE) Award of the National Science Foundation under Cooperative Support Agreement EAR-1851048. We used FPSPACK61 software to handle the focal mechanism obtained in the inversion. The ray parameter and travel-time are calculated with the TauP Toolkit62 for the calculation of the Green’s function. All the figures were generated with Generic Mapping Tools (v6.5.0)60.
Author information
Authors and Affiliations
Contributions
R.Y., Y.Y. and R.O. conceptualized this study. R.Y. and Y.Y. processed data and carried out the inversion analysis. R.Y. generated the figures. R.Y., Y.Y., R.O. and B.E. interpreted and discussed the results and data. R.Y. wrote the original manuscript. Y.Y., R.O. and B.E. substantially revised the manuscript. All authors approved the revised manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yamaguchi, R., Yagi, Y., Okuwaki, R. et al. The complex rupture evolution of the long and slow, tsunamigenic 2021 South Sandwich Islands earthquake. Sci Rep 15, 17706 (2025). https://doi.org/10.1038/s41598-025-02043-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-02043-6