Experimental and numerical study on flexural behavior of steel fiber reinforced high–strength concrete (SFRHC) beams

Abstract

This study investigates the flexural behavior of steel fiber reinforced high-strength concrete (SFRHC) beams through experimental testing and numerical analysis. Eleven beams were subjected to four-point bending tests, with three primary variables: steel fiber volume fraction, beam depth, and longitudinal reinforcement ratio. The experimental program examined the load-midspan deflection relationships and failure modes throughout the loading process, and the results were validated through finite element analyses. Results demonstrated that increasing both the steel fiber volume fraction and beam depth led to enhanced cracking loads and ultimate loads. While the longitudinal reinforcement ratio significantly influenced the ultimate load capacity, its effect on the cracking load was minimal. Based on these findings, a new formula was developed to predict the flexural capacity of SFRHSC beams, incorporating the crack-bridging effect of steel fibers in the cracked section. The proposed formula showed excellent agreement with the experimental results.

Introduction

Concrete is the most widely used building material in civil engineering because of simple construction technology, good compression performance, and working performance.However, the plastic deformation of ordinary concrete is small when it is destroyed, which has the possibility of sudden failure¹. In practical engineering, some fibers with high tensile strength, high ultimate elongation, and high toughness can be added to the concrete matrix to improve the performance of concrete. The inclusion of fibers enhances the toughness of concrete through distributed reinforcement, which effectively suppresses crack initiation and propagation². There are many kinds of fibers, such as steel fiber, carbon fiber, basalt fiber, and polypropylene fiber. Steel fiber is widely used because of its high strength and high elastic modulus. Compared with traditional concrete materials, the compressive properties of SFRC(Steel Fiber Reinforced Concrete) materials are not significantly improved^3,4, but the tensile strength^5,6 and bending toughness^7,8,9 is improved considerably. At the same time, SFRC can reduce the crack width and deflection of the structure and improve the bearing capacity, impact resistance, and ductility of the structure^10,11,12. Ning¹³ studied the influence of steel fiber on the flexural behavior of reinforced self-compacting concrete beams through seven full-scale steel fiber reinforced self-consolidating concrete beams. The results showed that the addition of steel fiber improves the ultimate flexural capacity and reduces the mid-span deflection of specimens. Doo¹⁴ studied and compared the flexural behavior of steel fiber ultra-high performance concrete beams with different lengths and those without fiber ultra-high performance concrete beams, and found that steel fiber significantly improved the bearing capacity and stiffness of the test beams after cracking. Mertol¹⁵ has carried out experimental research on SFRC beams and ordinary concrete beams with different reinforcement ratios and found that steel fiber can increase the ultimate bending load and ultimate deflection of test beams. Biolzi¹² studied the flexural–shear behavior of SFRC beams. The test results showed that steel fiber could increase the flexural capacity and ductility of beams. Mahmud¹⁶ has studied the size effect of beams with 2% steel fiber content through experiments. The results showed that the beam depth was in the range of 30–300 mm, and the influence of size change on the bearing capacity of beams could be neglected. Xu¹⁷ carried out the shear bearing capacity test of 9 concrete beams with different steel fiber contents and compared the test results between Chinese code and European code. Oezcan¹⁸ carried out four-point loading test and finite element comparative analysis on three steel fiber reinforced concrete beams, and found that the mid-span deflection and stress obtained by the finite element model were consistent with the test data obtained from reinforced concrete beams; The failure mechanism of steel fiber reinforced concrete beams simulated by finite element method is very close to the failure load measured during the test. Xu and Wu¹⁹ studied the failure mode of steel fiber-reinforced concrete specimens under four-point bending. The experimental results showed that increasing the volume ratio of steel fiber can reduce the generation and propagation of shear cracks and bonding cracks. The higher crack resistance and sewing ability of steel fiber can improve the stability of its bearing capacity.

Despite the widespread engineering applications of steel fiber reinforced concrete (SFRC) owing to its superior crack resistance and enhanced toughness, extant research has predominantly concentrated on low to medium strength concrete matrices. A comprehensive literature review reveals that contemporary SFRC investigations predominantly utilize concrete with compressive strength classifications ranging from C20 to C60. For instance, in the domain of seismic performance evaluation, Zhang et al.²⁰ confined their experimental scope to C60-grade SFRC; in durability studies, Liu et al.²¹ exclusively examined the chloride ion penetration resistance of SFRC within the C20-C40 strength spectrum; in flexural behavior investigations, El Bakzawy et al.²² limited their experimental program to C30-grade concrete when studying SFRC beam bending mechanisms and hybrid reinforcement configurations; and in bridge engineering implementations, the concrete strength parameters in Xiang et al.’s²³ research did not surpass 60 MPa. This current state of research presents a notable disparity with the escalating demand for high-performance concrete structures in advanced engineering applications. The present investigation systematically examines high-strength SFRC with compressive strengths ranging from 67.3 to 86.6 MPa (corresponding to C60-C80 classifications).This study significantly advances upon prior research by extending the investigated compressive strength range of SFRC by approximately 44%. Furthermore, it systematically investigates five distinct fiber volume fractions within the 0–2% range, enabling the establishment of more comprehensive parametric influence relationships. Consequently, this work offers a more robust foundation for design guidelines pertaining to high-performance concrete structures in advanced engineering applications.

In addition to concrete strength grade, steel fiber content is also a critical factor influencing SFRC performance, the steel fiber reinforced concrete test with insufficient steel fiber content shows that the increase in tensile strength is negligible, while the improvement of properties after cracking is limited²⁴. Therefore, the critical volume fraction of steel fiber was proposed to design a high–performance fiber–reinforced concrete mixture, which achieves strain hardening under direct tension and has advanced ductility and energy absorption capacity^25,26, such as steel fiber high–strength reinforced concrete (SFHRC). Yang²⁷ conducted an experimental study on ultra-high performance concrete flexural beams with a steel fiber volume ratio of 2%. The results showed that steel fiber could effectively control crack development under the same load level. Choi and Kim^28,29 studied the influence of different steel fiber volume fractions on the compressive strength and tensile strength of high–strength steel fiber reinforced concrete beams.

In the field of civil engineering, research on modeling strategies for high-performance concrete structures under flexure and fatigue has become increasingly important. To broaden the scientific context and maintain alignment with recent findings in the field, several key research directions deserve attention. Regarding post-tensioned systems, composite steel–concrete beams have gained widespread application in bridge construction due to their economic advantages, with finite element analysis by Hassanin et al.³⁰ showing that the degree of shear connection significantly affects fatigue life, demonstrating a clear delay in failure when composite action exceeds 80%. Related research by Hassanin et al.³¹ further explored the failure modes of composite beams under fatigue loading, identifying the welding collar at the base of shear studs as a structurally weak region and a critical factor affecting overall performance.In terms of fatigue behavior modeling, research on polyolefin fiber-reinforced concrete pavements by Vidyashree et al.³² demonstrates that structured and twisted fibers significantly enhance concrete’s mechanical properties and fatigue resistance, even reducing white topping thickness from 19 to 17 cm at optimal dosages, providing more economical and sustainable solutions. Studies on the damage behavior of steel fiber reinforced concrete by Faustmann et al.³³ have successfully improved the agreement between theoretical predictions and experimental results by modifying traditional damage laws based on residual flexural tensile strength, offering new insights for durability assessment of concrete structures.For hybrid fiber reinforcement approaches, Khaleel and Dawood³⁴ found that Ultra-High Performance Concrete (UHPC), despite its excellent strength and durability, exhibits brittleness under tensile and dynamic loads, while hybrid fiber systems significantly enhance overall material performance through synergistic effects between different fiber types, although challenges remain regarding high installation costs and long-term performance validation. Experimental research on hybrid fiber reinforced concrete (HFRC) slabs by Khan et al.³⁵ further confirms that specific combinations of steel fibers and polypropylene fibers effectively improve load-bearing capacity and ductility, achieving favorable crack control.These multidimensional research findings provide comprehensive references for modeling strategies of high-performance concrete structures under complex loading conditions, establishing a solid foundation for optimizing post-tensioned systems, precisely predicting fatigue behavior, and innovatively applying hybrid fiber reinforcement methods.

The related research indicated that the previous studies mainly focused on the flexural behavior of steel fiber reinforced concrete, with a small part involving the flexural behavior of steel fiber reinforced high–strength concrete (SFRHC). Therefore, 11 specimens were tested and simulated, and the effects of key parameters including the steel fiber volume fraction, the beam depth, and longitudinal reinforcement ratio on the flexural behavior of beams were studied. Based on the experimental results, the failure mode, load–deflection relationship, flexural capacity, and the strain distribution along the height of the cross-section were analyzed elaborately. Furthermore, considering the effect of steel fiber on the cracked sections after beam cracking, the calculation formula for predicting the flexural capacity of SFRHC beams was derived.

Experimental programs

Materials

The concrete mixture was prepared using Grade 42.5 Portland cement, aggregates, steel fibers, clean tap water, and a polycarboxylate-based high-range water-reducing admixture. Continuously graded limestone crushed stone with particle sizes ranging from 5 to 20 mm was used as the coarse aggregate. Well-graded natural sand with a fineness modulus of 2.75 served as the fine aggregate. The reinforcing steel fibers measured 32.14 mm in length and 0.9 mm in diameter, yielding an aspect ratio (lf/df) of 35.7. These fibers demonstrated a tensile strength of 600 MPa under uniaxial tension testing.

Specimen design

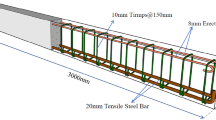
In this experimental study, eleven beam specimens were fabricated, comprising ten steel fiber reinforced high-strength concrete (SFRHC) beams and one reinforced high-strength concrete (RHC) beam as a control specimen. The investigation focused on three key parameters: steel fiber volume fraction, beam depth, and longitudinal reinforcement ratio. The detailed parameters and specimen designations are summarized in Table 1. All specimens were tested under four-point bending with a net span of 2700 mm and a concrete cover of 25 mm, as illustrated in Fig. 1. For each beam specimen, twelve companion test blocks of corresponding concrete type (RHC or SFRHC) were cast simultaneously. Following 28 days of standard curing, the mechanical properties including cube compressive strength, splitting tensile strength, and elastic modulus were determined according to GB/T 50081-2019³⁶. These test results are presented in Table 1.

Table 1 Detail parameters of the test specimens.

Fig. 1

Cross-section reinforcement details of beam specimens. (unit: mm).

The beam specimens were reinforced with HPB335 plain round bars of 10 mm diameter in the compression zone, while HRB400 deformed bars of 8mm, 14 mm, 16 mm, and 20 mm diameter were utilized in the tension zone. The cross-sectional views of each specimen are shown in Fig. 1. The mechanical properties of all reinforcing bars were experimentally determined and are presented in Table 2.

Table 2 Mechanical properties of steel bars.

Test procedure

According to the Technical Specification for Application of Steel Fiber Reinforced Concrete (JGJ/T 221)³⁷, the key to steel fiber reinforced concrete preparation lies in first mixing conventional concrete until homogeneous, then uniformly adding steel fibers in batches using mechanical methods, followed by appropriate vibration to ensure uniform fiber distribution without clustering or segregation phenomena. Through observation of the failure cross-sections of specimens with different steel fiber volume fractions(as shown in Fig. 2), it was evident that the steel fibers were uniformly distributed, confirming the effectiveness of this preparation technique.

Fig. 2

Failure cross-sections of specimens.

Regarding steel fiber distribution detection methods, in-situ CT technology can provide precise three-dimensional distribution data of steel fibers in concrete. Wang et al.³⁸ employed CT scanning technology to accurately extract three-dimensional coordinates and angular parameters of each steel fiber in concrete, reconstructing the spatial distribution model of fibers, as shown in the Fig. 3. Furthermore, Wang et al.³⁹, through systematic mechanical property testing and theoretical analysis, discovered that a 2% fiber content most significantly enhanced the mechanical properties of micro steel fiber reinforced concrete. Therefore, through in-situ CT technology, reconstructing the spatial distribution model of fibers enables quantitative assessment of the uniformity assurance effect of the preparation process specified in the technical specification, providing more intuitive and precise evidence for the scientific validity of the preparation technology.

Fig. 3

Comparison of internal fiber distribution³⁸.

The instrumentation layout for displacement and strain measurements is illustrated in Fig. 4. Seven LVDTs were installed along the beam length to monitor displacements at the midspan and supports. At the midspan section, five concrete strain gauges were vertically arranged at heights of 0, 100, 200, 250, and 300 mm from the beam soffit to measure the strain distribution. Crack widths were monitored using a crack width gauge with a precision of 0.02 mm.

Fig. 4

Test setup. (unit: mm).

The flexural tests were conducted using a 2000 kN hydraulic servo testing machine under four-point bending configuration in accordance with GB/T 50152-2012⁴⁰. Prior to formal testing, specimens underwent 2–3 preloading cycles at loads below 70% of the calculated cracking load to verify the testing setup and ensure proper instrument connectivity. The loading protocol consisted of three phases: pre-cracking loads applied in 5 kN increments, post-cracking loads in 15 kN increments, and near-failure loads in 5 kN increments, with a minimum of 10 loading stages for each specimen. At each load step, after load stabilization, measurements including applied load, concrete strains, reinforcement strains, and deflections were recorded using the DH3816 data acquisition system. Additionally, crack patterns were mapped and individual crack widths were measured.

Experimental results

Load–midspan deflection relationship

Based on the experimental observation and measured load versus midspan deflection curves of the specimens, entire 11 specimen beams had normal section reinforcement failure, as shown in Fig. 5 (The complete dataset is available in Supplementary Table S1) Longitudinal tensile reinforcement firstly yielded, and then the concrete at the top of the midspan section was crushed. According to the load–deflection curve of the specimen beams, the specimens under bending were considered to experience three stages until failure.

Fig. 5

Load–deflection relationship of specimens with different (a) steel fiber volume fraction, (b) beam depth, and (c) longitudinal reinforcement ratio.

Start loading to cracking stage

During the initial loading stage, all specimens exhibited linear elastic behavior, characterized by a linear relationship between applied load and midspan deflection. This stage demonstrated rapid load increase with minimal deflection development. When the tensile stress in the concrete between the loading points reached its ultimate tensile strength, cracking initiated. The onset of cracking marked a reduction in the effective section properties and flexural stiffness, resulting in a distinct change in the slope of the load–deflection response curve.

As illustrated in Fig. 5a, the load–deflection responses of both RHC and SFRHC beams exhibited nearly identical linear behavior during the elastic stage. However, SFRHC beams demonstrated higher cracking loads, indicated by the delayed occurrence of the curve’s turning point. This observation suggests that while steel fibers had minimal influence on the initial stiffness, they effectively enhanced the cracking resistance of the specimens.

Figure 5b demonstrates that increasing the beam depth led to steeper load–deflection curves, accompanied by higher cracking loads at the inflection points. This indicates that greater beam depth simultaneously enhanced both the elastic stiffness and cracking resistance of the specimens.

The influence of longitudinal reinforcement ratio is shown in Fig. 5c, where steeper load–deflection curves were observed with increasing reinforcement ratios. Notably, specimens B-F2.1 and B-F2.7 exhibited identical cracking loads to specimen B-F1.39, indicating that while the longitudinal reinforcement ratio significantly affected the elastic stiffness, it had negligible impact on the cracking load.

Cracking to steel yield stage

Following initial cracking, the specimens entered an elastic–plastic phase characterized by accelerated deflection development and progressive reduction in load–deflection curve slope until reinforcement yielding occurred. As shown in Fig. 5a, specimen B-F0 exhibited a distinct bilinear response, with a steep initial slope in the pre-cracking phase followed by a significant reduction in stiffness after cracking, resulting in a pronounced turning point. In contrast, fiber-reinforced specimens demonstrated more gradual transitions at the cracking point with less severe stiffness degradation. This behavior can be attributed to the fiber bridging mechanism in the tension zone, where steel fibers partially carried the tensile stresses across cracks, thereby enhancing both the tensile capacity and overall flexural stiffness of the specimens.

As evidenced in Fig. 5b and c, the post-cracking stiffness increased substantially with greater beam depth and longitudinal reinforcement ratio. These observations confirm that both parameters effectively enhanced the structural stiffness during the transition from cracking to yielding stages.

Failure modes

The crack patterns of test specimens are illustrated in Fig. 6. Upon reaching the cracking load, initial vertical cracks emerged at the bottom surface within the constant moment region between the loading points. This cracking initiated when the tensile stresses at the beam soffit exceeded the tensile strength of SFRHC. While the initial crack widths were comparable between RHC and SFRHC beams, the SFRHC specimens exhibited significantly reduced crack heights. This behavior demonstrates the effectiveness of steel fiber reinforcement in restraining crack propagation, thereby enhancing both the structural integrity and stiffness of the specimens.

Fig. 6

Crack distribution diagram of test and simulation, when steel fiber volume fraction changes: (a) 0%; (b) 0.5%; (c) 1.0%; (d) 1.5%; and (e) 2.0%.

As the applied load increased, crack formation intensified within the pure bending region, with rapid vertical propagation and symmetrical distribution on both sides of the beam. At approximately 60% of the ultimate load, the crack pattern in the pure bending region was fully established, with the initial crack remaining the most prominent. SFRHC beams exhibited distinct cracking characteristics compared to their RHC counterparts, featuring higher crack density, reduced crack spacing, and limited crack heights. The presence of multiple fine cracks with limited propagation height and width demonstrated the activation of the fiber bridging mechanism at this loading stage.

With further load application, vertical crack propagation in the pure bending region stabilized. At approximately 85% of the ultimate load, audible cracking sounds were detected, followed by rapid upward progression of several dominant cracks accompanied by significant widening. Secondary splitting cracks developed around these primary cracks, while existing secondary and diagonal cracks interconnected with the primary cracks through a network of fine fissures. As the loading approached ultimate capacity, several dominant cracks in the pure bending region penetrated through to the compression zone, forming plastic hinges.

The ultimate failure mode of both RHC and SFRHC beams was characterized by concrete crushing in the compression zone coupled with tensile reinforcement yielding. However, the RHC specimens exhibited more extensive damage, featuring a larger compression failure zone and severe deterioration of the concrete cover. Increasing steel fiber volume fraction led to notable improvements in failure characteristics, including reduced compression damage zone, enhanced concrete cover integrity, and minimal surface spalling.

Cracking load

Figure 7 illustrates the comparative analysis of cracking loads (Fcr) among all test specimens. Relative to the control RHC beam (B-F0), specimens incorporating steel fiber volume fractions of 0.5%, 1.0%, 1.5%, and 2.0% demonstrated cracking load enhancements of 40%, 80%, 80%, and 100%, respectively. These results clearly demonstrate the significant contribution of steel fiber reinforcement to the enhancement of initial cracking resistance in SFRHC beams.

Fig. 7

Cracking load of all the tested specimens.

The influence of beam depth was also evident, as specimens B-H250, B-H300, and B-H350 exhibited increases in cracking load of 60%, 60%, and 116%, respectively, compared to the reference specimen B-H200. This trend highlights the substantial impact of section depth on the cracking resistance of SFRHC beams.

Furthermore, increasing the longitudinal reinforcement ratio from 0.77% (B-R0.77) to higher ratios of 1.39%, 2.1%, and 2.7% (specimens B-F15H300R1.39, B-R2.1, and B-R2.7) resulted in a consistent 29% enhancement in cracking load. These findings suggest that the longitudinal reinforcement ratio has a moderate yet consistent influence on the cracking behavior of SFRHC beams.

Ultimate load

Figure 8 presents a comparative analysis of ultimate load (Pu) and flexural stiffness across all test specimens. When compared to the control RHC beam (B-F0), specimens incorporating steel fiber volume fractions of 0.5%, 1.0%, 1.5%, and 2.0% (B-F05, B-F1, B-F15H300R1.39, B-F2) exhibited increases in ultimate load of 2%, 5%, 8%, and 19%, accompanied by corresponding enhancements in flexural stiffness of 2%, 10%, 37%, and 45%, respectively. The magnitude of improvement demonstrated a positive correlation with fiber volume fraction, confirming that increased steel fiber content enhances both ultimate bearing capacity and flexural rigidity.

Fig. 8

(a) Ultimate load and (b) Flexural stiffness of all the tested specimens.

The influence of beam depth was particularly pronounced, as specimens B-H250, B-F15H300R1.39, and B-H350 showed substantial improvements compared to the reference specimen B-H200. Ultimate load capacity increased by 34%, 64%, and 94%, while flexural stiffness demonstrated even more significant enhancements of 92%, 182%, and 273%, respectively, with increasing beam depth. These results underscore the substantial impact of section depth on structural performance parameters.

The variation in longitudinal reinforcement ratio also yielded significant effects. Increasing the reinforcement ratio from 0.77% (B-0.77) to 1.39%, 2.1%, and 2.7% (B-F15H300R1.39, B-R2.1, B-R2.7) resulted in ultimate load improvements of 50%, 98%, and 120%, respectively. Corresponding enhancements in flexural stiffness were observed at 2%, 10%, 37%, and 45%. These findings demonstrate the substantial influence of longitudinal reinforcement ratio on both load-bearing capacity and flexural behavior.

Load–strain relationship

Figure 9 (The complete dataset is available in Supplementary Table S2) depicts the strain distribution along the height of the midspan section for specimens B-F0 and B-R2.7 under various loading conditions, with compressive and tensile strains denoted by negative and positive values, respectively. Analysis of the strain profiles reveals that magnitudes in the compression zone were consistently lower than those in the tension zone. The intersection point of these strain distribution curves indicates the position of the neutral axis, which exhibited an upward migration from the section’s centroidal axis as loading increased. The strain distribution demonstrated a predominantly linear relationship along the section height at all loading stages, validating the plane section assumption commonly adopted in beam theory.

Fig. 9

The strain of concrete along with the height of cross-section: (a) B-F0; and (b) B-R2.7.

The FE analysis

A comprehensive numerical investigation was conducted using ABAQUS 6.14⁴¹ finite element (FE) software to further examine the flexural behavior of steel fiber reinforced high-strength concrete beams. The analysis focused on specimens B-F0, B-F05, B-F1, B-F15H300R1.39, and B-F2, leveraging ABAQUS’s established capability in simulating the nonlinear response of reinforced concrete elements. This section presents a detailed description of the three-dimensional FE models developed for the analysis.

Material modeling

Based on the stress characteristics of the test specimens, the concrete damaged plasticity (CDP) model was implemented to simulate the concrete behavior. This model incorporates linear and isotropic elastic material properties while requiring five key parameters to define the failure criterion: shape factor (k_c), stress ratio (f_b0/f_c0), eccentricity (ε), viscosity (μ), and dilation angle (ψ). Following ABAQUS guidelines, these parameters were assigned values of 0.667, 1.16, 0.1, 0.005, and 30°, respectively. The CDP model utilizes distinct stress–strain relationships to characterize both compressive and tensile behavior of concrete, while the reinforcing steel bars were modeled using an idealized elastic–plastic stress–strain relationship.

To efficiently simulate the reinforcing effect of steel fibers, this study adopts a macroscopic phenomenological approach rather than discrete fiber modeling, reflecting the influence of fibers on the overall mechanical properties of the composite by modifying key parameters within the concrete constitutive relationship. The uniaxial compressive response of SFRC is based on the mathematical model proposed by Lu et al.⁴², which introduces the steel fiber characteristic parameter λ_f (reflecting the combined effect of fiber volume fraction V_f and aspect ratio l_f/d_f) to modify the shape parameter α_cf (governing the descending branch shape and reflecting compressive toughness) of the stress–strain curve, effectively reflecting the fibers’ contribution to the material’s ductile failure mode. The uniaxial tensile behavior is based on the constitutive relationship established by Zhang et al.⁴³, which utilizes the parameter α_tf (controlling the shape of the post-cracking softening response in tension) to describe the significant role of fibers in improving performance during this phase.

Boundary

The finite element model employs C3D8R elements (8-node reduced integration 3D solid elements) for concrete and T3D2 elements (2-node linear 3D truss elements) for reinforcing bars. C3D8R elements were selected for their computational efficiency and ability to mitigate shear locking phenomena commonly encountered in concrete structural analysis. T3D2 elements, which resist only axial forces, effectively represent the mechanical behavior of steel reinforcement. This element combination adequately captures the nonlinear response of reinforced concrete members under the investigated loading conditions^43,44. Figure 10 (The complete dataset is available in Supplementary Table S3) illustrates the assembly configuration and boundary conditions of the beam model. To mitigate stress concentration effects, rigid cushion blocks of 10mm thickness were introduced at both support and loading points, with Tie constraints implementing the connection between these blocks and the beam. In order to effectively capture the overall mechanical response of the structure while managing computational expense, a simplified assumption of perfect bond between the steel reinforcement and concrete was employed. Specifically, this connection is implemented in the model using the embedded element technique, which assumes full kinematic constraint. The validity and effectiveness of this approach for predicting the macroscopic structural response have been demonstrated in numerous studies^45,46,47,48. For instance, Lee et al.⁴⁸, utilizing finite element models based on the perfect bond assumption, achieved good correlation with experimental findings. They reported a mean ratio of simulated-to-measured load capacity of 1.02 with a standard deviation of just 0.04, alongside well-matched load–displacement curves. The overall errors were maintained within 10%, representing an acceptable level of accuracy for engineering applications. This evidence further substantiates the suitability of the adopted model simplification for the research objectives herein.In the iterative solution process, a displacement-based convergence criterion was employed as the primary basis for determining computational convergence. This criterion functions by monitoring the change in nodal displacements during the iterations. Specifically, it was set such that convergence for an increment was considered achieved, indicating a stable displacement field, when the ratio of the L2 norm of the displacement correction vector to the L2 norm of the total displacement increment vector for the current step fell below the convergence tolerance of 1.0 × 10⁻⁵.

Fig. 10

Details of the simulated specimen.

A comprehensive mesh sensitivity analysis was conducted through numerical simulations employing mesh sizes of 30 mm, 40 mm, and 50 mm. The load-midspan deflection relationships for specimen B-F1 under varying mesh configurations are presented in Fig. 11. The results demonstrate that simulations utilizing a 30 mm mesh size exhibited optimal correlation with experimental data. A comprehensive mesh sensitivity analysis was conducted using mesh sizes of 30 mm, 40 mm, and 50 mm. Figure 8 illustrates the load-midspan deflection relationships for specimen B-F1 under various mesh configurations. The results indicate that simulations with a 30 mm mesh size demonstrated optimal correlation with experimental data. This finding aligns with the perspective of Aziza et al.⁴⁹, who emphasized that selecting an appropriate mesh size is crucial for accurately estimating the ultimate load-carrying capacity of reinforced concrete beams. Although Özbayrak et al.⁵⁰ determined 25 mm as the optimal mesh size in their study, considering the specific characteristics of the components in this research and computational resource limitations, the 30 mm mesh size exhibited the best balance between accuracy and efficiency in our analysis. Therefore, this study adopted a 30 mm mesh size for all subsequent numerical simulations, which effectively captures the nonlinear structural behavior while maintaining reasonable computational costs.

Fig. 11

Mesh size effect of specimen B-F1.

Validation of the FE model

Figure 12 (The complete dataset is available in Supplementary Table S4) presents a comparative analysis of experimentally and numerically obtained load-midspan deflection curves, while Fig. 6 illustrates the corresponding crack propagation patterns. In the elastic stage, minor discrepancies are observed between experimental and FE results, primarily attributed to the reduction in flexural stiffness caused by concrete microcracking—a phenomenon not captured by the FE model under low stress conditions. The experimental and FE results demonstrate excellent agreement during both elastic–plastic and plastic stages, with no significant load degradation observed in the latter phase. The deviation in ultimate load predictions between experimental and FE results remains within 8.4% across all specimens. These comparisons validate the FE model’s capability to accurately predict both the load–deflection response and failure mechanisms of the tested specimens.

Fig. 12

FE analysis versus experimental deflection observations of the beams. (a) V_f = 0%, (b) V_f = 0..5%, (c) V_f = 1%, (d) V_f = 1.5%, (e) V_f = 2%.

Figure 13 illustrates the stress distribution contours within the concrete specimens. tresses in the compression zone, with stress patterns varying according to steel fiber content. At low fiber volume fractions, stress propagation extends into the tensile zone, resulting in wider crack formations. However, when the steel fiber volume fraction reaches 2%, stresses remain predominantly concentrated in the compression zone with minimal extension into the tensile region, leading to the formation of fine cracks only. These numerical observations align with experimental findings, demonstrating that increasing steel fiber content results in reduced crack widths and the development of dense microcrack networks.

Fig. 13

Von mises stress of concrete for specimens with steel fiber.

The stress distribution in the reinforcing bars is depicted in Fig. 14. At failure, the bottom longitudinal reinforcement exhibits complete yielding, with stress levels reaching 550 MPa.

Fig. 14

Von mises stress of steel bars for specimens with steel fiber.

Calculation method of flexural capacity

Fundamental assumptions

In accordance with the Chinese Code for Design of Concrete Structures (GB 50010-2010)⁵¹, the following fundamental assumptions are established for predicting the flexural capacity of SFRHC beams:

• (1) The height-strain relationship presented in Fig. 9. Confirms that cross-sections maintain their planarity throughout the loading process until failure, validating the plane section assumption.

• (2) The contribution of steel fibers to tensile resistance must be incorporated into flexural capacity calculations, as these fibers bear a portion of the tensile stresses within the beam’s tension zone.

• (3) Perfect bond conditions are assumed between reinforcing bars and steel fiber reinforced high-strength concrete, precluding any bond-related failure mechanisms.

Materials constitutive model

Concrete

The compressive stress–strain relationship of SFRHC is evaluated by Eq. (1).¹⁷

$$\begin{aligned} \sigma & = (1 - d_{fc} )E{}_{fc}\varepsilon \\ d_{fc} & = \left\{ \begin{gathered} 1 - \frac{{\rho_{fc} n}}{{n - 1 + x^{n} }}(x \le 1) \hfill \\ 1 - \frac{{\rho_{cf} }}{{\alpha_{fc} (x - 1)^{2} + x}}(x > 1) \hfill \\ \end{gathered} \right. \\ \rho_{fc} & = \frac{{f_{fc,r} }}{{E_{fc} \varepsilon_{fc,r} }} \\ n & = \frac{{E_{fc} \varepsilon_{fc,r} }}{{E_{fc} \varepsilon_{fc,r} - f_{fc,r} }} \\ x & = \varepsilon /\varepsilon_{fc,r} \\ \alpha_{fc} & = (0.157f_{fc}^{0.785} - 0.905)\left[ {(1 - 0.0192(l_{f} /d_{f} )V_{f}^{0.08} } \right] \\ \varepsilon_{fc,r} & = (700 + 172\sqrt {f_{fc} } )(1.0 + 0.189\lambda_{f} ) \times 10^{ - 6} \\ \lambda_{f} & = V_{f} l_{f} /d_{f} \\ \end{aligned}$$

(1)

where f_fc is the compressive strength of SFRHC; l_f, df, V_f are the length, diameter, and volume fraction of steel fiber, respectively; α_fc is the shape parameter of the descending section of the stress–strain curve of SFRHC under uniaxial compression; f_fc,r is the compressive strength value of SFRHC; ε_fc,r is the peak compressive strain of SFRHC corresponding to uniaxial compressive strength f_fc,r; d_fc is the damage evolution parameter of SFRHC under uniaxial compression.

steel bar

The simplified ideal elastic–plastic stress–strain relationship is adopted for longitude reinforcement, which can be expressed as Eq. (2). According to the code GB50010-2010⁵¹, the ultimate tensile strain of longitudinal tensile reinforcement is taken as 0.01.

$$\sigma_{{\text{s}}} = E_{{\text{s}}} \varepsilon_{{\text{s}}} \le f_{y}$$

(2)

where σ_s is the tensile stress of steel bars; ε_s is the tensile strain of steel bars. f_y is the design value of reinforcement strength.

Calculation of flexural capacity

When the SFRHC beam was damaged, the longitudinal tensile steel bars in the pure bending section yield first, and then the concrete in the compression zone reached the ultimate compressive strain. Figure 15a illustrates the geometric configuration of the rectangular cross-section and the position of tensile reinforcement. Figure 15b,c displaces the stress and strain distributions of SFRHC beams. The equivalent compression zone height is the measured compression zone height multiplied by the coefficient β; Compressive stress is the axial compressive strength of steel fiber reinforced concrete multiplied fc by a coefficient α. Assuming that the height of equivalent rectangular compressive stress distribution of the compression zone is x, according to the plane section assumption, the compressive strain at any place in the compression zone is ε_fc:

$$\varepsilon_{{{\text{fc}}}} { = }\frac{{\varepsilon_{{{\text{fu}}}} }}{x}y$$

(3)

where εfu is the ultimate compressive strain of SFRHC, ${{{\upvarepsilon}}}_{{f}{u}}=0.0033-\left({{f}}_{{c}{u},{k}}-50\right)\times {10}^{-5},{{{\upvarepsilon}}}_{{c}{u}}\le 0.0033.$ ${\mathbf{f}}_{\mathbf{c}\mathbf{u},\mathbf{k}}$ is the standard value of compressive strength of concrete cube.

Fig. 15

Stress and strain distributions of the strengthened beams under bending failure: (a) Cross section; (b) Strain distribution; (c) Stress distribution; and (d) Equivalent rectangular compressive stress distribution.

The micro–pressure strain of a certain unit dε_fc in the compression zone can be obtained by differentiating the two sides of Eq. (3):

$${\text{d}}\varepsilon_{{{\text{fc}}}} { = }\frac{{\varepsilon_{{{\text{fu}}}} }}{x}{\text{d}}y \Rightarrow {\text{d}}y = \frac{x}{{\varepsilon_{{{\text{fu}}}} }}{\text{d}}\varepsilon_{{{\text{fc}}}}$$

(4)

The resultant force C and the bending moment of the resultant force C on the neutral axis can be expressed by

$$C = b\int_{0}^{x} {\sigma_{{{\text{fc}}}} \left( {\varepsilon_{{{\text{fc}}}} } \right){\text{d}}y}$$

(5)

$$Cy_{{\text{c}}} = b\int_{0}^{x} {\sigma_{{{\text{fc}}}} \left( {\varepsilon_{{{\text{fc}}}} } \right)y{\text{d}}y}$$

(6)

where b is the width of beam cross-section, yc is the distance from the resultant action point in the compression zone to the neutral axis. Substituting Eq. (4) into (5) and (6), the resultant force and the bending moment can be expressed by

$$C = \frac{bx}{{\varepsilon_{{{\text{fu}}}} }}\int_{0}^{{\varepsilon_{{{\text{fu}}}} }} {\sigma_{{{\text{fc}}}} \left( {\varepsilon_{{{\text{fc}}}} } \right){\text{d}}\varepsilon_{{{\text{fc}}}} }$$

(7)

$$Cy_{{\text{c}}} { = }b\frac{{x^{2} }}{{\varepsilon_{{{\text{cu}}}}^{2} }}\int_{0}^{{\varepsilon_{{{\text{fu}}}} }} {\sigma_{{{\text{fc}}}} \left( {\varepsilon_{{{\text{fc}}}} } \right)\varepsilon_{{{\text{fc}}}} {\text{d}}\varepsilon_{{{\text{fc}}}} }$$

(8)

Consequently, combining Eqs. (7) and (8), the distance y_c can be evaluated by

$$y_{{\text{c}}} = \frac{x}{{\varepsilon_{{{\text{fu}}}} }}\frac{{\int_{0}^{{\varepsilon_{{{\text{fu}}}} }} {\sigma_{{{\text{fc}}}} \left( {\varepsilon_{{{\text{fc}}}} } \right)\varepsilon_{{{\text{fc}}}} {\text{d}}\varepsilon_{{{\text{fc}}}} } }}{{\int_{0}^{{\varepsilon_{{{\text{fu}}}} }} {\sigma_{{{\text{fc}}}} \left( {\varepsilon_{{{\text{fc}}}} } \right){\text{d}}\varepsilon_{{{\text{fc}}}} } }}$$

(9)

The actual stress distribution of the cross-section and the equivalent rectangular stress distribution of the cross-section have the same position of the resultant force acting point. The equilibrium equation can be obtained from Fig. 15c,d:

$$h_{0} - \left( {x - y_{{\text{c}}} } \right) = h_{0} - \frac{\beta x}{2}$$

(10)

where h₀ is the effective height of the section. Substituting Eqs. (9) into (10), the equivalent rectangular stress distribution compression zone height reduction factor β can be expressed by

$$\beta = 2 - \frac{2}{{\varepsilon_{{{\text{cu}}}} }}\frac{{\int_{0}^{{\varepsilon_{{{\text{fu}}}} }} {\sigma_{{{\text{fc}}}} \left( {\varepsilon_{{{\text{fc}}}} } \right)\varepsilon_{{{\text{fc}}}} {\text{d}}\varepsilon_{{{\text{fc}}}} } }}{{\int_{0}^{{\varepsilon_{{{\text{fu}}}} }} {\sigma_{{{\text{fc}}}} \left( {\varepsilon_{{{\text{fc}}}} } \right){\text{d}}\varepsilon_{{{\text{fc}}}} } }}$$

(11)

If $k = \frac{1}{{\varepsilon_{{{\text{fu}}}} }}\frac{{\int_{0}^{{\varepsilon_{{{\text{fu}}}} }} {\sigma_{{{\text{fc}}}} \left( {\varepsilon_{{{\text{fc}}}} } \right)\varepsilon_{{{\text{fc}}}} {\text{d}}\varepsilon_{{{\text{fc}}}} } }}{{\int_{0}^{{\varepsilon_{{{\text{fu}}}} }} {\sigma_{{{\text{fc}}}} \left( {\varepsilon_{{{\text{fc}}}} } \right){\text{d}}\varepsilon_{{{\text{fc}}}} } }}$, Eq. (11) can be simplified as

$$\beta = 2 - 2k$$

(12)

As the actual stress distribution of the cross-section is equal to the area of the equivalent rectangular stress distribution of the cross-section, it can be obtained according to Fig. 15c,d:

$$\int_{0}^{x} {\sigma_{{{\text{fc}}}} \left( {\varepsilon_{{{\text{fc}}}} } \right){\text{d}}y} = \alpha f_{{{\text{fc}}}} \beta x$$

(13)

Substituting Eqs. (4) into (13):

$$\frac{x}{{\varepsilon_{{{\text{fu}}}} }}\int_{0}^{{\varepsilon_{{{\text{fu}}}} }} {\sigma_{{{\text{fc}}}} \left( {\varepsilon_{{{\text{fc}}}} } \right){\text{d}}\varepsilon_{{{\text{fc}}}} } = \alpha f_{{{\text{fc}}}} \beta x$$

(14)

Substituting Eqs. (12) into (14), the reduction coefficient of concrete compressive strength in compression zone with equivalent rectangular stress distribution ${\varvec{\upalpha}}$ can be expressed by

$$\alpha = \frac{{\int_{0}^{{\varepsilon_{{{\text{fu}}}} }} {\sigma_{{{\text{fc}}}} \left( {\varepsilon_{{{\text{fc}}}} } \right){\text{d}}\varepsilon_{{{\text{fc}}}} } }}{{2\left( {1 - k} \right)\varepsilon_{{{\text{fu}}}} f_{{{\text{fc}}}} }}$$

(15)

The cross-sectional equilibrium conditions shown in Fig. 15d are as follows:

$$\alpha f_{{{\text{fc}}}} \beta xb = A_{{\text{s}}} f_{{\text{y}}} + f_{{{\text{ftu}}}} \left( {h - x} \right)b$$

(16)

where h is the section beam depth; ${{f}}_{{f}{t}{u}}$ is the equivalent tensile stress of SFRHC in the tensile zone. From Eq. (14), it can be obtained that the height $x$ of the beam compression zone is:

$$x = \frac{{A_{{\text{s}}} {\text{f}}_{{\text{y}}} + {\text{f}}_{{{\text{ftu}}}} bh}}{{\alpha f_{{{\text{fc}}}} \beta b + {\text{f}}_{{{\text{ftu}}}} b}}$$

(17)

The distance between the resultant force points of compression zone and tension zone and the resultant force points of reinforcement can be obtained as follows:

$${M}_{\text{fu}}=\alpha {f}_{\text{fc}}b\beta x\left({h}_{0}-\frac{\beta }{2}x\right)-{f}_{\text{ftu}}b\left(h-x\right)\left(\frac{h-x}{2}-{a}_{s}\right)$$

(18)

where a_s is the distance from the resultant force point of reinforcement to the edge of the tension zone, f_ftu = f_tβ_tuλ_f, according to CECS 38: 2004⁵², β_tu = 1.3.

Formula validation

Table 3 presents a comparative analysis between experimental and predicted flexural capacities. The analysis reveals a mean experimental-to-predicted ratio of 1.01 with a coefficient of variation (COV) of 0.08. These statistical indicators demonstrate the high accuracy and reliability of the proposed analytical model in predicting the flexural capacity of SFRHC beams.

Table 3 Comparisons of test and predicted flexural capacity.

Conclusion

This study presents a comprehensive investigation of the flexural behavior of steel fiber reinforced high-strength concrete (SFRHC) beams through integrated experimental, numerical, and theoretical approaches. The investigation encompasses failure modes, parametric analysis, and ultimate load capacity. Based on the research findings, the following conclusions are drawn:

• (1) The flexural response of SFRHC beams exhibits three distinct stages: initial loading to crack initiation, crack propagation to steel reinforcement yielding, and post-yield behavior until ultimate failure.

• (2) Both the steel fiber volume fraction and beam depth significantly enhance the ultimate load capacity and flexural stiffness of SFRHC beams. While the longitudinal reinforcement ratio effectively improves ultimate load capacity and flexural stiffness, its influence on cracking load remains minimal.

• (3) The finite element analysis demonstrates excellent correlation with experimental results in terms of deflection patterns and failure mechanisms. Numerical results confirm that increasing steel fiber content leads to reduced crack widths and promotes the formation of dense microcrack networks.