Introduction

Boolean networks (BNs) are a special kind of nonlinear systems with logical operations1,2. The model of BNs was established by Kauffman to study gene regulatory networks (GRNs)3. Furthermore, BNs with inputs are referred to Boolean control networks (BCNs), which is a correct method to describe the dynamics of GRNs4. For some basic theory and applications of BNs, please refer to5,6. However, due to the lack of mathematical methods for handling logical processes, it becomes very inconvenient to study the control issues of BNs7.

Recently, a new matrix product, called semi-tensor product of matrices, has provided great convenience for the study of BNs8. Based on the characteristics of matrix product, an algebraic state space representation (ASSR) framework has been constructed for the research of BNs. Therefore, researchers can use the ASSR to investigate BNs through the traditional control theory9. In the past twenty years, many excellent results have been achieved for BNs via the ASSR framework10,11. Observability and controllability for BNs were investigated in12,13. Stability and stabilization of BCNs were investigated in14,15,16.

Control design is always a core issue in control theory17,18. Recently, many control design methods have been introduced to address the control problems of BCNs through the ASSR19. Furthermore, how to design appropriate control techniques to reduce control costs is an important topic in modern control theory. As we all know, sampled-data control (SDC) is an effective technique, which reduces the update frequency of the controller and significantly reduces the computational burden20,21. In22, a self-triggered implementation of the proposed event-triggered sampling scheme was presented. Based on the ASSR framework, SDC method is introduced into the control of BCNs19,23, and some basic results are proposed for the sampled-data stabilization and controllability of BCNs24. There are two types of SDC: uniform SDC and nonuniform SDC (NSDC). Since the sampling length of NSDC is time-varying, it can more effectively utilize information resources than uniform SDC25, which also makes the controller design more challenging.

In GRNs, time delay is generally used to represent slow biochemical reactions26. In addition, external environmental factors, such as nutrient concentration and temperature may also lead to time delays in GRNs. For example, the coupled oscillatory biochemical network in cell cycle is simplified as the delayed BN27:

$$\begin{aligned} \left\{ \begin{array}{lll} C_{1}(t+1)=\lnot \big (C_{1}(t-2)\wedge C_{2}(t-1) \big ),\\ C_{2}(t+1)=\lnot \big (C_{1}(t-1)\wedge C_{2}(t-2) \big ),\end{array}\right. \end{aligned}$$
(1)

where \(C_{1}(t)\) and \(C_{2}(t)\) represent the state of two cells at time t, and time delays are caused by the delayed translocation between cells. In the past ten or more years, delayed BNs have attracted the research interest of many scholars. Delayed BNs were firstly investigated through the ASSR in8. Subsequently, delayed BCNs (DBCNs) were also well investigated in some works12,28. In29, fault detectability of asynchronous DBCNs with sampled-data control was investigated.

As is well known, constraints play a very important role in nonlinear systems30. In GRNs, it is necessary to impose constraints on certain gene states that may lead to diseases and treatment options that may lead to serious complications31. For example, in WNT5A gene networks, states of the WNT5A=1 are undesirable as they accelerate the opportunity for transfer32. State inequality constraints, as an important form of constraints, often appear in the control logic design of dynamic systems33. They are usually physical constraints of the system and have wide practical applications34. For example, in a semi-batch reactor, due to the volume constraint of the reactor, only a limited amount of substrate can be fed. Similarly, for safety reasons, one may not want the reactor to operate above a certain maximum temperature. In a feed batch bioreactor, there may be constraints on cell mass concentration (beyond which oxygen transfer is restricted) or substrate concentration (beyond which unexpected side reactions may occur). However, there are no relevant results on the investigation of DBCNs with state inequality constraints via NSDC.

In this paper, based on the ASSR framework, we analyze the inequality constrained set reachability and inequality constrained set stabilization of DBCNs with state inequality constraints via NSDC. The main contributions can be summarized in two aspects: (i) State inequality constraints are introduced into DBCNs, and an inequality constrained controllability matrix is constructed for studying the inequality constrained set stabilization of DBCNs. (ii) NSDC provides us with more control schemes to achieve control objectives and reduce control costs. The traditional control and uniform SDC can be considered as a special case of NSDC.

The remainder of this paper is organized as follows: Section “Problem formulation” presents the equivalent system of DBCNs with state inequality constraints through the ASSR framework. The inequality constrained controllability matrix and nonuniform sampled-data inequality constrained reachability are considered in section “Inequality constrained set reachability”. The time-variant state feedback inequality constrained set stabilization of DBCNs is studied in section “Inequality constrained set stabilization”. Section “Illustrative example” and section “Conclusions” provide an illustrative example and a brief summary, respectively.

Notations: \(\mathbb {R}\), \(\mathbb {Z}\), \(\mathbb {N}\) and \(\mathbb {Z_{+}}\) represent the set of real numbers, integers, nonnegative integers and positive integers, respectively. \(\textbf{0}_{s}:=(\underbrace{0,\cdots ,0}_{s})^{\top }\). \(\textbf{1}_{s}:=(\underbrace{1,\cdots ,1}_{s})^{\top }\). \(I_s\) denotes the s-order identity matrix. \((A)_{s, m}\) denotes the (s, m)-th element of matrix A. \(Col_{i}(A)\) denotes the i-th column of matrix A. \(\mathscr {D}:=\{0, 1\}\), \(\mathscr {D}^m:=\underbrace{\mathscr {D}\times \cdots \times \mathscr {D}}_{m}\). \(\Delta _s:=\{\delta _s^i: i=1, \cdots , s\}\), where \(\delta _s^i=Col_{i}(I_s)\). \(A_{s\times m}\) is called a (s, m) logical matrix, if \(Col_{i}(A_{s\times m})\in \Delta _s, i=1, \cdots , m\). \({\mathscr {L}}_{s\times m}\) denotes the set of \(s\times m\) logical matrices. \(W_{[s,m]}\) and \(M_{r,n}\) are swap matrix and power-reducing matrix, respectively8. \([a, b)|_{\mathbb {Z}}=\{a, \cdots , b-1\}\subseteq \mathbb {Z}, \ a, b \in \mathbb {Z}, a<b\). \(\lfloor c\rfloor\) represents the maximum integer not greater than c. Denote \(a_{1}\widetilde{\bigwedge } a_{2}=\min \{a_{1}, a_{2}\}\). In this paper, the default matrix product is semi-tensor product (\(\ltimes\))8.

Problem formulation

Consider the following DBCN:

$$\begin{aligned} \left\{ \begin{array}{lll} x_{1}(t+1)=\kappa _{1}(X(t-\varsigma +1), \cdots , X(t), U(t)),\\ ~~~~\vdots \\ x_{n}(t+1)=\kappa _{n}(X(t-\varsigma +1), \cdots , X(t), U(t)),\end{array}\right. \end{aligned}$$
(2)

where \(\varsigma \in \mathbb {Z_{+}}\) is the time delay, \(X(i):=(x_{1}(i), \cdots , x_{n}(i))\in \mathscr {D}^n\), \(i=-\varsigma +1,\cdots , 0, 1, \cdots\) denote the state, here \(U(t):=(v_{1}(t), \cdots , v_{m}(t))\in \mathscr {D}^{m}\) denotes the control input, and \(\kappa _{i}: \mathscr {D}^{n\varsigma +m} \rightarrow \mathscr {D}\), \(i=1,\cdots ,n\) are Boolean functions. Assume that \(Y_{0}:=(X(-\varsigma +1),\cdots ,X(0))\in \mathscr {D}^{n\varsigma }\) denotes the initial state trajectory.

Furthermore, consider state inequality constraints for binary variables \(x_{j}(i)\in \mathscr {D}\), \(j=1,\cdots ,n\):

$$\begin{aligned} a\le f(x_{1}(i), \cdots , x_{n}(i))\le b, \end{aligned}$$
(3)

where \(f: \mathscr {D}^{n} \rightarrow \mathbb {R}\) is the inequality constrained function, and \(a,b\in \mathbb {R}\) are inequality constrained boundaries.

For DBCN (2), we assume that \(f(x_{1}(i), \cdots , x_{n}(i))\) satisfies the following linear form:

$$\begin{aligned} f(x_{1}(i), \cdots , x_{n}(i))=(2^{0}, 2^{1}, \cdots , 2^{n-1})(x_{1}(i), \cdots , x_{n}(i))^{\top }.\end{aligned}$$
(4)

It is worth pointing out that all possible states in \(\mathscr {D}^n\) correspond one-to-one to indicator set \([0, 2^{n})|_{\mathbb {Z}}\), and some other types of inequalities (nonlinear) can be transformed into linear constraint forms of (4) through column expansion35.

Fig. 1
figure 1

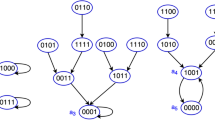
Network of the cell apoptosis network (5).

Full size image

Example 1

Consider the cell apoptosis network36

$$\begin{aligned} \left\{ \begin{array}{lll} IAP(t+1)=\lnot C3a(t)\wedge TNF(t),\\ C3a(t+1)=\lnot IAP(t)\wedge C8a(t),\\ C8a(t+1)=C3a(t)\vee TNF(t), \end{array}\right. \end{aligned}$$
(5)

where IAP, C3a, and C8a represent concentration levels (low or high) of apoptosis inhibitor protein, active cystatin 3, and active cystatin8, respectively; the concentration level of tumor necrosis factor (TNF) is considered as a control input. The network graph of (5) is shown in Fig. 1.

Set \(x_1(t)=IAP(t)\), \(x_2(t)=C3a(t)\), \(x_3(t)=C8a(t)\), \(v(t)=TNF(t)\), and

$$f(X(t))=(2^{0},2^{1},2^{2})(X(t))^{\top }=2^{0}x_{1}(t)+2^{1}x_{2}(t)+2^{2}x_{3}(t).$$

From \(\mathscr {D}^3=\{(0, 0, 0),(1, 0, 0),(0, 1, 0),\) (1, 1, 0), (0, 0, 1),  (1, 0, 1),  (0, 1, 1),  \((1, 1, 1)\}\), the corresponding indicator can be obtained as \(f(0, 0, 0)=0, f(1, 0, 0)=1,\) \(f(0, 1, 0)=2, f(1, 1, 0)=3, f(0, 0, 1)=4, f(1, 0, 1)=5, f(0, 1, 1)=6,\) \(f(1, 1, 1)=7.\)

In practice, the concentration ratio of IAP, C3a, and C8a can only be effective within an indicator range, so only the data within the range needs to be considered. For example, the indicator range requires \(2\le f(X(t))\le 5\), then the corresponding solution set is \(C_{x}=\{(0, 1, 0),(1, 1, 0),(0, 0, 1)\), \((1, 0, 1)\}\), that is, the states of system (5) are constrained to \(C_{x}.\)

Firstly, we give the definitions of NSDC and nonuniform sampled-data inequality constrained set stabilization5.

Definition 1

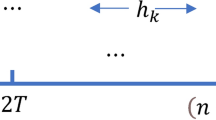
Given a set of sampling points \(\{t_{h}: h\in \mathbb {N}\}\) with \(t_0=0\). \(\{U(t): t\in \mathbb {N}\}\subseteq \mathscr {D}^{m}\) is said to be an NSDC, if

$$\begin{aligned} U(t)=U(t_{h}), t\in [t_{h}, t_{h+1})| _{\mathbb {Z}}, t_{h+1}-t_{h}=\tau _{h}, \end{aligned}$$
(6)

where the interval length \(\tau _{h}\in \mathbb {Z}_+\) between sampling points are time-variant.

Especially, when \(\tau _{h}=\tau\) holds for any \(h\in \mathbb {N}\), the definition of uniform SDC can be given, where \(\tau \in \mathbb {Z}_+\) is called the sampling period37.

Definition 2

Let a state inequality constraint (3) and a nonempty state set \(\mathscr {E}_{e}\) that satisfies (3) be given. DBCN (2) is said to be nonuniform sampled-data inequality constrained set stabilizable to \(\mathscr {E}_{e}\), if for any \(Y_{0}\) that satisfies (3), there exist a time-variant state feedback NSDC

$$\begin{aligned} v_{i}(t)=g_{i}(t_{h}, X(t_{h}-\varsigma +1), \cdots ,X(t_{h})), t\in [t_{h}, t_{h+1})| _{\mathbb {Z}} \end{aligned}$$
(7)

with \(g_{i}: \{t_{h}: h\in \mathbb {N}\}\times \mathscr {D}^{n\varsigma }\rightarrow \mathscr {D}, \ i=1,\cdots ,m\) being time-variant logical functions, and a positive integer T such that \(X(t)\in \mathscr {E}_{e}, \forall \ t\ge T\), and \(a\le f(X(t))\le b, \forall \ t \ge 1\).

Secondly, based on the ASSR8, we provide the equivalent algebraic form of DBCN (2).

Identifying \(1\sim \delta _{2}^{1}\), \(0\sim \delta _{2}^{2}\). Setting \(x(t)=\ltimes _{i=1}^n x_i(t)\in \Delta _{2^n}\), \(v(t)=\ltimes _{i=1}^m v_i(t)\in \Delta _{2^m}\), \(y(t)=\ltimes _{i=t-\varsigma +1}^t x(i) \in \Delta _{2^{n\varsigma }}\), we can convert DBCN (2) into the algebraic form

$$\begin{aligned} \left\{ \begin{array}{lll} x_1(t+1)=K_{1}v(t)y(t),\\ ~~\vdots \\ x_n(t+1)=K_{n}v(t)y(t),\end{array}\right. \end{aligned}$$
(8)

where \(K_{i}\in \mathscr {L}_{2\times {2^{n\varsigma +m}}}\) is the structural matrix of \(\kappa _i\), \(i=1,\cdots ,n\). Multiplying the n equations in (8), we can obtain the following form of (8):

$$\begin{aligned} x(t+1)=Kv(t)y(t), \end{aligned}$$
(9)

where \(K\in \mathscr {L}_{2^n\times 2^{n\varsigma +m}}\) satisfies \(Col_{j}(K)=\ltimes _{i=1}^{n}Col_{j}(K_{i})\), \(j=1,\cdots ,2^{n\varsigma +m}\). For detailed instructions on how to use the ASSR to represent logical functions, please refer to8.

In addition, from (4) and the construction of \(x(t)=\ltimes _{i=1}^n x_i(t)\in \Delta _{2^n}\), we can easily obtain the following result.

Proposition 1

If \(f(p_{1}, \cdots , p_{n})=p,\ (p_{1}, \cdots , p_{n})\in \mathscr {D}^n\), then \(\delta _{2^{n}}^{p+1}=\delta _{2}^{p_{n}+1}\ltimes \cdots \ltimes \delta _{2}^{p_{1}+1}\in \Delta _{2^n}\) holds.

Based on Proposition 1, we present the following algorithm to determine the solution set for the state inequality constraint (3).

Algorithm 1
figure a

Construction of the solution set for the state inequality constraint (3).

Full size image

Similar to DBCN (2), we can convert the NSDC (7) into the algebraic form:

$$\begin{aligned} v(t)=G(t_{h}) y(t_{h}), \ t\in [t_{h}, t_{h+1})| _{\mathbb {Z}}, \end{aligned}$$
(10)

where \(G(t_{h})\in {\mathscr {L}}_{2^{m}\times 2^{n\varsigma }}\) is referred to as the time-variant state feedback sampled-data gain matrix.

In order to unify the dimensions of states in system (9), we convert system (9) into the augmented form

$$\begin{aligned} y(t+1)= & \ltimes _{i=t-\varsigma +2}^{t+1}x(i)\nonumber \\= & (\textbf{1}_{2^n}^{\top } \otimes I_{2^n})y(t)x(t+1) \nonumber \\= & (\textbf{1}_{2^n}^{\top } \otimes I_{2^n})y(t)Kv(t)y(t)\nonumber \\= & (\textbf{1}_{2^n}^{\top } \otimes I_{2^n})(I_{2^{n\varsigma }}\otimes K)W_{[2^{m},2^{n\varsigma }]}v(t)y^2(t)\nonumber \\= & (\textbf{1}_{2^n}^{\top } \otimes I_{2^n})(I_{2^{n\varsigma }}\otimes K)W_{[2^{m},2^{n\varsigma }]}(I_{2^m}\otimes M_{r,2^{n\varsigma }})v(t)y(t)\nonumber \\:= & \overline{K}v(t)y(t), \end{aligned}$$
(11)

where \(\overline{K}=(\textbf{1}_{2^n}^{\top } \otimes I_{2^n})(I_{2^{n\varsigma }}\otimes K)W_{[2^{m},2^{n\varsigma }]}(I_{2^m}\otimes M_{r,2^{n\varsigma }})\in \mathscr {L}_{{2^{n\varsigma }}\times {2^{n\varsigma +m}}}.\)

Assume \(C_{x}=\{\delta _{2^n}^{\psi _{1}}, \cdots , \delta _{2^n}^{\psi _{\beta }}\}\subseteq \Delta _{2^{n}}\), where \(\psi _{1}<\cdots <\psi _{\beta }\). Correspondingly, the states of (11) are constrained to

$$\begin{aligned} C_{y}=\{y=\ltimes _{i=1}^{\varsigma } x^{i} : x^{i}\in C_{x}\}:=\{\delta _{2^{n\varsigma }}^{\mu _{1}}, \cdots , \delta _{2^{n\varsigma }}^{\mu _{\beta ^{\varsigma }}}\},\end{aligned}$$
(12)

where \(\mu _{1}<\cdots <\mu _{\beta ^{\varsigma }}\). For the nonempty set \(\mathscr {E}_{e}\subseteq C_{x}\) in Definition 2, we denote

$$\begin{aligned} \widehat{\mathscr {E}}_{e}=\{y=\ltimes _{i=1}^{\varsigma } x^{i} : x^{i}\in \mathscr {E}_{e}\}\subseteq C_{y}. \end{aligned}$$
(13)

Finally, we study the relation between nonuniform sampled-data inequality constrained set stabilizable to \(\mathscr {E}_{e}\) of DBCN (2) and nonuniform sampled-data inequality constrained set stabilizable to \(\widehat{\mathscr {E}}_{e}\) of system (11). Before this, we first provide the definition of nonuniform sampled-data inequality constrained set stabilizable to \(\widehat{\mathscr {E}}_{e}\) for (11).

Definition 3

For the nonempty set \(\widehat{\mathscr {E}}_{e}\subseteq C_{y}\), system (11) is said to be nonuniform sampled-data inequality constrained set stabilizable to \(\widehat{\mathscr {E}}_{e}\), if \(\forall \ y_{0} \in C_{y}\), there exist an NSDC (10) and an integer \(\widehat{T}>0\) such that \(y(t)\in \widehat{\mathscr {E}}_{e}, \forall \ t\ge \widehat{T}\), and \(y(t)\in C_{y}, \forall \ t \ge 0.\)

Then, we have the following result.

Proposition 2

DBCN (2) is nonuniform sampled-data inequality constrained set stabilizable to \(\mathscr {E}_{e}\), if and only if system (11) is nonuniform sampled-data inequality constrained set stabilizable to \(\widehat{\mathscr {E}}_{e}.\)

Proof

(Necessity) From Definition 2, for any \(y_{0}=\ltimes _{i=-\varsigma +1}^0 x(i)\in C_{y}\), there exist a time-variant state feedback NSDC sequence and a positive integer T such that \(x(t)\in \mathscr {E}_{e},\ \forall \ t \ge T\), and \(x(t)\in C_{x},\ \forall \ t\ge 1\), which implies \(y(t)=\ltimes _{i=t-\varsigma +1}^t x(i) \in \widehat{\mathscr {E}}_{e}, \ \forall \ t \ge T+\varsigma -1\), and \(y(t)=\ltimes _{i=t-\varsigma +1}^t x(i)\in C_{y}, \ \forall \ t\ge 1\). From Definition 3, system (11) is nonuniform sampled-data inequality constrained set stabilizable to \(\widehat{\mathscr {E}}_{e}\).

(Sufficiency) From Definition 3, for any \(y_{0}\in C_{y}\), there exist a time-variant state feedback NSDC sequence and a positive integer \(\widehat{T}\) such that \(y(t) \in \widehat{\mathscr {E}}_{e}, \ \forall \ t \ge \widehat{T}\), and \(y(t)\in C_{y}\), \(\forall \ t\ge 1\). From the construction of \(\widehat{\mathscr {E}}_{e}\) and the unique factorization of \(y(t)=\ltimes _{i=t-\varsigma +1}^t x(i)\), we have \(x(t)\in \mathscr {E}_{e}\), \(\forall \ t \ge \widehat{T}\), and \(x(t)\in C_{x}\), \(\forall \ t \ge 1\). From Definition 2, DBCN (2) is nonuniform sampled-data inequality constrained set stabilizable to \(\mathscr {E}_{e}\). \(\square\)

Inequality constrained set reachability

In this section, by constructing an inequality constrained controllability matrix, we investigate the nonuniform sampled-data inequality constrained set reachability of the augmented system (11).

Firstly, we give the concept of nonuniform sampled-data inequality constrained set reachability of system (11).

Definition 4

Given a nonempty set \(\widehat{\mathscr {E}}_{d}\subseteq C_{y}\) and an initial state \(y_{0} \in C_{y}\). \(\widehat{\mathscr {E}}_{d}\) is called nonuniform sampled-data inequality constrained set reachable from \(y_{0}\) at sampling point \(t_{h}\) under NSDC, if one can find an NSDC sequence \(\big \{v(0),v(1),\cdots\) \(,v(t_{h}-1)\big \}\subseteq \Delta _{2^{m}}\) such that \(y(t_{h})\in \widehat{\mathscr {E}}_{d}\) and \(y(t)\in C_{y}\), \(\forall \ 1 \le t \le t_{h}\).

Secondly, we construct the inequality constrained controllability matrix.

For system (11), split \(\overline{K}\) into \(2^m\) equal blocks as

$$\begin{aligned} \overline{K}=[Blk_1(\overline{K})~\cdots ~Blk_{2^m}(\overline{K})]. \end{aligned}$$
(14)

Then, \(Blk_i(\overline{K})\) corresponds to the control \(\delta _{2^m}^i\), \(i=1,\cdots ,2^m\). In order to reduce the computational complexity caused by state inequality constraints, define \(E\in \mathbb {R}^{2^{n\varsigma }\times 2^{n\varsigma }}\) with

$$\begin{aligned} Row_{i}(E)=\left\{ \begin{array}{lll} (\delta _{2^{n\varsigma }}^{i})^{\top },\ \ i\in \{\mu _{1}, \cdots , \mu _{\beta ^{\varsigma }}\},\\ \textbf{0}_{2^{n\varsigma }}^{\top },\ \hbox {otherwise}.\end{array}\right. \end{aligned}$$
(15)

Let

$$\begin{aligned} Blk_i(\widehat{\overline{K}})=E \big (Blk_i(\overline{K})\big ) E^{\top }, i=1,\cdots ,2^m. \end{aligned}$$
(16)

Intuitively, \(Blk_i(\widehat{\overline{K}})\) is obtained from \(Blk_i(\overline{K})\) by substituting zeros in the corresponding rows and columns with indices \(\{1,\cdots , {2^{n\varsigma }}\} \setminus \{\mu _{1}, \cdots , \mu _{\beta ^{\varsigma }}\}\). Then, the inequality constrained controllability matrix is constructed as follows:

$$\begin{aligned} Q_{\tau _{h}}=\sum _{i=1}^{2^{m}}\Big (Blk_{i}(\widehat{\overline{K}})\Big )^{\tau _{h}}, \end{aligned}$$
(17)

where \(\tau _{h}=t_{h+1}-t_{h}, h\in \mathbb {N}.\)

Finally, we present a criterion for the nonuniform sampled-data inequality constrained set reachability by (17).

Theorem 1

Given a nonempty set \(\widehat{\mathscr {E}}_{d}\subseteq C_{y}\) and an initial state \(y(0)=\delta _{2^{n\varsigma }}^{\mu _{\theta }}\in C_{y}\). \(\widehat{\mathscr {E}}_{d}\) is nonuniform sampled-data inequality constrained set reachable from y(0) at sampling point \(t_{h}\) under NSDC, if and only if

$$\begin{aligned} \sum _{\delta _{2^{n\varsigma }}^{\mu _{h_{i}}}\in \widehat{\mathscr {E}}_{d}}(Q_{\tau _{h-1}}\cdots Q_{\tau _{0}})_{\mu _{h_{i}},\mu _{\theta }}\ge 1. \end{aligned}$$
(18)

Proof

(Necessity) Assuming that \(\widehat{\mathscr {E}}_{d}\) is inequality constrained set reachable from \(y(0)=\delta _{2^{n\varsigma }}^{\mu _{\theta }}\) at \(t_{h}\) under NSDC, we prove (18) by induction.

For \(h=1\), from Definition 4, there exist \(v(0)=\delta _{2^{m}}^{\xi _{0}}\), \(\cdots ,v(t_{1}-1)=\delta _{2^{m}}^{\xi _{0}}\) and \(y(t_{1})=\delta _{2^{n\varsigma }}^{\mu _{{\tilde{1}}_{i}}}\in \widehat{\mathscr {E}}_{d}\) such that \(\delta _{2^{n\varsigma }}^{\mu _{{\tilde{1}}_{i}}}=\Big (Blk_{\xi _{0}}(\widehat{\overline{K}})\Big )^{\tau _{0}}\) \(\delta _{2^{n\varsigma }}^{\mu _{\theta }}\) and \(y(t)\in C_{y}\), \(\forall \ 1 \le t \le t_{1}\). Thus, \(\Big (\big (Blk_{\xi _{0}}(\widehat{\overline{K}})\big )^{\tau _{0}}\Big )_{\mu _{{\tilde{1}}_{i}},\mu _{\theta }}=1\), which shows that

$$\begin{aligned} \sum _{\delta _{2^{n\varsigma }}^{\mu _{1_{i}}}\in \widehat{\mathscr {E}}_{d}}(Q_{\tau _{0}})_{\mu _{1_{i}},\mu _{\theta }} \ge \Big (\sum _{j=1}^{2^{m}}\big (Blk_{j}(\widehat{\overline{K}})\big )^{\tau _{0}}\Big )_{\mu _{{\tilde{1}}_{i}},\mu _{\theta }} \ge \Big (\big (Blk_{\xi _{0}}(\widehat{\overline{K}})\big )^{\tau _{0}}\Big )_{\mu _{{\tilde{1}}_{i}},\mu _{\theta }}=1, \end{aligned}$$
(19)

that is, (18) holds for \(h=1.\)

Assume that (18) holds for some \(h=\lambda >1\), that is

$$\begin{aligned} \sum _{\delta _{2^{n\varsigma }}^{\mu _{\lambda _{i}}}\in \widehat{\mathscr {E}}_{d}}(Q_{\tau _{\lambda -1}}\cdots Q_{\tau _{0}})_{\mu _{\lambda _{i}},\mu _{\theta }}\ge 1.\end{aligned}$$
(20)

Then, there exist \(v(t)|_{t=t_{0}}^{t_{1}-1}=\delta _{2^{m}}^{\xi _{0}}, \cdots , v(t)|_{t=t_{\lambda -1}}^{t_{\lambda }-1}=\delta _{2^{m}}^{\xi _{\lambda -1}}\) and \(y(t_{\lambda })=\delta _{2^{n\varsigma }}^{\mu _{{\tilde{\lambda}}_{i}}}\in \widehat{\mathscr {E}}_{d}\) such that

$$\begin{aligned} \Big (\big (Blk_{\xi _{\lambda -1}}(\widehat{\overline{K}})\big )^{\tau _{\lambda -1}} \cdots \big (Blk_{\xi _{0}}(\widehat{\overline{K}})\big )^{\tau _{0}}\Big )_{\mu _{{\tilde{\lambda}}_{i}},\mu _{\theta }}=1, \end{aligned}$$
(21)

where \(v(t)|_{t=t_{h}}^{t_{h+1}-1}=\delta _{2^m}^{\xi _{h}}\) denotes an NSDC sequence \(\{v(t_{h})=\delta _{2^m}^{\xi _{h}},\cdots ,v(t_{h+1}-1)=\delta _{2^m}^{\xi _{h}}\}\subseteq \Delta _{2^{m}}\), \(h\in \mathbb {N}\).

We prove that (18) holds for \(h=\lambda +1\). By (21) and Definition 4, there exist \(v(t)|_{t=t_{0}}^{t_{1}-1}=\delta _{2^{m}}^{\xi _{0}}, \ \cdots ,\ v(t)|_{t=t_{\lambda -1}}^{t_{\lambda }-1}=\delta _{2^{m}}^{\xi _{\lambda -1}},\) \(v(t)|_{t=t_{\lambda }}^{t_{\lambda +1}-1}\) \(=\delta _{2^{m}}^{\xi _{\lambda }}\) and \(y(t_{\lambda +1})=\delta _{2^{n\varsigma }}^{\mu _{\widetilde{(\lambda +1)}_{i}}}\in \widehat{\mathscr {E}}_{d}\) such that the trajectory from \(\delta _{2^{n\varsigma }}^{\mu _{\theta }}\) to \(\delta _{2^{n\varsigma }}^{\mu _{\widetilde{(\lambda +1)}_{i}}}\) can be decomposed to the trajectory from \(\delta _{2^{n\varsigma }}^{\mu _{\theta }}\) to

$$\begin{aligned} y(t_{\lambda }) =\Big (\big (Blk_{\xi _{\lambda -1}}(\widehat{\overline{K}})\big )^{\tau _{\lambda -1}} \cdots \big (Blk_{\xi _{0}}(\widehat{\overline{K}})\big )^{\tau _{0}}\Big )\delta _{2^{n\varsigma }}^{\mu _{\theta }} =\delta _{2^{n\varsigma }}^{\mu _{{\tilde{\lambda}}_{i}}}\in C_{y} \end{aligned}$$
(22)

at sampling point \(t_{\lambda }\) and the trajectory from \(\delta _{2^{n\varsigma }}^{\mu _{{\tilde{\lambda}}_{i}}}\) to \(\delta _{2^{n\varsigma }}^{\mu _{\widetilde{(\lambda +1)}_{i}}}\) in \(\tau _{\lambda }\) steps. Then, from (19) and (22), we have

$$\begin{aligned} \Big (\big (Blk_{\xi _{\lambda }}(\widehat{\overline{K}})\big )^{\tau _{\lambda }}\Big ) _{\mu _{\widetilde{(\lambda +1)}_{i}},\mu _{{\tilde{\lambda}}_{i}}}=1 \quad \text {and}\quad \Big (\big (Blk_{\xi _{\lambda -1}}(\widehat{\overline{K}})\big )^{\tau _{\lambda -1}} \cdots \big (Blk_{\xi _{0}}(\widehat{\overline{K}})\big )^{\tau _{0}}\Big )_{\mu _{{\tilde{\lambda}}_{i}},\mu _{\theta }}=1, \end{aligned}$$

which show that

$$\begin{aligned}&\sum _{\delta _{2^{n\varsigma }}^{\mu _{(\lambda +1)_{i}}}\in \widehat{\mathscr {E}}_{d}}(Q_{\tau _{\lambda }}Q_{\tau _{\lambda -1}}\cdots Q_{\tau _{0}})_{\mu _{(\lambda +1)_{i}},\mu _{\theta }} \ge \sum ^{2^{n\varsigma }}_{j=1}(Q_{\tau _{\lambda }})_{\mu _{\widetilde{(\lambda +1)}_{i}},j} (Q_{\tau _{\lambda -1}}\cdots Q_{\tau _{0}})_{j,\mu _{\theta }}\\&\quad \ge \Big (\big (Blk_{\xi _{\lambda }}(\widehat{\overline{K}})\big )^{\tau _{\lambda }} \Big )_{\mu _{\widetilde{(\lambda +1)}_{i}},\mu _{{\tilde{\lambda}}_{i}}} \Big (\big (Blk_{\xi _{\lambda -1}}(\widehat{\overline{K}})\big )^{\tau _{\lambda -1}} \cdots \big (Blk_{\xi _{0}}(\widehat{\overline{K}})\big )^{\tau _{0}}\Big )_{\mu _{{\tilde{\lambda}}_{i}},\mu _{\theta }} =1. \end{aligned}$$

Thus, (18) holds for \(h=\lambda +1.\) By induction, the necessity is proved.

(Sufficiency) Assume that (18) holds, that is,

$$\begin{aligned} \sum _{\delta _{2^{n\varsigma }}^{\mu _{h_{i}}}\in \widehat{\mathscr {E}}_{d}}(Q_{\tau _{h-1}}\cdots Q_{\tau _{0}})_{\mu _{h_{i}},\mu _{\theta }}=\sum _{\delta _{2^{n\varsigma }}^{\mu _{h_{i}}}\in \widehat{\mathscr {E}}_{d}}\Big (\sum _{j=1}^{2^{m}}\big (Blk_{j}(\widehat{\overline{K}})\big )^{\tau _{h-1}}\cdots \sum _{j=1}^{2^{m}}\big (Blk_{j}(\widehat{\overline{K}})\big )^{\tau _{0}}\Big )_{\mu _{h_{i}},\mu _{\theta }} \ge 1. \end{aligned}$$

Then, there exist \(v(t)|_{t=t_{0}}^{t_{1}-1}=\delta _{2^{m}}^{\xi _{0}}, \cdots , v(t)|_{t=t_{h-1}}^{t_{h}-1}=\delta _{2^{m}}^{\xi _{h-1}}\) and \(y(t_{h})=\delta _{2^{n\varsigma }}^{\mu _{\widetilde{h}_{i}}}\in \widehat{\mathscr {E}}_{d}\) such that

$$\begin{aligned} \Big (\big (Blk_{\xi _{h-1}}(\widehat{\overline{K}})\big )^{\tau _{h-1}}\cdots \big (Blk_{\xi _{0}}(\widehat{\overline{K}})\big )^{\tau _{0}}\Big )_{\mu _{\widetilde{h}_{i}},\mu _{\theta }}=1. \end{aligned}$$

Thus, \(y(t_{h})=\delta _{2^{n\varsigma }}^{\mu _{\widetilde{h}_{i}}}=\Big (\big (Blk_{\xi _{h-1}}(\widehat{\overline{K}}) \big )^{\tau _{h-1}}\cdots \big (Blk_{\xi _{0}}(\widehat{\overline{K}})\big )^{\tau _{0}}\Big )\delta _{2^{n\varsigma }}^{\mu _{\theta }} \in \widehat{\mathscr {E}}_{d}.\)

Finally, we prove \(y(t)\in C_{y}, \ \forall \ 1 \le t \le t_{h}\) by reduction to absurdity. In fact, if there exists \(1 \le t^{\prime }< t_{h}\) satisfying \(y(t^{\prime })\notin C_{y}\), then by (16), \(y(t)=\textbf{0}_{2^{n\varsigma }}\) for any \(t^{\prime }< t\le t_{h}\), which is a contradiction to \(y(t_{h}) \in \widehat{\mathscr {E}}_{d}.\)

Thus, from Definition 4, \(\widehat{\mathscr {E}}_{d}\) is inequality constrained set reachable from y(0) at \(t_{h}\) under NSDC. \(\square\)

Example 2

Consider DBCN (2) with equivalent algebraic form (11), where \(\varsigma =1\), \(C_{x}=\Delta _{2^{3}}\), and \(\overline{K}=\delta _{8}[1 ~ 7 ~ 8~ 3 ~ 4 ~ 5~ 7 ~ 6~3 ~ 6~ 3 ~ 2\) 4 6 7 8]. Assume \(\widehat{\mathscr {E}}_{d}=\{\delta _8^7\}\), \(y(0)=\delta _{8}^1.\)

  1. (i)

    Suppose \(\tau _{h}=1, \forall \ h\in \mathbb {N}\). According to Theorem 1, \(\widehat{\mathscr {E}}_{d}\) is inequality constrained set reachable from \(\delta _{8}^1\) at time \(t=7\) under the traditional state feedback control sequence \(\{v(0)=\delta _{2}^2,v(1)=\delta _{2}^1,v(2)=\delta _{2}^1,v(3)=\delta _{2}^1,v(4)=\delta _{2}^2,v(5)=\delta _{2}^2, v(6)=\delta _{2}^1\}\);

  2. (ii)

    Suppose \(\tau _{h}=\tau =2, \forall \ h\in \mathbb {N}\), where \(\tau =2\) is the sampling period. According to Theorem 1, \(\widehat{\mathscr {E}}_{d}\) is unreachable from \(\delta _{8}^1\) under any state feedback uniform SDC sequence;

  3. (iii)

    Suppose \(\tau _{0}=2,\tau _{1}=4,\tau _{2}=1,\tau _{3}=2,\cdots\). According to Theorem 1, \(\widehat{\mathscr {E}}_{d}\) is inequality constrained set reachable from \(\delta _{8}^1\) at sampling point \(t_{4}\) under the state feedback NSDC sequence \(\{v(t)|_{t=t_{0}}^{t_{1}-1}=\delta _{2}^2,v(t)|_{t=t_{1}}^{t_{2}-1}=\delta _{2}^1,v(t)|_{t=t_{2}}^{t_{3}-1}= \delta _{2}^2,v(t)|_{t=t_{3}}^{t_{4}-1}=\delta _{2}^1\}\).

Fig. 2
figure 2

State trajectories in (i) and (iii).

Full size image

Remark 1

Traditional state feedback control15 and state feedback uniform SDC37 can be viewed as a special case of NSDC. NSDC can provide us with more control schemes to achieve control objectives and reduce control costs (see Fig. 2).

Inequality constrained set stabilization

Based on the inequality constrained set reachability, we investigate the nonuniform sampled-data inequality constrained set stabilization.

Firstly, we introduce the concept of the largest nonuniform sampled-data inequality constrained invariant subset.

Definition 5

A nonempty subset \(\mathscr {E}^{\prime }\subseteq C_{y}\) is referred to as a nonuniform sampled-data inequality constrained invariant subset, if for any \(y(0)\in \mathscr {E}^{\prime }\), one can find a state feedback NSDC \(v(t_{0})\in \Delta _{2^{m}}\) such that \(y(t)\in \mathscr {E}^{\prime }\) holds for any \(t \le \overline{\tau }\), \(\overline{\tau }=\max \{\tau _{h}, h\in \mathbb {N}\}.\)

From Definition 5, the union of inequality constrained invariant subsets is still an inequality constrained invariant subset.

Definition 6

Given a nonempty set \(\mathscr {E}\subseteq C_{y}\), \(I(\mathscr {E})\) is said to be the largest nonuniform sampled-data inequality constrained invariant subset of \(\mathscr {E}\), if \(I(\mathscr {E})\) is the union of all nonuniform sampled-data inequality constrained invariant subsets contained in \(\mathscr {E}.\)

From Definition 6, the construction method of the largest nonuniform sampled-data inequality constrained invariant subset \(I(\mathscr {E})\) is given as fellow:

  1. (i)

    Set \(\Gamma _{0}:=\{\mu :\delta _{2^{n\varsigma }}^\mu \in \mathscr {E}\}\);

  2. (ii)

    Set \(\Gamma _{j}:=\Big \{\mu \in \Gamma _{j-1}:\ \hbox {there exists an integer}\) \(\ 0< \xi _{\mu }\le 2^{m},\ \hbox {such that}\widetilde{\bigwedge }_{l=1}^{\overline{\tau }}\Big (\sum _{i\in \Gamma _{j-1}}\big (\big (Blk_{\xi _{\mu }}(\widehat{\overline{K}})\big )^{l}\big )_{i,\mu }\Big )=1\Big \}, \ j\in \mathbb {Z}_{+};\)

  3. (iii)

    Find the smallest positive integer \(q\le |\mathscr {E}|\) such that \(\Gamma _{q}=\Gamma _{q+1}\);

  4. (iv)

    \(I(\mathscr {E})=\{\delta _{2^{n\varsigma }}^\mu :\mu \in \Gamma _{q}\}\).

Secondly, given \(\chi \in \mathbb {Z}_{+}\), we define the nonuniform sampled-data inequality constrained reachable sets as

$$\begin{aligned}&E_{\tau _{\chi -1}}(I(\widehat{\mathscr {E}}_{e}))=\Big \{\delta _{2^{n\varsigma }}^{\alpha }\in C_{y}:\hbox {there exists an integer} \ 1\le \xi _{\alpha }\\&\quad \le 2^{m}, \hbox {such that}\sum _{\delta _{2^{n\varsigma }}^{\mu _{\chi _{i}}}\in I(\widehat{\mathscr {E}}_{e})}\big (\big (Blk_{\xi _{\alpha }}(\widehat{\overline{K}})\big )^{\tau _{\chi -1}}\big )_{\mu _{\chi _{i}},\alpha }=1\Big \}, \end{aligned}$$

and

$$\begin{aligned}&E_{\tau _{\chi -2}+\tau _{\chi -1}}(I(\widehat{\mathscr {E}}_{e}))\\&\quad =\Big \{\delta _{2^{n\varsigma }}^{\alpha }\in C_{y}:\hbox {there exists an integer} 1\le \xi _{\alpha }\\&\quad \le 2^{m},\ \hbox {such that}\sum _{\delta _{2^{n\varsigma }}^{\mu _{(\chi -1)_{i}}}\in E_{\tau _{\chi -1}}(I(\widehat{\mathscr {E}}_{e}))}\big (\big (Blk_{\xi _{\alpha }}(\widehat{\overline{K}})\big )^{\tau _{\chi -2}}\big ) _{\mu _{(\chi -1)_{i}},\alpha }=1\Big \}. \end{aligned}$$

Keeping this procedure going, we define

$$\begin{aligned} & E_{\Sigma _{i=0}^{\chi -1}\tau _{i}}(I(\widehat{\mathscr {E}}_{e}))=\Big \{\delta _{2^{n\varsigma }}^{\alpha }\in C_{y}:\hbox {there exists an integer} 1\le \xi _{\alpha }\\ & \quad \le 2^{m},\ \hbox {such that}\sum _{\delta _{2^{n\varsigma }}^{\mu _{1_{i}}}\in E_{\Sigma _{i=1}^{\chi -1}\tau _{i}}(I(\widehat{\mathscr {E}}_{e}))}\big (\big (Blk_{\xi _{\alpha }}(\widehat{\overline{K}})\big )^{\tau _{0}}\big ) _{\mu _{1_{i}},\alpha }=1\Big \}. \end{aligned}$$

Thus, by the construction process of the largest nonuniform sampled-data inequality constrained invariant subset, if \(I(\widehat{\mathscr {E}}_{e})\ne \emptyset\), \(\delta _{2^{n\varsigma }}^{\alpha }\in E_{\Sigma _{i=0}^{\chi -1}\tau _{i}}(I(\widehat{\mathscr {E}}_{e}))\), then \(\delta _{2^{n\varsigma }}^{\alpha }\in E_{\Sigma _{i=0}^{q}\tau _{i}}(I(\widehat{\mathscr {E}}_{e})), \forall \ q\ge \chi -1\). Hence, we have the following result on the inequality constrained reachable sets.

Proposition 3

If \(I(\widehat{\mathscr {E}}_{e})\ne \emptyset\), then \(E_{\Sigma _{i=0}^{\chi -1}\tau _{i}}(I(\widehat{\mathscr {E}}_{e})) \subseteq E_{\Sigma _{i=0}^{\chi }\tau _{i}}(I(\widehat{\mathscr {E}}_{e}))\) holds for any \(\chi \in \mathbb {Z}_{+}.\)

Finally, based on the inequality constrained reachable sets, we provide the result on the inequality constrained set stabilization.

Theorem 2

System (11) is nonuniform sampled-data inequality constrained set stabilizable to \(\widehat{\mathscr {E}}_{e}\) under a time-variant state feedback NSDC (10), if and only if

  1. (i)

    \(I(\widehat{\mathscr {E}}_{e})\ne \emptyset\);

  2. (ii)

    there exists an integer \(1\le \chi \le \beta ^{\varsigma }\) such that \(E_{\Sigma _{i=0}^{\chi -1}\tau _{i}}(I(\widehat{\mathscr {E}}_{e}))=C_{y}\).

Proof

(Necessity) Obviously, from Definition 3, (i) holds. Now, we prove (ii).

From Definition 3, there exist an integer \(T > 0\) and a time-variant state feedback NSDC such that

$$\begin{aligned} y(t)\in I(\widehat{\mathscr {E}}_{e}), \forall \ t\ge T, \ \forall \ y(0)\in C_{y}. \end{aligned}$$
(23)

Take \(\hat{T}\) to represent the smallest integer \(T>0\) that satisfies (23). By reduction to absurdity, we prove \(\hat{T}<\beta ^{\varsigma }\overline{\tau }\). If \(\hat{T}\ge \beta ^{\varsigma }\overline{\tau }\), we have \(y(t_{h})\notin I(\widehat{\mathscr {E}}_{e}), h=0,\cdots ,\beta ^{\varsigma }\). However, since system (11) with the state inequality constraint has at most \(\beta ^{\varsigma }\) different states, there exist different \(h_{1}, h_{2}\in \{0,1,\cdots ,\beta ^{\varsigma }\}\) such that \(y(t_{h_{1}})=y(t_{h_{2}})\). Hence, under the NSDC, starting from \(y^{\prime }(0)=y(t_{h_{1}})\), the state trajectory forms a cycle, which contradicts the fact that system (11) is inequality constrained set stabilizable to \(\widehat{\mathscr {E}}_{e}\) under the NSDC.

Setting \(\chi =\lfloor \hat{T}/\overline{\tau }\rfloor +1\le \beta ^{\varsigma }\), we have \(E_{\sum ^{\chi -1}_{i=0}\tau _{i}}(I(\widehat{\mathscr {E}}_{e}))=C_{y}\). Thus, (ii) holds.

(Sufficiency) Assume that (i) and (ii) hold. For each \(y(0)=\delta _{2^{n\varsigma }}^{\alpha }\in E_{\Sigma _{i=0}^{\chi -1}\tau _{i}}(I\) \((\widehat{\mathscr {E}}_{e}))=C_{y}\), there exists an integer \(0<\xi _{\alpha }\le 2^{m}\) such that \(E_{\Sigma _{i=1}^{\chi -1}\tau _{i}}(I(\widehat{\mathscr {E}}_{e}))\) is inequality constrained set reachable from \(\delta _{2^{n\varsigma }}^{\alpha }\) in \(\tau _{0}\) steps under the NSDC \(v(t_{0})=\delta _{2^{m}}^{\xi _{\alpha }}\). Set \(G(t_{0})=\delta _{2^{m}}[\eta _{1}^{t_{0}}~\cdots ~\eta _{2^{n\varsigma }}^{t_{0}}]\), where

$$\begin{aligned} \eta _{i}^{t_{0}}\in \left\{ \begin{array}{lll} \{\xi _{\alpha }\}, \ \hbox {if} \ i=\alpha , \alpha =\mu _{1}, \cdots ,\mu _{\beta ^{\varsigma }} ,\\ \{1,\cdots , 2^{m}\},\ \hbox {otherwise}. \end{array} \right. \end{aligned}$$
(24)

Under the NSDC \(v(t_{0})=G(t_{0})y(0)\), let

$$\begin{aligned} \Upsilon _{\tau _{0}}(y(0))&=\Big \{y(t_{1})\big |y(t_{1})=(\overline{K}v(t_{0}))^{\tau _{0}}y(0)\in C_{y}, y(0)\in E_{\sum ^{\chi -1}_{i=0}\tau _{i}}(\widehat{\mathscr {E}}_{e})\Big \}\\&:=\Big \{\delta _{2^{n\varsigma }}^{\alpha _{1}^{1}},\cdots ,\delta _{2^{n\varsigma }}^{\alpha _{\varrho _{1}}^{1}}\Big \} \subseteq E_{\Sigma _{i=1}^{\chi -1}\tau _{i}}(I(\widehat{\mathscr {E}}_{e})). \end{aligned}$$

For each \(\delta _{2^{n\varsigma }}^{\alpha _{j}^{1}}\in \Upsilon _{\tau _{0}}(y(0))\), \(j=1,\cdots ,\varrho _{1}\), there exists an integer \(1\le \xi _{\alpha _{j}^{1}}\le 2^{m}\) such that \(E_{\Sigma _{i=2}^{\chi -1}\tau _{i}}(I(\widehat{\mathscr {E}}_{e}))\) is inequality constrained set reachable from \(y(t_{1})=\delta _{2^{n\varsigma }}^{\alpha _{j}^{1}}\) in \(\tau _{1}\) steps under the NSDC \(v(t_{1})=\delta _{2^{m}}^{\xi _{\alpha _{j}^{1}}}\). Set \(G(t_{1})=\delta _{2^{m}}[\eta _{1}^{t_{1}}~\cdots ~\eta _{2^{n\varsigma }}^{t_{1}}]\), where

$$\begin{aligned} \eta _{i}^{t_{1}}\in \left\{ \begin{array}{lll} \{\xi _{\alpha _{j}^{1}}\}, \ \hbox {if} \ i=\alpha _{j}^{1}, \ j=1,\cdots ,\varrho _{1},\\ \{1,\cdots , 2^{m}\},\ \hbox {otherwise}. \end{array} \right. \end{aligned}$$
(25)

Under the NSDC \(v(t_{1})=G(t_{1})y(t_{1})\), let

$$\begin{aligned} \Upsilon _{\tau _{1}+\tau _{0}}(y(0))&=\Big \{y(t_{2})\big |y(t_{2})=(\overline{K}v(t_{1}))^{\tau _{1}}y(t_{1})\in C_{y}, y(t_{1})\in \Upsilon _{\tau _{0}}(y(0))\Big \}\\&:=\Big \{\delta _{2^{n\varsigma }}^{\alpha _{1}^{2}},\cdots ,\delta _{2^{n\varsigma }}^{\alpha _{\varrho _{2}}^{2}}\Big \} \subseteq E_{\Sigma _{i=2}^{\chi -1}\tau _{i}}(I(\widehat{\mathscr {E}}_{e})). \end{aligned}$$

Keeping this procedure going, we have \(G(t_{i})=\delta _{2^{m}}[\eta _{1}^{t_{i}}~\cdots ~\eta _{2^{n\varsigma }}^{t_{i}}], \ i=0,\cdots ,\) \(\chi -1\). Under the NSDC

$$\begin{aligned} v(t_{\chi -1})=G(t_{\chi -1})y(t_{\chi -1}), \end{aligned}$$

let

$$\begin{aligned} \Upsilon _{\Sigma _{i=0}^{\chi -1}\tau _{i}}(y(0)) =\Big \{y(t_{\chi })\big |y(t_{\chi })=(\overline{K}v(t_{\chi -1}))^{\tau _{\chi -1}}y(t_{\chi -1})\in C_{y}, y(t_{\chi -1})\in \Upsilon _{\Sigma _{i=0}^{\chi -2}\tau _{i}}(y(0))\Big \} \subseteq I(\widehat{\mathscr {E}}_{e}). \end{aligned}$$

From (i) and the largest nonuniform sampled-data inequality constrained invariant subset, for each \(\delta _{2^{n\varsigma }}^{\alpha }\in I(\widehat{\mathscr {E}}_{e})\), there exists an integer \(0<\xi _{\alpha }\le 2^{m}\) such that \(y(t)=(\overline{K}\delta _{2^{m}}^{\xi _{\alpha }})^{t-t_{h}}\delta _{2^{n\varsigma }}^{\alpha }\in I(\widehat{\mathscr {E}}_{e}), \forall \ t_{h}\le t\le t_{h+1}, \forall \ h\ge \chi .\) Set \(G(t_{h})=\delta _{2^{m}}[\eta _{1}^{t_{\chi }}~\cdots ~\eta _{2^{n\varsigma }}^{t_{\chi }}]\), where

$$\begin{aligned} \eta _{i}^{t_{\chi }}\in \left\{ \begin{array}{lll} \{\xi _{\alpha }\}, \ \hbox {if} \ i=\alpha ,\\ \{1,\cdots , 2^{m}\},\ \hbox {otherwise}. \end{array} \right. \end{aligned}$$
(26)

For each \(y(t_{h})\in I(\widehat{\mathscr {E}}_{e})\), under the NSDC \(v(t_{h})=\delta _{2^{m}}[\eta _{1}^{t_{\chi }}~\cdots ~\eta _{2^{n\varsigma }}^{t_{\chi }}]y(t_{h})\), we have \(y(t)\in I(\widehat{\mathscr {E}}_{e}), \forall \ t_{h}\le t\le t_{h+1},\ h\ge \chi .\)

Thus, we obtain the time-variant state feedback NSDC as follows:

$$\begin{aligned} v(t) =G(t_{h})y(t_{h}) =\left\{ \begin{array}{lll} \delta _{2^{m}}[\eta _{1}^{t_{h}}~\cdots ~\eta _{2^{n\varsigma }}^{t_{h}}]y(t_{h}), \ h=0,\cdots ,\chi -1,\\ \delta _{2^{m}}[\eta _{1}^{t_{\chi }}~\cdots ~\eta _{2^{n\varsigma }}^{t_{\chi }}]y(t_{h}), \ h\ge \chi . \end{array} \right. \end{aligned}$$
(27)

\(t\in [t_{h}, t_{h+1})| _{\mathbb {Z}}\), under which system (11) is nonuniform sampled-data inequality constrained set stabilizable to \(\widehat{\mathscr {E}}_{e}\). \(\square\)

Corollary 1

For \(\mathscr {E}_{e}\subseteq C_{x}\) given in Definition 2, DBCN (2) is nonuniform sampled-data inequality constrained set stabilizable to \(\mathscr {E}_{e}\) by a time-variant state feedback NSDC (7), if and only if (i) and (ii) of Theorem 2hold.

Remark 2

The state constraints in BNs are generally directly given a state constraint set, while state inequality constraints require solving the state constraint set based on the constraints satisfied by the state. Meanwhile, this paper provides a method for determining the state constraint set based on the state inequality constraints. This provides technical support for studying the stabilization problem of BNs under different constraint conditions.

Illustrative example

Example 3

Consider the apoptosis network (5):

$$\begin{aligned} \left\{ \begin{array}{lll} x_{1}(t+1)=\lnot x_2(t-1)\wedge v(t),\\ x_{2}(t+1)=\lnot x_1(t-1)\wedge x_3(t-1),\\ x_{3}(t+1)= x_2(t-1)\vee v(t), \end{array}\right. \end{aligned}$$
(28)

with the state time delay \(\varsigma =2\) and the state inequality constraint

$$\begin{aligned} 2\le 2^{0}x_{1}(i)+2^{1}x_{2}(i)+2^{2}x_{3}(i)\le 4, \ i=-1, 0, 1, \cdots . \end{aligned}$$
(29)

Setting \(x(t)=\ltimes _{i=1}^3 x_i(t)\), \(y(t)=x(t-1)\ltimes x(t)\), from system (11), we have

$$\begin{aligned} y(t+1)=\overline{K}v(t)y(t), \end{aligned}$$
(30)

where

$$\begin{aligned} \overline{K}=\delta _{64}[&7~15~23~31~39~47~55~63~7~15~23~31~39~47~55~63~3~11~19~27~35~43~51~59~3~11~19~27~35~43~51~59\\&5~13~21~29~37~45~53~61~7~15~23~31~39~47~55~63~1~~9~17~25~33~41~49~57~3~11~19~27~35~43~51~59\\&7~15~23~31~39~47~55~63~7~15~23~31~39~47~55~63~8~16~24~32~40~48~56~64~8~16~24~32~40~48~56~64\\&5~13~21~29~37~45~53~61~7~15~23~31~39~47~55~63~6~14~22~30~38~46~54~62~8~16~24~32~40~48~56~64]. \end{aligned}$$

By Algorithm 1, we have \(C_{x}=\{\delta _{8}^{2}, \delta _{8}^{6}, \delta _{8}^{7}\}.\)

Next, we study the nonuniform sampled-data inequality constrained set stabilization of system (28) with \(\mathscr {E}_{e}=\{\delta _{8}^{6}, \delta _{8}^{7}\}\)

and

$$\begin{aligned} \tau _{h}=\left\{ \begin{array}{lll} 2, \ h=2i,\\ 1,\ h=2i+1, \end{array} \right. i\in \mathbb {N}. \end{aligned}$$
(31)

From (12) and (13), we have \(C_{y}=\{\delta _{64}^{10}, \delta _{64}^{14}, \delta _{64}^{15}, \delta _{64}^{42}\), \(\delta _{64}^{46}, \delta _{64}^{47}, \delta _{64}^{50}, \delta _{64}^{54}, \delta _{64}^{55}\}\) and \(\widehat{\mathscr {E}}_{e}=\{\delta _{64}^{46}, \delta _{64}^{47}, \delta _{64}^{54}, \delta _{64}^{55}\}.\)

By the proof process of Theorem 1, we have \(I(\widehat{\mathscr {E}}_{e})=\widehat{\mathscr {E}}_{e}\) and \(E_{\tau _{0}}(I(\widehat{\mathscr {E}}_{e}))=C_{y}\). From Corollary 1, system (28) is inequality constrained set stabilizable to \(\mathscr {E}_{e}\). In addition, by Theorem 2, the time-variant state feedback sampled-data gain matrix is designed as

$$\begin{aligned} G(t_{0})=\delta _{2}[\eta _{1}^{t_{0}}~\cdots ~\eta _{64}^{t_{0}}], \ G(t_{h})=\delta _{2}[\eta _{1}^{t_{h}}~\cdots ~\eta _{64}^{t_{h}}], \end{aligned}$$
(32)

where

$$\begin{aligned} \eta _{i}^{t_{0}}\in \left\{ \begin{array}{lll} \{2\}, \ i=47,50,54,55\\ \{1,2\},\ \hbox {otherwise}\end{array}\right. , \ \eta _{i}^{t_{h}}\in \left\{ \begin{array}{lll} \{2\}, \ i=47,54,55\\ \{1,2\},\ \hbox {otherwise}\end{array}\right. , ~~h\ge 1. \end{aligned}$$

Remark 3

According to Example 3, the convergence speed of the proposed control algorithm can be controlled by (17). Using the traditional control15, it needs two state feedback controllers to make all states reach \(\mathscr {E}_{e}\). However, using the nonuniform sampled-data control, it only need one state feedback controller to make all states reach \(\mathscr {E}_{e}\). Therefore, it reduces the frequency of controller updates, and the amount of calculation will be reduced.

Conclusions

In this paper, we have analyzed the nonuniform sampled-data set stabilization of DBCNs with state inequality constraints via time-variant state feedback NSDC. We have presented an effective criterion for the nonuniform sampled-data inequality constrained set reachability of DBCNs under NSDC by constructing an inequality constrained controllability matrix. By virtue of the inequality constrained reachable set and the largest inequality constrained invariant subset, we have proposed a procedure to design time-variant state feedback nonuniform sampled-data stabilizers for DBCNs. In future works, we will further investigate the stabilization and synchronization of stochastic Boolean networks with state inequality constraints by establishing a new algebraic representation. It is worth pointing out that stochastic Boolean networks with state inequality constraints have more possibilities in the state transition process, which will bring greater challenges to research.