Introduction

Gamma dosimeters play a critical role in measuring and monitoring ionizing radiation levels in diverse fields. They are indispensable in fields such as radiation therapy, the nuclear industry, medical diagnostics, and environmental monitoring1. Gamma radiation detection must be precise to ensure safety and optimize its application. Conventional dosimeters based on gamma radiation-induced physical and chemical changes include thermoluminescent dosimeters and optically stimulated luminescence dosimeters. To meet the rigorous demands of modern applications, there is a growing demand for advanced dosimetric materials that exhibit higher sensitivity, precision, and reliability2.

A nanocomposite material comprises one or more nanoscale substances mixed with a bulk-phase material. Nanocomposites can be classified into three main types based on their matrix materials: ceramic matrix nanocomposites, metal matrix nanocomposites, and polymer matrix nanocomposites. A polymer or copolymer with nanoparticles or nanofillers dispersed within the polymer matrix constitutes a polymer nanocomposite. Nanocomposites, due to nanoscale fillers incorporated in a polymer matrix, have shown great promise as radiation-sensing materials because of their remarkable optical, electrical, and mechanical characteristics2,3,4.

When nanocomposites interact with gamma radiation, the polymer’s optical and structural properties, such as its absorption, photoluminescence, and refractive index, change. Due to its flexibility, chemical stability, and capacity to build nanocomposite structures, poly(ethylene oxide) (PEO), a widely studied polymer, is particularly suitable for such applications. PEO-based nanocomposites exhibit changes in optical transparency and structural organization upon gamma irradiation, enabling accurate dosimetric measurements. Owing to its exceptional properties, including chemical stability, heat resistance, and flexibility, PEO is widely used as a flexible polymer in various radiation-sensitive applications. PEO has been extensively researched for radiation-sensitive applications, such as gamma dosimeters, due to gamma radiation’s significant impact on its optical and structural properties5,6. Furthermore, thermo-sensitive polymer gels have been investigated for their gamma sensitivity. These gels exhibit property changes such as color or optical clarity in response to gamma exposure, enabling visual detection. Specifically, reversible thermo-sensitive polymer gels have been proposed to enhance superheated emulsion (bubble) detectors by extending their operational temperature range and improving their gamma response7.

Porous silicon (PSi) is a versatile material with excellent optical properties such as a large surface area, and tunable porosity. PSi is a popular choice for sensors, optoelectronics, and biomedical devices owing to these properties. PSi is highly sensitive to environmental changes, particularly to radiation effects, due to its extremely high surface-to-volume ratio. Furthermore, PSi’s refractive index modulation under gamma radiation forms the basis for its application in photonic dosimeters, which requires precise optical responses1,8,9.

Polymers and other materials can be incorporated into PSi’s matrix thanks to its unique microstructure consisting of interconnected pores9. This enhances PSi’s optical responsiveness to external stimuli. Gamma radiation exposure causes high-energy photons to interact with PSi, altering its refractive index. Ionization, atomic displacements, and changes in the dopant or infiltrating substance, like polymers, are the results of these interactions8. In PSi infiltrated with a doped polymer (PEO-based nanocomposites), the refractive index rises as gamma doses increase, indicating structural alterations and increased optical density. This characteristic is very helpful in photonic crystal structures (PhCs) that use PSi as a component layer10.

Photonic crystals are artificial periodic optical nanostructures that manipulate the propagation of electromagnetic waves by creating photonic bandgaps11,12,13,14,15,16,17. With novel optical characteristics that are extremely sensitive to radiation exposure, research in photonic structures has created new possibilities for creating gamma dosimeters with improved performance. There are several features and considerations to make while building the best PhCs as radiation dosimeters. The most important property is the material’s susceptibility to radiation. It is essential to consider the material’s sensitivity to radiation interaction18,19,20,21. Ref18. used 2D- silicon PhCs as gamma densitometry in the visible range and achieved sensitivity 150 nm/RIU. Ref22. designed PhC fiber used as radiotherapy dosimeters. According to studies, PSi-based PhCs are very effective radiation dosimeters because gamma radiation can cause alterations in their resonant wavelengths and photonic bandgap23,24. This sensitivity results from the PSi layers’ structural integrity and accurate modulation of the refractive index, even at different radiation dosages25. Ref8. investigated a 1D- defective PhC as gamma densitometry and achieved high sensitivity 205 nm/RIU.

Quasi-periodic structures have attracted significant interest in their ability to engineer wave interactions beyond the limits of periodic structures, offering unique properties like fractal bandgaps, localized states, and anomalous dispersion26,27,28,29. Recent advances in Thue-Morse, Fibonacci, and Rudin-Shapiro structures demonstrate their potential for applications in high-efficiency filters30,31,32,33,34,35, and topological photonics36. The family of photonic structures known as Thue-Morse quasi-periodic PhCs is distinguished by an aperiodic, randomized layer arrangement. In contrast to periodic or random systems, these structures display unique optical characteristics such as band gaps and localized modes. Thue-Morse PhCs are perfect for use in optical sensing because of their aperiodicity, which increases their sensitivity to outside influences37. When materials like PSi and nanocomposites are included in Thue-Morse quasi-periodic PhCs, it becomes possible to develop advanced dosimetry devices with extremely sensitive and adjustable optical responses to gamma radiation38,39,40.

In considering everything discussed above, we provide a novel theoretical study of the gamma-ray radiation dosimeter based on different structures of a 1D-quasi periodic-PhC. The structures consisted of aluminum oxide (\(\:{Al}_{2}{O}_{3}\)) as layer B and PSi infiltrated with PEO nanocomposite as layer A. These structures are five various generalized TMS (GTMS) configurations were examined throughout first, second, and third generations. The aim of studing these structures is to analyze their transmittance behavior and achieve high sensitivity with a high-quality factor for any gamma radiation dose without using defect layer. The proposed study indicate that the 3GTM(2,1) and GTMS(1,2) configurations hold strong potential for advanced radiation dosimetry applications, offering superior sensitivity and quality factors compared to many conventional designs.

Theoretical model and basic equations

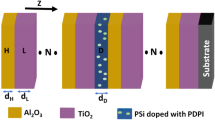
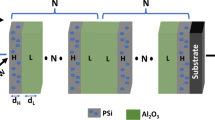
The proposed structures are mainly consisting of layer A and layer B. Layer A is \(\:PSi\) with 10% polymer nanocomposite (PEO) inside the pores, and layer B is \(\:{Al}_{2}{O}_{3}\). The thicknesses of \(\:A\) and \(\:B\) are 200 nm and 120 nm. PEO is considered the active material for gamma doses.

The following formulas (λ in µm) can be used to compute the RIs of \(\:{Al}_{2}{O}_{3}\) according to the Sellmeier equation by fitting the experimental data in Ref41., and the PSi containing \(\:\text{P}\text{E}\text{O}\:\)according to Bruggeman’s effective equations42:

$$\:n_{\text{A}\text{l}2\text{O}3}=-2.012168+\frac{\:4.352187{\lambda\:}^{2}}{{\lambda\:}^{2}-{0.045773}^{2}}+\frac{\:0.117166{\lambda\:}^{2}}{{\lambda\:}^{2}-{0.187027}^{2}}$$
(1)
$$\:{\text{n}}_{\text{P}\text{S}\text{i}}^{\:}=0.5\sqrt{{\uppsi\:}+\sqrt{{{\uppsi\:}}^{2}+8\:{\text{n}}_{\text{s}\text{i}}^{2}\:{\text{n}}_{\text{P}\text{E}\text{O}\:}^{2}}}, \:{\uppsi\:}=3\:\text{P}\:\left({\text{n}}_{\text{P}\text{E}\text{O}}^{2}-{\text{n}}_{\text{s}\text{i}}^{2}\right)+\left(2\:{\text{n}}_{\text{s}\text{i}}^{2}-{\text{n}}_{\text{P}\text{E}\text{O}\:}^{2}\right),$$
(2)

where P is the volume fraction of PEO in the PSi matrix, and \(\:{\text{n}}_{\text{S}\text{i}}^{\:}=3.7\). The RI and thermo-optic coefficient of Si is slightly affected with gamma doses up to 1000 kGy and 66.5 kGy (less than \(\:5\times\:{10}^{-5}\) and \(\:2.3\times\:{10}^{-4}\)), respectively43. Ahmed et al.44 used Monte Carlo codes to study the effect of gamma doses on Si-PhC. They found that dispersion, thermo-optic coefficient, temperature sensitivity, characteristic group index, peak center, and peak width are constant for high doses up to 1 MGy. The optical properties of \(\:{Al}_{2}{O}_{3}\) seem to be not changed by changing the gamma doses (even at 46 KGy)41. \(\:{Al}_{2}{O}_{3}\) can be stabilized with PSi45,46,47. To ensure precise and effective infiltration of polymer nanocomposites into porous silicon (PSi), several proven methods are available based on recent research. These methods vary depending on the pore size, and desired application48,49,50,51,52.

The RI of PEO can be calculated at different doses of gamma as follows (\(\:300\:\text{n}\text{m}\le\:\lambda\:\le\:800\:\text{n}\text{m},\) and \(\:\lambda\:\) should be in µm in equations)6:

At a gamma dose of 0 Gy:

$$\:{n}_{\text{P}\text{E}\text{O}\:}=-\:50.99\:{\lambda\:}^{3}\:+\:109.7{\:\lambda\:}^{2}\:-\:78.54\:\lambda\:+\:20.21$$
(3)

At a gamma dose of 100 Gy:

$$\:{n}_{\text{P}\text{E}\text{O}\:}=1267.32{\:\lambda\:}^{6}-\:4530.09\:{\lambda\:}^{5}+\:6714.24\:{\lambda\:}^{4}\:-\:5289.53{\:\lambda\:}^{3}+\:2341.49{\:\lambda\:}^{2}-\:554.456\:\lambda\:+\:61.5716$$
(4)

At a gamma dose of 200 Gy:

$$\:{n}_{\text{P}\text{E}\text{O}\:}=41.43\:{\lambda\:}^{4}\:-\:101.9{\:\lambda\:}^{3}+93.13{\:\lambda\:}^{2}-\:37.84\:\lambda\:+14.15$$
(5)

The transfer matrix method (TMM) is used to calculate the transmittance (T) of normal incident (\(\:\theta\:\:=\:0\)) transverse electric EMWs from the air passing through Thue-Morse Quasi-periodic PhC at different doses of gamma radiation as follows53,54,55,56,57,58,59,60,61:.

$$\:T\left(\%\right)=100\times\:\frac{{p}_{s}}{{p}_{0}}{\lfloor\:t\:\rfloor}^{2}$$
(6)

where,

$$\:t=\frac{2{p}_{0}}{\left({A}_{11}+{A}_{12}{p}_{s}\right){p}_{0}+\left({A}_{21}+{A}_{22}{p}_{s}\right)}$$
(7)
$$\:\left|\begin{array}{cc}{A}_{11}&\:{A}_{12}\\\:{A}_{21}&\:{A}_{22}\end{array}\right|={\left({a}_{H}{a}_{L}\right)}^{N}{\left({a}_{L}{a}_{H}\right)}^{N},$$
(8)
$$\:{p}_{i}={n}_{i}\:cos\left({\theta}_{i}\right),\:$$
(9)

where \(\:i=0\:\)(for air)\(\:,\:\text{H}\:\)(for PSi infiltrated with PEO)\(\:,\:\text{L}\:\)(for \(\:{Al}_{2}{O}_{3}\))\(\:,\text{a}\text{n}\text{d}\:\text{s}\:\left(\text{f}\text{o}\text{r}\:\text{s}\text{u}\text{b}\text{s}\text{t}\text{r}\text{a}\text{t}\text{e}\right).\) The RIs of substrate and air are 1.52 and 1, respectively.

$$\:{a}_{H}=\left[\begin{array}{cc}cos{\sigma}_{H}&\:\left(-\frac{i}{{p}_{H}}\right)sin{\sigma}_{H}\\\:-i{p}_{H}sin{\sigma}_{H}&\:cos{\sigma}_{H}\end{array}\right],$$
(10)
$$\:{a}_{L}=\left[\begin{array}{cc}cos{\sigma}_{L}&\:\left(-\frac{i}{{p}_{L}}\right)sin{\sigma}_{L}\\\:-i{p}_{L}sin{\sigma}_{L}&\:cos{\sigma}_{L}\end{array}\right],$$
(11)
$$\:{\sigma}_{H}=\frac{2\pi\:}{\lambda}{d}_{H}{n}_{H}cos{\theta}_{H}$$
(12)
$$\:{\sigma}_{L}=\frac{2\pi\:}{\lambda}{d}_{L}{n}_{L}cos{\theta}_{L}$$
(13)

Results and discussions

Figure 1a plots the refractive index of a PEO against the wavelength of light (300–800 nm) using both experimental data6 (marked as stars) and the fitted data (continuous lines) mention in Sect. 2 for varying gamma radiation dosages (0 Gy, 100 Gy, and 200 Gy). According to the agreement between experimental and fitted data, the refractive index behavior of the material at various gamma dosages is accurately predicted by the fitted model (created with MATLAB). The refractive index changes with increasing gamma radiation dose (from 0 Gy to 200 Gy), especially at shorter wavelengths. Changes in the molecular alignment of the polymer or structural density are probably the causes of the increase in refractive index with increasing gamma radiation62. Exposure to gamma radiation frequently results in cross-linking in polymer nanocomposites, which raises their density and refractive index. This behavior is in line with research on radiation-sensitive polymers and nanocomposites based on PEO63. So, this material is suited for optical sensing and dosimetry due to its sensitivity to gamma radiation, as seen by its increased refractive index at 200 Gy compared to 0 Gy.

Figure 1b shows the effect of PSi on the refractive index of the gamma-irradiated material (PEO). For PSi infiltrated with gamma-irradiated material (PEO), the Bruggeman or Maxwell-Garnett theories are frequently used to describe the refractive index as mentioned in Eq. (2). These models take into account the optical characteristics of PEO. The porous structure of PSi and the initial characteristics of the infiltrating PEO are the main factors that govern the refractive index. The refractive index fluctuation is usually more pronounced at shorter wavelengths (300–500 nm) because of larger dispersion effects. Since there is less material dispersion in the longer wavelength range, the refractive index stabilizes as the wavelength increases (beyond 600 nm), thus the impact of gamma radiation may seem less noticeable.

At 0 Gy, the refractive index shows how PSi and unirradiated PEO interact at baseline. Throughout the wavelength range, the values are comparatively constant. In comparison to 0 Gy, the refractive index rises at 100 and 200 Gy, with the effects being more pronounced at shorter wavelengths. The shift indicates gamma radiation-induced structural alterations in PEO. By comparing different doses, the shift demonstrates a dose-dependent rise in refractive index, hence validating the composite material’s gamma radiation sensitivity.

PSi containing 10% PEO is used to minimize changes in refractive index under radiation exposure. When pure PEO layers are used, the refractive index increases significantly with radiation, as clearly shown in Fig. 1(a). This causes the photonic bandgap and resonant peaks to shift markedly toward higher wavelengths, moving them outside the relevant experimental range (we can’t guess the experimental refractive index outside the range of concern). Additionally, resonant peaks originally located within the bandgap may shift out, while new peaks can appear from the lower-wavelength side—both of which are undesirable for sensing applications. We optimized the ratio of PEO in PSi by getting refractive indices that make all bandgaps (at 0 Gy, 100 Gy, and 200 Gy) inside the wavelength range of concern6.

Fig. 1
figure 1

(a) Experimental6 and fitted refractive index of PEO, and (B) refractive indices of PSi infiltrated with PEO at \(\:P=10\:\%\) at different doses.

Full size image

The following parts examine the optical properties of GTMS-based quasi-periodic PhCs for a range of generations and configurations. Five constructions are the subject of the study: GTM(1,1), GTM(2,1), GTM(3,1), GTM(1,2), and GTM(1,3). The structural design and associated transmittance spectra of each building are examined at different dosages of gamma radiation (0 Gy, 100 Gy, and 200 Gy). For every configuration, the analysis is separated into two main parts: (1) the PhC construction, which describes the alternating layer arrangement, and the quasi-periodic sequence used, and (2) the transmittance spectra, which shows the evolution of the photonic bandgap and its sensitivity to changes in the refractive index caused by gamma radiation. The optical behavior of these structures is further clarified by the generational analysis (first, second, and third) that shows the effects of growing quasi-periodicity. The goal of this methodical technique is to determine the ideal mix of material layers and quasi-periodic order to produce the most flexible and sensitive PhC design for gamma dosimetry applications.

The recursive relation can be defined as: \(\:{S}_{q}={S}_{q-1}^{m}{\stackrel{-}{S}}_{q-1}^{n}\:\)for \(\:q\ge\:1\) (integer). For GTMS (m=1, n=1), the initial sequences being \(\:{\:S}_{0}=A\) and\(\:\:{S}_{1}=AB\)30,64,65, where m and n are the successive repetitions of the sequences with m = 1 and n = 1. For the second sequence, \(\:{S}_{2}={S}_{1}^{1}{\stackrel{-}{S}}_{1}^{1}=2\text{G}\text{T}\text{M}\:\left(1,\:1\right)=ABBA\). On the other hand, the third sequence can be represented as\(\:{\:S}_{3}={S}_{2}^{1}{\stackrel{-}{S}}_{2}^{1}=3\text{G}\text{T}\text{M}\:\left(1,\:1\right)=ABBABAAB\), etc. For simplicity, each \(\:A\) is converted to \(\:AB\), and each \(\:B\) is converted to \(\:BA\).

For GTMS (2, 1), the initial sequences being \(\:{\:S}_{0}=A\)and\(\:\:{S}_{1}=AAB\). For the second sequence, \(\:{S}_{2}={S}_{1}^{1}{\stackrel{-}{S}}_{1}^{1}=2\text{G}\text{T}\text{M}\:\left(2,\:1\right)=AABAABBAA\). On the other hand, the third sequence can be represented as\(\:{\:S}_{3}={S}_{2}^{1}{\stackrel{-}{S}}_{2}^{1}=3\text{G}\text{T}\text{M}\:\left(2,\:1\right)=AABAABBAABAAAABAAB\), etc. For simplicity, each \(\:A\) is converted to \(\:AAB\), and each \(\:B\) is converted to \(\:BAA\).

For GTMS (3, 1), the initial sequences being \(\:{\:S}_{0}=A\)and\(\:\:{S}_{1}=AAAB\). For the second sequence, \(\:{S}_{2}={S}_{1}^{1}{\stackrel{-}{S}}_{1}^{1}=2\text{G}\text{T}\text{M}\:\left(3,\:1\right)=\) AAABAAABAAABBAAA. On the other hand, the third sequence can be represented as \(S_{3}=S_{2}^{1}\bar{S}_{1}^{2}= \:3{\rm GTM \:(3,1)}=\) AAABAAABAAABBAAAAABAAABAAABBAAAAAABAAABAAABBAAABAAAAAAABAAABAAAB, etc. For simplicity, each \(\:A\) is converted to \(\:AAAB\), and each \(\:B\) is converted to \(\:BAAA\). We selected five GTMS configurations to evaluate the impact of increasing quasi-periodicity and dielectric contrast on dosimeter sensitivity and quality. The following study is limited to theoretical modeling, and further experimental validation is required to confirm the observed sensitivity trends under real-world conditions.

GTM(1,1)

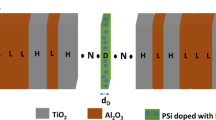
The GTMS (1,1) quasi-periodic PhCs for the following four generations: zeroth (0 GTM(1,1)), first (1 GTM(1,1)), second (2 GTM(1,1)), and third (3 GTM(1,1)) are constructed in Fig. 2. The structure is built on alternating layers, A and B, where layer A is PSi infiltrated with PEO, and layer B is made of \(\:{Al}_{2}{O}_{3}\). The most basic structure is the zeroth generation (Fig. 2a), which comprises just one layer of material A. The sequence changes according to the recursive Thue-Morse rule, which states that each sequence is created by attaching the complement of the one before it, as the generation order rises. In the first generation (Fig. 2b), for example, layers A and B alternate, whereas in the second generation (Fig. 2c), the structure is extended by repeating the pattern in a quasi-periodic fashion as follows: ABBA. The third generation (Fig. 2d) adds even more complexity, making the layer arrangement more complex (ABBABAAB). One essential feature of Thue-Morse quasi-periodicity is the hierarchical sequence generation, which adds special optical features including numerous photonic band gaps and improved tunability.

Depending on the structural complexity, the photonic bandgap properties are generated by the interaction of low-refractive-index (\(\:{Al}_{2}{O}_{3}\)) and high refractive-index (PSi + PEO). Quasi-periodic ordering improves light localization and adds special optical characteristics, which makes these PhCs perfect for gamma dosimetry and other applications requiring accurate light manipulation66.

Fig. 2
figure 2

GTMS (1,1) quasi-periodic PhC using layer A (\(\:PSi\) infiltrated by PEO) and layer B (\(\:{Al}_{2}{O}_{3}\)) (a) zeroth, (b) first, (c) second, and (d) third generations.

Full size image

Figure 3a-c studies the transmittance spectra \(\:1{\text{G}\text{T}\text{M}\left(\text{1,1}\right)}^{4}\), \(\:2{\text{G}\text{T}\text{M}\left(\text{1,1}\right)}^{2}\) and 3GTMS (1,1) structures under gamma radiation (0 Gy, 100 Gy, and 200 Gy) doses in range (500–800 nm) wavelength. The superscripts (4 and 2) in these structures donate to the repetitions of the GTMS (1,1) unit cell. Figure 3a-c illustrates how the quasi-periodic layer arrangement affects the PhC’s optical characteristics with the GTMS (1,1) structures. Interference and creation of a photonic bandgap are caused by changes between refractive-index materials (PSi infiltrated with PEO and \(\:{Al}_{2}{O}_{3}\)). The high refractive index contrast between PSi infiltrated with PEO and \(\:{Al}_{2}{O}_{3}\)made them suitable for creating photonic bandgaps. The spectral response of the PhC becomes more complex as the quasi-periodic order increases gradually from one to third generation. In higher generations, the position, width, and quantity of photonic bandgaps are directly influenced by the increased layer thickness and improved structural symmetry. Since the refractive index of PSi and PEO layers is sensitive to radiation exposure, this hierarchical design is especially useful for applications like gamma dosimetry. Therefore, by examining their transmittance spectra, the different optical characteristics of these structures can be used to detect and measure gamma radiation.

Figure 3a shows the transmittance of the first generation of the GTMS (1,1) structure which is repeated four times. Because there are fewer layers and a simpler structure, the bandgap is comparatively narrow. Due to gamma-induced modifications in the refractive indices of the component materials, a small redshift of the bandgap is seen at 100 Gy. At 200 Gy, the redshift increases, and the bandgap’s depth increases, suggesting radiation-induced defects and degeneration in the structural homogeneity. Figure 3b shows the transmittance of the second generation of the GTMS (1,1) structure which is repeated two times. It is noted that the resonance peak appears and is like a defect mode. This behavior reflects the increased structural complexity and sensitivity to changes in refractive index brought on by gamma radiation. With an increase in the gamma dose from 0 Gy to 200 Gy, the resonance peak shifts to higher wavelengths from 549.95 nm to 620.37 nm with a high intensity of approximately (95%), respectively. Figure 3c shows the most intricate transmittance spectra of the third generation of the GTMS (1,1) characterized by the localized defect mode at higher wavelengths compared to the second generation in Fig. 3b. A defect mode appears at 619.42 nm with intensity (72.84%) at 0 Gy gamma irradiation dose. Once, increased to 100 Gy, and 200 Gy, the defect mode appears at 673.61 nm, and 687.68 nm with intensity (72.77%, and 76.04%), respectively.

These data demonstrate that as quasi-periodicity increases, sensitivity to gamma radiation gradually improves. The interaction between material sensitivity and quasi-periodic ordering highlights the promise of PhCs based on GTMS in radiation dosimetry and other optical applications.

Fig. 3
figure 3

Transmittance for GTM (1,1) quasi-periodic PhC sequences; (a) \(\:1{\text{G}\text{T}\text{M}\left(\text{1,1}\right)}^{4}\), (b) \(\:2{\text{G}\text{T}\text{M}\left(\text{1,1}\right)}^{2}\), and (c) 3GTM (1,1), at different gamma doses.

Full size image

GTM(2,1)

In this section, using the two layers of type A (PSi + PEO) and one layer of type B (\(\:{Al}_{2}{O}_{3}\)) the GTMS (2,1) sequence is built according to the Thue-Morse quasi-periodic rule as shown in Fig. 4a-d. As the most basic building block, the zeroth-generation structure starts with a single (A) layer. The first generation’s expansion of the sequence is (AAB). The second generation uses the replacement rule to create (AABAABBAA), and the third generation changes the sequence to (AABAABBAAAABAABBAABAAAABAAB). By altering the refractive index contrast and quasi-periodicity of the system, these designs introduce a distinctive spatial arrangement of dielectric materials that have a major impact on the optical properties.

Compared to GTMS(1,1), this hierarchical structure offers a clear advantage in managing photonic bandgaps. Controlling light propagation depends heavily on the layered configuration of GTMS(2,1) across generations, especially in photonic systems exposed to external influences such as gamma radiation.

Fig. 4
figure 4

GTMS (2,1) quasi-periodic PhC using layer A (PSi infiltrated by PEO) and layer B (\(\:{Al}_{2}{O}_{3}\)) (a) zeroth, (b) first, (c) second, and (d) third generations.

Full size image

Figure 5a–c shows the transmittance spectra of GTMS(2,1) structures for the first, second, and third generations with different repeated unit cells at gamma doses of 0 Gy, 100 Gy, and 200 Gy. Due to their intricate quasi-periodic sequences and light interactions with alternating layer types, these generations exhibit distinct optical properties. Figure 5a presents the transmittance spectra for the first generation, \(\:1{\text{G}\text{T}\text{M}\left(\text{2,1}\right)}^{4}\), revealing a single major photonic bandgap between 613.60 nm and 646.08 nm. The \(\:1{\text{G}\text{T}\text{M}\left(\text{2,1}\right)}^{4}\) structure shows a major photonic bandgap that broadens and redshifts with increasing gamma doses due to radiation-induced changes in the refractive index of PSi/PEO. Compared to \(\:1{\text{G}\text{T}\text{M}\left(\text{1,1}\right)}^{4}\), the bandgap in \(\:1{\text{G}\text{T}\text{M}\left(\text{2,1}\right)}^{4}\) occurs at a longer wavelength, changes in the optical properties of the constituent layers.

Figure 5b shows the transmittance of the second generation repeated two times unit cell (\(\:2{\text{G}\text{T}\text{M}\left(\text{2,1}\right)}^{2}\)). The sequences of this generation are more complicated than the first generation, leading to an increase the interferences. This leads to the formation of the localized defect mode with high intensity and sharpness. By comparing this structure with the before structure \(\:2{\text{G}\text{T}\text{M}\left(\text{1,1}\right)}^{2}\), we noticed that the current structure (\(\:2{\text{G}\text{T}\text{M}\left(\text{2,1}\right)}^{2}\)) gave resonance peak (like defect mode) with high intensity and more sharpener. For the effect of gamma-ray radiation (from 0 Gy to 200 Gy) on the defect mode, the defect mode shifts to a higher wavelength with high intensity. This indicates that gamma radiation enhanced the refractive index of layer A, enhanced the contrast between layer A and dielectric layer B, and reflected in the transmittance spectra of this structure.

Figure 5c shows the transmittance of the third generation 3GTM (2,1). This generation is a highly complicated quasi-structure, leading to stronger interferences and creating highly localized defect modes more sensitive to any dose of gamma-ray radiation. At 0 Gy, the defect mode appears at 516.19 nm with intensity reaching 100%. Once the gamma dose is applied, this defect mode shifts at more distance of wavelengths (Ex; 570.88 nm, and 586.89 nm at 100 Gy, and 200 Gy, respectively. This behavior is based on the higher refractive index of layer A (PSi infiltrated with PEO) increases the strength of the localization and the path length. In addition, the intensity of this defect mode decreases (to 77.55%, and 67.27%) by increasing the gamma-ray doses (100 Gy, and 200 Gy), respectively. As gamma doses increase, the intensity of light transmitted through the defect mode decreases, primarily due to the combined effects of absorption, scattering, and alterations in the refractive index. Besides, increasing the thickness of photonic crystal multilayer films typically reduces transmittance due to enhanced interference, stronger absorption, and more pronounced photonic bandgaps67,68,69,70. This indicates that this structure is highly sensitive to any optical properties’ changes in the structure. Compared to the third-generation structure 3GTM (1,1) discussed in the previous section, the 3GTM (2,1) structure is better suited for use as a gamma dosimeter. This is due to its highly localized defect mode, which exhibits significant sensitivity to variations in gamma-ray radiation doses.

Fig. 5
figure 5

Transmittance for GTM (2,1) quasi-periodic PhC sequence; (a) \(\:1{\text{G}\text{T}\text{M}\left(\text{2,1}\right)}^{4}\), (b) \(\:2{\text{G}\text{T}\text{M}\left(\text{2,1}\right)}^{2}\), and (c) 3GTM (2,1), at different gamma doses.

Full size image

GTM(3,1)

Figure 6a-d shows the construction of the quasi-periodic GTM(3,1) in the zeroth, first, second, and third generation. The zeroth generation comprises just one layer A. This is the most basic version of the GTMS(3,1) structure, devoid of periodicity and layering. The first generation comprises one B layer after three A layers. The setup is as follows: AAAB. The first-generation structure was repeated to develop the second generation, which had a more intricate arrangement. It comprises several A and B layers arranged as follows: AAABAAABAAABBAAA. By further repeating the second-generation pattern, the third generation is created, which results in an extremely complex layer sequence: (.AAABAAABAAABBAAAAAABAABAAABBAAAAABAAABAAABBAAABAAAAAABAAABAAAB). This configuration adds a great deal of complexity and strengthens the optical interactions inside the structure.

Fig. 6
figure 6

GTMS (3,1) quasi-periodic sequences using layer A (PSi infiltrated by PEO) and layer B (\(\:{Al}_{2}{O}_{3}\)) (a) zeroth, (b) first, (c) second, and (d) third generations.

Full size image

Figure 7a-c shows the transmittance spectra of GTMS(3,1) structures are examined for first, second, and third generations with different repeated unit cells at different gamma doses (0 Gy, 100 Gy, and 200 Gy(. Figure 7a shows the transmittance of the first generation of GTMS(3,1) which repeated four times (\(\:1{\text{G}\text{T}\text{M}\left(\text{3,1}\right)}^{4}\)). This configuration gives a broadened band gap before the effect of gamma-ray radiation (0 Gy). Comparing this structure (\(\:1{\text{G}\text{T}\text{M}\left(\text{3,1}\right)}^{4}\)) with the first generation of the before structures (\(\:1{\text{G}\text{T}\text{M}\left(\text{1,1}\right)}^{4}\)) and (\(\:1{\text{G}\text{T}\text{M}\left(\text{2,1}\right)}^{4}\)), we found that this structure gives a broader band gap at longer wavelengths. The reason behind that is related to the high complexity of this structure and the increase in the number of A layers, which increased the number of interferences and enhanced the optical properties of this structure. Besides, increasing the number of successive layers of A increases the thickness. According to the quarter-wavelength condition (\(\:nd=\lambda\:/4\))71, the central wavelength of the band gap (\(\:\lambda\:\)) is directly proportional to the thickness of layers.

At 100 Gy, the band gap shifts to lower wavelengths, and at 100 Gy, the band gap shifts again to higher wavelengths but less than the band gap at 0 Gy. This behavior is due to the complexity of this structure.

The transmittance of the second-generation structure, which is repeated two times (\(\:2{\text{G}\text{T}\text{M}\left(\text{3,1}\right)}^{2}\)), is shown in Fig. 7b. This structure shows a high sharpener band gap and is like (two localized defect modes) at 0 Gy. This band gap gives the same behavior as the (\(\:1{\text{G}\text{T}\text{M}\left(\text{3,1}\right)}^{4}\)) at 100 Gy and 200 Gy. The transmittance of the third-generation structure (3GTM(3,1)) gives several localized defect modes at each gamma radiation dose, as shown in Fig. 7c. While GTM(3,1) exhibits improved light localization, it is not suited for use as a gamma dosimeter due to its high density of defect modes. When exposed to gamma rays, the structure should show a single, distinct defect mode with a notable intensity shift for gamma dosimetry applications. However, several localized defect modes in GTM(3,1) make it more difficult to analyze gamma-radiation-induced transmittance variations. Because of the numerous modes, it is more difficult to observe changes in position or intensity caused by radiation, which makes this structure less useful for sensing purposes.

Fig. 7
figure 7

Transmittance for GTM(3,1) quasi-periodic PhC sequence; (a) \(\:1{\text{G}\text{T}\text{M}\left(\text{3,1}\right)}^{4}\), (b) \(\:2{\text{G}\text{T}\text{M}\left(\text{3,1}\right)}^{2}\), and (c) 3GTM(3,1), at different gamma doses.

Full size image

GTM(1,2)

In this section, the study depends on the increase of dielectric layers B rather than layer A. Figure 8a-d shows the construction of the GTMS(1,2) in the zeroth, first, second, and third generation. As is known, the zeroth generation is the simplest structure with no periodicity and consists of a single layer A. For the arrangements layer of the first generation will be one layer of A followed by two layers of B (ABB). By applying a quasi-periodic rule to the first-generation structure, the second generation is created. The layers are set up as follows: ABBBBABBA. With more B-layers than A-layers, this structure adds a greater degree of quasi-periodicity. The quasi-periodic arrangement is further extended in the third generation, resulting in a more intricate structure with the layer sequence as follows: ABBBBABBABBABBAABBBBABBAABB. More layers and complex arrangement enhance the creation of photonic bandgaps and interference effects.

In the GTMS(1,2) structures, the proportion of A-layers to B-layers is 2:1. The transmission spectra are considerably impacted by this enhanced B-layer presence in the following ways:

Fig. 8
figure 8

GTMS(1,2) quasi-periodic sequences using layer A (PSi infiltrated by PEO) and layer B (\(\:{Al}_{2}{O}_{3}\)) (a) zeroth, (b) first, (c) second, and (d) third generations.

Full size image

The 1GTM(1,2) structure is repeated four times in this arrangement. As illustrated in Fig. 9a, the transmittance spectra at gamma dosages of 0 Gy, 100 Gy, and 200 Gy indicate a distinct principal photonic bandgap. Because of the higher dielectric homogeneity caused by the greater number of B-layers, the principal photonic bandgap is wider. Gamma-induced changes in the A-layer’s refractive index cause the bandgap to slightly redshift at larger doses. Changes in the A-layer refractive index cause redshifts in the bandgap for gamma dosages of 0 Gy, 100 Gy, and 200 Gy. Nevertheless, these shifts are not as noticeable as in structures with fewer B-layers. Comparing between the structures \(\:1{\text{G}\text{T}\text{M}\left(\text{1,2}\right)}^{4}\), and \(\:1{\text{G}\text{T}\text{M}\left(\text{2,1}\right)}^{4}\), Wider bandgaps that are less sensitive to small variations in refractive index are the result of the increased B-layers, which also improve transmittance stability across the bandgap. For \(\:1{\text{G}\text{T}\text{M}\left(\text{2,1}\right)}^{4}\), the increased number of layers A enhanced the refractive index contract and the structure more sensitive to gamma-ray radiation. Wider photonic bandgaps that are less sensitive to small variations in refractive index are the result of the increased B-layers, which also improve transmittance stability across the bandgap.

Figure 9b, shows the transmittance spectra of \(\:2{\text{G}\text{T}\text{M}\left(\text{1,2}\right)}^{2}\) which repeated two times in this arrangement. This structure produces clear, easily monitored localized fault modes, which are essential for gamma sensing. Changes in the A-layer refractive index cause redshifts in the defect modes for gamma dosages of 0 Gy, 100 Gy, and 200 Gy. Nevertheless, these shifts are not as noticeable as in systems with fewer B-layers. If we compare this structure with \(\:2{\text{G}\text{T}\text{M}\left(\text{1,2}\right)}^{2}\) with \(\:2{\text{G}\text{T}\text{M}\left(\text{2,1}\right)}^{2}\), the defect modes are sharper and more sensitive to gamma-ray radiation in \(\:2{\text{G}\text{T}\text{M}\left(\text{2,1}\right)}^{2}\).

Without repetition, the third-generation structure is depicted in Fig. 9c, which displays transmittance spectra with a low-intensity (65.61%) localized defect mode at 0 Gy. The structural changes induced by gamma radiation are reflected in the defect modes’ shift to longer wavelengths and increase in intensity to (88.18%, and 95.36%) when the gamma dose rises to 100 Gy and 200 Gy, respectively.

Fig. 9
figure 9

Transmittance for GTM(1,2) quasi-periodic PhC sequence; (a) \(\:1{\text{G}\text{T}\text{M}\left(\text{1,2}\right)}^{4}\), (b) \(\:2{\text{G}\text{T}\text{M}\left(\text{1,2}\right)}^{2}\), and (c) 3GTM (1,2), at different gamma doses.

Full size image

GTM (1,3)

As in all sections before, we analyze new structure from quasi-periodic (GTM(1,3)) in which the ratio of layers (1 A:3B). Figure 10a-d shows the construction of this structure in the zeroth, first, second, and third generation. The first generation presents a simple quasi-periodic sequence with three B-layers after one A-layer: ABBB. By repeating the first-generation pattern into a more intricate sequence, the second generation expands the structure: ABBBBBBABBBABBBA. This configuration results in more interfaces and a significant dielectric contrast by increasing the dominance of B-layers. The third generation builds on the second-generation sequence, generating a highly complex structure with many more layers: ABBBBBBABBBABBBABBBABBBABBBAABBBBBBABBBABBBAABBBBBBABBBABBBAABBB. This complex arrangement results in a highly varied photonic response by increasing the number of contacts and enhancing interference effects.

Fig. 10
figure 10

GTMS(1,3) quasi-periodic sequences using layer A (PSi infiltrated by PEO) and layer B (\(\:{Al}_{2}{O}_{3}\)) (a) zeroth, (b) first, (c) second, and (d) third generations.

Full size image

The transmittance spectra of the first generation which was repeated four times at 0 Gy, 100 Gy, and 200 Gy shown in Fig. 11a-c. At 0 Gy, the band gap with very low width and less intensity appears in Fig. 11a. The reason behind this behavior is the lower number of layers A compared to the increased number of layers B. At higher doses (100 Gy, and 200 Gy) the refractive index of layers A increased and led to an increase in the width of the band gap and shifted to higher wavelengths. In the second generation which was repeated two times, the defect mode appeared with high intensity (95.50%) at a wavelength (606.75 nm) at 0 Gy, as shown in Fig. 11b. By increasing the gamma dose to 100 Gy and 200 Gy, the defect mode shifts to higher wavelengths (647.10 nm, and 659.79 nm) and becomes a sharpener with stability in the intensity (≈ 95%). The single generation 3GTM(1,3) structure exhibits complicated transmittance spectra due to multiple interferences between large numbers of layers. As shown in Fig. 11c, the defect mode appears at wavelength (511.41 nm) with low intensity (39.68%). The defect mode shifts toward longer wavelengths and highly decreases in intensity (14.80%, and 5.38%) when the gamma dose increases to 100 Gy and 200 Gy because of changes in the refractive index and scattering effects.

In conclusion from this section, increases in layer B relative to layer A led to a decrease in the refractive index contrast between the two layers, which broadens the band gap, small red shift to a higher wavelength, and lowers the intensity of the defect modes.

Fig. 11
figure 11

Transmittance for GTM(1,3) quasi-periodic PhC sequence; (a) \(\:1{\text{G}\text{T}\text{M}\left(\text{1,3}\right)}^{4}\), (b) \(\:2{\text{G}\text{T}\text{M}\left(\text{1,3}\right)}^{2}\), and (c) 3GTM(1,3), at different gamma doses.

Full size image

Sensitivity and quality factor (Q-factor) are two important factors used to assess the performance of quasi-periodic PhCs for gamma dosimetry. Sensitivity, which measures how well the structure senses changes in refractive index caused by radiation, is defined as the shift in defect mode wavelength (Δλ) per unit gamma dose. The Q-factor, which is defined as \(\:Q=\:\lambda\:/FWHM\), where \(\:\lambda\:\) is the resonant wavelength and FWHM is the full-width at half-maximum of the defect mode, indicates how well-localized a defect mode is. The sensitivity and Q-factor of the many different structures show distinct variations in the second and third generations in the two ranges of gamma doses (0–100 Gy, and 100–200 Gy) as shown in Table 1. Sensitivity and Q-factor are exchanged off in the study of various structures. The structures with high Q-values typically have lesser sensitivity.

Out of all the structures that were examined, \(\:2{\text{G}\text{T}\text{M}\left(\text{2,1}\right)}^{2}\)and 3GTM(2,1) had remarkably high Q-factors (892.2 and 1715.9, respectively) and a moderate sensitivity of 0.55 nm/Gy. Sharp and well-localized defect modes are indicated by these high Q-values, which are advantageous for accurate wavelength identification. Nevertheless, structures from GTMS(1,3), especially 3GTM(1,3), have the highest Q-factor (1929), but their poor defect mode response to radiation results in a relatively low sensitivity of 0.15 nm/Gy, making them less appropriate for gamma sensing.

However, the GTMS(1,2) structures, especially\(\:2{\text{G}\text{T}\text{M}\left(\text{1,2}\right)}^{2}\), provide a better-balanced performance with an appropriately high Q-factor of 473 and S = 0.5 nm/Gy. In comparison to higher-order structures, this equilibrium maintains better sensitivity while maintaining effectively acute defect modes. In comparison, 3GTM(1,2) shows a considerable performance trade-off with a lower Q-factor (414.8) and a little lower sensitivity (0.49 nm/Gy).

All things considered, \(\:3\text{G}\text{T}\text{M}\left(\text{2,1}\right)\), and 2GTM(1,2) are the best-performing structures for gamma dosimetry because they offer the best sensitivity and Q-factor balance, ensuring significant and apparent changes in the defect mode while preserving sufficient sharpness for accurate dose measurements.

Structures with too low Q-value, such 3GTM(1,1) (Q = 33.8), lack spectral resolution for accurate detection, whereas structures with too high a Q-value, like 3GTM(1,3), are less useful because of their low sensitivity. Consequently, the best option for gamma dosimetry applications are \(\:3\text{G}\text{T}\text{M}\left(\text{2,1}\right)\), and \(\:2{\text{G}\text{T}\text{M}\left(\text{1,2}\right)}^{2}\).

Table 1 Sensitivity, and quality factor of the different quasi-periodic phcs.
Full size table

As indicated in Table (2), the performance of the proposed GTMS-based quasi-periodic PhCs as gamma dosimeters is compared with previously published structures in the field of research. In contrast, our \(\:3\text{G}\text{T}\text{M}\left(\text{2,1}\right)\), and GTMS(1,2)-based structures maintain great sensitivity and flexibility under gamma irradiation while offering more stable and well-defined defect modes. These findings demonstrate that the \(\:3\text{G}\text{T}\text{M}\left(\text{2,1}\right)\), and GTMS(1,2) configuration are promising candidates for advanced radiation dosimetry applications since they perform better in terms of sensitivity and quality factors than many traditional designs.

Table 2 Evaluation of different gamma sensors:.
Full size table

Conclusion

In this study, we evaluated the viability of many quasi-periodic PhC structures depending on the GTMS as gamma dosimeters by designing and analyzing them. To verify the optical response of the structures, fitting equations for experimental data were included in the theoretical calculations based on the transfer matrix method. A thorough evaluation of the impact of structural complexities on radiation sensitivity, defect mode creation, and transmittance spectra has been performed. The structures were made of aluminum oxide as layer B and PSi injected by PEO nanocomposite as layer A. The best configurations for gamma dosimetry among the configurations under study were 3GTM(2,1) and \(\:2{\text{G}\text{T}\text{M}\left(\text{1,2}\right)}^{2}\). With a sensitivity of 0.55 nm/Gy and a quality factor of 1715.9, 3GTM(2,1) showed remarkably strong defect mode localization, which qualifies it for extremely sensitive detection. With a sensitivity of 0.5 nm/Gy and a quality factor of 473, \(\:2{\text{G}\text{T}\text{M}\left(\text{1,2}\right)}^{2}\)demonstrated a well-balanced performance that makes it extremely useful for gamma-sensing applications. The suggested designs offer better sensitivity, tunability, and defect mode stability than traditional dosimeters described in the comparsion. Future studies will concentrate on investigating substitute materials with distinct optical characteristics and examining more quasi-periodic structures to boost sensitivity and enhance the tunability of defect modes in order to better optimize the performance of GTMS-based PhCs. The goal of these efforts is to improve theoretical models and find setups that optimize photonic structures’ gamma radiation sensitivity.