The regulation scheme of a double-rotor wind turbine during operation based on the transmission modes of rotors

Abstract

Current research on double-rotor wind turbines (DRWT) primarily focuses on aerodynamic performance and wake characteristics. Addressing the specific control challenges during operation, this study first establishes a geometric model of the Counter-rotating Double-Rotor Wind Turbine (C-DRWT) and an integrated drivetrain model from the dual rotors to the gearbox. Subsequently, based on the structural characteristics of C-DRWT and its operational wind speed range, three gearbox operating modes and three transmission configurations for the dual rotors are defined under necessary assumptions (e.g., assuming power/torque/speed parameters of both rotors remain below rated values). Finally, utilizing parameters from the NREL 5 MW reference wind turbine, torque-speed characteristic curves for three operational phases of C-DRWT are calculated and established. With power optimization as the control objective, the control strategies and detailed implementation schemes for each operational phase are elucidated through specific wind speed examples. The analysis demonstrates that C-DRWT can extend the effective operational wind speed range, thereby reducing downtime and lowering energy costs. This theoretical framework provides strategic guidance and operational protocols for practical implementation of C-DRWT systems.

Introduction

In recent decades, wind power technology has developed rapidly, and new types of wind turbines have emerged continuously. From the initial small single-rotor wind turbine (SRWT)¹ to the recent high-power wind turbines that are capable of generating tens of megawatts², the scale of wind turbines is ever-growing. Consequently, two intractable problems have arisen: the difficulty in blade manufacturing and transportation caused by the increases in blade lengths, and the sharp decrease in the life of the gearbox resulting from the excessive stress on key parts of the gearbox^3,4.

To resolve the above problems related to SRWTs, wind power companies such as MAAG and BOSCH have applied power distribution technology to the gearboxes of large wind turbines⁵. In this way, the huge torque transmitted by the rotor can be reduced into two parts, and then are combined before being transmitted to the parallel gear stage, which reduces about half of the stress on the planetary gear and its bearings⁶. However, this resolution is not convenient for manufacturing, installation, transportation, and maintenance of the blades.

The Key Research Laboratory of Advanced Materials in Tsinghua University has designed a novel folding blade consisting of two parts: a root blade fixed on the rotor hub and a top blade connected with the root blade through a hinge⁷. While, in the double-rotor turbine with wind or hydraulic proposed by Nomesh technologies⁸, the double-rotor is used as two inputs, and the power transmitted by the two rotors is combined with the differential planetary stage and then transmitted to the generator.

This development provides viable solutions to two major challenges in megawatt-scale wind turbines: (1) the manufacturing, transportation, and installation difficulties caused by the dramatic increase in blade length, and (2) the high gearbox failure rates resulting from substantial input torque. Building on this concept, this paper proposes a contra-rotating dual-rotor wind turbine (C-DRWT) structure, comprising an upwind rotor (UR) and a downwind rotor (DR). The downwind rotor is mounted on a support frame located in the peripheral annular region of the upwind rotor’s swept area to minimize or avoid the wake effects from the upwind rotor.

Double-rotor wind turbines (DRWTs)

There have been many studies on the double-rotor wind turbines (DRWTs). Researchers from Iowa State University⁹ studied the aerodynamic and wake characteristics of a two-rotor wind turbine. It was concluded that the power output and the wind load on the blades of DRWT are both higher than those of the traditional SRWT at the same condition. Wang et al.¹⁰ carried out an experimental analysis on the aerodynamic performance of the DRWT. The results showed that the wind load of the co-rotating DRWT (CO-DRWT) was higher than that of counter-rotating (CR-DRWT), which could generate 7.2% more power than the CO-DRWT. Wei Cai et al.¹¹ developed a mechanical model of a DRWT and proposed a novel cross-coupling control strategy. They investigated the influence of blade pitch angle and rotor speed on the power output of the DRWT. Simulation experiments demonstrated that the proposed control strategy could effectively optimize the power generation performance of the DRWT. Thomas Amoretti and other scholars¹² also studied the power generation of dual-rotor wind turbines and through blade element momentum (BEM) theory models, demonstrated that dual-rotor wind turbines generate 10.6% more electricity compared to single-rotor wind turbines. Scholars at City University of Hong Kong¹³ studied the wake characteristics of the vertical axis wind turbine (VAWT); they found that the wake of a counter-rotating VAWT was symmetric. Yang et al.¹⁴ proposed the layout criterion of double rotors based on different requirements in practice after studying the relative position relationship between the two rotors in a DRWT.

The aforementioned research primarily focuses on the aerodynamic performance, wake characteristics, and dual-rotor configuration of DRWTs, emphasizing their advantages over SRWTs (Single-Rotor Wind Turbines) in terms of power generation capacity. However, these studies do not directly address the drivetrain or gearbox of DRWTs, nor do they reveal or propose detailed operational control strategies for DRWTs during operation (e.g., blade pitch angle, rotor speed, and tip-speed ratio). Yet, these factors are critical for the stable operation and efficient power generation of DRWTs. Currently, most research on wind turbine operation and control strategies is tailored to SRWTs, where the technology has already matured significantly.

The regulation and control schemes of SRWTs

There have been many studies on the regulation schemes and control processes of SRWTs^15,16,17. Based on the control objectives, the operation region can be divided into three parts¹⁸, as shown in Fig. 1. In region 1, the wind turbine is shutdown beneath the cut-in wind speed. In region 2, the maximum power absorption is realized by controlling the rotational speed of the rotor when the wind speed is between the cut-in and the rated speeds. In region 3, the objective is to stabilize the output power near the rated power by adjusting the blade pitch angle and the generator torque when the wind speed is between the rated and cut-out speeds.

Fig. 1

The operation region of SRWT.

Research on the operation and regulation of wind turbines has mainly focused on the control of the blade pitch angle and power. Chen et al.¹⁹ proposed an adaptive control method of the pitch angle, which was verified by simulation experiments. Allah Rakhio Junejo et al.²⁰ designed a power controller for a vertical-axis wind turbine (VAWT) and demonstrated that it could achieve a 25% higher power output compared to conventional controllers. A control method of the active power was proposed²¹ that has been proven to be effective by FAST (Fatigue, Aerodynamics, Structures, and Turbulence) model. Yan et al.²² established a probabilistic model for the power curve of wind turbine based on Monte Carlo, neural network and fuzzy clustering methods. The results showed that fuzzy clustering was superior to other methods. The scholars at Politecnica University²³ also carried out the control problem of the blade pitch angle after the wind speed was higher than the rated speed. Xu et al. in the Hong Kong Polytechnic University²⁴ designed a pitch angle controller. They verified the correctness of the proposed method through wind tunnel experiments.

To address the design deficiencies in DRWTs, R. Bontempo et al.²⁵ proposed an innovative design strategy for contra-rotating wind turbines. This approach optimizes the blade geometry of both rotors while explicitly accounting for the mutual wake interference between them, ultimately maximizing the overall power output of the system. Errami et al.²⁶ studied all the operating regions of direct-driven wind turbines and proposed a nonlinear push-back control strategy. Mostafa et al.²⁷ presented the operating range of the horizontal axis wind turbine with variable speed and pitch. They proved that the proposed control strategy was superior to the traditional control strategy by simulation experiments. An integral adaptive sliding mode controller was designed²⁸ that could maintain the maximum power output at the optimal speed of the wind turbine. Various other studies based on the maximum power outputs of wind turbines by different technologies have been conducted^29,30,31.

The above studies focused on the operation and control of SRWTs, as described by Amira Elkodama et al. in Reference ³² regarding several advanced control methods for wind turbines (classical, soft computing, and artificial intelligence (AI)), soft computing control algorithms—such as fuzzy logic control (FLC), sliding mode control (SMC), and maximum power point tracking (MPPT)—can achieve 5% higher power output in small-scale wind turbines and 2% higher power output in megawatt-scale turbines compared to traditional control methods in blade pitch and yaw control applications.

Similar problems exist for C-DRWTs, such as, the regulation scheme, the operation, and the transmission modes; however, there have been few studies investigating the regulation schemes of C-DRWTs. Due to the structural characteristics of C-DRWTs, the operation and regulation of SRWTs cannot be directly applied in C-DRWTs. Instead, it is necessary to have corresponding regulation schemes for different transmission modes. In this paper, regulation schemes for C-DRWTs under different transmission modes are proposed and analyzed, which provides a framework for further research on the control process of C-DRWTs.

The main contents of this paper are as follows. The second section is the introduction and analysis of the structural characteristics of the C-DRWT. Based on the characteristics of the transmission system, three transmission modes of the double rotor under three working patterns of the gearbox are discussed. The third section analyzes the three transmission modes of the C-DRWT in detail and proposes regulation schemes, and the characteristic curves of the torque and speed tracking are presented to achieve the regulation objective under different transmission modes. The fourth section presents a summary of the research content. The last section discusses the future work.

Structural characteristics and transmission modes based on working patterns of gear box

Structure and characteristics of rotors

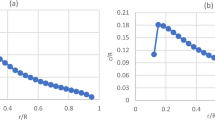
Figure 2¹³ is just described the geometric size relationship for the upwind rotor (UR) and the downwind rotor (DR). The UR has the same structure as the rotor of a traditional SRWT. The blades of DR need to be supported by a support rod designed to reduce the overlapping swept area of the blades of the two rotors in the radial direction as much as possible to decrease the wake effect of the UR on the DR.

The two rotors of the C-DRWT are set up in the coordinate system, with the rotation center of the UR as the zero, the radial direction of the UR blade as the Y-axis, and the connection between the rotation centers of the UR and the DR as the Z-axis. The nacelle is not shown in Fig. 2.

Fig. 2

Geometric model of UR and DR.

${R_{UR}}$ and ${R_{DR}}$ are the blade lengths of the UR and the DR respectively, while ${R_1}$ and r are the radial positions of tip and root of DR blades respectively. The relationship among ${R_{DR}}$, ${R_1}$ and r can be obtained as ${R_1}={R_{DR}}+r$.

Working patterns of gear box and transmission modes of rotors

The mechanism schematic of the C-DRWT is shown in Fig. 3. The UR and DR are connected to separate the drive shafts. The wind energy is converted into mechanical energy and transmitted to the gearbox via a spindle, which is then transmitted to the main shaft of the generator after the speed is increased via the gearbox.

As shown in Fig. 3, the UR and DR coaxially rotate in the reverse direction (the coaxial rotation will form a power backflow in the transmission, so the rotation directions of the two rotors are opposite). During the operation and regulation of the turbine, the blade of the DR is fixed on a nut, as shown in Fig. 3, and it can move radially along the support rod under the action of a screw that is fixed to bevel gear ${g_2}$. The rotation of bevel gear ${g_2}$ is realized by the worm gear and the bevel gears ${g_1}$ and ${g_2}$. Due to the self-locking property of the worm gear, there is no relative movement between the DR and its support frame. When the radial position of the DR needs to be adjusted, the control motor (not shown in Fig. 3) mobilizes on the worm, which can drive the bevel gear actuating the DR to move radially along the support rod.

As shown in Fig. 3, if the ring gear or the planet carrier of the first differential planetary stage is braked, it will become a planetary system with a single degree of freedom. Based on this behavior, the gear box of the C-DRWT can have three working patterns: differential mode, planet carrier input (PCI) with the ring gear immobilized, and ring gear input (RGI) with the planet carrier immobilized. In these three patterns, the increase ratio of the gear box decreases successively, and the working process of the gearbox is also set to transition from differential mode to PCI and then to RGI.

Fig. 3

The gearbox structure of C-DRWT.

One rotor of the C-DRWT is connected to the ring gear, and the other is connected to the planet carrier of the first planetary stage in Fig. 3, that is, the transmission modes of the UR and DR are suitable for the working patterns of the gear box, which is converted from a double-rotor input to a DR in single-input mode and then to a UR in single-input mode.

To increase the power generation of the C-DRWT, the swept area of the rotors should be as large as possible. In the current design, the UR and DR can both absorb wind energy, i.e., the transmission mode of the C-DRWT is a double-rotor input using the differential mode of the gear box. When the wind speed increases, to allow the power of the double rotor reach the rated power of the C-DRWT, the wind energy absorbed by the two rotors should be restricted by adjusting the pitch angle of the UR blades and the radial position of the DR blades.

When the UR and DR are regulated to their critical values, but their total power is still higher than the rated power of the C-DRWT, the ring gear of the gearbox and UR are both braked, and the transmission mode of the C-DRWT is converted into a DR in single-input mode using the PCI of the gearbox.

When the wind speed increases ulterior and the radial position of DR blades reaches the critical maximum value, the planet carrier of the gear box can be braked slowing the DR. The braking of the ring gear can be stopped, and transmission mode of the C-DRWT is converted into a UR single-input mode using the RGI of the gearbox.

Figure 4 delineates the effective wind speed boundaries of C-DRWT for stable turbine operation. This analytical framework builds upon the foundational topology outlined in Fig. 1, with explicit visual codification of three distinct operational paradigms governing dual-rotor coordination and gearbox kinematic configurations across defined wind velocity intervals.

Fig. 4

Operational modes and wind speed ranges of C-DRWT.

The three working patterns of the gearbox and the corresponding transmission modes of the rotors of the C-DRWT under different wind speed scopes are analyzed as follows.

(1) Gearbox operates in differential mode.

The wind speed interval is $v \in \left[ {{v_{cut - in}},{v_{UR - b}}} \right)$, ${v_{cut - in}}$ is the cut-in speed of C-DRWT, and ${v_{UR - b}}$ is the wind speed when the UR begins to be braked. The transmission mode of the C-DRWT is a double-rotor input.

At this moment, the gear box operates in differential mode, with both the ring gear and the planet carrier as inputs. Both rotors absorb wind energy and transfer it to the gearbox. The power of the C-DRWT is the total power of the two rotors.

The wind speed within its limits can be classified into two subintervals according to whether the total power from the two rotors reaches the rated power of the C-DRWT.

The wind speed scope of subinterval-I is $v \in \left[ {{v_{cut - in}},{v_{rated}}} \right)$, ${v_{rated}}$ is the rated wind speed of the C-DRWT. Within this limits, the power of the C-DRWT is below the rated power and the double-rotor of the C-DRWT is in the state of maximum wind energy absorption. Since the torque transmitted by the planet carrier and the ring gear of the first planetary stage need to satisfy the relationship during differential operation, the regulation of the DR requires the maximum power point to be selected within the adjustable range of the radial position of the DR blades based on the operation state of the UR. The target of regulation in this phase is to maximize the total power of the UR and DR.

The wind speed limits of subinterval-II is $v \in \left[ {{v_{rated}},{v_{UR - b}}} \right)$. The target of power regulation in this phase is to keep the total power of the UR and DR close to the rated power of the C-DRWT. This is realized by adjusting the pitch angle of the UR blades, the radial position of the DR blades and the torque of the generator.

(2) Gearbox operates in PCI mode.

The wind speed limits is$v \in \left[ {{v_{UR - b}},{v_{DR - b}}} \right)$, and ${v_{DR - b}}$ is the wind speed when the DR starts to be braked. The transmission mode of the C-DRWT is DR single-input mode.

By this time, the ring gear of the first planetary stage is braked with the UR, and only the DR rotates the planet carrier to transfer power. The C-DRWT is equivalent to the fixed-pitch SRWT with only the DR in operation, and the overall power of the C-DRWT is the power of the DR. The regulation objective at this stage is still to maintain the power of the DR near the rated power of the C-DRWT, which is regulated by the radial movement of the DR blades combined with the generator torque.

(3) Gearbox operates in RGI mode.

The wind speed range is $v \in \left[ {{v_{DR - b}},{v_{cut - out}}} \right)$, where ${v_{cut - out}}$ is the cut-out wind speed of the C-DRWT. The transmission mode of the C-DRWT is UR single-input mode.

At this point, the plant carrier of the first planetary stage of the gear box is braked with the DR, and only the UR rotates the ring gear to transfer power. The C-DRWT is equivalent to a variable-pitch SRWT with only the UR operating normally, and the overall power of the C-DRWT is the power of the UR. The regulation objective at this stage is still to maintain the power of the UR near the rated power of the C-DRWT, which is regulated by the pitch angle of the DR blades combined with the generator torque.

Based on the discussion above, the working patterns of the gearbox and the operating modes of the C-DRWT within the three wind speed ranges are summarized in Table 1.

Table 1 Three operating modes of C-DRWT and working patterns of gearbox.

Power analysis of three transmission modes

Wind turbines operate in different modes depending on the wind speed. For the C-DRWT, the transmission mode of its rotor varies with different wind speed. This is mainly reflected in the regulation of the rotor’s power generation.

In this section, the power generation of the C-DRWT, the pitch angle of the UR blades, and the radial position of the DR blades under each transmission mode are analyzed.

The power generation of the blades is directly related to the aerodynamic parameters, and the following equation of the wind energy absorbed by the blades that is transformed into electric power can be obtained³³.

$$P=\frac{1}{2}{C_p}\rho A{v^3}$$

(1)

where, ${C_p}$ is the wind energy utilization factor, $\rho$ andν are the air density and incoming flow wind speed, and A is the swept area of the blades.

The swept areas ${A_{UR}}=\pi R_{{UR}}^{2}$, ${A_{DR}}=\pi \left( {R_{{DR}}^{2}+2{R_{DR}}r} \right)$ and the wind energy utilization coefficients of the UR and DR were substituted into Eq. (1), and equations for the wind power absorbed by the UR and DR were obtained as follows:

$${P_{UR}}=\frac{1}{2}\pi \rho {C_{{p_{UR}}}}R_{{UR}}^{2}{v^3}$$

(2)

$${P_{DR}}=\frac{1}{2}\pi \rho {C_{{p_{DR}}}}\left( {R_{{DR}}^{2}+2{R_{DR}}r} \right){v^3}$$

(3)

where, ${C_{{p_{UR}}}}$ and ${C_{{p_{DR}}}}$ are the wind energy utilization coefficients of the UR and DR. The total power of the C-DRWT, ${P_t}$, is the sum of the wind power absorbed by the UR and DR

$${P_t}={P_{UR}}+{P_{DR}}.$$

Analysis of double rotor input

For the double-rotor input, the wind speed is $v \in \left[ {{v_{in}},{v_{UR - b}}} \right)$, and the gearbox of the C-DRWT works in differential mode. The power of the C-DRWT is the sum of the power absorbed by the UR and DR from the wind.

$${P_t}=\frac{1}{2}\pi \rho {v^3}\left[ {{C_{{p_{UR}}}}R_{{UR}}^{2}+{C_{{p_{DR}}}}\left( {R_{{DR}}^{2}+2{R_{DR}}r} \right)} \right]$$

(4)

where, ${R_{DR}}$ is the length of the blade of the DR.

When the wind speed is in subinterval-I, that is $v \in \left[ {{v_{cut - in}},{v_{rated}}} \right)$, the power of the C-DRWT, ${P_t}$, is below the rated power, and the regulation objective of the power is to make ${P_t}$ optimal, i.e., to make the UR and DR absorb as much wind energy as possible. The blades of UR can be placed in the maximum windward state so that the wind energy utilization coefficient is optimal. The radial position of the DR blades should select the point with the maximum DR power within adjustable limits.

When the wind speed is in subinterval-II, that is, $v \in \left[ {{v_{rated}},{v_{UR - b}}} \right)$, the power of the C-DRWT, ${P_t}$, increases to the rated power. By coupling the pitch angle regulation of the UR blades and the radial movement of the DR blades with the regulation of the generator torque, the output power ${P_t}$ is stabilized near the rated power ${P_N}$.

Analysis of downwind rotor (DR) single-input mode

When the wind speed increases to ${v_{UR - b}}$, it is necessary to brake the UR and keep the DR in operation, and the working pattern of the gear box changes to PCI. The wind speed is $v \in \left[ {{v_{UR - b}},{v_{DR - b}}} \right)$, and C-DRWT is in DR single-input mode. The C-DRWT can be regarded as an SRWT with a fixed pitch, and the total power can be obtained as follows:

$${P_t}={P_{DR}}=\frac{1}{2}\pi {C_{{p_{DR}}}}\rho \left( {R_{{DR}}^{2}+2{R_{DR}}r} \right){v^3}$$

(5)

The regulation objective of the power is still to keep ${P_t}$ stabilized at the rated power ${P_{DR}}={P_N}$. The pitch angle of the DR blades is constant, but its radial position is adjustable. The regulation of the DR can refer to the regulation of the SRWT, and the radial movement of the DR blades can be regulated meanwhile.

Analysis of UR single-input

When the wind speed increases to ${v_{DR - b}}$, it is necessary to brake the DR and release the UR simultaneously. The gearbox is in RGI mode. The wind speed is $v \in \left[ {{v_{DR - b}},{v_{cut - out}}} \right)$, and the C-DRWT operates in UR single-input mode.

The C-DRWT can be regarded as an SRWT with a variable pitch. According to Eq. (2), the total.

power of the C-DRWT can be obtained as follows:

$${P_t}={P_{DR}}=\frac{1}{2}\pi {C_{{p_{DR}}}}\rho \left( {R_{{DR}}^{2}+2{R_{DR}}r} \right){v^3}$$

(6)

The regulation objective of the power is still to keep ${P_t}$ stabilized at the rated power ${P_N}$.

The pitch of the UR blades is variable. With the increase in the wind speed, the power of the UR can be maintained near the rated power by adjusting the pitch angle of the UR blades.

When the wind speed increases continuously and reaches the cut-out wind speed of the C-DRWT, ${v_{cut - out}}$, the C-DRWT should be cut off from the grid, and the shutdown should be carried out at the same time.

Regulation schemes under three transmission modes

The regulation of the C-DRWT during operation refers to the determination of the relationship between the rotational speeds and torques of the two rotors of the C-DRWT based on the requirements of the wind speed and generator. By adjusting the pitch angle of the UR blades and the radial position of the DR blades, the output power requirements of the C-DRWT under different transmission modes can be realized.

This section proposes regulation schemes for the three transmission modes in Table 1, including the torque and speed characteristic curves of the UR and DR, which are tracked during the regulation phase.

The regulation strategy of the C-DRWT includes two regulation stages. When the total power is below the rated power, the C-DRWT must be maintained in a state of maximum power output. After increasing to the rated power, it needs to maintain C-DRWT in the state of the rated power output. The pitch angle of the UR blades is adjustable, while that of the DR is fixed. The existing wind turbines with a fixed pitch operate with variable or constant speeds. Many limitations exist in constant-speed turbines, such as low power coefficients and the need to absorb energy from the grid to maintain constant-speed operation. Hence, this section only proposes a regulation scheme for the case in which the DR blades have a fixed pitch with a variable speed, and the characteristic curves of the torque and speed of the UR and DR are obtained.

Central ideas and process of regulation scheme

There are two main stages in the existing operation process of an SRWT between the cut-in and the cut-out wind speed: (1) Between the cut-in speed and the rated speed, the rotor is in the state of maximum wind energy absorption, that is, the wind energy utilization coefficient is a maximum,${C_{{p_{\hbox{max} }}}}$. (2) The wind speed is between the rated speed and the cut-out speed, and the power of the rotor is kept near the rated power by adjusting the generator torque and the pitch angle of the blades. The operation and regulation of the C-DRWT can also be generally divided into these two stages.

Due to the different structures of the double rotor, the regulation scheme during operation in each stage needs to be determined separately. In this paper, the variable-speed UR and the fixed-pitch, variable-speed, and radially removable DR are discussed in detail.

During the regulation of the C-DRWT, the required power values of the C-DRWT at different wind speed limits were taken as the regulation objectives, which were achieved by adjusting the pitch angle of the UR (changing the wind energy utilization coefficient, ${C_{{p_{UR}}}}$) and the radial position of the DR blades (changing the swept area of the DR and the wind energy utilization coefficient, ${C_{{p_{DR}}}}$). In addition, the relationship between the torques and speeds of the two rotors and the wind speed is used to determine the characteristic curves of the torque and speed.

The wind energy utilization coefficient of the wind turbine is related to the tip speed ratio and pitch angle of the blades as follows³⁴:

$${C_p}\left( {\lambda ,\beta } \right)={k_1}\left( {\frac{{{k_2}}}{{{\lambda _i}}}+{k_3}\beta +{k_4}} \right){e^{\frac{{{k_5}}}{{{\lambda _i}}}}}+{k_6}\lambda$$

(7)

where, ${\lambda _i}=\frac{1}{{\lambda +{k_7}\beta }}+\frac{{{k_8}}}{{1+{\beta ^3}}}$, $\lambda =\frac{{\omega R}}{v}$, and ${k_1}\sim {k_8}$ are the constants, $\beta$, $\omega$, and R are the pitch angle, speed, and radius of the blade, respectively, and ν is the wind speed.

The aerodynamic torque of the wind turbine is also related to the wind speed and rotational speed of blades, as follows³⁴:

$$T=\frac{1}{2}\pi \rho {R^3}{C_q}\left( {\lambda ,\beta } \right){v^2}$$

(8)

where, ${C_q}\left( {\lambda ,\beta } \right)$ is the torque coefficient of the blades, and ${C_q}\left( {\lambda ,\beta } \right)=\frac{{{C_p}\left( {\lambda ,\beta } \right)}}{\lambda }$.

In the C-DRWT, the pitch angle of the UR blades is adjustable, but the blade length is constant. Thus, the wind energy utilization coefficient ${C_{{p_{UR}}}}$ is determined by the pitch angle ${\beta _{UR}}$ and rotational speed ${\omega _{UR}}$, as follows:

$${C_{{p_{UR}}}}\left( {{\beta _{UR}},{\omega _{UR}}} \right)={k_1}\left( {\frac{{{k_2}}}{{{\lambda _{{i_{UR}}}}\left( {{\beta _{UR}},{\omega _{UR}}} \right)}}+{k_3}{\beta _{UR}}+{k_4}} \right){e^{\frac{{{k_5}}}{{{\lambda _{{i_{_{{UR}}}}}}\left( {{\beta _{UR}},{\omega _{UR}}} \right)}}}}+{k_6}{\lambda _{UR}}\left( {{\omega _{UR}}} \right)$$

(9)

where, ${\lambda _{{i_{UR}}}}=\frac{1}{{{\lambda _{UR}}+{k_7}{\beta _{UR}}}}+\frac{{{k_8}}}{{1+\beta _{{UR}}^{3}}}$, and ${\lambda _{UR}}=\frac{{{\omega _{UR}}{R_{UR}}}}{v}$.

The derivation of Eq. (9) involves substituting the pitch angle ${\beta _{UR}}$ and rotational speed ${\omega _{UR}}$ of UR into Eq. (7). In Eq. (7), ${C_p}$ is defined as a function of $\lambda$ and $\beta$, where both $\lambda$ and ${\lambda _i}$ are dependent variables of $\beta$ and $\omega$. Consequently, in Eq. (9), ${\lambda _{UR}}$ and ${\lambda _{i{}_{{UR}}}}$ can be expressed in terms of ${\omega _{UR}}$ and ${\beta _{UR}}$, thereby reformulating ${C_{{p_{UR}}}}$ as a function of ${\beta _{UR}}$ and ${\omega _{UR}}$.

The pitch angle ${\beta _{DR}}$ of the DR blades is constant, but the radial position of the blade is adjustable. Thus, the wind energy utilization coefficient ${C_{{p_{DR}}}}$ is determined by the radial position r of the blades and the rotational speed ${\omega _{DR}}$, as follows:

$${C_{{p_{DR}}}}\left( {{\omega _{DR}},r} \right)={k_1}\left( {\frac{{{k_2}}}{{{\lambda _{{i_{DR}}}}\left( {{\omega _{DR}},r} \right)}}+{k_3}{\beta _{DR}}+{k_4}} \right){e^{\frac{{{k_5}}}{{{\lambda _{{i_{DR}}}}\left( {{\omega _{DR}},r} \right)}}}}+{k_6}{\lambda _{DR}}\left( {{\omega _{DR}},r} \right)$$

(10)

where, ${\lambda _{{i_{DR}}}}=\frac{1}{{{\lambda _{DR}}+{k_7}{\beta _{DR}}}}+\frac{{{k_8}}}{{\beta _{{DR}}^{3}+1}}$, and ${\lambda _{DR}}=\frac{{{\omega _{DR}}\left( {r+{R_{DR}}} \right)}}{v}$.

Equation (10 describes the wind energy capture coefficient ${C_{{p_{DR}}}}$ for the DR blade. Unlike Eq. (9), where the blade pitch angle ${\beta _{DR}}$ of the DR is fixed, the radial displacement r varies. Consequently, ${\lambda _{DR}}$ and ${\lambda _{{i_{DR}}}}$ become dependent on ${\omega _{DR}}$ and r, making ${C_{{p_{DR}}}}$ a function of ${\omega _{DR}}$ and r.

The torques of the UR and DR can be written as follows:

$${T_{UR}}=\frac{1}{2}\rho \pi R_{{UR}}^{3}{C_{{q_{UR}}}}\left( {{\beta _{UR}},{\omega _{UR}}} \right){v^2}$$

(11)

$${T_{DR}}=\frac{1}{2}\rho \pi R_{{DR}}^{3}{C_{{q_{DR}}}}\left( {{\omega _{DR}},r} \right){v^2}$$

(12)

In Eqs. (11) and (12),${C_{{q_{UR}}}}\left( {{\beta _{UR}},{\omega _{UR}}} \right)$ is the torque coefficient of the UR, and ${C_{{q_{UR}}}}\left( {{\beta _{UR}},{\omega _{UR}}} \right)=\frac{{{C_{{p_{UR}}}}\left( {{\beta _{UR}},{\omega _{UR}}} \right)}}{{{\lambda _{UR}}}}$.${C_{{q_{DR}}}}\left( {{\omega _{DR}},r} \right)$ is the torque coefficient of the DR, and ${C_{{q_{DR}}}}\left( {{\omega _{DR}},r} \right)=\frac{{{C_{{p_{DR}}}}\left( {{\omega _{DR}},r} \right)}}{{{\lambda _{DR}}}}$.

Based on the above, the process of determining the regulation scheme proposed in this paper is as follows.

• (1) Determine the limits where the wind speed is located according to the current wind speed.

• (2) The working pattern of the gear box and the transmission mode of the C-DRWT are determined by step 1.

• (3) The relationship between the objective power, the torque and the speed of the rotors are determined. The pitch angle of the UR and the radial position of the DR blades are determined by Eqs. (2) and (3), and the relationship between the torque and rotational speed of the UR and DR are determined by Eqs. (11) and (12).

• (4) The pitch angle of the UR and the radial position of the DR blades are adjusted to achieve the power regulation objective, and the characteristic curves of the torque and speed are drawn according to the relationship between the torque and speed obtained in step 3.

• (5) If the wind speed fluctuates within the prescribed limits, the control strategy remains unchanged. Otherwise, the process returns to Step 1 and re-regulates.

Within the aforementioned regulatory processes, stages (3) and (4) constitute the pivotal computational phases determining C-DRWT’s two critical control parameters: the pitch angle of UR blades and the radial position of DR blades. These stages span the complete drivetrain assembly comprising dual rotors, gearbox, and generator, systematically solving kinematic models for each transmission mode under power optimization objectives. The detailed computational methodology were illustrated in Fig. 5 (Subinterval-I of the double rotor input mode), Fig. 8 (Subinterval-II of the double rotor input mode), Fig. 11 (DR in single-input mode) and Fig. 13 (DR in single-input mode).

Fig. 5

Regulation process of UR and DR in subinterval-I.

Fig. 6

Characteristic of torque and speed of UR in subinterval-I. (a) Characteristic surface of UR in subinterval-I. (b) Characteristic curve of UR in${v_1}$.

Fig. 7

Characteristic of torque and speed of DR in subinterval-I. (a) Characteristic surfaces of DR in subinterval-I. (b) Characteristic curves of DR in ${v_1}$.

Fig. 8

Regulation process of UR and DR in subinterval-II.

Regulation schemes of C-DRWT

Taking the transmission parameters and control parameters of NREL 5 MW wind turbine (as shown in Table 2) as reference, the relevant parameters of C-DRWT are calculated as shown in Table 3.

Table 2 The operation parameters of NREL 5 MW wind turbine.

Table 3 The operation parameters of C-DRWT.

Regulation scheme of double rotor input

The UR and DR operate simultaneously, and the gearbox is in differential mode. In the regulation process, the torque matching of a planetary gear and the speed relationship between the input and output must be considered.

According to the structural characteristics of the gearbox shown in Fig. 3, the following torque relationship between the UR and DR in stable operation must be satisfied:

$$\frac{{{T_{DR}}}}{{{T_{UR}}}}= - \frac{{{p_1}+1}}{{{p_1}}}$$

(13)

where, ${p_1}$ is the ratio of the number of teeth between the ring gear and the sun gear of the first planetary stage, and ${p_1}={z_{{b_1}}}/{z_{{a_1}}}$. The torque ratio of the UR to the DR is negative because the torque directions of the UR and the DR were considered. In the structure of Fig. 3, the UR and DR are rotated in reverse to avoid power backflow inside the gearbox. Therefore, the directions of their torques and speeds were opposite.

The speed relationship between the input and output of the gear box is as follows:

$${\omega _{UR}}{p_1} - {\omega _{DR}}\left( {{p_1}+1} \right)=\frac{{{\omega _g}}}{{{i_2}{i_{pa}}}}$$

(14)

where, ${\omega _{UR}}$ and ${\omega _{DR}}$ are the rotational speeds of the UR and DR, respectively, ${\omega _g}$ is the rotational speed of the generator, and ${i_2}$, ${i_{pa}}$ are the transmission ratios of the second planetary stage and parallel stage, respectively.

According to the definition of power, the power formulas of the UR and DR can be obtained as follows:

$${P_{UR}}={T_{UR}}{\omega _{UR}}$$

(15)

$${P_{DR}}=\frac{{{T_{UR}}{\omega _g}}}{{{p_1}{i_2}{i_{pa}}}} - {T_{UR}}{\omega _{UR}}$$

(16)

By substituting Eqs. (15) and (16) into ${P_t}={P_{UR}}+{P_{DR}}$, the total power of the C-DRWT can be obtained as follows:

$${P_t}=\frac{{{T_{UR}}{\omega _g}}}{{{p_1}{i_2}{i_{pa}}}}$$

(17)

As described in Section 2.3.1, when the C-DRWT operated with a double rotor input, there were two subintervals within its wind speed limits. Next, different regulation schemes are discussed for each subinterval.

Subinterval-I

When operating in this subinterval, $v \in \left[ {{v_{cut - in}},{v_{rated}}} \right)$, the C-DRWT operates below the rated power. The wind energy utilization coefficient of the UR is in a state of maximum ${C_{{p_{UR\hbox{max} }}}}$. The blades of the DR have a fixed pitch. To satisfy Eqs. (13) and (14), the radial position that maximizes the power of the DR is selected within the adjustable limits of the radial position of the DR.

The power regulation objective is to maximize the total output power of the two rotors. In this paper, ${P_{UR}}$ is guaranteed to be the largest, and the radial position of DR blades r is adjusted to make ${P_{DR}}$ as large as possible, as follows:

$${P_t}=\frac{1}{2}\pi \rho {v^3}\left[ {{C_{{p_{UR}}_{{\hbox{max} }}}}R_{{UR}}^{2}+{C_{{p_{DR}}}}\left( {R_{{DR}}^{2}+2{r_{opt}}{R_{DR}}} \right)} \right]$$

(18)

where, ${r_{opt}}$ is the radial position of the DR blades when ${P_{DR}}$ is optimal.

Based on Eqs. (9) and (12), (13), (14), the regulation process of the pitch angle of the UR blades and the radial position of the DR blades is shown in Fig. 5.

The detailed operation of the regulation process in Fig. 5 is described.

Firstly, regulating the pitch angle ${\beta _{UR}}$ to ${\beta _{UR\hbox{min} }}$ in the light of Eq. (18). Figure 6(a) plots the characteristic surface of the UR draw on Eq. (11). When the wind speed is ${v_1}$, where ${v_1} \in \left[ {{v_{cut - in}},{v_{rated}}} \right)$, the characteristic curve ${T_{UR}}{\text{-}}{\omega _{UR}}$ is described as Fig. 6(b). For obtained the maximum value of ${C_{{p_{UR}}}}$, the derivative of Eq. (9) with respect to ${\omega _{UR}}$ was calculated as ${\omega _{UR1}}$ in Fig. 6(b). Thereout, the torque of UR, ${T_{UR1}}$, could also be confirmed as the point A in Fig. 6.

From Eq. (13), the torque of DR, ${T_{DR}}$, could be solved as ${T_{DR1}}$. In order to optimize the power of DR, regulating the rotational speed of generator, ${\omega _g}$, to acquired the optimal speed of DR as ${\omega _{DR1}}$. Figure 7(a) shows the characteristic surface of DR draw on Eq. (12). The blue and pink semitransparent planes in the figure are represented ${\omega _{DR}}{\text{=}}{\omega _{DR1}}$ and ${T_{DR}}{\text{=}}{T_{DR1}}$ respectively. The point B is the final solution. In Fig. 7(b), the radial position of DR, r, could be ensured as ${r_1}$. Therefore, it is needed to regulate the radial pisition of DR to ${r_1}$.

The above regulation process is based on the premise that all parameters have solutions in their limits. Equation (13) shows that the ratio of the UR torque to the DR torque, ${{{T_{DR}}} \mathord{\left/ {\vphantom {{{T_{DR}}} {{T_{UR}}}}} \right. \kern-0pt} {{T_{UR}}}}$, depends on the parameters of the planetary stage determining whether the adjusted parameters have solutions, so this problem should be taken into account when designing the planetary stage of the C-DRWT and the value of ${{{T_{DR}}} \mathord{\left/ {\vphantom {{{T_{DR}}} {{T_{UR}}}}} \right. \kern-0pt} {{T_{UR}}}}$ should be distributed reasonably according to Eq. (13).

Subinterval-II

When operating in the subinterval-II, $v \in \left[ {{v_{rated}},{v_{UR - b}}} \right)$, the power of the C-DRWT has reached the rated power. With the increase in the wind speed, the pitch angle of the UR and the radial position of the DR blades should be adjusted simultaneously to stabilize the total power near the rated power.

According to Eqs. (9)–(14) and (17), the regulation process of the pitch angle of the UR and the radial position of the DR blades is shown in Fig. 8.

Figures 9 and 10 show the characteristic surfaces and curves of UR and DR in subinterval-II. When the wind speed is ${v_2}$, where ${v_2} \in \left[ {{v_{rated}},{v_{UR - b}}} \right)$, it is necessary to regulate the pitch angle of the UR to the value of ${\beta _{UR2}}$. The torque-speed relationship of UR expressed in Eq. (11) can be described as the red curve in Fig. 9. The point C is the regulation results of UR in the state of ${\beta _{UR}} \to {\beta _{UR2}}$.

The torque and speed of the DR, ${T_{DR}}$ and ${\omega _{DR}}$, can be calculated as ${T_{DR2}}$ and ${\omega _{DR2}}$ in line with Eqs. (13), (14). Just as the semitransparent surfaces ${T_{DR}}{\text{=}}{T_{DR2}}$ and ${\omega _{DR}}{\text{=}}{\omega _{DR2}}$ in Fig. 10(a). The point D in Fig. 10 means regulating the radial position of the DR to the value of ${r_2}$.

The regulation progress aforementioned is under the condition that the solutions of ${\beta _{UR}}$, ${\omega _{UR}}$ and the radial position of the DR blades, r, are existing. Otherwise, there should be a tiny increment to the pitch angle of the UR, i.e. ${\beta _{UR}}{\text{+}}\Delta {\beta _{UR}}$, and the above progress should also be reregulated.

Fig. 9

Characteristic torque and speed of UR in subinterval-II. (a) Characteristic surface of UR in${v_2}$. (b) Characteristic curves of UR in${v_2}$.

Fig. 10

Characteristic of torque and speed of DR in subinterval-II. (a) Characteristic surface of DR in${v_2}$. (b) Characteristic curves of DR in${v_2}$.

Regulation scheme of DR in single-input mode

In this stage, $v \in \left[ {{v_{UR - b}},{v_{DR - b}}} \right)$, the objective of the power regulation is to keep the output power of the DR close to the rated power of the C-DRWT. The relationship between the rotational speed of the DR and the generator speed is as follow:

$$- {\omega _{DR}}\left( {{p_1}+1} \right)=\frac{{{\omega _g}}}{{{i_2}{i_{pa}}}}$$

(19)

According to the definition of power and Eq. (19), the power of the DR is as follow:

$${P_{DR}}= - {T_{DR}}\frac{{{\omega _g}}}{{\left( {{p_1}+1} \right){i_2}{i_{pa}}}}$$

(20)

Based on Eqs. (10), (12) and (19), (20) above, the regulation process of the radial position of the DR blades is shown in Fig. 11.

When the wind speed is ${v_3}$, where ${v_3} \in \left[ {{v_{UR - b}},{v_{DR - b}}} \right)$, the characteristic surface of DR could be described as Fig. 11 drived from Eq. (12). Here, the torque of the DR is acquired as ${T_{DR3}}$ in accordance with Eq. (20) accompanied by regulating the generator torque, ${T_g}$. Subsequently, the rotational speed of DR could calculated as ${\omega _{DR3}}$ by Eq. (19). Just as the semitransparent planes ${T_{DR}}{\text{=}}{T_{DR3}}$ and ${\omega _{DR}}{\text{=}}{\omega _{DR3}}$ in Fig. 12(a) and (b). The point E indicates the final solution of the DR, then the radial position of the DR blades should be regulated to ${r_3}$.

Fig. 11

Regulation process of DR in single-input mode.

Fig. 12

Characteristic of torque and speed of DR in single-input mode. (a) Characteristic surface of DR in single-input mode. (b) Characteristic curves of DR in single-input mode.

Regulation scheme of UR in single-input mode

The wind speed increases to $v \in \left[ {{v_{DR - b}},{v_{cut - out}}} \right)$ during this stage. The objective of power regulation is to keep the output power of the UR close to the rated power of the C-DRWT. The speed relationship between the input and output can be obtained as follow:

$${\omega _{UR}}{p_1}=\frac{{{\omega _g}}}{{{i_2}{i_{pa}}}}$$

(21)

The negative sign in Eq. (21) represents the speed of the UR is opposite to the speed of the generator. According to the definition of power and Eq. (21), the power of the UR can be obtained as follow:

$${P_{UR}}={T_{UR}}\frac{{{\omega _g}}}{{{p_1}{i_2}{i_{pa}}}}$$

(22)

According to Eqs. (6), (11) and (21), (22), the regulation process of the pitch angle of the UR blades is shown in Fig. 13.

Figure 14 shows the characteristic of the torque and speed of the UR in single-input mode when the wind speed is ${v_4}$. The characteristic surface of the UR could be depicted in Fig. 14 by Eq. (11). Firstly, it is required to regulate the generator torque. Thereout, the generator speed, ${\omega _g}$, could also be known. Sequentially, the torque of the UR would be calculated as ${T_{UR4}}$ according to Eq. (22), and the rotational speed of the UR should also be determined as ${\omega _{UR4}}$. So that they could be described as the semitransparent planes ${T_{UR}}{\text{=}}{T_{UR4}}$ and ${\omega _{UR}}{\text{=}}{\omega _{UR4}}$ in Fig. 14(a) and (b). The point F is the impact point which indicates that the pitch angle of the UR should be regulated to ${\beta _{UR4}}$.

Fig. 13

Regulation process of UR in single-input mode.

Fig. 14

Characteristic of torque and speed of UR in single-input mode. (a) Characteristic surface of UR in single-input mode. (b) Characteristic curves of UR in single-input mode.

Conclusion

This paper proposed a regulation strategy for the C-DRWT. Theoretical analysis and calculations showed that this regulation strategy could expand the wind speed range for effective power generation (compared with an SRWT of the same power), and provided a theoretical basis for the control algorithm of the C-DRWT during its later operation. According to the wind speed and the structural characteristics of the gearbox, the different components of the first planetary stage could be braked to decrease the increasing ratio of the gearbox. Hence, the three working patterns of the gearbox correspond one-to-one with the three transmission modes of the double-rotor as follows: differential mode→double rotor input mode, PCI→DR single-input mode, RGI→UR single-input mode. Regulation schemes of the UR and DR under each transmission mode are also proposed.

• (1) When the wind speed is between the cut-in speed and the UR braking speed, the gearbox is in differential mode with the maximum increasing ratio, and the C-DRWT is in double rotor input mode. When the wind speed is below the rated, the UR is regulated to achieve the state of maximum absorption of wind energy. Second, the radial position of the DR blades is regulated to maximize the power of the DR. After the wind speed reaches the rated speed, the total power of the C-DRWT should be maintained near the rated power by regulating the pitch angle of the UR blades and the radial position of the DR blades.

• (2) When the wind speed is between the UR braking speed and the DR braking speed, the gearbox is in PCI mode. The increasing ratio is slightly lower than that in differential mode. The C-DRWT is in DR single-input mode. The objective is still to maintain the output of the rated power by regulating the radial position of the DR blades and the torque of generator.

• (3) When the wind speed is between the DR braking speed and the cut-out speed, the gearbox is in RGI mode. The increasing ratio is slightly less than that in PCI mode. The C-DRWT is in UR single-input mode, and the objective is to stabilize the output of the rated power by regulating the pitch angle of the UR blades and the torque of the generator.

It is worth noting that the regulation strategy proposed in this paper is derived from an in-depth theoretical study of the relationships between the aerodynamic parameters (such as torque, rotational speed, pitch angle, etc.) of the UR and DR and the design parameters of the gearbox (such as gear ratio, speed increase ratio, etc.) based on the structural characteristics of the C-DRWT. That is to say, this paper does not yet include the verification results of relevant data from experimental operations necessary for the implementation of the regulation strategy. It is merely a feasible scheme proposed theoretically. Therefore, in future research work, we will manufacture a prototype of the C-DRWT and build a test platform to conduct comprehensive and systematic experiments on the regulation schemes, collect and analyze experimental data, and verify the feasibility and robustness of the regulation strategy.

Further research

The regulation scheme proposed in this paper provides a foundation for the overall operation of C-DRWT. A specific control algorithm based on the regulation scheme needs to be developed, and it should be combined with the regulation scheme and applied in the actual operation of the C-DRWT to verify the effectiveness of the regulation scheme proposed in this paper. In future research, a prototype could be made for experiments or simulations in Matlab Simulink. The transition between the three transmission modes of the C-DRWT and the continuous operation in the case of abrupt wind speed changes have not been studied. Theoretically, the regulation scheme should be required to achieve a smooth transition between two adjacent transmission modes and operate continuously in the case of abrupt wind speeds. These problems are important directions of future research.