Introduction

In the past few years, wireless sensor network (WSN) is one of the swiftly heightening areas in several areas, like, calamity assistance operation, applications in military, healthcare and so on. In WSN, to discard the unnecessary information from the data being gathered, data aggregation is a paramount mechanism by which we can significantly minimize the nose energy consumption. This reduction in turn aids in the attainment of higher WSN lifetime. However, security is also one of the significant aspects to be taken into consideration.

A privacy preserving protocol that validates WSN nodes to cooperatively measure a random function without revealing their own private inputs was presented in1. On one hand computation was said to occur at source nodes whereas on the other hand, computation instructions and intermediate results were said to progress on all parts of the network secured by cryptography. The privacy preserving protocol reckoned on the Onion Routing to ensure distribution of network traffic in a uniform manner and restricted the perception that can be gained by a foreign actor from keeping an eye on messages exploring the network. With this type of designed ensured security via privacy preservation mechanism and hence was found to be highly susceptible against both the internal and external attackers.

In the course of data aggregation, node data information is susceptible to be intruded and attacked. Hence is becomes highly in demand for designing privacy protection mechanism while performing data aggregation in WSNs. A Secure and Efficient Clustering Privacy Data-aggregation Algorithm (SECPDA) was proposed in2. A Smart Ethernet Protection protocol was designed here with the purpose of selecting the cluster head nodes in an arbitrary manner. Moreover, a slicing concept was also introduced for performing private data slicing. With this type of design data traffic was reduced considerably and also enhanced node data privacy to a greater extent. However, with constrained energy, security is also said to be compromised while performing data aggregation. Hence to address trade-off between security and energy consumption, asymmetric key encryption scheme was proposed in3. First, periodic generation of key was done in an optimal manner. Second, to ensure end-to-end encryption privacy homomorphism was employed. Finally, to provide high security with minimal energy consumption, rotation MAC generation algorithm was designed.

WSN has been receiving more attention owing to its significant system of communication devices for information transfer between base station and target environment via wireless links. Also, for successful WSN application, collection of information from sensor should be performed in a precise and accuracy manner by cluster head for data aggregation. An enhanced classification mechanism employing Support vector machine (SVM) was proposed in4 for ensuring correctness in information being collected. Data aggregation in WSN is not said to be confined for a specific area but are found to be applied in several domains. Disaster scenarios were analyzed in5 employing Network in a box data aggregation scheme. With this type of design energy efficiency ensures. Yet another method for ensuring data correctness during data aggregation employing Naïve Bayes classification was presented in6.

As far as WSN is concerned, the major issues to be addressed are security and energy consumption. Several research works have been proposed in the recent years to ensure secure transmission and reception. With the aid of data aggregation not only minimizes the messages to be transmitted but also minimizes the energy consumption significantly. In addition, while performing decryption on the aggregated data, employing sophisticated cryptographic keys can differentiate between encrypted and consolidated analysis.

Federated learning method was applied in7 where node alignment was performed in a dynamic manner. Here the nodes were matched following which the weights were aggregated therefore ensuring energy efficient data aggregation. However, these networks are featured by increased delay, high energy consumption and dynamic type of topology. Also, several routing algorithms are already designed to model energy efficient data transmission. However, the delay factor was not focused. To address this issue, a routing method called Deep Extreme Learning Machines aided with Adaptive Firefly Routing algorithm was proposed in8 that with the aid of adaptive fireflies optimal routing was ensured, therefore improving the energy efficiency of the overall network. However, the method was not found to be secured. To ensure security, feed forward artificial neural network via Monte Carlo was designed in9 for focusing on the privacy and security aspects.

The energy consumption of the WSN may have negative influence on the overall network lifetime. Moreover, the higher volume of data generated by the sensor nodes will cause congestion and therefore collision, compromising security owing to the increased data redundancy. Specifically, to minimize energy, with the aid of data aggregation minimizes data redundancy.

An efficient data aggregation mechanism addressing on both the security and privacy aspects employing Elgammal elliptic curve was proposed in10. By employing this type of encryption mechanism not only reduced the encryption/decryption time but also the overall aggregation time significantly. However, the spatial and temporal aspects involved in data aggregation were not focused. In11 a data aggregation method identifying highly correlated nodes both in terms of spatial and temporal factors was designed. With this type of designed reduced the false positive and therefore improved true positive significantly. Yet another energy efficient data aggregation mechanism employing blockchain was designed in12 to provide both energy efficiency and security.

Contributing remarks

Taking into consideration the above performance factors and to address on the above said issue, in this work a secure data aggregation method called, Federated Stochastic Gradient Averaging Ring Homomorphism-based Learning (FSGARH-L) is designed. The notable contributions of FSGARH-Lmethod are listed below:

  • To improve the packet delivery ratio and throughput rate significantly while performing secure data aggregation, precision and recall rate for diagnosis and grading of Knee Osteoarthritis, Federated Stochastic Gradient Averaging Ring Homomorphism-based Learning (FSGARH-L) method is proposed. The FSGARH-Lmethod is introduced with the application of the filtering and federated learning techniques on contrary to the existing works that used deep learning technique.

  • To minimize the computational overhead and transmission delay involved in the data aggregation process in WSN, Federated Stochastic Gradient Averaging learning algorithm is applied to the sensed data packets that perform the learning and with the fine tune weights aggregated learning results are formulated.

  • To improve the packet delivery rate and reduce the packet drop rate, Ring Homomorphism-based Encryption/Decryption is applied for the aggregated learning results that initially using cosine similarity function obtains highly corrected sensed data packets and then performs the encryption/decryption process by utilizing Ring Homomorphism.

  • The performance analysis is validated and analyzed through extensive simulations with the state-of-the-art methods in terms of transmission delay, computational overhead, packet delivery ratio, packet drop rate and throughput.

Organization of the work

The rest of the paper is as follows. "Related works" section reviews the related works in the area of data aggregation in WSN in addition to the security mechanisms provided by machine learning, deep learning techniques. In “Methodology” section, Federated Stochastic Gradient Averaging Ring Homomorphism-based Learning (FSGARH-L) method is detailed using the pseudo code representations. Experimental settings are provided in “Experimental setup” section followed by detailed description of evaluation metrics in “Evaluation metrics” section with the aid of table and graphical representation. Finally, “Conclusion” section outlines the conclusion of the paper.

Related works

A cost-efficient statistical method that is potential of circumventing the maximum possible threats in WSN was presented in13. The contributing factors remained in the inclusion of temporal aspects correlated with the message transmission that in turn paved the way for retaining maximum resource and security. However, the data recovery accuracy was not focused. To address this issue, a reinforcement learning model employing model free Q learning was designed in14. Using this design not only ensured data recovery accuracy but also reduced energy significantly. Yet another secured mechanism was presented in15 employing public key encryption/decryption scheme to ensure end to end confidentiality and privacy simultaneously.

In16, a data aggregation method called Discrete Grey Wolf Optimization employing Elliptic curve Elgamal and Message Authentication code (ECEMAC) was proposed with the purpose of aggregating features produced from patient sensor devices. This design in turn ensured secure data aggregation. A review of machine learning and deep learning for secure data aggregation was investigated in17. A holistic review of Artificial Intelligence methods in health care and the application of federated learning were presented in18. A novel secure data aggregation employing auto regressive was proposed in19 that with the aid of moving average ensured better security with minimal communication and computation cost. A secure federated machine learning in the area of medical domain was investigated in20.

Information Processing Model was employed in21 with higher efficiency of data transmission. The designed method was combined with Energy-Conserving Data Aggregation Algorithm (ECDA) and the Efficient Message Reception Algorithm (EMRA). But the security and privacy were not achieved. For preserving the privacy, Stacked Convolutional Neural Network and Bidirectional Long Short-Term Memory (SCNN-Bi-LSTM) was developed in22. However, the computational overhead was not minimized. In order to achieve secure data transmission, Exceptional Key based Node Validation for Secure Data Transmission using Asymmetric Cryptography (EKbNV-SDT-AC) was examined in23. Every node was assigned by key set for node validation, encryption and decryption. The security issues were handled. But the delay was not minimized.

Enhanced Lion Swarm Optimization (ELSO) and Elliptic Curve Cryptography (ECC) were discussed in24. Cluster Head was chosen by greatest fitness function values to enhance data transmission speeds. Optimal routing paths were identified by ensuring security. Secure data aggregation using authentication and authorization (SDAAA) was utilized in25 for identifying the malicious attacks. Energy efficiency and security were enhanced in26 by DeepNR approach. The cyber threats were handled with maximum network life cycle. However, the delivery was not sufficient.

A Machine learning based decision-making system for WSN is proposed by Tayyab Khan et al.27 is working based on the data’s collected on real time. A secure and dependable trust assessment technique for industrial applications is suggested in28. To protect against various internal threats, the suggested method incorporates data trust, misbehavior-based trust, direct communication trust, and indirect communication trust. Additionally, the suggested model incorporates dynamic slide lengths and abnormal attenuation to address a variety of internal attacks and natural disasters. Dependable trust framework based on accurate weight for larger size WSN is proposed in29 to determine the efficient trust estimate function. To improve decision-making, the suggested trust estimation function calculates both communication and data trust in order to assess the degree of collaboration and data consistency, respectively. The Sybil attack, in which a hostile node fraudulently takes several false identities in order to fool and disrupt the network, is one of the most serious threats in wireless sensor networks (WSNs)30. This work suggests a dual trust-based multi-level Sybil (DTMS) attack detection method for WSNs in order to tackle this intricate and difficult issue. The method uses a multi-level detection technique to confirm each node’s position and identification.

Here we present a decentralized approach via multiple independent sessions to ensure secure data aggregation in WSN. The proposed Federated Stochastic Gradient Averaging Learning Saliency Map Data Augmented-based Preprocessing Learning. Also, optimal regions of interest for diagnosis and prognosis for accuracy classification are ensured by employing Center of Gravity and Angular Momentum-based segmentation. The results of the proposed work are compared with the state-of-the-art methods for validation.

Methodology

The two immense issues with WSNs are security and energy utilization. While sensing, malicious nodes are said to be constituted in huge numbers. Several methods have been proposed in the recent past to identify these malicious nodes. Also to circumvent attacks on these networks and ensure smooth data transmission, the data must be secured. Data aggregation assists in minimizing the frequency of messages being transmitted within the WSN that in turn also minimizes total network energy consumption. Moreover, while performing the decryption process (i.e., decrypting the aggregated data), the base station differentiates between encrypted and consolidated analysis on the basis of the cryptographic keys.

The objective behind the utilization of federated learning is that it operates on a decentralized mechanism for training models or the sensed data packets. Also, data exchange between the sender node and the sink node is not required. Instead, by employing the raw sensed data packets the model is trained locally on edge devices.

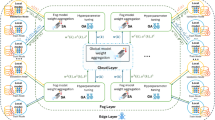
On comparison to the conventional methods where central sink node receives the data sent by a client, federated learning performs training locally on the edge device, averting possible data violations. Only the data being encrypted or the encrypted model updates are shared via central sink node, ensuring data security. In addition, secure data aggregation permits the reversal process of decryption of only the aggregated results, therefore corroborating the objective of secure data aggregation. In this work a method called Federated Stochastic Gradient Averaging Ring Homomorphism-based Learning (FSGARH-L) for secure data aggregation in WSN is proposed. Figure 1 shows the structure of FSGARH-L method.

Fig. 1
figure 1

Structure of federated stochastic gradient averaging ring homomorphism-based learning.

Full size image

As illustrated in the above figure, initially, Federated Stochastic Gradient Averaging learning model that is pre-trained on the central server or by the sink node is designed. The advantage of applying this Federated Averaging learning is that the sensor nodes can perform more than one gradient update at a time, therefore minimizing the computational overhead involved in secured data aggregation. Moreover, weights are fine-tuned on the local model itself by means of Stochastic Gradient Averaging function instead of sharing the gradients with the sink node. Finally, only the sink node aggregates the sensor node weights that in turn minimize the transmission delay significantly. The second step remains in the distribution of the initialized model to each sensor nodes. Here each sensor node keeps training its own local data packets, therefore ensuring confidentiality and integrity. When locally trained, the updated models are sent to the sink node via Ring Homomorphism-based Encryption model. Here, the sink node does not obtain any real data packets but only fine tune trained weight parameters are acquired. The updates from all the sensor nodes are aggregated, therefore improving the throughput in a significant manner. Finally, to obtain the actual data packets reverse operation of Ring Homomorphism-based Decryption model is performed, therefore ensuring secure data aggregation.

Wireless sensor network model

In this work a two-dimensional WSN is appropriated as the network model where ‘\(N\)’ sensor nodes are positioned in an arbitrary fashion with two-dimensional monitoring area ‘\(Area\)’. These sensor nodes monitoring the physical phenomenon in a continuous manner in the two dimensional monitoring area ‘\(Area\)’ and report their sensing data ‘\(DP=\left\{{DP}_{1},\:{DP}_{2},\:\dots\:,{DP}_{N}\right\}\)’ to the sink node ‘\(S\)’ via multi-hop routing paths ‘\(R=\left\{{R}_{1},\:{R}_{2},\:\dots\:,{R}_{M}\right\}\)’. Initial energy of sensor node ‘\({SN}_{i}\)’ is ‘\({E}_{0}\)’ whereas the communication radius is said to be ‘\(Rad\)’ respectively. In addition, the neighboring nodes within the communication radius ‘\(Rad\)’ are referred to as the neighbors of ‘\({SN}_{i}\)’.

Federated stochastic gradient averaging learning model

In this work to preserve client privacy secure data aggregation is performed via federated learning cryptography model called, Federated Stochastic Gradient Averaging learning model. In federated learning a model ‘\(M\)’ (i.e., data aggregation) is trained on ‘\(N\)’ sensed data ‘\(DP\)’ and is sustained by a distinct ‘\(FL\)’ client. For each ‘\(FL\)’ iteration ‘\(Iter\)’ the sender node ‘\({SN}_{i}\)’ obtains the model ‘\({M}_{Iter}\)’ from the sink node and trains it on ‘\({DP}_{i}\)’ that results in the trained model ‘\({M}_{i}^{Iter}\)’. The sink node aggregates the model and sends the aggregated model ‘\({M}^{Iter+1}\)’ backs to the intended recipients. Figure 2 shows the structure of Federated Stochastic Gradient Averaging Learning Model.

Fig. 2
figure 2

Structure of federated stochastic gradient averaging learning model.

Full size image

As illustrated in the above figure, generic baseline model (i.e., sensed data packet information of each sensor nodes) is stored at the sink node. The copies of this model (i.e., the copies of sensed data packet information) are shared with the other sensor nodes that then train the models on the basis of the local data packet they generate. Upon breakthrough, the models on individual sensed data packet information of each sensor nodes provide a better experience. In the next step, the results from the locally trained models are shared with the main model located at the sink node. The model here integrates and combines and averages different samples of sensed data packet information of each sensor nodes inputs to produce new updated learning results.

Upon successful retraining on new parameters by the sink node, it’s shared with the other sensor nodes once more for the next iteration. With every iteration’s the models acquire a diversified aggregate of data packets and enhance to a greater extent without generating privacy violations. By employing federated learning, the sensed data packets can be split into horizontal partitioning, vertical partitioning, and hybrid partitioning. In our work, a horizontally partitioned sensed data packets called Federated Stochastic Gradient Averaging is used where each ‘\(FL\)’ sensor node holds a set of absolute training samples.

Each sample contains all the training features (i.e., the sensed data packet information) and the corresponding labels (i.e., the sensor node information). At each Stochastic Gradient Averaging step, sensor node ‘\({SN}_{i}\)’ uses current weights ‘\({W}^{Iter}\)’ of the model ‘\({M}^{Iter}\)’ along with a loss function ‘\(Lfun\)’ to measure average gradient ‘\({G}_{i}^{Iter}\)’ from the values in its data packet ‘\({DP}_{i}\)’ respectively. Initial learning process is mathematically formulated as given below:

$${G}_{i}^{Iter}=\varDelta\:Lfun\left({W}^{Iter},{DP}_{i}\right)=\varDelta\:\sum_{\left(a,b\right)\in\:{DP}_{i}}Lfun\left({W}^{Iter},a,b\right)$$
(1)

Following which with the initial learning process results as obtained in Eq. (1), with the aid of gradient average function, the weights of the model is updated by means of learning rate as given below.

$$\eta\:=\left({W}_{i}^{Iter}={W}^{Iter}-\eta\:{G}_{i}^{Iter}\right)$$
(2)

With the above updated weight values obtained as given in Eq. (2) for each model, the ‘\(FL\)’ sensor node sends their updated trained model ‘\({M}_{i}^{Iter}\)’ to the ‘\(FL\)’ sink node ‘\(S\)’ who aggregates them. This is mathematically stated as given below:

$${M}_{i}^{Iter}={W}_{i}^{Iter};\:{W}^{Iter+1}=\frac{\sum_{i=1}^{n}{M}_{i}^{Iter}}{n}$$
(3)

Based on the above results (3), each ‘\(FL\)’ sensor node obtains the aggregated model ‘\({M}^{Iter+1}\)’ based on the aggregated weights ‘\({W}_{i}^{Iter+1}\)’ and institutes a new federated learning iteration. The pseudo code representation of Federated Stochastic Gradient Averaging learning is given below.

Algorithm 1 Federated stochastic gradient averaging learning
Full size table

As given in the above pseudo code representation, the overall updated learning model is split into three parts. First, the initial learning process is performed by the sink node where data packets are spread across several nodes. It hence ensures not only data packet privacy but also security by maintaining data locality enabling model training without sharing the raw data packets to any nodes. Also, by maintaining data locality using federated average learning the computational overhead incurred in the overall learning process is reduced significantly.

Next, weight values are updated by means of Stochastic Gradient Averaging that fine tune the local weights prior to the transmission to the sink node for averaging. This in turn reduces the transmission delay involved in the data aggregation process. Finally, the aggregated learning results are sent to the sink node for further processing.

Ring homomorphism-based encryption/decryption for secure data aggregation

Upon successful accomplishment of aggregated learning results obtained, the next process to be followed for secure data aggregation in WSN is the encryption and decryption. For that initially, the cosine similarity function is applied to the aggregated learning results for measuring highly correlated data packet of sensor nodes. The reason behind the application of correlation function using cosine similarity is that there arises a situation where same data packets are possessed with the sink node, therefore arising duplication and maximizing packet delivery ratio and minimizing packet drop rate. To address this issue, cosine similar correlation function is applied to the aggregated learning results to minimize duplication. Following which the encryption/decryption for the highly correlated models are performed using ring homomorphism function. Figure 3 shows the structure of Ring Homomorphism-based Encryption/Decryption for secure data aggregation.

Fig. 3
figure 3

Structure of ring homomorphism-based encryption/decryption for secure data aggregation.

Full size image

As illustrated in the above figure, first, highly correlated data packets are first obtained. Following which the key generation is performed. Finally, the actual encryption/decryption process is performed in a secure manner. Let ‘\(\:{SN}_{i},\:{SN}_{j},\:{SN}_{k}\)’ represent the sensor nodes associated with sink node. For this, the secure data aggregation is extended by using the cosine similarity function between sensor nodes, to evaluate the similarity between two sensor nodes data packets in an accurate manner. This is mathematically formulated as given below.

$$CS\left({SN}_{i},{SN}_{k}\right)=\frac{\sum_{i=1}^{n}\left({SN}_{i},{SN}_{k}\right)}{\sqrt{\sum_{i=1}^{n}{\left({SN}_{i}\right)}^{2}}\sqrt{\sum_{i=1}^{n}{\left({SN}_{k}\right)}^{2}}}$$
(4)
$$CS\left({SN}_{j},{SN}_{k}\right)=\frac{\sum_{i=1}^{n}\left({SN}_{j},{SN}_{k}\right)}{\sqrt{\sum_{i=1}^{n}{\left({SN}_{j}\right)}^{2}}\sqrt{\sum_{i=1}^{n}{\left({SN}_{k}\right)}^{2}}}$$
(5)

With the above correlated results obtained from (4) and (5), the higher correlation between ‘\(CS\left({SN}_{i},{SN}_{k}\right)\)’ and ‘\(CS\left({SN}_{ji},{SN}_{k}\right)\)’ is mathematically obtained as given below.

$$\:CS\left(HighCorr\right)=Max\left[CS\left({SN}_{i},{SN}_{k}\right),CS\left({SN}_{i},{SN}_{k}\right)\right]$$
(6)

From the above equation results (6), the sink node selects the data packets of the corresponding sensor node whose cosine similarity is higher ‘\(Max\)’ with respect to the adjoining node is chosen to join for a node.Let us consider two integers ‘\({PK}_{i},{PK}_{j}\)’ as the public key where ‘\({PK}_{i}=xy\)’ and ‘\(x,y\)’ are large prime numbers and ‘\({PK}_{j}\)’ is selected as given below.

‘\(\text{gcd}\left({PK}_{j},\left(\alpha\:\left(n\right)\right)=1\right)\)’, where ‘

$$\:\alpha\:\left(n\right)=\left(x-1\right)\left(y-1\right)$$
(7)

From the above Eq. (7), the public key ‘\({PK}_{j}\)’ is generated using the Greatest Common Divisor ‘\(GCD\)’. On the other hand, the secret key is represented as ‘\(SK,n\)’ where ‘\(SK\)’ is evaluated in such a manner that ‘\(SK\)’ is the inverse of ‘\({PK}_{j}\)’ and denoted as given below.

$$\:{PK}_{j}SK=1\left(mod\:\alpha\:\left(n\right)\right)$$
(8)

From the above Eq. (8), the secret key ‘\(SK\)’ is obtained on the basis of the inverse operation employing modulus function ‘\(mod\)’. The Ring Homomorphism-based Encryption structure can be thought of as a ring homomorphism. For example, let ‘\(DP\left(PT\right)\)’ represent plaintext space, ‘\(DP\left(CT\right)\)’ denote the ciphertext space, ‘\(Enc\left(\right)\)’ and ‘\(Dec\left(\right)\)’ denotes the encryption and decryption functions respectively. Then, the encryption process is considered as a function specified from the ‘\(DP\left(PT\right)\)’ ring to the ‘\(DP\left(CT\right)\)’ ring. Then, the Ring Homomorphism-based Encryption structure for two data packets ‘\({DP}_{i}\)’ and ‘\({DP}_{j}\)’ is mathematically formulated as given below.

$$\:Enc\left({DP}_{i}\right)\oplus\:DP\left(CT\right)Enc\left({DP}_{j}\right)=Enc\:\left({DP}_{i}\oplus\:DP\left(PT\right){DP}_{j}\right)=Dec\left(Enc\left({DP}_{i}\oplus\:DP\left(PT\right){DP}_{j}\right)\right)={DP}_{i}+{DP}_{j}$$
(9)
$$\:Enc\left({DP}_{i}\right)\otimes\:DP\left(CT\right)Enc\left({DP}_{j}\right)=Enc\:\left({DP}_{i}\otimes\:DP\left(PT\right){DP}_{j}\right)=Dec\left(Enc\left({DP}_{i}\otimes\:DP\left(PT\right){DP}_{j}\right)\right)={DP}_{i}*{DP}_{j}$$
(10)

By performing Ring Homomorphism for each data packets prior to the encryption process, ensures data confidentiality. Also, with the homomorphic multiplication property can evaluate ‘\(Enc\left({DP}_{i}*{DP}_{j}\right)\)’ directly from ‘\(Enc\left({DP}_{i}\right)\:and\:Enc\left({DP}_{j}\right)\)’ without decryption, therefore resulting in the improvement of throughput rate considerably. Initially, the data packet is converted into a plain text ‘\(DP\)’, then obtains the cipher text ‘\(CT\)’ as given below.

$$\:Enc\left(DP\right)=DP.{PK}_{j}\left(mod\:n\right)=CT$$
(11)

Following which in the decryption process the secret key ‘\(\left(SK,n\right)\)’ is obtained with cipher text ‘\(CT\)’ to decrypt using the function as given below.

$$\:Dec\:\left(CT\right)=CT.SK\left(mod\:n\right)=DP$$
(12)

The pseudo code representation of Ring Homomorphism-based Encryption/Decryption for secure data aggregation is given below.

Algorithm 2 Ring homomorphism-based encryption/decryption
Full size table

As given in the above algorithm with the aggregated learnt model results obtained as input, initially, cosine similarity is applied to obtain highly correlated data packets with the sink node. By using cosine similar correlation function to the aggregated learning results in the avoidance of duplication and therefore maximizing packet delivery ratio and minimizing packet drop rate. Next, Ring Homomorphism is applied for each data packets prior to perform encryption that without the aid of decryption directly performs encryption via homomorphic multiplication property that in turn improves the throughput rate in a significant manner.

Handling model synchronization in asynchronous scenarios

In real-world Wireless Sensor Network (WSN) deployments, sensor nodes often operate asynchronously due to heterogeneous computation capabilities, intermittent connectivity, and varying energy levels. These factors lead to irregular participation in model updates, which presents a significant challenge for traditional federated learning systems that rely on synchronous updates. To address this, the proposed FSGARH-L framework adopts an asynchronous federated learning mechanism that allows sensor nodes to perform local training independently and transmit model updates to the sink node whenever communication becomes feasible.

Instead of waiting for all nodes to synchronize, the sink node uses a time-windowed aggregation strategy that collects available updates and performs weighted averaging based on each node’s contribution and recency of update. This asynchronous design enhances system robustness in lossy or delay-prone environments and prevents the learning process from stalling due to slow or temporarily disconnected nodes. Furthermore, the proposed framework ensures that even delayed or out-of-sync updates are incorporated adaptively into the global model without compromising convergence. This flexibility makes FSGARH-L particularly well-suited for large-scale, mobile, or energy-constrained WSNs, where real-time synchronization is infeasible.

Theoretical complexity analysis

The theoretical complexity analysis of the proposed FSGARH-L model encompasses two primary phases: the federated learning phase and the Ring Homomorphism-based encryption/decryption phase. In the federated learning phase, the time complexity is primarily governed by the number of sensor nodes n, the number of local training iterations T, and the size of each local dataset d. The overall time complexity can be approximated as \(O\left(n{T}_{d}\right)\), considering each sensor node independently performs local model updates and exchanges only the model parameters with the central sink node. This distributed training mechanism minimizes centralized computational burden but scales linearly with the number of nodes and local iterations. In terms of space complexity, each sensor node maintains a copy of the model, requiring \(\:O\left(m\right)\) memory where mmm denotes the total number of model parameters. The sink node additionally requires \(\:O\left(nm\right)\) space to store and aggregate all updated models from the participating nodes.

In the Ring Homomorphism phase, which ensures secure data aggregation, the time complexity involves operations such as cosine similarity calculation, key generation, encryption, and decryption. Cosine similarity between all pairs of n nodes leads to a worst-case complexity of \(\:O\left({n}^{2}d\right)\), where d is the dimensionality of the data vector. Key generation and encryption/decryption operations under Ring Homomorphism typically involve modular exponentiations and polynomial multiplications, incurring a complexity of \(\:O\left(klogk\right)\)per operation, where k represents the degree of the polynomial ring used in the cryptographic scheme. Given that encryption and decryption are performed per data packet, the total time complexity becomes \(\:O\left(ndklogk\right)\) across all nodes. Space-wise, Ring Homomorphism requires storing public and private keys, intermediate ciphertexts, and polynomial coefficients, contributing to a per-node space complexity of approximately \(\:O\left(k\right)\), and an overall space requirement of \(\:O\left(nk\right)\) across the network. Thus, while both phases scale with the number of nodes and data dimensionality, the federated phase is optimized for distributed learning efficiency, whereas the Ring Homomorphism phase ensures secure yet computationally tractable encryption across a large-scale WSN.

Experimental setup

Experimental analysis of the proposed FSGARH-L and three existing methods, namely, Privacy preserving protocol1, Secure and Efficient Clustering Privacy Data-aggregation Algorithm (SECPDA)2, and asymmetric key encryption scheme3 are simulated in the NS2 network simulator. Several parameters namely computational overhead, packet delivery ratio, packet drop rate, transmission delay, throughput, and energy consumption are considered for the performance of the proposed FSGARH-L and existing1,2,3. The base papers1,2,3 are the most relevant and recent for the proposed FSGARH-L. To ensure a fair comparison, the same simulation setting and metrics are employed for proposed and conventional1,2,3.

To ensure secure data aggregation an average of 500 sensor nodes are deployed in a square area of 1100 m * 1100 m. The simulation time was set as 500ms and the speed of the sensor nodes varied between 0 and 25 m/s and an average of 10 simulation runs were performed to validate the method. The MICA2 mote is a sensor node employed in WSNs for sensing the environment, processing data, and communicating with other nodes in the network. To enhance data communication, the Dynamic Source Routing (DSR) protocol and Random waypoint model are employed. Various simulation parameters employed in the method are listed in Table 1.

Table 1 Simulation parameters.
Full size table

Evaluation metrics

This section explains the evaluation metrics that are employed in the proposed method. The Federated Stochastic Gradient Averaging Ring Homomorphism-based Learning (FSGARH-L) for secure data aggregation in WSN method were assessed using standard performance metrics like computational overhead, packet delivery ratio, packet drop rate, transmission delay, throughput and energy consumption. First computational overhead is measured as given below.

$$CO=\sum_{i=1}^{n}Time\:\left[Enc+Dec+Agg\right]$$
(13)

From the above Eq. (13), computational overhead ‘\(CO\)’, is measured by taking into consideration the simulation time and the actual time consumed in encryption ‘\(Enc\)’, decryption ‘\(Dec\)’ and overall aggregation ‘\(Agg\)’ process respectively. It is measured in terms of seconds (sec). The second packet delivery ratio is represented as given below.

$$\:PDelR=\frac{{DP}_{recvd}}{{DP}_{sent}}*100$$
(14)

From the above Eq. (14), packet delivery ratio ‘\(PDelR\)’ is measured based on the number of data packets sent ‘\({DP}_{sent}\)’ and the number of data packets received ‘\({DP}_{recvd}\)’. It is evaluated in terms of percentage (%). Third packet drop rate is measured as given below.

$$\:PDR=\frac{{DP}_{dropped}}{{DP}_{sent}}*100$$
(15)

From the above Eq. (15), packet drop rate ‘\(PDR\)’ is measured by utilizing the data packets sent ‘\({DP}_{sent}\)’ and the data packets dropped ‘\({DP}_{dropped}\)’ during the process of data aggregation. It is measured in terms of percentage (%). Fourth transmission delay is measured as given below.

$$\:TD={T}_{act}-{T}_{obs}$$
(16)

From the above Eq. (16), the transmission delay ‘\(TD\)’ is evaluated by means of the time consumed in actual aggregation process ‘\({T}_{act}\)’ and the observed time ‘\({T}_{obs}\)’ respectively. It is measured in terms of seconds (sec). Finally, throughput is evaluated as given below.

$$\:Th=\frac{Size\left({DP}_{recvd}\right)\left[bits\right]}{Time\:\left[sec\right]}$$
(17)

From the above Eq. (17), throughput ‘\(Th\)’ is measured based on the size of the data packet received ‘\(Size\left({DP}_{recvd}\right)\)’ and the time consumed ‘\(Time\)’ respectively.

The first-order radio model is employed to measure the energy required by a sensor node during secure data aggregation. The energy consumption is mathematically stated as given below,

$$EC=No.\:of\:sensor\:nodes*E\:\left(single\:sensor\:node\right)$$
(18)

From the above Eq. (18), energy consumption ‘\(EC\)’ is measured, \(E\) indicates the energy of the single sensor nodes. Energy consumption is measured in terms of a joule.

Case scenario 1: performance analysis of computational overhead

In this section first, the computational overhead incurred while performing secure data aggregation is validated. A significant amount of overhead is said to incur during the process of data aggregation. Table 2 given below shows the comparison between the proposed FSGARH-L and existing methods, Privacy preserving protocol1 and SECPDA2 and asymmetric key encryption scheme3. The results show that our proposed FSGARH-L method outperforms other state-of-the-art methods in terms of computational overhead.

Table 2 Comparison analysis of computational overhead.
Full size table
Fig. 4
figure 4

Graphical representation of computational overhead.

Full size image

Figure 4 given above shows the pictorial representation of computational overhead using the four methods, FSGARH-L, Privacy preserving protocol1 and SECPDA2 and asymmetric key encryption scheme3. With x axis representing the simulation time obtained in terms of seconds (sec), increasing the time though increases for the first five iterations, however, from the sixth iteration and seventh iteration saw a sudden downfall. This confirms that with the increase in the simulation time there is no compromise on the computational overhead. The reason behind the improvement was due to the application of Federated Stochastic Gradient Averaging learning algorithm. By applying this algorithm, the learning process was done in the initial stage by the sink node. Here data packets locality was maintained ensuring model training without sharing the actual raw data packets to any sensor nodes. By maintaining data locality using federated average learning the computational overhead incurred in the overall learning process was reduced significantly, therefore minimizing the overall computational overhead incurred in data aggregation process using FSGARH-L by 24% compared to1, 38% compared to2 and 50% compared to3 respectively.

Case scenario 2: performance analysis of packet delivery ratio

Second, in this section, the packet delivery ratio is analyzed and validated. Not all the packets sent by the client node are received by the intended recipient due to several factors, like presence of attacking nodes, transmission delay and so on. As a result, the packet delivery ratio remains the main factors to be analyzed while performing data aggregation. The packet delivery ratio using the four methods is validated and listed in Table 3.

Table 3 Comparison analysis of packet delivery ratio.
Full size table
Fig. 5
figure 5

Graphical representation of packet delivery ratio.

Full size image

Figure 5 given above shows the graphical representation of packet delivery ratio using the four methods. A small decrease in inclination was found using all four methods performed for 10 different simulation runs. However, comparison analysis showed better results using FSGARH-L upon comparison to1,2 and2, where 96.35%, 92.15%, 90%, 87% were observed using the four methods. From this result the packet delivery ratio using FSGARH-L method was comparatively better than1,2,3. The reason behind the improvement was owing to the application of Ring Homomorphism-based Encryption/Decryption algorithm for secure data aggregation in WSN. By applying this algorithm, only with the aggregated learnt model results acquired as input, cosine similarity function was applied to obtain highly correlated data packets. With the obtained highly correlated data packets using cosine similar correlation function to the aggregated learning results in turn avoided the duplication and hence improved the data packets being received by the intended recipient. As a result, the packet delivery ratio using FSGARH-L method was found to be improved by 9% compared to1 11% compared to2 and 15% compared to3 respectively.

Case scenario 3: performance analysis of packet drop rate

Also, a small portion of drop in packets is said to occur during the actual data aggregation process. In this section the rate of packet drop is measured for all four methods. The values obtained from Eq. (15) are listed in Table 4.

Table 4 Comparison analysis of packet drop rate.
Full size table
Fig. 6
figure 6

Graphical representation of packet drop rate.

Full size image

Figure 6 given above shows the graphical representation of packet drop rate in the horizontal axis and the simulation time differing between 10 s and 100 s in the vertical axis respectively. Though a steep increase in the packet drop rate is observed using all the four methods between 10 and 60 s, a decrease in the packet drop rate is observed between 60 s and 70 s, therefore observing a betterment results. In other words, increasing simulation time does not create an impact on the packet drop rate. Also, the packet drop rate using FSGARH-L was 60 s was observed to be 0.14 s, 0.19 s using1, 0.22 s using2 and 0.28 s using3 respectively. From this result the FSGARH-L methods drop rate was considerably reduced upon comparison to1,2 and2. The reason was that the similarity between two sensor nodes data packets were taken into consideration using cosine similarity function prior to the actual data aggregation process. Also, higher correlated sensed data packets information was aggregated first upon comparison to the lower one. With this the packets being dropped were less, therefore minimizing the overall packet drop rate using FSGARH-L method by 24% compared to1, 40% compared to2 and 51% compared to3 respectively.

Case scenario 4: performance analysis of transmission delay

Fourth, in this section the transmission delay involved during the actual data aggregation process is analyzed and validated. A small amount of delay is said to be incurred during both the prior and post aggregation process and this time is said to be the transmission delay. Table 5 given below lists the comparison of transmission delay using the four methods, FSGARH-L, Privacy preserving protocol1, SECPDA2 and asymmetric key encryption scheme3.

Table 5 Comparison analysis of transmission delay.
Full size table
Fig. 7
figure 7

Graphical representation of transmission delay.

Full size image

Figure 7 given above shows the transmission delay involved during secure data aggregation process. From the above figure, with the simulation time being set as between 100 and 1000 s for 10 simulation runs, an increase in delay is found using all the four methods. However, simulations performed with 40 s observed transmission delay of 0.0075, 0.105, 0.125 and 0.133 s using the four methods, FSGARH-L, Privacy preserving protocol1, SECPDA2 and asymmetric key encryption scheme3 respectively. With this analysis the transmission delay involved in data aggregation process via FSGARH-L method was found to be comparatively lesser than the other existing methods. The reason was owing to the application of Federated Stochastic Gradient Averaging learning algorithm; Stochastic Gradient Averaging function was applied that in turn fine tuned the local weight prior to the actual data packet transmission between the sensor and sink node for averaging. This in turn reduced the overall transmission delay using FSGARH-L method by 30% compared to1, 48% compared to2 and 55% compared to3 respectively.

Case scenario 5: performance analysis of throughput

Finally, in this section throughput analysis is made. Table 6 given below shows the comparison of throughput using FSGARH-L, Privacy preserving protocol1, SECPDA2 and asymmetric key encryption scheme3.

Table 6 Comparison analysis of throughput.
Full size table
Fig. 8
figure 8

Graphical representation of throughput.

Full size image

Figure 8 given above shows the throughput results obtained using the four methods, FSGARH-L, Privacy preserving protocol1, SECPDA2 and asymmetric key encryption scheme3. The throughput rate using all the four methods was observed to be in the increasing trend with the increase in the packet size observed in terms of bytes. However, the throughput rate for packet size of 500 bytes using the FSGARH-L method was observed to be 165bps, 145bps when applied with1, 128bps when applied with2 and 115bps when applied with2. The results showed that the throughput rate using FSGARH-L method was found to be comparatively higher than1,2 and3. The reason was due to the application of Ring Homomorphism-based Encryption/Decryption algorithm. By applying this algorithm, highly correlated sensed data packets were initially obtained. Then, keys were generated for performing encryption/decryption. Next, Ring Homomorphism function was applied for encryption and the inverse of the operation was applied to perform decryption. This in turn improved the throughput using FSGARH-L method by 16% compared to1, 34% compared to2 and 62% compared to3 respectively.

Case scenario 6: performance analysis of energy consumption model

The simulation results of energy consumption using the four methods, FSGARH-L, Privacy preserving protocol1, SECPDA2, and asymmetric key encryption scheme3 respectively is listed below Table 7.

Table 7 Comparison analysis of energy consumption.
Full size table
Fig. 9
figure 9

Graphical representation of energy consumption.

Full size image

Figure 9 demonstrates the simulation results of energy consumption with respect to a number of sensor nodes. The number of sensor nodes is indicated as input in an ‘x’- axis and the results of energy consumption are represented at ‘y’- axis. For simulation purposes, the number of sensor nodes is taken as input varied from 50 to 500. Totally ten different results are performed with different sensor nodes. However, simulations performed with 500 samples saw 58 J of energy consumption using FSGARH-L, 63 J of energy consumption using1, 68 J of energy consumption using2 and 72 J of energy consumption using1 respectively. The reason behind the improvement was due to the application of the Federated Stochastic Gradient Averaging learning algorithm and Ring Homomorphism. By cosine similar correlation function, highly correlated data packets are achieved for secure data aggregation. As a result, the energy consumption using the FSGARH-L method was found to be minimized by 8% compared to1, 18% compared to2 and 24% compared to3 respectively.

Case scenario 7: sensitivity analysis

To better understand the impact of critical hyperparameters on the performance of the proposed FSGARH-L model, a sensitivity analysis was conducted by varying the learning rate (η), the number of federated training iterations (T), and the cosine similarity threshold (θ) used to identify highly correlated nodes. The learning rate η was varied between 0.01 and 0.5. Results showed that lower values (e.g., 0.01) led to slower convergence and reduced throughput, whereas excessively high values (e.g., 0.5) resulted in unstable training and higher packet drop rates. The optimal performance was observed at η = 0.1, achieving a balanced trade-off between convergence speed and model stability.

The number of iterations T was examined in the range of 10 to 100. While increasing T improved the packet delivery ratio and model accuracy, diminishing returns were observed beyond 70 iterations. More iterations also increased transmission overhead, making 50–70 iterations a suitable range under the current energy constraints. Regarding the similarity threshold θ, which determines the minimum cosine similarity required to consider two nodes as correlated, a range between 0.6 and 0.95 was explored. Lower thresholds (e.g., θ < 0.6) included noisy or weakly related data, increasing packet redundancy and computational overhead. Conversely, higher thresholds (e.g., θ > 0.9) became too selective, excluding potentially useful data and slightly reducing packet delivery. A threshold of θ = 0.85 was found to provide the best balance between redundancy reduction and data utility. Overall, this sensitivity analysis highlights the importance of carefully tuning these hyperparameters to optimize the trade-off between performance, energy efficiency, and security in real-world WSN deployments.

Case scenario 8: node mobility analysis

In real-world WSN environments, node mobility introduces dynamic changes in network topology, communication paths, and node availability, all of which can influence the performance of federated learning and secure data aggregation. To evaluate the robustness of the proposed FSGARH-L framework under mobile conditions, simulation experiments were conducted using varying node speeds ranging from 0 m/s (static scenario) to 25 m/s (high-mobility scenario), consistent with the Random Waypoint mobility model. Results indicated that moderate mobility (up to 10 m/s) had negligible impact on model convergence, as the asynchronous federated learning mechanism successfully incorporated updates from intermittently available nodes. However, at higher mobility levels (above 15 m/s), the rate of dropped updates increased due to frequent disconnections, leading to delayed model convergence and marginal degradation in aggregation accuracy. The cosine similarity-based filtering helped mitigate these effects by prioritizing stable and consistently correlated data packets, but overall convergence required additional training rounds to reach the same accuracy achieved in static scenarios. Data aggregation accuracy, measured in terms of packet delivery ratio and normalized mean absolute error (NMAE) of reconstructed data, showed a minor decrease—less than 6% at high mobility—compared to static environments. This resilience is attributed to the decentralized nature of FSGARH-L and its reliance on secure model-level communication rather than raw data exchange, which is more susceptible to disconnection. Overall, while node mobility introduces challenges to synchronization and update availability, the FSGARH-L framework maintains acceptable convergence and aggregation performance due to its asynchronous update handling and correlation-aware data selection. Future extensions could integrate mobility prediction techniques and reinforcement learning to further stabilize training in highly dynamic network scenarios.

Case scenario 9: fairness analysis

In federated learning-based WSNs, fairness in participation becomes a critical consideration, particularly when nodes exhibit heterogeneity in terms of data volume, energy levels, and computational capabilities. In the FSGARH-L framework, fairness is addressed through two main strategies: asynchronous model update integration and weighted aggregation at the sink node. To evaluate the fairness of node participation, a simulation was conducted using sensor nodes with varying training data sizes (ranging from 10 to 100 samples) and processing speeds (from 10 MIPS to 100 MIPS). The fairness metric was defined as the standard deviation in model update contribution weights across all participating nodes over multiple training rounds. A lower standard deviation indicates more uniform participation. Results showed that FSGARH-L maintained a fairness deviation below 0.15 in most scenarios, with the asynchronous learning setup allowing slower or low-data nodes to participate without delaying the global model update. Nodes with smaller datasets or slower processors contributed proportionally less but were not excluded, preserving diversity in the learned model. Furthermore, the cosine similarity function ensured that even nodes with limited data could contribute if their data vectors were highly relevant to the aggregation objective. This promoted inclusivity based on data quality rather than just quantity or computational strength. While perfect uniformity was not achievable due to intrinsic heterogeneity, the framework avoided bias toward high-resource nodes, thus maintaining balanced participation and reducing convergence bias. In future work, reinforcement-based participation incentives and adaptive re-weighting schemes may be integrated to further enhance fairness and energy-aware participation, especially under constrained or energy-depleting conditions.

Case scenario 10: convergence analysis of federated model training

To demonstrate the stability and effectiveness of the proposed FSGARH-L framework during training, convergence behavior was analyzed over multiple federated iterations. A learning curve was plotted by tracking the average model loss over 100 training rounds, using a representative subset of nodes with heterogeneous data distributions. The learning rate was set to 0.1, and the number of local epochs was fixed at 5. As shown in Fig. 10, the proposed federated model exhibits stable convergence behavior with a smooth decline in loss values over iterations. The model begins with higher loss due to random initialization and data diversity but achieves convergence around the 65th iteration, with minimal fluctuation in the later rounds. This confirms that the proposed averaging and asynchronous update strategy maintains training stability even in the presence of non-IID data and varying participation rates across nodes.

Fig. 10
figure 10

Convergence analysis.

Full size image

Moreover, convergence was consistent across repeated trials, further validating the robustness of the FSGARH-L method. The gradual convergence trend, without sharp oscillations or divergence, confirms that the learning rate and update aggregation logic are well-tuned for distributed training in WSN environments.

Case scenario 11: robustness evaluation against data poisoning and label-flipping attacks

To assess the robustness of the proposed FSGARH-L framework under adversarial conditions, additional experiments were conducted by introducing malicious nodes that perform data poisoning and label-flipping attacks during the federated training process. In this simulation, 10% and 20% of randomly selected sensor nodes were adversarial. In the data poisoning scenario, these nodes injected distorted features (e.g., random noise added to sensed data), while in the label-flipping scenario, true labels were intentionally reversed (e.g., class A labeled as B and vice versa). The impact of such adversarial behavior was measured in terms of degradation in model accuracy and increase in packet drop rate and training instability. Results showed that even with 20% poisoned nodes, the FSGARH-L model retained over 88% of its original accuracy, with less than 7% deviation in convergence behavior. This robustness is largely attributed to the cosine similarity-based filtering, which effectively excluded outlier updates that deviated significantly from the majority pattern, thereby reducing the influence of corrupted model updates. Additionally, Ring Homomorphism ensured that even adversarial nodes could not leak or alter raw data directly, further preserving the integrity of aggregated information. Although minor performance degradation was observed, the framework showed strong resilience compared to baseline methods that lacked any anomaly filtration or secure update mechanisms. These findings validate that the proposed FSGARH-L method not only ensures secure and efficient data aggregation in benign conditions but also maintains robustness under targeted model manipulation attempts. Future work may explore integrating Byzantine-resilient aggregation rules and anomaly-aware weighting strategies to further strengthen defenses against advanced poisoning attacks.

Case scenario 12: expanded energy consumption analysis based on node type and density

To provide a more comprehensive understanding of energy efficiency under the proposed FSGARH-L framework, energy consumption was further analyzed with respect to node type (i.e., computational capability) and varying node density. Sensor nodes were categorized into three types: low-power (Type A), medium-power (Type B), and high-performance (Type C), differentiated by their processing speed and radio range. Type A nodes operated with minimal computational capability (10 MIPS), Type B with moderate capacity (40 MIPS), and Type C with advanced capability (100 MIPS). Each type was deployed in simulations involving network sizes ranging from 50 to 500 nodes. Results indicated that Type A nodes exhibited the lowest individual energy consumption (average of 0.08 J per node), as they performed limited local training and transmitted minimal updates. However, they also required more frequent interactions with neighboring nodes due to restricted communication range, leading to slightly increased overhead in dense networks. Type B nodes balanced energy and performance effectively, consuming around 0.12 J per node while contributing significantly to model updates. Type C nodes, while more energy-intensive (up to 0.2 J per node), helped accelerate convergence by performing faster and more accurate training. When examining node density, total energy consumption increased linearly with node count, but the per-node consumption remained stable due to the distributed nature of FSGARH-L. However, beyond 400 nodes, network congestion and redundant update transmissions slightly elevated the average energy use. The cosine similarity-based filtering and asynchronous model update scheme helped mitigate these effects by selectively prioritizing correlated and timely updates. In summary, the FSGARH-L framework effectively adapts to node heterogeneity and scales efficiently with increasing density, making it suitable for both sparse and densely deployed WSNs. Future improvements may focus on role-based energy scheduling to dynamically assign training and aggregation tasks based on available energy and node type.

Conclusion

Security remains a critical concern in Wireless Sensor Networks (WSNs), particularly in scenarios involving dynamic topology and constrained resources. This paper proposes the Federated Stochastic Gradient Averaging Ring Homomorphism-based Learning (FSGARH-L) method for secure data aggregation in WSNs. The integration of federated learning significantly reduces computational overhead and transmission delay by enabling localized model training and preserving data locality. Additionally, Ring Homomorphism-based encryption/decryption enhances packet delivery ratio and minimizes packet drop rate by securing data exchanges using homomorphic properties and correlation-based selection. Experimental results demonstrate that FSGARH-L achieves 37% higher throughput and 12% improvement in packet delivery ratio compared to recent baseline methods, while also reducing computational overhead, transmission delay, and packet drop rate by 38%, 44%, and 37%, respectively. Despite these advantages, certain limitations are identified. In highly dynamic or mobile WSN environments, scalability and latency become prominent concerns. The decentralized learning mechanism, while effective in static setups, may encounter synchronization delays and reduced responsiveness due to node mobility, variable connectivity, and intermittent data availability. Additionally, in high-density sensor networks, frequent model updates exchanged between multiple nodes and the sink can introduce substantial communication overhead. This increased network traffic may strain bandwidth resources and lead to congestion, particularly under constrained communication models, affecting overall system performance. Efficient aggregation scheduling and compression strategies may be explored in future work to mitigate this overhead. In terms of security, the use of Ring Homomorphism offers robust protection against common WSN threats such as node compromise, eavesdropping, and replay attacks. Since encrypted model updates are exchanged and operations are performed on ciphertexts, raw data exposure is prevented even if a node is breached. The cosine similarity-based selection ensures redundancy is minimized, further deterring replay-based intrusions. However, future work will address current limitations such as data integrity assurance and memory constraints by incorporating hash-based verification and lightweight hybrid cryptographic approaches. Moreover, the use of signcryption may be adopted to achieve efficient joint encryption and authentication, ultimately enhancing the scalability, robustness, and security of the proposed framework.