Introduction

Permanent magnet synchronous motors (PMSM) are increasingly recognized for their wide range of applications in industrial automation and renewable energy1. This recognition stems from its high power output, low energy consumption, excellent performance, long lifetime and minimal noise level2. To address the challenges faced in optimizing the performance of PMSMs, in the field of position sensorless control3,4 such as Extended Kalman Filter (EKF)5,6, Model-Referenced Adaptive Control (MRAC)7, Sliding Mode Observer (SMO)8, and Nonlinear Magnetic Chain Observer (NMCO)9,10 have been explored by an increasing number of scholars.

Compared to the Lomborg sliding film observer, the EKF exhibits superior convergence performance at low speeds, although its effectiveness relies heavily on the precise tuning of the noise matrix parameters, which often requires extensive simulation and calibration work. Bolognani et al. proposed an all-digital position sensor-less drive technique that is reduced to be limited to current and DC link voltage sensors, which greatly reduces the use of sensors and improves the reliability and economy of the system11. Barut M et al. implemented a two-input extended Kalman filter estimator that simultaneously estimates the stator resistance, rotor resistance, and load torque variations based on two extended induction motor models12. Kim et al. proposed a high performance embedded permanent magnet synchronous motor drive without rotary position sensor using a reduced order EKF with lower order state variables greatly reducing the computational load and computational error13.Bolognani S et al. combined a novel self-tuning process to bring the EKF drive closer to the actual product, with an algorithm based on full normalization14.

Studies15,16 have utilized real-coded genetic algorithms to augment sensorless control systems for PMSMs, resulting in the development of a fully normalized EKF algorithm that improves the adaptability of various control systems. However, these optimization techniques are very complex and require a large amount of training data and long training time, posing challenges for practical engineering applications. Literature17 introduced fuzzy logic system into EKF for estimating the noise covariance matrices Q and R in sensorless DC brushless control systems, but the control rules of the fuzzy logic system will directly affect the estimation accuracy of KF. Literature18 proposed a new interest-based method for estimating the noise covariance matrix of a system, which can adjust Q in real time, and verified its effectiveness in a DC sensorless control system19. Compared with other improved methods, the main advantages of this method are its simple structure and small computational effort20. However, estimating the noise covariance still requires traversing new intervals at each historical moment, which is not practical for the implementation of the algorithm21. Literature22 applied the SageHusa Kalman filtering algorithm to position sensorless control systems for PMSMs and permanent magnet synchronous linear motors, both of which use the SageHusa noise estimator to achieve a recursive estimation of R, which is then further solved to find Q. However, the conventional SageHusa noise estimator leads to the failure of observer convergence.

The aim of this paper is to address the limitations of traditional methods by improving the Sage-Husa noise estimator integrated within the EKF framework of a PMSM sensorless control system. While previous implementations utilize the Sage-Husa estimator for recursive estimation of the noise covariance matrices Q and R, they often encounter the problem of non-convergence. Our proposed improvement retains the advantages of fast convergence and adaptability, while significantly improving the stability and estimation accuracy of the observer. The next sections describe our approach in detail, show experimental results, and discuss the implications of our findings for future PMSM applications.

PMSM mathematical model

In the d-q axis reference coordinate system, if the magnetic saturation effect is not considered, the extended reverse potential Eq. (1) of the PMSM is shown below:

$$\left[ {\begin{array}{*{20}{c}} {{u_d}} \\ {{u_q}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} {{R_s}+s{L_d}}&{ - {\omega _e}{L_q}} \\ {{\omega _e}{L_q}}&{{R_s}+s{L_d}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{i_d}} \\ {{i_q}} \end{array}} \right]+{E_a}\left[ {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right]$$
(1)

where \(\:{\text{u}}_{\text{d}}\) and \(\:{\text{u}}_{\text{q}}\) represent the d-q axis voltage, while \(\:{\text{i}}_{\text{d}}\) and \(\:{\text{i}}_{\text{q}}\) represent the d-q axis current. Rs denotes the stator winding resistance; \(\:{\text{L}}_{\text{d}}\) and \(\:{\text{L}}_{\text{q}}\) stand for the d-q axis inductance. \(\:{{\upomega\:}}_{\text{e}}\:\)signifies the rotational speed of the magnetic flux, and Eq. (2)\(\:\:{\text{E}}_{\text{a}}\:\)denotes the amplitude of the extended counter electromotive force of the PMSM expressed as:

$${E_a}=({L_d} - {L_q}){\omega _e}{i_d} - ({L_d} - {L_q})\frac{{d{i_q}}}{{dt}}$$
(2)

By performing the inverse Park transformation on Eq. (1), the extended inverse electromotive force model in the \(\:{\upalpha\:}-{\upbeta\:}\) axis coordinate system can be obtained:

$$\left[ {\begin{array}{*{20}{c}} {{u_\alpha }} \\ {{u_\beta }} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} {{R_s}+s{L_d}}&{ - {\omega _e}({L_d} - {L_q})} \\ {{\omega _e}({L_d} - {L_q})}&{{R_s}+s{L_d}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{i_\alpha }} \\ {{i_\beta }} \end{array}} \right]+{E_a}\left[ {\begin{array}{*{20}{c}} { - \sin {\theta _e}} \\ {\cos {\theta _e}} \end{array}} \right]$$
(3)

The Eq. (4) of motion for PMSM is:

$${J_m}\frac{{d{\omega _m}}}{{dt}}={T_e} - {T_L} - {B_m}{\omega _m}$$
(4)

Assumptions

In the theoretical calculation process, motor damping is typically neglected. It is assumed that the external load torque changes slowly and can be compensated for by the PI controller in the integral link. Consequently, the motor load is disregarded to simplify the model, as demonstrated below:

$${J_m}\frac{{d{\omega _m}}}{{dt}}={T_e}=\frac{3}{2}{p_n}{i_q}[{i_d}({L_d} - {L_q})+{\psi _f}]$$
(5)

where\(\:{\:\text{T}}_{\text{e}}\:\)is the motor torque,\(\:{\:\text{p}}_{\text{n}}\)is the number of motor pole pairs,\(\:{\:\text{J}}_{\text{m}}\) is the motor inertia momentum, and ψf is the motor magnetic chain.

Observer design

In this paper, Kalman Filtering is employed to estimate EMF of PMSM with high accuracy and robustness. By choosing\(\:{\:\text{i}}_{{\upalpha\:}}\)and\(\:{\:\text{i}}_{{\upbeta\:}}\)as state variables and incorporating them as extended state variables, the full-order state equations of the PMSM are formulated as follows:

$$\frac{d}{{dt}}\left[ {\begin{array}{*{20}{c}} {{i_\alpha }} \\ {{i_\beta }} \end{array}} \right]= - \frac{1}{{L_{{_{d}}}^{\prime }}}\left[ {\begin{array}{*{20}{c}} {{R_s}}&{{\omega _e}({L_d} - {L_q})} \\ { - {\omega _e}({L_d} - {L_q})}&{{R_s}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{i_\alpha }} \\ {{i_\beta }} \end{array}} \right]+\frac{1}{{L_{{_{d}}}^{\prime }}}\left[ {\begin{array}{*{20}{c}} {{u_\alpha } - {e_\alpha }} \\ {{u_\beta } - {e_\beta }} \end{array}} \right]$$
(6)
$$\frac{d}{{dt}}\left[ {\begin{array}{*{20}{c}} {{e_\alpha }} \\ {{e_\beta }} \end{array}} \right]={\omega _e}\left[ {\begin{array}{*{20}{c}} { - {e_\beta }} \\ {{e_\alpha }} \end{array}} \right]+\frac{d}{{dt}}{\omega _e}\left[ {\begin{array}{*{20}{c}} {{e_\alpha }} \\ {{e_\beta }} \end{array}} \right]={\omega _e}\left[ {\begin{array}{*{20}{c}} { - {e_\beta }} \\ {{e_\alpha }} \end{array}} \right]$$
(7)

In Eq. (6),\(\:{\text{L}}_{\text{d}}^{{\prime\:}}\)presents the dynamic inductance, which maintains the same value as the steady-state inductance when magnetic saturation of the magnetic chain is not taken into account. \(\:{e}_{\alpha\:}\) and \(\:{e}_{\beta\:}\) indicate the back electromotive force of the \(\:{\upalpha\:}-{\upbeta\:}\) axis.

Improved sage-huse for full-order EKF observer

The state space equation of the PMSM nonlinear system can be expressed as:

$$\dot {x}(t)=f[x(t)]+Bu(t)+\sigma (t)$$
(8)
$$Z(t)=h[x(t)]+\mu (t)$$
(9)

The input state variables, control variables, and output state variables needed to extend the Kalman observer are selected as:\(\:\text{x}\left(\text{t}\right)={[{\text{i}}_{{\upalpha\:}},{\text{i}}_{{\upbeta\:}},{\text{e}}_{{\upalpha\:}},{\text{e}}_{{\upbeta\:}}]}^{\text{T}}\), \(\:\text{u}\left(\text{t}\right)={[{\text{u}}_{{\upalpha\:}},{\text{u}}_{{\upbeta\:}}]}^{\text{T}}\), \(\:\text{Z}\left(\text{t}\right)={[{\text{i}}_{{\upalpha\:}},{\text{i}}_{{\upbeta\:}}]}^{\text{T}}\).\(\:{\upsigma\:}\left(\text{t}\right)\) is the system noise and \(\:{\upmu\:}\left(\text{t}\right)\) is the measurement noise.

$$f(x)=\left[ {\begin{array}{*{20}{c}} {{f_1}} \\ {{f_2}} \\ {{f_3}} \\ {{f_4}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} { - \frac{{{R_s}}}{{{L_d}}}{i_\alpha } - \frac{{{\omega _e}({L_d} - {L_q})}}{{{L_d}}}{i_\beta } - \frac{1}{{{L_d}}}{e_\alpha }} \\ { - \frac{{{R_s}}}{{{L_d}}}{i_\beta }+\frac{{{\omega _e}({L_d} - {L_q})}}{{{L_d}}}{i_\alpha } - \frac{1}{{{L_d}}}{e_\beta }} \\ { - {\omega _e}{e_\beta }} \\ {{\omega _e}{e_\alpha }} \end{array}} \right]$$
(10)
$$B=\left[ {\begin{array}{*{20}{c}} {\frac{1}{{{L_d}}}}&0 \\ 0&{\frac{1}{{{L_d}}}} \\ 0&0 \\ 0&0 \end{array}} \right]$$
(11)

where \({t_k}=k{T_s},\,\,{t_{k - 1}}=(k - 1){T_s}\), Ts is the sampling time, and linearization is performed to obtain the Jacobi matrix F and H, and the state transfer matrix\(\:{\Phi\:}\), respectively:

$$F(x(t))=\frac{{\partial f}}{{\partial x}}\left| {_{{x=x(t)}}} \right.=\left[ {\begin{array}{*{20}{c}} { - \frac{{{R_s}}}{{{L_d}}}}&{ - \frac{{{\omega _e}({L_d} - {L_q})}}{{{L_d}}}}&{ - \frac{1}{{{L_d}}}}&0 \\ {\frac{{{\omega _e}({L_d} - {L_q})}}{{{L_d}}}}&{ - \frac{{{R_s}}}{{{L_d}}}}&0&{ - \frac{1}{{{L_d}}}} \\ 0&0&0&{{\omega _e}} \\ 0&0&{{\omega _e}}&0 \end{array}} \right]$$
(12)
$$\Phi ({t_k},{t_{k - 1}},x({t_{k - 1}})) \cong I+F{T_s}=\left[ {\begin{array}{*{20}{c}} {1 - \frac{{{R_s}{T_s}}}{{{L_d}}}}&{ - \frac{{{\omega _e}{T_s}({L_d} - {L_q})}}{{{L_d}}}}&{ - \frac{{{T_s}}}{{{L_d}}}}&0 \\ {\frac{{{\omega _e}{T_s}({L_d} - {L_q})}}{{{L_d}}}}&{1 - \frac{{{R_s}{T_s}}}{{{L_d}}}}&0&{ - \frac{{{T_s}}}{{{L_d}}}} \\ 0&0&1&{ - {T_s}{\omega _e}} \\ 0&0&{{T_s}{\omega _e}}&1 \end{array}} \right]$$
(13)
$$H(x(t))=\frac{{\partial h}}{{\partial x}}\left| {_{{x=x(t)}}} \right.=\left[ {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&1&0&0 \end{array}} \right]$$
(14)

After formulating a discrete model of the non-linear PMSM system, the Sage-Husa adaptive EKF algorithm is utilized for estimating the state variables using the measured input and output data. The Sage-Husa algorithm demonstrates improved adaptability to the system’s non-linear and non-Gaussian characteristics compared to conventional Kalman Filtering methods, thus enhancing the rate of noise estimation convergence while accommodating the adaptive capabilities of the dynamic system.

Step 1: Forecasting.

In the following Eq. (15),\(\:{\stackrel{\sim}{x}}_{k}\) represents the a priori state value, while\(\:{\:\widehat{q}}_{k}\:\)signifies the system noise’s mean value computed using the Sage-Huse noise estimator.

$${\tilde {x}_k}={\hat {x}_{k - 1}}+{T_s}(F({\hat {x}_{k - 1}})+B{u_{k - 1}})+{\hat {q}_k}$$
(15)

In the following Eq. (16), \(\:{\stackrel{\sim}{\text{P}}}_{\text{k}}\) represents the a priori error covariance matrix, while\(\:{\widehat{Q}}_{k}\) denotes the system noise matrix at the kth iteration.

$${\tilde {P}_k}=\Phi {\hat {P}_{k - 1}}{\Phi ^T}+{\hat {Q}_k}$$
(16)

The difference between the best predicted value and the measured value is called new interest:

$${\varepsilon _k}={Z_k} - H{x_k} - {\hat {r}_k}$$
(17)

Step 2: Update.

In the following Eq. (18),\(\:{\widehat{R}}_{k}\) represents the measurement noise matrix at the kth iteration, and the Kalman Filter gain is:

$${K_k}=\frac{{{{\tilde {P}}_k}{H^T}}}{{H{{\tilde {P}}_k}{H^T}+{{\hat {R}}_k}}}$$
(18)

The updated optimal estimate is:

$${\hat {x}_k}={\tilde {x}_k}+{K_k}{\varepsilon _k},{K_k} \in \left[ {0,{H^ - }} \right]$$
(19)

The updated optimal covariance matrix is:

$${\hat {P}_k}=(1 - {K_k}H){\tilde {P}_k}$$
(20)

The Sage-Husa noise estimator is a commonly used noise mean and covariance estimation method, which is combined with the KF to form the Sage-Husa Kalman Filter. The traditional Sage-Husa noise estimator simultaneously estimates the mean of system noise\(\:{\:\widehat{\text{q}}}_{\text{k}}\:\)and measurement noise\(\:{\:\widehat{\text{r}}}_{\text{k}}\)in the Kalman Filter.The recursive formula for these estimates involves subtraction operations to ensure unbiased covariance estimation.However, this algorithm’s straightforward implementation can compromise the semi-positive definiteness of the noise covariance matrix, resulting in observer dispersion. To address this issue, a stabilization coefficient\(\:{\lambda\:}_{s}({\lambda\:}_{s}>0)\)is introduced to enhance observer stability. Its respective recursive expression is:

$${\hat {q}_k}=(1 - {b_k}){\hat {q}_{k - 1}}+{b_k}({\hat {x}_k} - {\Phi _{k - 1}}{\hat {x}_{k - 1}})$$
(21)
$${\hat {Q}_k}=(1 - {d_k}){\hat {Q}_{k - 1}}+{d_k}({K_k}{\varepsilon _k}\varepsilon _{k}^{T}K_{k}^{T})+{\lambda _s}({\hat {P}_k} - {\Phi _{k - 1}}{\hat {P}_k}\Phi _{{k - 1}}^{T})$$
(22)
$${\hat {r}_k}=(1 - {b_k}){\hat {r}_{k - 1}}+{b_k}({Z_k} - {H_k}{\hat {x}_{k - 1}})$$
(23)
$${\hat {R}_k}=(1 - {d_k}){\hat {R}_{k - 1}}+{d_k}({\varepsilon _k}\varepsilon _{k}^{T}) - {\lambda _s}({H_k}{\hat {P}_{k - 1}}H_{k}^{T})$$
(24)

The variables\(\:{d}_{k}\)and \(\:{b}_{k}\)and represent the weighting coefficients in the noise covariance matrix, while\(\:\gamma\:\)represents the reserve coefficient for the noise mean. The coefficients\(\:{d}_{k}\)are determined based on the values provided in Eq. 25, primarily influenced by the magnitude of the new interest rate.

$${d_k}=\frac{{tr[{\varepsilon _k}]}}{{\gamma \cdot tr[{{\hat {q}}_k}+{{\hat {r}}_k}]}} \in (0,1)$$
(25)

In order to prevent observer dispersion, the covariance matching principle is used to determine the:

$$\varepsilon _{k}^{T}{\varepsilon _k}>\gamma \cdot tr[{H_k}{\hat {P}_{k - 1}}H_{k}^{T}]$$
(26)

When\(\gamma =1\), constitutes the most stringent convergence criterion. If Eq. (24) holds it means that the observer has diverged, at which point the system noise covariance\({\widehat {Q}_k}\)computed in Eq. (22) is not usable and the estimate\({\widehat {Q}_{k - 1}}\)from the previous moment can be chosen instead.

NQPLL

The extended inverse potential amplitude is essential in traditional PLL parameter design, leading to the utilization of a NQPLL for extracting rotor speed and position information. The normalized extended inverse electromotive force is subsequently integrated into the QPLL. Block diagram of NQPLL structure is as shown in Fig. 1.

Fig. 1
figure 1

Block diagram of NQPLL structure.

Full size image

The normalized error signal can be expressed as:

$$\Delta e=\frac{1}{{\sqrt {\hat {e}_{\alpha }^{2}+\hat {e}_{\beta }^{2}} }}( - {\hat {e}_\alpha }\cos {\hat {\theta }_e} - {\hat {e}_\beta }\sin {\hat {\theta }_e})=\sin ({\theta _e} - {\hat {\theta }_e})$$
(27)

When \({\theta _e} - {\widehat {\theta }_e}<\pi /2\), the normalized error signal can be simplified as:

$$\Delta e={\theta _e} - {\hat {\theta }_e}$$
(28)

The simplified block diagram of the structure represents the transfer function as:

$${G_{PLL}}(s)=\frac{{{{\hat {\theta }}_e}}}{{{\theta _e}}}=\frac{{{k_{pp}}s+{k_{pi}}}}{{{s^2}+{k_{pp}}s+{k_{pi}}}}$$
(29)

In the block diagram of the NQPLL structure,\(\:{k}_{pp\:}\)and\(\:{k}_{pi\:}\)represent the proportional and integral gains of the PI regulator. The PLL parameters are fine-tuned using the pole configuration method. Here,\(\:{\omega\:}_{p}\:\)specifies the bandwidth of the NQPLL, with a typical selection of\(\:{\:k}_{pp}=2{\omega\:}_{p}\) and \(\:{k}_{pi}={\omega\:}_{p}^{2}\).

LPF

Due to the nonlinearity of the inverter with magnetic field space harmonics, which lead to the presence of high-frequency harmonics in the extended reaction potential, the estimated position may incorporate sub-harmonics. To mitigate this concern, a low-pass filter is utilized to dampen resonance in the signal. The transfer function is expressed as follows:

$${G_{LPF}}(s)=\frac{{{{\hat {\omega }}_e}}}{{{\omega _e}}}=\frac{{{k_F}s}}{{{k_F}s+1}}$$
(30)

where\({k_F}\)is the coefficient in the low-pass filter.

Speed loop controller design

SMC

The error between the rotor speed estimated by the observer and the reference speed to the speed loop controller, whose controller uses a slip film controller with greater immunity and robustness, and whose slip film controller is designed as follows:

Define the state variables of the SMC controller of the PMSM system as:

$$\left\{ {\begin{array}{*{20}{c}} {{x_1}{\text{=}}{\omega _{ref}} - {\omega _m}} \\ {{x_2}={{\dot {x}}_1}= - {{\dot {\omega }}_m}} \end{array}} \right.$$
(31)

where \(\:{x}_{1}\:\)represents the rotor speed error,\(\:{\omega\:}_{ref}\)denotes the set reference speed, and \(\:{\omega\:}_{m}\)signifies the estimated rotor speed. In theoretical calculations, motor damping is often disregarded to derive the equation of state for the velocity error:

$$\left\{ {\begin{array}{*{20}{c}} {{{\dot {x}}_1}={x_2}=\frac{1}{J}({T_L} - {K_t}{i_q})} \\ {{{\dot {x}}_2}= - \frac{{{K_t}}}{J}{{\dot {i}}_q}} \end{array}} \right.$$
(32)

By making the above equation\({\dot {i}_q}=u\), the equation of state can be made as follows:

$$\left[ {\begin{array}{*{20}{c}} {\mathop {{x_1}}\limits^{.} } \\ {\mathop {{x_2}}\limits^{.} } \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} 0&1 \\ 0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_1}} \\ {{x_2}} \end{array}} \right]+\left[ {\begin{array}{*{20}{c}} 0 \\ { - \frac{{{K_t}}}{J}} \end{array}} \right]u$$
(33)

where u is the SMC control law, \({K_t}=3/2 \cdot {p_n}{\psi _f}\), J is the inertial momentum;

Define the synovial surface as:

$$s=c{x_1}+{x_2},c>0$$
(34)

In this context, \(\:{x}_{2}\) represents the first-order derivative of the rotational speed error, with c being the adjustable parameter. The following equation is derived:

$$\dot {s}=c{\dot {x}_1}+{\dot {x}_2}=c{x_2}+{\dot {x}_2}=c{x_2} - \frac{{{K_t}}}{J}u$$
(35)

The convergence rate of the slip flux controller is designed as \(\:\dot{s}=(-{k}_{sp}\bullet\:\sqrt{\left|s\right|}-{k}_{si}/S),{k}_{sp}、{k}_{si}>0\). The integral term S, denoted by \(\:{k}_{si}/S\), indicates integration, while all other terms are associated with sliding mode surfaces.

The SMC control law expression is:

$$u=\frac{J}{{{K_t}}}\left( {c{x_2}+{k_{sp}}\sqrt {\left| s \right|} \operatorname{sgn} (s)+\frac{{{k_{si}}}}{s}\operatorname{sgn} (s)} \right)$$
(36)

MTPA

Utilizing the PMSM electromagnetic torque formula, the Lagrange pole method is applied to determine an optimal set of combinations\(\:{i}_{d}\)and\(\:{i}_{q}\), enabling the implementation of maximum torque-current ratio control.

The maximum current formula is as follows:

$$i_{{_{s}}}^{2}=f({i_d},{i_q})=i_{d}^{2}+i_{{_{q}}}^{2}$$
(37)

Considering the electromagnetic torque equation, the partial derivative with respect to the independent variable \(\:{i}_{q}\) is:

$$\frac{{\partial (i_{{_{s}}}^{2})}}{{\partial ({i_q})}}=2{i_d} - \frac{{2({L_d} - {L_q})i_{q}^{2}}}{{{\psi _f}+({L_d} - {L_q}){i_d}}}=0$$
(38)

The final derivation\({i_d},{i_q}\)of equation:

$${i_d}=\frac{{ - {\psi _f}+\sqrt {\psi _{{_{f}}}^{2}+4{{({L_d} - {L_q})}^2}i_{q}^{2}} }}{{2({L_d} - {L_q})}}$$
(39)
$${i_q}=\sqrt[4]{{\frac{{\frac{4}{9}T_{{_{e}}}^{2} - \frac{4}{3}{T_e}{\psi _f}{i_q}}}{{4{{({L_d} - {L_q})}^2}}}}}$$
(40)

Simulation results

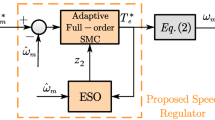
In Fig. 2, the speed loop contains two modules: SMC and MTPA. It takes the observed rotor speed estimation error \(\:{\varDelta\:\omega\:}_{m}\) as input, calculated the electromagnetic torque\(\:\:{T}_{e}\:\)through the slip film controller designed in this paper, and then realize the maximum torque current ratio control through MTPA to find the optimum\(\:{i}_{d}\)and\(\:{i}_{q}\). Initially, the sampling of motor parameters \(\:{i}_{a}\), \(\:{i}_{b}\), and \(\:{i}_{c}\)is conducted. Following the Clark transformation and Park transformation to get a comparison, the PI regulator in the current loop outputs axis voltage. Subsequently, after inverse Park transformation into the voltage of the axis, the SVPWM algorithm modulation, written using a MATLAB function, generates the coded values for the state of the three half-bridges at that particular moment in time. These coded values are then utilized to control the switching state of the IGBT inverter, thereby driving the motor. The observer contains three modules: ISH-FEKF, NQPLL & LPF, whose derivation equations are shown above. All of them are simulation models built by math module.

Fig. 2
figure 2

Simulation model for PMSM position sensorless control systems.

Full size image

The parameters of the two PMSM control system are shown in Table 1, and since the maximum speed of PMSM1 is 1600 rpm, PMSM2 is used to test the estimation accuracy of the observer at 2000 rpm and 3000 rpm. The PI parameters of the speed and current loops are parameterized using a typical type II system, which suppresses the overshoot and unstable fluctuations in the speed waveform so that the current system’s can perform well.

Table 1 PMSM control system parameters.
Full size table

The convergence and stability of the conventional EKF observer have been rigorously evaluated. The control system parameters are simulated and tested using a parameter identification algorithm to establish the initial values of the process noise matrix Q and the measurement noise matrix R. These initial values are set in a manner that ensures optimal performance across different speed bands. The noise covariance matrix (QR) of the conventional EKF observer for PMSM1 and PMSM2 is presented in Eqs. (41) and (42).

$${Q_1}{\text{=}}\left[ {\begin{array}{*{20}{c}} {0.001}&0&0&0 \\ 0&{0.1}&0&0 \\ 0&0&{10}&0 \\ 0&0&0&{0.01} \end{array}} \right]\,\,\,\,\,\,\,\,{Q_2}{\text{=}}\left[ {\begin{array}{*{20}{c}} {0.0001}&0&0&0 \\ 0&{0.25}&0&0 \\ 0&0&1&0 \\ 0&0&0&{0.001} \end{array}} \right]$$
(41)
$${R_1}{\text{=}}\left[ {\begin{array}{*{20}{c}} {0.1}&0 \\ 0&{0.1} \end{array}} \right]\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{R_2}{\text{=}}\left[ {\begin{array}{*{20}{c}} {0.1}&0 \\ 0&{0.1} \end{array}} \right]$$
(42)

The comparison of observed speeds within each speed domain of 500 rpm, 1000 rpm, and 1500 rpm is examined, as illustrated in Fig. 3. The total sampling time of the motor system is set to 10 s, with a sampling period of 1e-4. fpwm is 10 kHz. In Fig. 3, the black waveform represents the actual RPM of the motor controlled by the Hall sensor, the red waveform illustrates the observed RPM from the conventional EKF, the green waveform depicts the observed RPM from the EKF incorporating Sage-Husa, and the red waveform exhibits the observed RPM from the full-order EKF enhanced with the proposed Sage-Husa modifications in this study.

At 500 rpm, the motor reaches steady-state within 0.4 s after startup and acceleration, with minimal overshooting. The traditional EKF displays evident error fluctuations of approximately 3 rpm, while both SH-EKF and ISH-FEKF exhibit negligible observation errors. However, the SH-EKF observation waveforms demonstrate noticeable distortion, whereas the ISH-FEKF observation waveforms exhibit slight shifts.

As the motor speed increases to 1000 rpm, the traditional EKF shows an observation error of around 5 rpm. The performance of the traditional Sage-Husa variant deteriorates, resulting in increased waveform distortion and observation errors ranging from 3 to 5 rpm. The ISH-FEKF demonstrates optimal observation performance stability in this scenario. Upon reaching 1500 rpm, the observation error of the traditional EKF observer escalates to about 10 rpm. The SH-EKF observer struggles to maintain stability in the high-speed domain, whereas the ISH-FEKF observer showcases robust observation performance and stability at 1500 rpm.

Fig. 3
figure 3

Comparison of observed speeds at 500 rpm, 1000 rpm and 1500 rpm speed changes.

Full size image

Upon reaching 1500 rpm, the observation error of the traditional EKF observer escalates to about 10 rpm. The SH-EKF observer struggles to maintain stability in the high-speed domain, whereas the ISH-FEKF observer showcases robust observation performance and stability at 1500 rpm.

Figure 4 illustrates the comparison of motor torque among different observers within the PMSM position sensor-less system, wherein the torque reflects the error in the observed speed. At a motor speed of 500 rpm, the motor torque values for the traditional EKF observer range from 0.145 to 0.15 rad, for the SH-EKF observer range from 0.14 to 0.15 rad, and for the ISH-FEKF observer range from 0.128 to 0.132 rad. The ISH-FEKF observer demonstrates improved stability and reduced motor torque by approximately 0.015 rad compared to the SH-EKF observer.

As the motor speed increases to 1000 rpm, the motor torque controlled by the traditional EKF observer ranges from 0.2 to 0.218 rad, by the SH-EKF ranges from 0.182 to 0.212 rad, and by the ISH-FEKF ranges from 0.182 to 0.195 rad. Compared to the traditional EKF observer, the ISH-FEKF observer reduces the motor torque by around 0.023 rad, and compared to the SH-EKF observer, the reduction is about 0.015 rad, with significantly decreased fluctuation range observed in the SH-EKF.

Upon reaching a motor speed of 1500 rpm, the motor torque controlled by the traditional EKF observer ranges from 0.228 to 0.252 rad, the SH-EKF observer exhibits instability, and the ISH-FEKF observer ranges from 0.202 to 0.22 rad. The ISH-FEKF observer achieves a torque reduction of 0.026 rad compared to the traditional EKF observer.

Fig. 4
figure 4

Comparison of motor torque during sudden speed change.

Full size image

Figure 5 illustrates the ISH-FEKF observation of the rotor position error within each speed domain during sudden speed changes. The estimation accuracy of the rotor position can be maintained at 0.0001 rad across varying speeds. A specific setting incorporated in the ISH-FEKF observer is 0.01, enhancing the observer’s convergence performance. This setting ensures improved performance in achieving observer convergence during sudden speed changes.

Figure 6a displays the observed speeds of the traditional EKF at 2000 rpm and 3000 rpm. In the graph, the blue curve represents the actual motor speed, while the red curve depicts the observed speed. At a reference speed of 2000 rpm, the EKF observation curve fluctuates between 1958 and 1978 rpm, resulting in an error of approximately 20–40 rpm compared to the actual motor speed. When the reference speed is set to 3000 rpm, the EKF observation curve fluctuates within the range of 2940–2990 rpm, with an error ranging from 5 to 55 rpm.

Figure 6b illustrates the observation speeds of the ISH-FEKF using the filtered curve. By employing filtering technology, the FEKF observation speed exhibits reduced fluctuation in the observation speed curve. At 2000 rpm, the error with the actual motor speed is approximately 24 rpm, while at 3000 rpm, this error decreases to 0-18 rpm, leading to a reduction of about 30 rpm compared to the traditional EKF observer.

Fig. 5
figure 5

Rotor position observation error in different speed range.

Full size image
Fig. 6
figure 6

Comparison of observed rotational speeds at 2000 rpm and 3000 rpm speed changes. (a) The observed speeds of the traditional EKF. (b) The observation speeds of the ISH-FEKF.

Full size image

Figure 7 presents a comparative analysis of motor torque under sudden load fluctuations, with the implementation of a sliding mode controller to address disruptive factors such as load variations and enhance response speed. In the context of simulation testing, a specific load is applied to the motor with a reference speed of 1000 rpm. The conventional PI controller results in motor speed lag, where adjusting the proportional term to suppress overshooting concurrently has a significant impact on response speed, leading to a noticeable decline in speed post-load addition.The utilization of the sliding mode controller effectively alleviates the aforementioned issues, with poor parameter settings potentially causing sliding mode chattering.

The value of c in the SMC module is 26,\(\:{k}_{si}\) is 3.2, and \(\:{k}_{sp}\:\)is 0.225. The duration for the rotor to transition from start-up acceleration to a steady state is reduced from 0.4 s to 0.25 s.

Figure 8 displays the results of the motor forward and reverse tests conducted at 200 rpm and 500 rpm. The speed tracking performance is excellent in the low-speed range at both 200 rpm and 500 rpm, as evidenced by the electrical angle changes depicted in Fig. 9a,b respectively. Notably, the response time for speed increase and decrease at 500 rpm is under 0.04 s, significantly quicker than that observed at 200 rpm. However, it is observed that the observer exhibits fluctuations during forward and reverse movements at medium and high rotational speeds, with a higher likelihood of fluctuations occurring at higher rotational speeds.

Fig. 7
figure 7

Comparison of motor torque during sudden load change.

Full size image
Fig. 8
figure 8

200 rpm and 500 rpm motor forward and reverse test.

Full size image
Fig. 9
figure 9

Change of phase angle forward and reverse rotation (a) 200 rpm/min (b) 500 rpm/min.

Full size image

Physical results

The experimental platform of this study, as illustrated in Fig. 10, primarily comprises three components: the motor body, the drive control circuit, and the host computer. In this research, an adaptive extended Kalman Filter observer is employed in the sensorless control system for PMSM. Specific configuration operations carried out on the main MCU STM32G4 include enabling the Uart serial port to output waveforms of three-phase currents and motor speed for display on the VOFA host computer. Three-phase current sampling is performed using a combination of op-amps and ADC. TIM1, ADC, COMP analog comparator, and DAC are utilized to generate three-phase complementary PWM waves with dead-time and basic overcurrent protection. Additionally, GPIO controls LED and captures input key signals. The DAC converts digital signals within the MCU to analog outputs for debugging in an oscilloscope. The rated input voltage of the drive control circuit board is 24 V. It is connected to the motor’s three-phase lines and sequentially linked to ST-Link’s TX, RX, DIO, CLK for communication with the PC. Finally, the sensorless algorithm developed in MATLAB Simulink is used to generate embedded code, which is then burned into the drive control circuit board for experimental testing.

Fig. 10
figure 10

PMSM drive control experiment platform.

Full size image

The tracking performance of the conventional EKF and ISH-FEKF observers at 500 rpm, 1000 rpm and 1500 rpm is tested under the PMSM1 control system. Figure 11a shows the real-time RPM curve observed by the EKF when the reference speed is set to 500 rpm, and it can be seen that the real-time RPM curve is controlled in the range of 480–518 rpm for 4 s, with about rpm error. Figure 11b shows the real-time speed curve observed by ISH-FEKF when the reference speed is set to 500 rpm, and it can be seen that the real-time speed curve is controlled to float in the range of 482-517 rpm, and there is about rpm error. The experimental results show that at 500 rpm, the observation accuracy of the two observers is similar.

Fig. 11
figure 11

Comparison of real-time speed profiles observed by the observer at 500 rpm. (a) EKF. (b) ISH-FEKF.

Full size image

Figure 12a shows the real-time speed curve observed by EKF when the reference speed is set to 1000 rpm, and it can be seen that the real-time speed curve in 2s is controlled to float in the range of 982–1018 rpm, and there is about rpm error. Figure 12b shows the real-time speed curve observed by ISH-FEKF when the reference speed is set to 1000 rpm, and it can be seen that the real-time speed curve is controlled to float in the range of 985–1012 rpm. The experimental results show that at 1000 rpm, the error interval of ISH-FEKF observation is narrowed down by 3–6 rpm compared with that of the conventional EKF observer, and as the rotational speed increases, the fluctuation of the observed rotational speed curves increases, and the real-time rotational speed curves observed by ISH-FEKF are obviously larger than that of the conventional EKF.

Fig. 12
figure 12

Comparison of real-time RPM profiles observed by the observer at 1000 rpm. (a) EKF. (b) ISH-FEKF.

Full size image

Figure 13a depicts the real-time speed curve observed by the EKF when the reference speed is set to 1500 rpm. It is evident that the real-time speed curve fluctuates within the 1478–1522 rpm range within 1 s, with an approximate rpm error. In Fig. 13b, the real-time speed curve observed by the ISH-FEKF at a reference speed of 1500 rpm shows fluctuations within the range of 1488–1512 rpm, with a similar approximate rpm error. The experimental findings demonstrate that at 1500 rpm, the error interval observed by the ISH-FEKF observer is reduced by 10 rpm compared to the traditional EKF observer. While the accuracy of the ISH-FEKF observer improves with higher speeds, the inevitable level of fluctuations also escalates due to the adaptive parameters. The test results closely align with the simulation outcomes.

Fig. 13
figure 13

Comparison of real-time RPM profiles observed by the observer at 1500 rpm. (a) EKF. (b) ISH-FEKF.

Full size image

It is tested whether the observer designed in this paper can converge quickly to ensure the normal operation of the motor at 3000 rpm. As shown in Fig. 14 (a) (b), the experimental results show that at 2000 rpm, the error interval of the traditional EKF observation is about 20–40 rpm, and the error interval of the ISH-FEKF observation is about 10–15 rpm, which is narrowed down by 10–25 rpm compared with the conventional EKF observation, and the optimization of the LPF parameter should alleviate the problem, which is probably due to the adaptive parameter leading to the observation of the waveform appearing high-frequency spike signals several times. Optimization of the LPF parameters should alleviate the problem.

Fig. 14
figure 14

Comparison of real-time RPM profiles observed by the observer at 2000 rpm. (a) EKF. (b) ISH-FEKF.

Full size image

As shown in Fig. 15a, b, the experimental results show that at 3000 rpm, the error interval of traditional EKF observation is about 55–70 rpm, and the error interval of ISH-FEKF observer is about rpm under the ideal condition of stable signal without sharp pulse signal, which is narrowed down by rpm in comparison. In Figs. 14 and 15, the red waveform is the stator current and the green waveform is the electrical angle, and the electrical angle observed by ISH-FEKF is smoother in comparison.

Fig. 15
figure 15

Comparison of real-time RPM profiles observed by the observer at 3000 rpm. (a) EKF. (b) ISH-FEKF.

Full size image

Conclusion

In this research, we introduce an improved Sage-Huse adaptive Kalman observer for sensorless position control of PMSM. The study involves testing the traditional EKF and the adaptive EKF with the addition of the Sage-Huse noise estimator using MATLAB Simulink. The estimation performance of the conventional EKF observer in the system is evaluated, highlighting the issue of increased dispersion after incorporating Sage-Huse. Subsequently, we identify the dispersion problem and enhance the observer accordingly. The sensorless control algorithm is developed by integrating SMC and MTPA, followed by simulation tests under various conditions such as fixed load and variable speed, fixed speed and variable load, as well as forward and reverse rotation. The effectiveness of the ISH-FEKF observer is demonstrated in experiments conducted on the PMSM drive control platform utilizing the STM32G4 master MCU. Through experimental tests ranging from 500 to 3000 rpm, the results demonstrate that the ISH-FEKF observer can sustain a high level of estimation accuracy despite fluctuations in reference speed and the system environment. However, it may also exhibit potential instability, resulting in heightened fluctuations. At 3000 rpm, while ensuring the motor’s normal operation, the ISH-FEKF observer demonstrates a narrower error margin in rpm compared to the traditional EKF observations. The ISH-FEKF observer maintains excellent estimation accuracy across various speed ranges and control systems by incorporating new information to update the noise covariance between Q and R based on the error between predicted and measured values. The observer showcases superior performance in terms of accuracy, adaptability, and rapid convergence compared to the conventional EKF, which struggles with varying speed conditions due to its reliance on QR integration based on the current system state. The proposed ISH-FEKF observer stands out for its high accuracy, adaptability, and efficient convergence properties.