Feasibility study of multi Laue lens based SPECT with a dedicated 3D reconstruction algorithm using Monte Carlo simulations

Abstract

The development of in-vivo imaging techniques has significantly advanced biomedical science and cancer diagnosis, yet their limited spatial resolution constrains their utility in small-animal studies and early-stage tumour detection. This study introduces a novel SPECT system employing X-rays and gamma-rays focusing optics—traditionally used in astronomy—to enhance spatial resolution in small object imaging at sub-millimetre scales without compromising sensitivity. Current SPECT imaging techniques rely on absorptive collimation, which creates a trade-off between sensitivity and resolution, often limiting spatial resolution and hindering the examination of various biomedical research areas, thereby restricting the accurate identification of small lesions. Our innovative design utilizes an array of Laue lenses, which can focus gamma rays without the drawbacks of traditional collimators, thereby achieving ultra-high spatial resolution. This approach is motivated by the need for improved imaging capabilities that allow for the detection of subtle physiological changes and tumour evolution in transgenic models, which are critical for advancing personalized medicine and significantly impacting early-stage tumour detection. A custom Monte Carlo simulation models the system’s spatial resolution and sensitivity, supported by a tailored 3D reconstruction algorithm that complements the system’s geometry. Findings reveal that our proposed system can achieve a spatial resolution of 0.1 mm full width at half maximum (FWHM) and a sensitivity of 1,670 cps/µCi. This setup allows the discrimination of adjacent volumes as small as 0.113 nL, far surpassing the capabilities of existing SPECT systems, including the SIEMENS parallel LEHR and multi-pinhole (5-MWB-1.0) Inveon SPECT, which are limited to a 2 mm resolution due to inherent resolution-sensitivity trade-offs. The proposed design could revolutionize SPECT imaging, significantly impacting transgenic animal research and early-stage tumour detection with its sub-millimetre resolution, ultimately enabling more precise and effective diagnostic capabilities in preclinical studies.

Introduction

The study of SPECT functional images is a unique probe for revealing physiological processes at organs’ cellular and molecular levels. In SPECT, a tracer is injected intravenously into the patient’s bloodstream, interacting with the body’s metabolism and distributing appropriately in the organs of interest¹. This process enables visualization of metabolic activity, which is critical for accurate diagnosis and treatment planning. Gamma photons are emitted isotropically due to the radioactive decay of the radioisotope and are detected by a scintillator detector. Then, information about the incidence angle of the photons detected is required to reconstruct the radioisotope’s original location. Therefore, a collimator is used to project back the rays from the specific detector position to the gamma rays source². Significant advancements in the multidisciplinary field of molecular imaging have sparked a biomedical revolution³. However, current gamma rays detection methods heavily rely on conventional collimation techniques, which present significant limitations in sensitivity and resolution. Up to this point, gamma rays have been detected using parallel and multi-pinhole conventional collimators. The collimator is a crucial component of the imaging chain that controls the final functional image’s noise, resolution, and sensitivity levels⁴. These limitations underscore the need for innovative approaches to imaging that can enhance both resolution and sensitivity in small-animal studies and early-stage tumour detection. In parallel hole SPECT, most photons that reach the collimator are absorbed by its septa, while other ones pass through the narrow field of view and contribute to the signal in the detector. Thus, the resolution and sensitivity of the corresponding system are primarily determined by the collimator’s radius, depth, and septal thickness^5,6.

Additionally, imaging with gamma rays emitted by radionuclides used in SPECT imposes additional challenges in minimizing collimator penetration and scatter without negatively impacting spatial resolution or sensitivity⁷. Compared to parallel hole collimators, a pinhole collimator can help reduce the compromise between sensitivity and spatial resolution². However, it too suffers from sensitivity resolution trade-offs and degraded Signal to Noise Ratio (SNR), particularly for small radiating sources that may represent early-stage tumours^8,9. This highlights the critical need for improved collimation techniques that can effectively balance sensitivity and resolution, especially in detecting small lesions.

A significant disadvantage of a single pinhole collimator is its limited Field of View (FOV) and low sensitivity. The use of multi-pinhole collimators can improve sensitivity and obtain a larger FOV while still achieving an adequate spatial resolution compared to the pinhole collimator^10,11. The geometry of single and multi-pinhole collimators substantially impacts image quality and is critical for SPECT imaging. Utilizing a multi-pinhole collimator is a typical approach to boosting system sensitivity. However, due to the system’s magnification, the FOV, and the detector area, the number and placement of pinholes in the collimator are constrained¹¹. When pinholes are positioned closely together, projections on the detector may be multiplexed. This overlap causes image artefacts and adds complexity to the 3D reconstruction algorithms due to the uncertainty of which pinhole the photon has passed through¹⁰. The requirement for increased sensitivity to identify malignant tumours in the sub-millimetre range may necessitate extending the size of the detectors to compensate for the low sensitivity of smaller detectors. However, increasing the detector size reduces the SNR Field because the SNR deteriorates with the square root of the counts in the background¹⁰.

There is a compelling need to increase image resolution to detect tumours in their earliest stages. Moreover, conventional imaging techniques such as SPECT and PET can be utilized to localize and image physiological functions in small animals with a spatial resolution of 1–2 mm¹². One option to increase spatial resolution is to focus the gamma rays; however, this is not possible to do with conventional refractive optics¹³. The use of grazing incidence optics has been proposed for small animal radionuclide imaging in the case of $\:27.5\:\text{k}\text{e}\text{V}\:$gamma rays emitted by ¹²⁵I^14,15. The system is based on using reflective optics with three nested mirrors to focus the radiation. The system is theoretically able to achieve sub-millimetre spatial resolution with comparable sensitivity to the conventional parallel collimators. However, because the critical angle for total reflection is inversely proportional to photon energy and a medical device must be as compact as possible, this approach is unsuitable. Throughout the 1980s, the Argonne group began seven research projects examining various designs for Laue lens crystals to focus high-energy photons in the field of astrophysics^16,17,18. The Argonne crystal diffraction group took the first step in applying the Laue lens diffraction concept to nuclear imaging in the 1990s. In 2000, researchers started to study the opportunity of using diffracting lenses to image radioactivity by developing the world’s first lens system capable of focusing photons with energies of $\:\:140\:\text{k}\text{e}\text{V}\:$emitted by ^99mTc¹⁹. This advancement highlights the potential of Laue lens systems to overcome limitations inherent in traditional collimators. Due to the detector’s small area, a high SNR was attained. Additionally, even with low activity sources, the detection effectiveness remained excellent. In 2005, a diffraction-based imaging system for detecting gamma rays in the range of $\:100-200\:\text{k}\text{e}\text{V}\:$was proposed^20,21. This presentation of Laue lens diffraction with a focus on nuclear medicine prompted a strong scientific interest in this application. Paterno et al.²² presented a gamma rays focusing study for SPECT, based on the Laue lens diffraction concept, with the major aim of determining a high-resolution image on the detector plane. In this work, we investigate the opportunity to focus gamma rays by means of Laue lenses to achieve a sub-millimetre spatial resolution. They consist of a compact arrangement of crystals in concentric rings to focus the gamma rays by means of diffraction. Laue lenses offer a promising approach for bypassing the constraints of non-focusing detection methods, including geometrical and quantum optics^14,15.

In this work, we propose a SPECT imaging system akin to the light field camera, which might offer significant post-processing capabilities, such as refocusing the image after it has been collected and shifting the point of view²³. A plenoptic camera is not substantially different from a conventional one, except that a micro-lens array is placed right in front of the imaging sensor, allowing the directions and intensities of light rays to be concurrently recorded²³. However, finding a microlenses array that operates well for gamma rays to replicate the vision of light field imaging in gamma rays remains challenging¹³. To apply the light field concept to existing diagnostic imaging systems, optics capable of focusing gamma rays are required. Tahtali sparked the research that led to the incorporation of light field imaging technology into CT imaging systems by developing a new imaging approach capable of storing both the directional and photon intensity information of incident X-rays, by employing a multi-pinhole camera similar to optical light field technology to obtain simultaneous projections from numerous X-rays sources²⁴. However, achieving the concept of a light field utilizing a gamma-focusing element remains a challenge.

This research addresses some open design questions, including how to combine the Laue lens geometry with standard gamma cameras. Also, it presents the first attempt to develop a novel 3D image reconstruction study for an array of Laue lenses in a SPECT gamma camera environment. This research addresses three main challenges. First, achieving a sub-millimetre resolution that is important to understand the fundamental mechanisms underlying brain function and human neurological disorders in transgenic animals^25,26. Secondly, a key objective of this study is to develop methods for the detection of cancer during its early evolutionary stages. This is particularly critical as nanolitre volumes are known to play a substantial role in the manifestation and progression of cancer. Thirdly, the research explores potential solutions to reduce the radiotracer doses administered to patients while simultaneously improving resolution.

Methods

This section describes the methods used to model and characterize the design of the proposed multi-lens-based SPECT system, shown in Fig. 1a. To model and study the envisioned system behaviour, we developed two different studies in Mathematica²⁷ and MATLAB²⁸. The Mathematica-based study was specifically developed to design and optimize the Laue lens tailored for a SPECT medical imaging application using a genetic algorithm. Genetic algorithms are adaptive heuristic search algorithms based on the principles of natural selection and genetics²⁹, allowing for the optimization of lens parameters to maximize photon diffraction sensitivity. Key components of the Mathematica study included analytical modelling to solve the Bragg diffraction equations, calculating the Bragg angles relevant to 140 keV photon energy, and assessing the diffraction efficiency of materials such as Aluminium and Copper. Additionally, the software enabled the visualization of the lens geometry, optimizing the arrangement of crystals for enhanced photon focusing.

The second MATLAB study was implemented for the modelling of the SPECT gamma camera integrated with the designed Laue lens to characterize the multi-lens-based SPECT. This included the development of a Monte Carlo simulation to evaluate photon propagation and the forward projection of gamma rays through the lens³⁰. The Monte Carlo simulations in MATLAB were based on the standard forward projection and ray tracing concept, starting by generating photons with specific energies, such as 140 keV for Technetium-99 m, along with their emission directions from a radiopharmaceutical source. The paths of these photons were tracked as they interacted with the Laue lens, capturing both successful diffraction events and those that passed through without interaction. Additionally, MATLAB simulated the detection process, recording the energy and location of focused photons when they hit the detector surface. This data facilitated the assessment of the Point Spread Function (PSF), as well as the system’s resolution and sensitivity.

The forward projection algorithms developed for multi-lens-based SPECT would undoubtedly differ from the approach for conventional parallel or multi-pinhole SPECT; however, we tweaked the method to analyse the acquired images from an array of Laue lenses in a planer plane. Furthermore, we developed a customized 3D image reconstruction algorithm in MATLAB to reconstruct the projection images resulting from the focused photons. The purpose of the reconstruction algorithm is to calculate an accurate 3D radioactivity distribution from the acquired projections. Validating the reconstruction algorithm for the new proposed SPECT design is crucial. To this end, we conducted validation studies that addressed two essential parameters, the mapping of the depth and shift information in the 3D reconstructed images of the multi-lens-Based SPECT and the sensitivity mapping over the FOV. The performance parameters of the proposed design were assessed against the existing parallel LEHR and multi-pinhole Inveon SPECT based on two figures of merits, sensitivity, and resolution, which were inferred based on standard methods. We used simple phantoms, described in the coming sections, for the initial characterization of the system.

Optimization of the Laue lens design

The Laue lens is a diffractive optical element traditionally used in high-energy physics and astronomy, adapted in this study for nuclear imaging applications such as SPECT. The lens operates by diffracting incoming gamma rays through crystal planes, following the principles of Bragg diffraction²⁹. While the Laue lens was originally developed for astrophysical applications, its use in medical imaging, as demonstrated in this work, represents a novel adaptation. The system was specifically designed for energies in the 100–200 keV range, typical of nuclear imaging tracers. The adaptation involved reducing the lens size and reconfiguring the geometry to suit the clinical environment, where space is limited, and the imaging system must be compact and efficient.

A tracking Monte Carlo genetic algorithm in Mathematica³¹ was developed and used to model and optimize the Laue lens design, which we propose to couple to the SPECT system. The optimization criteria are based on attaining the highest photon diffraction sensitivity, defined as the number of diffracted photons divided by the number of photons emitted by an isotropic source and the smallest focal length necessary to obtain a compact design. The Laue lens design is optimized based on the initial input parameters, the photon energy, the desired focal length, and sensitivity²⁹. Once the initial parameters are defined, the number of crystals in each ring, the angular velocity, the thickness of diffracting planes, the material type, and the crystal configurations are computed. For the initial prototype and system practicality, each ring’s crystals are assumed to be identical in material and size. However, each ring is built with a unique number of crystals and would have a distinct Bragg’s angle.

For the crystal selection and arrangement, the Laue lens is constructed using high-quality diffractive crystals. For the Ring configuration and geometry, the Laue lens utilized in this study comprises multiple concentric rings, with each ring designed to diffract photons at different Bragg angles. This configuration is essential for achieving sharp focus and high-resolution imaging. Regarding the Laue lens’s size, it was optimized specifically for clinical use, a departure from the traditionally larger lenses typically used in astrophysical applications. The compact design of the lens facilitates practical integration into existing SPECT systems without compromising the high resolution necessary for detailed medical imaging. By reducing the size of the lens, the design minimizes the challenges associated with alignment and positioning, making the system more user-friendly and efficient in real-world applications.

Based on the genetic algorithm in Mathematica²⁹, a total of 606 crystals made from aluminium (Al), silver (Ag), and copper (Cu) mosaic crystals were selected for the lens design, which are found to be (using Mathematica simulations²⁹) the best materials for obtaining a small focal length combined with the best sensitivity. Each crystal has a surface of 1.0 × 1.0 mm² with a thickness of 50 μm, and the mosaicity of the crystals is 30 arcsec. The approximate total area of the crystals in one lens is 460 mm², excluding the white spaces between the Laue lens rings.

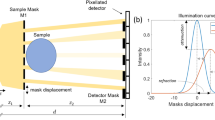
The Laue lens is optimized for 140 keV, the energy of the gamma rays emitted by ⁹⁹Tc. The design considers the distances L_s and L_d representing the distances between the lens and the gamma rays source and the lens and the detector plane, respectively (see Fig. 1a). To facilitate effective patient positioning during treatment, the focal length of the lens is configured to maintain a lens-to-target distance of 50 cm, allowing for adequate patient positioning throughout the system’s motion during treatment. In the initial experiment, we employed a configuration akin to a 3 × 3 pinhole collimator but incorporated nine Laue lenses. This strategic choice was aimed at optimizing both spatial resolution and FOV. Each lens plays a critical role in collecting and focusing gamma rays, thereby enhancing the overall sensitivity of the imaging system. The arrangement of multiple lenses allows for a broader FOV while maintaining high spatial resolution, which is essential for accurately detecting small lesions and improving image quality. Figure 1b shows the optimized Laue lens, and Table 1 lists the designed lens features.

Fig. 1

Multi Laue lens design: (a) Illustration of the proposed multi-lens-based SPECT design showing the focused gamma rays, the array of nine Laue lenses at the pinhole centres and the detector with the clinical collimator removed. L_s and L_d are the distances from the lens to the source and from the lens to the detector, respectively. (b) The proposed Laue lens is optimized using Monte Carlo simulations; the legend indicates the material of each element of the Laue lens.

Table 1 Parameters of the generated Laue lens design.

Multi-lens-based SPECT geometry

The designed system consists of nine Laue lenses (called here Laue-collimator) placed at the pinhole centres in a geometry similar to a multi-pinhole collimator with the clinical collimator removed. Figure 1a shows the conceptual illustration of the proposed multi-lens-based SPECT. The lenses are placed in a 3 × 3 array for the initial geometry. The Laue-collimator is positioned at equal distances from the source and the detector plane. The pitch or the distance between the centres of adjacent Laue lenses is equal to the lenses’ diameter. The active area of the detector module is matched to the envisaged Laue-collimator, which has a 150 × 150 mm² active area. The collimator of lens-based SPECT design is intended to be simple yet practical.

Study of the system characteristics

The multi-lens-based SPECT scans were performed for 360° rotation with 10° steps. We used one-point, three-point sources and a customized phantom with three cylindrical capillaries placed inside a cylindrical volume, represented in Fig. 2. Using standard phantoms in our evaluation of the newly developed SPECT system ensures controlled conditions for precise assessment of spatial resolution and sensitivity. This methodology establishes a reliable baseline, emphasizing the novelty and advantages of our design compared to conventional imaging techniques. The activity of the different point sources or volumes was selected to imitate cases of a suspicious mass or tumour in its initial stage compared to the background. The three-sphere phantom consists of spherical sources with a 0.03 mm radius, and the spheres are spaced by 0.1 mm from centre to centre (See Fig. 2a). Each sphere has an activity of 0.1 mCi. Sub-millimetre-sized spheres were chosen because the proposed crystal lens system has lower background noise and maintains the same overall sensitivity for small sources; thus, it should provide higher sensitivity than existing full-body scanners for sub-millimetre small sources^15,30. The phantom used for resolution studies consists of cylindrical capillaries with a 0.03 mm radius, and the cylinders are spaced by 0.1 mm from centre to centre (See Fig. 2b). Each cylinder has an activity of 0.1 mCi. The cylinders are placed in a cylinder of 0.5 mm in height and 0.5 mm in diameter. Then, a customized phantom, shown in Fig. 2c, was used to study system performance in lesion detection. It consists of a sphere with a 0.03 mm radius (representing a defect) placed inside a cylinder (representing the background), which represents the simplified geometry of a cylinder with 0.2 mm height and 0.2 mm diameter. The activity in the sphere is three times higher than the one of the rest of the cylinder. The different activity mimics the cancerous tumour with higher radio tracer absorption of the gamma rays.

Fig. 2

Customized phantoms: (a) Three spheres with a radius equal to 0.03 mm and spaced by 0.1 mm from centre to centre were used to validate the systems’ resolution. (b) Top view of the customized resolution phantom with small cylindrical capillaries, the red volumes represent three cylindrical capillaries with 0.03 mm in radius and spaced by 0.1 mm from centre to centre are placed inside a cylinder which represents the background, with 0.5 mm height and 0.5 mm diameter. (c) Customized cylinder-sphere phantom used to study the system performance in lesion detection, a sphere with a 0.03 mm radius (representing a defect) placed inside a cylinder, which represents the background, with 0.2 mm height and 0.2 mm diameter.

The resolution of the Laue lens for a particular radiation wavelength depends on the crystals’ mosaicity. To this end, the spatial resolution in each direction (x, y, z) has been studied using two standard methods. The first is based on finding the FWHM of the point spread function generated from the Gaussian distribution of the 3D reconstructed image of a single sphere point source. Photons emitted by a point-shaped source reaching the scintillator are counted for each angle of the rotation of the Laue lens system. The signal profiles (corresponding to 2D images) are used to generate a 3D image of the gamma rays source. The signal profile in the 3D image is fitted with a Gaussian, and the full width at half-maximum (FWHM) is calculated and used to determine the resolution along the specified direction (x, y and z). The second is based on determining the spatial resolution (minimum resolvable distance between multiple source points that the Laue lens system can separate) with the phantoms sketched in Fig. 2a and b.

A spherical source of 0.03 mm radius radiating 10⁵ photon/projection was used to evaluate the sensitivity. The sensitivity of the Laue lens is calculated as the ratio of N_*/N₀, where N₀ is the number of gamma rays incident on the Laue lens, and N_* is the number of gamma rays emerging from the lens after diffraction. This is done by placing a ray counter counting gamma rays at the entrance and exit of the Laue lenses volumes (See Appendix A). The work has been performed with Monte Carlo simulations implemented in MATLAB. The sensitivity is studied by placing the three-sphere phantom (see Fig. 2a) at various axial shifts and distances from the Laue lenses’ axis with respect to its centre within the lenses’ FOV to represent different experimental scenarios. For an isotropic source, the lens’s sensitivity is calculated as the product of the ratio of the proportion of diffracted photons (ratio of N_*/N₀) and Ω_s, as shown in Eq. (1):

$$\:{\varOmega\:}_{s\:}=\:\left(\frac{A\_Lens}{4\times\:pi\times\:\:{\left(Ls\right)}^{2}}\right),$$

(1)

where $\:A\_Lens$ is the geometrical area of the lens and $\:Ls$ is the vertical source-to-lens distance. $\:{\varOmega\:}_{s\:}$ is the solid angle subtended by the active region of the lens and is calculated as the ratio of the geometrical area of the lens and the surface of the sphere with L_s as the radius (isotropic photon source). The sensitivity is calculated for each individual lens independently, as it depends on the relative position of the lens and the photon source (See Appendix A).

Forward projection algorithm

The forward projection algorithm is a mathematical model to simulate the path of gamma rays and calculates their probability of detection by the gamma camera. This generates expected data that can be compared to experimental measurements to reconstruct the patient’s internal activity distribution³². The algorithm calculates the probability that a gamma photon will be transmitted, absorbed, or diffracted (once the Bragg conditions are met) based on the angle of incidence on the Laue rings, which have different orientations. As shown in Fig. 3, the absorbed rays will be stopped, while the diffracted and transmitted photons will reach the detector plane. To accurately simulate the environment, photons are generated using a Monte Carlo approach that models isotropic emission from a point source, primarily at an energy of 140 keV, corresponding to the emissions of Technetium-99 m (99mTc), a widely utilized radiopharmaceutical in SPECT imaging. The algorithm generates random azimuthal and polar angles for each point (photon) within the phantom, which represent the radiated gamma photons. The projection path is determined based on these angles, and the photons either pass through, are absorbed, or diffract off the Laue crystals depending on their incident angle. The generated photons interact with the crystal lattice of the Laue lens, adhering to Bragg’s law of diffraction. The diffraction behaviour is characterized by the rocking curve of the Laue crystal, which is influenced by fundamental parameters, including crystal properties and the energy of the incident photons. Upon striking the Laue lens, the photons’ paths are traced to ascertain whether they are diffracted or absorbed. This simulation accounts for successful diffraction events, wherein the photons meet the Bragg condition, as well as unsuccessful interactions where photons pass through without engagement. Absorbed rays are effectively halted, while the diffracted photons continue towards the detector plane. For detection, a pixelated detector is employed within the MATLAB simulations. This detector captures the positions of photons that have been diffracted by the Laue lens, thereby contributing to the overall image reconstruction process and enhancing spatial resolution. The pixel value corresponds to the sum of the activity along the path of the gamma photons. The lens and detector assembly rotates around the phantom in defined angle increments, repeating this rotation until a comprehensive 360-degree scan of the object is achieved. This process generates a set of projection images, which are then used to estimate the distribution of the gamma rays within the scanned object. The pseudo-code for the lens-based SPECT forward projection algorithm, which encompasses detailed procedures for photon generation, interaction modelling, and detection processes, is provided in Appendix B.

Fig. 3

Forward projection algorithm: Gamma rays are emitted from the source on the right and are incident on the Laue lens (black lines). When passing through the Laue lens, the rays can be either absorbed (red), transmitted (yellow) or diffracted (blue). The projection images are obtained from the signal of the diffracted rays, while the transmitted rays should be absorbed by an appropriate shielding.

3D image reconstruction

The first effort to develop a method to reconstruct 3D images when using an array of Laue lenses is presented in this section. When compared to parallel pinhole SPECT, in a multi-lens-based SPECT, 3D image reconstruction is complicated by the refraction of the gamma rays. This means that the rays cannot be projected back in a straightforward manner to the voxel corresponding to the point of origin of the photon and that the reconstruction algorithm needs to take into account the effects of diffraction. The complexity of the 3D reconstruction algorithm in the context of the multi-lens-based SPECT arises from the inherent characteristics of this highly multiplexed imaging system. The system’s design allows for the detection of a significant portion of emitted photons while concentrating the activity in focal spots distributed across different regions of the detector. However, the overlapping nature of these projections introduces considerable intricacy and imposes additional constraints on the development of an efficient reconstruction algorithm. Addressing this challenge was the primary objective of our study, as we sought to successfully reconstruct the array projection of the Laue lenses in three dimensions. This Endeavor represented the first noteworthy effort in achieving such a reconstruction, underscoring the significance and novelty of our findings.

Based on the raytracing concept, The 3D image reconstruction algorithm employs a modified filtered back-projection (FBP) technique tailored to the unique geometries of the system. The algorithm processes non-zero pixels from the detector, converting their coordinates into XYZ format. Random points within each lens are generated, followed by back-projecting gamma rays towards these points based on randomly assigned azimuthal and polar angles. This ensures accurate directionality for the emitted radiations. The reconstruction accounts for which lens each radiation emanates from and evaluates the likelihood of absorption, diffraction, or transmission.

Rays meeting the Bragg angle condition are identified as diffracted and back-projected to the voxel of interest, while those that do not satisfy this requirement are disregarded. A fast voxel traversal method, coupled with Siddon’s tracing algorithm, is employed to calculate the lengths of ray intersections with voxel volumes. The effectiveness of the algorithm is illustrated through various figures showing the defined detector setup and back-projected rays converging at the voxel volume.

To ensure the 3D reconstruction algorithm’s reliability, the phantom under study is placed at different depths along Z and shifts in the X and Y directions from the centre of each lens of the Laue collimator. The focal spot will be adjusted for various shifts from the lens axis. Based on the generated 3D reconstructed images, the depth and shift information is determined using the pixel coordinates (pixel locations) and voxel size (the size of the individual volumetric pixels in the reconstructed image). The image as a 3D volume is composed of voxels arranged in a grid with dimensions of 256 voxels along the X-axis, 256 voxels along the Y-axis, and 256 voxels along the Z-axis. Each voxel represents a small 3D element of the image and has a width of -5 to 5 units along each axis. The uncertainty in the measurements is equivalent to half of the voxel width, which is 5/256 divided by two. The units are in mm, then 0.00977 would be the uncertainty. Equation 2 is used to calculate both the shifts in X and Y directions and the distances along the Z axis in the 3D reconstructed image.

$$\:\text{D}\text{e}\text{p}\text{t}\text{h},\:\text{S}\text{h}\text{i}\text{f}\text{t}\:(\text{x},\text{y},\text{z})\:=\:{Bound}_{Min}+\:{Pixel\:Location}_{(x,y,z)Reconstructed}\:-\frac{{Bound}_{min}-{Bound}_{Max}}{Voxel\:Size}$$

(2)

where $\:{Bound}_{Min}$and $\:{Bound}_{Max}\:$are the minimum and maximum bounds, respectively. $\:{Pixel\:Location}_{Reconstructed}\:$is the pixel location of the phantom in the reconstructed images. This calculation scales the pixel location to fit within the specified range of bounds and provides a depth value relative to the lower bound of the range (Fig. 4).

Fig. 4

Multi Laue lens back projection: Rays are back projected from the non-zero pixels on the detector plane through the Laue lens volume based on the Law of Laue lens diffraction to the voxel volume, which should correspond to the emission point of the gamma rays; the rays converge at the voxel volume. Different rays colours represent focused rays from different lenses.

Results

Projection and the 3D reconstructed image

Figure 5 shows an exemplary part of the thirty-six projection images of the multi-lens-based SPECT generated by rotating the Laue collimator around the three-point sources phantom (see Fig. 2a) with a 10⁰-step angle. The X-axis and Y-axis represent the column and row indexes of the pixelated projection image. Figure 6a-c show the 2D XZ, XY, and YZ slices of the 3D reconstructed image, respectively. Figure 6d shows the 3D volume of the reconstructed image. By referring to the phantom in Fig. 2a, the lens-based SPECT allows resolving adjacent volumes as small as 0.113 nL, which is substantially smaller than any conventional SPECT system can resolve.

Fig. 5

Projection images: Multi-Laue lens projections of 3 spheres rotated at 10-degree step angles. The x-axis represents the column index, and the y-axis represents the raw index of the pixelated projection image. The rotation is with respect to the X-axis shown in Fig. 4. Step angles are indicated to the left of the figures.

The 3D reconstructed phantom’s depth (displacement of the phantom along the Z-axis) information from the photon distribution in the focal plane/detector was compared against the exact depth that we applied to the source phantom to ascertain the system’s ability to accurately map and preserve the depth information along the Z-axis. Similar work was repeated for the 3D reconstructed lateral shifts (with respect to the Laue lens axis) information. Table 2 shows a comparison between the exact phantom shifts and depths applied to the phantom and the corresponding values obtained from the 3D reconstructed images. The results clearly indicate that the detected shifts and depth information of the phantom in the reconstructed images align well with the specific phantom shift we enacted. The array of Laue lenses can project different views of the object under study. Figure 7 shows a multi-Laue SPECT projection image of a point source with a radius of 0.03 mm showing a zoomed view of the red highlighted projection behind the upper right Laue lens, a zoomed view of the green highlighted projection behind the lower middle Laue lens and a zoomed view of the white highlighted projection behind the cantered Laue lens. The projection image associated with each lens represents a different view of the scanned object. Based on these results, the proposed system is envisioned to be akin to a light field camera, with each lens looking at the same target but from different angles^8,30. It is worth mentioning that the multi-lens-based SPECT is a highly multiplexed system, one Laue lens would project on the adjacent lens’s focal spot for larger shifts from the lens axis, resulting in a multiplexed projection. The Laue lenses would collect gamma rays from a wide area and focus them onto their respective focal points on the detector plane; the locations of the focal points are determined by the source’s shifts from the lenses’ axes. Any shift in the source’s position relative to a lens axis is replicated on the detector plane but in the opposite direction. By encoding the angular resolution with a higher spatial resolution, Laue lenses in SPECT systems enable sampling of the radiation. This method allows for the refocusing of SPECT images while preserving the spatial resolution, in an approach akin to light field imaging (see Appendix D).

Fig. 6

3D Reconstructed images: (a) 2D XZ slice of the 3D reconstructed image. (b) 2D XY slice of the 3D reconstructed image. (c) 2D YZ slice of the 3D reconstructed image. (d) The 3D volume of the reconstructed image. The units of measurement are in mm.

The data from the entire set of Laue lenses can be used to produce a 3D image containing information on the size of the tumour and its location up to submillimeter accuracy/up to 0.08 mm. Figure 8 shows the Gaussian fitted point source of 0.03 mm radius of the 3D reconstructed image. The plateau signal around the peak of the Gaussian fitted curve is a distribution of the background region in the cylindrical phantom. The Laue lens reduces blurring, ordinarily caused by radiation penetration and scattering in the aperture edge material common in a conventional collimator. This is evident from the sharp-fitted Gaussian of the 3D reconstructed images.

Table 2 Applied (ground truth) phantom shifts and depth versus the reconstructed ones in 3D. The uncertainty affecting the results is half the voxel width.

Fig. 7

Different views of the scanned phantom: Multi Laue SPECT projection image of a point source with a radius of 0.03 mm showing a zoomed view of the red highlighted projection behind the upper right Laue lens, a zoomed view of the green highlighted projection behind the lower middle Laue lens and a zoomed view of the white highlighted projection behind the cantered Laue lens. The x-axis represents the column index, and the y-axis represents the raw index of the pixelated projection image. In this image, the cooler yellow indicates higher photon intensity, while the blue colour corresponds to lower photon intensity.

Fig. 8

Gaussian fitted point source: Gaussian fitted point source of 0.03 mm radius of the 3D reconstructed image.

As we mentioned, the resolution study encompassed two distinct approaches. Firstly, the analysis of FWHM was conducted using the 3D reconstructed images. Secondly, a resolution phantom was employed to examine resolution characteristics.

The results indicated that the system could completely resolve three-point sources (See Fig. 1a) and three cylindrical capillaries with a radius of 0.03 spaced by 0.1 (See Fig. 1b) from centre to centre. The FWHM was determined to be 0.1 mm. Remarkably, both methodologies yielded consistent results, revealing that the multi-lens-based SPECT system possesses a resolution of 0.1 mm. The sensitivity of the multi-lens-based SPECT using an array of nine Laue lenses in a flat plane was determined as follows:

$$\:{Sensetivity}_{Multi\_Laue\_SPECT\:}=6.2\times\:{10}^{-5}\:\:(hits/emitted)\:\cong\:\:57\:\frac{cps}{MBq}$$

(3)

Comparative analysis

To provide a quantitative performance assessment and to evaluate the proposed system’s performance, we conducted a comparative study with conventional SPECT. In particular, the image quality of the lens-based SPECT was quantitatively compared with that of clinically used low-energy high-resolution LEHR SPECT, and multi-pinhole Inveon SPECT. Monte Carlo simulations of single point sources were used to compare the multi-lens-based SPECT point-spread functions and determine sensitivity, resolution, and PSF broadening. Table 3 shows the comparison between LEHR, Inveon, and lens-based SPECT in terms of system resolution and sensitivity. Case studies were then performed to evaluate further the applicability of the proposed Laue lens SPECT system.

Table 3 Comparison between LEHR, Inveon, and lens-based SPECT in terms of system resolution and sensitivity.

Case study: lesion detection

The customized cylinder-sphere phantom (See Fig. 2c) was conducted with a tomographic acquisition consisting of 36 projections, and scans were simulated for 360° rotation with a 10° step angle. The radius of rotation (ROR) (distance from the lens to the source) was 50 cm. Figure 9a shows the zoomed projection view on the detector plane for the cantered Laue lens. Figure 9b shows the XY slice of the 3D reconstructed image. A 0.1 mCi source emits $\:3.7\times\:{10}^{6}$gamma rays per second. With such activity and a multi-lens-based SPECT sensitivity of $\:6.2\times\:{10}^{-5}$, the radiation count rate is the product of the activity and the sensitivity as below:

$$\:{Gamma-ray\:counts}_{Multi\:Laue\:SPECT}\:\:=\:{3.7\times\:10}^{6}{\times\:6.2\times\:10}^{-5}=229\:\frac{counts}{second}$$

(4)

Fig. 9

Lesion Detection: (a) Zoomed view of the projection image behind the central lens. The x-axis represents the column index, and the y-axis represents the raw index of the pixelated projection image. (b) XY slice of the 3D reconstructed image. The x-axis represents the x pixel location, and the y-axis represents the y pixel location.

Clinically, organs that contain a large amount of blood retain approximately 2.2 µCi per cc of radioactivity. A malignancy maintains approximately six times this amount, or about thirteen µ Curies per cc¹⁵. Therefore, for an array of nine Laue lenses, we obtain a count rate for the malignant tumour of:

$$\:13\:{\upmu\:}Ci\:x\:3.7\:{10}^{4\:\:}x\:6.2\:{\times\:10}^{-5}\frac{hits}{emitted}\:=\:30\frac{counts}{second}\:\:$$

(5)

However, it should be noted that the tumour volume is not the only radioactive source in a clinical scan. Surrounding organs next to the tumour absorb some of the radiopharmaceuticals as well, and the absorption is proportional to the volume of that organ. Consequently, these organs cause background noise. Despite this, the high count rate enabled the clear detection of the tumour, with the radiotracer uptake in the tumour being about 6 times that of the surrounding tissue, allowing it to be distinguished from the background.

Discussion

The multi-lens-based SPECT system uses a novel design that enables high resolution image acquisition. The system is aimed at oncology applications, thyroid, and breast SPECT imaging to take advantage of its high-resolution feature for early detection of tumours. The proposed system offers an exceptional sensitivity/resolution trade-off and is envisioned to be fitted with a field of view big enough to cover most vital mouse organs. The advantage of the focusing feature is that it allows for acquiring a significant number of projections from a single point of focus. Extending the FOV is feasible by moving the object. This adjusts the Laue lenses to focus on different sections of the animal. Another advantage of using Laue lenses is the capability to adjust the lens shape with ultra-high spatial resolution and sensitivity to identify sub-µCi sources. This is an example of the lens system’s customization in medical imaging. The Laue lens’s achievable resolution and sensitivity are decoupled from the geometry and depend solely on the size and orientation of the crystals, in contrast to the existing parallel SPECT systems that suffer from resolution-sensitivity trade-off. The spatial resolution is boosted by a factor of two by scaling down the lens system by a factor of two, while the lens’s sensitivity to a small source is not affected because all angles remain constant¹⁷. Furthermore, downsizing would lessen the background provided by residual activity in non-cancerous tissue by four and sixteen times, respectively. As a result, the signal-to-background ratio and the signal-to- noise ratio rise by four and sixteen times, respectively¹⁷ this is in contrast to the LEHR SPECT, where the septa are used to prevent septal penetration at the cost of sensitivity and resolution. However, conventional planar performance metrics may not be applied to the proposed system.

The challenge is to develop new conceptual metrics to be able to characterize this system against “conventional ones” and to demonstrate how this concept applies to practical/clinical use. The National Electrical Manufacturers Association (NEMA) has established procedures to standardize the specifications of instrument performance. These, however, apply only to conventional systems and may not apply to systems with a different concept, like the adoption of the Laue lens, as the basis of its design. Consequently, direct comparisons to conventionally required results acquisition are not always meaningful. Nonetheless, we aimed to conduct a series of case studies to demonstrate performance. The performance parameters obtained may lay a foundation for future performance metrics suitable for non-traditional instruments, such as the lens-based SPECT. Our results indicate that, compared to the multi-pinhole Inveon and parallel LEHR collimators, the multi-lens-based SPECT offers significantly higher spatial resolution (by a factor of about 10) and comparable sensitivity. In contrast to methods that rely on absorptive collimation like single- or multiple-pinhole cameras, the use of refractive optics decouples spatial resolution from sensitivity. Our feasibility studies have refined and applied ray-tracing routines to design focusing optics for small animal studies. This study aims to develop a means of performing gamma rays imaging of small animals that would not rely on parallel hole collimators, as a method of offering the best prospect for achieving submillimeter spatial resolution. The novel approach relies on the Laue lens as a focusing element. The spatial resolution achievable is decoupled from the sensitivity and depends solely on the mosaicity and orientation of the crystals, in contrast to the existing collimators that suffer from resolution-sensitivity trade-off. However, despite the promising results, our work bears a number of limitations. The conducted case studies demonstrate the system’s practicality to accurately map 3D images of the scanned small phantoms. To the extent that the superliner position holds, any general object is considered to be made up of point sources and will be correctly imaged. However, there are definite limitations to high-resolution imaging of large objects. As mentioned earlier, the multi-lens-based SPECT is a highly multiplexed imaging system, with projections allowing for detecting a more significant fraction of emitted photons while still projecting activity concentrated in focal spots on different areas on the detector. The overlapping projections add complexity and put further restrictions on developing an efficient reconstruction algorithm. This was the main challenge of this study and the first attempt to reconstruct the Laue lenses’ array projection successfully. A future reconstruction algorithm that accounts for the probabilistic distribution behind each Laue lens will be considered. Furthermore, for the sake of reducing the uncertainty in the reconstructed image, we aim to develop a reconstruction algorithm for non-multiplexed projections by placing a slant between the Laue lenses.

Future research in this field should include the investigation of other possible approaches to boost the sensitivity gain, for example, by placing the lenses in a tiled plane in such a way that the field of view of the Laue lenses that are placed in different planes are converging. By optimizing the angles between the modular planes, it would be possible to see different views of the phantom based on the projection images from the individual Laue lenses. Extending and optimizing the Laue lens design to different radiotracers, such as ¹²³I, will be considered in future studies. The phantom must be rotated to focus on different sections, or the Laue lenses collimator plane must be rotated to increase the field of view. As a result, the area with the most significant sensitivity is scanned throughout the volume of interest. A submillimeter resolution and precise source localization could be achieved by placing the envisioned Laue collimator on a mechanical system/arm that adapts the focal length in response to the desired depth.

Fabricating a physical prototype of this miniature Laue lens SPECT system should be a major source of future investigation and conducting physical experiments, as the scale of our 2 mm diameter lens falls outside the conventional fabrication techniques, 3D printing and micro-machining being too coarse and lithography and nano-fabrication techniques are too fine. A hybrid technique needs to be developed. Further bio-chemical applications can be in the imaging of proteins and viruses. Non-medical applications of the Laue lens, which are currently limited to astronomical imaging, can be envisioned when miniature versions can be manufactured, such as enhanced radiological detectors and surveying equipment.

Feasibility of the study

The proposed Laue lens-based SPECT system demonstrates promising advancements in nuclear imaging; however, its feasibility hinges on both theoretical modelling and practical implementation. Initial Monte Carlo simulations have successfully modelled the system’s behaviour, highlighting its potential for improved spatial resolution and sensitivity. The tailored simulation environments assessed various case studies using different phantoms, indicating that while ideal conditions were assumed for preliminary evaluations, realistic physical interactions—such as nuclear event counts and attenuation within the Laue lens volume—enhance the validity of the results. Given the innovative nature of the design, the outcomes from these simulations indicate a high likelihood of successful integration into clinical practice. Nonetheless, manufacturing the Laue lens presents significant challenges, particularly in achieving the precise alignment of diffractive crystals. Collaborations with experts in nanotechnology fabrication are underway to address these obstacles, though limitations in crystal thickness and alignment precision remain. To further substantiate the system’s viability, future work will focus on refining simulations to incorporate realistic phantoms, accounting for scattering and attenuation effects, while developing a clear pathway for transitioning from simulations to physical prototypes. Importantly, the successful reconstruction of 3D images from the lens projections has validated the proposed system’s ability to achieve sensitivity levels comparable to existing clinical SPECT systems, thus reinforcing its potential to enhance diagnostic imaging capabilities. The combination of advanced simulation techniques and ongoing collaborative efforts strongly supports the feasibility of realizing this innovative imaging technology.

In future work, we are focusing on advancing the Monte Carlo simulations to determine the accurate FOV and optimal detector size for the multi-Laue lens geometry. This will improve the precision of the lens design and its application in imaging systems. The imageable area in a Laue lens system is defined by the field of view (FOV), which differs from that of optical lenses. In Laue lenses, the FOV is not determined by the active area of the lens or the total area of the crystals. Instead, it is determined by the crystal’s mosaicity and is calculated through a different geometric analysis. To determine the FOV accurately, Monte Carlo simulations are employed, enabling precise modelling of photon diffraction and detection. The FOV of the Laue lens is influenced by the offset angle of the source. When the source is displaced within the arcminute range, the number of photons focused by the lens does not change significantly. This means that the lens can focus a similar number of photons from both on-axis and off-axis sources. For off-axis sources, the diffraction of photons spreads them over a larger area on the detector. While the number of photons remains similar, the spatial distribution becomes more dispersed, requiring a larger detector to capture all diffracted photons.

The size of the FOV is determined by the radius of the detector. As the source moves off-centre, the lens can focus photons from a larger area. If the source is offset beyond the FOV, the photons form a ring with a radius greater than that of the detector, and they are discarded as they fall outside the lens’ capacity to focus them effectively. Increasing the detector size would enhance the FOV, allowing the system to capture photons from a wider range of off-axis sources.

Conclusion

We described the development and analysis of a new SPECT system design that, through a novel approach to focused gamma rays, could provide improved performance compared to conventional SPECT. Physical principles governing the design of this system are presented, along with a series of measurements analysing various characteristics of the generated projections and 3D reconstructed images. Our results show that the multi-lens-based SPECT has far superior spatial resolution and similar sensitivity compared to LEHR and Inveon’s multi-pinhole. The achieved resolution is outstanding and would open SPECT to other applications like oncology, thyroid, breast, and infant SPECT imaging, and with new possibilities for the sub-organ-level study and early detection of lesions. The detector sensitivity, projection resolution, and reconstruction resolution of the multi-lens-based SPECT system were all assessed. Monte Carlo simulations were utilized to create a specialized 3D image reconstruction algorithm that accurately determines the 3D distribution of radioactivity from focused projections. This algorithm ensures that the pixel values in the reconstructed images accurately represent the actual concentrations of radiopharmaceuticals within the subject.

The advantage of focusing on the gamma rays is that it allows for the acquisition of a high number of photons from a specific location of interest. Additionally, the resolution is independent of the lens’ radius, number of rings, and geometry, overcoming the sensitivity-resolution trade-off that represents a dilemma in the current parallel and multi-pinhole collimators. The system’s novelty relies on the ability to view the data from every lens separately to capture a specific view of the object, or it can be integrated to generate a three-dimensional image from the three modules, including accurate information about the object’s size and location. The developed Monte Carlo model will be applied for further studies on the development and evaluation of the system and effort will be devoted to optimizing the methods for image projection and reconstruction.