Hybrid stochastic and robust optimization of a hybrid system with fuel cell for building electrification using an improved arithmetic optimization algorithm

Abstract

This paper proposes a hybrid stochastic-robust optimization framework for sizing a photovoltaic/tidal/fuel cell (PV/TDL/FC) system to meet an annual educational building demand based on hydrogen storage via unscented transformation (UT), and information gap decision theory-based risk-averse strategy (IGDT-RA). The hybrid framework integrates the strengths of UT for scenario generation and IGDT-RA (hybrid UT-IGDT-RA) for optimizing the system robustness and maximum uncertainty radius (MRU) of building energy demand and renewable resource generation. The deterministic model focuses on minimizing the cost of energy production over the project’s lifespan (CEPLS) and considers a reliability constraint defined as the demand shortage probability (DSHP). The study utilizes an improved arithmetic optimization algorithm (IAOA) to optimize component sizes and MRUs, incorporating a neighborhood search operator to enhance performance and prevent premature convergence. The deterministic findings revealed that the PV/TDL/FC system configuration offers the lowest CEPLS and the highest reliability level (lowest DSHP) compared to the hybrid PV/FC and TDL/FC configurations. Additionally, these results indicated that enhancing the reliability of the energy supply for the educational building entails higher CEPLS, particularly due to increased costs associated with hydrogen storage. The robust framework findings for the PV/TDL/FC system using IGDT-RA show that for an uncertainty budget of 21%, the MRUs for educational building demand and renewable generation are obtained at 10.34% and 2.65%, respectively, which are higher compared to other configurations. This indicates that the hybrid PV/TDL/FC system is more robust in handling worst-case scenario uncertainties. Furthermore, the hybrid UT-IGDT-RA outcomes found that the stochastic scenarios incorporated to simulate a range of uncertainties beyond the conventional IGDT-RA based-nominal scenario, and it provides a broader range of robust solutions, enabling operators to align strategies with their risk tolerance and improves system flexibility, and decision-making precision in the face of uncertainties.

Introduction

Carbon emission restrictions and corresponding policies have driven the energy sector toward more sustainable and efficient resource utilization¹. In 2021, there was a significant resurgence in global CO2 emissions, increasing by nearly 5%², with electricity generation accounting for approximately 40% of this increase³. As a result, there has been a concerted effort to enhance the adoption of renewable energy sources, thereby decreasing reliance on fossil fuels. Off-grid hybrid renewable energy systems have increasingly been spotlighted for their capacity to generate clean energy due to various factors, such as the depletion of fossil fuel reserves, rising fuel prices, and the growing impact of global warming^1,2. Utilizing energy-source-based system is advocated as an effective strategy to mitigate environmental issues and improve the reliability of energy supply^3,4. The most viable renewable sources for fulfilling energy demands are off-grid hybrid systems that employ photovoltaic (PV) and wind turbine (WT) technologies⁵. These renewable energy sources are particularly beneficial in areas where traditional electric grids are not economically viable due to the high costs associated with setting up transmission lines, especially in remote locations^6,7. To enhance system efficiency and maintain continuous power supply, storage systems can be integrated with hybrid systems, compensating for the intermittent nature of PV and WT outputs, which may not always meet demand^8,9. Among storage options, fuel cells (FCs) and batteries are predominantly utilized. Batteries provide short-term energy storage, seamlessly integrating with renewable energy setups^10,11, while FCs, powered by hydrogen, offer long-term storage solutions thanks to their quick activation and high energy density¹². An FC generates energy by converting hydrogen fuel on demand, whereas batteries reserve energy for later use¹³. Optimal sizing of storage components is crucial for the effectiveness of hybrid systems, as it determines a system’s capability to meet energy demands reliably and economically¹³. However, hybrid systems face several challenges, including variable system loads and the unpredictability of energy production sources^14,15. These uncertainties can lead to deviations from the ideal system sizing, achieved through optimization. It is essential to thoroughly investigate these uncertainties to optimally plan and size these energy systems, as they significantly influence the overall cost and reliability of energy generation¹⁵.

Numerous research studies have been carried out to look into the size of various renewable energy system topologies with energy storage corresponding to various aims, restrictions, and solvers. Table 1 summarizes the research that has been done, and each study’s contribution is summarized in an approach that draws attention to the contrasts between the current study and the evaluated literature. Particle swarm optimization (PSO) and genetic algorithms are used in¹⁶ to size a hybrid PV/WT/FC energy system to reduce the weighted average cost of energy while preserving a particular renewable energy fraction¹⁷. presents the hybrid PV/WT/FC system sizing to meet annual loads while reducing net present cost and boosting system reliability as measured by the chance of a power supply failure using a cuckoo search algorithm. To reduce the cost of energy purchase and sales to the utility grid utilizing a hybrid artificial bee colony-PSO, the techno-economic sizing of a PV/FC energy system to feed a retail center is described in¹⁸. For increasing the energy resources contributions in the hybrid system and to evaluate the employing FCs feasibility as a storage or backup system rather than battery banks, a PV/WT/FC energy is sized in¹⁹ using a shuffled frog leaping algorithm (SFLA). In²⁰, scaling of a PV/WT/FC/Battery/Diesel energy system is carried out utilizing multi-objective NSGA-II to find the ideal capacity of the system devices to reduce the generation cost. Sizing of a PV/WT/biomass/battery system is implemented using the gradient artificial hummingbird algorithm (GAHA) in²¹ to reduce the energy cost and get the best system configuration. Using a mixed-integer linear programming technique, a two-layer sizing strategy using energy resources and battery storage is proposed in²² to determine the ideal capacity while taking the system cost into account²³. describes how to size a PV/WT/Battery system utilizing HOMER Pro software to create a logical, straightforward methodology for optimal energy system planning. A strategy for a PV/WT/Battery/Diesel system sizing is provided in²⁴ to reduce the overall cost using a multi-objective GA. In²⁵, a multi-objective NSGA-II is used to size a hybrid PV/WT/Battery energy system optimally while meeting the reliability requirement to reduce annualized energy cost. In²⁶, the whale optimization algorithm (WOA) is used to size a PV/WT/Tidal(TDL)/FC energy system to reduce the system’s energy cost. A grid-connected PV/TDL energy system’s size optimization is built in²⁷ utilizing a pattern search method and various optimization algorithms that take into account many optimization goals. Using the DICOPT solver, the size of a PV/WT/Battery/Geothermal energy system is provided in²⁸ dependent on the location for recharging electric vehicles. The GA is used in²⁹ to design a home PV/FC system sizing that minimizes costs and power supply. According to³⁰, size optimization of a PV/WT integrated with electric vehicles is carried out while taking into account varying electric vehicle levels of penetration and satisfying load requirements. The size of a hybrid WT/TDL energy system was optimized in³¹ to decrease the levelized electricity cost while considering the significant variability of renewable power. A PV/Biomass/Battery energy system’s size is provided in³² utilizing a discrete harmony search (DHS) to maximize system component sizing while minimizing the net present cost subject to reliability limit.

Table 1 The literature review summary.

In³³, a hybrid PV/WT/Battery integrated with electric vehicles is optimized to minimize the energy cost employing a linearized stochastic algorithm structure that takes into account generation uncertainty through a roulette wheel process along with appropriate probability distribution functions. In³⁴, probabilistic scaling of a PV/WT/Battery energy system is carried out utilizing simulation and an improved Crow search algorithm (ICSA), minimizing active losses and improving voltage profile while taking into account variable network demand and renewable generation. A PEM and manta ray foraging optimization algorithm are used in³⁵ to propose efficient energy management for an PV/WT integrated with electric vehicles that take into account liquid air energy storage and the load while taking into account the uncertainties of renewable power. To reduce the cost of energy, the probabilistic sizing of an HPV/Biomass/Battery energy system is investigated in³⁶ utilizing the aggrandized class topper optimization (ACTO), PSO, and JAYA algorithms. In³⁷, a point estimate method (PEM) and improved gradient based algorithm is presented for sizing a hybrid PV/Hydrokinetic/FC system in form of a stochastic optimization framework considering uncertainty. The stochastic methods such as the PEM presented in³⁷ are not able to determine the maximum radius of uncertainty parameters and cannot, like robust optimization methods, measure the system’s robustness to the worst scenario of uncertainty and prediction errors. In³⁸, a robust planning framework is presented for allocation of a hybrid PV/WT/Battery in the radial electrical distribution network for minimization of power losses cost, purchasing power from the hybrid system and the post incorporating the uncertainty via an information gap decision theory (IGDT) for short-term study. In³⁹, planning of a PV/CHP/Battery/TES Microgrid system is presented using a stochastic programming via the IGDT considering multiple uncertain parameters. In⁴⁰, robust operation of a PV/WT/CHP/Battery/TES Microgrid is implemented using the IGDT as a short-term study for minimization of the operating cost of the Microgrid to meet the thermal and electrical demands.

According to the review of the literature on the optimization of the hybrid systems presented in Table 1, the research gaps are still presented as follows:

• The TDL energy sources with the capacity to generate clean energy as well as the unrestricted supply of canals and rivers have a significant potential in the hybrid systems for power generation, which have been less thoroughly investigated and utilized in such systems. The TDL turbines are efficient in the production of electricity for locations with sufficient water flow potential because they harness the kinetic energy of flowing water in canals and rivers. The review of the literature revealed that further research and consideration are required for the integration and use of these kinds of clean and cost-free energy sources in hybrid systems, as well as for their connection to storage devices inside the hybrid system.

• The difficulty in sizing of the hybrid systems is related to the energy sources and load demands’ uncertainties, which are unavoidably extremely effective in sizing output as well as cost and reliability indicators. On the other hand, the storage level in the hybrid systems will constantly change depending on the state of the uncertainties at hand and how well these adjustments work to achieve both the lowest cost and the highest reliability level.

• The Monte Carlo simulation and the PEM are the most popular stochastic techniques currently being utilized to address the sizing issue of hybrid systems according to Refs^{33,34,35,36,37}. Due to their reliance on probability distribution functions, these methods typically demand a large amount of historical data with specific uncertain behavior and a great deal of scenario definition, which has resulted in a huge increase in their computing cost.

• Because the risk is not taken into account in the stochastic sizing model^{33,34,35,36,37}, the energy system operator is concerned about the risks of adverse deviation of data with uncertainty from their predicted values and the additional and likely cost of the project as a result of these uncertainties. However, from the perspective of a hybrid system operator, the hybrid system should be operated optimally, and the management of system reserve power should be established in a way that allows the risk associated with uncertainties to be controlled more efficiently to prevent decreasing the system’s reliability. To control the difficulties linked to the reliability of the load and ensure the efficient and reliable functioning of the system, a framework for the optimal sizing of the hybrid system should also be supplied while taking the risk of uncertainties into account.

• One of the best techniques for assessing the uncertainty of systems is the information gap decision theory (IGDT)^38,39,40. The goal of the IGDT approach is to establish the largest radius of uncertainty permitted for the problem’s non-deterministic parameters, taking into account that the problem’s objective function falls within the decision-maker’s permitted range. IGDT offers a deterministic framework that does not require detailed probability distribution functions (PDFs) of uncertain parameters, making it highly advantageous in scenarios with limited or incomplete data. Unlike MCS, which relies on repeated random sampling and extensive computational resources to estimate probabilistic outcomes, IGDT directly focuses on worst-case scenarios, providing a computationally efficient way to evaluate system robustness. This approach allows decision-makers to assess the trade-offs between robustness and cost while avoiding the complexity of probabilistic modeling. Moreover, IGDT’s structured methodology provides clear insights into the maximum uncertainty levels the system can handle, enabling risk-averse and reliable decision-making. These attributes make IGDT particularly suitable for applications where data scarcity, computational efficiency, and worst-case scenario analysis are critical.

• The conventional IGDT-RA approach’s reliance on a deterministic scenario (normal scenario) limits its ability to account for uncertainties, leading to potential suboptimal decision-making in hybrid system optimization. It overlooks risks from unexpected deviations in uncertain parameters. However, incorporating Unscented Transformation (UT)⁴¹ into the IGDT-RA framework addresses this limitation by generating multiple scenarios (positive and negative deviations), enabling more robust and risk-averse decisions. This integration improves system performance by better capturing uncertainties and allowing for more reliable sizing and operation of hybrid systems. According to the review of the literature, to the authors’ knowledge, no study has been done that focuses on the sizing of a PV/TDL/FC energy system based on hydrogen storage utilizing a hybrid UT with IGDT-risk-averse strategy for scenario generation, and optimizing the system robustness.

The paper elaborates on its contributions in addressing identified research gaps through several key methodologies and findings, as summarized below:

• Deterministic sizing of the PV/TDL/FC Energy System: The hybrid PV/TDL/FC energy system that utilizes hydrogen storage is initially sized deterministically without considering the uncertain parameters to supply the educational building load to minimize the cost of energy production over the project’s life span and meet the reliability targets, satisfied by the demand shortage probability (DSHP).

• Robust sizing of the PV/TDL/FC Energy System: A stochastic-robust sizing framework named Hybrid UT-IGDT-RA is proposed which improves the robustness and performance of the PV/TDL/FC energy system in condition of uncertainty. By incorporating the UT to generate the uncertainty scenarios, the method provides a more comprehensive understanding of uncertainty. It enhances decision-making by determining the maximum uncertainty radius (MRU) for energy demand and renewable power, allowing for better optimization of hybrid system components. This approach addresses the limitations of deterministic model-based IGDT and offers a more robust, risk-averse solution for energy system sizing and operation.

• Optimization Algorithm Enhancement: To optimize the optimization variables of the problem, an improved arithmetic optimization algorithm (IAOA) is employed. This enhanced version is chosen over the traditional arithmetic optimization algorithm (AOA)⁴² due to its straightforward implementation, simplicity, and effective convergence capabilities. However, recognizing the limitations of meta-heuristic algorithms, which can get stuck in local optima in complex systems, a neighborhood search operator^43,44 is incorporated to boost the algorithm’s performance and prevent premature convergence. The AOA offers several advantages that make it a highly effective and practical choice for solving optimization problems. Its straightforward implementation ensures that researchers and practitioners can easily integrate it into various problem-solving frameworks without requiring extensive algorithmic customization or domain-specific tuning. The algorithm’s simplicity stems from its reliance on basic arithmetic operations, which reduces computational complexity and makes it accessible for a wide range of applications, including those with limited computational resources⁴². These attributes collectively highlight the AOA as a versatile and efficient tool for addressing optimization challenges in diverse fields.

• The efficacy of IAOA is then compared with both the traditional AOA and PSO⁴⁵ in deterministic sizing scenarios to determine the best solution.

• Analysis of deterministic and robust sizing strategies: The paper presents the optimal power dispatch and operation of renewable energy resources within a hybrid system that includes a fuel cell and hydrogen storage. It also examines how uncertainties affect the operational strategy of the system in both deterministic and robust sizing scenarios.

• Evaluation of System Robustness: The study assesses the robustness of the hybrid PV/TDL/FC system against worst-case scenarios of uncertainty. This assessment helps in understanding how well the system can perform under adverse conditions, thereby providing effective insights into its reliability and efficiency. The hybrid UT-IGDT-RA approach offers a wider array of robust solutions, allowing operators to tailor strategies according to their risk preferences. It enhances system reliability, adaptability, and decision-making accuracy under uncertainty, surpassing the traditional IGDT-RA method.

The structure of this paper is as follows: The hybrid system operation and modeling are presented in Sect. 2. The model of cost, reliability, and system component constraints with suggested optimization solver are presented in Sect. 3. The modeling of the robust sizing based on the hybrid UT-IGDT-RA is formulated in Sect. 4 along with a description of the execution process. The deterministic and robust sizing findings are given in Sect. 5. Finally, Sect. 6 wraps up the research findings.

Hybrid system operation and modelling

Operation

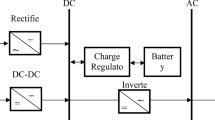
Before beginning any phase of optimal sizing, modeling is a crucial step. In earlier investigations, a variety of modeling methodologies were established to represent the hybrid system components. Three main components are present in a PV/TDL/FC system integrated with hydrogen storage, as depicted in Fig. 1. These are the PV generator, the TDL, and the fuel cell system, which consists of the electrolyzer, hydrogen tank, and FC.

Fig. 1

Block diagram of the PV/TDL/FC system.

The flowchart of the operating the PV/TDL/FC system is depicted in Fig. 2 and the different phases are described below:

• If total power produced using the PV/TDL/FC system is more than the educational building load, the extra power is transferred to the electrolyzer to generate the hydrogen ($\:\left({P}_{PV}\left(t\right)+{P}_{TDL}\left(t\right)\right)>\frac{{P}_{Edub}\left(t\right)}{{\eta}_{Inv}}$) and in this case, the EL and HS are in ON mode, and FC is in OFF mode. Where, $\:{P}_{PV}\left(t\right)$ is PV power at time t, TDL power at time t, $\:{P}_{Edub}\left(t\right)$ is demand of educational building at time t, and $\:{\eta}_{Inv}$is inverter efficiency.

• If the overal power produced by the PV/TDL/FC system is equal to the educational building demand ($\:\left({P}_{PV}\left(t\right)+{P}_{TDL}\left(t\right)\right)=\frac{{P}_{Edub}\left(t\right)}{{\eta}_{Inv}}$), in this case, the building demand is fully supplied. In this case, the EL, HS, and FC are in OFF mode.

• If the total power produced via the PV/TDL/FC system is lower than the educational building load, the deficit power is compenstaed by the fuel cell by receiving the hydrogen from hydrogen tank ($\:\left({P}_{PV}\left(t\right)+{P}_{TDL}\left(t\right)\right)<\frac{{P}_{Edub}\left(t\right)}{{\eta}_{Inv}}$) and in this case, the HS, and FC are ON mode, and EL is in OFF mode. In this case, if the FC cannot fully supply the lack of building demand, then part of the load will be cut off.

Fig. 2

Operation of the PV/TDL/FC system.

Modeling

In this section, the mathematical modeling of each part of the PV/TDL/FC system is presented.

PV

The extracted power from PV array based on the solar radiation emitted to panel, rated power of each PV panel, and maximum power point tracking efficiency is calculated by^3,6,7,12

$$\:{P}_{PV}=\frac{{IRR}_{PV}}{{IRR}_{PV-Ref}}\times\:{P}_{PV-Nominal}\times\:{{\upepsilon\:}}_{\text{m}\text{p}\text{p}\text{t}}$$

(1)

Where,$\:{\:P}_{PV}$ is the PV power,$\:\:{IRR}_{PV}$ is irradiance emmited to the PV panel surface, $\:{IRR}_{PV-Ref}\:$indicates reference standard $\:{IRR}_{PV}$ and equals to 1000 W/m²,$\:\:{P}_{PV-Nominal}$ is the nominal PV array power, and $\:{{\upepsilon\:}}_{\text{m}\text{p}\text{p}\text{t}}$ denotes to the PV maximum power point tracking efficiency.

TDL

The TDL systems with horizontal axis turbines work similarly to hydropower plants, which harness the power of moving water to create electricity. The cut-in, cut-out, and nominal water flow are used to determine the extracted TDL power Eqs^26,27,31 as follows:

$$\:{P}_{TDL\:=}\left\{\begin{array}{c}\:\:\:0\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:;{V}_{TDL}\le\:{V}_{TDL-cutin},{V}_{TDL}\ge\:{V}_{TDL-cutout}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:\:0.5\delta\:A{C}_{P}{{V}_{T}}^{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:;\:{V}_{TDL-cutin}<{V}_{TDL}<{V}_{TDL-Nominal}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\\\:{\:P}_{HKT-Nominal}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:;\:{V}_{TDL-Nominal}\le\:{V}_{TDL}\le\:{V}_{TDL-cutout}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\end{array}\right.$$

(2)

Where, $\:{P}_{TDL}\:$and $\:{\:P}_{TDL-Nominal}$ refer to the TDL extracted power and TDL rated power (kW), respectively, $\:{V}_{TDL}$ is the water flow, $\:{V}_{TDL-cutin}$ indicates cut-in water flow, $\:{V}_{TDL-Nominal}$ denotes nominal water flow, and $\:{V}_{TDL-cutout}$ clear cut-out water flow (m/s). $\:A$ refers to the turbine cross-sectional area (m²), $\:\delta\:$ denotes fluid densitz (kg/m²), and $\:{C}_{P}$ presents coefficient of the power.

EL

Hydrogen and oxygen are created by EL utilizing water electrolysis. The electrolyzer is employed in the hybrid system applications when there is an excess of power. In other words, the electrolyzer produces hydrogen using surplus power so that it can be provided to the load in condition of a power shortage. The model equation for this process is written as follows^12,13,26:

$$\:{P}_{EL-HS}={P}_{HS-EL}\times\:{\epsilon}_{EL}$$

(3)

Where, $\:{\epsilon}_{EL}$ denotes EL efficiency (%), and $\:{P}_{HS-EL}$ indicates transferred power to the EL from the renewable energy resources (kW).

HST

One of the crucial components of the FC system for storing hydrogen is the HST^12,13,26. The HST acts as a backup power in the hybrid system that includes the FC, and it significantly influences system reliability and electrical scheduling. The hydrogen generated is stored in the HST when there is a surplus of power, and it is injected to the FC to supply the load when there is a shortage of power. The model equation for the FC is as follows^12,13,26:

$$\:{E}_{HST}\left(t\right)=\:{E}_{HST}\left(t-1\right)+\left({P}_{\text{E}\text{L}-\text{H}\text{S}\text{T}}\right(t)-{\text{P}}_{\text{H}\text{S}\text{T}-\text{F}\text{C}}(t)\times\:{\epsilon}_{HST})\times\:t$$

(4)

Where,$\:\:{E}_{HST}\left(t\right)$ and $\:{E}_{HST}(t-1)$ are HST hydrogen energy at time t and t-1, respectively. $\:{P}_{\text{E}\text{L}-\text{H}\text{S}\text{T}}\left(t\right)$ is EL power to HST at time t (kW), $\:{\text{P}}_{\text{H}\text{S}\text{T}-\text{F}\text{C}}\left(\text{t}\right)$ denotes power delivered from the HST to FC (kW). $\:{\epsilon}_{HST}$ is HST efficiency (%).

Mass of the hydrogen in the tank is compaued by^12,13

$$\:{{\Pi\:}}_{HST}\left(t\right)=\frac{{E}_{HS}\left(t\right)}{{{\Theta\:}}_{H2}}$$

(5)

Where, $\:{{\Pi\:}}_{HST}\left(t\right)$ is hydrogen mass in the tank (kg) at time t, and $\:{{\Theta\:}}_{H2}$ denotes quantity of the hydrogen heating (39.7 kWh/kg)¹².

FC

When there is a power shortage in the hybrid system, the FC produces electricity by accepting hydrogen, which can increase the load’s dependability. The FC production model’s equation is as follows^12,13:

$$\:{P}_{FC-Inv}={P}_{HST-FC}\times\:{\epsilon}_{FC}$$

(6)

Where, $\:{\epsilon}_{FC}$ denotes the FC efficiency (%).

Inverter

The inverter, which is the last component of the hybrid system, converts DC electricity to AC power using the following model equation ^12,13:

$$\:{P}_{Inv-Edub}=({P}_{FC-Inv}+{P}_{Gen-Inv})\times\:{\epsilon}_{Inv}$$

(7)

Where,$\:\:{P}_{Inv-Edub}$ is the delivered power from inverter to the educational building load (kW), $\:{\epsilon}_{Inv}$ is the efficiency of inverter (%), and $\:{P}_{Ren-Inv}$ is the hybrid system power (PV, and TDL power) injected to the inverter (kW).

Optimal sizing

In this section, the PV/TDL/FC system sizing for electrifying an educational building is formulated. The goal is to minimize the CEPLS while still meeting the demand shortage probability (DSHP) constraint using an improved arithmetic optimization algorithm (IAOA).

Objective function

In this work, the aim function that the hybrid system can provide a reliable energy supply for educational buildings is the CEPLS minimization^3,6,7,12,13. According to the lifespan of renewable resources, the project has a 20-year lifetime. The CEPLS is defined by

$$\:CEPLS={\varpi}_{CAP}+{\varpi}_{O\&MAIN}+{\varpi}_{REP}$$

(8)

Where, $\:{\varpi}_{CAP},\:$$\:{\varpi}_{O\&MAIN}$, and $\:{\varpi}_{REP}$ are capital, operation and maintenance, and replacement costs, respectively and these costs are formulatedas follows:

$$\begin{aligned} \varpi _{{CAP}} & = \varpi _{{PV - cap}} \times \:\partial _{{PV}} + \varpi _{{TDL - cap}} \times \:\partial _{{TDL}} + \varpi _{{EL - cap}} \times \:\partial _{{EL}} + \varpi _{{HST - cap}} \times \:\partial _{{HST}} + \varpi _{{FC - cap}} \times \:\partial _{{FC}} \\ & \quad + \varpi _{{Inv - cap}} \times \:\partial _{{Inv}} \\ \end{aligned}$$

(9)

Where, $\:{\varpi}_{PV-cap}$, $\:{\varpi}_{TDL-cap}$, $\:{\varpi}_{EL-cap}$, $\:{\varpi}_{TDL-cap}$, $\:{\varpi}_{FC-cap}$, and $\:{\varpi}_{Inv-cap}$ are capital cost of PV, TDL, EL, HST, FC, and inverter, respectively. $\:{\partial}_{PV}$, $\:{\partial}_{TDL}$, $\:{\partial}_{EL}$, $\:{\partial}_{HST}$, $\:{\partial}_{FC}$, and $\:{\partial}_{Inv}$ refer to the PV, TDL, EL, HST, FC, and inverter, respectively. The capacity of each of these devices is considered as a unit.

$$\begin{aligned} \varpi _{{O\& MAIN}} & = {{\Upsilon }} \times \left( {\varpi _{{{\text{PV - OM}}}} \times \:\partial _{{{\text{PV}}}} {\text{ + }}\varpi _{{TDL - OM}} \times \:\partial _{{TDL}} + \varpi _{{EL - OM}} \times \:\partial _{{EL}} + \varpi _{{HST - OM}} \times \:\partial _{{HST}} + \varpi _{{FC - OM}} } \right. \\ & \quad \left. { \times \partial _{{FC}} + \varpi _{{Inv - OM}} \times \partial _{{Inv}} } \right) \\ \end{aligned}$$

(10)

$$\:\text{{\rm\:Y}}=\frac{{\left(1+\left(Ir\right)\right)}^{Plf}-1}{Ir{\left(1+\left(Ir\right)\right)}^{Plf}}$$

(11)

$$\:Ir=\frac{NoIr-\text{A}\text{n}\text{I}\:}{1+\text{A}\text{n}\text{I}\:}$$

(12)

Where, $\:{\varpi}_{PV-OM}$, $\:{\varpi}_{TDL-OM}$, $\:{\varpi}_{EL-OM}$, $\:{\varpi}_{HST-OM}$, $\:{\varpi}_{FC-OM}$, and $\:{\varpi}_{Inv-OM}$ are operation and maintenance cost of PV, TDL, EL, HST, FC, and inverter, respectively. $\:\text{{\rm\:Y}}$ is the factor of yearly payments present value, $\:Plf$ represent the project lifespan,$\:\:Ir$ is real interest rate, $\:NoIr$ is nominal interet rate, and AnI is the annual inflation.

$$\:{\varpi}_{REP}={\tau\:\:\times\:({\varpi}_{PV-rep}\times\:{\partial}_{PV}+\varpi}_{TDL-rep}\times\:{\partial}_{TDL}+{\varpi}_{EL-rep}\times\:{\partial}_{EL}+{\varpi}_{HST-rep}\times\:{\partial}_{HST}+{\varpi}_{FC-rep}\times\:{\partial}_{FC}+{\varpi}_{Inv-rep}\times\:{\partial}_{Inv})$$

(13)

$$\:\tau\:=\sum\:_{n=1}^{Nrep}\frac{1}{{\left(1+\left(\frac{NoIr-\text{A}\text{n}\text{I}\:}{1+\text{A}\text{n}\text{I}}\right)\right)}^{clf\times\:n}}$$

(14)

Where, $\:\tau\:$ is net present value of constant payments. $\:{\varpi}_{PV-rep}$, $\:{\varpi}_{TDL-rep}$, $\:{\varpi}_{EL-rep}$, $\:{\varpi}_{FC-rep}$, $\:{\varpi}_{Inv-rep}$ are replacement cost of photovoltaic, tidal, electrolyzer, H₂ tank, fuel cell, and inverter, respectively. $\:clf$ is useful lifetime of each device, and $\:Nrep$ is number of replacements for each device.

Constraints

DSHP

Reliability is one of the important indicators in the sizing of the hybrid system with the aim of improving the load supply level^3,6,7,12,13. In this work, the demand shortage probability (DSHP) is considered to evaluate the hybrid system reliability to supply the educational building demand. The DSHP is formulated by

$$\:DSHP=\frac{\sum\:_{t=1}^{T}[{P}_{Edub}\left(t\right)-{(P}_{Gen-Inv}\left(t\right)\times\:{\epsilon}_{Inv}+{P}_{FC-Inv}\left(t\right)\times\:{\epsilon}_{Inv})]}{\sum\:_{t=1}^{T}\left[{P}_{Edub}\left(t\right)\right]}$$

(15)

The DSHP constraint is defined by

$$\:DSHP\le\:\:{DSHP}_{max}$$

(16)

Where, $\:{DSHP}_{max}$ denotes maximum value of the $\:DSHP$.

Components

The following are the minimum and maximum constraints on the size of the hybrid system’s components:

$$\:{\partial}_{PV}^{min}\le\:{\partial}_{PV}\le\:{\partial}_{PV}^{max}$$

(17)

$$\:{\partial}_{TDL}^{min}\le\:{\partial}_{TDL}\le\:{\partial}_{TDL}^{max}$$

(18)

$$\:{\partial}_{EL}^{min}\le\:{\partial}_{EL}\le\:{\partial}_{EL}^{max}$$

(19)

$$\:{\partial}_{HST}^{min}\le\:{\partial}_{HST}\le\:{\partial}_{HST}^{max}$$

(20)

$$\:{\partial}_{FC}^{min}\le\:{\partial}_{FC}\le\:{\partial}_{FC}^{max}$$

(21)

$$\:{\partial}_{Inv}^{min}\le\:{\partial}_{Inv}\le\:{\partial}_{Inv}^{max}$$

(22)

$$\:{E}_{HST}^{min}\le\:{E}_{HST}\le\:{E}_{HST}^{max}$$

(23)

$$\:{{\Pi\:}}_{HST}^{min}\le\:{{\Pi\:}}_{HST}\le\:{{\Pi\:}}_{HST}^{max}$$

(24)

Where, $\:{\partial}_{PV}^{min}$, $\:{\partial}_{TDL}^{min}$, $\:{\partial}_{EL}^{min}$, $\:{\partial}_{HST}^{min}$, $\:{\partial}_{FC}^{min}$, and $\:{\partial}_{Inv}^{min}$are minimum number of photovoltaic, tidal, electrolyzer, H₂ tank, fuel cell, and inverter, respectively. Also, $\:{\partial}_{PV}^{max}$, $\:{\partial}_{TDL}^{max}$, $\:{\partial}_{EL}^{max}$, $\:{\partial}_{HST}^{max}$, $\:{\partial}_{FC}^{max}$, and $\:{\partial}_{Inv}^{max}$are maximum number of PV, TDL, EL, HST, FC, and inverter, respectively.$\:\:{E}_{HST}^{min}$ and $\:{E}_{HST}^{max}$ denote lower and upper HST energy, respectively, and $\:{{\Pi\:}}_{HST}^{min}$ and $\:{{\Pi\:}}_{HST}^{max}$ are lower and upper mass of the hydrogen in the tank, respectively.

Proposed optimizer

A new, improved solver named the improved arithmetic optimization algorithm (IAOA), which is presented in the following, is used to find the PV/TDL/FC system’s optimal size.

Conventional AOA

Mathematical arithmetic operators (AOs), such as multiplication (M), division (D), subtraction (S), and addition (A), without using their derivatives, are the basis for the arithmetic algorithm for optimization (AOA)⁴². Arithmetic is a key component of the theory of numbers, and AOs are the conventional computing tools for learning statistics. Simple calculations are used for optimizing by the AOA.

• Preparation phase.

At the beginning of the optimization process, a stochastic set of potential solutions (X) is generated. The best response is one that comes close to being the current best⁴².

$$X = \left[ {\begin{array}{*{20}c} {x_{{{\text{1,1}}}} } & {X_{{{\text{1,2}}}} } & \cdots & \cdots & {x_{{1,j\,}} } & {x_{{1,n - 1}} } & {x_{{1,n}} } \\ {x_{{{\text{2,1}}}} } & {X_{{{\text{2,2}}}} } & \cdots & \cdots & {x_{{2,j}} } & \cdots & {x_{{2,n}} } \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {x_{{N,1}} } & {X_{{N,1}} } & \cdots & \cdots & {x_{{N,j}} } & {x_{{N,n - 1}} } & {x_{{N,n}} } \\ \end{array} } \right]$$

(25)

In the beginning, the AOA must choose between both exploration and extraction. As a result, (26) computes the mathematical optimization function (MOF) and applies it to the search process⁴².

$$\:MOA(C\_Iter)=Min+C\_Iter\times\:\left(\frac{Max-Min}{M\_Iter}\right)$$

(26)

Where, C_Iter refers to the current iteration, M_Iter represents the largest number of iterations, and lower and upper also signify the least and lowest amounts of the $\:MOA$, $\:MOA(C\_Iter)$ reflects the monetary function’s amount over the course of t-iteration.

• Exploration phase.

Calculations utilizing specific AOs establish which relates to the discovery seeking phase employing either the division (D) or multiplication (M) operator. Due of their wider spread, the M and D operators are unable to achieve the goal as quickly as the S and A operators. The discovery search phase will find the most ideal response after several repetitions. By interacting with one another, M and D operators help with the execution phase of the optimization process⁴².

Fig. 3

Update the operators of AOA to the optimum area⁴².

The AOA’s exploration operators assess the search space in conjunction with the two M and D operators to identify the best solution. How to set the used operators to the ideal area is shown in Fig. 3⁴². The D operation is dependent on r2 < 0.5 throughout this phase, and the M is disregarded once the D operation is over. M is turned on once D has finished serving its purpose. The exploratory phase position adjustment by⁴²

$$\:{x}_{i,j}(C\_Iter+1)=\left\{\begin{array}{c}\frac{best\left({x}_{j}\right)}{(MOP+\epsilon\:)\times\:\left(\right(U{B}_{j}-L{B}_{j})\times\:\mu\:+L{B}_{j})}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}r2<0.5\\\:best\left({x}_{j}\right)\times\:MOP\times\:\left(\right(U{B}_{j}-L{B}_{j})\times\:\mu\:+L{B}_{j}),\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}otherwise\end{array}\right.$$

(27)

Where x_{i, j} (C_Iter) indicates the jth scenario of the ith response in the present iteration, best (x_j) symbolizes the jth circumstance for the best answer, marks a zero, and xi, (C_Iter + 1) is the ith subsequent answer, xi, (C_Iter + 1) signals the ith subsequent solution. The terms UBj and LBj specify the maximum and minimum bounds of the j location, respectively, and µ denotes a restricted factor (in this case, 0.5)⁴².

$$\:MOP(C\_Iter)=1-\frac{C\_Ite{r}^{1/\alpha\:}}{M\_Ite{r}^{1/\alpha\:}}$$

(28)

where MOP refers to the mathematical possibility of the optimizer, $\:C\_Iter$ signifies the present iteration and MOP (C_Iter) stands for the fitness metric. A critical characteristic that corresponds to high sensitivity to state the precision of the utilization phase is (equal to 5); M_Iter reflects the iterations as a higher iterations quantity⁴².

• Exploitation phase.

During the usage phase, subtraction (S) or addition (A) processes produce additional density. S and A operators, in contrast to M and D, can hit the target with less scatter. After several iterations, the near-optimal solution may be found during the operational phase. As shown analytically by⁴², the S and A explore the search space with multiple concentrations in order to enhance the result.

$$\:{x}_{i,j}(C\_Iter+1)=\left\{\begin{array}{c}best\left({x}_{j}\right)-(MOP+\epsilon\:)\times\:\left(\right(U{B}_{j}-L{B}_{j})\times\:\mu\:+L{B}_{j})\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}r3<0.5\\\:best\left({x}_{j}\right)+(MOP+\epsilon\:)\times\:\left(\right(U{B}_{j}-L{B}_{j})\times\:\mu\:+L{B}_{j}),\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}otherwise\end{array}\right.$$

(29)

Operator A is neglected until the exploitation of operator D is finished during the phase of operation, where operator S is dependent on r3 < 0.5. As the S operator completes, the A operator begins. The region of optimal trapping is forbidden by the operators S and A. As a result, this process increases the effectiveness of the technique to achieve the best result. The present location can be found to be among a region that corresponds to the search space conditions D, M, S, and A. The D, M, S, and A deliberately change their locations inside the solution circumstance by deciding that it is near to the ideal answer. The AOA begins the stages by analyzing a random responses set. The commencement of the stochastic variables within the minimum and maximum values is how the circumstance vector is defined. Each iteration changes the location and each population member step. Utilization for modifying the location until the convergence criteria are met, at which point the best variables are found using the best fitness.

Improved AOA (IAOA)

The MOP variant in conventional AOA plays a key role in regulating the algorithm’s exploration stage. It has been discovered that exponentially decreasing conversion parameters, or MOPs, have better-searching precision than linearly reducing parameters. High responsiveness is required by parameters to express the accuracy of the exploration phase. The parameter is regarded as equal to 5 in the conventional AOA. The study’s interpretation of the symbol is [0, 5]. The updated MOP formulation included in the enhanced AOA is provided by

$$MOP(C\_Iter)=\alpha \times {e^{\frac{{C\_Iter}}{{M\_Iter}}}}$$

(30)

Additionally, new descendants must be generated promptly when the algorithm is not updated in a while. In order to enhance the capability of the AOA, a neighbourhood search operator is used in this study^43,44. The precise procedure is as follows:

$$\:{X}_{i}={r}_{1}\times\:{X}_{i}+{r}_{2}\times\:{x}_{best}+{r}_{3}\times\:({X}_{1}-{X}_{2})$$

(31)

Where TXi is the trial version of the parent solution X_i produced by the neighbourhood search operator, Gbest is the globally optimal solution discovered using the conventional AOA, and X₁ and X₂ are the two solutions that were randomly chosen to be distinct from X_i. Additionally, r₁, r₂ and r₃ are random values that fall between (0, 1) and meet the equation r₁ + r₂ + r₃ =1. The ability to update the current agent to any location in the search space thanks to the trial solution considerably enhances the algorithm’s capability to explore and avoid premature convergence.

Hybrid stochastic-robust approach (UT-IGDT-RA)

UT based-stochastic model

The unscented transformation (UT) approach to parameter modeling is used in this work. The capacity of UT to handle nonlinear transitions⁴¹ and provide very appropriate predictions of PDFs has earned it widespread recognition. The dimension of the source vector for uncertainties (U) in this approach is indicated by the letter n. Additionally, for every uncertain parameter, 2n + 1 scenarios are generated. This study incorporates the unscented transformation (UT) method for parameter modeling. UT is well-known for its capability to address nonlinear transitions⁴¹ and very suitable estimations of probability distribution functions. In this method, n denotes the dimension of the input vector for uncertainties (U). Also, 2n + 1 scenarios are produced for each uncertain parameter. Because no scenario lowering approach is applied to this limited number of situations, the computation time is greatly decreased. y = f(x), where x ∈ Rⁿ is the uncertain input vector and y ∈ R^r is the uncertain outcome vector with r components, x ∈ Rⁿ represents the problem with its stochastic, nonlinear, and uncertain characteristics. x’s mean and covariance are displayed as µ_x and σ_x. The symmetric and asymmetric components of σ_x are used to determine the variance and covariance of uncertainty, respectively. The UT method’s implementation is to determine the results’ mean and covariance amounts, or µ_y and σ_y. The steps listed below provide an explanation of this⁴¹:

Step 1: From uncertainty of input data, select 2n + 1 samples⁴¹:

$$x_{0} = \mu _{x}$$

(32)

$$x_{s} = \mu _{x} + \sqrt {\frac{n}{{1 - W^{0} }}\sigma _{x} } \,\,\,\,\,\,\,\forall s = 1,2,...,n$$

(33)

$$x_{s} = \mu _{x} - \sqrt {\frac{n}{{1 - W^{0} }}\sigma _{x} } \,\,\,\,\,\,\,\forall s = 1,2,...,n$$

(34)

Where, W⁰ denotes the mean value µ_x weight.

Step 2: Evaluate each sample point’s weighting factor⁴¹:

$$W^{0} = W^{0}$$

(35)

$$W_{s} = \frac{{1 - W^{0} }}{{2n}}\,\,\,\,\,\,\,\forall s = 1,2,...,n$$

(36)

$$W_{{s + n}} = \frac{{1 - W^{0} }}{{2n}}\,\,\,\,\,\,\,\forall s + n = n + 1,n + 2,...,2n$$

(37)

$$\sum\limits_{{s = 1}}^{n} {W_{s} } = 1$$

(38)

Step 3

In accordance with Eq. (27), sample 2n + 1 points to the nonlinear function that produces the outputting samples.

$${y_s}=f({x_s})$$

(39)

Step 4

Evaluate σ_y and µ_y of the variableθ.

$${\mu _y}=\sum\limits_{{s=1}}^{n} {{W_s}{\theta _s}}$$

(40)

$${\sigma _y}=\sum\limits_{{s=1}}^{n} {{W_s}\left( {{\theta _s} - {\mu _y}} \right)} - {\left( {{\theta _s} - {\mu _y}} \right)^T}$$

(41)

Conventional IGDT-RA based-robust model

The Information Gap Decision Theory (IGDT) facilitates the development of a system ideal for managing the fluctuation range of uncertain variables. IGDT is a non-probabilistic approach that deals with uncertainty by capturing the interval of error between actual observations and predictions without relying heavily on extensive historical data. Additionally, the IGDT framework enables decision makers to pursue two distinct strategies: robust, which focuses on safeguarding against worst-case scenarios, and opportunistic, which aims to exploit favorable outcomes. Typically, an IGDT model consists of three main elements: the system model, the uncertainty model, and the performance metrics. According to sources^{38,46,47,48,49}, an optimization problem within this framework can be structured to include both quality and inequality constraints.

$$\begin{aligned} & {\text{min}}\,f\left( {X,\vartheta } \right) \\ & g\left( {X,\vartheta } \right) = 0 \\ & h\left( {X,\vartheta } \right) \le 0 \\ \end{aligned}$$

(42)

where X and u, respectively, stand in for the vector of decision and the uncertain input data and y = f(X,$\:\:\vartheta\:$) signifies cost.

The uncertain input data of predicted values are represented by $\:\stackrel{-}{\vartheta\:}$ and the set U, referred to as having the uncertainty set, is characterized as all quantities $\:\vartheta\:$ with a departure over the predicted quantities of no more than $\:\alpha\:\stackrel{-}{\vartheta\:}$^46,47.

$$\:U\left(\alpha\:,\vartheta\:\right)=\left\{\vartheta\::\:\left|\frac{\vartheta\:-\stackrel{-}{\vartheta\:}}{\stackrel{-}{\vartheta\:}}\right|\le\:\alpha\:\right\}$$

(43)

Where, $\:\alpha\:$ is uncertain parameter’s uncertainty radius.

In the IGDT-RA model, the decision-maker feels met if the costs are equal to or below a certain critical threshold. The aim of the risk-averse decision-maker in this IGDT model is to expand the uncertainty radius for uncertain parameters as much as possible. This approach ensures that any deviation in the input data from the set of uncertain parameters does not result in costs exceeding this critical threshold. The structure of the risk-averse IGDT-based model is as follows:

$$\begin{aligned} & {\text{max}}\,\alpha \left( {X,\vartheta } \right) \\ & f\left( {X,\vartheta \,} \right) \le f_{{cr}} \quad \forall \vartheta \in U \\ & g\left( {X,\vartheta } \right) = 0\quad \forall \vartheta \in U \\ & h\left( {X,\vartheta } \right) \le 0\quad \forall \vartheta \in U \\ & f_{{IGDT - RA,max}} = (1 + \sigma ) \times \overline{{f_{{Deterministic}} }} \\ \end{aligned}$$

(44)

In the risk-averse Information Gap Decision Theory (IGDT-RA) model, the robustness boundary is defined relative to the deterministic optimal cost, $\:\stackrel{-}{{f}_{Deterministic}}$ ​, which is achieved when the uncertain inputs of the deterministic problem match the nominally expected uncertain data. The maximum acceptable cost in this model is denoted as $\:{f}_{IGDT-RA,max}$​, and this represents the critical cost variance rate or the uncertainty budget. Essentially, the primary aim of IGDT-RA is to ensure that minimum requirements are met by strategically setting decision variables to shield the decision-maker from the risks associated with undesirable deviations from uncertain input data. The system’s robustness, encompassing $\:{\alpha}_{Load}$ and $\:{\alpha}_{Gen}$, is evaluated in the IGDT-RA against the most adverse uncertainty scenarios while adhering to the established sizing constraints. The decision-making solution in the IGDT-RA model ensures that the expected demand and generation are capable of being met within the defined uncertainty range. The cost value determined in the deterministic sizing process is referred to as $\:{CEPLS}_{Deterministic}$​ in the deterministic sizing of the hybrid system. This model considers uncertainties in building demand and renewable energy sources during robust sizing. Thus, the objective is to maximize the uncertainty radius for $\:{\alpha}_{Load}$ and $\:{\alpha}_{Gen}$ while taking into account the designated uncertainty budgets. The Risk-Averse Strategy for decision-making is formulated using the principles of IGDT.

$$\begin{aligned} & max\:\left( {\alpha _{{Load}} ,\alpha _{{Gen}} } \right) \\ & subjected\:to\:CEPLS_{{IGDT - RA}} \le \:(1 + \sigma \:) \times \:CEPLS_{{Deterministic}} ,\:\:\:\sigma \: \in \:\left[ {{\text{0,1}}} \right) \\ & P_{{LD,t}} = (1 + \alpha _{{Load}} ) \times \:\mathop P\limits^{ - } _{{LD,t}} \\ & P_{{Gen,t}} = (1 + \alpha _{{Gen}} ) \times \:\mathop P\limits^{ - } _{{Gen,t}} \\ & {\text{Constraints}}\:{\text{Eqs}}.\:\left( {15} \right) - \left( {24} \right) \\ \end{aligned}$$

(45)

Where, $\:{CEPLS}_{IGDT-RA}$ is the CEPLS taking into account the uncertainty budget rising in the robust sizing. $\:{\stackrel{-}{P}}_{LD,t}$ and $\:{\stackrel{-}{P}}_{Gen,t}$ are building demand and producing renewable resources at time t using a deterministic sizing strategy, respectively.

The flowchart of the robust sizing implementation via the IGDT-RA and IAOA is demonstrated in Fig. 4 and its steps are as follows:

Step 1) Begin by gathering data for the hybrid system, which should include local solar irradiance and wind speed measurements, building energy requirements, as well as the technical and financial specifications of the system components, and the parameters for the algorithm.

Step 2) Select the unceryainty budget ($\:\sigma\:$) considering$\:\:CEPL{S}_{IGDT-RA}\le\:(1+\sigma\:)\times\:CEPL{S}_{IGDT-RA},\text{\hspace{0.17em}\hspace{0.17em}}\sigma\:\in\:\text{\hspace{0.17em}}\left[\text{0,1}\right)$.

Step 3) Initiate the decision variables including hybrid system components and uncertainty radius of building demand and renewable resources generation in allowable range for each population.

Step 4) Compute the IGDT-OF as $\:IGDT-OF=-0.5\times\:{\alpha}_{Load}-0.5\times\:{\alpha}_{Gen}$ for each population satisfying the constraints and the corresponding member with minimum $\:IGDT-OF$ value (maximum $\:{\alpha}_{Load}\:$and$\:{\:\alpha}_{Gen}$) is considered as best solution.

Step 5) Update the algorithm’s population.

Step 6) Calculate the IGDT-OF for the refreshed population that meets the established criteria. The optimal solution is identified as the individual with the smallest IGDT-OF value. If this value is lower than the one obtained in Step 4, proceed to update the solution with it.

Step 7) Use the new MOP and neighborhood search operator to update the algorithm’s population again.

Step 8) Apply the neighborhood search operator to the latest population that fulfills the criteria and compute the IGDT-OF.

Step 9) Replace the best solution obtained in Step 6, with the new solution achieved in step 8, if its IGDT-OF value shows improvement over the result from Step 6.

Step 10) Check if the convergence criteria are satisfied. If they are, proceed to Step 11; otherwise, revert to Step 2.

Step 11) Conclude the process and print the best solution.

Fig. 4

Flowchart of the proposed robust sizing implementation via the conventional IGDT-RA and IAOA.

The IGDT serves as the theoretical foundation for modeling uncertainties in the energy demand and renewable generation, allowing the characterization of robustness through the maximum uncertainty radius (MRU). The IGDT framework defines the robustness criteria and establishes the relationship between the uncertainty budget and the system’s performance under worst-case scenarios. The AOA, in its improved form (IAOA), is employed as the optimizer to efficiently search for the optimal system configuration and corresponding MRUs that satisfy the robustness criteria while meeting the cost and reliability constraints. By leveraging the exploration and exploitation capabilities of the IAOA, the proposed framework ensures accurate and computationally efficient determination of MRUs, directly linking IGDT’s robustness measures with the optimization process. This synergy between IGDT and IAOA allows for a seamless integration of uncertainty modeling and optimization, enabling the robust design of the hybrid energy system.

The IGDT-based robust framework evaluates the system’s performance under worst-case uncertainty scenarios by gradually increasing the uncertainty budget, which represents the deviation from expected demand or generation values. The maximum level of robustness is achieved when the MRU reaches a point where further increases in the uncertainty budget do not affect the system’s ability to meet operational and reliability constraints. This saturation point reflects the system’s capacity to handle uncertainties without additional compromise in cost or reliability. The greatest risk corresponds to the boundary condition at this maximum uncertainty radius, where the system is designed to operate under the most adverse conditions anticipated. This process is systematically integrated with the IAOA, which optimizes the component sizing to balance cost, reliability, and robustness, ensuring that the system can withstand the highest levels of uncertainty effectively.

The hybrid UT-IGDT-RAS model

This section outlines the hybrid UT-IGDT-RA approach combining the UT with IGDT-RA for stochastic-robust optimization. The hybrid method integrates the strengths of UT for scenario generation and IGDT-RAS for optimizing the system sobustness under uncertainty.

Formulation of hybrid UT-IGDT-RA Method

The hybrid method is structured as follows:

Step 1: UT Scenario Generation.

• Input Data: Define uncertainty parameters, including load demand (P_LD) and generation (P_Gen), and assign mean (µ) and covariance (σ) values.

• Scenario Creation: Generate 2n + 1 scenarios based on the UT rules, where n is the dimension of the uncertainty parameter set. Nominal, positive deviation, and negative deviation scenarios are created.

• Weights are assigned to scenarios. Where λ is a scaling parameter.

Step 2: Robust Optimization Using IGDT-RA.

• Objective Function: Maximize the uncertainty radius ($\:{\alpha}_{Load}$ and $\:{\alpha}_{Gen}$) while meeting reliability and cost constraints.

• Constraints: Ensure demand and generation balance, reliability thresholds, and system operational limits.

Step 3: Combine UT and IGDT-RA.

• For each UT scenario, apply IGDT-RA to find maximum uncertainty radius and corresponding CEPLS values.

• Output three robust solutions: base scenario, positive deviation, and negative deviation.

Step 4: Decision-Making.

- The energy operator selects the robust solution based on risk tolerance or observed uncertainties.

Algorithm steps for hybrid UT-IGDT-RA

• Initialize Data: Define input parameters, constraints, and objectives.

• Generate UT Scenarios: Create 2n + 1 scenarios using the UT method.

• Perform IGDT-RA Optimization: Apply IGDT-RA for each scenario to compute $\:{\alpha}_{Load}$ and $\:{\alpha}_{Gen}$.

• Evaluate Robustness: Compare uncertainty radius and cost (CEPLS) across scenarios.

• Decision Selection: Present results to the energy operator for selecting the best solution.

• Output Results: Provide the final configuration, uncertainty radius, and CEPLS.

Simulation results and discussion

Results of the accurate sizing of an off-grid PV/TDL/FC energy system based on hydrogen storage are presented in this section to fulfill the annual load requirement of an educational building and minimize the cost of electricity through the life span of the project. The hybrid UT-IGDT-RA technique and the IAOA solver are used to resolve the robust sizing problem. In this study, the performance of the robust sizing model and the deterministic sizing model are compared while considering the generation uncertainties of renewable resources and the load for educational buildings. Additionally, the effectiveness of the suggested IAOA has been evaluated in comparison to the traditional AOA⁴² and particle swarm optimization (PSO)⁴⁵ techniques. The user experience and multiple simulation executions to achieve the best solution and prevent unnecessary increases in the computational cost are the reasons for choosing these numbers, which are considered to be 50, 200, and 25, respectively, for each algorithm’s population, maximum iteration, and number of independent executions in each simulation scenario. Each algorithm’s adjusting parameters are also chosen based on the information given in the related Refs^42,45.

The following simulation scenarios are provided to evaluate the proposed approach.

Scenario#1) Deterministic sizing for three hybrid system configurations as:

• PV/TDL/FC.

• PV/FC.

• TDL/FC.

Scenario#2) Robust sizing for three configurations based on the IGD-RAS as:

• PV/TDL/FC.

• PV/FC.

• TDL/FC.

Scenario#3) Hybrid Stochastic-Robust sizing method for three configurations based on the UT-IGD-RAS as:

• PV/TDL/FC.

• Comparison with WT/TDL/FC.

The aim of the research is to determine the robustness value of each system combinations in condition of worst uncertainty scenario, which is obtained via the UT-IGDT-RA approach and the IAOA solver.

System data

The irradiance and water flow experimental data applied for sizing the hybrid system are related to Yazd city, Iran (latitude: 31^o53^’, longitude: 54^o21)²⁶. Figures 5 and 6 show, respectively, the hourly profiles of irradiance and water flow during a year (8760 h). The hourly load demand profile for an educational building with a peak demand of approximately 50.22 kW and a total annual electrical consumption of 277,686.5 kWh is also depicted in Fig. 7. Additionally, the educational building’s load specifications are included in Table 2. It should be noted that usage of the devices shown in Table 2 varies seasonally and in response to customer demands and environmental factors. However, the max load is 50.22 kW in size. Additionally, Table 3 provides technical and financial information on each of the system’s components. The project life span is similar to the useful life time of the renewable energy sources (20 years). In addition, Ref¹². states that the chosen interest and inflation rates are 9% and 3%, respectively.

Fig. 5

Profile of solar radiation during a year²⁶.

Fig. 6

Profile of water flow during a year²⁶.

Fig. 7

Profile of the educational building load during a year²⁶.

Table 2 Estimation of each type of educational building load^50,51.

Table 3 Technical and cost components data applied in the sizing problem^12,26.

Results of deterministic sizing (Scenario#1)

Optimal configuration

In this section, deterministic sizing of various hybrid system configurations including PV/TDL/FC, HPV/FC, and TDL/FC is presented via the IAOA method. The process of sizing convergence of different system configurations is shown in Fig. 8. As it is clear, the PV/TDL/FC system has obtained the optimal solution with the lowest CEPLS cost, and then the TDL/FC configuration has the lowest sizing cost. Also, the HPV/FC configuration has the highest cost among different configurations.

Fig. 8

Convergence process of deterministic sizing of PV/TDL/FC system sizing.

The set of optimal solutions including the decision variables and also the cost and reliability values obtained by the IAOA method for different system configurations including PV/TDL/FC, PV/FC, and TDL/FC are given in Tables 4 and 5. As the results demonstrated, the optimal configuration with the simultaneous participation and overlapping of PVs and TDLs units with hydrogen reserve energy has been able to achieve a lower sizing cost in addition to further improving the reliability of the educational building. The sizing cost of PV/TDL/FC, HPV/FC, and TDL/FC configurations is obtained at 1.436 M$, 2.824 M$, and 1.756 M$, respectively, and the DSHP value is achieved at 0.0090, 0.0095, and 0.0093, respectively, which clears the better economic-technical performance of the PV/TDL/FC configuration.

Table 4 Deterministic sizing results for different systems.

Table 5 Deterministic results of reliability and cost for different system configurations.

Figure 9, shows the production change curve of each configuration of the hybrid system. In the HPV/FC, only the PV arrays generate power, and in the TDL/FC configuration, only the TDL units provide the generated power to supply the load. In the PV/TDL/FC configuration, PV and TDL sources play the role of generating power in the system.

Fig. 9

Generation of the different configurations of (a) PV/FC. (b) TDL/FC. (c) PV/TDL/FC.

In Fig. 10, the changes in hydrogen energy stored in the tank for different configurations are illustrated. As is clear from the figure, the TDL/FC configuration is highly dependent on hydrogen storage to supply the building load. The lowest dependence is related to the HPV/FC configuration, which, of course, is known to have a very high sizing cost. On the other hand, the dependence of the best configuration, PV/TDL/FC, on hydrogen storage is balanced. According to Fig. 10, in the hours when the production resources are not able to supply the building load, with the discharge of hydrogen to the FC, the lack of educational building is compensated, and in these hours the behavior of the energy curve of the tank is downward (for example, from 2500:00 to 2800:00 in PV/TDL/FC configuration). Also, during the hours when renewable resources can supply the load of the educational building, in this case, excess power is tranferred to the EL, and as a result, the produced hydrogen is delivered to the hydrogen tank such as hours 800:00 to 1100:00. Therefore, in different configurations, electrical scheduling has been done to supply the load building using hydrogen reserve power management.

Fig. 10

Hydrogen storage energy in deterministic sizing of different hybrid system configurations.

Considering that the behavior of the irradiance data as well as the water flow is stochastic, a hybrid system consisting of renewable production resources is not capable to fully supply the demand alone. For this reason, they are integrated with storage to create electrical scheduling and supply with a high level of reliability. On the other hand, even with a storage device, part of the load may be cut off. So here is defined the reliability index as DSHP_max=1%. In Fig. 11, the changes of DSHP are shown, which are observed in some hours of the PV/TDL/FC, it is not able to supply the load, although the total disconnected building load is not more than 1% of the total load according to the provided reliability condition (DSHP_max=1%).

Fig. 11

DSHP changes in deterministic sizing of the PV/TDL/FC configuration.

Reliability effect

In this section, the effect of DSHP_max reliability constraint changes on the PV/TDL/FC sizing and cost and reliability results. The results of this evaluation are given in Tables 6 and 7. The base simulation is implemented for the value of 1%. The results show that by reducing the DSHP_max, which means that the probability of not supplying the building load is reduced, the production level of resources and the storage device increases. On the other hand, the cost of sizing has increased due to the increase in the amount of production and storage level of hydrogen. Therefore, providing load with higher reliability requires spending more cost. The sizing cost for values of 1%, 3%, and 5% of DSHP_max are calculated at 1.436 M$, 1.193 M$, and 1.031 M$, respectively.

Table 6 The PV/TDL/FC sizing results considering different DSHP_max.

Table 7 The PV/TDL/FC reliability and cost results considering different DSHP_max.

The changes in the solution set and hydrogen storage energy due to the changes in the DSHPmax are demonstrated on the PV/TDL/FC configuration sizing in Figs. 12 and 13, which indicates the increase (decrease) in the production and storage level due to the decrease (increase) in the DSHP_max constraint.

Fig. 12

Changes of the solution set considering different DSHP_max.

Fig. 13

Hydrogen storage energy in PV/TDL/FC sizing considering different DSHP_max.

Superiority of the proposed optimizer

The performance of the IAOA to solve the deterministic sizing problem is evaluated in comparison with the traditional AOA and PSO methods. The convergence process of problem solving by different algorithms is shown in Fig. 14. As it is clear, the IAOA is able to converge to the best solution faster than other algorithms.

Fig. 14

The convergence curve of algorithms in PV/TDL/FC sizing.

The numerical outcomes of the different optimizers in solving the deterministic problem with DSHP_max=1%, including the set of optimal solutions and the statistical analysis values of the cost, as well as the confidence index, are given in Tables 8 and 9. According to the presented results, it is clear that the IAOA has obtained a lower cost and better statistic analysis criteria than other algorithms. The amount of sizing cost for IAOA, AOA, and PSO algorithms is 1.436 M$, 1.445 M$ 1.460 M$, respectively, and the value of the DSHP index for the presented algorithms is obtained 0.0090, 0.0098, and 0.0095, respectively, which results indicate the efficient, cost-effective and reliable performance of the IAOA algorithm to solve the sizing problem.

Table 8 The PV/TDL/FC sizing results for different optimization algortihms.

Table 9 The PV/TDL/FC reliability and cost results for different optimization algortihms.

Results of robust sizing (Scenario#2)

The outcomes of robust sizing using the IGDT-RA are reported in this section, accounting for the educational building load demand as well as the renewable resources production uncertainties. Using the IGDT-RA and the IAOA meta-heuristic solver, the decision variables in this method, such as the maximum uncertainty radius of renewable resource output and load demand, have been identified. In other words, the goal of this research is to estimate each hybrid system configuration’s robustness value under the worst-case scenario of uncertainty. In other words, the energy operator can make rational and accurate judgments based on the behavior of uncertain parameters by measuring the rate of robustness. The suggested method is applied to the configurations PV/TDL/FC, HPV/FC, and TDL/FC, and the outcomes are examined.

PV/TDL/FC system

In this section, numerical results of robust sizing of the PV/TDL/FC configuration are presented using the IGDT-RA and IAOA solver in Table 10. Uncertainty budgets for values below 3% and 21%, corresponding values of $\:{\alpha}_{Load}$ and $\:{\alpha}_{Gen}$ are saturated and CEPLS values remain unchanged. For uncertainty budgets of 3%, 9%, 15%, and 21%, $\:{\alpha}_{Load}$ values are obtained at 3.21%, 5.20, 7.52%, and 10.34%, respectively, and $\:{\alpha}_{Gen}$ values are achieved at 1.52%, 1.93%, 2.28%, and 2.65%, respectively. Also, the CEPLS cost for uncertainty budgets of 3%, 9%, 15%, and 21% is calculated as 1.479 M$, 1.565 M$, 1.651 M$, and 1.737 M$, respectively. Therefore, the maximum uncertainty radius of the building load demand for the uncertainty budget of 21% equals 10.34% and the maximum uncertainty radius of each PV and TDL source for the uncertainty budget of 21% equals 2.65% or for the entire production of the PV/TDL/FC configuration is set at 5.30%. According to Table 10, it can be seen that in the condition of uncertainty budget deviation from 3 to 21%, the values of $\:{\alpha}_{Load}$ and $\:{\alpha}_{Gen}$ have increased by 222% and 74%, respectively.

Table 10 Results of uncertainty radius considering different uncertainty budgets ($\:\sigma\:$) for the PV/TDL/FC configuration

In Fig. 15, the changes of $\:{\alpha}_{Load}$ and $\:{\alpha}_{Gen}$ with respect to the changes of uncertainty budget σ is shown. As can be seen, with the increase in σ, the $\:{\alpha}_{Load}$ as well as the $\:{\alpha}_{Gen}$ have increased. According to this figure, the maximum uncertainty radius of building load and renewable production is found 10.34% and 2.65%, respectively.

Fig. 15

Variation of (a) $\:{\alpha}_{Load}$ versus $\:\sigma\:$ (b) $\:{\alpha}_{Gen}$ versus $\:\sigma\:$ for the PV/TDL/FC configuration

The change curve of power dispatch based on energy management for PV/TDL/FC configuration for two deterministic and IGDT-RA sizing is presented in Fig. 16. Obviously, with the increase in the uncertainty budget, the load demand has increased, and of course, to cover this increase, the production of renewable resources has also increased. Comparison of Fig. 16a with Fig. 16b shows the increase in the level of load demand and production of resources, as well as the increase in the FC production in the mode of robust sizing based on IGDT-RA compared to the deterministic sizing. According to Fig. 16, during the hours of 01:00 to 07:00 of the simulation, the load of the building is provided by TDL and the FC. At 08:00, PV sources generate power by receiving irradiance and enter the production cycle. During the hours of 08:00 to 17:00, the load of the educational building has been supplied with the participation of renewable PV and TDL resources. In addition, during the hours of 08:00 to 17:00, excess power over the load requirement is delivered to the EL to produce hydrogen, and during these hours, the most power is transferred to the EL and the excess power from 17:00 to 24:00 is transferred to the electrolyzer but with less capacity. Therefore, in the early hours of 01:00 to 07:00, the hydrogen-based storage system with the TDL in the absence of PV sources played a major role in meeting the building’s demand.

Fig. 16

Power dispatch of different system components during a day for the PV/TDL/FC configuration (a) Risk-neutral strategy. (b) Risk-adverse strategy.

PV/FC system

In this section, the numerical outcomes of robust sizing for PV/FC configuration utilizing IGDT-RA and IAOA solver are given in Table 11. Corresponding $\:{\alpha}_{Load}$ and $\:{\alpha}_{Gen}$ are saturated for uncertainty budget values below 3% and 17%, respectively but CEPLS values stay constant. For uncertainty budgets of 3%, 9%, 15%, and 17%, the corresponding $\:{\alpha}_{Load}$ values are obtained 3.04%, 4.83, 6.68%, and 8.75%, while the corresponding $\:{\alpha}_{Gen}$values are achieved 2.97%, 3.75%, 4.43%, and 4.80%. Additionally, 2.915, 3.085, 3.254, and 3.339 are determined as the CEPLS for uncertainty budgets of 3%, 9%, 15%, and 17%, respectively. As a result, for the 17% uncertainty budget, the maximum uncertainty radius for demand is found to be 8.75%, and the maximum uncertainty radius for each TDL resource is found to be 4.80%. Table 1 shows that the values of $\:{\alpha}_{Load}$ and $\:{\alpha}_{Gen}$ have increased by 187% and 62%, respectively, in the case of the uncertainty budget variation from 3 to 17%.

Table 11 Results of uncertainty radius considering different uncertainty budgets ($\:\sigma\:$) for the PV/FC configuration

In Fig. 17, the variations of $\:{\alpha}_{Load}$ and $\:{\alpha}_{Gen}$ with respect to the changes of uncertainty budget σ is illustrated. As can be seen, with the uncertainty budget increasing the values of building demand uncertainty radius as well as the renewable resources production uncertainty radius have increased. According to this figure, the demand maximum uncertainty radius and each renewable production is obtained 8.75% and 4.80%, respectively.

Fig. 17

Variation of (a) $\:{\alpha}_{Load}$ versus $\:\sigma\:$ (b) $\:{\alpha}_{Gen}$ versus $\:\sigma\:$ for the PV/FC configuration

In Fig. 18, the power dispatch of the HPV/FC configuration components is demonstrated for two deterministic and robust (IGDT-RA) sizing approaches. As is widely known, both the demand for buildings and the output of PV sources have expanded under conditions of rising σ. According to Fig. 18 and the comparison of power dispatch in two deterministic and robust approaches, it is obvious that the level of FC production has increased to compensate for the increase in load with the increase in the uncertainty budget and as a result of the increase in renewable production. As shown in Fig. 18, the building load is supplied from 01:00 to 07:00 by releasing hydrogen into the FC, and the building demand is met using FC power alone, without the assistance of PV generation power. The PV sources commence the production cycle at 7:00 am and handle the entire system load until 6:00 pm. Additionally, from 7:00 to 18:00, the system’s excess electricity is fed into the electrolyzer where it is used to create hydrogen. This hydrogen is then stored in the hydrogen tank and from 18:00 to 24:00, when the PV sources are unable to generate electricity, the FC is in charge of injecting and supplying electricity to the load.

Fig. 18

Power dispatch of different system components during a day for HPV/FC configuration (a) Risk-neutral strategy. (b) Risk-adverse strategy.

TDL/FC system

In this section, numerical results of robust sizing for HPV/FC configuration using IGDT-RA and IAOA solver are presented in Table 12. For uncertainty budgets values below 3% and 17%, correspond and $\:{\alpha}_{Load}$ and $\:{\alpha}_{Gen}$ saturated and CEPLS values remain constant. For uncertainty budgets of 3%, 9%, 15%, and 19%, $\:{\alpha}_{Load}$ values are found at 3.15%, 4.96, 6.85%, and 9.17%, respectively, and $\:{\alpha}_{Gen}$ values are obtained at 3.01%, 3.80%, 4.49%, and 5.10%, respectively. Also, the CEPLS for uncertainty budgets of 3%, 9%, 15%, and 19% is calculated as 1.808, 1.913, 2.019, and 2.089, respectively. So, for the uncertainty budget of 19%, the demand maximum radius of uncertainty is found 9.17% and the maximum uncertainty radius of each TDL resource is found 5.10%. Based on Table 12, it can be seen that in the condition of the uncertainty budget deviation from 3 to 19%, the values of $\:{\alpha}_{Load}$and $\:{\alpha}_{Gen}$ have increased by 191% and 69%, respectively.

Table 12 Results of uncertainty radius considering different uncertainty budgets ($\:\sigma\:$) for TDL/FC configuration

In Fig. 19, the variations of $\:{\alpha}_{Load}$ and $\:{\alpha}_{Gen}$ with respect to the changes of uncertainty budget σ is illustrated. As can be seen, with the uncertainty budget increase, the values of building demand uncertainty radius as well as the renewable power uncertainty radius have increased. According to this figure, the maximum uncertainty radius of load and production of each renewable source is obtained 9.17% and 5.10%, respectively.

Fig. 19

Variation of (a) $\:{\alpha}_{Load}$ versus $\:\sigma\:$ (b) $\:{\alpha}_{Gen}$ versus $\:\sigma\:$ for the TDL/FC configuration

Figure 20, shows how the sources of electricity generation contributed to meeting the building load. With the help of TDL and the FC resources, required power of the building at 01:00 is supplied. The FC is used to satisfy the building demand from 02:00 to 05:00, and from 06:00 to 08:00, it collaborates with TDL resources to fulfill the building load requirement. The TDL resources are in charge of supplying the load from 08:00 to 24:00. In the meantime, the electrolyzer receives the surplus electricity over the load requirement and uses it to generate hydrogen. The created hydrogen is then put into the hydrogen tank where it can be used to power the building during times of system power deficit. As a result, the energy management approach is such that the FC makes up for the absence of load power during the hours when the TDL resources are unable to provide the system load in order to increase the reliability of the building’s load. A comparison of the data from two deterministic and robust approaches revealed that the robust model’s level of production, the level of FC power production has increased to account for the growth in the building’s load level.

Fig. 20

Power dispatch of different system components during a day for TDL/FC configuration (a) Risk-neutral strategy. (b) Risk-adverse strategy.

Results comparison of different configurations

The size outcomes of several hybrid system configurations are provided in this study utilizing the IGDT-RA technique and the IAOA solver. Table 13 shows the findings in relation to the output of renewable resources per the maximum amount of uncertainty budget and the maximum uncertainty radius of educational building load demand and renewable resources generation. As can be observed, when evaluated with the other configurations, the PV/TDL/FC configuration has the maximum percentage of $\:{\alpha}_{Load}$ and $\:{\alpha}_{Gen}\:$under the circumstance of the biggest uncertainty budget. With the highest uncertainty radius of production and load demand equal to 5.30% and 10.34%, respectively, the system is more robust to the worst uncertainty scenario associated to the PV/TDL/FC configuration. In other words, as compared to other configurations, the PV/TDL/FC configuration has achieved greater robustness in terms of prediction errors brought on by uncertainties. Moreover, HPV/FC has the least level of robustness under circumstances where the uncertainty budget changes the least. The uncertainty model based on the IDGT is not based on the probability distribution, so it can be said that, in contrast to the stochastic approach like Monte Carlo simulation, this method is very suitable for cases with severe uncertainties and in the absence of access to adequate historical data.

Table 13 Comparing the robustness of different system configurations for the maximum amount of uncertainty budget.

Results comparison with WT-based hybrid topology system

Deterministic results comparison

In this section, optimization of the hybrid system including the wind turbine (WT) as WT/TDL/FC configuration has been implemented considering the wind speed profile based on Ref²⁶. , and its results have been compared and analyzed with PV/TDL/FC sizing. The set of optimal solutions including the decision variables and the cost and reliability results obtained by the IAOA are given and compared in Tables 14 and 15. As can be seen, the sizing cost of the WT/TDL/FC and PV/TDL/FC hybrid systems to provide the same annual load is M$1.648 and M$1.431, respectively. Also, the reliability of the system is obtained 0.0092 and 0.0090 for WT/TDL/FC and PV/TDL/FC hybrid systems. Therefore, considering the wind turbine compared to the photovoltaic panels, it has increased the cost by 23.62% and weakened the reliability by 2.22%. The high cost of sizing based on wind turbines versus photovoltaic panels is due to the weak wind speed potential for the study area, which has no economic and technical justification, and for this reason, the PV/TDL/FC system is optimally sized to supply the annual load in this study. In addition, the cost of energy has increased from $0.2586 to $0.2966 in condition of using wind turbines instead of photovoltaic panels in the hybrid system configuration.

Table 14 Deterministic sizing results comparison for PV/TDL/FC and WT/TDL/FC systems using the IAOA.

Table 15 Deterministic results of reliability and cost for PV/TDL/FC and WT/TDL/FC systems using the IAOA.

Robust results comparison

In this section, numerical results of robust sizing of the PV/TDL/FC and WT/TDL/FC configurations are compared using the IGDT-RA and IAOA solver in Table 16 considering uncertainty budgets of 3%, 9%, 15%, and 21%. In WT/TDL/FC configuration robust sizing, $\:{\alpha}_{Load}\:$for uncertainty budgets of 3%, 9%, 15%, and 21% are obtained at 3.01%, 4.83, 7.26%, and 9.92%, respectively, and $\:{\alpha}_{Gen}$ are achieved at 1.46%, 1.87%, 2.13%, and 2.54%, respectively. Also, the CEPLS cost for uncertainty budgets of 3%, 9%, 15%, and 21% is calculated as 1.693 M$, M$1.794, M$1.891, and M$1.993, respectively. Therefore, the maximum uncertainty radius of the building load demand for WT/TDL/FC configuration and the uncertainty budget of 21% equals 9.92% and the maximum uncertainty radius of each WT and TDL source for the uncertainty budget of 21% equals 2.54% or for the entire production of the WT/TDL/FC configuration is set at 5.08%. Based on the comparison of the results of different configuration, it can be seen that the WT/TDL/FC configuration has a lower level of robustness compared to the PV/TDL/FC configuration.

Table 16 Results of uncertainty radius with different uncertainty budgets ($\:\sigma\:$) for the PV/TDL/FC and WT/TDL/FC systems using the IAOA

Results of hybrid stochastic-robust sizing (Scenario#3)

In this section, numerical results of hybrid stochastic-robust sizing of the PV/TDL/FC, and WT/TDL/FC configurations are presented using the UT-IGDT-RA and IAOA solver in Table 17. For uncertainty budgets of 3%, 9%, 15%, and 21% for PV/TDL/FC system, $\:{\alpha}_{Load}$ values are obtained at 3.21%, 5.20, 7.52%, and 10.34%, for normal scenario, 2.82%, 4.67%, 7.05%, and 10.10% for negative deviation scenario, and 3.68%, 5.96%, 8.27%, and 10.70% for positive deviation scenario, respectively, and $\:{\alpha}_{Gen}$ values are achieved at 1.52%, 1.93%, 2.28%, and 2.65%, for normal scenario, 1.47%, 1.86%, 2.21%, and 2.58% for negative deviation scenario, and 1.59%, 2.00%, 2.35%, and 2.71% for positive deviation scenario, respectively. Also, the CEPLS cost for maximum uncertainty budget of 21% for megative deviation, normal, and positive deviation scenarios are calculated at 1.518 M$, 1.737 M$, and 1.977 M$, respectively. Also, for WT/TDL/FC system considering uncertainty budget of 21%, $\:{\alpha}_{Load}$ are obtained at 9.77%, 9.92, and 10.14% for negative deviation, normal, and positive deviation scenarios, and $\:{\alpha}_{Gen}$ are obtained at 2.475%, 2.54, and 2.615% for negative deviation, normal, and positive deviation scenarios and the CEPLS cost of WT/TDL/FC system for maximum uncertainty budget of 21% for megative deviation, normal, and positive deviation scenarios are calculated at 1.716 M$, 1.993 M$, and 2.282 M$, respectively (Table 18).

Table 17 Results of uncertainty radius considering $\:\sigma\:=21\%$ for different scenarios of PV/TDL/FC configuration

Table 18 Results of uncertainty radius considering $\:\sigma\:=21\%$ for $\:\%$ for different scenarios of the WT/TDL/FC configuration

In Fig. 21, the changes of $\:{\alpha}_{Load}$ and $\:{\alpha}_{Gen}$ of PV/TDL/FC system with respect to the changes of uncertainty budget σ is shown. As can be seen, with the increase in σ, the $\:{\alpha}_{Load}$ as well as the $\:{\alpha}_{Gen}$ have increased for negative deviation, normal and positive scenarios. According to this figure, the maximum uncertainty radiuss of building load and renewable production for normal scenario are found 10.34% and 2.65%, for negative scenario are determined 10.19%, and 2.61%, and for positive deviation scenario are calculated 10.50%, and 2.705%, respectively.

Fig. 21

Variation of (a) $\:{\alpha}_{Load}$ versus $\:\sigma\:$ (b) $\:{\alpha}_{Gen}$ versus $\:\sigma\:$ for different scenaios of the PV/TDL/FC configuration

The results of the Hybrid UT-IGDT-RA and the Conventional IGDT-RA (Normal Scenario) approaches highlight key differences in handling uncertainties, particularly in terms of maximum uncertainty radius and cost-effectiveness (CEPLS). Below is an in-depth analysis from the perspective of an energy system operator under uncertainty:

• Conventional IGDT-RA (Normal Scenario):

Uisng of the conventional IGDT-RA, a baseline approach to quantify the robustness of the system is presented. The maximum uncertainty radius for building load and renewable generation ($\:{{\upalpha\:}}_{\text{L}\text{o}\text{a}\text{d}}$=10.34%, and $\:{{\upalpha\:}}_{\text{G}\text{e}\text{n}}$=2.65%) are slightly conservative, as this method does not account for possible deviations (positive or negative). While providing reliable robustness, it does not fully exploit potential opportunities or risks arising from uncertainty.

• Hybrid UT-IGDT-RA (Positive and Negative Deviations).

The hybrid UT-IGDT-RA approach Incorporates stochastic scenarios to simulate a range of uncertainties beyond the nominal scenario. The positive deviation scenario that accounts for optimistic outcomes where renewable generation or load may exceed nominal expectations. Maximum radius of ​$\:{{\upalpha\:}}_{\text{L}\text{o}\text{a}\text{d}}$=10.50%, and $\:{{\upalpha\:}}_{\text{G}\text{e}\text{n}}=$2.705% show an improved ability to handle higher uncertainties compared to the normal scenario. Negative deviation scenario that considers pessimistic outcomes, where load or generation might underperform. Maximum radius of ​$\:{{\upalpha\:}}_{\text{L}\text{o}\text{a}\text{d}}$=10.10%, and $\:{{\upalpha\:}}_{\text{G}\text{e}\text{n}}=$2.85% are slightly lower, reflecting a cautious approach. The hybrid approach shows improved flexibility by considering both extremes of uncertainty (positive and negative), enabling energy operators to adapt more effectively to varying conditions.

• CEPLS Cost Comparison.

In positive deviation scenario, a higher CEPLS (1.977 M$) reflects increased system capacity to manage optimistic uncertainties. This cost reflects investments to enhance system flexibility and exploit favorable conditions. Also, in negative deviation scenario: Lower CEPLS (1.518 M$) shows a cautious investment approach to mitigate risks associated with pessimistic scenarios. The hybrid approach provides a range of costs for decision-makers, offering flexibility in aligning investments with risk tolerance. Operators with higher budgets can opt for the positive deviation strategy, while those constrained by costs may prioritize negative deviation scenarios.

• Comparative Insights: PV/TDL/FC vs. WT/TDL/FC Systems.

Higher robustness in $\:{{\upalpha\:}}_{\text{L}\text{o}\text{a}\text{d}}$​ and $\:{{\upalpha\:}}_{\text{G}\text{e}\text{n}}$ values across scenarios, with better cost-effectiveness (lower CEPLS) compared to WT/TDL/FC. Reflects the suitability of PV/TDL/FC for locations with stronger solar and tidal resources.

• Decision-Making for Energy System Operators.

Robustness vs. Cost Trade-off: The hybrid approach offers a spectrum of options for uncertainty handling. Operators can choose between scenarios based on their priorities (risk-averse vs. opportunity-seeking). Normal scenarios based on the IGDT-RA offer balanced solutions but may lack adaptability to extreme uncertainties.

Strategic Implications: The positive deviation scenario is uitable for operators looking to maximize system reliability and exploit potential surpluses in renewable generation. Ideal for locations with high variability but high potential.

Also, the negative deviation scenario is suitable for budget-constrained operators or risk-averse strategies focusing on worst-case scenario preparedness.

System Selection: The PV/TDL/FC system is superior in robustness and cost, making it the preferred choice for long-term investments.

• Decision-making Eenhancement under uncertainty.

The Hybrid UT-IGDT-RA approach enhances decision-making under uncertainty by combining the deterministic IGDT-RA method with stochastic scenario modeling (UT). Compared to the normal scenario. It provides a broader range of robust solutions, enabling operators to align strategies with their risk tolerance. It enhances adaptability to both positive and negative uncertainties, crucial for dynamic and uncertain environments. This hybrid method significantly improves system reliability, flexibility, and decision-making precision in the face of uncertainties, outperforming the conventional IGDT-RA approach.

Conclusion

In this research, the focus was on the hybrid stochastic-robust optimization of an PV/TDL/FC system, specifically aimed at optimizing hydrogen reserve capacity to meet the annual energy needs of an educational building using the UT-IGDT-RA over a 20-year period. Initially, the study employed deterministic sizing across various hybrid system configurations using the innovative meta-heuristic IAOA solver. This approach was directed at minimizing the CEPLS while adhering to the DSHP constraints. The impact of varying the reliability constraints on system sizing and DSHP was also examined. Subsequently, robust sizing was applied using the UT-IGDT-RA approach to accommodate the MRU of demand from the educational building and generation from renewable resources across different system configurations. The findings from the research are detailed as follows:

• Deterministic Sizing Outcomes: The study revealed that the optimal hybrid system configuration, integrating PV and TDL units with hydrogen storage, significantly reduced the CEPLS while enhancing the reliability for the educational building. Specifically, the configurations of PV/TDL/FC, HPV/FC, and TDL/FC recorded CEPLS values of M$1.431, M$2.824, and M$1.756 respectively, with DSHP values of 0.0090, 0.0095, and 0.0093, respectively. These results highlight the superior economic and technical performance of the PV/TDL/FC configuration.

• Effect of Reliability Constraint Variations: Changing the reliability constraint demonstrated a direct impact on resource production and hydrogen storage levels. Higher reliability levels required increased expenditure on CEPLS. Specifically, DSHP values at 1%, 3%, and 5% resulted in sizing costs of M$1.431, M$1.193, and M$1.031 respectively, indicating the trade-off between cost and reliability.

• Comparison of Deterministic and Robust Sizing: The comparison between the two sizing approaches showed that increasing the uncertainty budget led to higher demand and renewable production power. Particularly during early hours when PV power is unavailable, the system relied on the FC assisted by TDL to supply power, underscoring hydrogen’s critical role as a reserve power source in enhancing reliability.

• Robust Sizing Findings: The robust sizing results for the PV/TDL/FC, HPV/FC, and TDL/FC configurations indicated that the maximum uncertainty radius (both demand and generation) reach saturation levels at uncertainty budgets of 21%, 17%, and 19% respectively, beyond which the CEPLS values remain unchanged. The highest uncertainty radius for building demand and resource production in the PV/TDL/FC configuration were 10.34% and 5.30%, respectively.

• Strategic Implications of Robust Approach: The robust approach, which caters to a risk-averse sizing problem, facilitates robust decision-making in the face of uncertainties. Decisions within the IGDT framework are formulated based on discrepancies between predicted and actual uncertainty parameters.

• Sizing Considering the WT resources: The high cost of sizing based on WTs versus PVs is due to the weak wind speed potential for the study area, which has no economic and technical justification. Also, the WT/TDL/FC configuration has a lower level of robustness compared to the PV/TDL/FC configuration in condition of considering uncertainties.

• The Hybrid UT-IGDT-RA approach enhances decision-making under uncertainty by combining the IGDT-RA method with stochastic scenario modeling (UT). It provides a broader range of robust solutions, enabling operators to align strategies with their risk tolerance, and also enhances adaptability to both positive and negative uncertainties, crucial for dynamic and uncertain environments. This hybrid method significantly improves system reliability, flexibility, and decision-making precision in the face of uncertainties, outperforming the conventional IGDT-RA approach.

• Recommendations for Future Work: For further research, it is suggested to explore the robust sizing of an PV/TDL/FC energy system augmented with batteries and electric parking lots using the IGDT-RA approach within a multi-energy storage system framework.