Medical image segmentation based on frequency domain decomposition SVD linear attention

Abstract

Convolutional Neural Networks (CNNs) have achieved remarkable segmentation accuracy in medical image segmentation tasks. However, the Vision Transformer (ViT) model, with its capability of extracting global information, offers a significant advantage in contextual information compared to the limited receptive field of convolutional kernels in CNNs. Despite this, ViT models struggle to fully detect and extract high-frequency signals, such as textures and boundaries, in medical images. These high-frequency features are essential in medical imaging, as targets like tumors and pathological organs exhibit significant differences in texture and boundaries across different stages. Additionally, the high resolution of medical images leads to computational complexity in the self-attention mechanism of ViTs. To address these limitations, we propose a medical image segmentation network framework based on frequency domain decomposition using a Laplacian pyramid. This approach selectively computes attention features for high-frequency signals in the original image to enhance spatial structural information effectively. During attention feature computation, we introduce Singular Value Decomposition (SVD) to extract an effective representation matrix from the original image, which is then applied in the attention computation process for linear projection. This method reduces computational complexity while preserving essential features. We demonstrated the segmentation validity and superiority of our model on the Abdominal Multi-Organ Segmentation dataset and the Dermatological Disease dataset, and on the Synapse dataset our model achieved a score of 82.68 on the Dice metrics and 17.23 mm on the HD metrics. Experimental results indicate that our model consistently exhibits segmentation effectiveness and improved accuracy across various datasets.

Introduction

With the continuous development of deep learning theory, medical imaging technology and neural networks have achieved a high degree of integration in the field of medical imaging. Neural networks facilitate the extraction of low-dimensional local features and the fusion of high-dimensional abstract semantic features from common radiological imaging modalities such as Computed Tomography (CT), Magnetic Resonance Imaging (MRI), and Positron Emission Tomography-Computed Tomography (PET-CT)^1,36. This approach helps improve the efficiency of radiologists’ complex and repetitive screening tasks, reducing the likelihood of missed and incorrect diagnoses. Neural networks have a wide range of applications in medical imaging, with the most common tasks being disease classification and lesion segmentation. Lesion segmentation, in particular, is a crucial foundational research area for automating patient diagnosis in outpatient settings and enabling intelligent clinical surgical planning². Combining medical imaging with deep learning enables automatic segmentation of lesion structures using neural networks, which has become a significant research area in medical artificial intelligence.

In the early stages of neural networks, CNNs based on convolutional kernel filters were primarily used to perform local feature extraction and semantic segmentation on the raw data of medical images³. Compared to traditional digital image processing techniques such as wavelet transforms⁴, Markov random fields⁵, and random forests⁶, CNNs—by employing loss functions for constraint and automatic learning of hyperparameters—have achieved significant improvements in various segmentation metrics. Current mainstream CNNs, such as Fully Convolutional Networks (FCN)⁷, ResNet⁸, and U-Net⁹, have made groundbreaking advancements in semantic segmentation tasks for lesions in medical images.

Related work

U-Net segmentation method

The U-Net architecture, with its symmetric U-shaped structure consisting of an encoder and a decoder, can effectively concatenate convolutional features extracted from downsampling layers with diluted global features in upsampling layers to achieve precise segmentation. This design helps to mitigate the loss of local details in spatial structures for high-level semantic information. The U-Net network structure has shown significant advantages in medical image segmentation tasks, achieving notable improvements in classification accuracy and segmentation precision metrics on CT and MRI images.

CT and MRI image segmentation based on U-Net

The U-Net network is primarily used in image segmentation tasks targeting various organs and lesions, such as the spine¹⁰, breast cancer¹¹, and lung lesions¹². In lung segmentation tasks, U-Net can accurately identify and segment regions of lung tumors or nodules. Chen et al.¹³ proposed embedding dilated convolutions into the downsampling layers of the U-Net network to expand the receptive field of the convolutional kernels, thereby enhancing the breadth of contextual information. Dilated convolutions can better capture boundary details when extracting lung features. U-Net is widely used in lung nodule screening, where it can automatically segment lung nodules. S. Akila Agnes et al.¹⁴ proposed a network framework combining wavelet transforms with U-Net + + to perform multi-scale feature decomposition, thereby more precisely capturing the fine-grained boundary information of lung nodules. By accurately segmenting lung nodules, this approach reduces doctors’ workload and improves early diagnosis of lung cancer. In addition to lung applications, the U-Net network is also frequently used for liver segmentation in abdominal CT imaging tasks. The 3D structure of liver tumors provides crucial guidance for clinicians in both early diagnosis and the formulation of surgical plans. Li et al.¹⁵ introduced a method that incorporates supervised learning into the bottleneck layer of the U-Net network, embedding supervision signals to enhance the feature extraction capability of abstract semantic information. In cases where tumor boundary geometry is ambiguous, the bottleneck feature’s supervision signal enables the extraction of both local and global features for complex tumor morphologies, allowing for fine-grained segmentation of liver tumor boundaries.

U-Net al.so demonstrates significant advantages in segmenting brain structures in MRI images and has achieved outstanding results in brain tumor segmentation tasks. Allah et al.¹⁶ proposed the Edge U-Net network, which integrates tumor boundary information into the traditional U-Net architecture to achieve precise localization of brain tumors. This is mainly done by combining edge features with regional features, enabling fine-grained boundary segmentation while accurately capturing the overall spatial structure. Since MRI images provide good contrast for soft tissues, Edge U-Net effectively identifies tumors of various sizes and shapes, addressing the limitations of traditional U-Net networks in handling complex morphologies.

Shortcomings of convolutional neural networks

In terms of data processing, medical imaging datasets are generally smaller and have more inconsistent sample quality compared to general datasets like ImageNet1K, which often leads to suboptimal experimental results for conventional segmentation networks on medical imaging datasets¹⁷. The U-Net network introduced a U-shaped structure that combines features of different dimensions extracted by downsampling with the diluted global features of upsampling, achieving a contextual fusion of local and global features. As a result, it has achieved state-of-the-art (SOTA) performance in various medical image segmentation experiments⁹. However, medical images often present the challenge of high resolution for single samples. For example, standard CT images have pixel dimensions of 512 × 512 × 512. Due to hardware limitations, it is usually necessary to crop 3D images, such as CT and MRI, into 2D slices for training, which leads to a loss of spatial context. Furthermore, medical image segmentation targets, such as tumors and herniated discs, often have complex three-dimensional spatial structures, making it difficult for traditional CNNs to capture the overall spatial structure of foreground regions during training. Additionally, lesion areas may extend across multiple slices, making it challenging for CNNs to locate the diseased regions accurately. For example, in spine vertebra segmentation tasks, it is difficult to identify the overall boundary structure of the target lesion¹⁸.

Regarding feature extraction through convolutional kernels, CNN architectures like U-Net primarily operate by using self-learned convolutional kernels to perform multi-level feature extraction. There is a positive correlation between the size of the target in the foreground region and the receptive field of the convolutional kernel. For common organs and tissues, if the target region exceeds the boundaries of the convolutional kernel’s receptive field, it can result in segmentation discontinuities and insufficient overall segmentation accuracy¹⁹.

Attention-based segmentation methods

Due to the receptive field limitations of convolutional kernels, CNNs struggle to comprehensively learn and capture overall features as the network depth increases. With the introduction of the Transformer structure²⁰ in ViT²¹, the self-attention mechanism, based on data self-correlation, enables context learning on local data patches and facilitates information exchange and global modeling across patches. However, since the ViT network directly processes raw data, its segmentation accuracy does not achieve significant improvements over some CNN architectures. The Swin Transformer²² was later proposed, which enhances image-based Transformers by dividing raw data into a series of patches, allowing for global data interaction. This improved segmentation performance in general image segmentation tasks.

In recent years, researchers have developed Swin Unet²³ based on the Swin Transformer, applying it to small-scale medical image datasets, such as the Synapse multi-class segmentation task. This approach replaces convolutional kernels with a purely Transformer-based structure utilizing the encoder-decoder framework of U-Net. Other researchers have proposed integrating Transformer structures as a complementary method to CNNs. For example, TransUNet²⁴ employs the Transformer structure as a powerful encoder within the U-Net network to extract local spatial information for fine-grained, precise segmentation. The nnFormer network²⁵ innovatively combines convolution with three types of attention mechanisms to capture long-range dependencies. It employs local and global volumetric self-attention to construct a feature pyramid and provide an expanded receptive field, while skip attention bridges the gap between encoder and decoder.

The UNETR network²⁶ takes an innovative approach by using the Transformer structure as a strong encoder and combining it with a CNN decoder to merge features of different resolutions, effectively extracting spatial structural information from 3D medical images and segmenting target regions. Wu et al. proposed a structure called D-former²⁷, which, compared to architectures like UNETR, uses dilated convolutions to expand the receptive field and enhance local feature extraction capabilities. This approach improves the accuracy in smoother regions of 3D medical images without increasing computational complexity.

While the Transformer structure exhibits superior learning capabilities and higher segmentation accuracy on medical image datasets, the traditional self-attention mechanism often overlooks high-frequency signals, such as textures and contours, when learning lesion regions in medical images, leading to an inability to segment local details in target regions²⁸. Additionally, since the self-attention mechanism extracts the self-correlation of the raw data, the complexity of the sample space reaches $O({n^2})$, which results in limitations in time and speed when computing attention matrices on high-resolution medical images²⁹. R. Agarwal et al.³⁰. proposed a multi-scale dual-channel feature embedding decoder structure based on the Swin Transformer network, validated through segmentation experiments on biomedical images. The study demonstrated that leveraging multi-scale features can achieve superior segmentation accuracy and model robustness in complex biomedical datasets. P. Ghosal et al.³¹ proposed a Transformer-based compound attention-embedded dual-channel encoder-decoder framework designed for precise segmentation of multiple sclerosis lesions in brain MRIs. By integrating compound attention mechanisms with the global feature modeling capability of Transformers, the model achieves accurate detection of multiple sclerosis lesions in the brain while significantly enhancing sensitivity and specificity. X. Guo et al.³² proposed a Transformer-based uncertainty-guided CNN-Transformer hybrid model, UCTNet, for medical image segmentation. This model leverages the advantages of Transformers in global feature modeling and capturing long-range dependencies in medical images, while integrating CNN’s ability to extract high-frequency information and local features. By fusing global and local features, the model achieves a more comprehensive feature representation. Furthermore, with uncertainty guidance, the model precisely localizes segmentation regions, significantly enhancing the accuracy of the segmentation results.

Contribution

Our main contributions are as follows:

• (1) To address the limitation of Transformer structures in extracting high-frequency signals, we propose constructing a Laplacian pyramid in different frequency domains. By selectively extracting and fusing attention features from high-frequency and low-frequency signals, we effectively capture both smooth regions and boundary regions.

• (2) To tackle the challenge of high computational complexity in self-attention mechanisms for high-resolution medical images, we introduce a linear attention mechanism based on SVD. This method extracts the essential content from the original data and incorporates it into the attention mechanism as a linear projection matrix, achieving linear computational complexity.

• (3) We proposed an enhanced skip connection structure. By applying SVD decomposition to the features extracted from downsampling, we captured frequency domain information at different levels, enabling effective feature fusion of high-frequency and low-frequency signals in the decoder. This approach retains overall features while enhancing high-frequency signals, such as textures and boundaries.

Methodology

Data collection and processing

In this study, we selected the publicly available SynapseCT abdominal multi-organ 3D dataset and the ISIC 2018 skin lesion dataset for experiments and validation. The Synapse dataset is commonly used to evaluate and compare various medical image segmentation models. It includes CT scans of eight major abdominal organs, including but not limited to the liver, stomach, and kidneys. The dataset contains 30 patient cases, with each sample consisting of 85 to 198 cross-sectional images. The data is stored in NIFTI format.

The ISIC 2018 dataset, released by the International Skin Imaging Collaboration, is focused on the diagnosis and classification of skin lesions, aiming to improve early diagnosis of conditions such as melanoma and dermatofibroma. It contains a total of 10,015 images, with 2,594 images specifically designated for segmentation experiments. The dataset includes two categories: lesion foreground and normal region. Detailed information on both datasets is summarized in Table 1.

Table 1 Synapse dataset and ISIC2018 dataset details.

Network architecture

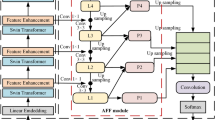
The encoder-decoder U-shaped structure effectively fuses local features extracted by downsampling with global contextual information recovered by the decoder, enabling efficient feature extraction. Therefore, the overall network architecture proposed in this paper adopts an encoder-decoder U-shaped structure. The overall architecture is illustrated in Fig. 1. The encoder structure includes four downsampling layers, each consisting of two Laplacian Transformer Blocks and a Patch Merging module. For the input raw data$X \in {{\mathbb{R}}^{H \times W \times C}}$, a Patch Embedding operation is first performed, segmenting the raw data matrix into multiple patches and feeding them into the Laplacian Transformer Block.

Traditional Transformer structures often lack focus on high-frequency information, such as tumor boundaries and overall spatial structures of the spine, while learning contextual information. However, in medical datasets, texture and structural information about target regions are crucial for early diagnosis and surgical planning. To enhance the global information extraction capability of the self-attention mechanism for high-frequency signals, we designed a Laplacian pyramid-based self-attention mechanism. For the input raw image data X, multi-frequency domain features are extracted using Gaussian blur kernels of different sizes, constructing a Laplacian pyramid based on the differentiated information between various frequency domains. Attention features are computed on different frequency features of the Laplacian pyramid, enabling contextual information extraction for medical images.

When calculating self-attention feature maps for the Laplacian pyramid, the conventional self-attention matrix, where the Query and Key attention features undergo a softmax operation in sample space $N \times N$, leads to a computational complexity of $O({n^2})$. Inspired by this, we introduce an SVD-based data decomposition during the self-attention computation for various frequency domain features, reducing dimensionality by transforming the data sample space into a subspace while preserving the rank integrity of the original sample space.High-resolution medical images often lose substantial spatial information during resampling and cropping. While traditional U-shaped structures fuse fine-grained downsampled features and upsampled overall features through skip connections, the semantic differences between the encoder’s extracted features and the decoder’s recovered features can lead to a loss of high-frequency information, specifically in local details. To address this, we designed an enhanced skip connection structure, as shown in Fig. 1. The high-frequency domain features extracted by the Laplacian Transformer Block from the encoder’s low-resolution deep features undergo SVD decomposition to obtain effective subspaces S and U. This linearly maps the Value and Key matrices from $n \times d$ dimensions to $k \times d$, where k is much smaller than n, reducing the overall computational complexity from $O({n^2})$to $O(kn)$. This improves the computational efficiency of the self-attention mechanism while ensuring high-frequency feature extraction.

To further enhance the global feature extraction capability of the self-attention mechanism in medical images, we input the extracted attention features A into a Dynamic Evolution Self-attention structure (DES) using a residual structure. The DES structure dynamically adjusts attention weights, compensating for the self-attention mechanism’s limitations in focusing on short-range dependencies, thereby improving the model’s overall generalization ability while ensuring effective extraction of high-frequency information.

Fig. 1

The overall structure of the network.

The decoder structure consists of four layers of Laplacian Transformer Blocks and Patch Expanding modules. The Laplacian Transformer Block performs global feature fusion on low-resolution deep features of various sizes extracted by the encoder, while the Patch Expanding module is responsible for transforming low-dimensional deep features into high-dimensional global features, restoring the global semantic information of the image.

SVD linear attention

The traditional self-attention mechanism primarily extracts the self-correlation within the raw data.

X, where n represents the sample data size and d represents the feature dimension of the data. The traditional attention calculation formulas are shown in (1) and (2):

$$Attention=soft\hbox{max} \left( {\frac{{Q{K^T}}}{{\sqrt {{d_k}} }}} \right) \in {{\mathbb{R}}^{n \times n}}$$

(1)

$$Output=A \cdot Value \in {{\mathbb{R}}^{n \times d}}$$

(2)

Due to the high resolution of medical images, the computational complexity remains $O({n^2})$ even when calculating attention on multiple cropped patch data blocks. We perform Singular Value Decomposition on the original data matrix$X \in {{\mathbb{R}}^{n \times d}}$, dividing it into three components: $U \in {{\mathbb{R}}^{n \times r}}$,$\sum \in {{\mathbb{R}}^{r \times r}}$ and ${V^T} \in {{\mathbb{R}}^{r \times d}}$, where r represents the rank of the matrix. The principal component matrices $U \in {{\mathbb{R}}^{n \times r}}$ and ${V^T} \in {{\mathbb{R}}^{r \times d}}$, extracted from the original data decomposition, are embedded into the traditional attention computation process to project the Key and Value matrices, reducing the feature dimension from d to $(r \ll d)$. This approach not only addresses the issue of high computational complexity in traditional attention mechanisms for high-resolution medical images but also retains the essential components of the original data, enabling selective preservation of contextual information. The overall computational process of the SVD-based linear attention mechanism is shown in Fig. 2, where the raw data Xrepresents the original data matrices from different frequency domains in the constructed Laplacian pyramid.

Fig. 2

SVD linear attention structure.

Additionally, since medical images exhibit a substantial amount of redundant data in their voxel values when observed in three-dimensional structures (for example, the high similarity in voxel values in abdominal cavity regions), the overall voxel value distribution approximates a Gaussian distribution. Inspired by this phenomenon, we propose performing SVD decomposition on the raw data to extract the effective data subspace from the sample space and retain the top K significant singular vectors from this subspace. The SVD decomposition of the raw data and its computational process are shown in Eq. (3):

$$X=u\sum {v^T},X \in {{\mathbb{R}}^{n \times d}}$$

(3)

Where u and v represent matrices. For a given matrix X, a rank inequality is introduced. For matrices u and v, the rank of the product matrix uv satisfies the following equality (4) and inequality (5):

$$R=u\sum$$

(4)

$$r(R) \leqslant \hbox{min} (r(u),r(\sum ))=r(\sum )=r(X)$$

(5)

Since $X=u\sum {v^T}$, it can therefore prove Eq. (6).

$$r(X)=r(u\sum {v^T}) \leqslant \hbox{min} (r(u),r(\sum ),r(v))=r(\sum )$$

(6)

The ranks of the u and v matrices, decomposed by SVD, are lower than the rank of the original data X. Therefore, we sort the u and u matrices and extract the top K largest significant values. The effective data subspace matrices u and v, extracted from the sample space of the original data, are then replaced with the linear projection matrices S and U in the linear attention matrix. The revised attention calculation formulas are shown in Eqs. (7) and (8):

$${A_{svd}}=soft\hbox{max} \left( {\frac{{Q{{({u^T}K)}^T}}}{{\sqrt {{d_k}} }}} \right) \in {{\mathbb{R}}^{n \times k}}$$

(7)

$$Output=A \cdot {v^T}V \in {{\mathbb{R}}^{n \times d}}$$

(8)

By analyzing the computational complexity of the SVD-based linear attention mechanism, it is found to be $O(nk)$, where K is a linear constant significantly smaller than the number of samples n. Compared to the traditional self-attention computational complexity $O({n^2})$, it is evident that our proposed SVD linear attention mechanism effectively reduces the overall computational complexity of attention.

The algorithmic flow of the SVD linear attention mechanism is shown in Algorithm 1.

Algorithm 1

SVD-based linear attention.

Laplacian transformer block

In traditional medical image segmentation models, the encoder or feature extractor has a strong capability for learning low-frequency signals in foreground regions during training. As a result, it performs relatively well in extracting smooth areas of the target during segmentation prediction. However, in clinical settings, precise boundary delineation of lesions or organs is essential for accurate evaluation. For instance, the area and thickness of a tumor are critical clinical indicators for determining whether conservative treatment or surgical intervention is appropriate. While the traditional self-attention mechanism can capture global information by extracting context from each layer’s input, i.e., the raw data, it often lacks effectiveness in extracting high-frequency information such as textures and precise boundary regions.

To address the limitations of self-attention mechanisms, we propose applying different frequency domain signal processing to the raw data in each downsampling layer to extract various frequency domain signals, such as low- and high-frequency components. A Laplacian Pyramid splits an image into layers of different detail levels—smooth background (low frequency) and sharp edges (high frequency). This allows our model to focus on important features, such as boundaries and textures. Linear attention is then used to project the effective data subspaces from different frequency domains linearly.

The computational process of the Laplacian Transformer Block is illustrated in Fig. 3. Initially, the raw data X undergoes a Gaussian kernel pyramid extraction to effectively isolate high- and low-frequency components, using Gaussian kernels of various sizes. The formula for the Gaussian kernel is shown in Eq. (9), and we use four different sizes of Gaussian kernels for extraction. Subtracting the output of a larger variance Gaussian kernel (7 × 7) from that of a smaller variance Gaussian kernel (5 × 5) can isolate high-frequency signals. As shown in Fig. 3, this subtraction effectively removes low-frequency information while retaining edges and fine details, which are crucial for capturing high-frequency components such as boundaries and textures. High-frequency signals are obtained by subtracting adjacent layers in the Gaussian pyramid, where each layer represents a different level of detail. This yields a feature pyramid ${I_k}$, containing signals ranging from low to high frequency, as shown in Eqs. (10) and (11). By computing ${I_k} - {I_{k+1}}$at the k-th layer, we construct the Laplacian pyramid ${L_k}$, which primarily includes three levels: low-to mid-frequency features $LMf$, mid-to high-frequency features$MHf$, and high-frequency features $Hf$.

$$K(x,y) = \exp \left( { - \frac{{\left\| {x - y} \right\|^{2} }}{{2\sigma ^{2} }}} \right),\;\sigma \in \{ 1,3,5,7\}$$

(9)

$${I_k}=I \cdot {K_{{\sigma _k}}},k \in \{ 1,3,5,7\}$$

(10)

$${L_k}={I_k} - up({I_{k+1}}),k \in \{ 1,2,3\}$$

(11)

For each of the four downsampling layers, we use three levels of Laplacian pyramids constructed from four different Gaussian blurs to distribute low- and high-frequency signals evenly across the three feature levels. This provides mid-low, mid-high, and high-frequency domain features necessary for SVD-based data subspace decomposition in the next step. By performing SVD decomposition on these three frequency domains, we obtain three sets of u and v matrices containing low-mid, mid-high, and high-frequency information. These are then introduced into the linear attention mechanism, where the Key and Value matrices undergo data subspace-based linear projection. This approach effectively extracts contextual information across high, medium, and low-frequency domains while reducing the computational complexity of attention calculations within the overall model. Finally, the extracted low-frequency smooth regions and high-frequency textured boundary regions from the high, medium, and low-frequency domains are aggregated through an overlay operation, achieving fusion of the entire frequency domain information at different scales.

Fig. 3

Laplacian transformer block structure.

The algorithmic flow of SVD linear attention mechanism based on Laplacian pyramid is shown in Algorithm 2.

Algorithm 2

Linear attention in different frequency domains based on Laplace pyramid.

Evaluation metrics

In this experiment, the Synapse dataset is used for a multi-label organ segmentation task. For segmentation tasks in medical images, we use the Dice coefficient to measure the segmentation accuracy of low-frequency signals in the foreground regions. The calculation principle of the Dice coefficient is shown in Eq. (12):

$${\text{Dice}}=\frac{{2{\text{TP}}}}{{2{\text{TP}}+{\text{FP}}+{\text{FN}}}}$$

(12)

In the formula above, TP represents the number of pixels where both the network’s predicted result and the actual label are positive, while FP denotes the number of false positives, i.e., cases where the predicted result is positive but the label is negative. FN represents the number of pixels where the prediction is negative but the label is also negative.

In addition to using the Dice coefficient to measure segmentation accuracy in smooth regions, we also introduce the 95% Hausdorff Distance (HD) to evaluate the continuity of high-frequency signals, specifically boundary regions, in the foreground segmentation. The calculation principle of the Hausdorff Distance is shown in Eq. (13):

$${H_{95\% }}(x,y)=\hbox{max} \left\{ {\mathop {\sup }\limits_{{x \in X}} \mathop {\inf }\limits_{{y \in Y}} dis(x,y),\mathop {\sup }\limits_{{y \in Y}} \mathop {\inf }\limits_{{x \in X}} dis(x,y)} \right\}$$

(13)

In the formula above, X represents the label, while Y denotes the inference result. $dis$ indicates the Euclidean distance between x and y.

The ISIC 2018 dataset focuses primarily on different skin diseases, so the data is in 2D form. To better evaluate the segmentation performance of various models in this experiment, we not only use the Dice coefficient from Eq. (12) but also select Specificity (SP), Sensitivity (SE), and Accuracy (ACC) as additional metrics for a more comprehensive assessment. The calculation principles for SE, SP, and ACC are shown in Eqs. (14), (15), and (16), respectively.

$${\text{SP=}}\frac{{{\text{TN}}}}{{{\text{(TN+FP)}}}}$$

(14)

$${\text{SE=}}\frac{{{\text{TP}}}}{{{\text{(TP+FN)}}}}$$

(15)

$${\text{ACC=}}\frac{{{\text{(TP+TN)}}}}{{{\text{(TP+TN+FP+FN)}}}}$$

(16)

Where TN is true negative represents the case where the prediction is positively labelled as negative.

Result

Experimental environment and loss function

For the model proposed in this paper, we chose the PyTorch framework for development. The experiments were conducted on an NVIDIA RTX 4090 (24GB) GPU. All training batches used the SGD optimizer, with a weight decay of 0.0001 and an initial learning rate set to 0.001. We selected a combined loss function, incorporating both BCE and Dice loss functions. The loss function is shown in Eq. (17):

$${\text{ }}Loss=\alpha [y\log (p)+(1 - y)\log (1 - p)] - \beta \frac{{2TP}}{{(2TP+FP+FN)}}$$

(17)

In the above equation y represents the true label and p represents the predicted probability.

Comparative experiments with synapse dataset

In this comparative experiment, we selected the Synapse abdominal multi-organ segmentation dataset for training and testing. This dataset includes eight categories: aorta, gallbladder, left kidney, right kidney, liver, pancreas, spleen, and stomach. Among these, the gallbladder and pancreas are relatively small targets in abdominal segmentation compared to other organs. To validate the segmentation performance and accuracy of our proposed model in medical imaging, we tested six mainstream segmentation network frameworks on the Synapse dataset. The six segmentation frameworks include the purely CNN-based U-Net, the CNN + Transformer fusion network Att-Unet, and the pure Transformer network Swin-Unet. By comparing our model with various network frameworks, we aimed to demonstrate the effectiveness and superiority of our proposed model.

The quantitative experimental results are presented in Tables 2 and 3. Table 2 shows the average Dice score for the eight organs and the overall average Dice accuracy of the model, while Table 3 displays the average HD distance for the eight organs. Analyzing the results in Table 2, we observe that our proposed model achieved the highest Dice score in the segmentation tasks for six organs: gallbladder, left kidney, liver, pancreas, spleen, and stomach. For the average Dice score across all eight organs, our model achieved the highest score of 82.68. Compared to the pure CNN network U-Net, our model’s Dice score improved by an average of 6.15%. When compared to the SOTA model Swin-Unet within pure Transformer networks, our Dice score showed an average increase of 3.81%. Furthermore, compared to the next-best segmentation model in our experiments, HiFormer-S, we achieved a significant improvement of 2.44%.

From the Dice score of individual categories to the overall framework’s average Dice score, our model consistently demonstrated significant improvements in segmentation accuracy, validating the effectiveness of our proposed model in multi-organ segmentation tasks. To validate the versatility of our proposed model on both lumbar spine and pelvic datasets, this study compared the segmentation accuracy with three classic segmentation models and the current SOTA segmentation model, nnUnet, among others.

Table 2 Segmentation comparison experiments on synapse dataset dice (%) metrics results collated.

Table 3 Synapse multi-organ segmentation comparison trial 95% HD metrics results.

The Dice metric in Table 2 evaluates the model’s segmentation performance in smooth regions of the foreground, i.e., low-frequency signal areas. In addition to assessing the segmentation accuracy of low-frequency signals, the overall experimental results for the HD metric, which evaluates boundary continuity, are presented in Table 3. Analyzing the results in Table 3, our model achieved the shortest HD distance of 13.97 mm in the pancreas region. For other organ categories, the HiFormer-S model achieved SOTA accuracy for the HD metric. However, our proposed model shows only a 2 mm difference in average HD distance compared to HiFormer-S, and still achieved a performance improvement of 0.2 mm over the next-best segmentation model, LeVit-Unet-384. This demonstrates the effectiveness of our proposed model in boundary continuity segmentation tasks.

To provide a more intuitive display of the segmentation performance of the seven models, we visualized the segmentation results on the Synapse dataset in Fig. 4. In this figure, (a) represents the original image, (b) represents the ground truth labels, and (c)-(i) show the segmentation results of the seven comparative algorithms selected for this experiment. As seen in Fig. 4, compared to the pure CNN network (c) U-Net, our model demonstrates significantly superior segmentation in both smooth regions and high-frequency regions, such as boundaries. Compared to the pure Transformer network (d) Swin-Unet, our model also performs better in high-frequency regions, such as boundaries and texture structures, for organs like the right kidney, outperforming other models.

Fig. 4

Visualisation of test set predictive segmentation results for the 7-class model on the Synapse dataset, with red frames representing under-segmented regions and yellow frames representing over-segmented regions.

According to the results in Table 4, the proposed model demonstrates significant advantages in computational efficiency. Compared to other mainstream models, the proposed model has a parameter size of 28.35 M, which is significantly lower than TransUNet’s 96.07 M and close to Swin-Unet’s 27.17 M, indicating a good balance between performance and complexity. Additionally, its floating-point operations (FLOPs) are only 44.7 GFLOPs, lower than U-Net’s 45.6 GFLOPs and Swin-Unet’s 62.7 GFLOPs, and far below TransUNet’s 88.9 GFLOPs. These results indicate that the proposed model, by optimizing computational complexity, can not only efficiently process high-resolution medical images but also achieve higher computational efficiency in practical applications.

Table 4 Comparison of model parameters and floating point operations (FLOPs) on the synapse dataset for four models.

ISIC2018 dataset comparison experiment

The Synapse dataset tests each network framework’s ability to extract spatial structural information from target regions. To further verify our proposed model’s ability to capture different spatial structures comprehensively, we conducted benchmark experiments on the ISIC 2018 dataset using seven segmentation networks. The experimental results are presented in Table 5. In the 2D segmentation task, our model achieved the highest Dice score of 92.16. Compared to the SOTA model HiFormer-S, our Dice score improved by an average of 2.24%, demonstrating superior segmentation performance in smooth regions.

Table 5 ISIC2018 experimental algorithm comparison results.

For the SE metric, our model achieved the highest score of 92.84, with an average improvement of 6.4% over the other six networks. In terms of ACC, our model reached an accuracy of 96.35%, which is an improvement of 0.97% compared to the next-best model, Swin-Unet.

We visualized the segmentation results of the ISIC 2018 dataset and presented them in Fig. 5. Here, (a) is the original image, (b) is the ground truth, and (c)-(f) compare the top 4 networks in terms of ACC: TransUNet, Swin-Unet, HiFormer-S, and our model. From Fig. 5, it can be seen that (f) our model exhibits better continuity in boundary regions, i.e., high-frequency areas, compared to (c) TransUNet and (d) Swin-Unet. In comparison to the next-best segmentation model (e) HiFormer-S, our model shows superior segmentation accuracy in smooth regions.

Fig. 5

Visualisation of network segmentation results for the top 4 ACC scores of the ISIC2018 dataset.

The analysis of the four metrics and visualization results demonstrates our model’s superior segmentation performance on the ISIC 2018 dataset, further validating its segmentation effectiveness across different datasets.

Ablation experiment

To robustly evaluate our model’s robustness and analyze its statistical significance, we conducted seven repeated experiments on the Synapse and ISIC 2018 datasets using the baseline U-Net network. In each experiment, we added a single variable, i.e., one improvement module. By conducting ablation experiments on the same network framework, we can intuitively analyze the actual impact of individual improvements on segmentation performance and accuracy. The individual improvement modules we selected include the Transformer Block (TB), Laplacian Pyramid(LP), Laplacian Transformer Block (LTB), Enhanced Skip Connection (ESC), and SVD Linear Attention (SLA). The ablation experiment results on the Synapse dataset are shown in Table 5.

After introducing the Laplacian pyramid module (U-Net + LP), the model showed significant improvements in both Dice and HD95 metrics. Specifically, compared to the baseline U-Net, Dice increased by 0.36%, and HD95 was significantly reduced by 14.32 mm. This result demonstrates that the Laplacian pyramid module effectively enhances the model’s ability to capture high-frequency signals, such as boundaries and textures.Analyzing the data in Table 6, we can see that the U-Net + TB group, which embedded the TB module into the convolutional layer of U-Net, improved overall segmentation accuracy by 1.84 and reduced the HD distance by 10.89 mm compared to the baseline U-Net model. This demonstrates that the TB structure enhances the basic U-Net model’s contextual feature extraction capabilities.

Table 6 Results of ablation experiments on the synapse dataset.

The U-Net + LTB group, compared to the U-Net + TB group, achieved an average Dice score improvement of 0.31% and reduced the HD distance by 2.79 mm by introducing the Laplacian pyramid for high-frequency signal decomposition and feature extraction. The results confirm that the Laplacian pyramid enhances feature extraction for high-frequency signals, such as boundaries. The U-Net + ESC group, which added Enhanced Skip Connection, showed some improvement over the baseline U-Net in both Dice and HD metrics, demonstrating that constructing a Laplacian pyramid from features extracted by the encoder’s downsampling, followed by SVD decomposition and linear attention feature extraction, effectively enhances the fusion of deep and local features in the decoder.

The U-Net + TB + SLA group achieved similar segmentation accuracy in Dice and HD metrics compared to the U-Net + TB group, while reducing computational complexity and maintaining segmentation accuracy stability. Furthermore, the U-Net + LTB + SLA group, compared to the U-Net + TB + SLA group, improved the Dice score by 1.9% and reduced the HD distance by 5.23 mm, showing that high-frequency signal extraction from the Laplacian pyramid contributes to overall segmentation accuracy.Finally, our proposed model, which incorporates all improvement modules, achieved the highest Dice score of 82.68 and the shortest HD distance of 17.23 mm, indicating that our enhancements effectively boost segmentation accuracy across eight organ categories.

Ablation experiments were conducted on the ISIC 2018 dataset using the same setup to validate the robustness and effectiveness of our proposed improvements across different datasets. The experimental results are presented in Table 7. The results of the ablation experiments in Table 7 show that adding the Laplacian pyramid module (U-Net + LP) led to improvements in both the Dice and ACC metrics. Specifically, compared to the baseline U-Net, Dice increased by 0.56% and ACC improved by 1.12%. These findings indicate that the Laplacian pyramid module effectively enhances segmentation accuracy and continuity. Analyzing the data, we can see that the U-Net + TB, U-Net + LTB, and U-Net + ESC groups all achieved improvements over the baseline U-Net in Dice, SE, SP, and ACC metrics, verifying the effectiveness of individual improvement modules on segmentation accuracy.

Table 7 Ablation experiment segmentation results for the ISIC2018 dermatology dataset.

The U-Net + LTB + SLA group showed a Dice score increase of 0.85% and an ACC improvement of 1.34 over the U-Net + TB + SLA group. The U-Net + LTB + SLA group also achieved the highest SP score of 97.34, indicating enhanced recognition of non-boundary regions through high-frequency signal extraction. Our model reached SOTA segmentation performance across all three metrics, with a Dice score of 92.16, SE of 92.84, and ACC of 96.35.

Testing and validation on two datasets with different spatial structures demonstrate that the LTB improvement module and SLA attention mechanism effectively enhance attention to different frequency domain signals, thereby improving the model’s ability to capture high-frequency structures and overall features. These results confirm the effectiveness of our proposed improvements.

Summary

This paper first proposes a method for constructing Laplacian pyramids of different frequencies based on data at various scales, addressing the challenge traditional Transformers face in learning high-frequency contextual information in medical image features. To tackle the issue of high complexity in the sample space when calculating attention features on the frequency-varied characteristics extracted from the Laplacian pyramid, we propose using SVD to decompose the original data matrix to obtain principal component matrices. These matrices then linearly project the Query and Value matrices, enabling effective dimensionality reduction for self-attention in high-dimensional sample spaces. Finally, the extracted high- and low-frequency features are effectively fused, allowing traditional self-attention to capture local textures and edge information in medical images while reducing overall computational complexity.