Comparative analysis of seasonal wind power using Weibull, Rayleigh and Champernowne distributions

Abstract

Accurate statistical modeling of wind speed variability is crucial for assessing wind energy potential, particularly in regions with low wind speeds and significant calm hours. This study evaluates the Champernowne distribution as a novel model for wind speed analysis, comparing its performance with the two-parameter Weibull, three-parameter Weibull, and Rayleigh-Rice distributions. Wind speed data at 10 m hub height over three years (2021–2023) from Ben Guerir, Morocco, were analyzed using statistical metrics such as Root Mean Square Error (RMSE), Mean Absolute Error (MAE), Mean Bias Error (MBE), Coefficient of Determination (R²), Akaike Information Criterion (AIC), and Bayesian Information Criterion (BIC). The Champernowne distribution outperformed the other models across all metrics, achieving the lowest RMSE (0.00036), MAE (0.00022), AIC (650.52), and BIC (689.46), and the highest R² (0.99998). Its ability to capture calm hours and extreme wind speeds provided more accurate power density estimates, with errors averaging 23%, compared to 33% and 42% for the Weibull and Rayleigh-Rice distributions, respectively. Despite low mean wind speeds (2.7 m/s), Ben Guerir’s ground-based power density ranged from 18 to 54 W/m². The results suggest that conventional large-scale wind energy projects are unsuitable for Ben Guerir. Instead, small Vertical-Axis Wind Turbines (VAWTs) or alternative strategies should be considered. The Champernowne distribution’s robustness makes it a valuable tool for wind energy assessments, especially in regions with intermittent wind patterns, providing a foundation for more accurate modeling and energy planning.

Introduction

In recent times, global energy consumption has been on a steady rise, attributed to the progress in economic and societal advancements across both established and emerging nations.

In 2019 world energy production reached 14,736 Mtoe, a 2.2% increase compared to 2018 ¹. Energy demand rose by 3.5% in the OECD (Organization for Economic Co-operation and Development) countries. It has also increased by 0.38% in non-OECD. ¹.

For 2019, Africa produced 5.9% of the world’s energy (Fig. 1), ranking 5th with 869.4 Mtoe of energy produced, and having 1.2% of growth in energy production compared to 2018.

Fig. 1

Distribution of total energy production by region in 2019 (source: Statista.com).

In the energy share, wind energy increase of production accelerated in 2019 by 12%. Fossil fuels accounted for more than 81% of production in 2019, as in 2018 ^1,2.

Over the past two decades, numerous studies have focused on electricity generation through wind turbines and water pumping via direct mechanical methods from wind energy conversion systems ². Although wind speed data in hourly time series format can be extensive, a concise set of key parameters can be employed to determine wind characteristics and assess the wind energy potential within this extensive dataset.

Renewable energy, with wind energy at the forefront, has emerged as a pivotal solution. Morocco’s wind resources are located in the areas along the coast of the Atlantic Ocean and the Mediterranean Sea, as well as in certain mountainous areas. In this context, Morocco has implemented an energy strategy that includes the creation of several Renewable Energy projects. As of 2023, with new operational projects (Table 1), Morocco had an installed wind power capacity of around 2.09 GW which represents a share of around 18% in the total installed capacity ^3,4, with the goal to generate up to 50% of the electricity (installed power) from renewable sources by 2030.

Table 1 Wind projects in Morocco ⁴.

However, to enhance the electrical output performance of wind farms in specific locations, a meticulous examination of local wind characteristics is imperative ^5,6. Notably, scholars have increasingly focused on evaluating wind energy potential across various global regions through diverse probability density functions (PDFs) ^7,8,9,10.

This paper concentrates on applying a Champernowne distribution to characterize wind speed probability patterns at the Green Energy Park (GP) station in Ben Guerir (Fig. 2). The results are then to be compared to the three and two-parameters Weibull and Rayleigh-Rice PDF for the same area.

Fig. 2

Green Energy Park facility and the anemometer.

Literature review

Pandeya and Prajapati et al. ¹¹ conducted a study aimed at estimating the wind energy potential and comparing six different methods for estimating Weibull parameters at two potential locations in Nepal. Wind data were collected at a height of 2 m and extrapolated to a height of 50 m to determine average wind speed, Weibull parameters, and wind power density. The evaluation of the six parameter estimation methods revealed that the empirical method of Justus and Lysen demonstrated the highest accuracy, while the graphical method performed the poorest. Using the empirical method of Lysen, the average wind power density was estimated as 336.07 W/m² for Jumla and 326.73 W/m² for Okhaldhunga, indicating that both locations possess a moderate potential for wind energy extraction.

Similarly, Akdag et al.¹², presented a comprehensive analysis of the Turkish wind energy landscape on 14 sites using the two-parameter Weibull PDF. Subsequently, the researchers scrutinize the influx of new wind power plant license applications in Türkiye to gauge investment interest. Capacity factors ranging from 19.7 to 56.8% were computed, alongside production costs of electrical energy varying between 1.73 and 4.99 $cent/kWh. Jowder et al.¹³ have performed the same analysis in Bahrain using the two-parameter Weibull PDF to analyze wind speed data at 10 m, then extrapolated to 30 m and 60 m. Weibull was also used as a statistical model by Mpholo et al. ¹⁴, who have performed a wind potential assessment at two locations in Lesotho.

Altunkaynak et al. ¹⁵, explore the relationship between wind power and wind speed, through statistical parameters derived from the two-parameter Weibull PDF. Additionally, the study outlines a straightforward procedure for calculating wind power at specific risk levels, typically 5% or 10%.

Fyrippis et al. ¹⁶, conducted a study on the wind power potential of Koronos village (Greece) using the two-parameter Weibull and the Rayleigh PDFs. For this site, through statistical metrics the authors have determined that the Weibull model provided a better fit to the actual data. Same conclusions were made by Shu et al. ¹⁷ while investigating wind energy potential in Hong Kong.

Dong and Wang et al. ¹⁸, embarked on a comprehensive study aimed at optimizing wind resource assessment and selecting appropriate wind turbines in Huitengxile, Inner Mongolia, China. Gamma, Rayleigh, Lognormal and Weibull PDFs have been compared, and Weibull distribution has been evaluated as the best fit for the studied area, while two intelligent optimization algorithms—Differential Evolution (DE), and Genetic Algorithm (GA)—were suggested as best parameters estimators of the Weibull distribution, compared to the traditional estimator such as moment method, maximum likelihood method, cumulative probability method. These were found inadequate due to the wide range of wind speed data.

Za’rate-Minano et al. ¹⁹, suggested two methods for creating wind speed series using stochastic differential equations and have chosen the Weibull distribution as a statistical model. The goal was to simulate wind speed patterns that closely match the historical wind speed data from a specific location.

Harris Cook et al. ²⁰ suggested the use of the Weibull distribution as an appropriate model for estimating the wind energy potential for three different locations: Changi, Singapore and Rome. The authors have used the Offset Elliptical Normal model (OEN) as a theoretical base to present the Weibull distribution as an effective model to represent wind speed behavior.

However, the study by Shonhiwa and Makaka et al.²¹ to assess wind resources in Mthatha (South Africa) showed that the three-parameter Weibull distribution outperforms the two-parameter Weibull distribution, because the third parameter (threshold parameter) which account of the occurrence of low wind speeds, more effectively, which is the case for Mthatha, with an annual wind speed average of 3.3009 m/s.

For Morocco-based recent studies using the two-parameter Weibull distribution in wind-rich areas, Daoudi et al. conducted three interrelated studies focused on optimizing wind energy utilization. The first study used the Data Envelopment Analysis (DEA) method to prioritize 14 offshore Moroccan wind sites, identifying Dakhla, Laâyoune, and Tanger as having the highest potential based on wind power density and seabed characteristics ²². The second study examined the techno-economic feasibility of two onshore wind farms in Tantan province, achieving energy costs as low as 3.45 US cents per kWh ²³. The third study explored integrating wind energy and hydrogen production for greenhouse agriculture, highlighting Dakhla and Essaouira as key sites capable of meeting electricity demands and producing significant hydrogen quantities to support sustainable agricultural practices ²⁴.

Numerous techniques are available in the literature for fitting wind speed data to the Weibull distribution and determining its parameters. These methods encompass the least-squares method (LSM), the order statistics method (OSM), the maximum likelihood method (MLM), the modified maximum likelihood method (MMLM), the energy pattern factor method (EPFM), the empirical method of Lysen (EML), and the method of moments (MOM) ^{25,26,27,28,29}.

Studies in the literature commonly rely on statistical analysis, assuming that the Weibull distribution, or its special case, the Rayleigh distribution, provides a reasonable approximation of wind speed patterns ¹³.

While Rayleigh-Rice PDF has shown good performance in some cases, the Weibull distribution has been recommended due to the ease of estimating the Weibull distribution parameters to match the empirical distribution of wind observations ¹⁰.

Relevance of the study

The present study aims to evaluate the applicability of the Champernowne distribution in modeling wind speed characteristics in regions with a high prevalence of minimal wind speeds. While the Champernowne distribution has been extensively explored in economic studies, its application to wind speed analysis remains limited, with Bahraoui et al. ²¹ being the sole documented example in recent literature. Their findings indicated that the Champernowne distribution provided a superior fit for wind-rich areas in Northern Morocco, capturing wind power intensity more accurately compared to other models.

This paper presents a comparative analysis of the Champernowne distribution, the two-parameter and three-parameter Weibull distributions, and the Rayleigh-Rice distribution, utilizing the least-squares method for parameter estimation. To enhance the study’s relevance, the analysis utilizes minutely wind speed data collected from Ben Guerir, Morocco, spanning three years: 2021, 2022, and 2023, instead of relying solely on hourly data from a single year.

While previous research highlights that the least-squares method, often referred to as the "graphical method," may lack accuracy and robustness compared to the maximum likelihood approach, it remains one of the few methods, alongside the method of moments, capable of accommodating null wind speed data. This is a critical consideration for the present study, as null wind speed values provide essential insights into variability and fluctuations in wind behavior, particularly in regions with low wind potential.

For energy applications, the Champernowne distribution’s four parameters make it particularly versatile, enabling it to accommodate variable behaviors observed in wind speed histograms. This flexibility is especially valuable in microclimate contexts, where wind exhibits complex patterns and variability.

In the context of the future of green hydrogen production, both globally and in Morocco ²⁴, incorporating the Champernowne distribution alongside existing wind models enables the inclusion of extremes and variability. This approach supports advanced multi-scenario analyses, which can more effectively simulate market dynamics, production fluctuations, and pricing trends, thereby providing valuable insights to guide policy decisions and investment strategies.

Moreover, accurate distribution is essential for data correction and realistic gap-filling in wind data analysis, particularly when addressing large gaps. Relevance of the Study.

Understanding and accurately modeling wind speed is of paramount importance in wind assessments due to its direct influence on power density calculations. The power density ($Pd{P}_{d}$), a key metric for evaluating wind energy potential, is defined as ${\text{P}}_{\text{d}}=\frac{1}{2}\uprho {\text{v}}^{3}$, where $v$ is the wind speed and $\uprho$ is the air density. Through a logarithmic transformation ${\text{lnP}}_{\text{d}}=\text{ln}\left(\frac{1}{2}\right)+{ln\rho }+3\text{lnv}$ and subsequent differentiation: $\frac{{\text{dP}}_{\text{d}}}{{\text{P}}_{\text{d}}}=3\frac{\text{dv}}{\text{v}},$ it becomes evident that power density is highly sensitive to wind speed variability. Specifically: $\Delta {\text{P}}_{\text{d}}=3 {\Delta v}.$

Considering the previous demonstration, a 10% overestimation in wind speed ($\Delta v/v=0.1$) leads to a 30% overestimation in power density ($\Delta Pd/Pd=0.3$. This amplification of error highlights the critical importance of accurate wind speed modeling in assessing wind energy potential and subsequent well-informed decisions.

Accordingly, the present paper aims to highlight the importance of accurate statistical techniques and comparative error analysis to enhance the accuracy and reliability of wind energy potential assessments. The Champernowne distribution offers a framework capable of capturing a wide range of wind behaviors, contributing to the existing literature by improving the assessment of wind speed variability and ensuring that corrected and gap-filled data align closely with observed physical phenomena.

Finally, with regard to non-energy applications, incorporating the Champernowne distribution broadens the toolkit available in the existing literature for analyzing wind speed data. The study’s relevance is interdisciplinary, as accurately characterizing wind speed behavior is crucial not only for energy applications but also for non-energy domains such as pollution dispersion modeling, fire mitigation, and agricultural planning.

Data and methods

Area study

For the present work, access to ground-based wind speed data for the years 2021, 2022, and 2023 was provided by the Green Energy Park (GEP), located in Ben Guerir, Morocco.

The selection of the Ben Guerir station was motivated by its seasonal climate fluctuations, including variations in wind speeds, which make it an ideal site for studying wind variability across different time periods and validating statistical models for diverse wind regimes. Ground-based data available from this location further support the analysis. For instance, in 2022, wind speeds at Ben Guerir exhibited an average value of 2.7 m/s with a standard deviation of 1.9 m/s. Minimum wind speeds of 0 m/s were recorded, while peaks reached 18 to 25 m/s over the 3 years. The station is geographically located at: (i) Latitude: 32.2212°; (ii) Longitude: − 7.9289°; (iii) Altitude: 446 m. The estimated power density in Benguerir at a height of 10 m ranges between 35 and 59 W/m² according to the Global Wind Atlas.

The anemometer (Fig. 2) is positioned at a height of 10 m above ground level, providing wind speed measurements corresponding to this specific elevation.

The preliminary step in any data processing workflow involves data filtering. For this study, six key characteristics were evaluated to assess the quality of the dataset ²². These characteristics include coherence, accuracy, completeness, reliability, relevance, and validity.

While all six characteristics are essential for ensuring data quality, their relative importance depends on the context and specific objectives of the analysis. In this study, completeness and coherence were identified as the most critical factors. A quality assessment performed on the ground-based data confirmed complete coherence in terms of quantities and units, alongside 100% completeness.

Wind speed and direction

The monthly averages of wind speed and direction for the years 2021, 2022, and 2023 are presented in Fig. 3. To enhance readability and better capture wind speed patterns, the time series data from 2022 were selected for further representation.

Fig. 3

Wind speed and directions averages (2021–2023).

The variability of wind speed demonstrates notable patterns, with peaks observed, especially in May and June, followed by a steady decline towards the end of the year. The wind directions present significant deviations in specific periods like February 2022.

Wind rose diagrams depict wind direction and associated frequencies (Figs. 4, 5, 6 and 7) and are categorized by wind speed for four distinct seasons in 2022: (i) Season 1 (January 1–March 31), (ii) Season 2 (April 1–June 30), (iii) Season 3 (July 1–September 30), and (iv) Season 4 (October 1–December 31). The focus on 2022 provides a detailed seasonal analysis of wind behavior.

Fig. 4

Wind rose (01 January–31 March).

Fig. 5

Wind rose (01 April–30 June).

Fig. 6

Wind rose (01 July–30 September).

Fig. 7

Wind rose (01 October–31 December).

The wind rose diagrams indicate that wind speeds at 10 m are predominantly concentrated in the Eastern sector (Northeast, East, Southeast). However, for wind turbine design or applications requiring wind data at different heights, additional processing is necessary. While wind speed can be extrapolated to other heights using Hellman’s exponential law ^30,31:

$${v}_{{z}_{1}}={v}_{{z}_{0}}{\left(\frac{{z}_{1}}{{z}_{0}}\right)}^{{\alpha }}$$

(1)

where, ${\text{v}}_{{\text{z}}_{1}}$ represents the wind speed at the target altitude ${\text{v}}_{{\text{z}}_{0}}$ is the wind speed at the reference altitude (10 m in our case), ${\alpha }$ is the exponent of the power law, which depends on local conditions and typically varies between 0.1 and 0.4 for terrestrial regions.

Adjustments for wind direction involve more complex phenomena such as the Ekman spiral ³², which accounts for the Coriolis effect and vertical wind shear.

Weibull distribution

The Weibull distribution is widely used in literature for describing wind speed data in many regions around the world and it parameter estimation is well documented^{9,11,12,16,20,24,25,33,34,35,36,37,38,39,40}. In wind speed characterization, the variation in wind speed is captured by Weibull distribution two functions: the probability density function (PDF) and the cumulative density function (CDF). There are 2 types of Weibull distributions: the two-parameter Weibull distribution (2WPDF), and the three-parameter Weibull distribution (3WPDF).

A random variable, y, here the wind speed (m s⁻¹) has a f(y) three-parameter Weibull distribution if its PDF expressed as:

$$\text{f}\left(\text{y}\right)=\left\{\begin{array}{c}{{\frac{\text{k}}{\text{s}-\upvarepsilon }\left(\frac{\text{y}-\upvarepsilon }{\text{s}-\upvarepsilon }\right)}^{\text{k}-1}\text{e}}^{-{\left(\raisebox{1ex}{$\text{y}-\upvarepsilon $}\!\left/ \!\raisebox{-1ex}{$\text{s}-\upvarepsilon $}\right.\right)}^{\text{k}}}, y\ge 0\\ 0 , y<0\end{array}\right.$$

(2)

The cumulative of such a distribution is expressed as the following:

$$\text{g}\left(\text{y}\right)=\left\{\begin{array}{c}{1-\text{e}}^{-{\left(\raisebox{1ex}{$\text{y}-\upvarepsilon $}\!\left/ \!\raisebox{-1ex}{$\text{s}-\upvarepsilon $}\right.\right)}^{\text{k}}}, y\ge 0\\ 0 , y<0\end{array}\right.$$

(3)

In Eqs. (2) and (3), ε is the location parameter, k is the shape parameter (dimensionless number), s is the scale parameter. ε and s have the same dimensions as y in (m s^-1).

In several papers, the Weibull distribution has 2 parameters because the studies focus on regions with high and frequent wind speeds, calm hours are ignored ³³. In that case, the Weibull distribution is rewritten as:

$$\text{f}\left(\text{y}\right)=\left\{\begin{array}{c}{{\frac{\text{k}}{\text{s}}\left(\frac{\text{y}}{\text{s}}\right)}^{\text{k}-1}\text{e}}^{-{\left(\raisebox{1ex}{$\text{y}$}\!\left/ \!\raisebox{-1ex}{$\text{s}$}\right.\right)}^{\text{k}}}, y\ge 0\\ 0 , y<0\end{array}\right.$$

(4)

The cumulative distribution function of the 2WPDFt is expressed as:

$$\text{g}\left(\text{y}\right)=\left\{\begin{array}{c}1-{\text{e}}^{-{\left(\raisebox{1ex}{$\text{y}$}\!\left/ \!\raisebox{-1ex}{$\text{s}$}\right.\right)}^{\text{k}}}, y\ge 0\\ 0 , y<0\end{array}\right.$$

(5)

One advantage of Eq. (2) is that it allows for the possibility of obtaining a non-zero probability when wind speed is zero, which is not the case for Eq. (1) (f(0) = 0). For specific locations such as Ben Guerir, where extreme events wind speeds can be observed, identifying calm hours can offer valuable insights into the characteristics of wind patterns and help in planning and decision-making for future projects related to wind energy or other applications.

To estimate parameters for both forms of Weibull distribution, the least squares method has been used. This involves minimizing the sum of squared errors (SSE), which quantifies the squared differences between actual observations and predicted values. The results are presented in Sect. 2.7. .

Rayleigh-Rice distribution

The Rayleigh-Rice distribution, named after Stephen O. Rice, published his work in 1945 where he extends Rayleigh’s work to account for a non-zero mean ⁴¹. That distribution is often used as an alternative to the Weibull distribution to describe wind speed statistical behavior ^42,43. The Rice distribution is indeed expressed with parameters K, and μ, where μ represents the non-central parameter, which is the mean or expected value of the distribution. These parameters are used to define a non-central Rice distribution, which allows for the presence of both a signal component (μ) and Gaussian noise. The PDF of such a Rayleigh-Rice distribution with y as the variable is expressed as:

$$\text{f}\left(\text{y};\text{K},\upsigma ,\upmu \right)=\frac{\text{y}}{{\upsigma }^{2}}{\text{e}}^{-\left({\text{y}}^{2}-2{\upmu y}+{\upmu }^{2}+{\text{K}}^{2}\right)/\left(2{\upsigma }^{2}\right)}{\text{I}}_{0}\left(\frac{\text{Kx}}{{\upsigma }^{2}}\right)$$

(6)

For this PDF y is the wind speed, ${\text{I}}_{0}$ is the modified Bessel function of the first kind and order 0, K is the Rician parameter. The Rayleigh-Rice cumulative distribution function is expressed as:

$$\text{F}\left(\text{y};\upsigma ,\text{s}\right)=1-{\text{Q}}_{1}\left(\frac{\upnu }{\upsigma },\frac{\text{y}}{\upsigma }\right)$$

(7)

In Eq. (7), Q1 is the Marcum Q-function ⁴⁴ of the first order is expressed as:

$${\text{Q}}_{1}\left(\frac{\text{s}}{\upsigma },\frac{\text{y}}{\upsigma }\right) ={\int }_{\frac{\text{y}}{\upsigma }}^{\infty }\text{f}\left(\text{y};\text{K},\upsigma ,\upmu \right)\hspace{0.17em}\text{dy}$$

(8)

The parameter estimation process was conducted using the Least Squares Method (LSM), with the corresponding results detailed in “Parameter estimation methods”.

Champernowne distribution

The Champernowne distribution is defined as: The function is originally defined by the following equation:

$$\text{f}\left(\text{y};\text{c},{\alpha },\uplambda ,{\text{y}}_{0}\right)=\frac{\text{c}}{\text{cosh}\left[{\alpha }\left(\text{y}-{\text{y}}_{0}\right)\right]+\uplambda }\forall \text{ y }\in ]-{ \infty }, +\infty [,\text{ c}\ge 0,\uplambda \ge 0,{ \alpha }\ge 0 ,$$

(9)

where n is an amplitude parameter, and ${\varvec{\uplambda}}$ is a horizontal translation parameter. ${\varvec{\uplambda}}$ and n are dimensionless parameters, and α is a positive parameter, y₀ is the median of the dataset, defined as the central value within a set of observed data, arranged in ascending order. In the context of this study, where y represents wind speed—a strictly positive quantity—Eq. (9) can be reformulated as follows:

$$\text{f}\left(\text{y};\text{c},{\alpha },\uplambda ,{\text{y}}_{0}\right)=\frac{\text{c}}{\text{cosh}\left[{\alpha }\left(\text{y}-{\text{y}}_{0}\right)\right]+\uplambda }\forall \text{ y }\in [0, +\infty [,\text{ c}\ge 0,\uplambda \ge 0,{ \alpha }\ge 0 ;$$

(10)

The Champernowne distribution was first proposed by D. G. Champernowne in 1937 at a conference at the Oxford Meeting of Econometrics Society to describe a family of curves for the graduation of pretax income distributions ^45,46.

It was further developed and discussed by the author in 1952, where methods are described for fitting the distribution parameters. Since then, the Champernowne distribution is discussed and used in econometrics to model income distribution^{47,48,49,52–56}.

Results and discussion

Parameter estimation methods

For the four distributions, the parameters have been determined using the least squares method (LSM). For the current study, this can be expressed as follows:

$$\text{SSE}={\sum }_{\text{k}=0}^{\text{n}}|\text{hist}\left({\text{y}}_{\text{k}}\right)-\text{f}\left({\text{y}}_{\text{k}};{\upalpha },\uplambda ,{\text{y}}_{0}\right){|}^{2}\text{\circledR }0$$

(11)

In Eq. (11), SSE is the objective function to minimize, $\text{hist}\left({\text{y}}_{\text{k}}\right)$ represent the histogram of wind speeds, n is the number of observations. Tables 2, 3 and 4 presents the estimated parameter for each period and distribution from June to December 2022.

Table 2 Parameter estimation for two and three-parameter Weibull PDFs (2WPDF and 3WPDF).

Table 3 Parameter estimation for Rayleigh-Rice distribution.

Table 4 Champernowne distribution parameters.

Distribution comparison

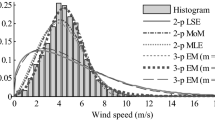
After determining the various parameters for each distribution, histograms were generated alongside the PDFs of the two-parameter Weibull, three-parameter Weibull, Rayleigh-Rice, and Champernowne distributions for each period, as illustrated in Fig. 8.

Fig. 8

Seasonal PDFs comparison of wind speed models (2021–2023).

For the original Champernowne distribution, for l > 1, the CDF has been calculated and is expressed as:

$${\text{F}}\left(\text{y;}{\alpha}{,\lambda,}{\text{y}}_{0}\right)= \frac{\text{c ln}\left(\frac{\left(\sqrt{\left({{{\lambda}^2}-1}\right)}{+\lambda}\right){\text{e}}^{{\alpha}{\text{y}}}\text{+}{\text{e}}^{\alpha {\text{y}}_{0}} }{\left(\sqrt{\left({{{\lambda}^2}-1}\right) \, }{-\lambda}\right){\text{e}}^{{\alpha}{\text{y}}}{\text{- e}}^{\alpha {\text{y}}_{0}}}\right)}{\alpha \sqrt{\left({{{\lambda}^2}-1}\right)} \, }$$

(12)

However, because of the complex form of the Eq. (12), for values different from 1 and since it is not normalized, the Champernowne CDF can be approximated by a Fisk distribution (l = 1, 2c = ${\alpha }$) Eq. (12) is reduced to a Fisk CDF⁵⁷:

$$\text{F}\left(\text{y};{\alpha },\uplambda ,{\text{y}}_{0}\right)= \frac{{\text{e}}^{{\alpha}{\text{y}}}}{\left({\text{e}}^{{\alpha}{\text{y}}}+{\text{e}}^{\alpha {\text{y}}_{0}}\right)}$$

(13)

In Fig. 9, the Champernowne CDF, approximated by a Fisk CDF, exhibits a distinctive non-zero value at 0, indicating the presence of a probability density even during calm wind conditions. Exceptions to this behavior are observed during Jul–Sep 2021, Apr–Jun 2022, Jan–Mar 2023, and Jul–Sep 2023. These characteristic underscores notable irregularities in the wind speed distribution, particularly pronounced from April to September where discrepancies usually occur, and the mean wind velocities are higher (Fig. 3).

Fig. 9

Seasonal Fisk CDFs using Champernowne parameters (2021–2023).

Statistical performance indicators

To determine the performance of the four models in relation to the observed data, standard statistical metrics were considered:

• The Akaike Information Criterion

  $${\text{AIC}}=2\text{k}-2\text{ln}\left(\mathcal{L}\right)$$

  (14)

• Bayesian Information Criterion (BIC)

  $$\text{BIC}=\text{kln}\left(\text{n}\right)-2\text{ln}\left(\mathcal{L}\right)$$

  (15)

  where k is the number of estimated parameters, while $\text{ln}\left(\mathcal{L}\right)$: is the natural logarithm of the PDF values.

• The Root Mean Square Error (RMSE)where ${y}_{i}$ is the observed data points, $n$ the number of observations, $\widehat{{y}_{i}}$ the predicted data points. The mean is expressed as:

  $${\text{RMSE}}=\sqrt{\frac{1}{\text{n}}{\sum }_{\text{i}=1}^{\text{n}}{\left({\text{y}}_{\text{i}}-\widehat{{\text{y}}_{\text{i}}}\right)}^{2}}$$

  (16)

• The Mean Bias Error (MBE)where ${y}_{i}$ is the observed data points, $n$ the number of observations, $\widehat{{y}_{i}}$ the predicted data points. The mean is expressed as:

  $${\text{MBE}}=\frac{1}{n}{\sum }_{i=1}^{n}\left({y}_{i}-\widehat{{y}_{i}}\right)$$

  (17)

• The Mean Absolute Error (MAE)where ${y}_{i}$ is the observed data points, $n$ the number of observations, $\widehat{{y}_{i}}$ the predicted data points. The mean is expressed as:

  $${\text{MAE}}=\frac{1}{n}{\sum }_{i=1}^{n}\left({y}_{i}-\widehat{{y}_{i}}\right)$$

  (18)

• The Determination Coefficient (R²)where ${y}_{i}$ is the observed data points, $n$ the number of observations, $\widehat{{y}_{i}}$ the predicted data points. The mean is expressed as:

  $${\text{R}}^{2}=1-\frac{{\sum }_{\text{i}=1}^{\text{n}}{\left({\text{y}}_{\text{i}}-\widehat{{\text{y}}_{\text{i}}}\right)}^{2}}{{\sum }_{\text{i}=1}^{\text{n}}{\left({\text{y}}_{\text{i}}-\overline{\text{y} }\right)}^{2}}$$

  (19)

$$\overline{y }=\frac{1}{n}{\sum }_{i=1}^{n}{y}_{i}$$

(20)

In the performance analysis, models were assessed using several statistical metrics, where lower values of RMSE, MAE, MBE, AIC, and BIC indicate superior performance. Conversely, higher R² values, closer to 1, denote greater model accuracy. The best-performing metrics are emphasized for clarity and comparison.

Over the three considered years, from January to March, the Champernowne distribution demonstrated better accuracy across multiple metrics when compared to other models as shown in Table 5. It consistently achieved the highest R² values (R² of 0.999986902 for 2023). Additionally, it delivered the lowest RMSE, MAE, MBE, and MAE values. Furthermore, its lowest AIC and BIC scores highlight the Champernowne model’s balance between fit and complexity, making it a robust choice for wind speed distribution modeling.

Table 5 Performance metrics for wind speed models—January–March (2021–2023).

However, despite its strengths, the Champernowne model exhibited a slight weakness in handling the central tendencies or tails of certain datasets, as evidenced by its Mean Bias Error (MBE = 0.000547996) between January and March 2022 which was higher than the values achieved by the 2-parameter or 3-parameter Weibull models.

Comparatively, the Weibull distributions (2WPDF and 3WPDF) performed reliably but were generally outclassed by the Champernowne model in terms of capturing both low and extreme wind speeds. The Rayleigh-Rice model consistently lagged behind, exhibiting higher RMSE and MAE values, coupled with poorer AIC and BIC scores, which indicated its unsuitability for complex wind speed profiles.

From January to March, over the three analyzed years, the Champernowne distribution consistently exhibited better performance across most evaluation metrics, as shown in Table 6. For instance, it achieved the highest R² values across all years (e.g., R² = 0.999976971 for 2023 and R² = 0.999708078 for 2021). The Champernowne distribution outperformed other models in terms of RMSE, MAE, and AIC/BIC scores, except in 2022. Comparatively, the Weibull distributions (2WPDF and 3WPDF) provided reliable results but generally fell short of the Champernowne model. The Rayleigh-Rice (R.R) model, on the other hand, globally showed less accuracy with higher RMSE and MAE values and higher AIC/BIC scores.

Table 6 Performance metrics for wind speed models—April–June (2021–2023).

From July to September across the three years, the Champernowne distribution consistently exhibited superior performance metrics, as shown in Table 7. For between July and September 2023, the Champernowne model experienced minor performance deviations, characterized by a slightly negative MBE (− 0.00004), indicative of minimal overestimation in wind speed predictions with the second lowest AIC and BIC.

Table 7 Performance metrics for wind speed models—July–September (2021–2023).

Notably, the 3-parameter Weibull, despite the lowest AIC and BIC values, showed significant underperformance in 2023, with a remarkably high RMSE (0.0284) and a poor R² value of 0.9296. Raileigh-Rice distribution demonstrated for 2023, better accuracy, with improved RMSE, MAE and MBE, despite its highest AIC and BIC scores.

Spanning the months from October to December (2021–2023) Table 8 presents results where the Champernowne distribution displays a mitigated performance. While it consistently delivered strong results in 2022 and 2023, its performance in 2021 was notably weaker compared to the 3-parameter Weibull model (3WPDF) and compared to the previous months.

Table 8 Performance metrics for wind speed models—October–December (2021–2023).

Additionally, the AIC (651) and BIC (689) scores for the Champernowne model were less favorable than those of the 3WPDF model, indicating a slightly poorer balance between model complexity and fit in 2021.

In 2022 and 2023, the Champernowne model demonstrated robust performance, achieving the lowest RMSE, MAE and MBE, and AIC, despite being penalized by the second lowest BIC in 2023.

Power density calculation

A statistical probability density analysis was conducted, specifically focusing on the histogram of wind speeds at 10 m of hub height and its relation to mechanical power density analysis.

$${P}_{d}=\left(1/2\right)\uprho {\text{v}}^{3}$$

(21)

where ${P}_{d}$ is the power density, v is the wind speed, and ρ is the air density. The relative error ∆ was calculated between the observed data and the models. The highest the error, the worse the model is close to reality.

The results from Table 9 indicate that, for all cases from 2021 to 2023, the power density estimated using the Champernowne probability density function (PDF) consistently aligns more closely with the measured power density derived from ground-based data. The Champernowne distribution is followed in performance by the two-parameter Weibull PDF, while the Rayleigh-Rice and Weibull distributions exhibit comparatively weaker accuracy.

Table 9 Seasonal power density analysis in W/m² for each distribution.

Conclusions

A comprehensive seasonal analysis of wind speed and direction was conducted. Four statistical distributions were evaluated and compared. The analysis aimed to assess the variability of wind speeds and their implications principally for wind turbine design and energy estimation. Parameter estimation was performed using the Least Squares Method (LSM), chosen for its simplicity and its ability to account for null wind speeds—an essential consideration for studying wind speed variability in regions like Ben Guerir. The following conclusions were derived from the study:

• a.a.a. Site selection and potential transferability:

Ben Guerir has relatively low wind energy potential, with annual mean wind speeds between 1.8 m/s and 3.5 m/s, averaging 2.7 m/s. Despite this limitation, the site was selected due to its wind variability and the availability of a high temporal resolution of measurements. The models discussed in this study could be extended to areas with higher wind energy potential, where their application could yield more significant energy estimates.

• b.b.b. Champernowne distribution strengths and weaknesses:

The Champernowne distribution demonstrated overall best fit to the observed wind velocities probability distributions in Ben Guerir, as indicated by performance metrics and energy analyses (Tables 5, 6, 7, 8, 9). This model closely captured the characteristics of the wind speed distribution, particularly the intermittency and variability, and outperformed the other models, including the two- and three-parameter Weibull distributions. By including calm hours in its analysis, the Champernowne distribution avoided overestimating wind power potential. This is particularly important, as excluding calm hours—as observed in the two-parameter Weibull distribution—can lead to substantial overestimations of wind energy potential (Table 9).

The inclusion of a large proportion of calm hours in the dataset has the potential to skew the distribution curve toward a log-normal shape, leading to inaccuracies in wind speed and energy estimations especially during summer where calm days are followed by storms. Moreover, its four-parameter structure introduces complexity to the extraction of the cumulative distribution function (CDF), which may challenge its applicability in scenarios with limited computational resources. Future studies should address these shortcomings by exploring more efficient estimation techniques and analyzing its performance under varying data conditions.

• c.c.c. Comparison with Weibull distributions:

The two-parameter Weibull distribution, while widely used in wind energy studies for its simplicity, displayed some notable shortcomings in this analysis. By excluding calm hours, it systematically overestimated the wind energy potential, particularly in low wind speed conditions, and demonstrated reduced accuracy left of the median of the wind speed distribution. The three-parameter Weibull distribution, despite incorporating a third parameter, was unable to accurately capture wind speed fluctuations and exhibited Pareto-like behavior during periods of extended calm hours combined with high wind speeds. This pattern is often observed during summer and winter, where temperature gradients lead to significant variability in wind speed. However, its performance remained stable when the probability density for calm hours did not exceed 0.1 (Fig. 8).

• d.d.d. Rayleigh-Rice distribution limitations:

The Rayleigh-Rice distribution exhibited limited performance for wind speed data in Ben Guerir. Its heavier tail (Fig. 8) underestimated wind speeds in the 4–6 m/s range and assigned null probabilities to calm hours. While Drobinski et al. ⁴³ highlighted the Rayleigh-Rice distribution as a potential alternative to Weibull, it proved unsuitable for representing the wind potential in this study.

• e.e.e. Insights on wind energy development.

The analysis indicates that Ben Guerir is not suitable for conventional large-scale wind energy projects. In regions with low mean wind speeds, alternative strategies, such as wind speed augmentation mechanisms or specialized turbine designs, should be explored. Given that the ground-based power density ranges from 18 to 54 W/m² at a height of 10 m, small Vertical-Axis Wind Turbines (VAWTs) present a viable solution for harnessing the area’s wind energy potential. Additionally, small-scale turbines could complement larger systems in high wind power zones.

• f.f.f. Key implications for wind modeling.

The divergence in performance between energy analysis and wind speed modeling reflects the nonlinear relationship between wind speed and energy (linear vs. cubic functions). The study reaffirms the importance of relative error analysis, as overestimation left of the mean velocity in Weibull distributions highlights the need for refined modeling approaches. The Champernowne distribution’s stability and low relative error make it an advantageous choice for long-term wind variability analyses.

• g.g.g. Future directions.

This study’s findings demonstrate the versatility and robustness of the Champernowne distribution in capturing wind speed variability. Future work could explore its application to regions with more complex topographical features or integrate it into hybrid models for better prediction accuracy. Additionally, further refinement of its parameter estimation methods and CDF could improve its usability in computationally demanding scenarios.