Improved quadratic interpolation optimizer for stochastic short-term hydrothermal scheduling with integration of solar PV and wind power

Abstract

The quadratic interpolation optimization (QIO) introduces a novel approach inspired by the generalized quadratic interpolation (GQI) with dual mechanisms. Initially, QIO employs GQI in its exploration strategy, updating populations based on two randomly selected individuals. Subsequently, it incorporates another exploration strategy, updating populations based on the best solution and two randomly selected individuals. Despite QIO’s effectiveness in numerous optimization tasks, it exhibits limitations when addressing highly nonlinear and multidimensional problems, such as stagnation, susceptibility to local optima, low diversity, and premature convergence. In this study, we propose three enhancement strategies to refine traditional QIO, aiming to bolster its exploration and exploitation capabilities through Weibull flight motion, chaotic mutation, and PDO mechanisms. The resultant improved QIO (IQIO) is then applied to solve the short-term hydrothermal scheduling (STHS) problem, considering system uncertainties and the potential installation of PV and wind turbine generation units to reduce fuel costs and emissions. The STHS is solved with considering the system constraints including water discharge and reservoir storage, the generated powers by the hydro and thermal units as well as balanced powers. The dependent constraints are handled using weighted summation method. The efficacy of the proposed IQIO is demonstrated using the CEC 2022 test suite, and the obtained results are benchmarked against various competitive optimization methods. Statistical analysis of the results confirms a notable enhancement in the original QIO’s performance upon applying the suggested IQIO. Furthermore, the inclusion of renewable generation units by IQIO yields maximum reductions of 23.73% in costs and 45.50% in emissions, underscoring its potential for sustainable energy management.

Introduction

Background

The modern electric systems consist of intricate and extensive networks that combine transmission, generation, and distribution networks. As the demand for electrical energy increases, there is a need for new energy resources to contribute to the power systems, offering economic and environmental benefits. The reliance on fossil fuels is currently diminishing due to the positive impact of renewable resources on electrical power networks. These resources are frequently integrated into the power system networks. In the stochastic STHS problem, the goal is to maximize the utilization of hydro, PVs, and wind turbines during intervals when these resources are available, while reducing dependency on thermal units to lower fuel costs. Operational constraints, such as water discharge rate, fluctuating hourly reservoir inflow and storage, and capacity limits of hydro and thermal units, must be taken into account during operations.

Literature review

The analytical programming methods were utilized previously to solve the non-linear STHS problem. These programming methods are such as linear, quadratic, non-linear and interior^1,2,3,4 but these ways may not execute satisfactory due to challenge the complex constraints and non-linearity functions of the problem. Thus, the advance artificial intelligence approaches have been introduced later on to tackle such non-linear problems and they have utilized the randomly created solutions that are iteratively enhanced by the random operators. Due to randomness and parallel exploration mechanism, they have a high probability of attaining the global solution and avoid of being trap into local minima. The optimization is executed autonomously and unpretentiously by nature of problem.

Among these intelligence algorithms, in this literature few are discussed and involved to solve the STHS problem such as salp swarm algorithm (SSA)⁵, turbulent water flow optimization (TWFO)⁶, grey wolf optimization algorithm (GWO)⁷, flower pollination algorithm (FPA)⁸, arithmetic optimization algorithm (AOA)⁹, henry gas solubility optimization algorithm (HgSOA)¹⁰, elite collaborative search algorithm (eCSA)¹¹, chimp optimization algorithm (COA)¹², grasshopper optimization algorithm (GOA)¹³, teaching–learning optimization¹⁴, rigid cuckoo search algorithm (rCSA) ¹⁵, and so on.

For optimal planning and operation of small and large-scale hydro power considering renewable resources, it is the prodigious implication to define the state of enduring periodicity and random short-term change¹⁶. To model of uncertainty, the different approaches have been extensively utilized and investigated, and divided into three categories such as statistical modeling using Markov chain along with the time series method^17,18,19. It is an intricated approach to implement an extremely comprehensive model to tackle the variations of renewable resources. Most of the models are intended for a firm feature of output because these resources have a complex meteorological correlation and the time–space and may observe few uncertain unidentified correlations. The other model is auto-regressive moving average (ARMA) that create the several scenarios²⁰. The Monte Carlo simulation is a probabilistic approach to create the scenarios that rely on the precise probability distribution²¹.

In most topical years, the contribution of the renewable resources into the electric networks have the great importance and more popular in power systems. The most feasible resources such as wind and solar PV are frequently used for integration purposes. The authors in^22,23, used the chaos and chaotic-oppositional-based sine cosine algorithm and whale optimization algorithms to solve the STHS problem with solar PV and wind generation systems scheduling to alleviate the fuel cost and the environment emissions. The authors in²⁴, applied the particle swarm optimization technique to solve the hydrothermal problem using solar plant to decrease the fuel cost and emissions. The authors in²⁵, used the oppositional-based learning (OBL) approach to improve the overall response of grasshopper optimization algorithm, the OBL helps algorithm to improve its social bounding among the grasshoppers to attain the global solution. The proposed OBL based grasshopper algorithm is used to resolve the scheduling of the hydrothermal units by incorporating wind and solar PV to decrease the fuel cost. In²⁶, the levy spiral flight technique is applied to enhance the exploration strength of artificial hummingbird algorithm and solve the STHS problem considering uncertainty of wind and solar powers to reduce the fuel cost as objective. The authors in²⁷ used the Weibull and lognormal PDF to model the windspeed and solar irradiance without taken into account the uncertainties of wind and solar. To solve STHS problem integrated with solar and wind powers by applying the lightning attachment procedure optimizer, where the objective is to minimize the fuel cost. The authors in²⁸, proposed an intensified water cycle approach (IWCA) based on two novel modifications through local search and opposition-based learning approach to improve the exploitation and exploration phases of the algorithm. The proposed IWCA approach is further used to solve the standard hydrothermal scheduling problem. Moreover, to prove the effectiveness of the proposed IWCA, the developed approach was tested through statistical and non-parametric tests. The authors in²⁹, proposed an enhanced version of Harris hawk optimizer (EHHO) used to resolve the multiple objective STHS problem to minimize the fuel cost with emissions.

Research contribution

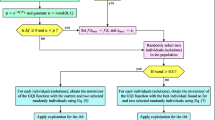
The graphical abstract to solve the stochastic STHS problem considering uncertain load power, the generated powers of PV and wind systems are illustrated in Fig. 1. The salient contributions are outlined below.

• 1. Enhancing the traditional QIO optimizer by incorporating Weibull flight motion, chaotic mutation, and PDO exploitation mechanisms to bolster both exploration and exploitation capabilities in the form of an improved version termed IQIO.

• 2. Addressing the short-term hydrothermal scheduling (STHS) problem, with and without the integration of Renewable Energy Resources (RERs), to minimize costs and emissions, while accounting for system losses and the valve point loading effect.

• 3. Employing statistical and non-parametric analyses on the CEC 2022 test suite to assess the efficacy of the proposed IQIO in comparison to established traditional optimizers, including SCSO, JSO, ZOA, DBO, EEFO, and QIO.

Fig. 1

The graphical abstract to solve the stochastic STHS problem with Solar and Wind considering power losses and valve-point loading effect.

The following sections of this paper are arranged as follows: Section "Stochastic STHS problem formulation" is the stochastic STHS problem formulation. Section "Modeling the uncertainties" depicts the models of uncertainties. Section "Methodology" explains the concept and the mathematical representation of the traditional and modified QIO. The experimental results are provided in section "The simulation results and analysis" while the summary of the main conclusion is outlined in section "Conclusion and future prospects".

Stochastic STHS problem formulation

This section provides a detailed discussion of the STHS formulation, specifically focusing on the uncertainties associated with solar and wind energy, taking into account VPLE (Variable Power Loss Estimation) as well as transmission losses. The objective is to achieve the optimal fuel cost while ensuring compliance with operational constraints. Subsequent sub-sections offer further insights into the relevant discussions.

Fuel cost minimization considering VPLE

The thermal units fuel cost at time $t$ considering VPLE is formulated as follows:

$$f_{it} \left( {P_{si}^{t} } \right) = \min .\mathop \sum \limits_{t = 1}^{T} \mathop \sum \limits_{i = 1}^{{N_{s} }} \left\{ {\partial_{i} + \varsigma_{i} P_{si}^{t} + \rangle_{i} (P_{si}^{t} )^{2} + \left| {\zeta_{i} \sin \left[ {\vartheta_{i} \left( {P_{si}^{\min i} - P_{si}^{t} } \right)} \right]} \right|} \right\}$$

(1)

where, ${\partial }_{i}$, ${\varsigma }_{i}$, ${\varrho }_{i}$, ${\zeta }_{i}$ and ${\vartheta }_{i}$ are the thermal unit cost coefficients of i^th generator with units ($/MW²h), ($/MWh), ($/h), ($/h) and (rad/MW), while ${P}_{si}^{mini}$ is referring to the least limit of the power generation for the associated thermal unit.

Solar PV and wind plant direct cost

The direct cost may not be imposed in these plants due to unuse of fossil fuel, but independent system operator (ISO) entails the initial paybacks adjustment in terms of renewal and maintenance costs³⁰. The ISO paid this cost in contradiction of scheduled power to the private suppliers. The direct cost of the ${j}^{th}$ wind plant is formulated as³¹:

$${C}_{wsch,j}^{t}\left({P}_{wsch,j}^{t}\right)={g}_{direct,j}\times {P}_{wsch,j}^{t}$$

(2)

where ${P}_{wsch,j}^{t},$ and ${g}_{direct,j}$ are the scheduled power and the direct cost coefficient of the ${j}^{th}$ wind plant. While the direct cost of the ${j}^{th}$ solar PV plant is formulated as:

$${C}_{sch,k}^{t}\left({P}_{psch,k}^{t}\right)={h}_{direct,k}\times {P}_{psch,k}^{t}$$

(3)

where ${P}_{psch,j}^{t}$ and, ${h}_{direct,k}$ are the scheduled power of the solar PV system and the direct cost coefficient.

Wind power uncertainty cost assessment

The ISO requires to keep the spinning reserves in order to ensure the continuous power supply, this is because of where the wind plant contribute its power under the estimation value, while the overestimation is required from the undetermined source. The reserve cost is formulated as³⁰:

$$\begin{array}{c}{C}_{rs,j}^{t}\left({P}_{wsch,j}^{t}-{P}_{win{d}_{ap},j}^{t}\right)={k}_{rs,j}\left({P}_{wsch,j}^{t}-{P}_{win{d}_{ap},j}^{t}\right)\\ ={k}_{rs,j}^{t}{\int }_{0}^{{P}_{wsch,j}^{t}} \left({P}_{wsch,j}^{t}-{p}_{w,j}\right){ f}_{w}\left({p}_{w,j}\right) d{p}_{w,j}\end{array}$$

(4)

where, ${k}_{rs,j}$ is the reverse cost coefficient, ${f}_{w}\left({p}_{w,j}\right)$ is the probability function of ${j}^{th}$ wind, while ${P}_{win{d}_{ap},j}^{t}$ is the actual power attained from the ${j}^{th}$ wind plant. If the plant supplies over to estimated value, then the state of the plant become considered as underestimation. In this state, the ISO is responsible to pay the extra amount for this excessive generation. The formulation is as follows³¹:

$$\begin{array}{c}{C}_{pc,j}^{t}\left({P}_{win{d}_{ap},j}^{t}-{P}_{ws,j}^{t}\right)={k}_{pc,j}\left({P}_{win{d}_{ap},j}^{t}-{P}_{wsch,j}^{t}\right)\\ ={k}_{pc,j}{\int }_{{P}_{wsch,j}^{t}}^{{P}_{wr,j}} \left({p}_{w,j}-{P}_{wsch,j}^{t}\right){ f}_{w}\left({p}_{w,j}\right) d{p}_{w,j}\end{array}$$

(5)

where, ${k}_{pc,j}$ is the penalty cost coefficient and ${P}_{wr,j}$ is referred to the ${j}^{th}$ plant output.

Solar PV uncertainty cost assessment

The solar PV plant has also the uncertain outputs as well as in under and overestimation states. The solar PV reserve cost is formulated as follows:

$$\begin{array}{c}{C}_{rs,k}^{t}\left({P}_{psch,k }^{t}-{P}_{photo-voltai{c}_{ap},k }^{t}\right)={k}_{rs,j}\left({P}_{psch,k }^{t}-{P}_{photo-voltaic\_ap,k }^{t}\right)\\ ={k}_{rs,k}{ \times f}_{s}\left({P}_{photo-voltai{c}_{ap},k }^{t}<{P}_{psch,k }^{t}\right)\times \\ \left[{P}_{ps,k}-E\left({P}_{photo-voltaic\_ap,k }^{t}<{P}_{psch,k }^{t}\right)\right]\end{array}$$

(6)

where, ${P}_{photo-voltaic\_ap,k }^{t}$ and ${k}_{rs,k}$ are the actual power attained from ${k}^{th}$ solar PV plant and reverse cost coefficient. The ${f}_{s}\left({P}_{photo-voltaic\_ap,k }^{t}<{P}_{psch,k }^{t}\right)$ is referring the probability of the deficiency of solar PV power i.e. ${P}_{psch,k }^{t}$ the real power minimum to the schedule, while $E\left({P}_{photo-voltaic\_ap,k }^{t}<{P}_{psch,k }^{t}\right)$ is the expectation of solar PV to the schedule power. The penalty cost is formulated for the underestimation of ${k}^{th}$ solar PV plant is formulated as³⁰:

$$\begin{array}{c}{ C}_{pc,k}\left({P}_{photo-voltai{c}_{ap},k }^{t}-{P}_{psch,k }^{t}\right)={k}_{pc,k}\left({P}_{photo-voltaic\_ap,k }^{t}-{P}_{psch,k }^{t}\right)\\ ={k}_{pc,k}{ \times f}_{s}\left({P}_{photo-voltai{c}_{ap},k }^{t}>{P}_{psch,k }^{t}\right)\times \\ \left[E\left({P}_{photo-voltaic\_ap,j}>{P}_{psch,k }^{t}\right)-{P}_{psch,k }^{t}\right]\end{array}$$

(7)

where, ${k}_{pc,k}$ is considering as the penalty cost coefficient, ${\times f}_{s}\left({P}_{photo-voltai{c}_{ap},k }^{t}>{P}_{psch,k }^{t}\right)$ is the probability of the deficiency of solar PV power i.e. ${P}_{ps,k }^{t}$ is the real power minimum to the schedule, while $E\left({P}_{photo-voltaic\_ap,j}>{P}_{psch,k }^{t}\right)-{P}_{psch,k }^{t}$ is the expectation of solar PV to the scheduled power.

Stochastic STHS to lessen the entire cost considering RERs uncertainty

The main objective of this research is to solve the stochastic STHS problem and lessen the cost of thermal units by installation of PV and wind turbine units considering uncertainties. The fuel cost formulation is given as follows:

$$Fobj=\sum_{t=1}^{T}\left\{\begin{array}{c}\sum_{i=1}^{{N}_{s}}{f}_{si}^{t}\left({P}_{si}^{t}\right)+\sum_{j=1}^{{N}_{wind}}\left[\begin{array}{c}{C}_{wsch,j}^{t}\left({P}_{wsch,j}^{t}\right)+{C}_{rs,j}^{t}\left({P}_{wsch,j}^{t}-{P}_{win{d}_{ap},j}^{t}\right)+\\ {C}_{pc,j}^{t}\left({P}_{win{d}_{ap},j}^{t}-{P}_{wsch,j}^{t}\right)\end{array}\right]\\ +\sum_{k=1}^{{N}_{photo-voltaic}}\begin{array}{c}[{C}_{s,k}^{t}\left({P}_{psch,k}^{t}\right)+{C}_{rs,k}^{t}\left({P}_{psch,k }^{t}-{P}_{photo-voltai{c}_{ap},k }^{t}\right)+\\ {C}_{pc,k}\left({P}_{photo-voltaic\_ap,k }^{t}-{P}_{psch,k }^{t}\right)] \$\end{array}\end{array}\right\}$$

(8)

where, $Fobj$ is the objective function of stochastic STHS problem which contains the entire operating cost of the thermal, solar PV and unit power units, while ${N}_{photo-voltaic}, {N}_{wind}$ and ${N}_{s}$ is the number of solar PV, wind and the thermal generator linked to the network.

System constraints

The stochastic STHS considering uncertainties of the wind and the solar PV powers must satisfy the balanced and inequality constraints.

Balance power constraints

The generated power from the thermal, the hydro, the wind and the PV power units should be equivalent to the total power demand.

$$\sum_{i=1}^{{N}_{s}} {P}_{si}^{t}+\sum_{\text{m}=1}^{{N}_{hydo}}{P}_{hm}^{t}+\sum_{\text{j}=1}^{{N}_{wind}}{P}_{wsch,j}^{t}+\sum_{\text{k}=1}^{{N}_{photo-voltaic}}{P}_{psch,k}^{t}-{P}_{L}^{t}={P}_{Dm}^{t} \forall t\in T$$

(9)

where, ${N}_{wind}$, ${N}_{photo-voltaic}$, ${N}_{hydo}$ and ${N}_{s}$ are referring to the number of the wind, solar PV, hydro and thermal generating units. ${P}_{L}^{t}$ is the transmission power losses, while ${P}_{Dm}^{t}$ is the uncertain load demand.

The generation of power from hydroelectric is depend on water discharge rate and reservoir water head. ${P}_{hm}^{t}$ is referring to the power generating from the hydro units and the related expression is given as follows:

$${P}_{hm}^{t}={C}_{1m}{\left({V}_{hm}^{t}\right)}^{2}{+C}_{2m}{\left({Q}_{hm}^{t}\right)}^{2}+{C}_{3m}{V}_{hm}^{t}{Q}_{hm}^{t}+{C}_{4m}{V}_{hm}^{t}+{C}_{5m}{Q}_{hm}^{t}+{C}_{6m} j\in {N}_{h} \forall t\in T MW$$

(10)

where, ${C}_{1m}, \dots ,$ ${C}_{6m}$ are the hydro generating power units’ coefficients, while, ${Q}_{hm}^{t}$ and ${V}_{hm}^{t}$ are the water discharge units and reservoir volume. ${P}_{L}^{t}$ is referred to the transmission losses can be formulated as follows:

$${P}_{L}^{t}=\sum_{i=1}^{{N}_{s}}\sum_{m=1}^{{N}_{s}}{P}_{i}^{t}{B}_{im}{P}_{m}^{t}+\sum_{i=0}^{{N}_{h}+{N}_{s}}{B}_{oi}{P}_{i}^{t}+{B}_{00} MW$$

(11)

where, ${B}_{00}$, ${B}_{im}$ and ${B}_{oi}$ are referring the coefficients of the transmission losses.

Moreover, the contribution of both renewable resources is relatively low compared to the hydro and thermal units. So, the defected power is contributed from the thermal units, which have been added and considered in objective, the expression is as follows:

$${k}_{L} {\left(\sum {P}_{G}^{t}-\sum {P}_{Dm}^{t}-{P}_{L}^{t}\right)}^{2}$$

(12)

where, ${k}_{L}$ is the penalty factor.

Network hydraulic constraints

It contains the equilibrium equation of water of the individual hydro plant associated to the bounds included initial, water discharge rates and contingent on the terminal reservoir volume storage. These bounds are decided by the limitations of the plant, state of physical reservoirs and associated to the multi-purpose predictability of the hydro systems.

Hydro reservoir network continuity equation

$$V_{hm}^{t} = V_{hm}^{t - 1} + I_{hm}^{t} - Q_{hm}^{t} - S_{Hm}^{t} + \mathop \sum \limits_{l = 1}^{{R_{um} }} \left( {Q_{hl}^{{t - d_{im} }} + S_{hl}^{{t - d_{im} }} } \right) ,j \in N_{h} , t \in T$$

(13)

where, ${Q}_{hm}^{t}$, ${S}_{hm}^{t}$, ${I}_{hm}^{t}$ and ${V}_{hm}^{t}$ are referring to the water discharge, spillage, water inflow and reservoir volume of the ${m}^{th}$ plant at time $t$, while ${R}_{um}$ represents the upstream hydro units overhead the reservoir.

Terminal and initial reservoir water discharge rate and volume storage limits

$${V}_{hm}^{min}\le {V}_{hm}^{t}\le {V}_{hm}^{max} ,j\in {N}_{h}, t\in T$$

(14)

$${Q}_{hm}^{min}\le {Q}_{hm}^{t}\le {Q}_{hm}^{max} ,j\in {N}_{h}, t\in T$$

(15)

where, ${Q}_{hm}^{max}$, ${V}_{hm}^{max}$ and ${Q}_{hm}^{min}$, ${V}_{hm}^{min}$ are referring to the water discharge and reservoir storage maximum and minimum rate and volume of the ${m}^{th}$ hydro plant.

Power generation constraints

Individual production unit has its own maximum and the minimum power output limits. The related representation is considered as follows:

$${P}_{hm}^{min}\le {P}_{hm}^{t}\le {P}_{hm}^{max} ,j\in {N}_{h} , t\in T$$

(16)

$${P}_{si}^{min}\le {P}_{si}^{t}\le {P}_{si}^{max} ,j\in {N}_{s} , t\in T$$

(17)

$${P}_{wsch,j}^{min}\le {P}_{wsch,j}^{t}\le {P}_{wsch,j}^{max} ,j\in {N}_{w} , t\in T$$

(18)

$${P}_{psch,k}^{min}\le {P}_{psch,k}^{t}\le {P}_{psch,k}^{max} ,j\in {N}_{pv} , t\in T$$

(19)

where, the Eqs. (16–19) referred to the maximum and the minimum limits of the hydro, thermal, wind and solar PV units.

Modeling the uncertainties

The modeling of uncertainties such as time-varying uncertain load demand, windspeed and solar irradiance are presented in this section. The monte-Carlo simulation (MCS) is used in this research work to create the set of scenarios for these uncertainties³². The MCS frequency is set to 800 and applied the reduction-based approach (RBA) to create the set of scenarios for these uncertainties. The number of desired scenarios is taken around 20, while their distribution of time-varying load demand, solar irradiance and windspeed with their means and standard deviation illustrations are presented in Figs.1,2,3

Fig. 2

The distribution of the uncertain time-varying load demand during the day ahead, (a) Boxplot distribution of time-varying load over time, (b) Distribution of loading over the generated scenarios, (c) Mean and standard response of loading (%)The distribution of uncertain time-varying load demand with mean and the standard values attained for the day-head interval are demonstrated in Figure.

Fig. 3

The distribution, mean and standard response uncertain of windspeed during the day ahead, (a) Boxplot distribution of windspeed over time, (b) Distribution of windspeed over the generated scenarios, (c)Mean and standard response of windspeed (m/sec).

Uncertain time-varying load demand

The normal probability density function (PDF) is used to model the time-varying uncertain load demand^33,34,35, the related mathematical formulation is given as follow³⁶:

$$f\left( {S_{L} } \right) = \frac{1}{{\sqrt {2\pi \sigma_{L} } }}\exp \left[ { - \frac{{\left( {S_{L} {-} \omega_{L} } \right)^{2} }}{{2\tau_{L}^{2} }}} \right]$$

(20)

where, ${\tau }_{L}$ and ${\omega }_{L}$ are referred to the mean and the standard deviation value.

Wind speed uncertainty modeling

The Weibull PDF is using for modelling the uncertainty in windspeed, the related expression is given as follows ³⁶:

$$f_{v} \left( v \right) = \left( {\frac{\beta shape}{{\alpha \_scale}}} \right) \times \left( {\frac{v}{\alpha \_scale}} \right)^{{\left( {\beta shape - 1} \right)}} \times e^{{ - \left( {{\raise0.7ex\hbox{$v$} \!\mathord{\left/ {\vphantom {v {\alpha \_scale}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\alpha \_scale}$}}} \right)^{\beta shape} }} for 0 < v < \infty$$

(21)

where, $\alpha \_scale$ and $\beta shape$ are the Weibull scale and the shape factors, the values of both factors are considered to 15 and 1.5³⁰, respectively. The mean is expressed as follows:

$${M}_{wbl}=\alpha \_scale\times\Gamma \times \left(1+{\beta shape}^{-1}\right)$$

(22)

where, $\Gamma$ is referred to the gamma function, which is formulated as follows:

$$\Gamma \left(x\right)={\int }_{0}^{\infty }{e}^{-t}{t}^{x-1}{d}_{t}$$

(23)

The distribution of the uncertain windspeed with mean and the standard values attained for the day-head interval are demonstrated in Fig. 3. The wind turbine output is calculated by using the following equation³⁷.

$${P}_{ws,j}^{t}=\left\{\begin{array}{c}0 for {v}_{w}^{t}<{v}_{cutin, } {v}_{w}^{t}>{v}_{\begin{array}{c}cutout\\ , \end{array}}\\ {P}_{wr,j}\times \left(\frac{{v}_{w}^{t}-{v}_{cutin}}{{v}_{rated}-{v}_{cutout}}\right) for {v}_{cutin}\le {v}_{w}^{t}\le {v}_{rated}\\ {P}_{wr,j} for {v}_{rated}\le {v}_{w}^{t}\le {v}_{cutout}\end{array}\right.$$

(24)

where, ${P}_{ws,j}^{t}$ and ${P}_{wr,j}$ are the output and the rated power of the ${j}^{th}$ turbine, while ${v}_{rated}$, ${v}_{cutout}$ and ${v}_{cutin}$ are the rated, cut-out and cut-in windspeeds with values 11, 25 and 4 m/sec, respectively.

The rated power for the wind unit is considered in this work is taken 175 $MW$. In cut-out and cut-in regions, the output of the wind turbine is equal to zero, while the maximum output can get in between those regions. Therefore, the probabilities among these regions are expressed as follow³¹:

$$\begin{array}{c}{f}_{\left({P}_{wj}^{t}\right)}=1-exp\left[-{\left(\frac{{v}_{in, }}{c}\right)}^{j}\right]+exp\left[-{\left(\frac{{v}_{out,}}{c}\right)}^{j}\right] \, {\text{f}}{\text{o}}{\text{r}} \, \left({P}_{wj}^{t}=0\right),\\ {f}_{\left({P}_{wj}^{t}\right)}=exp\left[-{\left(\frac{{v}_{r }}{c}\right)}^{j}\right]-exp\left[-{\left(\frac{{v}_{out }}{c}\right)}^{j}\right] \, {\text{f}}{\text{o}}{\text{r}} \, \left({P}_{wj}^{t}={P}_{wrj}^{t}\right).\end{array}$$

(25)

For continuous region, the probability of the wind unit is expressed as follows:

$$\begin{array}{c}{f}_{\left({P}_{wj}^{t}\right)}=\frac{j\left({v}_{r}-{v}_{in}\right)}{{c}^{k}*{P}_{wj}^{t}}{\left[{v}_{in}+\frac{{P}_{wj}^{t}}{{P}_{wrj}^{t}}\left({v}_{r}-{v}_{in}\right)\right]}^{j-1}\\ exp-\left(\frac{{v}_{in}+\frac{{P}_{wj}^{t}}{{P}_{wrj}^{t}}\left({v}_{r}-{v}_{in}\right)}{c}\right)\end{array}$$

(26)

Solar irradiance uncertainty modeling

The lognormal PDF is used here to model the uncertainty in solar irradiance, the mean and the standard deviation probability is formulated as follows:

$${f}_{photo\_voltaic}(G)=\frac{1}{G\sigma \sqrt{2\pi }}\text{exp}\left[\frac{-\left(\text{ln}x-{\mu }^{2}\right)}{2{\sigma }^{2}}\right]\text{ for }G>0$$

(27)

where, the mean and the standard deviation are taken 6 and 0.6, while for mean calculation the related expression is used:

$${M}_{Lgn}=\text{exp}\left(\mu +\frac{{\sigma }^{2}}{2}\right)$$

(28)

The output power from the solar PV is taken by using the following formulation:

$${P}_{psk}^{t}=\left\{\begin{array}{c}{P}_{rtd\_pwr}\times \left(\frac{{G}^{2}}{{G}_{std\_env}\times {R}_{Certain\_ir}}\right) for 0< G<{R}_{Certain\_ir}\\ {P}_{sr}\times \left(\frac{G}{{G}_{std\_env}}\right) for G>{R}_{Certain\_ir}\end{array}\right.$$

(29)

where, ${P}_{rtd\_pwr}$, ${G}_{std\_env}$ and ${R}_{Certain\_ir}$ are the rated power of solar PV taken as 100 $MW$, standard environment set to $1000 W/{m}^{2}$ and certain irradiance set to $120 W/{m}^{2}$ ²⁷, respectively.

The distribution of uncertain solar irradiance with mean and the standard values attained for the day-head interval are demonstrated in Fig. 4.

Fig. 4

The distribution, mean and standard response uncertain of solar irradiance during the day ahead, (a) Boxplot distribution of solar irradiance over time, (b) Distribution of solar irradiance over generated scenarios, (c) Mean and standard response of solar irradiance (W/m²).

Methodology

In this section, the novel strategy applied to traditional quadratic interpolation optimizer (QIO) optimizer to overcome the stagnation complications and improve the overall strength of the optimizer. To better understand the flow of study, this section is further divided into two sections, first part is to discuss the traditional QIO and second part is to discuss the different improvement strategies applied to the QIO to improve its exploration and exploitation abilities.

Quadratic interpolation optimizer

This quadratic interpolation optimizer is a math-based inspired meta-heuristic technique which is commonly used for the curve apt and mostly utilize for unary functions to find the minimum solution inside a definite interval³⁸. Quadratic interpolation is extensively used to approximate the minimum function. The QIO exploration and the exploitation phases details are given in the below sub-sections.

Exploration phase

In the exploration phase, the $QIO$ uses the generalized quadratic interpolation ($GQI$)³⁸ approach to indicate the promising regions during searching different regions, this approach can improve the exploration ability of the optimizer to improve the solution. In this approach, chosen of two individuals randomly in $GQI$ are jointly employed among the current individual and the population, so the minimizer of interpolation function shaped by the three positions. This third position is selected from the current population to create the new solution, which increases the overall diversity of the population. The related formulation is given as follows:

$${v}_{i}\left(t+1\right)={x}_{i,r1,r2}^{*}\left(t\right)+{w}_{1}\times \left({x}_{r3}\left(t\right)-{x}_{i,r1,r2}^{*}\left(t\right)\right)+round\left(0.5\times \left(0.05+{r}_{1}\right)\right)\times log\frac{{r}_{2}}{{r}_{3}}$$

(30)

$$x_{i,r1,r2}^{*} \left( t \right) = GQI \times (x_{i} \left( t \right),x_{r1} \left( t \right), x_{r2} \left( t \right), fit\left( {x_{i} \left( t \right)} \right), fit\left( {x_{r1} \left( t \right)} \right), fit\left( {x_{r2} \left( t \right)} \right))$$

(31)

here,$fit\left(.\right)$ refers to the fitness function, ${x}_{r1}$, ${x}_{r2}$ and ${x}_{r3}$ are the random positions of the different selected individuals from the current position, ${r}_{1}$, ${r}_{2}$ and ${r}_{3}$ are the random number values between 0 to 1, while $GQI\times ({x}_{i}\left(t\right),{x}_{r1}\left(t\right), {x}_{r2}\left(t\right), fit\left({x}_{i}\left(t\right)\right), fit\left({x}_{r1}\left(t\right)\right), fit\left({x}_{r2}\left(t\right)\right))$ indicates the $GQI$ function which uses the optimizer during functioning to obtain the minimizer of interpolation function (${x}_{i}$, $fit\left({x}_{i}\right)$), (${x}_{r2},fit\left({x}_{r2}\right)$) and (${x}_{r3},fit\left({x}_{r3}\right)$), respectively. The $QIO$ using a important parameter ${w}_{1}$ named exploration weight which depends on adaptive $b$ coefficient, which provides the balancing among the exploration to exploitation phase. The related formulation is given as follows:

$${w}_{1}=3\times {n}_{1}\times b$$

(32)

$$b=0.7\times a+0.15\times a\times \left(cos\left(\frac{5\times \theta \times t}{Tmax}\right)+1\right)$$

(33)

$$a= cos\left(\frac{\theta \times t}{2\times Tmax}\right)$$

(34)

here, ${n}_{1}$ refers to the normal distribution, $Tmax$ is the maximum number of iterations while $t$ indicates the number of iterations. In the intial process of iteration, the $b$ coefficient value increases gradually and ensuring a smooth change from exploration to exploitation phase.

Exploitation phase

During the exploitation phase of $QIO$, two selected individuals from the best and the current population are employed in $GQI$ to create the finest solution. It is auspicious for the optimizer to obtain the finest solution in the area nearby the minimizer. Thus, $QIO$ achieves the exploitation level, the current individual position is updated as:

$$v_{i} \left( {t + 1} \right) = x_{bst,r1,r2}^{*} \left( t \right) + w_{2} \times \left( {\begin{array}{*{20}c} {x_{bst} \left( t \right) - } \\ {round(1 + rand} \\ \end{array} } \right) \times \frac{{Upper_{b} - Lower_{b} }}{{Upper^{rD} - Lower^{rD} }} \times x_{i}^{rD} \left( t \right))$$

(35)

$$x_{bst,r1,r2}^{*} \left( t \right) = GQI \times (x_{bst} \left( t \right),x_{r1} \left( t \right), x_{r2} \left( t \right),fit\left( {x_{bst} \left( t \right)} \right), fit\left( {x_{r1} \left( t \right)} \right), fit\left( {x_{r2} \left( t \right)} \right))$$

(36)

$${w}_{2}= 3\times \left(1-\frac{t-1}{Tmax}\right)\times {n}_{2}$$

(37)

here, ${n}_{2}$ refers to the normal standard distribution, ${Upper}^{rD}$ and ${Lower}^{rD}$ are the upper and the lower bounds at the ${rD}^{th}$ dimesion, $rD$ is the random integer $1 to dim$, while ${w}_{2}$ is the weight exploitation factor. ${x}_{bst}$ is the best position, ${x}_{r1}$ and ${x}_{r2}$ are the randomly selected individuals employed in $GQI$ approach for creating minimizer ${x}_{bst,r1,r2}^{*}$, which is usually finest than the three individuals. The ${i}^{th}$ individual position is the updated by the following equation.

$${\text{x}}_{\text{i}}\left(\text{t}+1\right)= \left\{\begin{array}{c}{\text{x}}_{\text{i}}\left(\text{t}\right) fit\left({\text{x}}_{\text{i}}\left(\text{t}\right)\right)\le fit\left({\text{v}}_{\text{i}}\left(\text{t}+1\right)\right)\\ {\text{v}}_{\text{i}}\left(\text{t}+1\right) fit\left({\text{x}}_{\text{i}}\left(\text{t}\right)\right)>fit\left({\text{v}}_{\text{i}}\left(\text{t}+1\right)\right)\end{array}\right.$$

(38)

If the obtained candidate solution is observed better than the current solution, so the ${i}^{th}$ position will be replaced by using Eq. 36.

Modified quadratic interpolation optimizer

In this section, the traditional QIO is improved via Weibull flights motion, chaotic mutation and PDO mechanisms. The purpose of these modifications in QIO to enhance the exploration and exploitation abilities of the QIO to attain the global solution.

QIO with Weibull flight operator

In this step, QIO is modified via Weibull flight operator and the approach is effectively improved the performance of the other recent optimizers reported in^39,40,41. The cumulative Weibull flight is based on the two factors such as shape and scale, formulated as follows:

$$f\left( x \right) = \left( {\frac{shape}{{scale}}} \right) \times \left( \frac{x}{scale} \right)^{{\left( {v - 1} \right)}} \times e^{{ - \left( {{\raise0.7ex\hbox{$x$} \!\mathord{\left/ {\vphantom {x {sclae}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${sclae}$}}} \right)^{shape} }} for x \ge 0$$

(39)

These two factors can be attained from Weibull distribution considering the short and wide step movement. The wide step can be obtained as follows:

$$\text{Step}=wblrnd(\text{1,1},[1,D])\times sign(rand\left(1,D\right)-0.5)$$

(40)

where, $wblrnd$ is the randomly generated number from Weibull distribution while $sign$ gives the values from -1 to 1. The short step movement can be formulated as:

$$Step= \left\{\begin{array}{c}wblrnd\left(\text{0.5,1},\left[1,D\right]\right)\times 0.5\times sign\left(rand\left(1,D\right)-0.5\right)\\ \times norm\left({x}_{bst}-{x}_{i}\right), if {x}_{bst}\ne {x}_{i}\\ wblrnd\left(\text{0.5,1},\left[1,D\right]\right)\times 0.1\times sign\left(rand\left(1,D\right)-0.5\right), else\end{array}\right.$$

(41)

So, the new created populations’ location can be expressed as follows:

$${x}_{new,i}{=x}_{new,i}+Step$$

(42)

QIO with chaotic mutation using logistic map

In this step, QIO is modified with the chaotic mutation strategy^39,42 to enhance the strength of the traditional QIO optimizer. It is based on initializing the locations of the QIO population using the logistic map of chaotic for initial population diversity improvements by using the following expressions.

$$\xi^{\prime} = \mu \zeta \left( {1 - \xi } \right)$$

(43)

$$x_{i} \left( {t + 1} \right) = x_{i} \left( t \right) + \xi^{\prime} \times \left( {U_{b} - L_{b} } \right)$$

(44)

where, $\xi^{\prime}$ refers to the values of chaotic logistic map around$\xi^{\prime} \ne \left\{ {0.0, 0.25, 0.75, 0.5, 1.0} \right\}$, $\xi$ is a random factor values between $0\le \xi \le 1$, while $\mu$ is the constant factor and its value is selected to 4.

Exploitation based on prairie dog optimization (PDO) boosting mechanism

In this step, the conceptualized exploitation mechanism is taken based on Prairie dogs^43,44,45. In this mechanism, the communication among these dogs via producing the special sound in case of getting predators or food, which is formulated as follows:

$$\overrightarrow{{x}_{i}}\left(iter+1\right)=\overrightarrow{{x}_{bst}}-\overrightarrow{eC{x}_{bst}} \times \varepsilon -\overrightarrow{CPD}\times rand$$

(45)

$$\overrightarrow{CPD}=\frac{\overrightarrow{{x}_{bst}}-r\overrightarrow{{x}_{i}}}{\overrightarrow{{x}_{bst}}+\Delta }$$

(46)

$$\overrightarrow{eC{x}_{bst}}=\overrightarrow{{x}_{bst}}\times \Delta +\frac{\overrightarrow{{x}_{i}}\times mean\left(x\right)}{\overrightarrow{{x}_{bst}}\times \left({U}_{b}-{L}_{b}\right)+\Delta }$$

(47)

The flowchart of proposed improved IQIO used to solve the stochastic STHS problem considering time-varying load, windspeed and solar PV is given in Figs. 1 and 5. It should be highlighted here that the improved quadratic interpolation optimizer has high searching ability with high capability of exploitation and exploration mechanisms due to three integrated improvement strategies including the Weibull flight, chaotic mutation and PDO strategy. Hence, the proposed method can be applied for solving the high nonlinear optimization problems like stochastic short-term hydrothermal scheduling.

Fig. 5

The proposed improved IQIO to solve the stochastic STHS problem with solar PV and wind.

The simulation results and analysis

In this section, the proposed improved quadratic interpolation optimization (IQIO) algorithm is used to solve the STHS problem considering the uncertain time-varying load demand without and with installation of PV and wind turbine units to lessen the cost. The simulations are executed on PC core i9-13900H CPU @2.60 GHz 32 GB RAM on MATLAB software version R2023a. Moreover, to authenticate the efficacy of the IQIO and other well-known traditional optimizers are via statistical and nonparametric analysis such as Wilcoxon and Friedman using CEC2022 benchmark functions. For fair comparison, the selection parameters of the different optimizers are taken from Table 1, where the maximum number of iterations, number of runs and search agents are considered same during the execution of simulation.

Table 1 Selection parameters for different considered algorithms.

Application of the improved IQIO tested via CEC 2022 functions

In this section, to authenticate the effectiveness of the proposed IQIO optimizer is tested via CEC2022 functions. The details and discussions related to the statistical analysis, the convergence and the boxplot responses, and the nonparametric analysis such as Friedman and Wilcoxon are provided are in the following sub-sections.

Statistical analysis

The statistical analysis outcomes among proposed IQIO and other well-known optimizers such as SCSO, JSO, ZOA, DBO, EEFO and traditional QIO are conducted via CEC2022 standard benchmark function and their outcomes are tabulated in Table 2, with the average, the worst, the best, the standard deviation and the execution time response. By jugging Table 2, the IQIO gives its finest value with efficient mean response in functions CEC01. In function G2, the IQIO observed with the finest response but mean response is slight inferior to the traditional QIO, but superior to the other techniques. In functions G3, G4 and G5, the stable response attained by the IQIO with observed the finest mean and best response values to attain the solution. In function G6, the IQIO observed minor inferior to QIO but superior to other traditional optimizers. In function CEC07, the IQIO is superior but observed inferior in function CEC08. In functions CEC09 to CEC12, the stable response with the finest mean values attained by proposed IQIO. The statistical results indicated that the proposed IQIO has an efficient response to obtain the global solution by attaining the finest mean response. As we have seen that the higher execution time are taken by the IQIO mostly in the entire functions of CEC2022, it may due to the little higher complexity of the Weibull flight operator, chaotic mutation and PDO approaches but the overall response of the IQIO is observed still good and showed its superiority towards attaining the global solution.

Table 2 Statistical outcomes of IQIO and other well-known traditional optimizers tested via CEC2022 benchmark functions.

Convergence analysis

The convergence curve response getting by CEC2022 functions via proposed IQIO and other well-known optimizers are illustrated in Fig. 6. By observing the convergence behavior illustrated in Fig. 6, the best convergence response is attained by the proposed improved IQIO almost observed in the entire functions’ of CEC2022. The IQIO has observed the stable and fast convergence response to obtain the optimal solution.

Fig. 6

Convergence curves of the proposed IQIO and other optimizers tested via CEC2022.

Boxplot analysis

The representation of the boxplot analysis is demonstrated in Fig. 7, for the entire CEC2022 functions, which provides the proper illustration of the capriciousness ethics in dataset with detail such as median, upper and lower quartiles, outliers in dataset as well as minimum and the maximum values. In majority of CEC2022 functions, the response of the proposed IQIO has observed lean compare to the other well-known optimizer, which indicated towards the optimal response attained by the IQIO in entire functions.

Fig.7

Boxplot response of the proposed IQIO and other optimizers tested via CEC2022.

Non-parametric statistical analysis via Wilcoxon ranking test

In this sub-section, the non-parametric analysis is conducted via Wilcoxon ranking test for intricate distribution. The obtained ranking test P-values are tabulated in Table 2, and significantly compare their response with the efficient IQIO among other optimization standards. To verify the effectiveness of the IQIO, the Wilcoxon ranking test employed on CEC2022 benchmark functions. The level of significance is 5%, if the values are less than this value, so there will be the significance different among the optimizers. By observing the p-value response tabulated in Table 2, in the most of the CEC2022 is observed below 5% and few are more than it. The overall non-parametric test indicated the response of IQIO is generally obtained the optimal response compare to the other well-known optimizers.

Friedman’s test conducted via CEC2022 functions

To authenticate the efficacy of the proposed IQIO is verified via non-parametric test named Friedman mean rank test. This test analyzes the mean response of the entire optimizers to compare on each dataset to attain the significant difference among the optimizers. The mean response of the different optimizers is demonstrated in Fig. 8, where the results clear indicated that the finest mean value is attained by the IQIO variant during the test conducted on CEC2022 standard functions.

Fig. 8

Friedman’s response of different optimizers including proposed IQIO tested via CEC2022.

The overall result indicated that the best mean response attained by the IQIO, while the worst mean response is attained by the SCSO with the high mean value.

Stochastic STHS problem solution without and with uncertainties of RERs considering VPLE and transmission losses

In this section, the two different cases are considered to solve the STHS problem with uncertain time-varying load demand without and with presence of wind and solar uncertainties to lessen the fuel cost ($). In both cases, the VPLE and the transmission losses have been considered, while resolving the stochastic STHS problem. The related details of such cases are given in to the further sub-sections. The expected values of the solar irradiance (W/m²) and the wind speed (m/sec) are demonstrated in the Fig. 9a,b while the uncertain load demand for day a head is given in Tables 4b and 6b, respectively. It should be highlighted here that the prime objective is to reduce total cost, while the emission is not considered as objective function, but it is calculated only for all studied cases to assess the environmental effects only.

Fig. 9

The expected values of the wind speed and the solar irradiance (a) The expected solar irradiance, (b) The expected windspeed.

CASE I: STHS with uncertain load without RERs considering power losses and VPLE

In CASE I, contains 4 hydro plants optimize with 3 thermal plants considering the uncertain load to lessen the cost. The details of the price coefficients, uncertain load demand and the thermal generation capacities as well as the generation power coefficients are taken from ^27,49. The simulations are executed for this case, the related parameters are taken from Table 1. The simulations statistical outcomes such as the best, the average, the worst, the standard deviation the execution time as well as the significance p-values for this case are tabulated in Table 3. By observing Table 3, the optimal and the average response is attained by the proposed IQIO attained with the value around 41,829.58$ and 43,108.57$, while the worst cost 48,801.79$ is obtained by the SCSO optimizer, respectively.

Table 3 Statistical results for CASE 1 to solve the STHS problem without uncertainty of wind and Solar PV.

The boxplot and the convergence response of the different optimizers are illustrated in Fig. 10a,b where the fast and optimal response achieve by the proposed IQIO compared to the other mentioned optimizers. By judging from Table 3, the proposed IQIO is observed well and less reported to the other optimizers such as SCSO 14.2869, JSO 6.4979%, ZOA 14.2914%, DBO 7.5913%, EEFO 5.8557% and traditional QIO 1.3025%, respectively. The emissions are reported for this case attained around 2.3227e + 04. Moreover, to prove the effectiveness of the proposed IQIO is further compared with other state-of-the-art techniques, where the proposed IQIO is observed superior to others techniques provided in Table 4.

Fig. 10

Boxplot, convergence response reservoir volume for hydro plants, generated power response, and mismatch power response for CASE I without considering RERs (a) Boxplot response for objective to minimize fuel cost, (b) Convergence response for objective to minimize fuel cost (c) Reservoir Storage Volume for Hydro Plants VPLE with power losses ,(d) Generated Power Response of 4H + 3 T VPLE with Plosses, (e) Mismatching of Power.

Table 4 Comparisons of state-of-the-arts techniques for reduction of fuel cost ($) for Case I.

Figures 10c,d are demonstrated the hourly response of the reservoir storage volume for hydro plants and the generated power of hydrothermal units. While, Fig. 10(e) is demonstrated the mismatching of powers generated from hydrothermal units about 24-h time interval. Moreover, the water discharge rate, the response of hydrothermal power units is tabulated in Table 5, while rest of optimal outcomes such as thermal power units, uncertain load demand with losses and the overall emission for this case are tabulated in Table 6.

Table 5 The optimal values of water discharge rate and hydro power units for Case I.

Table 6 The optimal values of thermal power units, emissions, the uncertain time-varying load considering VPLE with transmission losses for Case I.

The overall results indicated towards the efficient response of the proposed IQIO optimizer to solve the STHS problem considering uncertain load, where the entire bounds are observed within their pre-define bounds.

CASE II: STHS with uncertainty of load demand and RERs considering power losses and VPLE

The CASE II contains 4 hydro and 3 thermal plants by inclusion of PV and wind turbine units considering the uncertain time-varying load demand with VPLE and power losses. The uncertainty of these RERs resources are considered in this approach, where the direct, the penalty and the reverse costs are also taken into the account ³¹. The Weibull and lognormal distribution functions are used to modeled the uncertainty of windspeed and solar irradiance while for time-varying response the normal PDF is used in this research. The rated capacity of the wind and the solar powers are taken around $100 MW$ and $175 MW$, respectively. The penalty and the reverse costs for the wind and the solar PV are chosen to 3 and 1.5. In addition, the scale and the shape parameters for wind powers are selected to 15 and 1.5, while mean and the standard parameters for PV are chosen to 6 and 0.6, respectively.

The simulations are executed by using the proposed IQIO and other well-known traditional optimizers to solve the STHS problem and minimize the fuel cost by considering solar and wind power. The statistical outcomes such as the average, the best solution, the worst solution, the standard deviation, the execution time as well as the significance p-values for this case are tabulated in Table 7. By jugging Table 7, the optimal and mean response is obtained by the proposed IQIO with the values around 31,904.15$ and 33,083.00$, while the worst mean and worst response attained by the ZOA optimizer with the values of around 36,747.44$ and 39,705.33$, respectively.

Table 7 Statistical results for CASE II to solve the STHS problem with uncertainty of wind and Solar PV.

The boxplot and the convergence response of the different optimizers are illustrated in Fig. 11a,b where the fast and efficient response attained by the proposed IQIO optimizer. By judging from Table 7, the proposed IQIO is observed well and less reported to the other optimizers such as SCSO 5.53%, JSO 11.30%, ZOA 13.18%, DBO 11.03%, EEFO 5.55% and traditional QIO 1.94%, respectively. The emissions are reported for this case attained around 2.3227e + 04, respectively. So, by comparing the case without considering RERs (wind and solar PV), the overall fuel cost is reduced to 23.73%, which seems the huge saving via obtained by integration of RER into the STHS problem. While, the emissions obtained in this case are observed around 1.2659e + 04 that is 45.50% reported less compared from the case without considering uncertainties.

Fig. 11

Boxplot, convergence response reservoir volume for hydro plants, generated power response, and mismatch power response for CASE II with RERs. (a) Boxplot response for objective to minimize fuel cost, (b) Convergence response for objective to minimize fuel cost, (c) Reservoir Storage Volume for Hydro Plants VPLE with power losses, (d) Generated Power Response of 4H + 3 T with Wind and Solar contribution, (e) Mismatching of powers.

Figures 11c,d are demonstrated the hourly response of the reservoir storage volume for hydro plants, generated power from hydrothermal with solar and wind power units. While, the Fig. 11(e), is demonstrated the mismatch of power generated from these resources during the 24-h time interval. Moreover, the water discharge rate, the response of hydrothermal power units, the uncertain time-varying load demand, inclusion of power losses, the underestimated and the estimated costs attained by the solar PV and wind powers are tabulated in Table 8 and 9. The overall results indicated towards the efficient response of the proposed IQIO to solve the STHS problem considering uncertain load, where entire bounds are within their pre-define bounds.

Table 8 The optimal values of water discharge rate and hydro power units for Case II.

Table 9 The optimal values of thermal power units, emissions, wind and PV related costs, the uncertain time-varying load considering VPLE with transmission losses for Case II.

By jugging the results provided in Table 9, the solar and wind power plants contributed their maximum power to the system, where the entire day-ahead generated power from these resources are observed 4804.75MW, that is around 26.84% contribution to the overall day-ahead power.

Conclusion and future prospects

In the work, the proposed improved quadratic interpolation optimization (IQIO) was successfully applied to solve the Short-Term Hydrothermal Scheduling (STHS) without and with optimal inclusion of Wind and PV to minimize the fuel cost and emission of the network. The proposed modification into the traditional QIO was applied based on Weibull flight motion, chaotic mutation, and PDO mechanisms, aimed to boost its exploration and exploitation capabilities. The effectiveness of the proposed IQIO optimizer is showcased through experiments conducted using the CEC 2022 test suite. During solution to stochastic STHS problem, the system uncertainties such as time-varying load, solar irradiance and wind speed have been considering. The optimal results attained by the proposed IQIO over to other state-of-the-art techniques and the related detail are listed below:

• The results demonstrate that optimal planning can lead to a significant reduction in fuel costs, achieving savings of approximately 23.73% along with a notable reduction in emissions by around 45.50%.

• The effectiveness of the proposed IQIO verified through statistical and non-parametric tests conducted via CEC 2022 test suite, where IQIO outperformed almost in entire functions.

For future prospective, the proposed IQIO holds promise for application in solving real-world engineering problems with ease. Furthermore, future iterations of the STHS problem could involve greater complexity and innovation by incorporating considerations such as Electric Vehicles (EVs) and storage systems.