Introduction

The reading man flap was first proposed in 2008 for the closure of circular skin defects by Mutaf et al.1. The design of the reading man flap consists of the angle of the quadrangular flap, the angle of the triangular flap and one central axis. The quadrangular flap and the triangular flap were designed in an unequal Z-plasty manner. The central axis of the unequal Z-plasty was a tangential line passing through the margin of the circular defect and perpendicular to the relaxed skin tension lines (RSTL). The angles and central axis combination suggested by Mutaf is 60o for the angle of the quadrangular flap, 45o for the angle of the triangular flap, with 1.5 times length of the diameter of the circular defects for the central axial length. Rhomboid flap, double opposing semicircular flaps and double rotation flaps were also used for the closure of circular skin defects. Compared with rhomboid flap in which tissue is borrowed from 1 direction, the reading man flap borrows tissue from 2 directions. Thus, it distributes tension and leads to lesser tissue distortion and displacement of the neighboring mobile anatomic landmarks. Techniques including double opposing semicircular flap and double rotation flaps, result in a considerably much longer scar than the reading man flap1.

The reading man flap has been widely used for closer of the circular skin defects of the face, trunk, and extremities2,3,4,5,6,7. Methods to optimize the angles and the central axis of the flap have been tried by the surgeons. Reconstruct malar and infraorbital circular defects was done using the transforming reading man flap by adopting measures, such as the angle of the quadrangular flap was set as 85°–90°, the angle of the triangular flap was set as 60°, and the length of the central axis was slightly shorter than the diameter of the defect2. Nagata reported 2 clinical cases in which intermediate-size plantar defects were reconstructed using the transforming reading man flap. The angle of the quadrangular flap was approximately 90°, and the angle of the triangular flap was 60°, the length of the central axis was designed to be 50% longer than the diameter of the circular defect3. Long-necked reading man flap was used to reconstruct the distal dorsal finger defect with the central axis extended to at least twice that of the defect, and two skin flaps were designed in a Z-plasty manner based on the size of the defect at the middle phalanx of the finger4. The large periorbital defects were also reconstructed using the transforming reading man flap with the angle of the quadrangular flap was 95°, the angle of the triangular flap was 55°, and the length of the central axis was designed to be 1–1.25 times the width of the primary defect5.

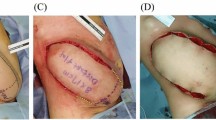
Tip necrosis appeared in few patients who underwent the surgery by using the reading man flap to repair the skin defect6,7. Redness, local small epidermal necrosis, and scab formation of the flap tip had been observed in the clinical practice (Figs. 1 and 2).

Fig. 1
figure 1

A 88-years-old male with squamous cell carcinoma of skin on back region is referred to our Hospital. (a) Preoperative appearance of the tumor. (b) The tumor was removed, and the reading man flap was designed. (c) Appearance immediately after surgery. (d) Appearance 12 days postoperatively.

Full size image
Fig. 2
figure 2

A 20-years-old male with dermatofibrosarcoma protuberans of the right shoulder is referred to our Hospital. (a) Before extended tumor resection. (b) After extended tumor resection, and the reading man flap was designed. (c) Appearance immediately after surgery. (d) Appearance 18 days postoperatively.

Full size image

Stress tends to be a key factor in the wound healing and scarring processes following reconstructive surgery. Acutely, local stress concentrations may cause vascular insufficiency and localized flap necrosis. Chronically, local stress concentrations may induce excessive wound tension resulting in dehiscence and/or hypertrophic scarring8,9,10,11,12.

Finite element method (FEM) has been widely adopted to solve the complex problem encountered in clinical practice by discretizing the complex environment into several elements. Optimized design for rhombic transposition flaps and flap suture and release state of A-T flap in surgery processes were performed by FEM13,14. Gaussian process (GP) surrogate models of local cutaneous flaps can be created based on the FEM to predict stress and strain for arbitrary material parameters15. A 3D wound flattening method for mapping skin mechanical properties based on finite element method was proposed16. A computational modelling framework is developed to test that continuous delivery of a specified level of negative pressure to the wound bed is important for promoting surgical wound healing17. The distortional strain energy can be symbolized by the Von Mises Stress, so it is often used in the analysis of soft tissue by researchers, and a common basis of comparison can be provided for other researchers.

Total of 8 cases based on the different angles and central axis lengths combination of the reading man flap were studied by FEM with the purpose of reducing the stress of the flap tip. Due to the mechanical properties of skin vary considerably, depending on many factors such as age and position of the body18,19,20, so different sets of material constants were studied and compared.

Methods

Ethics approval was obtained from the Institutional Review Board (No. M2024104) of Peking University Third Hospital with a wavier of informed consent. The methods of the study were conducted in accordance with relevant guidelines and regulations.

Finite element model of the reading man flap

In this paper, ANSYS software was used to create a 30 cm*30 cm*0.6 cm finite element model of the reading man flap. The element’s type used for the skin flap was solid185, defined by 8 nodes, with each node having 3 translational degrees of freedom along the x-y-z directions. This element possesses hyperelasticity, large deformation, and high strain capabilities. The element is of good applicability to simulate the stress and strain changes inside the skin after the flap transfer, providing a relatively realistic representation of the stress and strain changes before and after the transfer of the skin flap.

Geometric model of the reading man flap

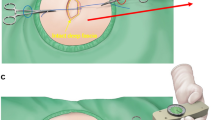
The typical preoperative marking and suturing of a reading man flap were displayed in Fig. 1 (b ~ c) and Fig. 2 (b ~ c), respectively, and the corresponding geometric reading man flap model was established as shown in Fig. 3. The brown circle showed the skin defects after the tumor incision. The diameter of the skin defects was D.

The reading man flap was consisted of one quadrangular flap(b-c-f-e), one triangular flap(b-c-a) and one central axis(bc). The central axis was a tangential line passing through the margin of the circular defect, perpendicular to the relaxed skin tension lines (RSTL). The length of the central axis was L. The length of ab, bc and cf. was same. The angle of the quadrangular flap was α, and the angle of the triangular flap was β, just as shown in Fig. 3.

After flap elevation, the quadrangular flap was subjected to forces in two directions, including a clockwise rotational force and an upward thrusting force. The triangular flap was subjected to forces along counterclockwise direction. Therefore, the quadrangular flap was moved to the defect area and the triangular flap was transposed to cover the quadrangular flap’s donor site.

Fig. 3
figure 3

Geometric model of the reading man flap.

Full size image

Material modeling

Young’s modulus and Poisson’s ratio of material parameters are key factors to the effectiveness and accuracy of the entire numerical simulation results. Poisson’s ratio and Young’s modulus of the skin were determined based on previous research. The values of Poisson’s ratio at the end of the hold for parallel and perpendicular stretching to relaxed skin tension lines (RSTL) were 1.92 ± 0.23 and 0.49 ± 0.062, respectively21. When planning the reading man flap, the central axis of the unequal Z-plasty was a tangential line passing through the margin of the circular defect and perpendicular to the relaxed skin tension lines (RSTL). The Poisson’s ratio of the flap was 0.49 when the finite element model of the flap is established. The Young’s modulus of human skin is varied between 1.09 kPa to 83.3 MPa at different positions, and they are extracted using different experimental methods such as suction, indentation, tension, and noninvasive ones18,22,23,24,25. The Young’s modulus of forearm of young people and elderly people, as well as forehead of young people were obtained by experimental methods of suction26,27. It provides more effective and reliable data for observing the stress distribution when using the reading man flap to repair skin defects at different ages and positions. The material properties were listed in Table 1.

Table 1 The material properties of the FE model26,27.
Full size table

Meshing and boundary conditions

On the basis of the above geometric model, mesh division was carried out. Firstly, the unit size was set. If the unit size was too large, simulation results may be distorted, and if the unit size was too small, simulation calculations may not converge. The demonstration of mesh independence is needed and a mesh convergence study was done, and the result was presented. The method is that, unit forces in three directions(X/Y/Z) at position C were applied and the stress levels at different grid sizes at the same distance from the loading point were analyzed, the result was just as shown in Fig. 4.

Fig. 4
figure 4

Stress levels at different grid sizes at the same distance under same load.

Full size image

It can be seen from Fig. 4, the internal force tends to converge as the element size decreases. Therefore, taking into account the above situation, this article would set the unit size to 8 mm; Secondly, set Mshkey to 0 to achieve free meshing, and set Mshape to 1 to achieve a triangular tetrahedral mesh structure. After grid partitioning, taking Condition 1 as an example, there were a total of 3585 nodes and 10,328 units, and there may be slight differences in the total number of points and units under different cases. Fixed constraints were used around the skin boundary, as well as all degrees of freedom of nodes on the constraint boundary. The finite element model of the reading man flap after mesh division was shown in Fig. 5 below.

Fig. 5
figure 5

The meshes of the reading man flap.

Full size image

Human skin is a soft material with nonlinear mechanical behavior that hardens with increasing external strain. The linear elastic material model based on average elastic modulus and Poisson’s ratio is often inaccurate. The use of hyperelastic material models such as Mooney Rivlin, Yeoh, Ogden, Veronda Westmann, and Martins models can accurately describe the nonlinear behavior of soft tissues28. At present, there is no experimental conditions available for the material characteristics of skin flaps, so the assumption of linear elastic modal is adopted. The results obtained from this calculation can provide some inspiration for similar research work. The limitation of the paper is the uncertainty of material property values. There is no doubt that there are significant differences in the characteristics of skin between individuals. The purpose of this article is to explore the conditions that may be encountered during reading man flap transfer, to obtain the optimal angles and central axis lengths combination with the purpose of reducing the stress of the flap tip, and the purpose can be achieved in a linear elastic modal. The tissue layer is considered to be linearly isotropic, orthotropic, nonlinear hyperelastic, or laterally anisotropic of most wound closure calculation models29.

Description of the reading man flap transfer

Numerical simulation analysis of the reading man flap transfer can be divided into the following steps which is shown in Fig. 6: (1) As the edge of the surrounding skin, the nodes on edges 1 and 4 side were fixed first. (2) The nodes on the side 6 were given a forced displacement, so that the nodes on the side 6 arrived at the corresponding position of the side 1 after the forced displacement. (3) The nodes on the side 3 were given a forced displacement, so that the nodes on the side 3 arrived at the corresponding position of the side 4 after the forced displacement. (4) The forced displacements were enforced to the nodes on the circumference of a circular wound perpendicular to a certain diameter, which was used as the axis of symmetry. (5) The nodes of the side 2 were given forced displacement so that the nodes of the side 2 were forced to move to the corresponding positions of the nodes of the side 5 after the forced displacement of the nodes of the side 2.

Fig. 6
figure 6

The numerical simulation analysis of the reading man flap transfer.

Full size image

Virtual experiment design

To obtain the optional angles and central axis lengths combination, and 8 cases in which α, β, and L were deemed as variables are established, just as shown in Tables 2 and 72 virtual experiments were conducted based on Tables 1 and 2. Stress concentration tended to appear at the flap tip which leading to dehiscence, skin necrosis, and hypertrophic scarring according to Clinical practice and literature references. The von Mises stresses at flap tip A, B, and C were extracted, just as shown in Fig. 7.

Fig. 7
figure 7

Stress extraction points of A, B and C at the flap tip.

Full size image
Table 2 Cases based on the two angles and the central axis.
Full size table

Results

Distribution of Von Mises stress

The distribution of von Mises stresses of the case 1 & young people forearm was shown in Fig. 8. The stress concentration positions displayed in the cloud map, matched with the actual stress concentration position of the flap in Fig. 1, and the effectiveness and reliability of the numerical simulation were proved. The model for characterizing the constitutive relationship of skin flap mechanical properties is one of the common models used in computational software, this model has been extensively validated by users of the software in civil engineering30,31,32.

Fig. 8
figure 8

The distribution of von Mises stresses of the case 1 & young people forearm.

Full size image

Statistical analysis of the stress at the tip of the reading man flap

The calculated von Mises stresses at the flap tip A, B, and C of 72 virtual experiments, just as shown in Fig. 9.

Fig. 9
figure 9

The von Mises stresses at the flap tip A, B, and C in different age.

Full size image

groups and different positions among 8 cases.

Statistical analysis of the above results data was carried out, where the minimum stress value among 8 cases for each material was set as the reference value and marked as “–“, values exceeding (0,5%] were marked as “1+”, values exceeding (5%,10%] were marked as “2+”, values exceeding (n*5%,(n + 1)*5%] were marked as (n + 1)+. Furthermore, the results with patterns in the range (–,2+] were marked as italics, results in the range (2+,10+) were marked as bolditalic, and results greater than or equal to 10 + were marked as bold. Finally, the stress variations in different age groups and different positions of different angles and central axis combinations were compared. Stresses comparison of the material parameters of the young forearm were statistically analyzed, and the statistical results were shown in Table 3.

Table 3 Statistical analysis of the stress at the tip of the reading man flap.
Full size table

The angles and central axis combination of the minimum stress of the flap tip was case 5(α = 60 °, β = 45 °, L = 2D) by comparing to the flap tips for each material. Since the material of the model was in the linear elastic stage within the deformation range, the analysis results obtained for different age groups and positions were consistent with the conclusions in Table 3.

The stress of the flap tip A was more sensitive to α & β than L. The stress of flap tip A increased significantly with the increase of α (note: case1 ~ case4, α is dependent variable, L is fixed value), the stress of flap tip A changed less with the increase of L(note: case1,case 5,case 6, L was dependent variable, α and β were fixed value). The result also could be drawn from case 4, case 7, case 8.

The averages and standard deviations of the stresses at the flap tips A, B, and C of 8 cases under different material parameters were obtained, just as shown in Table 4.

Table 4 The averages and standard deviations of the stresses under different material of 8 cases (unit: Pa).
Full size table

It can be seen from Table 4:

  1. (1)

    The average von Mises stress at the flap tip A of 8 cases was lower than that of B and C obviously. Therefore, higher risk of dehiscence, skin necrosis, and hypertrophic scarring may happen at the flap tip B and C belongs to the quadrangular flap.

  2. (2)

    The von Mises stresses at the flap tips of the elderly people forearm were higher than that of the young people forearm. Therefore, higher risk of complications may happen at the flap tips of the elderly people under the same design and position.

  3. (3)

    The von Mises stresses at the flap tips of the young people forehead were higher than that of the young people forearm under the same designed flap.

Discussion

The Young’s modulus of the forearm in the elderly people was greater than the forehead in young people, which was greater than the forearm in young people. Due to the same forced displacement given to each side of the flap in the model, the same strain was produced, so higher Young’s modulus with higher stress, just as shown in Eq. 1:

$$\sigma =e{\text{~~}}\xi {\text{,}}$$
(1)

Where σ was stress, ξ was strain and e was Young’s modulus.

Under the same designed flap, the von Mises stresses at the flap tips of the young people forehead were higher than that of the young people forearm. Therefore, higher risk of dehiscence and hypertrophic scarring may happen at the flap tips of the young people forehead. However, probability of skin necrosis of the young people forehead may be lower compared with the forearm due to the blood supply.

As we all known, more complicated situation needs to be faced in the actual clinical practice. For example, the hypertrophic scarring (position: flap tip B), dehiscence and skin necrosis (position: the suture of the upper edge of the quadrangular flap, the upper edge of the circular skin defect) generated at the quadrangular flap (just as shown in Fig. 2), that is because the wound occurs in the shoulder, and the stress distribution of the flap effected by the local bony bulge with activities of shoulder joint under the flap.

The numerical simulation analysis model established in this article was based on a relatively ideal model. However, the position of the suture line varied with surgeons when the circular defect was sutured actually. The choice of suture area between the flap tip C and the wound influenced by many factors, such as mechanical properties of the patient’s skin, the relationship between the donor site and the wound bed. Subsequently, the plane position of the flap tips B and C may change, but it will not affect the qualitative analysis conclusion that there are higher stresses at the flap tips B and C.

The stress distribution of the flap changed with the alteration of the suture way includes direction and position selection. Nevertheless the stress of the flap tip A was relatively fixed due to the relatively fixed suture way. Therefore, when the same designed flap was used to the same designed flap by different surgeons, the stress of the flap tips B and C may be different.

The suture of the flap can be conducted according to the result of the FE simulation, just because the best terminal position of the quadrangular flap can be obtained advance by FEM, and so the transferred quadrangular flap tip position can be marked referring to the result of the FE simulation.

Conclusion

The optimal angles and axis lengths combination with the purpose of reducing the stress of the flap tip is 60° for the angle of quadrangular flap, 45° for the angle of triangular flap, with 2 times length of the diameter of the circular defects for the central axial length. The quadrangular flap tip tends to be higher possibility of complications than the triangular flap tip. Stress of the triangular flap tip is more sensitive to the angles and axis length. Stress of the flap tip in elderly people is higher than that of the young with the same design and position, which leads to higher possibility of complications at the flap tip in elderly patients than young.