Predicting low ionospheric parameters and low frequency sky wave propagation strength using machine learning

Abstract

Studying the propagation prediction of low-frequency (LF) radio waves is very significant for supporting applications in fixed and mobile long-distance communication, remote navigation, and timing service. Therefore, to enhance the predicting accuracy of LF sky wave propagation, we proposed an improved method based on the machine learning method. Firstly, we employed a machine learning method to create a prediction model for the critical frequency of the low ionospheric E layer (f_oE), which significantly affects LF sky wave propagation. Secondly, we enhanced the method for predicting LF sky wave propagation based on the model of low ionospheric parameters. By comparing the measured data from East Asia and predicted data based on the wave-hop theory, the proposed method achieved a 6.16% improvement in LF sky wave field strength.

Introduction

The Low-frequency (LF) is defined as the frequency range between 30 kHz and 300 kHz. Thanks to their low signal attenuation, strong penetration ability, and resilience against both human-made and nuclear interference, LF radio waves are extensively utilized in navigation, control communications, and emergency command¹. LF radio waves propagate in two ways: ground waves and sky waves, and the latter can be reflected by the ionosphere, enabling long-distance propagation. In order to achieve an effective application and high-quality communication, LF radio wave propagation prediction has been a research hotspot in the past, remains so in the present, and will continue to be in the future.

In 1938, Booker extended the magneto-ionic theory² to address a series of issues related to the oblique incidence of LF sky waves on the ionosphere³. In 1962, Budden published Radio Waves in the Ionosphere, systematically providing the mathematical basis for the propagation of LF sky waves in the ionosphere⁴. Based on previous theories, Ferguson in 1985 proposed a model for the statistical treatment of the daytime ionosphere, which could be used for predicting LF sky wave propagation⁵. In 2003, Hayakawa’s research on LF propagation signals in the sub-ionosphere revealed earthquakes-related ionospheric disturbances⁶. Berenger in 2006 summarized the application of the Finite Difference Time Domain (FDTD) algorithm in LF propagation⁷. In recent years, Antunes de Sá used machine learning models to estimate lightning distance based on LF lightning signal data, which promoted the development of remote sensing of the ionosphere⁸. Gao et al. predicted the ionospheric reflection coefficient using ionosphere models, comparing and validating the impact of different lower ionospheric models on LF sky wave propagation⁹. In 2023, Hu et al. investigated the prediction of LF sky wave propagation under complex random ionospheric conditions, comparing the advantages of different FDTD algorithms¹⁰. In addition, as an international standard, Recommendation ITU-R P.684 is a widely accepted method for predicting LF sky wave propagation¹¹. It is not difficult to see that the ionosphere, as the main part of LF sky wave propagation channel, has great research potential.

To further enhance the prediction accuracy of LF sky wave propagation, we first propose a model for predicting the critical frequency of the low ionospheric E layer (f_oE) in East Asia based on statistical machine learning (SML) and spatial cubic spline interpolation (SCSI) methods. Based on this model, we improved the LF sky wave propagation prediction method based on wave-hop theory which can be used to calculate the field strength at frequencies below about 150 kHz. The structure of this paper is arranged as follows: Section “Method description” presents the current status of predictions for low ionospheric parameters, explains the overall method to constructing the model in this paper, and provides a flowchart for the entire modeling process. Section “Modeling of ionospheric parameters” details the entire process of establishing the f_oE prediction model based on SML and SCSI, including the principles, data, modeling process, and prediction results, demonstrating the model’s advantages in f_oE prediction and laying the foundation for field strength prediction. In Section “Improved prediction of sky wave propagation”, we enhance the LF sky wave propagation prediction method, providing the predicted results of relevant parameters and field strength, and proving the model’s advantages in field strength prediction. Finally, we summarize the whole work and analyze the future development direction.

Method description

For LF propagation, the low ionosphere plays a crucial role in the propagation of LF sky waves^12,13. In particular, the ionospheric parameters of the E layer are essential for accurate prediction of LF sky waves. Through the f_oE at the reflection position, we can determine the ionospheric reflection height, and then deduce the reflection coefficient, focusing factor, and other parameters. Therefore, accurately predicting f_oE has become very important in supporting the LF sky wave propagation prediction. The most commonly used model for f_oE prediction is the International Reference Ionosphere (IRI) model, which is the empirical standard model for predicting many ionospheric parameters. Currently, there are several versions such as IRI-2020, IRI-2016, and IRI-2012¹⁴. In 2007, Yue et al. developed an empirical model based on the data given by the ionospheric observation station in Wuhan and compared it with the IRI model, which is of great significance for the prediction of f_oE in East Asia¹⁵. In 2011, Chen et al. summarized some variation patterns of f_oE in the past 20 years based on the measured data of stations in different locations, which helped develop regional empirical models¹⁶. In 2013, based on the historical measured data of f_oE, Somoye et al. predicted the variation pattern of f_oE in Singapore, Slough, and other places by using standard deviation quotient and average values¹⁷. In the same year, Wongcharoen et al. studied the influence of solar activity index and ionospheric index on f_oE based on the measured data of f_oE over Chumphon, Thailand, which has guiding significance for the prediction of f_oE in this region¹⁸. Also in 2013, Abe et al. studied the correlation between f_oE changes and solar activities and obtained the pattern that f_oE increases with the increase of solar intensity, etc., which is conducive to modeling the f_oE¹⁹. As an international standard, ITU-R P.1239 provides the calculation method of monthly median values of f_oE²⁰.

However, at present, many scholars are focusing on the study of ionospheric parameter such as total electron content (TEC)^21,22,23. Due to the importance of f_oE in LF propagation, accurate prediction of f_oE urgently needs to keep up with the development of the times. Therefore, we first established a higher accuracy model of f_oE, and then improved the propagation prediction method of field strength and relative parameters in this paper. As shown in Fig. 1, the total research process includes.

• (1) The first part focuses on the prediction of f_oE. This is accomplished through the use of SML and SCSI. The SML method involves training models on extensive datasets, which include various influencing factors such as solar activity, and historical ionospheric data. By analyzing these factors, the models based on SML can learn patterns and relationships that enable them to predict future f_oE with high accuracy. This method is advantageous because it allows for continuous improvement as more data becomes available, making the predictions increasingly reliable over time. Building upon the time prediction using SML, we further employ the SCSI for spatial reconstruction. The SCSI is a mathematical method used to create smooth curves through a series of data points, refining and smoothing input data to achieve higher accuracy.

• (2) The second part is dedicated to predicting the LF sky wave field strength. Building upon the f_oE prediction earlier, we can improve the ionospheric reflection height based on the wave-hop theory, thereby enhancing the prediction accuracy of LF sky wave field strength. Wave-hop theory can provide a framework for understanding the propagation of LF sky wave in the ionosphere.

Fig. 1

Overall modeling process.

By fusing these two parts, we can more accurately predict LF sky wave propagation. Subsequent sections will elaborate on the detailed process of model establishment as delineated in this paper.

Modeling of ionospheric parameters

Modeling idea

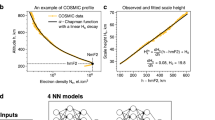
The SML uses data and statistical techniques to enhance system performance. One of its key advantages lies in its ease of understanding and explanation. Applied SML is a process of extracting data features, summarizing data models, discovering internal knowledge, and finally applying these to data^24,25. Like other processes that employ machine learning methods to solve problems, it’s crucial to pay attention to the four key aspects: data, model, algorithm, and strategy. Figure 2 shows the four aspects of modeling in this paper.

Fig. 2

Four aspects of modeling f_oE based on SML.

To be specific, the application of SML methods to build prediction models should be expanded from the following four directions:

• (1) Modeling data: The application of machine learning to problem-solving involves the identification of data features, which need to be consistent and clear across the dataset. Typically, a portion of the acquired dataset is used for model training, while the remainder is allocated for model evaluation. The quality of the data directly influences the quality of the model.

• (2) Model selection: This is the key to using machine learning to solve problems. We need to fully understand the purpose of modeling, the principle and the characteristics of the data, and other factors. Only in this way can we choose the appropriate modelset. If the selected model is not suitable for the problem, it will cause poor modeling accuracy and high modeling costs. Principal Component Analysis (PCA) is a widely used machine learning modeling method. It constructs new features on the basis of the original data features to achieve data dimensionality reduction. The PCA method transforms the original features into a combination of linearly independent basis functions. In the early twentieth century, Person proposed the application of PCA method to establish empirical models²⁶. Over half a century later, Dvinskikh introduced the PCA method into the establishment of empirical models of ionospheric parameters²⁷, creating a precedent in this field. Since then, the PCA method has increasingly been utilized in the establishment of various ionospheric models.

• (3) Model training: Based on the selected model, the appropriate algorithm is used to analyze the training dataset. This involves identifying statistical patterns between the input and output variables, solving for the correlation coefficient, and determining the specific form of the model expression. The Least Squares (LS) algorithm is a most commonly used algorithm in the field of function fitting²⁸, which is closest to the real case, and its purpose is to minimize the sum of squares of errors.

• (4) Model evaluation: Select appropriate statistics as criteria for evaluating the quality of the model. The smaller the difference between the predicted values based on the deterministic model and the data used for model evaluation, the better the model performance.

Taking into account the preceding descriptions, in order to obtain the predicted values of the monthly median f_oE of each station in November 2013 (comprising the monthly median hourly data for each month), the following details the process of establishing the f_oE prediction model based on the SML:

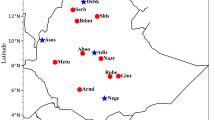
Step 1 Obtain f_oE measured data of four ionospheric observation stations in East Asia (Fig. 3 shows the location information of the four stations and the transmitter station) from 1998 to 2012 and the solar activity index data of the corresponding time.

Fig. 3

Observation stations of f_oE.

Step 2 Based on the PCA²⁹, choose the empirical orthogonal function set as the model set to analyze the time variation characteristics of a specific station, and establish the mapping relationship between f_oE (MHz) and the solar activity index. It is defined as follows:

$$f_{o} E\left( {X,m} \right) = \sum\limits_{k = 0}^{K} {\sum\limits_{j = 0}^{J} {\left[ {\mu_{k,j} X^{j} \cos \left( {\frac{2\pi km}{{12}}} \right) + \eta_{k,j} X^{j} \sin \left( {\frac{2\pi km}{{12}}} \right)} \right]} }$$

(1)

where m is the month from 1 to 12, X is the solar activity index chosen later, k from 1 to 4 can represent the time variation characteristics of 12, 6, 3, and 1 month³⁰, respectively. j is used to represent the variation characteristics of the solar activity index, which can be represented by functions of order 1, 2, 3 or higher. The optimal number is denoted as K and J. μ and η represent the correlation coefficients

Step 3 Determine the solar activity index X, select a set of solar activity index variation characteristics j and time variation characteristics k.

Step 4 Use the data from 1998 to 2009 as the training dataset for model training. Perform regression analysis using the LS algorithm based on the provided values of j and k. Calculate the correlation coefficients and establish the specific mapping relationship according to the following procedure:

$$\begin{array}{*{20}c} {\left( {BB^{T} } \right)\left[ {\begin{array}{*{20}c} {\mu_{b,0} } \\ {\mu_{b,1} } \\ \vdots \\ {\eta_{{k_{J - 1} }} } \\ {\eta_{{k_{J} }} } \\ \end{array} } \right] = B\left[ {\begin{array}{*{20}c} {f_{o} E_{{1^{\prime}}} } \\ {f_{o} E_{{2^{\prime}}} } \\ \vdots \\ {f_{o} E_{{z - 1^{\prime } }} } \\ {f_{o} E_{{z^{\prime}}} } \\ \end{array} } \right]} \\ \end{array}$$

(2)

where f_oE′ is the observation statistic value of f_oE, Z is the maximum observation count, T is transpose of the matrix, and B is defined as follows:

$$B = \begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} 1 & 1 & \ldots & 1 \\ {(X)_{1} } & {(X)_{2} } & \ldots & {(X)_{z} } \\ \vdots & \vdots & \vdots & \vdots \\ {(X)_{1}^{J - 1} \sin^{J - 1} \left( {\frac{2\pi km}{{12}}} \right)} & {(X)_{2}^{J - 1} \sin^{J - 1} \left( {\frac{2\pi km}{{12}}} \right)} & \ldots & {(X)_{z}^{J - 1} \sin^{J - 1} \left( {\frac{2\pi km}{{12}}} \right)} \\ {(X)_{1}^{J} \sin^{J} \left( {\frac{2\pi km}{{12}}} \right)} & {(X)_{2}^{J} \sin^{J} \left( {\frac{2\pi km}{{12}}} \right)} & \ldots & {(X)_{Z}^{J} \sin^{J} \left( {\frac{2\pi km}{{12}}} \right)} \\ \end{array} } \right]} \\ \end{array}$$

(3)

Step 5 Evaluate the model using the data from 2010 to 2012 by employing the Relative-Root-Mean-Square-Error (RRMSE) as the criterion for assessment. Suppose n₁ is the total number of f_oE from 2010 to 2012, f_oE_OBS and f_oE_PRE represent the measured f_oE data and predicted values respectively, it is defined as follows:

$$RRMSE = \sqrt {\frac{1}{{n_{1} }}\sum\limits_{i = 1}^{{n_{1} }} {\left( {\frac{{f_{o} E_{{OBS_{i} }} - f_{o} E_{{PRE_{i} }} }}{{f_{o} E_{{OBS_{i} }} }}} \right)^{2} } }$$

(4)

Step 6 Traverse k and j until the RRMSE between the model predicted values and the measured data is minimum. Identify the optimal values for k and j, denoted as K and J, respectively. Subsequently, establish the specific mapping relationship for the station based on these determined values.

Step 7 Repeat steps 2–6, analyze other stations and determine the corresponding mapping relationships.

Step 8 Predict the monthly median f_oE in November 2013. Then calculate the Root-Mean-Square Error (RMSE) between the predictions and the measured monthly median values of f_oE in November 2013. Suppose n₂ is the total number of measured monthly median values of f_oE in November 2013, it is defined as follows:

$$RMSE = \sqrt {\frac{1}{{n_{2} }}\sum\limits_{i = 1}^{{n_{2} }} {\left( {f_{o} E_{{OBS_{i} }} - f_{o} E_{{PRE_{i} }} } \right)^{2} } }$$

(5)

Modeling data

Following the modeling steps outlined in the above section, this section employs the Kokubunji station as an example (with other stations are similar) to illustrate the data required for modeling. All data come from official institutions and have been manually scaled by experienced specialists, ensuring their quality and reliability.

Firstly, we collect f_oE measured data³¹ from the Kokubunji station spanning from 1998 to 2012 with a sampling interval of 1 h. Then, the data are preprocessed to obtain the corresponding monthly median values of f_oE. However, as shown in Fig. 4a, there are instances of missing data. It is worth noting that during nighttime, f_oE values are relatively small, and the vertical incidence sounders used by the station have a measurement lower limit close to 1 MHz, making stable measurements challenging during this period. To ensure data reliability, we have excluded f_oE measured data below 1 MHz.

Fig. 4

Data required for modeling. (a) f_oE data. (b) SSN data.

Secondly, considering the significant impact of solar activity on the ionosphere, wherein the SSN commonly denotes solar activity intensity, particularly within the framework of the IRI model for predicting f_oE, this paper incorporates SSN as a solar activity index influencing f_oE variation^32,33. As shown in Fig. 4b, we collect SSN data³⁴ from 1998 to 2012, and obtain the monthly median SSN data after preprocessing. Similar to the measured data of f_oE, there are also instances of missing SSN data.

Due to the small proportion of missing data in the total, it will not affect training based on SML. Meanwhile, the missing data mainly exists after 2010 and is not used for training.

Modeling process and results

Based on the Eq. (1), taking the Kokubunji station as an example, the model is iterated through different j and k to train the model and evaluate the possible model sets respectively. Figure 5 shows the RRMSE obtained from the evaluation of models under various combinations of j and k.

Fig. 5

RRMSE under various combinations of j and k.

As shown in Fig. 5, it’s evident that the increase of j and k not only increases the computational complexity but RRMSE may not decrease. Although the computational complexity of j = 1 and k = 1 is the lowest, the corresponding RRMSE is obviously greater than that of other combinations of j and k. For practical engineering applications, although the RRMSE reaches its minimum when j = 2 and k = 2, the increase in computational complexity doesn’t significantly enhance accuracy compared to when j = 1 and k = 2. Consequently, J = 1 and K = 2 is chosen. Therefore, the mapping relationship between f_oE and SSN at the Kokubunji station can be expressed as follows:

$$f_{o} E(SSN,m) = \sum\limits_{k = 0}^{2} {\sum\limits_{j = 0}^{1} {\left[ {\mu_{k,j} (SSN)^{j} \cdot \cos \left( {\frac{2\pi km}{{12}}} \right) + \eta_{k,j} (SSN)^{j} \cdot \sin \left( {\frac{2\pi km}{{12}}} \right)} \right]} }$$

(6)

Once the model is trained, the coefficients μ_k,j and η_k,j can be obtained through regression analysis utilizing the LS method. By applying absolute values and logarithmic transformations to the coefficients, Fig. 6 illustrates the distribution of the correlation coefficients of the f_oE prediction model for the Kokubunji station with Japan Standard Time (JST). From Fig. 6, it is evident that most coefficients are relatively small but not zero. Notably, μ_0,0 has significant values and, like all coefficients except μ_0,1, exhibits a trend of being higher during the day and lower at night. Substituting k = 0 and j = 0 into Eq. (6), μ_0,0 serves as a constant term representing a baseline for f_oE prediction. Its prominent values indicate that this baseline plays a substantial role. Additionally, μ_2,0 at JST = 0 differs significantly from other times. Larger coefficients for higher-order terms indicate the model’s ability to effectively capture local features.

Fig. 6

Distribution of the coefficients μ_k,j and η_k,j with JST.

Based on the above steps, the specific form of the f_oE prediction model for the Kokubunji station can be obtained and the corresponding prediction model for each station can be obtained by further analysis. Figure 7 illustrates the variations of predicted monthly median f_oE values with JST at Kokubunji, Okinawa, Wakkanai, and Yamagawa stations predicted by the ITU model and the PRO model (the model proposed in this paper) in November 2013. Nighttime f_oE values are typically small, making them difficult to observe at ionospheric observation stations, thus impacting the accuracy of models relying on measured data. On this basis, referring to the ITU model and the actual situation at the four stations, a f_oE nighttime steady-state value close to the ITU model is selected in the PRO model. It can be seen that the variation pattern of f_oE predicted by both models is largely consistent within a 24-h period, with f_oE remaining relatively stable at night, increasing post-sunrise, peaking at noon, and decreasing into the night again. The ITU model tends to predict slightly smaller f_oE values at night compared to this paper’s model, while daytime predictions align more closely between the two models. As previously mentioned, the measurement lower limit of vertical incidence sounders is 1 MHz. It can be observed that around JST = 17–18, the measured values and the predictions from the PRO model exceed 1 MHz, while the ITU model’s predictions fall below this threshold, showing significant discrepancies. This difference can be attributed to two factors: first, the ITU model is derived from global ionospheric observation data, giving it a global and steady-state characteristic; second, during sunset, the ionosphere tends to experience fluctuations, resulting in variations in f_oE. The PRO model, based on measured data, effectively captures these fluctuations (such as in Fig. 7c when JST = 17), providing more accurate predictions compared to the ITU model. Based on the existing measured data, the RMSE of the two models at the four stations can be calculated. Using Eq. (7), the proportion of RMSE improvement of the PRO model relative to the ITU model can be determined. Statistics analysis shows that the PRO model achieves approximately 66.16% (Kokubunji), 66.38% (Okinawa), 73.21% (Wakkanai), and 3.97% (Yamagawa) higher accuracy in f_oE prediction compared to the ITU model at the four stations, respectively. Compared to the other three stations, the improvement at the Yamagawa station is less significant. This is because the f_oE values themselves are quite low, and the limited measured data make the overall improvement more sensitive to minor prediction errors. Specifically, at this station, the prediction errors of the PRO model are slightly larger than those of the ITU model at JST = 11 and 12, leading to a smaller improvement ratio. However, overall, the PRO model demonstrates highly accurate predictions. Moreover, the yellow bars, representing errors between predicted values and measured data based on the PRO model, are generally lower than the green bars, indicating smaller errors compared to the ITU model. Overall, the PRO model significantly improves f_oE prediction accuracy compared to the ITU model.

$$Improvement = \frac{{\left| {{\text{RMSE}}_{{{\text{ITU}}}} - {\text{RMSE}}_{{{\text{PRO}}}} } \right|}}{{{\text{RMSE}}_{{{\text{ITU}}}} }} \times 100\%$$

(7)

Fig. 7

Comparison of f_oE predictions of the two models at four stations. Black square: measurements (identified as Mea); Red dot: Predictions of the ITU model (identified as ITU); Blue triangle: Predictions of the PRO model (identified as PRO); Yellow bar: Error between measurements and ITU predictions (identified as |Mea-ITU|). Green bar: Error between measurements and PRO predictions (identified as |Mea-PRO|).

The SML method can obtain the predicted values of f_oE at specific observed stations. To obtain f_oE at any location, spatial reconstruction can be performed using interpolation methods. The commonly used interpolation methods include distance-weighted interpolation, SCSI, spherical harmonic functions, Kriging, etc.³⁵ Among these, the SCSI method is particularly noteworthy. It approximates sample points by defining cubic polynomials in a piecewise manner, making it widely applicable in mathematical modeling. This method excels in constructing smooth curves, boasting high accuracy and stability³⁶, hence its selection in this paper.

Here, we take the predicted f_oE values at four stations in November 2013 as sample values, and the f_oE of the target location can be reconstructed by the SCSI method. The SCSI is usually used for the analysis of one-dimensional data. However, in this paper, f_oE is predicted based on two-dimensional data based on longitude and latitude, so it is necessary to reduce the dimension of the data. Specifically, the Kriging method is based on Euclidean distance³⁷, whereas this paper uses Manhattan distance³⁸ for data dimensionality reduction³⁹ to complement the cubic spline interpolation. Using the intersection of the 0° magnetic longitude line and the 0° magnetic latitude line as the origin, eastward and northward are considered positive directions. the specific definition is as follows:

$$M_{i} = \mu_{i} + \eta_{i} \quad i = 0,1, \ldots ,n$$

(8)

where M_i is the Manhattan distance which can represent the location information of the i-th station, n + 1 is the number of ionospheric observation stations, and μ_i and η_i represent the magnetic latitude and magnetic longitude of the i-th station, respectively. Hence, the data point (μ_i, η_i, f_oE_i) can be denoted as (M_i, f_oE_i). Ionospheric observation stations at different locations can be regarded as different nodes on a curve, which can be divided into different intervals. Accordingly, in the interval [M_i, M_i+1], a cubic polynomial can be constructed and defined as follows:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{o} E_{i} (M) = a_{i} + b_{i} (M - M_{i} ) + c_{i} (M - M_{i} )^{2} + d_{i} (M - M_{i} )^{3} ,\quad i = 0,1, \ldots ,n - 1$$

(9)

where M represents the location information of the target location, and a_i, b_i, c_i, d_i are four correlation coefficients⁴⁰. The first and second derivatives of Eq. (9) are defined as follows:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{o} E_{i}^{\prime } (M) = b_{i} + 2c_{i} (M - M_{i} ) + 3d_{i} (M - M_{i} )^{2} \quad i = 0,1, \ldots ,n - 1$$

(10)

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{o}^{i} E_{i}^{\prime \prime } (M) = 2c_{i} + 6d_{i} (M - M_{i} ),\quad i = 0,1, \ldots ,n - 1$$

(11)

Based on the interpolation condition, all known sample points must pass through the curve, so there is:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{o} E_{i} (M_{i} ) = a_{i} = f_{o} E_{i} ,\quad i = 0,1, \ldots ,n - 1$$

(12)

and then according to the continuity condition⁴¹, there are:

$$\begin{aligned} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{o} E_{i}^{\prime } (M_{i + 1} ) = & \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{o} E_{i + 1}^{\prime } (M_{i + 1} )\quad i = 0,1, \ldots ,n - 2 \\ & \Rightarrow b_{i} + 2c_{i} (M_{i + 1} - M_{i} ) + 3d_{i} (M_{i + 1} - M_{i} )^{2} = b_{i + 1} \\ \end{aligned}$$

(13)

$$\begin{aligned} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{o} E_{i}^{\prime \prime } (M_{i + 1} ) = & \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{o} E_{i + 1}^{\prime \prime } (M_{i + 1} ) \\ & \Rightarrow 2c_{i} + 6d_{i} (M_{i + 1} - M_{i} ) = 2c_{i + 1} \\ \end{aligned}$$

(14)

set $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{o} E_{i}^{\prime \prime } (M_{i} )$ as U_i, there are:

$$c_{i} = U_{i} /2$$

(15)

$$d_{i} = (U_{i + 1} - U_{i} )/6(M_{i + 1} - M_{i} )$$

(16)

$$b_{i} = \frac{{f_{o} E_{i + 1} - f_{o} E_{i} }}{{M_{i + 1} - M_{i} }} - \frac{{(M_{i + 1} - M_{i} )}}{2}U_{i} - \frac{{(M_{i + 1} - M_{i} )}}{6}(U_{i + 1} - U_{i} )$$

(17)

By substituting Eqs. (12), (15), (16), and (17) into Eq. (13), a system of equations with a single unknown, U, is obtained, which can be handled and written as follows:

$$N_{i} = M_{i + 1} - M_{i}$$

(18)

$$H_{i} = f_{o} E_{i + 1} - f_{o} E_{i}$$

(19)

$$\begin{gathered} K\left[ {U_{0} \quad U_{1} \quad U_{2} \quad U_{3} \quad \ldots \quad U_{{n - 1}} \quad U_{n} } \right]^{T} \hfill \\ \quad \quad \quad \quad = 6\left[ {0\quad \frac{{H_{1} }}{{N_{1} }} - \frac{{H_{0} }}{{N_{0} }}\quad \frac{{H_{2} }}{{N_{2} }} - \frac{{H_{1} }}{{N_{1} }}\quad \frac{{H_{3} }}{{N_{3} }} - \frac{{H_{2} }}{{N_{2} }}\quad \ldots \quad \frac{{H_{{n - 1}} }}{{N_{{n - 1}} }} - \frac{{H_{{n - 2}} }}{{N_{{n - 2}} }}\quad 0} \right]^{T} \hfill \\ \end{gathered}$$

(20)

where K is the coefficient matrix of the equation and T stands for transpose of the matrix. Then we can solve for U based on the boundary conditions⁴¹. Based on the Not-A-Knot end conditions, K can be written as:

$${\varvec{K}} = \begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} { - N_{1} } & {N_{0} + N_{1} } & { - N_{0} } & 0 & 0 & \cdots & 0 \\ {N_{0} } & {2(N_{0} + N_{1} )} & {N_{1} } & 0 & 0 & \cdots & 0 \\ 0 & {N_{1} } & {2(N_{1} + N_{2} )} & {N_{2} } & 0 & \cdots & 0 \\ 0 & 0 & {N_{2} } & {2(N_{2} + N_{3} )} & {N_{3} } & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & {N_{n - 2} } & {2(N_{n - 2} + N_{n - 1} )} & {N_{n - 1} } \\ 0 & 0 & 0 & \cdots & { - N_{n - 2} } & {N_{n - 2} + N_{n - 1} } & { - N_{n - 1} } \\ \end{array} } \right]} \\ \end{array}$$

(21)

Based on the above steps, U_i can be solved and then we can obtain the coefficients of the interpolation function. According to the interval, we can select the corresponding SCSI function and get the corresponding f_oE.

To verify the effectiveness of the SCSI method, Table 1 compares the RRMSE between the f_oE predicted values and measured data over 24 h in November 2013 at four stations, based on reconstructions using the SCSI and Kriging methods, which is the traditional interpolation method of ionospheric parameters⁴². It can be seen that the RRMSE calculated using the SCSI interpolation method is consistently lower than those obtained using the Kriging interpolation method. Therefore, it is proved that the SCSI method can achieve more accurate spatial predictions in small areas, such as East Asia.

Table 1 RRMSE at four stations based on the two methods.

Figure 8a,b show the variation patterns of f_oE at JST = 12 in November 2013 in East Asia based on the ITU model and the PRO model, respectively. Darker colors denote smaller f_oE values. While the ITU model shows a decreasing trend in f_oE from south to north, the PRO model exhibits a decreasing trend from southwest to northeast. This difference mainly stems from the data sources used: the ITU model is built on data from 55 globally distributed ionospheric observation stations, whereas the PRO model relies on data from four ionospheric observation stations in East Asia, leading to location-related discrepancies. Figure 8c shows the error variation patterns of the two models. In the eastern part of the region, the predicted values of f_oE based on the PRO model are smaller than that of f_oE based on the ITU model, while the reverse is true in the western part of the region.

Fig. 8

Comparison of the f_oE variation patterns at JST = 12 in November 2013 based on the two models. (a) Results based on the ITU model. (b) Results based on the PRO model. (c) Bias between the ITU and PRO models.

Improved prediction of sky wave propagation

Improved reflection height

With f_oE of the reflection points and wave-hop theory, we can calculate its corresponding ionospheric reflection height, which is defined as follows:

$$R_{h} = 100 - G\sqrt {1 - (f - 10)/f_{o} E} \quad {\text{km}}$$

(22)

where G is a function related to f_oE¹¹, f is the frequency.

Figure 9a,b show the variation patterns of ionospheric reflection height R_h at JST=12 in November 2013 in East Asia based on the ITU and PRO models. As shown in Fig. 9a,b, R_h based on the ITU model exhibits an increasing trend from south to north, whereas that based on the PRO model demonstrates an increasing trend from southwest to northeast. Consequently, Fig. 9c shows the error distribution between the two models. In the western part of the region, the R_h predicted values based on the PRO model is smaller than those based on the ITU model, whereas the opposite is true in the eastern part.

Fig. 9

Comparison of the R_h from the two models at JST = 12 in November 2013. (a) Results based on the ITU model. (b) Results based on the PRO model. (c) Bias between the ITU and the PRO models.

Enhanced wave-hop method

Having the ionospheric reflection height R_h, various parameters necessary for calculating the LF sky wave field strength can be calculated. Here, the calculation method of LF sky wave field strength is first given as¹¹:

$$E_{s} = \frac{{600\sqrt {p_{t} } }}{P}(\cos \phi )^{2} C_{i}^{2} FC_{g}^{s - 1} A_{t} A_{r} \quad {\text{mV}}/{\text{m}}$$

(23)

where s is the sky wave hop number, and p_t is the transmitting power (kW). The other parameters are directly or indirectly affected by the ionospheric reflection height (R_h), which is described as follows:

• (1) φ is the elevation angle, which is defined as

  $$\phi = \arctan \left\{ {\cot \left( {\frac{D/s}{{2r}}} \right) - \frac{{r\csc \left( {\frac{D/s}{{2r}}} \right)}}{{(r + R_{h} )}}} \right\}\quad {\text{rad}}$$

  (24)

  where D is the great circle distance (km) between the transmitter and receiver, and r is the effective Earth radius (km).

• (2) P is the sky wave propagation path length (km), which is defined as:

  $$P = 2sr\sin \left( {\frac{D/s}{{2r}}} \right)\sec \left( {\varphi + \frac{D/s}{{2r}}} \right)\quad {\text{km}}$$

  (25)

• (3) F is the ionospheric focusing factor⁴³, which can be defined in different areas as follows:

  $$F = \left\{ \begin{gathered} {\text{Lighting}}\;{\text{area}} \hfill \\ \left( {\frac{{r + R_{h} }}{r}} \right)\left[ {\frac{{2\sin \left( {\frac{\beta }{2s}} \right)}}{\sin \theta }} \right]^{\frac{1}{2}} \left[ {\frac{{r + R_{h} - r\cos \left( {\frac{\beta }{2s}} \right)}}{{\left( {r + R_{h} } \right)\cos \left( {\frac{\beta }{2s}} \right) - r}}} \right]^{\frac{1}{2}} \times \rho , \hfill \\ {\text{Caustic}}\;{\text{point}} \hfill \\ \left( {\frac{2s}{{\sin \beta_{t} }}} \right)^{\frac{1}{2}} \left[ {\left( {\frac{{r + R_{h} }}{r}} \right)^{2} - 1} \right]^{\frac{1}{2}} \times 1.3466\left( \frac{wr}{3} \right)^{\frac{1}{6}} e^{{\frac{i\pi }{{12}}}} , \hfill \\ Shadow\;area \hfill \\ \left( {\frac{2s}{{\sin \beta }}} \right)^{1/2} \left\{ {\left[ {\left( {\frac{{r + R_{h} }}{r}} \right)^{2} - 1} \right]^{\frac{1}{2}} + \frac{{\beta - \beta_{t} }}{2s}} \right\} \times 1.3466\left( \frac{wr}{3} \right)^{\frac{1}{6}} e^{{\frac{i\pi }{{12}}}} \hfill \\ \end{gathered} \right.$$

  (26)

  where β is the angular distance between the transmitter and the receiver. When the reflection wave is tangent to the ground, β is β_t. w is the wavelength number (= 2π/λ), λ is the wavelength, ρ is the correction factor.

• (4) C_i is the ionospheric reflection coefficient, which is a function of the ionospheric incidence angle q, calculated by interpolation. q is also affected by the ionospheric reflection height and is defined as follows:

  $$q = \arcsin \left( {r\cos (\varphi )/\left( {r + R_{h} } \right)} \right)\quad {\text{rad}}$$

  (27)

• (5) A_t and A_r are antenna factors of the transmitting and receiving antenna, which are determined by the geographical environment and elevation angle φ. They are computed through interpolation.

• (6) C_g is the ground reflection coefficient, which is defined as follows:

  $$C_{g} = \left\{ {\begin{array}{*{20}l} {\frac{{v^{2} \sin (\varphi ) - \sqrt {v^{2} - \cos^{2} (\varphi )} }}{{v^{2} \sin (\varphi ) + \sqrt {v^{2} - \cos^{2} (\varphi )} }}} \hfill & {\varphi > 0} \hfill \\ {E_{D} /E_{F} } \hfill & {\varphi \le 0} \hfill \\ \end{array} } \right.$$

  (28)

  where v is related to the ground reflection point environment, E_D is the diffraction field strength, and E_F is the free space field strength⁴⁴.

With these parameters, we can predict the field strength using Eq. (23) and then calculate the RMSE between the predicted values and the measured field strength. Suppose n₃ is the total number of field strength data, E_OBS and E_PRE represent the measured field strength and predicted field strength respectively, it is defined as follows:

$${\text{RMSE}} = \sqrt {\frac{1}{{n_{3} }}\sum\limits_{i = 1}^{{n_{3} }} {\left( {E_{{OBS_{i} }} - E_{{PRE_{i} }} } \right)^{2} } }$$

(29)

Based on the comparison of ionospheric reflection height, we can further analyze the variation of relevant parameters based on the ITU and the PRO model in East Asia. Figure 10 shows the differences in relevant parameters over East Asia based on the two models (ITU and PRO). As can be seen from Fig. 10, the change in color represents a difference in the parameters based on the two models

• (1) As shown in Fig. 10a, the elevation angles calculated by the PRO model increase in the eastern part, whereas those decrease in the western part. The difference is greatest around the transmitter and in the northeast corner of this region.

• (2) As shown in Fig. 10b, the variation patterns of the sky wave propagation path length are similar to those of the elevation angle. The difference is also greatest around the transmitter and in the northeast corner of this region.

• (3) As shown in Fig. 10c, the ionospheric focusing factor calculated by the PRO model increases for most links in this region. The difference is greatest in the northeast corner of this region.

• (4) As shown in Fig. 10d, the ionospheric reflection coefficient decreases around the transmitter according to the PRO model. The difference is greatest in the western part of the transmitter.

• (5) As shown in Fig. 10e,f, the antenna factors of both the transmitter and receiver have a significant reduction in predicted results based on the PRO model, particularly in the western part of the region. The difference is greatest in the western part and northeast corner of this region.

Fig. 10

Differences of relevant parameters in East Asia based on the two models. (a) the difference in φ between the ITU model and the PRO model. (b) the difference in P between the ITU model and the PRO model. (c) the difference in F between the ITU model and the PRO model. (d) the difference in C_i between the ITU model and the PRO model. (e) the difference in A_t between the ITU model and the PRO model. (f) the difference in A_r between the ITU model and the PRO model.

Improved prediction of field strength

Figure 11 shows the map of the transmitter and receivers (Mapping software: The MathWorks Inc. (2024). MATLAB Online. Available: https://matlab.mathworks.com). We select this region due to the regional nature of the ionospheric data and the limited data available. The transmitter is at (37.4°N, 140.8°E). The receivers are arranged in a northeast-to-southwest direction over the Pacific Ocean, with the nearest receiver approximately 220 km from the transmitter and the farthest receiver about 2000 km away. We have a total of 55 different receiver stations. One of the receivers, located at (35.6°N, 139.5°E), is a fixed receiver and it measured field strength variations over 24 h. Figure 12 shows the spatiotemporal distribution of the measured and predicted field strength of 40 kHz LF sky waves within a range of 2000 km based on the ITU model and the PRO model, where the x-axis represents the propagation distance and the y-axis represents the JST. The larger the bubble, the lighter the color, and the greater the field strength. Upon analysis, the RMSE between the predicted field strength and the measured field strength of 78 point-to-point links using the ITU model is about 6.17 dB, while the RMSE between the predicted field strength and the measured field strength based on the model in this paper is approximately 5.79 dB. This represents a notable enhancement in accuracy of about 6.16 % compared to the ITU model, signifying significant improvement. It can be seen from the above section that the change in ionospheric reflection height leads to the change in relevant parameters. Combined with the wave-hop theory, it becomes apparent that alterations in one parameter influence others, rendering it difficult to isolate the impact of a single parameter change on field strength. Notably, all relevant parameters are either directly or indirectly linked to the elevation angle ψ, and even minor fluctuations in ψ induce changes in other parameters, consequently affecting field strength. Hence, the primary reason behind the enhanced accuracy in field strength prediction lies in the fluctuations of ψ triggered by variations in f_oE.

Fig. 11

Map of transmitter and receiver.

Fig. 12

Spatiotemporal distribution of field strength. (a): Measurement. (b): Predictions of the ITU model. (c) Predictions of the PRO model.

In Fig. 13, the overall error statistics are presented. The error distribution based on the two models conforms to a normal distribution. In Fig. 13a, there are 21 data points within the error range of − 0.5 to 2 dB, accounting for the largest proportion. Similarly, Fig. 13b depicts 20 data points within the error range of − 2.6 to − 0.4 dB, accounting for the largest proportion.

Fig. 13

Error statistics. Blue bar: Error. Red curve: normal distribution curve.

Conclusion

This paper proposes a prediction model for f_oE in East Asia utilizing the SML and SCSI methods. Comparing the ITU model and measured data, the proposed model can obtain reasonable variation patterns of f_oE and significantly improve the prediction accuracy of f_oE. Therefore, we believe that the SCSI method combined with the Manhattan distance has better prediction accuracy in a small range. Based on f_oE, the relatively improved parameters such as ionospheric reflection height, reflection coefficient, focusing factor, etc., are employed to improve the prediction of LF sky wave propagation, resulting in approximately 6.16 % improvement in accuracy for field strength prediction of LF sky wave propagation within 2000 km at 40 kHz compared to the ITU model.

Although existing established f_oE prediction methods have achieved a certain level of accuracy, validation reveals that prediction errors persist in some regions. To address this, the proposed model effectively captures the variation characteristics of f_oE in the East Asia region, thereby improving prediction accuracy and providing a novel approach for localized predictions.

In the future, a better mapping relationship between f_oE and solar activity index along with other parameters can be established by augmenting the sample size and utilizing prediction methods for other ionospheric parameters.