Introduction

Hepatitis B virus (HBV) is a major global public health issue, affecting an estimated 296 million people. HBV is a DNA virus that primarily targets hepatocytes, the cells that make up the liver. It can lead to both acute and chronic liver diseases, with severe consequences such as liver cirrhosis and hepatocellular carcinoma, which are associated with persistent HBV infection and are significant contributors to global disease and mortality rates1. HBV is mainly transmitted through direct contact with infected bodily fluids like blood. Individuals at higher risk include those receiving blood transfusions, intravenous drug users, and healthcare workers exposed to contaminated fluids. Additionally, mother-to-child transmission during childbirth is a key mode of infection, particularly in regions with high HBV prevalence. Despite the availability of antiviral treatme nts and effective vaccines, HBV remains a significant challenge, especially in low- and middle-income countries where healthcare access and vaccination efforts are limited. Consequently, the spread of the virus continues to grow.

Mathematical modeling plays a critical role in understanding HBV transmission and progression, supporting public health strategies aimed at mitigating its global impact. Researchers worldwide have developed various mathematical models to better understand and address the characteristics of the hepatitis B virus. For instance, Wang et al. modeled HBV disease with diffusion in2, and later conducted a stability analysis of HBV, focusing on cost-effectiveness in3. Delay differential models that account for time delays in HBV dynamics are discussed in4. Khan et al. introduced a model incorporating the effect of immigration in5, and later proposed models with three control parameters in6. Maynard et al. analyzed HBV control through vaccination in7, while Pang et al. explored the transmission dynamics of HBV considering the effects of vaccination in8. Age-structured HBV analysis was conducted in9, and a multi-group model was explored in10. These models offer diverse approaches to understanding and managing HBV transmission. However, these models are based on integer-order derivatives, which limit their ability to capture the memory and hereditary properties inherent in biological systems. Fractional-order models, which generalize integer-order models, offer the advantage of incorporating these memory and hereditary effects. Various definitions of fractional derivatives exist, with the Caputo, Caputo-Fabrizio (CF), and Atangana-Baleanu (AB) derivatives being the most prominent and widely applied by researchers. These fractional derivatives have been employed in various disease models, as demonstrated in references11,12,13,14,15,16,17,18,19,20,21. Specific studies related to HBV and other infectious diseases include the modeling and analysis of HBV with optimal controls22, and discussions on vaccination and treatment strategies with optimal control in23. Shat et al. used the Atangana-Baleanu operator to analyze HBV dynamics with treatment effects in24. Furthermore, the dynamics of tuberculosis (TB) using the Caputo derivative were explored in25, and fractional analysis of HBV dynamics with the Atangana-Baleanu derivative was conducted in26. Fractional modeling of HBV with hospitalization classes was presented in27, and TB transmission among children and adults was investigated in28. Novel models for coronavirus infection incorporating both singular and non-singular kernels were introduced in29, while fractional derivatives were applied to a two-species model in30. Tumor models have also been developed and discussed in31,32,33,34.

In this study, we propose a new mathematical model for the transmission dynamics of HBV by incorporating an additional treatment class and accounting for uncertainties in model parameters using Gaussian fuzzy numbers. The Caputo derivative is selected for this research among the several definitions of fractional derivatives because it can deal with initial circumstances in a way that is compatible with classical differential equations. In epidemiological models, the Caputo derivative is simpler to grasp and apply than the Riemann-Liouville derivative, which necessitates non-local initial conditions. The Caputo derivative captures the memory-dependent processes that are intrinsic to HBV dynamics in a simpler manner than Atangana-Baleanu derivatives. It is therefore especially well-suited for simulating the long-term effects of interventions in biological systems. To the best of the authors’ knowledge, previous studies have not addressed HBV transmission dynamics with both treatment interventions and fuzzification strategies. By utilizing a standard incidence approach, rather than the bi-linear incidence commonly employed in earlier models, our approach better captures the effects of treatment interventions. The incorporation of fuzzification through Gaussian fuzzy numbers helps to account for uncertainties in key parameters, leading to more reliable and realistic outcomes. This combination of treatment strategies and fuzzification enhances the model’s effectiveness in guiding strategies for controlling and reducing the impact of HBV.

Preliminaries

An essential tool for simulating complex biological systems with inherent uncertainties is fuzzy logic and fractional calculus. Long-term modeling is more accurate when fractional derivatives are used because they represent the memory and genetic characteristics of diseases. By taking into consideration uncertainty and parameter variability, fuzzy logic offers a more reliable framework for practical uses. All of these resources work together to guarantee the suggested HBV model’s validity and applicability.

Definition 1

35 The Caputo fractional derivative \(^{C}{\mathbb {D}}_t^\alpha\) of a function \(\eth (t)\) is defined by:

$$\begin{aligned} ^{C}{\mathbb {D}}_t^\alpha \{\eth (t)\} = \frac{1}{\Gamma (\vartheta -\alpha )} \int _{0}^{t} (t-\varrho )^{\vartheta -\alpha -1}\eth (t)^{(\vartheta )}(\varrho ) d\varrho , \hspace{1cm} \vartheta -1 < \alpha \le \vartheta . \end{aligned}$$
(1)

Definition 2

Let \(\eth (t)\) be a piecewise continuous function on the interval \([0,\infty ]\) of exponential order \(\delta\), the Laplace transform of \(\eth (t)\) , \(\tilde{\eth (s)}\) is given by

$$\begin{aligned} \tilde{\eth (s)}= \mathcal {L}[\eth (t)]=\int _{0}^{\infty } \textrm{e}^{-st}\eth (t) dt \hspace{1cm} s > \delta . \end{aligned}$$
(2)

and the inverse Laplace transform of \(\tilde{\eth (s)}\) is given by

$$\begin{aligned} \eth (t)= \mathcal {L}^{-1}[\tilde{\eth (s)}]=\int _{z-\iota \infty }^{z-\iota \infty } \textrm{e}^{st}\tilde{\eth (s)} dt \hspace{1cm} z= \Re (s) > z_{0}. \end{aligned}$$
(3)

The necessary properties of Laplace transform and its inverse are summarize in the following Lemma.

Lemma 1

36 Let \(\eth (t)\) , \(\varkappa (t)\) be a piecewise continuous function on the interval \([0,\infty ]\). If

\(\tilde{\eth (s)}= \mathcal {L}[\eth (t)]\), \(\tilde{\varkappa (s)}= \mathcal {L}[\varkappa (t)]\) and \(a,b \in \Re\) then

  1. 1.

    \(\mathcal {L}[a \eth (t) + b \varkappa (t)] = a \tilde{\eth (s)} + b \tilde{\varkappa (s)}\).

  2. 2.

    \(\mathcal {L}^{-1}[a \tilde{\eth (s)} + b\tilde{\varkappa (s)}] = a eth(t) + b\varkappa (t)\).

  3. 3.

    \(\lim _{{s \rightarrow \infty }} s\tilde{\eth (s)} = \eth (0)\).

  4. 4.

    \(\mathcal {L}\{t^{\alpha }\} = \frac{\Gamma (\alpha +1)}{s^{\alpha +1}}\) for \(\vartheta - 1< \alpha < \vartheta\).

  5. 5.

    \(\mathcal {L}\{{\mathbb {D}}_t^\alpha \{\eth (t)\}\} = s^{\alpha }\tilde{\eth (s)} - \sum _{k=0}^{\vartheta -1} s^{\alpha -k-1}\eth ^{(k)}(0)\), \(\vartheta - 1< \alpha < \vartheta\).

Definition 3

35 Let \(\Re\) be a real set. Then, a fuzzy set \(\tilde{\omega }\) in \(\Re\) can be characterized by a membership function \(\Omega _{\tilde{\omega }}\), where,\(\Omega _{\tilde{\omega }}\) : \(\Re \longrightarrow [0,1]\) An r-level set of \(\tilde{\omega }\) is \([\tilde{\omega }]^{r}\)=\({\omega \in \Re }:\Omega _{\tilde{\omega }}(\omega )\ge r\) for \(r\in [0,1]\)

There are following conditions for a fuzzy set \(\tilde{\omega }\) to be a fuzzy number:

  1. 1.

    \(\tilde{\omega }\) is normal, that is, for \(\omega _{0} \in \Re\) we have \(\Omega _{\tilde{\omega }}( \omega _{0})=1\) .

  2. 2.

    \(\tilde{\omega }\) is convex,that is \(\Omega _{\tilde{\omega }}(\epsilon \omega _{1}+(1-\epsilon )\omega _{2})\ge\) min \(\left\{ \Omega _{\tilde{\omega }}( \omega _{1}),\Omega _{\tilde{\omega }}( \omega _{2})\right\}\) for all \(\omega _{1},\omega _{2}\in \Re\) and \(\epsilon \in [0,1]\)

  3. 3.

    \(\tilde{\omega }\) is semicontinuous.

  4. 4.

    Te set \(\overline{\left\{ \omega \in \Re :\Omega _{\tilde{\omega }}(\omega )>0\right\} }\) is compact.

Definition 4

37 For an asymmetrical Gaussian fuzzy number \(\tilde{F} = (v, \sigma _l, \sigma _r)\), its membership function \(\Omega _{\tilde{F}}\) is as follows:

$$\epsilon _p = {\left\{ \begin{array}{ll} \exp \left[ - \frac{(z - v)^2}{2\sigma _l^2} \right] , & z \le v, \\ \exp \left[ - \frac{(z - v)^2}{2\sigma _r^2} \right] , & z \ge v. \end{array}\right. }$$

where, \(z \in \mathbb {R}\) represents the modal value, and \(\sigma _l\) and \(\sigma _r\) denote the left-hand and right-hand spreads, respectively, of the Gaussian distribution. In the case of a symmetric Gaussian fuzzy number, we have \(\sigma _l = \sigma _r = \sigma\).

Definition 5

37 The parametric form of a symmetric Gaussian fuzzy number \(\tilde{F} = (v, \sigma )\) can be written as:

$$\begin{aligned} \tilde{F} = [\underline{F(u)},\overline{ F(u)}] = \left[ v - \sqrt{-2 \log u} \sigma , v + \sqrt{-2 \log u} \sigma \right] . \end{aligned}$$

Definition 6

A fractional power series (FPS) about \(t=t_0\) is defined as

$$\begin{aligned} \sum _{i=0}^{\infty }\hbar _{i}(t-t_0)^{i}=\hbar _0+\hbar _{1} t+\hbar _{2} t^{2}+\hbar _{3} t^{3}+\cdots ; \end{aligned}$$

\(t_0\le t\le t+1\) , where the constants \(\hbar _{i}\) , \(i=0,1,2,\ldots\), are called the coefficients of the power series.

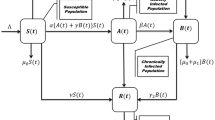
Table 1 Biological description and values of parameters for HBV model (5).
Full size table

HBV model transmission

To model the progression of Hepatitis B virus (HBV) infection, we begin with an existing system of fractional differential equations38 that describe various stages of infection and recovery. The population is divided into six compartments: Susceptible \(\mathbb {S}\), Exposed \(\mathbb {E}\), Acute Infected \(\mathbb {I}\), Asymptomatic \(\mathbb {A}\), Chronic \(\mathbb {C}\), and Recovered \(\mathbb {R}\). This model is then modified by adding a Treated \(\mathbb {T}\) compartment to account for individuals receiving treatment. The transitions between these compartments are governed by biological parameters with description are given in Table 1. To address uncertainties in the values of these parameters, we incorporate Gaussian fuzzy numbers, facilitating a more robust analysis under different conditions. Additionally, the model incorporates the memory effect inherent in biological systems by using Caputo fractional derivatives, making it particularly useful for examining the long-term effects of treatment strategies.

The incorporation of a treatment compartment is essential for accurately representing the entire range of disease progression and control during therapeutic intervention when simulating the transmission dynamics of the hepatitis B virus. By decreasing viral replication and subsequently the viral load in infected patients, antiviral therapy is essential for controlling chronic HBV infections. A more realistic depiction of the population receiving treatment is made possible by the inclusion of a treatment compartment, which takes into consideration their role in the systemic dynamics of the disease. Prolonged HBV infection frequently results in serious side effects including cirrhosis or hepatocellular cancer. The treatment compartment provides insights into the lowering of morbidity and death in treated populations by simulating how long-term antiviral therapy may modify the natural development of the disease. Biological description and values of parameters for HBV model (5) are given in Table 1.

Here, we create a deterministic mathematical model to show the dynamic behavior of HBV using seven ordinary differential equations (ODEs). At any given time t, the total human population, denoted by \(\mathbb {N}\), is divided into seven distinct categories: susceptible individuals \(\mathbb {S}\), exposed individuals \(\mathbb {E}\) acutely infected individuals \(\mathbb {I}\), asymptomatic individuals \(\mathbb {A}\), chronically HBV-infected individuals \(\mathbb {C}\), treated individuals \(\mathbb {T}\) and finally recovered individuals \(\mathbb {R}\). The sum of total human individual population defined as: \(\mathbb {N}=\mathbb {R}+\mathbb {T}+\mathbb {C}+\mathbb {A}+\mathbb {I}+\mathbb {E}+\mathbb {S}\). With the above discussion we formulated a HBV model which is given as follows:

$$\begin{aligned} {\mathbb {D}}_t\mathbb {S}(t)&=\Lambda - \beta (\mathbb {I} + \phi \mathbb {A}+ \epsilon \mathbb {C}) \mathbb {S} - \mu \mathbb {S}\nonumber \\ {\mathbb {D}}_t\mathbb {E}(t)&=\beta (\mathbb {I} + \phi \mathbb {A}+ \epsilon \mathbb {C}) \mathbb {S} - (\mu + \psi ) \mathbb {E}\nonumber \\ {\mathbb {D}}_t\mathbb {I}(t)&=\psi \theta \mathbb {E} - (\mu + \gamma + \eta + \kappa ) \mathbb {I}\nonumber \\ {\mathbb {D}}_t\mathbb {A}(t)&=\psi (1-\theta ) \mathbb {E} - (\mu + \tau + \nu +\zeta ) \mathbb {A}\nonumber \\ {\mathbb {D}}_t\mathbb {C}(t)&= \eta \mathbb {I} + \tau \mathbb {A} - (\mu + \varepsilon + \sigma +\delta ) \mathbb {C}+\omega \mathbb {T}\nonumber \\ {\mathbb {D}}_t\mathbb {T}(t)&=\gamma \mathbb {I} + \zeta \mathbb {A}+ \delta \mathbb {C}-(\mu +\omega +\varrho )\mathbb {T}\nonumber \\ {\mathbb {D}}_t\mathbb {R}(t)&=\kappa \mathbb {I} + \sigma \mathbb {C} + \nu \mathbb {A} +\varrho \mathbb {T} - \mu \mathbb {R} \end{aligned}$$
(4)

with the initial conditions

$$\begin{aligned} \mathbb {S}(0)=&\mathbb {S}_{{0}} \ge 0, \mathbb {E}(0)=&\mathbb {E}_{{0}} \ge 0, \mathbb {I}(0)=&\mathbb {I}_{{0}} \ge 0, \mathbb {A}(0)=&\mathbb {A}_{{0}} \ge 0, \nonumber \\ \mathbb {C}(0)=&\mathbb {C}_{{0}} \ge 0, \mathbb {T}(0)=&\mathbb {T}_{{0}} \ge 0, \mathbb {R}(0)=&\mathbb {R}_{{0}} \ge 0, \end{aligned}$$
(5)

Solution positivity

Lemma 1

38 Let \(\Theta (t) = (\mathcal {S}(t),\mathcal {E}(t),\mathcal {I}(t),\mathcal {A}(t),\mathcal {C}(t),\mathcal {T}(t),\mathcal {R}(t))\) be the solution corresponding to the model described by equations (4) with the initial conditions \(\Theta (0) \ge 0\). Then, the model (4) has the following properties:

  1. 1.

    The solution is non-negative for all \(t > 0\).

  2. 2.

    The total population \(\mathcal {N} = (\mathcal {S}(t)+\mathcal {E}(t)+\mathcal {I}(t)+\mathcal {A}(t)+\mathcal {C}(t)+\mathcal {T}(t)+\mathcal {R}(t))\) satisfies:

    \(\lim _{t \rightarrow \infty } \mathcal {N} \le \frac{\Lambda }{\mu },\)

Proof

Suppose \(t_1 = \sup \{ t> 0 : \Theta (t) > 0 \in [0,t] \}\), and thus \(t_1 > 0\). For \(t > t_1\), we have \(N_t = 0\). We analyze the non-negativity of each component of \(\Theta (t)\).

For the susceptible population \(\mathcal {S}(t)\), the differential equation is:

$$\frac{dS}{dt} =\Lambda - \beta (\mathbb {I} + \phi \mathbb {A}+ \epsilon \mathbb {C}) \mathbb {S} - \mu \mathbb {S},$$

where \(k =\beta (\mathbb {I} + \phi \mathbb {A}+ \epsilon \mathbb {C})\).

$$\frac{dS}{dt} =\Lambda - k \mathbb {S} - \mu \mathbb {S},$$

The equation can be shown as:

$$\begin{aligned} \frac{d}{dt} \left( \mathcal {S}(t) \exp \left( (\mu t) + \int _0^{t_1} k(q) \, dq \right) \right) = \Lambda \exp \left( (\mu t) + \int _0^{t_1} k(q) \, dq\right) , \end{aligned}$$
(6)

where \(t_1\) is the time when \(N_t\) is positive.

Thus,

$$\begin{aligned} \mathcal { S}(t_1) \exp \left( (\mu t_1) + \int _0^{t_1} k(q) \, dq\right) - S(0) = \Lambda \exp \left( (\mu x) + \int _0^x k(f) \, df \, dx\right) , \end{aligned}$$
(7)

so that

$$\begin{aligned} \mathcal {S}(t_1)&= S(0) \exp \left\{ -(\mu t_1 + \int _0^{t_1} k(q) \, dq)\right\} +\exp \left\{ -(\mu t_1 + \int _0^{t_1} k(q) \, dq)\right\} \nonumber \\&\times \int _0^{t_1} \Lambda \exp \left( (\mu x) +\int _0^x k(f) \, df\right) \, dx > 0. \end{aligned}$$
(8)

Since \(\mathcal { S}(0) \ge 0\) and \(\Lambda > 0\), \(\mathcal { S}(t)\) remains non-negative for all \(t > 0\). Similar analysis applies to \(E(t)\), \(I(t)\), \(A(t)\), \(C(t)\), \(T(t)\), and \(R(t)\), ensuring that these components remain non-negative. Adding all the equations, and arriving at,

$$\frac{dN}{dt} = \Lambda -\mu N - (\gamma +\kappa )\mathcal {I}- \nu \mathcal {A}- (\epsilon + \sigma )\mathbb {C}\le \Lambda -\mu N$$

Hence:

$$\lim _{t \rightarrow \infty } N \le \frac{\Lambda }{\mu }.$$

\(\square\)

Stability analysis of disease-free case

This section analyzes the stability of the HBV model with respect to the disease-free equilibrium (\(E_0\)). By setting the right-hand side of the HBV model (4) to zero, the following equilibrium state is obtained:

$$E_0 = \left( S(0), 0, 0, 0, 0, 0, 0\right) = \left( \frac{\Lambda }{\mu }, 0, 0, 0, 0, 0, 0\right) .$$

The basic reproduction number \(R_0\) is calculated using the next generation matrix approach for the HBV model (4). Focusing on the infected compartments \(E\), \(I\), \(A\), and \(C\), we derive the matrices \(F\) and \(V\) in accordance with the method detailed in39 and applied in40,41.

$$F = \begin{pmatrix} 0 & \beta \frac{\Lambda }{\mu } & \beta \phi \frac{\Lambda }{\mu } & \beta \epsilon \frac{\Lambda }{\mu } \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix}$$

and

$$V = \begin{pmatrix} \mu + \psi & 0 & 0 & 0 \\ -\psi \theta & \mu + \gamma + \eta + \kappa & 0 & 0 \\ -\psi (1 - \theta ) & 0 & \mu + \tau + \nu + \zeta & 0 \\ 0 & -\eta & -\tau & \mu + \epsilon + \sigma + \delta \end{pmatrix}$$

Let\(x_1=\mu + \psi\) \(x_2 = (\mu + \gamma + \eta + \kappa )\), \(x_3 = (\mu + \tau + \nu + \zeta )\) and \(x_4 = (\mu + \epsilon + \sigma + \delta )\).The basic reproduction number for the model is determined by the spectral radius of the matrix \(\mathcal {R}_0 = \rho (FV^{-1})\), as defined by the following equation:

$$\mathcal {R}_0^2 =\frac{\beta \Lambda \Psi \left( \theta {x_3} (\epsilon \eta + x_{4}) - (-1 + \theta ) x_{2} (\epsilon \tau + \Phi x_{4})\right) }{\mu {x_1} {x_2} {x_3} x_3}.$$

The basic reproduction number, \(\mathcal {R}_0\), in the context of the HBV (Hepatitis B Virus) model represents the average number of secondary human infections caused by a single infectious individual during their infectious period. This parameter is crucial as it indicates the potential for the HBV to spread within a community or population. Additionally, \(\mathcal {R}_0\) helps in assessing the proportion of the population that needs to be vaccinated to achieve disease eradication and control the outbreak effectively. In biological models, if \(\mathcal {R}_0 > 1\), the infection will spread within the population; if \(\mathcal {R}_0 < 1\), it will not. Generally, a higher \(\mathcal {R}_0\) value signifies greater difficulty in controlling the epidemic. Below, we demonstrate the local stability of the disease-free equilibrium (DFE) at \(E_0\).

Theorem 2

The disease-free equilibrium \(E_0\) is locally asymptotically stable for system (4) when \(\mathcal {R}_0 < 1\).

Proof

To prove the given theorem, we first compute the Jacobian matrix by evaluating model (1) at the disease-free equilibrium \(E_0\), which yields the following result:

$$J = \begin{bmatrix} - \mu & -\beta \frac{\Lambda }{\mu } & -\beta \frac{\Lambda }{\mu } & -\beta \epsilon \frac{\Lambda }{\mu } & -\beta \frac{\Lambda }{\mu } & 0 & 0 \\ 0 & -x_1 & 0 & 0 & 0 & 0 & 0 \\ 0 & \psi \theta & -x_2 & 0 & 0 & 0 & 0 \\ 0 & \psi (1 - \theta ) & 0 & -x_3 & 0 & 0 & 0 \\ 0 & \eta & \tau & 0 & -x_4 & \omega & 0 \\ 0 & \gamma & \zeta & \delta & 0 & -x_5 & 0 \\ 0 & 0 & \kappa & \nu & \sigma & \rho & -\mu \end{bmatrix}$$

From the matrix \(J(E_0)\) presented above, it is clear that the eigenvalues \(-\mu , -x_4 \text {and} x_5=\mu + \omega + \rho\) are all negative. The other four eigenvalues, which also possess negative real parts can be derived using the following equations: \(\lambda ^4 + \lambda ^3a_1 + \lambda ^2a_2 + \lambda a_3 + a_4 = 0,\)

where

$$\begin{aligned} \begin{aligned} a_1&= x_1 + x_2 + x_3 + \mu ,\\ a_2&= x_3\mu + x_2\left( x_3 + \mu \right) + x_1\left( x_2 + x_3 + \mu \right) ,\\ a_3&= x_1 x_3 \mu + x_2 x_3 \mu + x_1 x_2 (x_3 + \mu ),\\ a_4&= x_1x_2x_3\mu \left( 1 - \mathcal {R}_0^2\right) . \end{aligned} \end{aligned}$$

The coefficients represented by \(a_i \text {for} i = 1(1)4\) are positive for \(a_1, a_2, and a_3\), whereas \(a_4\) may assume positive or negative depending on the value of \(\mathcal {R}_0\). In case of disease-free equilibrium (DFE), where the value of the basic reproduction number should be less than 1, the last coefficient becomes positive when \(\mathcal {R}_0 < 1\). Consequently, all coefficients \(a_i\) for \(i = 1, 2, 3, 4\) are positive, and they must conform to the Routh-Hurwitz criteria. These criteria can be readily satisfied under the provided conditions \(a_1a_2a_3 > a_2^2 + a_1a_4\), where \(a_i > 0\) for all \(i = 1, 2, 3, 4\). This condition ensures that \(\Phi = a_1a_2a_3 - a_2^2 - a_1a_4 > 0\). Therefore, the satisfaction of the Routh-Hurwitz criteria guarantees the local asymptotic stability of the HBV model described by (5) at the disease-free equilibrium \(E_0\). \(\square\)

Existence and uniqueness theorem for the HBV model

Consider the HBV model described by the following system of ordinary differential equations as (4,5):

Theorem 3

Let

$$\textbf{y}(t) = \begin{pmatrix} S(t) \\ E(t) \\ I(t) \\ A(t) \\ C(t) \\ T(t) \\ R(t) \end{pmatrix}$$

and define the function \(f(t, \textbf{y})\) as:

$$f(t, \textbf{y}) = \begin{pmatrix} \Lambda - \beta (I(t) + \phi A(t) + \epsilon C(t)) S(t) - \mu S(t) \\ \beta (I(t) + \phi A(t) + \epsilon C(t)) S(t) - (\mu + \psi ) E(t) \\ \psi \theta E(t) - (\mu + \gamma + \eta + \kappa ) I(t) \\ \psi (1 - \theta ) E(t) - (\mu + \tau + \nu + \zeta ) A(t) \\ \eta I(t) + \tau A(t) - (\mu + \epsilon + \sigma + \delta ) C(t) + \omega T(t) \\ \gamma I(t) + \zeta A(t) + \delta C(t) - (\mu + \omega + \rho ) T(t) \\ \kappa I(t) + \sigma C(t) + \nu A(t) + \rho T(t) - \mu R(t) \end{pmatrix}.$$

Continuity: The function \(f(t, \textbf{y})\) is continuous with respect to \(t\) and \(\textbf{y}\) in a region containing the initial condition \((t_0, \textbf{y}_0)\).

Local Lipschitz Condition: The function \(f(t, \textbf{y})\) satisfies a local Lipschitz condition with respect to \(\textbf{y}\). Specifically, there exists a constant \(L\) such that:

$$\Vert f(t, \textbf{y}_1) - f(t, \textbf{y}_2) \Vert \le L \Vert \textbf{y}_1 - \textbf{y}_2 \Vert$$

for all \(\textbf{y}_1, \textbf{y}_2\) in the region.

Under these conditions, the Cauchy-Lipschitz theorem guarantees that there exists a unique solution \(\textbf{y}(t)\) to the initial value problem in some interval \([t_0 - \delta , t_0 + \delta ]\), where \(\delta > 0\) is dependent on the local behavior of \(f\) around \((t_0, \textbf{y}_0)\). Thus, the HBV model described by the above system of differential equations has a unique local solution for the given initial conditions.

Fuzzy fractional modeling of the HBV

In this section, we will concentrate on modeling a fuzzy fractional Hepatitis B Virus (HBV) system, which is a widely used in epidemic diseases models . The particular modified HBV system (4-5) is examined.

Using Definition 3, which is given in the following equations, the system (4) is described in fractional form. The modified HBV system in fractional form can be obtained by applying Definition 1.

$$\begin{aligned} ^{C}{\mathbb {D}}_t^\alpha \mathbb {S}(t)&=\Lambda - \beta (\mathbb {I} + \phi \mathbb {A}+ \epsilon \mathbb {C}) \mathbb {S} - \mu \mathbb {S}\nonumber \\ ^{C}{\mathbb {D}}_t^\alpha \mathbb {E}(t)&=\beta (\mathbb {I} + \phi \mathbb {A}+ \epsilon \mathbb {C}) \mathbb {S} - (\mu + \psi ) \mathbb {E}\nonumber \\ ^{C} {\mathbb {D}}_t^\alpha \mathbb {I}(t)&=\psi \theta \mathbb {E} - (\mu + \gamma + \eta + \kappa ) \mathbb {I}\nonumber \\ ^{C}{\mathbb {D}}_t^\alpha \mathbb {A}(t)&=\psi (1-\theta ) \mathbb {E} - (\mu + \tau + \nu +\zeta ) \mathbb {A}\nonumber \\ ^{C}{\mathbb {D}}_t^\alpha \mathbb {C}(t)&= \eta \mathbb {I} + \tau \mathbb {A} - (\mu + \varepsilon + \sigma +\delta ) \mathbb {C}+\omega \mathbb {T}\nonumber \\ ^{C}{\mathbb {D}}_t^\alpha \mathbb {T}(t)&=\gamma \mathbb {I} + \zeta \mathbb {A}+ \delta \mathbb {C}-(\mu +\omega +\varrho )\mathbb {T}\nonumber \\ ^{C} {\mathbb {D}}_t^\alpha \mathbb {R}(t)&=\kappa \mathbb {I} + \sigma \mathbb {C} + \nu \mathbb {A} +\varrho \mathbb {T} - \mu \mathbb {R} \end{aligned}$$
(9)

where \(\alpha\) is fractional parameter in a Caputo sense. We have incorporated gaussian fuzzy numbers to introduce uncertainty in the system by using the Defnition 3-5. In parametric form, they can be written as

$$\begin{aligned} \tilde{\beta }&=\left[ 0.042 - \sqrt{-\log (r) \cdot 2 \cdot (0.03086)^2}, 0.042 + \sqrt{-\log (r) \cdot 2 \cdot (0.03086)^2}\right] , \nonumber \\ \tilde{\psi }&=\left[ 0.004 - \sqrt{-\log (r) \cdot 2 \cdot (0.00294)^2}, 0.004 + \sqrt{-\log (r) \cdot 2 \cdot (0.00294)^2}\right] , \nonumber \\ \tilde{\eta }&=\left[ 0.02 - \sqrt{-\log (r) \cdot 2 \cdot (0.0147)^2}, 0.02 + \sqrt{-\log (r) \cdot 2 \cdot (0.0147)^2}\right] ,\nonumber \\ \tilde{\tau }&=\left[ 0.002 - \sqrt{-\log (r) \cdot 2 \cdot (0.00147)^2},0.002 + \sqrt{-\log (r) \cdot 2 \cdot (0.00147)^2}\right] ,\nonumber \\ \tilde{\sigma }&=\left[ 0.2 - \sqrt{-\log (r) \cdot 2 \cdot (0.147)^2}, 0.2 + \sqrt{-\log (r) \cdot 2 \cdot (0.147)^2}\right] ,\nonumber \\ \tilde{\varrho }&=\left[ 0.01 - \sqrt{-\log (r) \cdot 2 \cdot (0.00735)^2}, 0.01 + \sqrt{-\log (r) \cdot 2 \cdot (0.00735)^2}\right] \end{aligned}$$
(10)
$$\begin{aligned} \tilde{\mathbb {S}_{0}}&=\left[ \left( 1 -\sqrt{-\log (r) \cdot 2 \cdot (0.735)^2}\right) \cdot 60, \left( 1 + \sqrt{-\log (r) \cdot 2 \cdot (0.735)^2}\right) \cdot 60\right] , \nonumber \\ \tilde{\mathbb {E}_{0}}&=\left[ \left( 1 - \sqrt{-\log (r) \cdot 2 \cdot (0.735)^2}\right) \cdot 40, \left( 1 + \sqrt{-\log (r) \cdot 2 \cdot (0.735)^2}\right) \cdot 40\right] , \nonumber \\ \tilde{\mathbb {I}_{0}}&=\left[ \left( 1 - \sqrt{-\log (r) \cdot 2 \cdot (0.735)^2}\right) \cdot 3, \left( 1 + \sqrt{-\log (r) \cdot 2 \cdot (0.735)^2}\right) \cdot 3\right] ,\nonumber \\ \tilde{\mathbb {A}_{0}}&=\left[ \left( 1 - \sqrt{-\log (r) \cdot 2 \cdot (0.735)^2}\right) \cdot 2,\left( 1 + \sqrt{-\log (r) \cdot 2 \cdot (0.735)^2}\right) \cdot 2\right] ,\nonumber \\ \tilde{\mathbb {C}_{0}}&=\left[ \left( 1 - \sqrt{-\log (r) \cdot 2 \cdot (0.735)^2}\right) \cdot 1,\left( 1 + \sqrt{-\log (r) \cdot 2 \cdot (0.735)^2}\right) \cdot 1\right] ,\nonumber \\ \tilde{\mathbb {T}_{0}}&=0, \tilde{\mathbb {R}_{0}}=0 \end{aligned}$$
(11)

Thus, the fuzzy-fractional HBV system as follows

$$\begin{aligned} ^{C}{\mathbb {D}}_t^\alpha \tilde{\mathbb {S}(t)}&=\Lambda - \tilde{\beta } (\tilde{\mathbb {I}} + \phi \tilde{ \mathbb {A}}+ \epsilon \tilde{\mathbb {C}}) \tilde{\mathbb {S}} - \mu \tilde{ \mathbb {S}}\nonumber \\ ^{C}{\mathbb {D}}_t^\alpha \tilde{\mathbb {E}(t)}&=\tilde{\beta } (\tilde{\mathbb {I}} + \phi \tilde{ \mathbb {A}}+ \epsilon \tilde{\mathbb {C}}) \tilde{\mathbb {S}} - (\mu + \tilde{\psi }) \tilde{\mathbb {E}}\nonumber \\ ^{C} {\mathbb {D}}_t^\alpha \tilde{\mathbb {I}(t)}&=\tilde{\psi } \theta \tilde{\mathbb {E}} - (\mu + \gamma + \eta + \kappa ) \tilde{\mathbb {I}}\nonumber \\ ^{C}{\mathbb {D}}_t^\alpha \tilde{\mathbb {A}(t)}&=\tilde{\psi } (1-\theta )\tilde{ \mathbb {E}} - (\mu + \tau + \nu +\zeta ) \tilde{\mathbb {A}}\nonumber \\ ^{C}{\mathbb {D}}_t^\alpha \tilde{\mathbb {C}(t)}&= \tilde{\eta }\tilde{\mathbb {I}} + \tilde{\tau }\tilde{\mathbb {A}} - (\mu + \varepsilon + \tilde{\sigma }+\delta ) \tilde{\mathbb {C}}+\omega \tilde{ \mathbb {T}}\nonumber \\ ^{C}{\mathbb {D}}_t^\alpha \tilde{\mathbb {T}(t)}&=\gamma \tilde{\mathbb {I} }+ \zeta \tilde{\mathbb {A}}+ \delta \tilde{\mathbb {C}}-(\mu +\omega +\tilde{\varrho })\tilde{\mathbb {T}}\nonumber \\ ^{C} {\mathbb {D}}_t^\alpha \tilde{\mathbb {R}(t)}&=\kappa \tilde{\mathbb {I}} + \tilde{\sigma }\tilde{\mathbb {C}} + \nu \tilde{\mathbb {A}} +\tilde{\varrho } \tilde{\mathbb {T} } - \mu \tilde{\mathbb {R}} \end{aligned}$$
(12)

with fuzzy initial conditions

$$\begin{aligned} \tilde{\mathbb {S}}(0)= \tilde{\mathbb {S}_{0}}, \tilde{\mathbb {E}}(0)= \tilde{\mathbb {E}_{0}}, \tilde{\mathbb {I}}(0)= \tilde{\mathbb {I}_{0}}, \tilde{\mathbb {A}}(0)= \tilde{\mathbb {A}_{0}}, \tilde{\mathbb {C}}(0)= \tilde{\mathbb {C}_{0}}, \tilde{\mathbb {T}}(0)= \tilde{\mathbb {T}_{0}}, \tilde{\mathbb {R}}(0)=\tilde{\mathbb {R}_{0}} \end{aligned}$$
(13)

Solution methodology for fuzzy-fractional HBV model

In this section, we provide a detailed description of the steps involved in applying the Laplace Residual Power Series (LRPS) method to solve the fuzzy-fractional HBV system represented by equations (9) and (11). The fuzzy solution for the variable \(\tilde{\mathbb {S}}(t,r)\) is expressed as \(\tilde{\mathbb {S}}(t,r) = \left[ \underline{\tilde{\mathbb {S}}}(t,r), \overline{\tilde{\mathbb {S}}}(t,r)\right]\), where \(\overline{\tilde{\mathbb {S}}}(t,r)\) denotes the upper bound of the solution, and \(\underline{\tilde{\mathbb {S}}}(t,r)\) represents the lower bound.

By applying the Laplace transform to system (9) and (11), we obtain the following results:

$$\begin{aligned} \tilde{\mathbb {S}}(s,r)&=\frac{\tilde{\mathbb {S}_{0}}}{s}-\frac{1}{s^{\alpha }}\left[ \frac{\Lambda }{s} +\mathcal {L}\left( \tilde{\beta } (\mathcal {L}^{-1}\tilde{\mathbb {I}}(s,r) + \phi \mathcal {L}^{-1}\tilde{ \mathbb {A}}(s,r)+ \epsilon \mathcal {L}^{-1}\tilde{\mathbb {C}}(s,r)) \mathcal {L}^{-1}\tilde{\mathbb {S}}(s,r) \right) +\mu \tilde{ \mathbb {S}}(s,r)\right] \nonumber \\ \tilde{\mathbb {E}}(s,r)&=\frac{\tilde{\mathbb {E}_{0}}}{s}-\frac{1}{s^{\alpha }}\left[ \mathcal {L}\left( \tilde{\beta } (\mathcal {L}^{-1}\tilde{\mathbb {I}}(s,r) + \phi \mathcal {L}^{-1}\tilde{ \mathbb {A}}(s,r)+ \epsilon \mathcal {L}^{-1}\tilde{\mathbb {C}}(s,r)) \mathcal {L}^{-1}\tilde{\mathbb {S}}(s,r) \right) + (\mu + \tilde{\psi }) \tilde{\mathbb {E}}(s,r)\right] \nonumber \\ \tilde{\mathbb {I}}(s,r)&=\frac{\tilde{\mathbb {I}_{0}}}{s}-\frac{1}{s^{\alpha }}\left[ \tilde{\psi } \theta \tilde{\mathbb {E}}(s,r) + (\mu + \gamma + \tilde{\eta } + \kappa ) \tilde{\mathbb {I}}(s,r)\right] \nonumber \\ \tilde{\mathbb {A}}(s,r)&=\frac{\tilde{\mathbb {A}_{0}}}{s}-\frac{1}{s^{\alpha }}\left[ \tilde{\psi } (1-\theta )\tilde{ \mathbb {E}}(s,r) + (\mu + \tilde{\tau }+ \nu +\zeta ) \tilde{\mathbb {A}}(s,r)\right] \nonumber \\ \tilde{\mathbb {C}}(s,r)&=\frac{\tilde{\mathbb {C}_{0}}}{s}-\frac{1}{s^{\alpha }} \left[ \tilde{\eta }\tilde{\mathbb {I}}(s,r) + \tilde{\tau }\tilde{\mathbb {A}}(s,r) + (\mu + \varepsilon + \tilde{\sigma }+\delta ) \tilde{\mathbb {C}}(s,r)+\omega \tilde{ \mathbb {T}}(s,r)\right] \nonumber \\ \tilde{\mathbb {T}}(s,r)&=\frac{\tilde{\mathbb {T}_{0}}}{s}-\frac{1}{s^{\alpha }}\left[ \gamma \tilde{\mathbb {I} }(s,r)- \zeta \tilde{\mathbb {A}}(s,r)- \delta \tilde{\mathbb {C}}(s,r)+(\mu +\omega +\tilde{\varrho })\tilde{\mathbb {T}}(s,r)\right] \nonumber \\ \tilde{\mathbb {R}}(s,r)&=\frac{\tilde{\mathbb {R}_{0}}}{s}-\frac{1}{s^{\alpha }}\left[ \kappa \tilde{\mathbb {I}}(s,r) - \tilde{\sigma }\tilde{\mathbb {C}}(s,r) - \nu \tilde{\mathbb {A}}(s,r) -\tilde{\varrho } \tilde{\mathbb {T} }(s,r) + \mu \tilde{\mathbb {R}}(s,r)\right] \end{aligned}$$
(14)

Let we assume \(k^{th}\) fractional truncated series of \(\tilde{\mathbb {S}}^{k}(s,r),\tilde{\mathbb {E}}^{k}(s,r),\tilde{\mathbb {I}}^{k}(s,r),\tilde{\mathbb {A}}^{k}(s,r),\tilde{\mathbb {C}}^{k}(s,r),\tilde{\mathbb {T}}^{k}(s,r)\) and \(\tilde{\mathbb {R}}^{k}(s,r)\) as follows

$$\begin{aligned}&\tilde{\mathbb {S}}^{k}(s,r)= \sum _{n=0}^{k}\frac{\tilde{\mathbb {S}_{n}}}{s^{n\alpha +1}}, \tilde{\mathbb {E}}^{k}(s,r)= \sum _{n=0}^{k}\frac{\tilde{\mathbb {E}_{n}}}{s^{n\alpha +1}}, \tilde{\mathbb {I}}^{k}(s,r)= \sum _{n=0}^{k}\frac{\tilde{\mathbb {I}_{n}}}{s^{n\alpha +1}}, \tilde{\mathbb {A}}^{k}(s,r)=\sum _{n=0}^{k}\frac{\tilde{\mathbb {A}_{n}}}{s^{n\alpha +1}},\nonumber \\&\tilde{\mathbb {C}}^{k}(s,r)=\sum _{n=0}^{k}\frac{\tilde{\mathbb {C}_{n}}}{s^{n\alpha +1}}, \tilde{\mathbb {T}}^{k}(s,r)= \sum _{n=0}^{k}\frac{\tilde{\mathbb {T}_{n}}}{s^{n\alpha +1}}, \tilde{\mathbb {R}}^{k}(s,r)= \sum _{n=0}^{k}\frac{\tilde{\mathbb {R}_{n}}}{s^{n\alpha +1}} \end{aligned}$$
(15)

Where \(\tilde{\mathbb {S}_{n}},\tilde{\mathbb {E}_{n}},\tilde{\mathbb {I}_{n}},\tilde{\mathbb {A}_{n}},\tilde{\mathbb {C}_{n}},\tilde{\mathbb {T}_{n}}\) and \(\tilde{\mathbb {R}_{n}}\) are the unknown coefficients

\(k^{th}\) Laplace residual functions are

$$\begin{aligned} \mathcal {L}Res\tilde{\mathbb {S}}^{k}(s,r)&=\tilde{\mathbb {S}}^{k}(s,r)-\frac{\tilde{\mathbb {S}_{0}}}{s}+\frac{1}{s^{\alpha }}\left[ \frac{\Lambda }{s} +\mathcal {L}\left( \tilde{\beta } (\mathcal {L}^{-1}\tilde{\mathbb {I}}^{k}(s,r) + \phi \mathcal {L}^{-1}\tilde{ \mathbb {A}}^{k}(s,r)+ \epsilon \mathcal {L}^{-1}\tilde{\mathbb {C}}^{k}(s,r)) \mathcal {L}^{-1}\tilde{\mathbb {S}}^{k}(s,r) \right) \right] \nonumber \\&\quad +\frac{1}{s^{\alpha }}\left[ \mu \tilde{ \mathbb {S}}^{k}(s,r)\right] \nonumber \\ \mathcal {L}Res\tilde{\mathbb {E}}^{k}(s,r)&=\tilde{\mathbb {E}}^{k}(s,r)-\frac{\tilde{\mathbb {E}_{0}}}{s}+\frac{1}{s^{\alpha }}\left[ \mathcal {L}\left( \tilde{\beta } (\mathcal {L}^{-1}\tilde{\mathbb {I}}^{k}(s,r) + \phi \mathcal {L}^{-1}\tilde{ \mathbb {A}}^{k}(s,r)+ \epsilon \mathcal {L}^{-1}\tilde{\mathbb {C}}^{k}(s,r)) \mathcal {L}^{-1}\tilde{\mathbb {S}}^{k}(s,r) \right) \right] \nonumber \\&\quad + \frac{1}{s^{\alpha }}\left[ (\mu + \tilde{\psi }) \tilde{\mathbb {E}}^{k}(s,r)\right] \nonumber \\ \mathcal {L}Res \tilde{\mathbb {I}}^{k}(s,r)&=\tilde{\mathbb {I}}^{k}(s,r)-\frac{\tilde{\mathbb {I}_{0}}}{s}+\frac{1}{s^{\alpha }}\left[ \tilde{\psi } \theta \tilde{\mathbb {E}}^{k}(s,r) + (\mu + \gamma + \tilde{\eta } + \kappa ) \tilde{\mathbb {I}}^{k}(s,r)\right] \nonumber \\ \mathcal {L}Res \tilde{\mathbb {A}}^{k}(s,r)&=\tilde{\mathbb {A}}^{k}(s,r)-\frac{\tilde{\mathbb {A}_{0}}}{s}+\frac{1}{s^{\alpha }}\left[ \tilde{\psi } (1-\theta )\tilde{ \mathbb {E}}^{k}(s,r) + (\mu + \tilde{\tau }+ \nu +\zeta ) \tilde{\mathbb {A}}^{k}(s,r)\right] \nonumber \\ \mathcal {L}Res\tilde{\mathbb {C}}^{k}(s,r)&=\tilde{\mathbb {C}}^{k}(s,r)-\frac{\tilde{\mathbb {C}_{0}}}{s}+\frac{1}{s^{\alpha }} \left[ \tilde{\eta }\tilde{\mathbb {I}}^{k}(s,r) + \tilde{\tau }\tilde{\mathbb {A}}^{k}(s,r) + (\mu + \varepsilon + \tilde{\sigma }+\delta ) \tilde{\mathbb {C}}^{k}(s,r)+\omega \tilde{ \mathbb {T}}^{k}(s,r)\right] \nonumber \\ \mathcal {L}Res\tilde{\mathbb {T}}^{k}(s,r)&=\tilde{\mathbb {T}}^{k}(s,r)-\frac{\tilde{\mathbb {T}_{0}}}{s}+\frac{1}{s^{\alpha }}\left[ \gamma \tilde{\mathbb {I} }^{k}(s,r)- \zeta \tilde{\mathbb {A}}^{k}(s,r)- \delta \mathcal {L}Res\tilde{\mathbb {C}}^{k}(s,r)+(\mu +\omega +\tilde{\varrho })\tilde{\mathbb {T}}^{k}(s,r)\right] \nonumber \\ \mathcal {L}Res \tilde{\mathbb {R}}^{k}(s,r)&=\tilde{\mathbb {R}}^{k}(s,r)-\frac{\tilde{\mathbb {R}_{0}}}{s}+\frac{1}{s^{\alpha }}\left[ \kappa \tilde{\mathbb {I}}^{k}(s,r) - \tilde{\sigma }\tilde{\mathbb {C}}^{k}(s,r) - \nu \tilde{\mathbb {A}}^{k}(s,r) -\tilde{\varrho } \tilde{\mathbb {T} }^{k}(s,r) + \mu \tilde{\mathbb {R}}^{k}(s,r)\right] \end{aligned}$$
(16)

To determine unknown coefficients let we consider \(k=1\) in (15) as follows

$$\begin{aligned} \mathcal {L}Res\tilde{\mathbb {S}}^{1}(s,r)&=\tilde{\mathbb {S}}^{1}(s,r)-\frac{\tilde{\mathbb {S}_{0}}}{s}+\frac{1}{s^{\alpha }}\left[ \frac{\Lambda }{s} +\mathcal {L}\left( \tilde{\beta } (\mathcal {L}^{-1}\tilde{\mathbb {I}}^{1}(s,r) + \phi \mathcal {L}^{-1}\tilde{ \mathbb {A}}^{1}(s,r)+ \epsilon \mathcal {L}^{-1}\tilde{\mathbb {C}}^{1}(s,r)) \mathcal {L}^{-1}\tilde{\mathbb {S}}^{1}(s,r) \right) \right] \nonumber \\ &\quad +\frac{1}{s^{\alpha }}\left[ \mu \tilde{ \mathbb {S}}^{1}(s,r)\right] \nonumber \\ \mathcal {L}Res\tilde{\mathbb {E}}^{1}(s,r)&=\tilde{\mathbb {E}}^{1}(s,r)-\frac{\tilde{\mathbb {E}_{0}}}{s}+\frac{1}{s^{\alpha }}\left[ \mathcal {L}\left( \tilde{\beta } (\mathcal {L}^{-1}\tilde{\mathbb {I}}^{1}(s,r) + \phi \mathcal {L}^{-1}\tilde{ \mathbb {A}}^{1}(s,r)+ \epsilon \mathcal {L}^{-1}\tilde{\mathbb {C}}^{1}(s,r)) \mathcal {L}^{-1}\tilde{\mathbb {S}}^{1}(s,r) \right) \right] \nonumber \\ &\quad + \frac{1}{s^{\alpha }}\left[ (\mu + \tilde{\psi }) \tilde{\mathbb {E}}^{1}(s,r)\right] \nonumber \\ \mathcal {L}Res \tilde{\mathbb {I}}^{1}(s,r)&=\tilde{\mathbb {I}}^{1}(s,r)-\frac{\tilde{\mathbb {I}_{0}}}{s}+\frac{1}{s^{\alpha }}\left[ \tilde{\psi } \theta \tilde{\mathbb {E}}^{1}(s,r) + (\mu + \gamma + \tilde{\eta } + \kappa ) \tilde{\mathbb {I}}^{1}(s,r)\right] \nonumber \\ \mathcal {L}Res \tilde{\mathbb {A}}^{1}(s,r)&=\tilde{\mathbb {A}}^{1}(s,r)-\frac{\tilde{\mathbb {A}_{0}}}{s}+\frac{1}{s^{\alpha }}\left[ \tilde{\psi } (1-\theta )\tilde{ \mathbb {E}}^{1}(s,r) + (\mu + \tilde{\tau }+ \nu +\zeta ) \tilde{\mathbb {A}}^{1}(s,r)\right] \nonumber \\ \mathcal {L}Res\tilde{\mathbb {C}}^{1}(s,r)&=\tilde{\mathbb {C}}^{1}(s,r)-\frac{\tilde{\mathbb {C}_{0}}}{s}+\frac{1}{s^{\alpha }} \left[ \tilde{\eta }\tilde{\mathbb {I}}^{1}(s,r) + \tilde{\tau }\tilde{\mathbb {A}}^{1}(s,r) + (\mu + \varepsilon + \tilde{\sigma }+\delta ) \tilde{\mathbb {C}}^{1}(s,r)+\omega \tilde{ \mathbb {T}}^{1}(s,r)\right] \nonumber \\ \mathcal {L}Res\tilde{\mathbb {T}}^{1}(s,r)&=\tilde{\mathbb {T}}^{1}(s,r)-\frac{\tilde{\mathbb {T}_{0}}}{s}+\frac{1}{s^{\alpha }}\left[ \gamma \tilde{\mathbb {I} }^{1}(s,r)- \zeta \tilde{\mathbb {A}}^{1}(s,r)- \delta \mathcal {L}Res\tilde{\mathbb {C}}^{1}(s,r)+(\mu +\omega +\tilde{\varrho })\tilde{\mathbb {T}}^{1}(s,r)\right] \nonumber \\ \mathcal {L}Res \tilde{\mathbb {R}}^{1}(s,r)&=\tilde{\mathbb {R}}^{1}(s,r)-\frac{\tilde{\mathbb {R}_{0}}}{s}+\frac{1}{s^{\alpha }}\left[ \kappa \tilde{\mathbb {I}}^{1}(s,r) - \tilde{\sigma }\tilde{\mathbb {C}}^{1}(s,r) - \nu \tilde{\mathbb {A}}^{1}(s,r) -\tilde{\varrho } \tilde{\mathbb {T} }^{1}(s,r) + \mu \tilde{\mathbb {R}}^{1}(s,r)\right] \end{aligned}$$
(17)

Since for \(k=1\), \(\tilde{\mathbb {S}}^{1}(s,r)=\frac{\tilde{\mathbb {S}_{0}}}{s}+ \frac{\tilde{\mathbb {S}_{1}}}{s^{\alpha +1}} , \tilde{\mathbb {E}}^{1}(s,r)=\frac{\tilde{\mathbb {E}_{0}}}{s}+ \frac{\tilde{\mathbb {E}_{1}}}{s^{\alpha +1}} \cdots \tilde{\mathbb {R}}^{1}(s,r)=\frac{\tilde{\mathbb {R}_{0}}}{s}+ \frac{\tilde{\mathbb {R}_{1}}}{s^{\alpha +1}}\) we obtain following truncated series using in above system and multiply by \(s^{\alpha +1}\) to each equation of a system . Then we solve the following system

$$\begin{aligned}&\lim _{{s \rightarrow \infty }} \left( s^{\alpha +1}\mathcal {L}Res\tilde{\mathbb {S}}^{1}(s,r)\right) = 0, \lim _{{s\rightarrow \infty }}\left( s^{\alpha +1}\mathcal {L}Res\tilde{\mathbb {E}}^{1}(s,r)\right) = 0, \lim _{{s \rightarrow \infty }}\left( s^{\alpha +1}\mathcal {L}Res\tilde{\mathbb {I}}^{1}(s,r)\right) = 0,\nonumber \\&\lim _{{s \rightarrow \infty }}\left( s^{\alpha +1}\mathcal {L}Res\tilde{\mathbb {A}}^{1}(s,r)\right) =0, \lim _{{s \rightarrow \infty }}\left( s^{\alpha +1}\mathcal {L}Res\tilde{\mathbb {C}}^{1}(s,r)\right) = 0, \lim _{{s \rightarrow \infty }} \left( s^{\alpha +1}\mathcal {L}Res\tilde{\mathbb {T}}^{1}(s,r)\right) =0,\nonumber \\&\lim _{{s \rightarrow \infty }} \left( s^{\alpha +1}\mathcal {L}Res\tilde{\mathbb {R}}^{1}(s,r)\right) =0 \end{aligned}$$
(18)

to obtain the following outputs

$$\begin{aligned} \tilde{\mathbb {S}_{1}}&=-\mathbb {S}_{0} \mathbb {I}_{0} \beta - \mathbb {S}_{0} \mathbb {C}_{0} \beta \epsilon - \mathbb {S}_{0} \mu + \Lambda - \mathbb {S}_{0} \mathbb {A}_{0} \beta \phi \nonumber \\ \tilde{\mathbb {E}_{1}}&= \mathbb {S}_{0} \mathbb {I}_{0} \beta + \mathbb {S}_{0} \mathbb {C}_{0} \beta \epsilon - \mathbb {E}_{0} \mu + \mathbb {S}_{0} \mathbb {A}_{0} \beta \phi - \mathbb {E}_{0} \psi ,\nonumber \\ \tilde{\mathbb {I}_{1}}&= - \mathbb {I}_{0} \gamma -\mathbb {I}_{0}\eta -\mathbb {I}_{0} \kappa -\mathbb {I}_{0} \mu +\mathbb {E}_{0} \theta \psi ,\nonumber \\ \tilde{\mathbb {A}_{1}}&=-\mathbb {A}_{0} \mu -\mathbb {A}_{0}\tau -\mathbb {A}_{0}\nu -\mathbb {A}_{0} \zeta +\mathbb {E}_{0} \psi -\mathbb {E}_{0} \theta \psi ,\nonumber \\ \tilde{\mathbb {C}_{1}}&=-\mathbb {C}_{0} \delta + \mathbb {I}_{0} \eta - \mathbb {C}_{0} \mu - \mathbb {C}_{0}\xi - \mathbb {C}_{0} \sigma + \mathbb {A}_{0} \tau + \mathbb {T}_{0} \omega ,\nonumber \\ \tilde{\mathbb {T}_{1}}&=\mathbb {I}_{0} \gamma + \mathbb {C}_{0} \delta - \mathbb {T}_{0} \mu - \mathbb {T}_{0} \rho + \mathbb {A}_{0} \zeta - \mathbb {T}_{0} \omega ,\nonumber \\ \tilde{\mathbb {R}_{1}}&=\mathbb {I}_{0} \kappa -\mathbb {R}_{0} \mu +\mathbb {A}_{0}\nu +\mathbb {T}_{0} \varrho +\mathbb {C}_{0}\sigma \end{aligned}$$
(19)

In a same way unknown \(\tilde{\mathbb {S}_{n}},\tilde{\mathbb {E}_{n}}, \tilde{\mathbb {I}_{n}},\tilde{\mathbb {A}_{n}},\tilde{\mathbb {C}_{n}},\tilde{\mathbb {T}_{n}}\) and \(\tilde{\mathbb {R}_{n}}\) can be found.

Table 2 RPS solutions and residual errors for the fuzzy-fractional HBV Model at \(\alpha =1\) and \(r=1\).
Full size table
Table 3 RPS lower bound solutions and residual errors for the fuzzy-fractional HBV Model at \(\alpha =1\) and \(r=0.7\).
Full size table
Table 4 RPS upper bound solutions and residual errors for the fuzzy-fractional HBV Model at \(\alpha =1\) and \(r=0.7\).
Full size table
Figure 1
figure 1

Effect of \(\beta\) on HBV model.

Full size image
Figure 2
figure 2

Effect of \(\eta\) and \(\psi\) on HBV model.

Full size image
Figure 3
figure 3

Effect of \(\tau , \sigma\) and \(\varrho\) on HBV model.

Full size image
Figure 4
figure 4

Effect of different values of \(\alpha\) on HBV model.

Full size image
Figure 5
figure 5

Graphical representation of fuzzy-fractional HBV model at lower bound for various \(\alpha\).

Full size image
Figure 6
figure 6

Graphical representation of fuzzy-fractional HBV model at upper bound for various \(\alpha\).

Full size image

Discussion and analysis of fuzzy-fractional HBV model

The proposed model divides the population into several compartments Susceptible \(\mathbb {S}\), Exposed \(\mathbb {E}\), Acute Infected \(\mathbb {I}\), Asymptomatic \(\mathbb {A}\), Chronic \(\mathbb {C}\), Treated \(\mathbb {T}\), and Recovered \(\mathbb {R}\) to represent the various stages of Hepatitis B virus (HBV) infection. These compartments are selected based on the established clinical and biological stages of the disease. The parameters, including the infection rate \(\beta\), recovery rate \(\gamma\), and the rate of progression to chronic infection \(\eta\), are determined from existing empirical data, ensuring that the model reflects real-world HBV dynamics. The inclusion of the Treated \(\mathbb {T}\) compartment allows for an improved simulation of the effects of antiviral treatment on disease progression. Consider the HBV system modeled in fuzzy-fractional form as (10) with fuzzified initial conditions as:

$$\begin{aligned} \underline{\tilde{\mathbb {S}}(0)},\overline{\tilde{\mathbb {S}}(0)}&= \left[ \left( 1 -\sqrt{-\log (r) \cdot 2 \cdot (0.735)^2}\right) \cdot 60, \left( 1 + \sqrt{-\log (r) \cdot 2 \cdot (0.735)^2}\right) \cdot 60\right] \nonumber \\ \underline{\tilde{\mathbb {E}}(0)}, \overline{\tilde{\mathbb {E}}(0)}&= \left[ \left( 1 - \sqrt{-\log (r) \cdot 2 \cdot (0.735)^2}\right) \cdot 40, \left( 1 + \sqrt{-\log (r) \cdot 2 \cdot (0.735)^2}\right) \cdot 40\right] ,\nonumber \\ \underline{\tilde{\mathbb {I}}(0)},\overline{\tilde{\mathbb {I}}(0)}&= \left[ \left( 1 - \sqrt{-\log (r) \cdot 2 \cdot (0.735)^2}\right) \cdot 3, \left( 1 + \sqrt{-\log (r) \cdot 2 \cdot (0.735)^2}\right) \cdot 3\right] ,\nonumber \\ \underline{\tilde{\mathbb {A}}(0)},\overline{\tilde{\mathbb {A}}(0)}&= \left[ \left( 1 - \sqrt{-\log (r) \cdot 2 \cdot (0.735)^2}\right) \cdot 2,\left( 1 + \sqrt{-\log (r) \cdot 2 \cdot (0.735)^2}\right) \cdot 2\right] \nonumber \\ \underline{\tilde{\mathbb {C}}(0)},\overline{\tilde{\mathbb {C}}(0)}&=\left[ \left( 1 - \sqrt{-\log (r) \cdot 2 \cdot (0.735)^2}\right) \cdot 1,\left( 1 + \sqrt{-\log (r) \cdot 2 \cdot (0.735)^2}\right) \cdot 1\right] ,\nonumber \\ \underline{\tilde{\mathbb {T}}(0)},\overline{\tilde{\mathbb {T}}(0)}&= 0,\nonumber \\ \underline{\tilde{\mathbb {R}}(0)},\overline{\tilde{\mathbb {R}}(0)}&= 0 \end{aligned}$$
(20)

Using solution methodology given in section 8, we solve fuzzy-fractional system of HBV model after incorporating a treatment compartment and then extending it to a fuzzy-fractional model to capture the complex dynamics of HBV transmission, accounting for uncertainty and memory effects. Uncertainty was integrated into the fractional model using Gaussian fuzzy numbers, resulting in a fuzzy-fractional model. For the numerical analysis of the fuzzy-fractional HBV model, we applied the extended residual power series method (RPSM) to obtain approximate solutions and evaluate residual errors. Tables 2, 3, and 4 present these approximate solutions along with residual errors at fuzzy lower and upper bounds at integer order and various values of \(r-cut\). Graphical analysis, shown in Figs. 1, 2, and 3, explores the effects of various parameters on the HBV model. Figures 4, 5, and 6 illustrate the lower and upper bounds of the fuzzy-fractional model for different values of the fractional parameter \(\alpha\), demonstrating the range of outcomes under uncertainty, represented by Gaussian fuzzy numbers. These analyses provide valuable insights into the transmission dynamics of HBV and assess the robustness of model predictions under uncertain conditions and parameters.

Conclusion

Hepatitis B virus infection continues to pose a significant threat in both developed and developing countries, with a substantial number of cases still being reported. To mitigate the spread of this infection, it is crucial to provide timely treatment for individuals in the early stages of the disease, prevent the reuse of medical equipment, and raise awareness especially in rural areas about the risks of seeking treatment from non-professionals. In this study, a new mathematical model has been developed to analyze the dynamics of HBV in the presence of a treatment compartment. The simulation results offer valuable insights and can be highly beneficial to healthcare professionals and other stakeholders in the field. The primary objective was to evaluate the effects of treatment on disease transmission, incorporating uncertainty in the parameters by utilizing Gaussian fuzzy numbers, and to explore potential eradication strategies. A detailed stability analysis has been conducted, demonstrating that the proposed model is locally asymptotically stable at the disease-free equilibrium when \(R_0 < 1\). A semi-numerical approach was employed to investigate several mathematical aspects of the model, and graphical representations illustrate the effects of various parameters on different disease profiles at upper and lower bounds in a fractional-order environment. This analysis, which incorporates the novel assumptions of a treatment compartment and fuzzification within the model, provides deeper insights into HBV dynamics. The proposed methodology is expected to be particularly beneficial for researchers studying various aspects of HBV transmission and control.