Revisiting the Born–Infeld-AdS black hole phase structure through Landau theory and free energy landscape approaches

Abstract

In our present work, we probe the thermal phase transition structure, the dynamic and kinetic behavior of the Born–Infeld-AdS black hole. With the emergence of a triple point behavior and the possible ruling out the reentrant phase transition, for a certain parametric value of the charge parameter, we scrutinize the stochastic dynamics and the kinetic processes using the free energy landscape formalism. Such processes occur during the black hole phase transitions in terms of the Landau functional and equivalently by the Fokker–Planck equation in the context of black hole chemistry. Our analysis establishes a pertinent bridge between the thermal behavior among the different states of the Van-der-Waals-like fluids and the Born–Infeld-AdS black hole phases. To visualize the direct implications of the Landau functional of the usual Van-der-Waals-like fluids, we consistently employed the generic Landau formalism. We find that such investigations are worthy of study in implementing the continuous phase transition behavior during Hawking radiation. For more details, and in addition to the exploitation of the Landau functional, we introduce its convexity to determine its extreme points and the corresponding stable and unstable phases of the thermal black hole systems. We systematically study the behavior of the first-order and the second-order phase transitions and look into details of their evolution during thermal transitions. Moreover, knowing that the thermal phase transitions are controlled through a stochastic process depending upon an order parameter, the dynamics during its phases are determined through the fluctuating macroscopic variables, we recall the dynamical Fokker–Planck equation to furnish the advancement of such a process in the Born–Infeld-AdS background with a special focus on the probability distribution of the triple point. The evolution of the initial probability indicates that not only the initial small black hole to the final large black hole phase occurs, but also one has the equilibrium conditions established among the thermal radiations to the small black holes or the large black holes to thermal radiations and large black hole states. We also demonstrate the first passage time for the different black hole phase behaviors to determine their time scale using the Crank-Niclson method. Such a study has implications for the friction effects of the kinetic turnover of different black hole phases and consequently a direct connection to the microscopic degrees of freedom.

Introduction

In the realm of theoretical high-energy physics, the thermodynamics of black holes presents an intriguing and promising avenue for probing their quantum nature. This field offers a potential pathway towards the development of a quantum gravitational theory, particularly when examined within the framework of anti-de Sitter (AdS) space and conformal field theory (CFT)^1,2. The discovery of the Hawking-Page phase transition between the AdS thermal bath and large Schwarzschild-AdS black holes triggered a flurry of thermodynamic activities in the last few decades^{3,4,5,6,7,8,9,10,11,12,13,14}. Further, the black hole chemistry, i.e., the thermodynamics with a negative cosmological constant, made an open room to understand the different and new thermodynamics phenomena from the AdS/CFT perspectives^{15,16,17,18,19,20,21}. The gravitational viewpoint of the Van-der-Waals (VdW) fluid, the reentrant phase transition of the multicomponent liquids, the thermal behavior of the triple points, the polymer phases, and the superfluidity have uplifted the status of thermodynamics of a wide range of AdS black holes^{22,23,24,25,26,27,28,29,30,31,32,33,34,35,36}. Among various solutions, the Born–Infeld black holes in AdS spacetime have been of great importance^37,38. The Born–Infeld gravity is a nonlinear generalization of Maxwell’s electrodynamics calibrated by the Born–Infeld parameter which was originally used to establish a finite energy density model for the electron in the 1930s³⁹. Such kind of electrodynamics with the goal of avoiding divergences such as the infinite self-energy of a point charge are very important to understand the short-distance behavior of the electromagnetic field. Therewith, they arise naturally in the context of superstring theory and D-brane physics^{40,41,42,43,44}. Born–Infeld electrodynamics has been also explored in the context of cosmology, offering alternative models of the early universe^45,46,47. In a more recent development, Born–Infeld electrodynamics has been incorporated to modify the Einstein-Hilbert action, garnering significant attention and emphasis in literature^{48,49,50,51,52} from different physical point of views^{53,54,55,56,57,58,59,60,61,62}. In addition to this, such nonlinear solutions present some exotic thermodynamic behaviors. Indeed, the reentrant phase transition behaviors which were uncommon in the study of thermodynamics were first observed in the case of Born–Infeld AdS black holes in four-dimensional spacetime⁶³, instead, this phase transition was examined in the usual thermodynamic systems exhibiting the nicotine/water mixture⁶⁴. Otherwise, the reentrant phase transition (RPT) can be understood as a thermodynamic phenomenon of multicomponent liquids when the thermal system goes through multiple phases for a monotonic variation of any of the thermodynamic variables, provided the initial and the final states of the system shows the same macroscopic behaviors. After its inception for the conventional thermodynamic system, the reentrant phase transition has been reported for a wide class of AdS black hole systems^{17,65,66,67,68,69,70,71,72,73,74,75} apart from four-dimensional Born–Infeld AdS black holes. However, the Born–Infeld AdS black hole in dimensions greater than four does not show the reentrant phase transition⁷⁶.

The thermal properties of AdS black holes have surpassed the core idea of black hole mechanics and landed into much richer physics that is probed through the critical points and different tools^{77,78,79,80,81,82}. During the small to large phase transitions the thermodynamic properties change, which in turn affects the dynamic and kinetic processes that indicate the evolution of thermal systems through any thermodynamic process. Such dynamical evolution is systematically analyzed through Landau’s theory of free energy and controlled via the Landau functional^83,84. Rigorously speaking, during a phase transition, the system experiences a non-equilibrium state, and the Landau parameters play a pivotal role in discerning the thermal phase transition characteristics. This is particularly evident in systems such as VdW-type fluids or charged AdS black holes. As a result, the Landau functional manifests itself into a local minimum, effectively mimicking a second-order phase transition. On the other hand, in the case of first-order transitions spanning different phases, the Landau functional corresponds to a global minimum across the extended thermodynamic phases of AdS black hole systems.

Recently, the idea comprising the free energy landscape has been introduced from the perspectives of connecting the thermodynamic properties, the dynamics, and the kinetic transition processes through a stochastic process à la Fokker–Planck equation. In thermal statistical physics, the dynamical Fokker–Planck relation is employed to study the time profile of the probability density function for any generic observable⁸⁵. For black hole thermal systems, such notions were first explored in the context of the phase transition due to Hawking and Page and also for the massive gravity scenarios⁸⁶. The concept of representing the off-shell Gibbs free energy as dependent on the order parameter (e.g., the horizon radius), was the crucial identification behind such studies. The investigations of the free energy landscape are still under improvement, though people studied it for a wide range of black holes in Einstein as well as in modified gravity theories in asymptotically AdS spacetime.

Following the initial exploration of the dynamics of Schwarzschild-AdS spacetime within the framework of the free energy landscape proposal, this conceptualization has undergone successive expansions. Notably, it has been applied to charged AdS black hole systems⁸⁷, charge-neutral Gauss–Bonnet gravity theories⁸⁸ and their charged counterparts in four-dimensional spacetime⁸⁹. The investigation then delved into determining the dynamics of the triple point for six-dimensional electrically charged Gauss–Bonnet-AdS systems⁹⁰ and extended to incorporate modifications related to dark energy in charged AdS systems⁹¹. Additionally, it explored the black hole spacetime in the presence of a minimal coupling of general relativity to nonlinear electromagnetic sources^92,93, and more recently, Euler-Heisenberg-AdS black holes⁹⁴. The Analysis of the dynamical evolution is also involved by considering the effects of path integral and instanton approaches⁹⁵. For certain cases, the free energy landscape was extended to take into account the non-Markovian effects^96,97. This approach was further applied to rotating solutions, as seen in similar analyses of Kerr-AdS black holes⁹⁸. The free energy landscape problem underwent additional exploration through the generalized Fokker–Planck equation⁹⁹. Supplementary to recent developments, the topology of the free energy landscape and the identification of a dominant route in the dynamic and kinetic process during black hole phase alternation were analyzed for electrically charged AdS spacetime in Gauss–Bonnet gravity¹⁰⁰.

In our investigation, we will explore the thermal phase transition characteristics of AdS black holes within the Born–Infeld gravitational framework. Our focus entails a comprehensive examination of the free energy landscape for Born–Infeld-AdS black holes, employing both Landau theory and the Fokker–Planck equation. Our inquiry will be extended to the dynamic evolution of these black holes during thermal transitions and also probe reentrant phase transitions. A pivotal aspect of our study involves the Born–Infeld parameter, which significantly influences the horizon size. The radius of the horizon, in turn, serves as the order parameter. Our subsequent analysis will elucidate the dependency of the Landau functional or Gibbs free energy on the horizon radius, effectively forming a one-dimensional curve.

The structure of our paper unfolds as follows. In “Born–Infeld black hole in AdS spacetime and its thermodynamical criticality” section provides a comprehensive review of fundamental concepts related to Born–Infeld-AdS black holes, encompassing their solutions and relevant thermodynamic quantities of interest. Moving forward, we delve into an in-depth analysis of criticaxl points and their coordinates. The formalism of the Landau functional takes a central stage in “Born–Infeld AdS black hole phases picture from the Landau theory point of view” section, thereby shedding light on the dependence of free energy due to the Born–Infeld parameter. Afterward, in “Exploring free energy landscape through the Fokker–Planck equation: unveiling probabilistic dynamics” section, we shift our focus on the dynamic and kinetic processes governing the thermal system as it undergoes various phase transitions. This exploration is probed through the application of the Fokker–Planck equation. Our findings and overall conclusions are encapsulated in “Kinetics and fluctuations in the dynamics of Born–Infeld-AdS black hole state transitions” section, where we provide a concise summary and offer final remarks on the implications of our study.

Born–Infeld black hole in AdS spacetime and its thermodynamical criticality

The starting point is the action describing the four-dimensional general relativity where the Born–Infeld electrodynamics is considered³⁸

$$\begin{aligned} \mathcalligra{S} = \dfrac{1}{16 \pi } \int d^4x\sqrt{-g}\left[ R-2 \Lambda + 4 b^2 \left( 1 - \sqrt{1+\dfrac{F_{\mu \nu } F^{\mu \nu }}{2 b^2}}\right) \right] , \end{aligned}$$

(1)

in which R denotes the Ricci scalar curvature, $\Lambda$ is the cosmological constant expressed as $\Lambda = -3/l^2$, where l is the AdS radius and b stands for the Born–Infeld parameter having the dimension of mass and has a connection to the string tension $\alpha '$ as $b = 1 / \left( 2 \pi \alpha ' \right)$⁴⁴. The electromagnetic tensor field $F_{\mu \nu }$ is given in terms of the four potential $A_{\mu }$ by $F_{\mu \nu } = \partial _{\mu } A_{\nu }-\partial _{\nu } A_{\mu }$. The ansatz of the 4-dimensional static geometry with spherical symmetry has the following form

$$\begin{aligned} ds^2 = - f(r) dt^2 + \dfrac{dr^2}{f(r)}+ r^2 d\Omega ^2, \end{aligned}$$

(2)

where, $d\Omega$ is the line element on a unit $2$-sphere and the blackening function f(r) is obtained to be^37,38,50

$$\begin{aligned} f(r) = 1 + \dfrac{r^2}{l^2}-\dfrac{m}{r}+\dfrac{2 b^2 r^2}{3}\left( 1 - \sqrt{1+\dfrac{16 \pi ^2 Q^2}{b^2 r^2}}\right) +\dfrac{64 \pi ^2 Q^2}{3 r^2} _2\mathcalligra{F}_1\left[ \dfrac{1}{4}, \dfrac{1}{2}, \dfrac{5}{4}, - \dfrac{16 \pi ^2 Q^2}{b^2 r^2} \right] , \end{aligned}$$

(3)

with $_2\mathcalligra{F}_1\left[ a,b,c,d \right]$ is the hypergeometric function of the second kind, the black hole mass M can be expressed via the integration constant m as $M = m/8\pi$. The electric charge per unit volume $\omega =4\pi$ is denoted by Q. Within the spherical symmetric distribution, the only non-zero component is

$$\begin{aligned} A_t(r) = - \dfrac{4 \pi Q}{r} _2\mathcalligra{F}_1\left[ \dfrac{1}{4}, \dfrac{1}{2}, \dfrac{5}{4}, - \dfrac{16 \pi ^2 Q^2}{b^2 r^2} \right] . \end{aligned}$$

(4)

The limiting case of the Reissner–Nordstrom (RN)-AdS black hole^101,102 can easily be recovered by taking the limit $b \rightarrow \infty$ in the metric function and the gauge potential. The Hawking temperature of Born–Infeld AdS spacetime metric is found to be

$$\begin{aligned} T = \dfrac{1}{4 \pi } \left. \dfrac{\partial f(r)}{\partial r}\right| _{r=r_h} = \dfrac{1}{4 \pi r_h} + \dfrac{3 r_h}{4 \pi l^2} + \dfrac{b^2 r_h}{2\pi } \left( 1 - \sqrt{1+\dfrac{16 \pi ^2 Q^2}{b^2 r_h^2}}\right) . \end{aligned}$$

(5)

in which $r_h$ is the event horizon radius, obtained as the largest positive real solution of the blackening function, $f(r)=0$. The electric potential at spatial infinity relative to the event horizon reads as

$$\begin{aligned} \Phi = \dfrac{\partial M}{\partial Q} = \dfrac{4 \pi Q}{r_h} _2\mathcalligra{F}_1\left[ \dfrac{1}{4}, \dfrac{1}{2}, \dfrac{5}{4}, - \dfrac{16 \pi ^2 Q^2}{b^2 r_h^2} \right] . \end{aligned}$$

(6)

The first law of thermodynamics associated with the Born–Infeld-AdS black hole, is obtained by defining its key ingredients, namely entropy S, pressure P, and the volume V⁶³

$$\begin{aligned} \begin{aligned} S&=\int \dfrac{1}{T} \dfrac{\partial M}{\partial r_h} d r_h = \dfrac{r_h^2}{4}, \quad P = - \dfrac{\Lambda }{8 \pi }, \quad V = \dfrac{\partial M}{\partial P} = \dfrac{r_h^3}{4}, \\ \mathcalligra{B}&= \dfrac{\partial M}{\partial b} = \dfrac{b r_h^3}{6 \pi } \left( 1 - \sqrt{1+\dfrac{16 \pi ^2 Q^2}{b^2 r_h^2}}\right) + \dfrac{4 \pi Q^2}{3 b r_h} _2\mathcalligra{F}_1\left[ \dfrac{1}{4}, \dfrac{1}{2}, \dfrac{5}{4}, - \dfrac{16 \pi ^2 Q^2}{b^2 r_h^2} \right] , \end{aligned} \end{aligned}$$

(7)

the additional quantity $\mathcalligra{B}$ is conjugated to b which is interpreted as the Born–Infeld vacuum polarization⁶³, so that the first law and the related Smarr formula take the forms

$$\begin{aligned} \begin{aligned} dM&= T dS + \Phi dQ + V dP + \mathcalligra{B}db,\\ M&= 2 T S + \Phi Q - 2 P V - \mathcalligra{B} b. \end{aligned} \end{aligned}$$

(8)

We should keep in mind that the thermodynamic quantities M, Q, S, and V are written per unit volume $\omega$.

Following¹⁰³, we look into the Born–Infeld-AdS black hole critical behavior, where the black hole charge is allowed to vary but the cosmological constant remains a constant parameter. The specific heat at a constant charge is expressed as

$$\begin{aligned} C_Q = T\left( \dfrac{\partial S}{\partial T}\right) _Q, \end{aligned}$$

(9)

and the stability/instability during the phase transition can be found by considering the sign (positive/negative) of this quantity.

Note that Eq. (9) is also calculated with l and b taken as fixed. In addition, the Born–Infeld parameter significantly impacts the temperature of the black hole, particularly when the horizon radius is small. Depending on the value of the nonlinear parameter b, the BI-AdS black hole exhibits distinct behavior. For $Q \ge Q_m$, where $Q_m = \frac{1}{8\pi b}$ is the marginal charge, the black hole resembles a Reissner-Nordström-anti-de-Sitter (RN-AdS) black hole. Conversely, for $Q < Q_m$, it resembles a Schwarzschild-like black hole. Another important black hole charge, $Q_c$, emerges in the Reissner-Nordström configuration. The presence of this quantity associated with the critical behavior leads to a change in the phase structure.

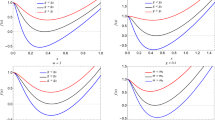
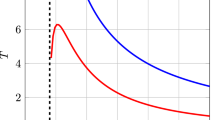
To unveil the thermal behavior of the Born–Infeld-AdS spacetime, we depict the variation of the temperature T and the specific heat $C_Q$ as a function of the event horizon radius $r_h$ within various values of the charge in Figs. 1 and 2 respectively.

Fig. 1

Temperature T in terms of the event horizon radius $r_h$ for different values of charge Q with $l=1$ and $b=3.5$. Herein $Q_{m}= 0.0113682$ and $Q_{c}= 0.0136024$.

Obviously, one can notice that the behavior of the temperature is highly influenced by the black holes’ charge for small $r_h$. So, for small $r_h$ values, we can Taylor expand the Hawking temperature as

$$\begin{aligned} T =\dfrac{2b}{r_h}\left( Q_m-Q \right) + \dfrac{r_h\left( 3+2 b^2l^2\right) }{4 \pi l^2}-\dfrac{b^3r_h^3}{16 \pi ^2Q} +\mathcalligra{O}(r_h^4), \end{aligned}$$

(10)

Besides, the large limit of $r_h$ corresponds to the Hawking temperature, $T=\frac{3 r_h}{4 \pi l^2}$ which is independent of the charge and which explains the linearly increasing behaviour of the temperature for the large $r_h$.

Fig. 2

The specific heat capacity $C_Q$ in terms of the event horizon radius $r_h$ for different values of charge Q with $l=1$ and $b=3.5$. Herein $Q_{m}= 0.0113682$ and $Q_{c}= 0.0136024$.

Depending on the value of Q, Born–Infeld-AdS black hole is identified as follow :

• For $Q < Q_m$, the black hole is ‘Schwarzschild-like’ (S-type). In the region of low temperature, black holes do not exist, much like in the Schwarzschild solution. The largest (smallest) branch of the isocharge, as shown in Fig. 1 is connected to the huge (small) black hole, which is locally stable (unstable), as illustrated by the positive (negative) values of specific heat at the constant charge in Fig. 2a. Indeed, in the largest (smallest) branch, the temperature is an increasing (decreasing) function in terms of the event horizon radius showing that the black hole is locally stable (unstable). Actually, in the situation of $Q < Q_m$, the extremal Born–Infeld-AdS black hole can not be found and therefore small charged black hole does not persist. This finding may be understood as screening effects on the electric field caused by the existence of the parameter b, which makes the role of charge less significant.

• When $Q_m\le Q < Q_c$, black hole is ‘Reissner–Nordstrom-like’ (RN-type). Due to the temperature crossing over from zero with decreasing $r_h$, we get an extremal black hole. Moreover, the system exhibits a phase transition behavior of first-order between a small black hole (SBH) and a large black hole (LBH) as one can notice from Fig. 2b,c. Indeed, as we can observe in Fig. 1, small and large black holes are both locally stable phases because the temperature is an increasing function in terms of horizon radius in these two regions.

• The situation $Q = Q_c$, associated with Fig. 2d, a critical behavior appears and phase transition is of a second-order that occurs between an SBH and an LBH.

• In the last case $Q > Q_c$, the black hole has a locally thermal stable phase forever, and the heat capacity is positive everywhere as is revealed in Fig. 2e. Moreover, the temperature is a monotonically increasing function in terms of horizon radius as is displayed in Fig. 1.

We proceed to determine the values of critical points relevant to the second-order phase transition in the Born–Infeld-AdS black hole previously discussed. With constant l and $Q = Q_c$, Fig. 1 illustrates that the critical points are identified through the inflection point, as characterized by

$$\begin{aligned} \left. \dfrac{\partial T}{\partial r_h}\right| _{Q_c} = 0 \quad \text {and} \quad \left. \dfrac{\partial ^2 T}{\partial r_h^2}\right| _{Q_c} = 0. \end{aligned}$$

(11)

Criticality is expected to have occurred on the right branch of the $T-r_h$ curve in the S-Type black hole, indicating thermal stability. Subsequently, the expressions for the formulas in Eq. (11) are derived by incorporating the temperature from Eq. (5) as follows

$$\begin{aligned} & - 2x^{2} + \left( {1 + \frac{3}{{2b^{2} l^{2} }} - \frac{1}{{2b^{2} r_{c}^{2} }}} \right)x + 1 = 0, \\ & x^{4} - \frac{{x^{2} }}{2} + \frac{x}{{4b^{2} r_{c}^{2} }} - \frac{1}{2} = 0, \\ \end{aligned}$$

(12)

in which, we have set

$$\begin{aligned} x = \left( 1+\dfrac{16 \pi ^2 Q_c^2}{b^2 r_c^4}\right) ^{-1/2}, \end{aligned}$$

(13)

and $r_c$ denotes the critical horizon radius. To ensure the positive definiteness of the values of the critical quantities, we impose the following constraint on x

$$\begin{aligned} 0 \le x \le 1. \end{aligned}$$

(14)

By the help of Eq. (12), one can obtain the following cubic equation

$$\begin{aligned} x^3 + p x + q = 0, \end{aligned}$$

(15)

in which, the quantities p and q stand for

$$\begin{aligned} p = - \dfrac{3}{2}, \quad q = \dfrac{1}{2}\left( 1+\dfrac{3}{2 b^2 l^2}\right) . \end{aligned}$$

(16)

Furthermore, given that q is a real-valued parameter and p is negative, the cubic equation exhibits either one or three real roots. The existence of these three roots is governed by the requirement $\Delta = 4 p^3 + 27 q^2\le 0$, and hence

$$\begin{aligned} b \ge b_0 = \sqrt{\dfrac{3}{2}\left( 1 + \sqrt{2}\right) } / l \approx 1.9029/l, \end{aligned}$$

(17)

and their form can be expressed as

$$\begin{aligned} x_k = \sqrt{2} \cos \left( \dfrac{1}{3}\arccos \left[ -\dfrac{\sqrt{2}}{2}\left( 1 + \dfrac{3}{2 b^2 l^2}\right) \right] - \dfrac{2 \pi k}{3}\right) , \quad k=0,1,2. \end{aligned}$$

(18)

The third root $x_2$ contravenes the condition specified in Eq. (14). Additional analysis by calculating the critical quantity for $x_1$ reveals that $r_c$ persists in the branch of critical isocharge where it is locally unstable for the S-type black holes^63,103. Consequently, the sole physically meaningful solution is $x_0$. While, in the $b < b_0$ scenario, a single real root is found and it is expressed as follows

$$\begin{aligned} x_3 = - \sqrt{2} \cosh \left( \dfrac{1}{3} {{\,\textrm{arccosh}\,}}\left[ -\dfrac{\sqrt{2}}{2}\left( 1 + \dfrac{3}{2 b^2 l^2}\right) \right] \right) , \end{aligned}$$

(19)

which breaks the rule obtained in Eq. (14). Henceforth, the criticality of the Born–Infeld-AdS black holes can only be seen for $b\ge b_0$. The critical quantities are revealed as soon as $x_0$ is available

$$\begin{aligned} \begin{aligned} r_c&=\sqrt{\dfrac{x_0}{2 b^2\left( 1 + x_0^2 - 2 x_0^4\right) }}, \\ Q_c&= \dfrac{1}{8 \pi b \sqrt{\left( 1+3 x_0^2-4 x_0^6\right) }},\\ T_c&= \dfrac{3 + 2 b^2 l^2\left( 1 + x_0 -2 x_0^3\right) }{4 \pi b l^2}\sqrt{\dfrac{x}{2\left( 1 + x_0^2-2 x_0^4\right) }}. \end{aligned} \end{aligned}$$

(20)

The critical charge $Q_c$ is larger than $Q_m$ where

$$\begin{aligned} b> b_1 = \sqrt{\dfrac{3}{2\left( \sqrt{6 \sqrt{3}-9}-1\right) }}/l \approx 2.8870/l. \end{aligned}$$

(21)

Thus for $b\ge b_1$, the criticality is the mimicker of the RN-type black hole. On the contrary, for $b_0 \le b \le b_1$, the criticality occurs at the right branch of $(T-r_h)_{Q_c}$ curve of the S-type black hole^63,103.

As b attains large values, the Taylor expansion of the critical quantities gives rise to

$$\begin{aligned} \begin{aligned} r_c&=\dfrac{l}{\sqrt{6}} - \dfrac{7}{24 \sqrt{6} b^2}+\mathcalligra{O}\left( \dfrac{1}{b^4 } \right) , \\ Q_c&= \dfrac{l}{24 \pi } - \dfrac{7}{576 \pi l b^2}+\mathcalligra{O}\left( \dfrac{1}{b^4 } \right) ,\\ T_c&= \sqrt{\dfrac{2}{3 \pi ^2 l^2}} - \dfrac{1}{12 \pi \sqrt{6}b^2 l^3}+\mathcalligra{O}\left( \dfrac{1}{b^4 } \right) . \end{aligned} \end{aligned}$$

(22)

As expected, the first terms in all the quantities of Eq. (22) reproduce the same critical behaviors as that of the RN-AdS black holes¹⁰².

Born–Infeld AdS black hole phases picture from the Landau theory point of view

A brief review of Landau theory formalism

Landau estimated a system’s free energy from a perspective that displays the non-analytical nature during the phase transition and ends up capturing a significant amount of the physics. The system is defined through a global minimum of Landau free energy L as a function of order parameter. The quantity L called sometimes the Landau functional, which is related to the system’s Gibbs free energy and has an energy dimension, but it is not the same as given in^84,104.

Following⁸⁴, the Landau free energy can be constructed for a general thermodynamical system as

$$\begin{aligned} L = \int F\left( X,T,P,Q\right) dX. \end{aligned}$$

(23)

The thermodynamic system consisting of temperature T, pressure P, and charge Q are treated as independent parameters, whereas the parameter X is regarded as an auxiliary variable. The function $F\left( X,T,P,Q\right)$ represents various relationships that these four significant thermodynamic system parameters satisfy.

The equation of state (EOS) describing the thermal properties is expressed as $P = f(V, T, Q)$, where V is the volume which is in canonical conjugation of P. Based on the EOS, we may create the functional dependence of $F\left( X,T,P,Q\right)$ as

$$\begin{aligned} F\left( X,T,P,Q\right) = P - f(X, T,Q). \end{aligned}$$

(24)

Now, one can assert that a particular thermodynamic equation describing the system’s state under a particular set of certain physical conditions takes the form $F\left( X,T,P,Q\right) = 0$. The system’s preferred path is the one that causes its free energy to drop to its lowest value between many distinct paths that the system can take to attain equilibrium. We incorporate an auxiliary variable X which serves as an order parameter having a dimension of volume when the system is heading towards the equilibrium in the isothermal, isobaric, and isocharge environments. We can discover certain actual physical thermodynamic system operations by the use of this parameter. Thus, when the functional L takes the least possible value, it is considered as the most realistic state in which the system is described, the relations $F\left( X,T,P,Q\right)$ satisfied by the set $\left\{ X, T, P, Q\right\}$:

$$\begin{aligned} \dfrac{d L}{d X} = F\left( X,T,P,Q\right) = 0 \Longrightarrow X = V, \end{aligned}$$

(25)

The order parameter X can be viewed as a volume of the system as it approaches equilibrium or, less formally, as the volume of the system in a non-equilibrium state that does not meet the system’s equation of state. Although the equilibrium thermodynamic volume V fulfills the system’s equation of state and is the root of the function $F\left( X,T,P,Q\right) = 0$. Another benefit of creating Landau-free energy in this manner is that its convexity is connected to the thermal stability of the thermodynamical system

$$\begin{aligned} \delta \left. \left( \dfrac{d L}{d X}\right) \right| _{X=V} = - \dfrac{\partial f(V,T,Q)}{\partial V} \delta V, \end{aligned}$$

(26)

from which, one can notice that the extreme point is comparable to a potential well when $\partial f(V,T,Q)/\partial V < 0$ and the corresponding state is stable, while the corresponding thermodynamic state is unstable when $\partial f(V,T,Q)/\partial V > 0$ and the extreme point is similar to a potential barrier. Hence, $\gamma$-function as

$$\begin{aligned} \gamma (V) = \left( 3 V\right) ^{2/3} \dfrac{\partial L(V)}{\partial V}. \end{aligned}$$

(27)

The sign of $\gamma (V)$ serves as an indicator:

• It is negative (indicating a stable phase) when the thermodynamic volume V corresponds to a local minimum of the Landau functional L(X), where X is the order parameter, interpreted as a non-equilibrium volume

  $$\begin{aligned} \gamma (V) < 0 \iff \left. \dfrac{\partial L}{\partial X} \right| _{X=V} = 0 \quad \text {and} \quad \left. \dfrac{\partial ^2 L}{\partial X^2} \right| _{X=V} > 0 \end{aligned}$$

• The function $\gamma (V)$ is positive (indicating an unstable phase) when V corresponds to a local maximum of the Landau functional L(X)

  $$\begin{aligned} \gamma (V) > 0 \iff \left. \dfrac{\partial L}{\partial X} \right| _{X=V} = 0 \quad \text {and} \quad \left. \dfrac{\partial ^2 L}{\partial X^2} \right| _{X=V} < 0. \end{aligned}$$

• The function $\gamma (V)$ is zero (indicating a fixed point) when V corresponds to an inflection point of the Landau functional L(X).:

  $$\begin{aligned} \gamma (V) = 0 \iff \left. \dfrac{\partial L}{\partial X} \right| _{X=V} = 0 \quad \text {and} \quad \left. \dfrac{\partial ^2 L}{\partial X^2} \right| _{X=V} = 0. \end{aligned}$$

With the definition provided in Eq. (27), the derivative is taken with respect to the thermodynamic volume V rather than the order parameter X, and the term $(3V)^{2/3}$ serves as a scaling factor. Therefore, the sign of the $\gamma (V)$ function is related to the convexity of the Landau functional L(X) when $X = V$. Further, the sign of $\gamma (V)$ is not directly related to the sign of $F(X,T,P,Q) = P - f(X,T,Q)$, particularly when $X = V$. Indeed, according to Eq. (25), when $X = V$, we have $F(V,T,P,Q) = P - f(V,T,Q) = 0$ in all equilibrium states, which corresponds to the equation of state.

Born–Infeld-AdS black hole thermodynamics through Landau formalism

To delineate a comprehensive phase transitions framework and categorize their types, an exploration of the thermodynamic potential linked to the Born–Infeld-AdS black hole is crucial. In this context, we revisit the Gibbs free energy, which is computed from the Euclidean action with the appropriate boundary term in the canonical ensemble¹⁰¹, maintaining fixed Hawking temperature T, pressure P, and charge Q. Employing the Legendre transformation, the Gibbs free energy per unit volume $\omega$ can be derived as follows⁶³

$$\begin{aligned} \begin{aligned} G\left( T,P,Q\right)&= M - T S\\&= \dfrac{1}{48 \pi r_h}\left[ 3 r_h^2 - \dfrac{3 r_h^4}{l^2} - 2 b^2 \left( 1 - \sqrt{1+\dfrac{16 \pi ^2 Q^2}{b^2 r_h^4}}\right) + 128 \pi ^2 Q^2 _2\mathcalligra{F}_1\left[ \dfrac{1}{4}, \dfrac{1}{2}, \dfrac{5}{4}, - \dfrac{16 \pi ^2 Q^2}{b^2 r_h^2} \right] \right] , \end{aligned} \end{aligned}$$

(28)

in which, $r_h = r_h(T, Q, P)$ and $l = l(P)$. In the following, we shall assume the charge of the Born–Infeld-AdS black hole can vary, while the value of the pressure is fixed. Moreover, we shall take $b=3.5>b_1$, thus the critical behavior will take place in the RN-type black hole.

To better determination of the global stability of the black hole configuration under consideration, we introduce the on-shell free energy which accounts for transient black hole states, with respect to the relevant thermodynamic variables such as temperature, pressure, and charge⁹⁵. In other words, we define the on-shell free energy $\tilde{G}\left( T,P,Q\right)$ as the Gibbs free energy corresponding to the globally stable phase. Specifically, the Gibbs free energy G(T, P, Q) is a multivalued function in terms of T, describing both local stable and unstable black hole phases. The on-shell free energy $\tilde{G} \left( T,P,Q\right)$ can be expressed as:

$$\begin{aligned} \tilde{G} \left( T,P,Q\right) = \min \left( G\left( r_h,T,P,Q\right) \right) , \end{aligned}$$

(29)

such that $G\left( r_h,T,P,Q\right)$ represents the generalized off-shell Gibbs free energy for the transient black hole state, and is given by

$$\begin{aligned} \begin{aligned} G\left( r_h, T,P,Q\right)&= M (r_h,P,Q) - T S(r_h)\\&= - \dfrac{1}{24 \pi r_h}\left[ \dfrac{3 r_h^4}{l^2} + 6 \pi T r_h^3 -3 r_h^2 + 2 b^2 r_h^4 \left( 1 - \sqrt{1+\dfrac{16 \pi ^2 Q^2}{b^2 r_h^4}}\right) \right. \\&\quad \left. + 64 \pi ^2 Q^2 _2\mathcalligra{F}_1\left[ \dfrac{1}{4}, \dfrac{1}{2}, \dfrac{5}{4}, - \dfrac{16 \pi ^2 Q^2}{b^2 r_h^2} \right] \right] , \end{aligned} \end{aligned}$$

(30)

where the horizon radius $r_h$ serves as the order parameter, encompassing values from zero to infinity¹⁰⁵. The minimum of $G\left( r_h, T,P,Q\right)$ in Eq. (29) is determined with respect to the horizon radius $r_h$ (order parameter). Consequently, the on-shell free energy $\tilde{G} \left( T,P,Q\right)$ characterizes the global stability of the black hole^106,107. It’s worth knowing, that, the Generalized off-shell Gibbs free energy differs from the free Gibbs energy $G\left( T,P,Q\right)$ given in Eq. (28), where the temperature T represents the Hawking temperature. In the Generalized off-shell Gibbs free energy, denoted as $G\left( r_h,T,P,Q\right)$, the temperature T serves as a parameter that can be freely and independently chosen from $r_h$. Therefore, the Generalized off-shell Gibbs free energy, $G\left( r_h,T,P,Q\right)$, equals the Gibbs free energy presented in Eq. (28) only when the temperature T matches the Hawking temperature corresponding to the black hole state with the horizon radius $r_h$.

The phase structure of the Born–Infeld-AdS Black hole is characterized based on the value of Q in the following manner:

• For $Q = 0.005 < {Q_0 = 0.00922}$, we present various plots in Fig. 3 showcasing the temperature as a function of the horizon radius $r_h$ (Fig. 3a), Gibbs free energy with respect to temperature (Fig. 3b), Landau function L as a function of the parameter X at different temperatures (Fig. 3c), Landau function L in terms of the black hole volume V (Fig. 3d), $\gamma$-function with respect to the black hole volume V (Fig. 3e), and on-shell Gibbs free energy $\tilde{G}$ versus temperature (Fig. 3f). We observe that the black hole behaves like the Schwarzschild one revealing a Hawking-Page transition (black dot) between the thermal radiations phase and stable large black hole one at $T_{HP}=0.3065$. The unstable phase corresponds to the local maximum of the Landau function (blue dot) whereas the stable phase corresponds to the local minimum (red dot). Moreover, we notice that the Landau function is a decreasing function in terms of the black hole volume when the system is stable (dark red curve) and it is an increasing function when the system is unstable (dark blue curve). Thus the $\gamma$ function is negative in the large black holes phase and positive in the small black holes one. The zero of $\gamma$-function is associated with an unstable fixed point indicating that the temperature is (locally) minimal. We can interpret these results as the large black hole becoming larger and more stable when it gets hotter, whereas the small hole becomes smaller when it gets hotter because of evaporation. The pink region indicates the zone where the temperature is less than Hawking-Page one (pink curves) and only the thermal radiation phase is globally stable.

• Herein, all previous diagrams of Fig. 3 are reproduced but for $Q = Q_0 = 0.00922$ in Fig. 4.

  It is noteworthy that the temperature, expressed in terms of the horizon radius, exhibits an inflection point, signifying a discontinuity in the first derivative of the Gibbs free energy and inflection points in the Landau function (depicted by the green and dark cyan curves). Consequently, a novel black hole phase emerges, termed intermediate black holes (green dots), sharing similarities with the unstable small black holes, as illustrated in Fig. 4c, where this phase corresponds to a local maximum of the Landau function. Furthermore, Fig. 4d illustrates that the Landau function increases concerning the black hole volume, signifying instability. In Fig. 4e, the $\gamma$-function reveals two fixed points: one unstable, corresponding to a Hawking-Page-like scenario, indicating minimal temperature; the second semi-stable fixed point separates two unstable phases (small and intermediate black holes) and corresponds to an inflection point in the temperature behavior. Finally, Fig. 4f demonstrates that the black hole resembles AdS Schwarzschild black holes, where only thermal radiations and large black hole phases are globally stable.

• Now, the charge is set to $Q = 0.01$ in Fig. 5.

  The temperature curve, as a function of the horizon radius, exhibits two minima (gray points), one local ($r_h = 0.07$) and the other global ($r_h = 0.52$). Additionally, it features a local maximum at ($r_h=0.18$). These minima and maxima correspond to discontinuities in the first derivative of the Gibbs free energy and inflection points in the Landau function (magenta, green, and dark cyan curves). Consequently, we identify four distinct black hole phases: two stable phases, represented by large and stable small black holes (dark red and orange points, respectively), and two unstable phases, corresponding to unstable small and intermediate black holes (dark blue and green points, respectively), as illustrated in Fig. 5c. These phases align with the local minima and maxima of the Landau functional. Furthermore, Fig. 5d depicts that the Landau function decreases concerning black hole volume for the stable phases and increases for the unstable ones. Additionally, Fig. 5e reveals three fixed points in the $\gamma$-function: one unstable (right point) segregating the large black hole phase from the unstable intermediate black hole phase, indicating minimal temperature; the second stable (middle point) dividing the stable small black holes phase from the unstable intermediate black holes phase and corresponding to the temperature maximum; the third unstable (left point) acting as a boundary between the stable small black hole phase and the unstable phase, suggesting a local minimum in temperature. Moreover, we observe that stable black holes increase in size as they become hotter, whereas unstable ones decrease in size with increasing temperature. Finally, Fig. 5f indicates that the black hole resembles AdS Schwarzschild black holes, where only thermal radiations and large black hole phases are globally stable.

• The case of $Q = 0.010026$ is depicted in Fig. 6.

  At such a charge, the zeroth order phase transition occurs at the intersection point between the stable small black holes branch and the large black holes as depicted in Fig. 6b and which corresponds to an inflection point in Landau function in terms of the black hole volume (magenta curve). We illustrate such a phase transition that occurs at a constant temperature by the dashed magenta line in Fig. 6d,e. The zeroth order phase transition occurs between the unstable state (gray point) and the large black hole phase. We ought to mention that at this charge begins the appearance of first-order phase transition and reentrant phase transition which we shall examine in the next case. Finally, one can remark from Fig. 6f, that the black hole reminisces the AdS Schwarzschild black holes as in previous cases.

• Continuing our exploration of the phase picture, we now examine the case of $Q = 0.01009$ in Fig. 7. Specifically, we plot the temperature as a function of the horizon radius $r_h$ (Fig. 7a), Gibbs free energy with respect to temperature (Fig. 7b), Landau function L versus the parameter X across various temperatures (Fig. 7c), Landau function L in terms of the black hole volume V (Fig. 7d), $\gamma$-function in terms of the black hole volume V (Fig. 7e), and the on-shell Gibbs free energy-temperature ($\tilde{G}-T$) diagram (Fig. 7f).

  In this scenario, we observe a reentrant phase transition from Large Black Holes (LBH) to Small Black Holes (SBH) and back to Large Black Holes. As evident in Fig. 7b, a zeroth-order phase transition occurs between large and small black holes (indicated by the magenta dashed line), manifesting as a jump in the Gibbs free energy. Additionally, a first-order phase transition between small and large black holes is discernible (shown by the purple dashed line), characterized by the swallowtail shape in the Gibbs free energy curve. Figure 7d,e further highlight these transitions. Furthermore, it is noteworthy that the large black hole (red curve) can transition to a small black hole (following the magenta dashed line) while maintaining a constant temperature, and subsequently undergo a first-order transition back to a large black hole phase. Lastly, as indicated in Fig. 7f, the black hole exhibits behavior reminiscent of the Schwarzschild-AdS black hole.

• Increasing the charge to reach $Q =0.010128$ in Fig. 8.

  The system exhibits always a first-order phase transition between small black holes and large ones following the dashed purple line whereas the zeroth-order phase transition is carried out between two unstable points following the magenta line. From this electric charge, the zeroth order phase transition shall disappear as we will see next case. Therefore, the reentrant phase transition that characterized the Born–Infeld-AdS black hole will disappear. Finally, we see in Fig. 8f that the situation remains the same.

• In Fig. 9, we extend our analysis to $Q = 0.0105.$

  The key remark is the disappearance of the zeroth-order phase transition in Fig. 9, eliminating the possibility of a reentrant phase transition. The system now undergoes only a first-order phase transition between small and large black holes. The Hawking-Page-like transition persists between thermal radiations and stable small black hole, ensuring the absence of black holes below $T=0.226$. Finally, in Fig. 9f, two critical points are identified. The first corresponds to the Hawking-Page-like transition between thermal radiations and small black holes, while the second is associated with the first-order phase transition between small and large black holes. Consequently, three globally stable phases emerge: thermal radiations, small, and large black holes.

• The phase portrait corresponding to $Q =Q_m = 0.0113682$ is depicted in Fig. 10.

  Clearly, we are encountering a Reissner–Nordstrom-like senario, marked by a first-order phase transition between small and large black holes (indicated by the purple arrow), along with an unstable intermediate phase.

• Figure 11 is associated with the case $Q =Q_c = 0.0136024.$

  The panels unveil a critical behavior where (block dot, i.e, critical point) a second-order phase transition occurs between small and large black holes at exactly $T = 0.265$.

• The case related to $Q = 0.0154$ is illustrated in Fig. 12, where we have depicted just the temperature as a function of horizon radius $r_h$ (Fig. 12a), Gibbs free energy-temperature diagram (Fig. 12b), Landau function L in terms of the parameter X for different temperatures (Fig. 12c), then in terms of the black hole volume V in Fig. 12d panel. The last panel is devoted to $\gamma$-function versus the black hole volume V (Fig. 12e).

  We note the absence of a phase transition, as the system exhibits only one globally stable phase associated with the large black hole state. This observation is supported by the monotonous behavior of temperature concerning the horizon radius, where there is no indication of non-monotonicity. Additionally, the Landau function L displays only one minimum with respect to the parameter X. Furthermore, both the Gibbs free energy and Landau function exhibit monotonic trends relative to temperature, and the $\gamma$-function lacks any fixed point (zero point), consistently maintaining a strictly negative nature.

Fig. 3

(a) Temperature versus the event horizon radius $r_h$. (b) Gibbs free energy-temperature diagram. (c) Landau function L in terms of the parameter X for different temperatures. (d) Landau function L in terms of the black hole volume V. (e) $\gamma$-function in terms of the black hole volume V. (f) On-shell Gibbs free energy $\tilde{G}$ as a function of temperature T. The arrows indicate the evolution of the temperature and the pink region indicates where the thermal radiation phase is the global stable phase $(T<T_{HP})$ with $Q = 0.005$, $l=1$, and $b=3.5$.

Fig. 4

(a) Temperature versus event horizon radius $r_h$. (b) Gibbs free energy-temperature diagram. (c) Landau function L in terms of the parameter X for different temperatures. (d) Landau function L in terms of the black hole volume V. (e) $\gamma$-function in terms of the black hole volume V. (f) On-shell Gibbs free energy $\tilde{G}$ as a function of temperature T. The arrows indicate the evolution of the temperature and the pink region indicates where the thermal radiation phase is the global stable phase $(T<T_{HP})$ with $Q = 0.00922$, $l=1$, and $b=3.5$.

Fig. 5

(a) Temperature versus the event horizon radius $r_h$. (b) Gibbs free energy-temperature diagram. (c) Landau function L in terms of the parameter X for different temperatures. (d) Landau function L in terms of the black hole volume V. (e) $\gamma$-function in terms of the black hole volume V. (f) On-shell Gibbs free energy $\tilde{G}$ as a function of temperature T. The arrows indicate the evolution of the temperature and the pink region indicates where the thermal radiation phase is the global stable phase $(T<T_{HP})$ with $Q = 0.01$, $l=1$, and $b=3.5$.

Fig. 6

(a) Temperature versus the event horizon radius $r_h$. (b) Gibbs free energy-temperature diagram. (c) Landau function L in terms of the parameter X for different temperatures. (d) Landau function L in terms of the black hole volume V. (e) $\gamma$-function in terms of the black hole volume V. (f) On-shell Gibbs free energy $\tilde{G}$ as a function of temperature T. The arrows indicate the evolution of the temperature and the pink region indicates where the thermal radiation phase is the global stable phase $(T<T_{HP})$ with $Q = 0.010026$, $l=1$, and $b=3.5$.

Fig. 7

(a) Temperature versus the event horizon radius $r_h$. (b) Gibbs free energy-temperature diagram. (c) Landau function L in terms of the parameter X for different temperatures. (d) Landau function L in terms of the black hole volume V. (e) $\gamma$-function in terms of the black hole volume V. (f) On-shell Gibbs free energy $\tilde{G}$ as a function of temperature T. The arrows indicate the evolution of the temperature and the pink region indicates where the thermal radiation phase is the global stable phase $(T<T_{HP})$ with $Q = 0.01009$, $l=1$, and $b=3.5$.

Fig. 8

(a) Temperature versus the event horizon radius $r_h$. (b) Gibbs free energy-temperature diagram. (c) Landau function L in terms of the parameter X for different temperatures. (d) Landau function L in terms of the black hole volume V. (e) $\gamma$-function in terms of the black hole volume V. (f) On-shell Gibbs free energy $\tilde{G}$ as a function of temperature T. The arrows indicate the evolution of the temperature and the pink region indicates where the thermal radiation phase is the global stable phase $(T<T_{HP})$ with $Q = 0.010128$, $l=1$, and $b=3.5$.

Fig. 9

(a) Temperature versus the event horizon radius $r_h$. (b) Gibbs free energy-temperature diagram. (c) Landau function L in terms of the parameter X for different temperatures. (d) Landau function L in terms of the black hole volume V. (e) $\gamma$-function in terms of the black hole volume V. (f) On-shell Gibbs free energy $\tilde{G}$ as a function of temperature T. The arrows indicate the evolution of the temperature and the pink region indicates where the thermal radiation phase is the global stable phase $(T<T_{HP})$ with $Q = 0.0105$, $l=1$, and $b=3.5$.

The complete phase diagram of the Born–Infeld-AdS black hole is depicted in Fig. 13.

Fig. 10

(a) Temperature versus the event horizon radius $r_h$. (b) Gibbs free energy-temperature diagram. (c) Landau function L in terms of the parameter X for different temperatures. (d) Landau function L in terms of the black hole volume V. (e) $\gamma$-function in terms of the black hole volume V. (f) On-shell Gibbs free energy $\tilde{G}$ as a function of temperature T. The arrows indicate the evolution of the temperature. The arrows indicate the evolution of the temperature with $Q =Q_m = 0.0113682$, $l=1$, and $b=3.5$.

Fig. 11

(a) Temperature versus the event horizon radius $r_h$. (b) Gibbs free energy-temperature diagram. (c) Landau function L in terms of the parameter X for different temperatures. (d) Landau function L in terms of the black hole volume V. (e) $\gamma$-function in terms of the black hole volume V. (f) On-shell Gibbs free energy $\tilde{G}$ as a function of temperature T. The arrows indicate the evolution of the temperature. The arrows indicate the evolution of the temperature with $Q =Q_c = 0.0136024$, $l=1$, and $b=3.5$.

Fig. 12

(a) Temperature as a function of event horizon radius $r_h$. (b) Gibbs free energy as a function of temperature. (c) Landau function L in terms of the parameter X for $T = 0.25$. (d) Landau function L in terms of the black hole volume V. (e) $\gamma$-function in terms of the black hole volume V. The arrows indicate the evolution of the temperature with $Q =0.015>Q_c$, $l=1$ and $b=3.5$.

Fig. 13

(a) $Q-V$ diagram of Born–Infeld-AdS black hole; the flow indicates the temperature gradient. (b) Critical temperatures as a function of electric charge. (c) On-shell Gibbs free energy as a function of temperature and electric charge. $l=1$ and $b=3.5$.

In Fig. 13a, the $Q-V$ diagram is presented, illustrating the temperature gradient through directional arrows and revealing four distinct local phases: stable small black holes (SSBH), unstable small black holes (USBH), Intermediate black holes (IBH), and large ones (LBH). The gray zone signifies regions where black holes cannot exist and is delimited by the extremal black hole solution. The pink zone indicates the region where thermal radiation is the globally stable phase, corresponding to temperatures below the Hawking-Page temperature. Notably, locally stable black holes exhibit a right-oriented temperature gradient, signifying an increase in temperature as the black hole enlarges. Conversely, locally unstable black holes display a left-oriented temperature gradient, indicating an increase in temperature as the black hole diminishes, ultimately leading to evaporation. For a more in-depth exploration, Fig. 1b illustrates the Hawking-Page transition temperature $T_{HP}$, the first-order phase transition temperature $T_f$, and the zeroth-order phase transition temperature $T_z$ as functions of electric charge Q. Several observations can be drawn from this panel: firstly, the zeroth-order phase transition temperature $T_z$ consistently remains below the Hawking-Page transition temperature $T_{HP}$, rendering the occurrence of zeroth-order phase transitions implausible. Secondly, the first-order phase transition can manifest when $Q>Q_m$. Further insights are provided in Fig. 13c, where the on-shell Gibbs free energy-temperature T-electric charge Q diagram depicts the presence of three globally stable phases: large black holes, thermal radiations, and small black holes.

In summary, the phase diagram of the Born–Infeld-AdS black hole can be characterized by three specific electric charge values, outlined as follows:

• When $Q<Q_t = 0.0103638$, we have just two globally stable phases, thermal radiation, and a large black hole, then consequently there is only one possible phase transition which is the Hawking-Page phase transition. Therefore, there is neither first-order phase transition nor zeroth-order phase transition as it was shown in¹⁰³, where, the authors have shown that the reentrant phase transition occurs for $0.010026<Q<0.10128$ but they had not proved that the intermediate black holes are globally stable for these values of electric charge. To conclude, for $Q<Q_t$, the Born–Infeld-AdS black hole is Schwrazchild-like, there are only two globally stable phases that are connected by Hawking-Page phase transition. Moreover, there is no extremal (no vanishing temperature) which confirms the results of¹⁰⁸.

• For $Q_t<Q<Q_m = 0.0113682$, three globally stable phases persist, thermal radiation (pink zone), small stable black hole (SSBH), and large black hole (LBH) with two possible critical points as we have shown in Fig. 9. Indeed, there are two possible phase transitions, the first one is between thermal radiations and small black holes corresponding to Hawking-Page-like transition; the second one is the first order phase transition between small and large black holes like that observed in Reissner-Nordström-AdS black holes¹⁰¹. Moreover, reaching the charge $Q=Q_t$, the system exhibits a triple point where thermal radiation, small, and large black holes coexist together.

• In the $Q_m<Q<Q_c = 0.0136024$ scenario, the Born–Infeld-AdS black hole unveils similarities to the Reissner-Nordström-AdS black hole case. Indeed, two globally stable phases emerge, accompanied by a first-order phase transition between small and large black holes. Additionally, the system may reach an extremal state where the black hole becomes sufficiently small. Consequently, the presence of a thermal radiation phase is eliminated, and the Hawking-Page-like transition ceases to exist.

• In the situation where $Q>Q_c$, there is only a globally stable phase emerges (LBH), mirroring the characteristics of the large black holes phase observed in the Reissner-Nordström-AdS black hole. Furthermore, when $Q=Q_c$, the black hole undergoes a second-order phase transition between small and large black holes.

Therefore, one concludes that the Born–Infeld-AdS black hole can unveil a triple point where the three globally stable phases can coexist. In Fig. 14 we illustrate the temperature as a function of horizon radius $r_h$ (Fig. 14a), Gibbs free energy in terms of temperature (Fig. 14b), Landau function L in terms of the parameter X for different temperatures (Fig. 14c), and in terms of the black hole volume V Fig. 14d, $\gamma$-function versus the black hole volume V (Fig. 14e), and in the last panel (Fig. 14f), the on-shell Gibbs free energy $\tilde{G}$ as a function of temperature.

Fig. 14

(a) Temperature versus the event horizon radius $r_h$. (b) Gibbs free energy-temperature diagram. (c) Landau function L in terms of the parameter X for different temperatures. (d) Landau function L in terms of the black hole volume V. (e) $\gamma$-function in terms of the black hole volume V. (f) On-shell Gibbs free energy $\tilde{G}$ as a function of temperature T. The arrows indicate the evolution of the temperature. The arrows indicate the evolution of the temperature with $Q =Q_t = 0.0103638$, $l=1$, and $b=3.5$.

Figure 14 reveals that Hawking-Page phase transition temperature $T_{HP}$ coincides with first-order phase temperature $T_f$, which means that Hawking-Page transition and first-order phase transition occur simultaneously. Therefore, we have an equilibrium between thermal radiations, small black holes, and large black holes.

Having comprehensively portrayed the phase transition landscape of the Born–Infeld-AdS black hole utilizing the Landau functional formalism, our focus in the next section shifts to a novel thermodynamic tool borrowed from the field of dynamical systems. We will consider the Fokker–Planck equation, a concept widely employed in current literature to gain deeper insights into thermodynamic processes.

Exploring free energy landscape through the Fokker–Planck equation: unveiling probabilistic dynamics

It was recently developed in⁸⁶ a new method for examining the dynamic process of phase transition on the free energy landscape, demonstrating that a black hole can escape from one phase to another due to thermal fluctuations. Then in¹⁰⁵, the authors investigated the criticality of RN-AdS black holes from the perspective of the free energy landscape, obtaining the probability distribution of states and the time distribution of the first passage kinetic process of black hole state switching. Within this perception, we will probe the Born–Infeld-AdS black hole phase structure via such a formalism to probe its rich phase portrait.

To maintain consistency with the convention in¹⁰⁵ and for simplicity, the horizon radius $r_h$ will be referred to as r. Consequently, the Gibbs free energy, expressed in terms of the order parameter r, will be represented as G(r). In the subsequent analysis, aiming to uncover the system’s response to thermal fluctuations over time, we consider the probability distribution of these evolving states as a function of both the order parameter r and time t. Thus, $\rho (r, t)$ represents the probability distribution of the spacetime state within the ensemble.

The explicit Fokker–Planck equation for the probabilistic evolution on the free energy landscape is obtained to be^109,110

$$\begin{aligned} \dfrac{\partial \rho (r,t)}{\partial t} = D \dfrac{\partial }{\partial r}\left[ e^{-\beta G(r)} \dfrac{\partial }{\partial r}\left[ e^{\beta G(r)}\rho (r,t)\right] \right] , \end{aligned}$$

(31)

in which $\beta = 1/k_BT$ denotes the inverse temperature and $D = k_BT /\zeta$ stands for the diffusion coefficient with $k_B$ is the Boltzmann constant while $\zeta$ called dissipation coefficient. For commodity and by preserving the generality, one will set $k_B$ and $\zeta$ equal to the unity in the rest of our analysis.

The choice of boundary conditions for solving the Fokker–Planck equation depends on the specific question under consideration. Two distinct types of boundary conditions need to be enforced at the boundaries of the computational domain. For instance, at $r = r_0$, with $r_0$ is the boundary location, we provide the following boundary conditions

• A reflecting boundary condition:

  $$\begin{aligned} \left. \dfrac{\partial }{\partial r}\left[ e^{\beta G(r)}\rho (r,t)\right] \right| _{r=r_0} = 0. \end{aligned}$$

  (32)

• Then, an absorbing boundary condition:

  $$\begin{aligned} \rho (r_0,t) = 0. \end{aligned}$$

  (33)

In the canonical ensemble, we explore the temporal evolution of the probability distribution of states. Throughout this evolution, the reflecting boundary condition is applied to preserve probability conservation, and the initial condition is selected as a Gaussian packet which serves as an effective approximation of the $\delta$ distribution and is commonly employed in numerical computations

$$\begin{aligned} \rho (r,0) = \dfrac{1}{\sqrt{\pi }a} e^{-\left( r-r_i\right) ^2/a^2 }, \end{aligned}$$

(34)

with the parameter $a \le 0.01$ is the Gaussian wave packet width, and $r_i$ is the initial horizon radius.

By taking the partial derivative $\frac{\partial \rho (r,t)}{\partial t}$ null in the Fokker–Planck equation, one can achieve the final stationary distribution as $\rho (r,t_{\infty }) \propto \exp (-G(r)/T)$. This is in accordance with the Boltzmann link between free energy and equilibrium probability distribution. In fact, as a result of the long-time evolution, the stationary distribution reaches the equilibrium probability. Therefore, the maximum of the final stationary distribution is then used to define the thermodynamic stable state⁸⁷.

We propose investigating the time-dependent characteristics of black hole probability distributions in extended phase space at various electrical charges and temperatures. We will also discuss oscillations occurring during an evolutionary process within the context of phase transitions. Specifically, we examine instances where the probability of a thermodynamic state ‘k’, denoted as $\rho (r_k, t=0) = 0$, is initially higher than what it will be in the eventual equilibrium situation. That is to say

$$\begin{aligned} \exists \ t>0 \quad \rho (r_k,t) > \rho (r_k,t_{\infty }), \quad \text {with} \quad \rho (r_k,t=0) = 0. \end{aligned}$$

(35)

An oscillation is considered strong when the probability of the thermodynamic state ‘k’ exceeds that of the initial state ‘i’:

$$\begin{aligned} \exists \ t>0 \quad \rho (r_k,t) > \rho (r_i,t), \quad \text {with} \quad \rho (r_k,t=0) = 0 \quad \text {and}\quad \rho (r_i,t=0) = \max \left( \rho (r,t=0)\right) . \end{aligned}$$

(36)

An oscillation is categorized as weak when it does not exhibit strength condition and satisfies only the Eq. (35) criteria.

• Considering $Q = 0.01009$: in¹⁰³, authors affirmed that there is a reentrant phase transition between the small and large black hole, nevertheless, we shall show that there is no reentrant phase transition and only thermal radiations and large black holes phases are globally stable and most probable states. We plot in Fig. 15 the probability distribution $\rho (r,t)$ governed by Fokker–Planck equation for different temperatures with $Q = 0.01009$, $l=1$ and $b=3.5$. For $T = T_z = 0.2718$, and the y-axis is rescaled with a logarithmic scale such that $y\longrightarrow 10^{50(y-1)}\left( y \longleftarrow \dfrac{\log _{10}(y)}{50}+1\right)$. when it is supposed to occur a reentrant phase transition (zeroth order phase transition), we observe that the probability $\rho (r,t)$ which is initially centered around the small black hole state, $r_i = 0.0707$, leaks quickly to thermal radiations state, $r=0$, which is the only globally stable state where the probability is maximal. This outcome serves as additional evidence supporting the absence of a reentrant phase transition, as $\rho (r_{l},t_\infty )< \rho (r_{s},t_\infty )< \rho (r=0,t_\infty )$, where $r_l = 0.6332$ and $r_s = 0.0707$ are the large and the small black holes horizon radii respectively, and the thermal radiations is the most stable phase. Afterward, in the second line of the figure, we set $T = T_{HP} = 0.2783$ associated with the Hawking-Page transition, one can notice that the probability $\rho (r,t)$ which is initially centered around the large black hole state, $r_i = 0.7138$, leaks quickly to thermal radiations state, i.e $r=0$, then it comes back to form another peak around the large black hole state, and by the end, we have $\rho (r = 0,t) = \rho (r_l,t)$ traducing the coexistence of the large black hole and the thermal radiations where the probability is maximal. In the bottom panels where we have taken $T = 0.2937$, one can remark that the probability $\rho (r,t)$ which is initially centered around the large black hole state, $r_i = 0.8448$, leaks quickly to thermal radiations state ($r=0$), then as t increases, the thermal radiations phase probability decreases wheres the large black holes phase probability increases forming a peak around $r_l$. Therefore, the large black holes phase is the most probable and stable phase.

• For the charge value $Q = Q_t = 0.0103638$, corresponding to Fig. 14 where the existence of a triple point is demonstrated, we propose reaffirming this finding through the probability distribution. To achieve this, we illustrate in Fig. 16 the probability distribution $\rho (r,t)$ governed by the Fokker–Planck equation for various temperatures $Q = Q_t = 0.01009$, $l=1$ and $b=3.5$. Specifically, for $T = 0.25$,

  It is notable that the probability distribution $\rho (r,t)$, initially centered around the small black hole state at $r_i = 0.0805$, rapidly shifts towards the thermal radiation state at $r=0$. This transition corresponds to the only globally stable state, where the probability reaches its maximum value. Indeed, $\rho (r_{s},t_\infty )< \rho (r=0,t_\infty )$, where $r_s = 0.0805$ is the small black hole horizon radius, and then the thermal radiations is the most stable phase confirming our previous result that the thermal radiation is the only globally stable phase. Increasing the temperature to $T = T_t = 0.276$, we notice that the probability $\rho (r,t)$ centered initially around the large black hole state, $r_i = 0.6909$, leaks quickly to thermal radiations state, $r=0$, but after then it comes back to form two peaks around the small and the large black holes horizon radii. Thus, we are in presence of a triple point, i.e a location where the thermal radiations, small black holes, and large black holes coexist together. i.e., $\rho (r_{s},t_\infty ) = \rho (r_l,t_\infty )= \rho (r=0,t_\infty )$ where $r_s = 0.1177$ and $r_l = 0.6909$, the three phases are equiprobable and globally stable. Now reaching $T = 0.29$, we see that the probability distribution $\rho (r,t)$, initially centered around the large black hole state at $r_i = 0.8172$, rapidly transitions towards thermal radiation and small black hole states, forming a pattern similar to the triple point case. Subsequently, $\rho (r=0,t)$ and $\rho (r_s,t)$ decrease over time, while $\rho (r_l,t)$ increases to reach its maximum. Consequently, $\rho (r = 0,t_\infty )< \rho (r_s,t_\infty ) < \rho (r_l,t_\infty )$, where $r_s = 0.1418$ and $r_l = 0.8172$. The large black hole phase emerges as the most probable state and, ultimately, the only globally stable phase.

• Now, with $Q = 0.0105$ that corresponds to Fig. 9 and where we have unveiled the existence of two critical points at such a value of charge, that is to say, two-phase transitions occur, the first one is between thermal radiation and small black holes phases which is a Hawking-Page-like transition, while the second one is a first-order phase transition between small and black holes phases. We dipect in Fig. 17 the probability distribution $\rho (r,t)$ derived from the Fokker–Planck equation for different temperatures around thermal radiations-small black holes transition with $Q = 0.0105$, $l=1$ and $b=3.5$. For $T = 0.227$,

  Such a figure reveals serval remarks, one can first notice that the probability $\rho (r,t)$ which initially centered around the small black hole state, $r_i = 0.0599$, attains fast the thermal radiation state, $r=0$, which is the only globally stable state. Indeed, $\rho (r_{s},t_\infty )< \rho (r=0,t_\infty )$, where $r_s = 0.0599$, and then the thermal radiations is the most stable phase which confirms our previous finding that the thermal radiation is the only globally stable phase. Second, for $T = T_{HP} = 0.25708$, which corresponds to the Hawking-Page-like transition between thermal radiation and small black holes phases, the probability $\rho (r,t)$ centered around the small black hole state, $r_i = 0.1034$, arrives to thermal radiations state, $r=0$, then it comes back to form another peak around the small black hole state, and by the end, one achieves $\rho (r = 0,t) = \rho (r_s,t)$, at $r_s = 0.1034$, traducing the coexistence of the small black hole and the thermal radiations at the maximum of the probability. In the third scenario with $T = 0.272$, the probability distribution $\rho (r,t)$, initially concentrated at the small black hole state with $r_i = 0.1226$, transitions towards the thermal radiation state ($r=0$). As time t progresses, the probability associated with the thermal radiation phase decreases, while the probability of the small black hole phase increases, forming a prominent peak around $r_s$. Consequently, the small black hole phase emerges as the most probable and stable phase.

  Within Fig. 18, we depict the probability distribution $\rho (r,t)$ for different temperatures around small-large black holes transition with the same parameters as in Fig. 17.

  Figure 18 reveals that for $T = T_f = 0.2753$, corresponding to the first-order phase transition between small and large black hole phases, the probability distribution $\rho (r,t)$ initially centered around the large black hole state with $r_i = 0.6838$ switchs to the thermal radiation state ($r=0$). Subsequently, it bifurcates to form two peaks around the horizons of the small and large black holes. This indicates the existence of a critical point where both the small and large black hole phases coexist. Specifically, $\rho (r_{s},t_\infty ) = \rho (r_l,t_\infty )$, where $r_s = 0.1273$ and $r_l = 0.6838$, implying that both phases are equiprobable and globally stable. Upon reaching $T = 0.29$, the probability distribution $\rho (r,t)$ initially centered around the large black hole state with $r_i = 0.8177$ transitions to thermal radiations and small black hole states, creating a pattern reminiscent of a critical point scenario. Thereafter, $\rho (r_s,t)$ decreases with time, while $\rho (r_l,t)$ increases, reaching its maximum. As a result, $\rho (r_s,t_\infty ) < \rho (r_l,t_\infty )$, where $r_s = 0.1542$ and $r_l = 0.8177$, indicating that the large black hole phase is the most probable and ultimately the only globally stable phase.

Now, let’s examine the dynamics at the triple point, where three globally stable phases coexist: thermal radiation at $r = 0$, the small black hole at $r_s$, and the large black hole at $r_l$. For a clear illustration, we depict in Fig. 19 the evolution of $\rho (r_k,t)$ when the initial Gaussian wave packet peaks at large or small black hole states. In fact, the state k ranges $\{ 0, s, l\}$, radiation, small and large black holes, respectively.

Fig. 15

Probability distribution $\rho (r,t)$ governed by Fokker–Planck equation for different temperatures with $Q = 0.01009$, $l=1$ and $b=3.5$.

Fig. 16

Probability distribution $\rho (r,t)$ governed by Fokker–Planck equation for different temperatures with $Q =Q_t = 0.0103638$, $l=1$ and $b=3.5$.

Fig. 17

Probability distribution $\rho (r,t)$ governed by Fokker–Planck equation for different temperatures around thermal radiations-small black holes transition with $Q = 0.0105$, $l=1$ and $b=3.5$.

Fig. 18

Probability distribution $\rho (r,t)$ governed by Fokker–Planck equation for different temperatures around small–large black holes transition with $Q = 0.0105$, $l=1$ and $b=3.5$.

Fig. 19

Behaviors of the probability $\rho (r,t)$ at the triple point, when the initial Gaussian wave packet is peaked at the (a) large and (b) small black hole states, with $Q = Q_t = 0.0103638$, $T=T_t = 0.276$, $l=1$ and $b=3.5$.

We observe that the initially large value $\rho (r_{l,s},t = 0)$ in each case rapidly decays to a stationary value, while the other two states (initially zero) grow toward this value.

Henceforth, considering the first case shown Fig. 19a, the initial Gaussian wave packet $\rho (r,t = 0)$ peaks at the large black hole phase with $\rho (r_l,t = 0) = 56.4189$, while $\rho (r = 0,t = 0) \simeq \rho (r_s,t = 0) \simeq 0$. As the parameter t increases, $\rho (r_l,t)$ decreases (red curve), and $\rho (r=0,t)$ and $\rho (r_s,t)$ increase (blue and green curves respectively) as expected, with $\rho (r=0,t) < \rho (r_s,t)$ because the initial state must surmount two barriers to reach thermal radiations state as we can see in Fig. 20.

Fig. 20

Gibbs free energy via landscape at the triple point with $Q = Q_t = 0.0103638$, $T=T_t = 0.276$, $l=1$ and $b=3.5$.

Certainly, from Fig. 20, portraying the Gibbs free energy landscape at the triple point, we observe three wells (blue, green, and red dots) of equal depth, separated by two barriers (magenta and orange dots). In this scenario, a large black hole situated at $r_l$ must overcome both barriers to transition to $r = 0$. Notably, the transition rate from the large to the small black hole state surpasses the combined rate from the small to the large black hole and thermal states. Once $t > 20$, $\rho (r=0,t) = \rho (r_s,t) = \rho (r_l,t) = 0.4377$ , where the final stationary state is achieved. During the evolution, we notice that $\rho (r_s,t)$ increases to a maximum of 0.7043 at $t = 0.8544$ and then decreases with time to its stationary value of 0.4377. This behavior arises because the small black hole state can transition to both thermal radiation and large black hole states. The system tends to persist longer in the small black hole and thermal radiation states, attributed to the relatively smaller barrier between them compared to the large black hole state. As the small black hole and thermal radiation states become more populated, transitions back to the large black hole state occur. Due to the possibility that $\rho (r_s,t)$ and $\rho (r=0,t)$ can surpass $\rho (r_l,t)$, we characterize this behavior as a strong oscillatory phenomenon⁹⁰.

Considering second situation shown Fig. 19b, the initial Gaussian wave packet $\rho (r,t = 0)$ peaks at the small black hole phase with $\rho (r_s,t = 0) = 56.4189$, while $\rho (r = 0,t = 0) \simeq \rho (r_l,t = 0) \simeq 0$. As expected, $\rho (r_s,t = 0)$ decreases whereas $\rho (r=0,t = 0)$ and $\rho (r_l,t = 0)$ both increase. Beyond $t > 20$, the probabilities reach a stationary state where $\rho (r=0,t) = \rho (r_s,t) = \rho (r_l,t) = 0.4377$, resembling the previous case. Throughout the evolution, we note a leakage of probability from the small black hole state to both thermal radiation and large black hole states. The probability at $r=0$ increases more rapidly than $\rho (r_l,t)$ due to the lower barrier height depicted in Fig. 20. Furthermore, we observe a rapid increase in $\rho (r=0,t)$ to a peak value of 4.1097 at $t = 0.0245$, followed by a gradual decrease over time to its stationary value of 0.4377. Notably, for $t > 0.0205$, we find that $\rho (r=0,t)> \rho (r_s,t) > \rho (r_l,t)$, indicating the dominance of $\rho (r=0,t)$ among the three probabilities. This suggests a higher probability of the system residing in the thermal radiation state. Given the dominance of $\rho (r=0,t)$, this behavior, akin to the previous case, is characterized as a strong oscillatory phenomenon. Meanwhile, the evolution of $\rho (r_l,t)$ shows an increase to a maximum of 0.7043 at $t=0.8551$, followed by a gradual decrease to its stationary value of 0.4377. Since $\rho (r_l,t)$ consistently remains smaller than $\rho (r_s,t)$, this behavior is termed a weak oscillatory phenomenon⁹⁰.

Kinetics and fluctuations in the dynamics of Born–Infeld-AdS black hole state transitions

Herein, we will explore the kinetics of the first passage event transitioning from one black hole state to another in a triple-point scenario, where thermal radiation, large, and small black hole states coexist. To this end, we recall the the first passage time notion. The time required for the black hole state to transition into an unstable black hole phase, represented by the free energy peak, is defined as the first passage time. In other words, the mean first passage time represents the average timescale for a stochastic event to occur for the first time⁸⁷. Figure 20 illustrates three cases: thermal radiations to small black holes (case 1), small black holes to thermal radiations and large black holes (case 2), and large black holes to small black holes (case 3).

The distribution of first passage times is defined as $F_p(t)$, where $\Sigma (t)$ is the probability that the state of the black hole hasn’t performed a first passage by time t. $F_p(t)$ and $\Sigma (t)$ distributions are connected by

$$\begin{aligned} F_p(t) = - \mathcalligra{A} \dfrac{d \Sigma (t)}{d t}, \end{aligned}$$

(37)

where $\mathcalligra{A}$ is nothing than a normalization constant such that $\int _{0}^{+ \infty } F_p(t) dt = 1$. The quantity $\Sigma (t)$ is defined to be the probability of a black hole being present in the system at time t⁸⁷. Hence, we get

$$\begin{aligned} \Sigma _{1}(t) = \int _{0}^{r_1} \rho (r,t) dr, \end{aligned}$$

(38)

$$\begin{aligned} \Sigma _{2}(t) = \int _{r_1}^{r_2} \rho (r,t) dr, \end{aligned}$$

(39)

$$\begin{aligned} \Sigma _{3}(t) = \int _{r_2}^{+\infty } \rho (r,t) dr. \end{aligned}$$

(40)

We apply reflective boundary conditions at $r = 0$ and $r = +\infty$ (sufficiently large r) and absorbing boundary conditions at $r_1$ and $r_2$ peaks. We assumed that the time required to transition from the intermediate transition state of the black hole to the large black hole state is substantially shorter than the first passage time. Furthermore, if a black hole state makes the first passage via thermal fluctuation, the black hole state exits the system. In this case, the probability distribution’s normalization will not be kept.

Using Eqs. (37), (38), (39), (40) and the Fokker–Planck equation Eq. (31), with $\lim \nolimits _{r \rightarrow +\infty } \rho (r,t) = 0$ in hands, one can express the first passage rate $F_p(t)$ for the three cases as

$$\begin{aligned} F_{p1}(t)= & \mathcalligra{A}_1 \left( - \left. \dfrac{\partial \rho (r,t)}{\partial r}\right| _{r = r_1} +\dfrac{1}{T} \left. \rho (r,t) \dfrac{\partial G(r)}{\partial r}\right| _{r = 0}\right) , \end{aligned}$$

(41)

$$\begin{aligned} F_{p2}(t)= & \mathcalligra{A}_2 \left( - \left. \dfrac{\partial \rho (r,t)}{\partial r}\right| _{r = r_2} +\ \left. \dfrac{\partial \rho (r,t)}{\partial r}\right| _{r = r_1}\right) , \end{aligned}$$

(42)

$$\begin{aligned} F_{p3}(t)= & \mathcalligra{A}_3 \left. \dfrac{\partial \rho (r,t)}{\partial r}\right| _{r = r_2}. \end{aligned}$$

(43)

We may calculate the mean first passage time and its relative fluctuation using the time distributions. The average first passage time is given by

$$\begin{aligned} \left\langle t\right\rangle = \int _{0}^{+ \infty } t F_p(t) dt, \end{aligned}$$

(44)

while the relative fluctuation is obtained to be

$$\begin{aligned} \mathfrak {f} = \dfrac{\left\langle t^2\right\rangle - \left\langle t\right\rangle ^2}{\left\langle t\right\rangle ^2}. \end{aligned}$$

(45)

We propose focusing solely on the second and third cases, as the initial state in the first case aligns with the boundary at $r=0$, resulting in numerical instabilities. These instabilities arise from the performance limitations of our computational tools and the narrowness of the studied domain. The numerical results for $F_{p2}(t)$ and $F_{p3}(t)$ are illustrated in Fig. 21a.

Fig. 21

(a) First passage time distribution for cases 2 and 3. (b) First and second parts of the first passage time for $F_{p2}(t)$. (c) First passage time distribution for case 3 and the second part of the first passage time for $F_{p2}(t)$.

For each case, there is a single peak at $t_2 = 0.0041$ and $t_3 = 0.1986$, which can be interpreted as the length of time at which the system remains in its initial state for each before first transiting to another state. For the second case (green curve), the system transits to other states (thermal radiation and large black hole) after a short time, whereas for the third case (red curve), the system remains in the large black hole state longer. The mean first passage time for the second case is $\left\langle t_2\right\rangle = 0.0856$ with a relative fluctuation $\mathfrak {f}_2 = 2.3474$, whereas, for the third case, $\left\langle t_3\right\rangle = 3.3835$ with a relative fluctuation $\mathfrak {f}_3 = 1.9227$.

In order to understand the behavior observed in Fig. 19, we depict the two parts of $F_{p2}(t)$ in Fig. 21b where $F_{p21}(t)$ (magenta curve) is the distribution of first passage time from small black hole to thermal radiation, and $F_{p22}(t)$ (orange curve) is the distribution of first passage time from small black hole to the large black hole. Obviously, each distribution shows a single peak at $t_{21} = t_2 = 0.0041$ and $t_{22} = 0.1387$. The mean first passage time for each situation is $\left\langle t_{21}\right\rangle = 0.0612$ with a relative fluctuation $\mathfrak {f}_{21} = 2.9721$, and $\left\langle t_{22}\right\rangle = 0.2550$ with a relative fluctuation $\mathfrak {f}_{22} = 0.4081$.

Moreover, we remark that $\left\langle t_{21}\right\rangle < \left\langle t_{22}\right\rangle$, which means that when the initial state peaks at the small black hole phase, the system transits suddenly to thermal radiations phase in good agreement with Fig. 19b where $\rho (r=0,t)$ increases very quickly and passes over $\rho (r_s,t)$, whereas $\rho (r_l,t)$ increases slowly before to reach its maximum with $\rho (r_l,t)$ is always smaller than $\rho (r_s,t)$ because the transition to large black hole phase takes more time than the transition to thermal radiations which explains the weak oscillations observed in this case. Indeed, the barrier height between the small black hole and thermal radiation is smaller than that between small and large black holes. When the initial state peaks at the large black hole phase, the transition takes quite more time ($\left\langle t_{3}\right\rangle < \left\langle t_{2}\right\rangle$) to transit to the small black hole phase, and after then the system can transit quickly to thermal radiations phase. Moreover, we see in Fig. 21c that $F_{p22}(t) \ne F_{p3}(t)$, which means that the transition between small and large black holes is not symmetric with $\left\langle t_{3}\right\rangle < \left\langle t_{22}\right\rangle$. That is to say, a large black hole takes more time to transit to a small black hole even though the height of the barrier is the same. Nevertheless, the relative fluctuation of first passage time is very important in the transition from a large black hole to a small black hole ($\mathfrak {f}_{3}>\mathfrak {f}_{22}$), and that what could explain the strong oscillatory behavior observed in Fig. 19a.

Conclusion

The connection of gravity, thermodynamics, and quantum field theory is an essential tool to probe the quantum nature of black holes. The thermodynamic analysis and the phase transition behavior during the black hole evaporation might be a crucial area of investigation to determine the microscopic description of the black hole thermodynamics in particular, and the spacetime structure in general. One possible way to investigate such microscopic structure is by probing through the dynamic and kinetic evolution of the black hole during the thermal phase transitions. This paper is devoted to inquiring into the small black hole and the large black hole phases as well as the reentrant phase transition for the Born–Infeld-AdS black holes from the perspectives of the free energy landscape via the Landau free energy formalism and the stochastic processes through a certain probability distribution using the Fokker–Planck equation.

We started with a brief discussion of the Born–Infeld-AdS black hole solutions, the related thermodynamic quantities, and their thermal properties. We then moved on to compute the critical points characterizing different black hole configurations during the phase transitions. We systematically analyzed the profile of the heat capacity at a constant electric charge, Q, and studied its stable and unstable branches. Depending upon the values of the charge parameter, we categorically discussed the phase transition behavior. For $Q<Q_m$, $Q_m$ denotes some marginal charge expressed in terms of the Born–Infeld parameter, we had Schwarzschild-AdS-like behavior, whereas for $Q\ge Q_m$ we had the characteristics behavior of the heat capacity mimicking that of the Reissner-Nordstr$\ddot{o}$m-AdS black holes. The condition $Q_m\le Q<Q_c$, where $Q_c$ is the critical point, exhibited a first-order phase transition where a small-sized black hole transited into a large black one. At the critical value $Q=Q_c$ of the charge parameter, a second-order phase transition occurred between the small and large black holes. For other values of the charge parameter greater than $Q_c$, we observed that the black holes are locally stable, thereby indicating the positive heat capacity.

Next, we focused our attention on exploring the thermal phase transition behavior of the Born–Infeld AdS black holes by considering a general prescription of the Landau-free energy functional of the Van der Waals fluids. The Landau functional provided us with a phenomenological description of the Van der Waals fluids when it undergoes a second-order phase transition. The analysis was quite interesting for our present analysis of the Born–Infeld AdS black holes, for that, we had to take into account the parameter space $\lbrace X,T,P, Q\rbrace$ describing the state of the system pertaining to a set of physical conditions to be imposed. Such an analysis actually led us to connect the thermal behavior among the different states of the Van der Waals-like fluids and the Born–Infeld AdS black hole phases. For such purposes, we computed the convexity of the Landau functional to determine its extreme points and the corresponding stable and unstable phases of the thermal black hole systems. We plotted the temperature, T vs. the horizon radius, $r_h$, the Gibbs free energy, G as a function of temperature, T, the Landau functional as a function of the state variable X as well as the volumes, V for different values of the charge parameter Q. As a further investigation of the thermal systems, we also plotted the on-shell Gibbs free energy $\tilde{G}$ as a function of the temperature. For the charge parameter $Q=0.005<Q_0$, both small and large black hole phases were observed. It’s worth noting that $Q_0$ corresponds to the charge parameter value where the temperature profile, represented by the $T-r_h$ plot, exhibits an inflection point. Consequently, when $Q=0.00922=Q_0$, the first derivative of the Gibbs free energy became discontinuous, signifying a corresponding discontinuity in the Landau functional

Additionally, the dynamics of AdS black holes and their kinematic descriptions were effectively elucidated by examining the thermal fluctuations exhibited by the system throughout its evolution. Given that fluctuating variables necessitate a probability distribution during thermal phase transitions, incorporating time dependence became imperative. This description relied on the probability distribution of the spacetime state in the ensemble, denoted as $\rho (r, t)$. The thermal phase transitions were governed by a stochastic process and were contingent on the order parameter, with dynamics during its phases determined by fluctuating macroscopic variables. The entire evolution process was investigated through the Fokker–Planck equation. Given that transitions, such as from small to large black holes or reentrant phase transitions, involve sudden changes in the event horizon size, we identified the event horizon as an order parameter. Our analysis of stability and thermal phase transitions in Born–Infeld-AdS spacetime employed heat capacity and Gibbs-free energy. Rather than addressing phase transitions during dynamic evolution, we elevated the conventional Gibbs free energy to the status of generalized off-shell Gibbs free energy as a function of the order parameter. Analytical solutions for the order parameter are challenging, but numerical analysis yielded its lower bound. Utilizing the off-shell Gibbs free energy for various black hole configurations, we illustrated them for different temperature values.

During the small-large black hole phases, the switching process becomes faster than it existed earlier and the final stationary states should be of Boltzmann type. Such parables of the small-large black hole phases existed in the literature for a wide variety of AdS black hole systems. However, for the AdS black holes in Born–Infeld gravity, the notions of the reentrant phase transitions and the leaking of the small to radiation or the large to radiation phases was an exciting investigation. But in the process of the dynamical evolution, the charge parameter $Q=0.01009$, we ruled out the possible existence of the reentrant phase transition behavior as claimed in the previous literature¹⁰³. The systems instead of going through a reentrant phase transition, drained down to the pure thermal state and the large black hole phase reflecting the most probable states. At slightly larger values of $Q=Q_t=0.0103638$, the system co-existed as a triple point comprising of the small, large, and thermal phases as was confirmed by the probability distribution. Further slight increase in the charge value, the phase transitions were distilled into two distinct phases, namely, a Hawking-Page-like phase transition between small to radiation, and another first-order phase transition among the small and the large black holes. Lately, we determined the first passage time for the kinetic evolution of distinct black hole states, focusing on the triple point configuration. Notably, we detected a finite peak in the distribution of the first passage time for three distinguished scenarios: (1) transition from pure thermal radiation to a small black hole, (2) transition between a small black hole and a large black hole through pure thermal radiation, and (3) transition from a large black hole to a small black hole phase. These processes unfold within a brief interval of the first passage time.

Exploring the impact of friction on kinetic and dynamic processes constitutes a thriving and highly relevant area of research, as briefly demonstrated in our current work through the computation of the mean first passage time and corresponding fluctuations. In a dynamical system, friction is incorporated through microscopic descriptions, offering insights into the macroscopic behavior of AdS black holes, particularly in terms of the order parameter. A potential future direction for this research could involve a more in-depth examination of the microscopic degrees of freedom and interactions among black hole molecules during kinetic turnovers.