Introduction

In recent years, supercritical fluid (SCF) technology has garnered significant attention as an environmentally friendly option due to its unique characteristics such as low viscosity, high diffusion capabilities, strong solvation capacity, and excellent selectivity. Regarding polar compounds, while SC-CO2 has moderate or even minimal solubility, it remains the most prevalent SCF due to numerous unique traits like low critical temperature and pressure, non-flammability, non-explosiveness, non-toxicity, economic efficiency, and particularly its ease of separation and recycling1. SC-CO2 has demonstrated significant capabilities in diverse domains, energy2, comprising nanoparticle formation3, food4, extraction of essential oil5, seed oil6, solubility7, anti-cancer drugs8,9, polymer synthesis5, impregnation10, optimization and mathematical modeling11, etc. Several studies showed that the micronization of a drug leads to improving the performance and absorption in the body and reducing side effects initiated from using the drug12. For this purpose, various methods such as grinding, recrystallization, spray-drying, freeze-drying, and crystallization have been utilized up to now. These prevalent micronization techniques are associated with issues such as significant thermal stress, thermal degradation, broad particle size distribution, and elevated residual solvent in the end product. Recently, new SCF-based technologies have arisen to achieve a high-quality product with a consistent particle size distribution13.

The key and fundamental effective factor in SCF extraction processes is the precise understanding of the equilibrium solubility of substances. Despite various methods to experimentally determine drug solubility, a specific set of conditions and tools is necessary due to their intricate and sensitive designs14. The difficulty and expense of obtaining equilibrium data at high pressures and temperatures increase the need to estimate drug solubility in SC-CO215. The solubility of SDs in SCF can be estimated through thermodynamic equations of state (EoSs), fluid density-based experimental and semi-experimental models, solution activity coefficient-based models, and artificial intelligence techniques16.

Numerous experimental investigations were conducted in the field of the solubility measurement of SDs in SC-CO2, which are given in Table 1. Some of these researchers presented experimental and semi-experimental models as follows. Sodeifian et al. measured the solubility of imatinib mesylate in SC-CO2 and analyzed the data using two sets of procedures involving three EoSs and six semi-experimental models. Their findings highlighted the effectiveness of the Haghtalab et al. EoS with the VdW2 mixing rule over other models. They subsequently introduced a new model, named Sodeifian et al., which incorporates six adjustable parameters and accurately estimates the experimental solubility of imatinib mesylate17. Housaindokht and Bozorgmehr estimate the solubility of three SDs in SC-CO2. The estimation was performed by three EoSs (Peng-Robinson, modified Peng-Robinson and Pauzuki) as well as three mixing rules (VdW1, VdW2 and Adachi-Sugi). The optimal outcome was obtained from the Pauzuki equation with the VdW2 mixing rule18. Huang et al. measured the solubility of aspirin in SC-CO2 with and without two solvents of ethanol and methanol. Then they estimate experimental data with the Peng-Robinson EoS and VdW mixing rule. Peng-Robinson EoS with an average absolute relative deviation (AARD) of (14–23%) showed good accordance between both experimental and estimated data19. Ardestani et al. measured the solubility of capecitabine using seven experimental models and three EoSs combined with the mixing rule. The EoS of PR-VdW2 (AARD = 20.32%) could estimate the solubility better9.

Recently, machine learning technology has been widely used as estimation tools across various scientific fields, such as estimating the solubility of solid materials in SC-CO2. This approach will reduce massive numerical calculations and expenses if a suitable thermodynamic model is provided20. One of the most famous of them is the artificial neural networks (ANNs) operate as a powerful methodology for the comparison and modeling of complex nonlinear problems, facilitating the estimation of solutions for such challenges. Sodeifian et al. studied the solubility of six pharmaceutical compounds in SC-CO2 using four different models: cubic EoS, empirical and semi-empirical models, regular solution with the Flory-Huggins equation, and ANN. comparing results indicated that the ANN-based model provided the best results in terms of correlating the experimental solubility of the pharmaceutical compounds in SC-CO220. Yang et al. measured the solubility of silymarin in pure SC-CO2 and with a cosolvent. They used three semi-experimental models and one backpropagation artificial neural network (BPANN) model to estimate solubility and compared the results to experimental data. The BPANN model demonstrated higher accuracy, with an AARD of 1.14–2.15%21. Mehdizadeh and Movagharnejad estimated the solubility of thirty different compounds in SC-CO2 using seven semi-experimental models and compared the results to those obtained from an ANN. The ANN method showed greater precision, with an average relative deviation (ARD) of 5.3%, compared to 15.96% for the best semi-experimental equation. Additionally, the ARD of the semi-experimental equations varied significantly across different compounds, whereas the ANN method exhibited more consistent performance regardless of the material type22. Dadkhah et al. estimated the solubility of solid substances in SC-CO2 by employing the adaptive neuro-fuzzy inference system (ANFIS) model. The model’s input parameters include several thermodynamic properties of the compounds, such as critical temperature, critical pressure, acentric factor, critical molar volume, as well as operational temperature and pressure. The correlation coefficient and The Root Mean Square Error (RMSE) values for all the data were found to be 0.983 and 0.156, respectively. The results of the model comparison showed that the ANFIS model performs superiorly to the FFNN model in estimating the target data23. Pishnamazi et al. measured the solubility of busulfan, which is an SD to treat blood cancer, in SC-CO2 using five semi-experimental models, the KJ model (AARD = 7.57%) presented a more suitable estimation of solubility24. Zhu et al. estimated the solubility of busulfan in SC-CO2 using ANFIS. The results showed that the ANFIS model can be utilized to precisely estimate the solubility of drugs in supercritical solvents8.

The literature includes only a few general semi-empirical models for estimating the solubility of solids in SC-CO₂25,26,27. The primary drawback of these models is that the parameters of the model for a particular solid must be determined solely by utilizing its own experimental solubility datasets. This makes it difficult to use easily and restricts the model’s performance to apply for other SDs.

According to the literature, there is no rigorous model to estimate the solubility of a specific SD in SC-CO2 without needing its sufficient experimental datasets used to fit the coefficients of semi-empirical models. On the other hand, the empirical determination of the solubility of solids under broad conditions is not only often troubled but also requires a significant amount of cost to carry out28,29,30. To address this challenge, the present study aimed to estimate the solubility of SDs in SC-CO2 using AIMs. The selected models include GEP and ANFIS. These models offer several advantages, including reduced time required and the ability to model complex nonlinear processes due to having a number of controllable parameters, which enhances the algorithm compared to other methods31. In order to derive the rigorous AIMs, a comprehensive data collection including some SDs properties additional to operating conditions were gathered. Using SDs properties as the input variables enables the model to estimate the solubility of an SD in SC-CO2 without applying its particular experimental datasets. The input variables of the AIMs were operational temperature and pressure (T, P), SDs’ molecular weight (MWSDs), and melting point (MPSDs). Coefficient of determination (R2), root mean square error (RMSE), mean absolute error (MAE), and the percent of Average absolute relative deviation (AARD%), as statistical parameters, were employed to evaluate and validate the results and to select the best model.

Table 1 Experimental data of SDs solubility in the SC-CO2 at various operating conditions.
Full size table

Artificial intelligence modeling

Data gathering

The data required for the AIMs was collected by gathering a comprehensive data collection (1816 dataset) from previous studies, as shown in Table 1. Consistent with Fig. 1, the experimental data of T, P, MWSDs, and MPSDs variables were selected as the input variables to estimate the solubility of SDs in SC-CO2. In the current AIMs, a wide range of T, P, MWSDs, and MPSDs were investigated, as presented in Table 2.

Fig. 1
figure 1

Schematic diagram of the AIMs.

Full size image
Table 2 Ranges of input variables of the AIMs.
Full size table

Gene expression programming (GEP)

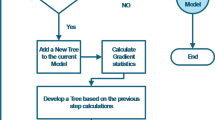
GEP is a combination of genetic algorithms and genetic programming that is based on Darwin’s theory and was developed by Ferreira in 199990. In this method, at the first stage, the initial population of chromosomes are generated randomly or based on input information. The chromosomes are then evaluated as expression trees. If an optimal solution is found, or the number of generations reaches a specified limit, evolution stops, and the best solution is presented. Otherwise, selection is performed, and the process is repeated for several generations to improve the quality of the population. Figure 2 presents the flowchart of GEP90. Figure 2 presents the flowchart of GEP.

Fig. 2
figure 2

The GEP flowchart90.

Full size image

Development GEP model

The procedure GEP utilizes to present a nonlinear function is mentioned below:

  • Entering data: 80% of datasets were selected for training, and 20% of them were selected for validation. The data was randomly selected and introduced to the software. Afterward, the estimator variables and response were identified.

  • The preparation of information: Given that the input variables had various ranges and entering raw-form data led to reducing the rate and accuracy of the model, a normalization process was employed to equalize the range of the data, as well as to accomplish better training. The Min-max normalization was conducted by Eq. (1):

$$\:{\text{v}}^{{\prime\:}}={(\text{v}}_{\text{n}\text{e}\text{w}-\text{m}\text{a}\text{x}}-{\text{v}}_{\text{n}\text{e}\text{w}-\text{m}\text{i}\text{n}})\text{*}\frac{\text{v}-{\text{v}}_{\text{m}\text{i}\text{n}}}{{\text{v}}_{\text{m}\text{a}\text{x}}-{\text{v}}_{\text{m}\text{i}\text{n}}}\:+{\text{v}}_{\text{n}\text{e}\text{w}-\text{m}\text{i}\text{n}}$$
(1)

Where \(\:{\text{v}}^{{\prime\:}}\) is the normalized data, \(\:{\text{v}}_{\text{m}\text{a}\text{x}}\) and \(\:{\text{v}}_{\text{m}\text{i}\text{n}}\) are the maximum and minimum values of the data and \(\:{\text{v}}_{\text{n}\text{e}\text{w}-\text{m}\text{a}\text{x}}\) and \(\:{\text{v}}_{\text{n}\text{e}\text{w}-\text{m}\text{i}\text{n}}\) are the range in which the datas were normalized, respectively91.

  • Adjusting parameters: The setting of GEP includes some steps as below:

  1. (1)

    The determination of the chromosome’s structure (number of chromosomes; head size; number of genes).

  2. (2)

    The determination of the linking function which determines the relationship between sub-ET (expression tree).

  3. (3)

    The determination of fitness function.

  4. (4)

    The selection of genetic operators, including mutation, IS transposition, RIS transposition, etc., and the determination of their rate.

  5. (5)

    The use of random numerical constants.

The optimal parameters concerning the GEP model settings are given in Table 3. The defaulted values of the software were used for other parameters92.

  • Selection of functions: as shown Table 4, a collection of functions was selected for modeling. Moreover, the stop condition was MAX fitness. The output of the model is shown in Fig. 3 as tree expression.

Table 3 Optimum parameter settings for the GEP model.
Full size table
Table 4 Mathematical functions used for the GEP model.
Full size table
Fig. 3
figure 3

Expression tree structure for the best GEP model.

Full size image

The adaptive neuro-fuzzy inference system (ANFIS)

ANFIS is a powerful technique in intelligent computational modeling. This method combines the learning capabilities of ANNs and the logical reasoning of Fuzzy Inference Systems (FIS) to overcome the disadvantages of each. FIS is designed based on “if-then” rules and appropriate membership functions to create an input-output relationship. ANFIS consists of six main sections: data preparation, ANFIS creation, variable selection, training, validation, and output generation, and includes five layers as shown in Fig. 4: Fuzzification Layer, Rule Layer, Normalization Layer, Defuzzification Layer, and Summary Layer. This structure allows ANFIS to effectively process inputs and generate accurate output93,94. The flowchart of ANFIS is presented in Fig. 5.

Fig. 4
figure 4

ANFIS structure.

Full size image
Fig. 5
figure 5

The ANFIS flowchart.

Full size image

Development ANFIS model

In order to develop AIM based on ANFIS the follow steps were done:

  • Entering data: Similar to the GEP model, 80% of datasets were selected for training, and 20% of them were selected for test and check.

  • The preparation of information: For the purpose of increasing accuracy and speed of AIM based on ANFIS, all datasets comprising the inputs and the targets were normalized between [− 1, 1] according to Eq. (1).

  • The preparation of information: For the purpose of increasing accuracy and speed of AIM based on ANFIS, all datasets comprising the inputs and the targets were normalized between [− 1, 1] according to Eq. (1).

Adjusting parameters:

In order to develop the satisfying AIM based on ANFIS, a Takagi–Sugeno fuzzy inference system was applied by using the fuzzy c-mean (FCM) clustering algorithm. The Gaussian membership function was selected for all independent variables comprising T, P and MWSDs. The output membership function was chosen linear. Additionally, the specifications of the developed ANFIS model are presented in Table 5.

Table 5 Specifications of the developed ANFIS model.
Full size table

Model selection

The AIMs were implemented many times to find the optimal setting of the parameters. The best model was selected by a multi-objective strategy as follows:

  1. (1)

    The selection of the simplest model though this parameter is not predominant

  2. (2)

    The training data have the highest value of fitness

  3. (3)

    The validation data have the highest value of fitness

The first objective should be controlled by the user. About the other objectives, the objective function (OBJ) by Eq. (2) was defined as a criterion for the accordance of the output estimated by the model with the output experimentally measured. The selection of the best model was conducted based on the minimum OBJ value that resulted in lower AARD%95.

$$\begin{aligned} OBJ = & \left( {\frac{{No_{{Training}} - No_{{Validaition}} }}{{No_{{Training}} }}} \right)\frac{{RMSE_{{Training}} + MAE_{{Training}} }}{{R_{{Training}}^{2} }} \\ & \; + \frac{{2No_{{Validaition}} }}{{No_{{Training}} }}{\text{~~}}\frac{{RMSE_{{Validaition}} + MAE_{{Validaition}} }}{{R_{{Validaition}}^{2} }} \\ \end{aligned}$$
(2)
$$\:{{R}_{i}}^{2}=\frac{{\left[\left(n\sum\:_{j=1}^{n}({T}_{j}{P}_{ij}\right)-\left(\sum\:_{j=1}^{n}{T}_{j}\right)\left(\sum\:_{j=1}^{n}{P}_{ij}\right)\right]}^{2}}{{\left[n\sum\:_{j=1}^{n}{{T}_{j}}^{2}-\right(\sum\:_{j=1}^{n}{T}_{j})}^{2}\left]\right[n\sum\:_{j=1}^{n}{{P}_{ij}}^{2}-{\left(\sum\:_{j=1}^{n}{P}_{ij}\right)}^{2}]}$$
(3)
$$\:RMSE=\sqrt{\frac{1}{n}\sum\:_{j=1}^{n}{({P}_{ij}-{T}_{j})}^{2}}$$
(4)
$$\:MAE=\frac{1}{n}\sum\:_{j=1}^{n}\left|{P}_{ij}-{T}_{j}\right|$$
(5)
$$\:AARD\%=\frac{100}{n}\sum\:_{j=1}^{n}(\frac{\left|{P}_{ij}-{T}_{j}\right|}{{T}_{j}}$$
(6)

where Notraining and Novalidation denote the number of training and validation data, respectively, and Pij is the value estimated by the individual model i for record j (out of n records). Tj is the target value for record j96.

The created objective function considers the variations of R2, RMSE, MAE, and AARD%, which are defined in Eqs. (3–6). The higher values of R2 and the lower values of RMSE, MAE and AARD% result in reducing the objective function. Consequently, it can present a more precise model. Furthermore, the abovementioned function considers the effects of splitting data sets to the training and validation sets95.

Results and discussion

To study the behavior of the AIMs selected based on the optimized parameters, the comparison of output of the models with the training and validation experimental data is shown in Figs. 6 and 7, respectively. The results and the statistical parameters of R2, RMSE, MAE, and AARD%, presented in Table 6 indicate that the ANFIS is more satisfactory and reliable in estimating the solubility of SDs in SC-CO2 than the GEP model. Since the ANFIS model showed the higher R2 and lower RMSE, MAE, and AARD% compared to GEP model, it was applied to compare the independent variables importance, to investigate the effect of them on the response, and finally to compare the model with semi-empirical ones.

Fig. 6
figure 6

Scattergram of the experimental data versus the estimation by GEP and ANFIS models for training datasets.

Full size image
Fig. 7
figure 7

Scattergram of the experimental data versus the estimation by GEP and ANFIS models for validation datasets.

Full size image
Table 6 Performance evaluation of the implemented correlation.
Full size table

As before mentioned, to evaluate the model accuracy, 10% of datasets was randomly considered as check data in the ANFIS model. Matching experimental and output values for check data including random SDs at various operating condition is clearly indicated in Fig. 8, The statistical analysis for the accordance investigation showed the R2 of 0.991, RMSE of 0.322, MAE of 0.153, and AARD% of 16.820%.

Fig. 8
figure 8

Investigation the accordance between experimental and output values for check data.

Full size image

Variable importance

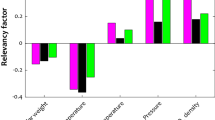
The sensitivity analysis of independent variables is conducted so as to estimate their relative importance in forecasting the dependent variable, which is significant to design better and optimize the related process97. GEP uses a complicated random method to calculate the variable importance of every single input variable. The importance of each independent variable is calculated by randomizing its input values and then by reducing R2 between the model output and the target. The results are normalized to nondimensionalize96. The relative importance of nondimensionalized numbers related to each independent variable produced in this study is shown in Fig. 9.

Fig. 9
figure 9

Variable importance chart for the GEP model.

Full size image

As can be seen, the independent variables of T, P, MWSDs, and MPSDs are denoted by d0, d1, d2, and d3. According to Fig. 9, MWSDs, P, MPSDs, and T have the highest effect in estimating the solubility in SC-CO2, respectively.

Investigation of the effect of independent variables on the solubility in SC-CO2

Temperature effect

In the equilibrium of a pure solid (component 1) with the SCF, by assuming that SC-CO2 is not solved in the solid, and the solid molar volume is not as a function of pressure, Eq. (7) can be written as follows:

$$\:{y}_{1}P{\phi\:}_{1}^{scf}={\phi\:}_{1}^{sat}{P}_{1}^{sat}{e}^{\left(\frac{{V}_{1}^{S}\left({P}_{1}-{{P}_{1}}^{sat}\right)}{RT}\right)}$$
(7)

where \(\:{y}_{1}\:\)is the molar fraction of the solvent in the vapor phase, T and P are the operational temperature and pressure, respectively, \(\:{\phi\:}_{1}^{scf}\) is the solid fugacity coefficient in the supercritical phase, \(\:{\:\phi\:}_{1}^{sat}\) is the vapor fugacity coefficient originated from the solid, \(\:{\:P}_{1}^{sat}\) is the solid saturation vapor pressure, \(\:{V}_{1}^{S}\) is the solid molar volume, P1 is the solid vapor pressure, and R is the universal gas constant98.

Since the temperature enhancement can lead to increasing the solvent vapor pressure, it can also be stated that the solubility of the solid component in SC-CO2 increases (see Eq. (7)). Despite the fact that increasing temperature will lead to decreasing the density of the solvent, the study of the effect of increasing temperature on the solubility of SDs in SC-CO2 indicated that the positive effect of vapor pressure of the drug component is dominant. Figure 10a and b indicates the positive effect of temperature on the solubility of SDs in SC-CO2. The literature research also showed the similar trend in examining the effect of operating temperature on the solubility of solid materials in SC-CO2 as Ref99.

Pressure effect

Operating pressure typically demonstrates a dual influence in investigating the solid solubility in SC-CO2. In assessing the impact of pressure, one must consider two significant variables: SC-CO2 density and solubilized vapor pressure. For this objective, there exists a cross-over region for drug solubility. This phenomenon transpires when the magnitude of the two determinants of SC-CO2 density and solute vapor pressure are equivalent73,75. In other word, as pressure rises at constant temperature constant, the density of the solvent rises, whereas the vapor pressure of the solute diminishes. At higher pressures, the extent of this density alteration becomes less pronounced, and the change in solute vapor pressure becomes more significant, effectively outweighing the impact of solvent density changes on the solubility of the solute. Since many drugs were used in this study and not all of them necessarily exhibited cross-over pressure, it is not possible to select a specific pressure or range as the crossover pressure. However, this phenomenon is clearly observable at a pressure of 215 bar and a temperature range of 308–328 K in Fig. 10b drawn for Galantamine. At pressures less than this region, the density effect dominates, and solubility increases with decreasing temperature. In contrast, above this region, the vapor pressure of the solute becomes a more significant factor, and higher solubility is observed at higher temperatures. The dual effect of temperature on the solubility of various drugs in supercritical carbon dioxide has been repeatedly studied in the literature58,62,79,81. In fact, the increase of pressure leads to reducing the intermolecular distance in SCF and as a result increasing the density, which heightens the solubility. Furthermore, the solvation power of SC-CO2 increases under the influence of increasing pressure. In the simplest binary solutions of SCF, the solvation phenomenon requires the soluble molecules to be surrounded by solvent because of local clustering of solvent molecules. In a cluster, the highest number of solvent molecules is aggregated around a soluble. The increase of the number of solvent-soluble interactions created by the displacement of solvent molecules towards the potential range of solvent-soluble interaction locally increases the average density of the solvent compared to the bulk, leading to enhancing the solubility100. Qingzhao Shi et al.101 also reached the similar results with this study during investigating the effect of pressure on the solubility of n-alkanes in SC-CO2. Figure 10a indicates the positive effect of increasing operating pressure and temperature on the solubility of Flutamide as an SD in SC-CO2. While the effect of pressure is more significant compared to temperature, which is also reported in Refs24,44,45,99. The results obtained from the sensitivity analysis of the independent variables of the model in Fig. 9 also confirms this finding. Furthermore, its three-dimensional surface plot was drawn as Fig. 10b to take a broader view of the operating condition effects on the ACDs solubility in the SC-CO2. As can be seen in Fig. 10, the maximum solubility of Flutamide and Galantamine is obtained in the highest operating conditions. Therefore, it is suggested that these two variables be at the highest possible value. On the other hand, due to the increase in the process cost, the cost of the supercritical process should be considered to determine the optimal operating conditions.

It is noteworthy, Fig. 10b confirms the results reported in the literature like the surface description of the estimated solubility data for salsalate based on ANN modeling reported by Nguyen et al.102 and for busulfan based on ANFIS modeling reported by Zhu et al.8. Since both of these models are provided only for a specific SD, the operating temperature and pressure were only their independent variables. While in the current model, using the physical properties of SDs as input model variables cause to the model applicability for solubility estimate of various SDs in the SC-CO2.

Fig. 10
figure 10

Two dimensional plot for Flutamide (a) and three dimensional plot for Galantamine (b) to investigate the effects of operating temperature and pressure on SD solubility in the SC-CO2.

Full size image

The effect of physical properties of SDs: MWSD and MPSD

The drugs with low molecular weight usually have higher solubility in SC-CO2. This is because smaller molecules can easily penetrate and interact with the molecular networks of carbon dioxide. Also, lower molecular weight usually means more surface area in contact with the solvent. Materials with higher molecular weight may have lower solubility in SC-CO2 due to their larger size and structural complexity28,103. In addition, the solubility of the substance depends on the type and chemical structure of the substance. SC-CO2 is a nonpolar solvent. Therefore, nonpolar drugs with high molecular weight are usually better dissolved in SC-CO2. On the other hand, polar drugs or drugs with polar groups may have lower solubility in SC-CO2. The type of bonds and molecular structure can also have a great effect on solubility. For example, drugs with strong hydrogen bonds may not dissolve in SC-CO287. In general, although molecular weight is one of the factors affecting solubility, it should be noted that other factors such as chemical structure, presence of functional groups, pressure and temperature also play an important role in estimating drug solubility in SC-CO2103.

The melting point can indicate the type of intermolecular bonds and the chemical structure of the drugs. Drugs with complex structures and strong bonds usually have higher melting points and may have lower solubility in SC-CO228,104. On the other hand, if the drug has functional groups that can interact with SC-CO2, it may have more solubility in SC-CO2, even if its melting point is high. Therefore, the solubility of a drug in SC-CO2 is strongly influenced by the type of interactions between drug molecules and SC-CO2103. Also, drugs with lower melting points usually have higher solubility in SC-CO₂. This is because, as the temperature decreases, the drugs can easily turn into a gas state and thus dissolve in SC-CO₂47.

Comparison the selected AIM with semi-empirical models

To compare the accuracy and ability of estimating SDs solubility in the SC-CO2 by the ANFIS model and previously reported models, the Flutamide SD was selected as a case study. As Table 7, the statistical parameters including R2, MAE, RMSE and AARD% showing the ANFIS model has more satisfactory results with higher accuracy than the other semi-empirical models.

Table 7 Comparison the ANFIS model with the previously semi-empirical models.
Full size table

Conclusion

The solubility estimation in SCF is an important step in the development of micro- and nanoscale particle production processes, as well as the extraction and purification of drugs. Alternatively, the time-consuming and costly access to solubility equilibrium data and the sensitivity of some drugs to heat, upsurge the necessity to model the solubility of drugs in SC-CO2. In this research, the solubility of SDs in SC-CO2 was modeled in a wide range of temperature and pressure (308–348.2 K and 80–400 bar) using AIMs based on GEP and ANFIS. The independent variables were T, P, MWSDs, and MPSDs. The collection of data for SDs in different operational conditions contains 1816 datasets, 80% of them were randomly selected for training, and the rest of them were for validation and test. The AIM output was selected through a multi-objective strategy that resulted in lower AARD% based on the simplest model having the highest fitness. The ANFIS model outperformed the GEP model in terms of accurate estimation, with statistical parameters such as R2, RMSE, MAE, and AARD% obtained in training and validation data equivalent to 0.991, 0.260, 0.167 and 13.890% and 0.990, 0.256, 0.157 and 15.273%, in that order. The RMSE, MAE and AARD% values not only are low, but they are very close together as much as possible, indicating the selected model has high precision in estimating the solubility. The sensitivity analysis of the optimized GEP model concerning the input variables was conducted. The results revealed that MWSDs, P, MPSDs, and T had the most influence in determining the solubility of SDs in SC-CO2, in that order. Increasing MWSDs as a consequence of increasing the number of carbon atoms leads to moving SDs towards nonpolarity. Hence, given the nonpolarity nature of SC-CO2, the increase of MWSDs enhances SDs solubility. Furthermore, the results showed that the positive effect of increasing temperature is dominant in such a way as to result in increasing the vapor pressure of SDs and consequently increasing the solubility in SC-CO2. Moreover, operating pressure significantly influences SDs solubility in SC-CO2, considering SC-CO2 density and solute vapor pressure. A cross-over region exists for drug solubility when the two determinants are equivalent. Other factors like chemical structure, functional group presence, and MPSDs also can play a significant role. Lower MPSDs exhibiting higher solubility due to gas-state dissolution. Eventually, in order to estimate the nonlinear relation between the input and output variables of the current research, the AIMs developed by ANFIS provides satisfactory results. Comparison the performance of the ANFIS model with the other semi-empirical models showed that the current model in addition to providing generalizability for various SDs by using MWSDs and MPSDs as the input model variables indicates more satisfactory results with higher accuracy.