Improved active current limiting control for flexible DC power grid to consider the effects of selective and higher fault resistance

Abstract

The current limiting control strategy of modular multilevel converters in flexible DC power grids can effectively reduce the requirements for line protection speed and the breaking capacity of DC circuit breakers (DCCB). However, it can easily lead to the interruption of power transmission at non-fault terminals and expanding the scope of the fault impact. Secondly, it did not consider the severity of matching faults, which may lead to excessive suppression of fault currents and reduce the sensitivity of the protection system. Therefore, this paper proposes an active current limiting control (ACLC) strategy with fault identification capability to further improve its selectivity and adaptability. Firstly, the starting element in the ACLC selectively identify fault areas based on the difference in the slope of the first backward traveling wave (TW) of the current. Secondly, a current limiting coefficient is constructed based on the slope of the first backward TW of current to achieve fault current limiting. On this basis, setting amplitude control to improve the adaptability of ACLC to fault resistance. Finally, a complete fault handling scheme was proposed, including ACLC, fault identification and fault isolation. The simulation results show that the proposed ACLC strategy is selective while reducing the technical requirements of DCCB. In addition, the adaptability of ACLC to fault resistance has also been improved.

Introduction

The rational development and utilization of energy is the key to solving resource and environmental problems¹. The flexible DC power grid has significant advantages in accepting renewable energy and is an inevitable trend for the future development of the power grid². The fault current in a flexible DC transmission system increases rapidly, making it crucial to quickly detect and isolate the fault³. At present, high-voltage DC circuit breakers (DCCB) are commonly used for fault isolation in flexible DC power grids⁴. However, the high technical requirements for DCCB make it expensive and reduce the economic efficiency of the system⁵. Higher requirements have been put forward for the breaking capacity of DCCB in DC power grids based on half bridge MMC (HB-MMC). This led to significant challenges in the design of DCCB. Therefore, limiting fault current is one of the solutions to reduce DCCB costs⁶. In addition, limiting the fault current can also ensure the safety of the converter and reduce the requirement for quick fault identification^7,8,9.

The current limiting scheme for fault current can be divided into two technical routes: improving equipment topology or improving MMC control. Improve equipment topology: Reference¹⁰ designs a resistive superconducting fault current limiter (SFCL) that can effectively suppress fault currents. Reference¹¹ proposes an improved hybrid DCCB that can effectively reduce the voltage and current stress of DCCB during DC fault current interruption. In addition, some scholars have achieved current limiting by improving the MMC topology. Reference¹² proposes a novel MMC topology that can block DC fault currents. Although the above technical approach can limit fault currents, it necessitates the addition of current-limiting devices or modifications to the DCCB and converter topology, which will reduce the economic efficiency of the power grid.

In contrast, active current limiting control (ACLC) achieved by changing the MMC control strategy is more economical. At present, ACLC based on MMC control is mainly achieved by reducing the DC voltage output by MMC. References^13,14,15 propose a current-limiting coefficient based on fault current to adjust the number of submodules (SMs) during the fault period, thereby achieving fault current limitation. Reference¹⁶ develops a bypass ratio function based on bridge arm current for bypassing SMs to limit fault current and analyzes its adaptability in both strong and weak AC systems. References^17,18 limit fault current by adjusting the MMC bridge arm voltage reference based on the fault current.

However, implementing a fault current suppression scheme based on changing the MMC control strategy has the following two issues. Firstly, regarding the startup issue of ACLC. Currently, ACLC primarily focuses on the fault current suppression effect, often overlooking the rationality of the startup conditions. ACLC mainly relies on detecting the current change rate and voltage drop as its starting conditions. References^16,18 respectively detect the amplitude of DC current and MMC bridge arm current as the starting conditions for ACLC. However, due to the sensitivity of setting the startup threshold or the lack of consideration for factors such as noise, ACLC fails to meet its selectivity requirements, which adversely affects the system. Therefore, the selectivity of ACLC also needs to be further improved. Secondly, most parameter settings in ACLC currently do not consider matching with the severity of the fault. This may lead to excessive suppression of fault current, reducing the sensitivity of the protection system. Therefore, the adaptability of ACLC still needs further improvement.

In addition, the coordination between ACLC and fault recognition still needs further improvement. References^19,20 analyze the impact of ACLC on fault traveling waves and propose corresponding protection principles. However, the concept of fault identification in protection can also be applied to provide valuable information for ACLC, helping to address its current issues.

Currently, the research on ACLC faces the following challenges:

• At present, the electrical quantities used for fault identification and their discrimination results have not been fully utilized in ACLC.

• At present, the ACLC strategy cannot meet its selectivity requirements and will expand the scope of fault influence, impacting the transmission power of non-fault terminals

• At present, most ACLCs have not considered matching the severity of the fault, which reduces the sensitivity of the protection system.

The electrical quantities used in the ACLC proposed in^13,15,21,22 are derived from DC lines. If the electrical quantities of the line can be effectively utilized to determine the fault area, the selectivity of ACLC can be improved. Reference²¹ proposes a staged ACLC based on this idea. However, there may be some issues with the coordination between ACLCs in different stages, and the suppression effect on fault current needs to be improved. On this basis, this article proposes an ACLC strategy. The proposed scheme has the following contributions:

• Based on the idea of fault identification, the use of electrical quantities from the line has improved the selectivity and adaptability of the ACLC, and has formed a complete fault handling plan, while effectively reducing the technical requirements for the DCCB.

• Fully utilize the single ended electrical quantities of the line to identify the fault area and use it as the starting criterion for ACLC, improving the selectivity of ACLC.

• Construct current limiting coefficient based on single ended electrical quantities information of the line, and set variable limiting amplitude control to adapt to higher fault resistance.

The rest of the paper is structured as follows. In section "The overall idea of ACLC strategy", the relationship between ACLC current limiting effect and startup time was explained, and the implementation approach of ACLC was presented. In section “ACLC starting element design”, the first backward TW of current of different fault areas was analyzed, and an overall ACLC was constructed. In section “The principle of ACLC”, the impact of ACLC on AC side current and MMC bridge arm current was explained, the time window for ACLC start criterion was specified, and ACLC startup threshold and control parameters were set. In section “Discussion on ACLC related issues”, the fault current suppression effect of ACLC, its coordination with DCCB, as well as its selectivity and adaptability were verified.

The overall idea of ACLC strategy

ACLC in flexible DC power grid should selectively avoid expanding the scope of fault impact. Secondly, ACLC also needs to respond quickly after a fault to reduce the fault current. Therefore, ACLC needs to balance selectivity and speed. The start time of ACLC after a fault is directly related to the limiting effect of fault current. Assuming ACLC is started at time t₁ and t₂ respectively, Fig. 1 shows the dynamic changes in DC side current.

Fig. 1

Illustration of the DC side current of the ACLC after startup at different times.

According to Fig. 1, the peak breaking current of DCCB is closely related to the fault isolation time and start-up time. In order to reduce DCCB costs and shorten fault isolation time, ACLC needs to be started as early as possible. Therefore, using the single ended electrical quantities of the line to identify fault areas as the starting criterion for ACLC can improve selectivity while meeting the requirement of rapidity. The method for obtaining of electrical quantities of lines in ACLC is shown in Fig. 2¹³. In Fig. 2, U_line and I_line represent the voltage and current measured at the installation site of the line protection.

Fig. 2

Measurement method of electrical quantities of lines in ACLC.

Secondly, this paper takes the half bridge MMC as the research object. During the fault process, the suppression of fault current is achieved by multiplying the MMC bridge arm voltage reference value by K_M¹⁸. Considering that in a weak AC system, in order to ensure that the wind turbines remains connected to the grid, the AC side voltage cannot be lower than 0.2 p.u., therefore the K_M range value is [0.2, 1]¹⁶, and the ACLC strategy principle is shown in Fig. 3.

Fig. 3

ACLC principle diagram.

In Fig. 3, U_pj^* and U_nj^* represent the reference voltages of the upper and lower bridge arms of the MMC. During the fault period, the coefficient K_M is used to reduce U_pj^* and U_nj^*, thereby changing the number of SMs input by MMC during the fault period and achieving the limitation of fault current.

The overall ACLC scheme timing diagram is shown in Fig. 4. In Fig. 4, t₀ is the time when the fault occurred. t_s is the ACLC startup time. t_b is the fault isolation time.

Fig. 4

The overall ACLC scheme timing diagram.

ACLC starting element design

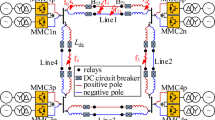
Four terminal MMC-HVDC grid is adopted as the study case in this paper, which the topology is shown in Fig. 5. In Fig. 5, f₀, f₁, and f₂ are situated at 20 km, 100 km, and 180 km, respectively, along Line1. According to the principle of selectivity, only the MMC of the two terminals of the faulty line starts ACLC. Taking the ACLC startup of MMC1 as an example, as shown in area A of Fig. 5.

Fig. 5

Schematic diagram of the startup range of ACLC for MMC1.

Based on the above content, fully utilizing the electrical quantities of the line to identify fault areas can improve the selectivity of ACLC. Secondly, ACLC must also satisfy the speed requirement. Therefore, fault traveling waves (TW) can be utilized to meet the requirements of selectivity and speed mentioned above. The analysis of TW at different fault locations is as follows.

Internal faults

In case of a positive pole-to-ground (P-PTG) fault, the characteristics of the first backward traveling wave of the current were analyzed. After a transmission line fault, there will be coupling between the positive and negative lines, which can be eliminated by Eq. (1).

$$\left[ \begin{gathered} F_{0} \hfill \\ F_{1} \hfill \\ \end{gathered} \right] = \frac{1}{\sqrt 2 }\left[ {\begin{array}{*{20}c} 1 & 1 \\ 1 & { - 1} \\ \end{array} } \right]\left[ \begin{gathered} F_{{\text{p}}} \hfill \\ F_{{\text{n}}} \hfill \\ \end{gathered} \right]$$

(1)

where F_p and F_n respectively represent the voltage or current at the positive and negative pole. F₁ and F₀ respectively represent the 1-mode fault component and 0-mode fault component of voltage or current. Due to the stability of the 1-mode component, this paper analyzes it using the 1-mode component. The propagation process of traveling waves along transmission lines can be represented by (2).

$$A(s) = \frac{1 - kl}{{1 + s\tau l}}e^{{ - s\frac{l}{V1}}}$$

(2)

where l is the transmission distance of the TW in the line. e^-sl/V1 represents the time delay of TW propagation in the line. k and τ respectively represent the amplitude attenuation effect and distortion effect of TW per unit length.

In case of measurement point RM1, the characteristics of the first backward traveling wave of the current were analyzed. Unless otherwise specified in this paper, backward TW represents the first backward TW of current. When the fault occurs at f₂ and the time delay is ignored, the complex frequency domain expression of TW at RM1 is shown in (3).

$$I_{{\text{b}}} (s) = \frac{{i_{{{\text{F1}}}} }}{s}\frac{{1 - kl_{1} }}{{1 + s\tau l_{1} }}$$

(3)

$$\left\{ {\begin{array}{*{20}l} {i_{{{\text{F1}}}} = \frac{{ - \sqrt 2 U_{{{\text{dc}}}} }}{{Z_{{{\text{C1}}}} + R_{{\text{f}}} }}} & {{\text{pole - to - pole fault}}} \\ {i_{{{\text{F1}}}} = \frac{{ - \sqrt 2 U_{{{\text{dc}}}} }}{{Z_{{{\text{C1}}}} + Z_{{{\text{C0}}}} + 4R_{{\text{f}}} }}} & {{\text{pole - to - ground fault}}} \\ \end{array} } \right.$$

(4)

where l₁ represents the distance from fault point f₂ to RM1. U_dc is the voltage at the fault point during normal system operation. Z_C0 and Z_C1 represent the 0-mode and 1-mode impedances of the DC line, respectively. The representation of I_b (s) in the time domain can be obtained through the Laplace inverse transform, as shown in (5).

$$I_{{\text{b}}} \left( t \right) = i_{{{\text{F1}}}} \left( {1 - kl_{1} } \right)(1 - e^{{ - t/\tau l_{1} }} )$$

(5)

According to (5), the waveform I_b(t) can be obtained as shown in Fig. 6.

Fig. 6

Backward TW at f₂ fault.

As shown in Fig. 6, when a fault occurs within the line, the waveform of TW is very steep. In the case of an internal fault, the traveling wave only undergoes the attenuation effect of the line, so its waveform change is not significant.

External faults

The equivalent circuit of f₃ fault is shown in Fig. 7.

Fig. 7

f₃ fault equivalent circuit.

In Fig. 7, I_F1 is the 1-mode fault traveling wave generated at the fault location. At this point, the complex frequency domain expression of TW at RM1 is shown in (6).

$$I_{{\text{b}}} \left( s \right) = \frac{{i_{{{\text{F}}1}} }}{s}\frac{{Z_{{{\text{C}}1}} }}{{sL_{{{\text{dc}}}} + Z_{{{\text{C1}}}} }}\frac{{1 - kL_{1} }}{{1 + s\tau L_{1} }}$$

(6)

where L₁ represents the length of the DC line Line 1. The representation of I_b (s) in the time domain can be obtained through the Laplace inverse transform, as shown in (7).

$$I_{{\text{b}}} \left( t \right) = (A_{1} + A_{2} e^{{ - t/(L_{{{\text{dc}}}} /Z_{{{\text{c1}}}} )}} + A_{3} e^{{ - t/\tau L_{1} }} )$$

(7)

$$\left\{ {\begin{array}{*{20}c} {A_{1} = i_{{{\text{F1}}}} (1 - kL_{1} )} \\ {A_{2} = i_{{{\text{F1}}}} (1 - kL_{1} )\frac{{L_{{{\text{dc}}}} }}{{Z_{{{\text{C1}}}} \tau L_{1} - L_{{{\text{dc}}}} }}} \\ {A_{3} = i_{{{\text{F1}}}} (1 - kL_{1} )\frac{{Z_{{{\text{C}}1}} \tau L}}{{Z_{{{\text{C1}}}} \tau L_{1} - L_{{{\text{dc}}}} }}} \\ \end{array} } \right.$$

(8)

According to (7), the waveform I_b(t) can be obtained as shown in Fig. 8.

Fig. 8

Backward TW at f₃ fault.

As shown in Fig. 8, in the case of an external fault, the CLR will significantly attenuate the traveling wave, resulting in a smoother waveform. Based on the above analysis, there is a significant difference in the traveling wave (TW) waveform between internal and external faults. This characteristic can be used as a starting criterion for ACLC. To further amplify the difference in the traveling wave (TW), its slope is calculated. Therefore, the ACLC start criterion is shown in (9).

$$\left| {k_{{{\text{ib}}}} (t)} \right| = \left| {\frac{{I_{{\text{b}}} (k + 1) - I_{{\text{b}}} (k - 1)}}{{2T_{{\text{S}}} }}} \right| > k_{{{\text{Ibset}}}}$$

(9)

where k_ib is the slope of I_b(t). T_S represents the sampling time interval of TW. k corresponds to a sampling point in the number of TW sampling points, where the first sampling point in TW corresponds to k = 1. k_Ibset is the start criterion threshold for ACLC, and its setting rules and values will be introduced in Sect. 5.

In addition, to prevent the coupling between the positive and negative poles from causing the MMC to mistakenly start ACLC, a pole selection criterion, as shown in Eq. (10), is defined.

$$M = \left( {\sum\limits_{n = 1}^{N} {\left| {\Delta i_{{\text{p}}} \left( n \right)} \right|} } \right)|\left( {\sum\limits_{n = 1}^{N} {\left| {\Delta i_{{\text{n}}} \left( n \right)} \right|} } \right)$$

(10)

$$\left\{ {\begin{array}{*{20}l} {M > M_{{{\text{set}}}} } & {{\text{ positive pole - to - ground fault}}} \\ {M_{{{\text{set}}}}^{{ - 1}} \le M \le M_{{{\text{set}}}} } & {{\text{ pole - to - pole fault}}} \\ {M < M_{{{\text{set}}}}^{{ - 1}} } & {{\text{ negative pole - to - ground fault}}} \\ \end{array} } \right.$$

(11)

where M is the selection factor. M_set is the pole selection setting value, which is set to 1.5 in this article. Δi_p and Δi_n are the positive and negative current fault components of the line measurement points.

The principle of ACLC

Construction of current limiting coefficient

Based on the above analysis, it can be concluded that the slope of the backward TW changes with the fault location. The backward TW can reflect the severity of the fault, and the K_M of ACLC can be constructed based on this characteristic. The maximum value of |k_ib(t)| within the limited current startup range is k_Ibmax, and the minimum value is k_Ibset. When |k_ib(t)| reaches its maximum value, it indicates that the most serious fault has occurred in the area, and the KM value should be set to the minimum value K_min. When |k_ib(t)| reaches its minimum value, it indicates that the slightest fault has occurred in the area, and the KM value should be set to its maximum, 1. Therefore, according to the idea of normalization, K_M is shown in (12).

$$K_{{\text{M}}} = {1 + }\left( {\frac{{\max (\left| {k_{{{\text{ib}}}} ({\text{t}})} \right|) - k_{{{\text{Ibset}}}} }}{{k_{{{\text{Ib}}\max }} - k_{{{\text{Ibset}}}} }}} \right) \times \left( {K_{\min } - {1}} \right)$$

(12)

The default K_min is 0.2, which can be substituted to obtain

$$K_{{\text{M}}} = {1} - {0}{\text{.8}}\left( {\frac{{\max (\left| {k_{{{\text{ib}}}} ({\text{t}})} \right|) - k_{{{\text{Ibset}}}} }}{{k_{{{\text{Ib}}\max }} - k_{{{\text{Ibset}}}} }}} \right)$$

(13)

According to (13), the number of SMs will be adjusted based on |k_ib(t)| after a fault occurs. But although the fault resistance will reduce the value of |k_ib(t)|, it will still make the K_M value smaller. This will result in over suppression of fault current and reduce the sensitivity of the protection system. In case of a PTG fault occurring at the midpoint of the line through a 200 Ω fault resistor, the DC side current before and after current limiting is shown in Fig. 9.

Fig. 9

DC side current under fault conditions with fault resistance.

According to Fig. 9, in the presence of fault resistance, ACLC will suppress the fault current and further weaken the fault characteristics. This is not conducive to identifying faults in the protection system. Therefore, ACLC needs to consider the handling plan for fault conditions with fault resistance.

ACLC variable amplitude control

In order to improve the adaptability of ACLC, K_M variable limit amplitude control is set up. When a fault occurs through a fault resistor, if ACLC cannot adapt to the fault resistor, it will further reduce the fault characteristics and affect the fault identification of the line. In addition, it is necessary to ensure the suppression effect of current under metallic faults. Therefore, k_limit is set as the switching condition for the limit amplitude. k_limit is the slope of the backward TW when there is a metallic fault at the end of the line, and a certain threshold is taken. Compare |k_ib(t)| with k_limit. When |k_ib(t)| is greater than k_limit, it is considered that a metallic fault has occurred in the line, K_min = 0.2. When |k_ib(t)| is less than k_limit, it is considered that the line has faulted through a fault resistance, K_min = U_min/U_dcn. U_min is the lowest voltage of the line. U_dcn is the rated voltage. ACLC’s variable amplitude control adjusts the lower limit of KM based on the voltage at the fault point, enhancing its adaptability to fault resistance. The control schematic diagram of ACLC is shown in Fig. 10. The parameter settings can be found in section “Discussion on ACLC related issues”.

Fig. 10

The ACLC control schematic diagram.

The fault conditions are the same as above. After ACLC adopts variable limit amplitude control, its DC side current is shown in Fig. 11.

Fig. 11

DC side current under variable limit amplitude control.

According to Fig. 11, the suppression of fault current is weakened under the variable limit amplitude control. Therefore, setting variable limit amplitude control can improve the adaptability of ACLC to fault resistance.

Performance characteristics of ACLC

After the DC side fault of the system, the equivalent diagram of the fault circuit is shown in Fig. 12. where L_arm, R_arm, and C_arm respectively represent the inductance, resistance and capacitance of the bridge arm in the MMC. L_eq1, R_eq1, and C_eq1 represent the equivalent inductance, resistance, and capacitance of the fault circuit. U_dc is the total capacitance–voltage of the SMs.

Fig. 12

Equivalent circuit diagram of DC side fault.

Then L_eq1, R_eq1, and C_eq1 are shown in (14).

$$\left\{ \begin{gathered} L_{{{\text{eq1}}}} = \frac{{2}}{{3}}L_{{{\text{arm}}}} + L_{{{\text{dc}}}} \hfill \\ R_{{{\text{eq1}}}} = \frac{{2}}{{3}}R_{{{\text{arm}}}} + R_{{{\text{dc}}}} + R_{f} \hfill \\ C_{{{\text{eq1}}}} = \frac{{6C_{SM} }}{{N_{{{\text{SM}}}} }} \hfill \\ \end{gathered} \right.$$

(14)

Due to the short discharge time and minimal voltage variation of capacitors, U_dc can be considered as a constant voltage source⁹. According to Fig. 12 and Kirchhoff’s voltage law, Eq. (15) can be obtained.

$$L_{{{\text{eq1}}}} \frac{{di_{{{\text{dc}}}} }}{dt} + R_{{{\text{eq1}}}} i_{{{\text{dc}}}} = U_{{{\text{dc}}}}$$

(15)

The fault occurred at t₀ and the DC side current before the fault was I_dc. According to (15), the expression for fault current can be obtained as shown in (16).

$$i_{{{\text{dc}}}} = \left( {I_{{{\text{dc}}}} - \frac{{U_{{{\text{dc}}}} }}{{R_{{{\text{eq1}}}} }}} \right)e^{{ - \frac{{R_{{{\text{eq1}}}} }}{{L_{{{\text{eq1}}}} }}(t - t_{0} )}} + \frac{{U_{{{\text{dc}}}} }}{{R_{{{\text{eq1}}}} }}$$

(16)

After ACLC, U_dc decreased by K_M times, as shown in (17).

$$U_{{{\text{dc2}}}} = K_{{\text{M}}} U_{{{\text{dc}}}}$$

(17)

The ACLC startup time is t_s. According to (15) and (17), the expression for the fault current after ACLC can be obtained, as shown in (18).

$$i_{{{\text{dc}}}}{\prime} = \left( {i_{{{\text{dc}}}} (t_{s} ) - \frac{{K_{{\text{M}}} U_{{{\text{dc}}}} }}{{R_{{{\text{eq1}}}} }}} \right)e^{{ - \frac{{R_{{{\text{eq1}}}} }}{{L_{{{\text{eq1}}}} }}(t - t_{{\text{s}}} )}} + \frac{{K_{{\text{M}}} U_{{{\text{dc}}}} }}{{R_{{{\text{eq1}}}} }}$$

(18)

Assuming fault time t₀ = 0ms and ACLC startup time t_s = 1 ms. According to (16) and (18), the waveform of the DC side current after ACLC can be obtained as shown in Fig. 13.

Fig. 13

The DC side fault current after ACLC.

As shown in Fig. 13, the mapping relationship between ACLC and fault current basically conforms to (18). In addition, it can be seen from Fig. 13 that ACLC can effectively suppress fault current after startup.

Discussion on ACLC related issues

AC side current and MMC bridge arm current

Reference²¹ provides a detailed analysis of the impact of ACLC on the AC side current and bridge arm current. The analysis results indicate that the AC current after ACLC is related to the AC side voltage of MMC. When reducing the inserted SMs through ACLC, it may cause overcurrent on the bridge arms of MMC. Therefore, it is necessary to suppress it to ensure the safety of MMC. Through analysis of the current inner loop control, it is known that it weakens the damping effect and accelerates the system’s response speed, resulting in overcurrent in the MMC bridge arm¹⁵. Therefore, in the d-axis current inner loop, the purpose of suppressing the bridge arm current can be achieved by adding a first-order low-pass filter¹⁵. When ACLC is started, the low-pass filter is connected in series to the d-axis current inner loop control. The control block diagram is shown in Fig. 14

Fig. 14

Bridge arm current suppression control of MMC.

In Fig. 14, T_d is the time constant of the low-pass filter. When a fault occurs at the local end of the line, switch to inner loop control, and the bridge arm current of MMC is shown in Fig. 15.

Fig. 15

Maximum bridge arm current of MMC.

As shown in Fig. 15, switching the d-axis current inner loop control after a fault can to some extent suppress the bridge arm current and prolong the MMC block time.

Time window for start criterion

This paper uses backward TW as the starting criterion for ACLC, therefore it is necessary to meet the relevant time constraints of backward TW. The wavelet transform modulus maxima (WTMM) is used to find out singular point and calibrate the arrival time of the fault traveling wave. It is necessary to ensure that the time window only includes the backward TW, with the first arrival time of the backward TW being t₁ and the second arrival time being t₂. TW arrival marker as shown in Fig. 16. Secondly, considering that ACLC should be started as early as possible, a time window of 0.5 ms should be selected. Therefore, the time window T₁ for the start criterion of ACLC is shown in (18).

$$T_{1} = \left\{ {\begin{array}{*{20}c} {0.{\text{5ms}}} & {t_{2} \ge {0}{\text{.5 + }}t_{1} } \\ {t_{2} - t_{1} } & {t_{2} < {0}{\text{.5 + }}t_{1} } \\ \end{array} } \right.$$

(18)

Fig. 16

The overall flow chart of ACLC scheme.

To ensure the integrity of obtaining backward TW, retain the TW data before t₁ 0.1 ms for computation. The fault pole selection criteria time window is also the same.

ACLC strategy flow chart

The overall flow chart of ACLC scheme proposed in this paper shown in Fig. 17.

Fig. 17

The overall flow chart of ACLC scheme.

When a fault occurs and the DC current is greater than 1.1 times the rated DC current or the DC voltage is less than 0.9 times the rated DC voltage, MMC enters the start judgment of ACLC strategy. Calculate and determine whether there is a fault in the line connected to this MMC according to (11). When it is determined that there is a fault in the line connected to this MMC, continue ACLC startup determination. Determine whether ACLC is started according to (9), and after starting, reduce the bridge arm reference voltage of MMC to K_M times. At the same time, a low-pass filter is connected in series to the d-axis current inner loop to limit the AC side current and the bridge arm current of the MMC. Simultaneously, the DCCB actions at both ends of the fault line isolate the fault. Finally, determine whether the fault current is less than 0.5 times the fault current to achieve the exit of ACLC. MMC returns to normal control mode after ACLC exits.

Determination of thresholds and control parameter settings

Thresholds for ACLC with PTG fault

Due to the difference in backward TW amplitude between pole-to-ground (PTG) faults and pole-to-pole (PTP) faults. Therefore, it is necessary to separately set the k_Ibset for PTG and PTP faults to ensure their reliability. System parameters are shown in Table 1. According to (9), the k_ib(t) under PTG fault can be obtained, as shown in Fig. 18.

Table 1 Specific system parameters and control parameters.

Fig. 18

The k_ib(t) of PTG faults at different locations.

The setting of ACLC startup threshold needs to consider the k_ib(t) when the most severe fault occurs outside the line, and multiply it by the reliability coefficient K_rel. According to Fig. 18, the |k_ib(t) at the most severe fault outside the line is 2029 (kA/s), and K_rel is taken as 1.5. Therefore, the startup threshold k_ibset1 of ACLC for PTG failure is 3043 (kA/s).

Thresholds for ACLC with PTP fault

According to (4), (5), and (7), and specific system parameters, the I_b (t) under PTP fault can be obtained as shown in Fig. 19. According to (9), the k_ib(t) under PTP fault can be obtained, as shown in Fig. 20. The principle of setting ACLC startup threshold under PTP fault is the same as above. According to Fig. 19, the |k_ib(t) at the most severe fault outside the line is 4540 (kA/s), and K_rel is taken as 1.5. Therefore, the startup threshold k_ibset2 of ACLC for PTP failure is 6810 (kA/s).

Fig. 19

The I_b(t) of PTP faults at different locations.

Fig. 20

The k_ib(t) of PTP faults at different locations.

Control parameter settings

Taking PTG malfunction as an example, the most serious fault is usually the local end of the line, the fault distance of 20 km. According to (5) and (9), the slope of backward TW can be obtained as shown in Fig. 21. According to Fig. 21, the k_Ibmax1 is 15,943 (kA/s). Due to the difference in k_ib(t) between PTG faults and PTP faults, k_Ibmax is set separately to ensure its effectiveness. The analysis method and parameter selection are the same as above. Under PTP fault, k_Ibmax2 is 35,786 (kA/s).

Fig. 21

The k_ib(t) of P-PTG faults at f₀.

k_limit is the slope of the backward TW when there is a fault at the end of the line and take a certain margin. Taking PTG malfunction as an example. According to (5) and (9), the slope of backward TW can be obtained as shown in Fig. 22. The fault distance of L₁.

Fig. 22

The k_ib(t) of P-PTG faults at f₂.

According to Fig. 22, the |k_ib(t)| at the end of the line is 14,050 (kA/s). Consider a certain margin, with a margin coefficient of 0.8, k_limit1 is 11,240 (kA/s). Due to the difference in k_ib(t) between PTG faults and PTP faults, k_Ibmax is set separately to ensure its effectiveness. The analysis method and parameter selection are the same as above. Under PTP fault, k_limit2 is 26,043 (kA/s).

Simulation and verification

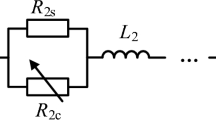
To verify the effectiveness of the ACLC proposed in this paper, a true bipolar ± 500kV four terminal DC power grid was built on the PSCAD simulation platform as shown in Fig. 5. MMC4 is controlled by constant DC voltage, while other MMCs are controlled by constant DC power. MMC adopts a half bridge SM topology, and the specific parameters of the flexible DC grid and MMC are shown in Table 1. The transmission line is an overhead line and is a frequency dependent model, as shown in Fig. 23. The system failure time is 1 s.

Fig. 23

DC lines model.

ACLC effect verification

ACLC trigger verification

In case of metal faults occurring at different positions, take measurement point RM1 as an example to verify whether MMC1 can correctly start ACLC. In case of PTG and PTP faults occurring at points f₂, f₃, and f₄, the |k_ib(t)| values are shown in Figs. 24 and 25. When the fault occurs at different locations, whether MMC1 starts ACLC are shown in Table 2.

Fig. 24

|k_ib(t)| under P-PTG fault.

Fig. 25

|k_ib(t)| under PTP fault.

Table 2 ACLC startup results at different fault locations.

As shown in Figs. 24, 25 and Table 2, ACLC can be accurately start under metal faults, improving the selectivity of ACLC. According to Table 2, the value of |k_ib(t)| will also change when the fault location is different. The verification confirms that |k_ib(t)| can sensitively reflect the severity of faults, demonstrating its feasibility for constructing ACLC. It should be noted that there is a fault with f₆, and based solely on the information from measurement point RM1, MMC1 does not start ACLC. However, the final result of ACLC startup also needs to be based on the information from measurement point RM2. Due to the symmetry of the system, if the start result of ACLC can be correctly determined based on the information of measurement point RM1, then the other measurement points can also be correctly determined. Therefore, the verification of the remaining measurement points will not be repeated.

Verification of ACLC fault current suppression effect

Set metal fault at the midpoint f₁ of the line and compare its current limiting effect with ACLC proposed in^13,18. In order to observe the trend of fault current changes more intuitively, the DCCB remained closed during the fault period. The DC side current measured at RM1 are shown in Figs. 26 and 27.

Fig. 26

DC side current under PTG fault.

Fig. 27

DC side current under PTP fault.

Considering that the fault identification time is 3 ms and the DCCB disconnection time is 4 ms, the main focus is on comparing the current changes 7 ms after the fault. Reference¹³ uses the current change rate as the criterion for starting ACLC, and constructs a current limiting coefficient based on the current amplitude and current change rate to reduce SMs input during faults. However, due to the use of current change rate as the starting criterion for ACLC, its anti-noise ability needs further verification. Secondly, fluctuations in current change rate can lead to unstable current limiting coefficient, which may affect its current limiting effect. Therefore, compared with before ACLC, under the action of ACLC in¹³, the current amplitude decreased by 34.19% 7 ms after the fault occurred, as shown in Fig. 26. Reference¹⁸ uses current amplitude as the criterion for starting ACLC, and constructs a current limiting coefficient based on the current amplitude to reduce SM input during faults. Therefore, compared with before ACLC, under the action of ACLC in¹⁸, the current amplitude decreased by 41.88% 7 ms after the fault occurred, as shown in Fig. 26. However, the starting threshold of this ACLC is the rated value of the DC current, which will expand the range of fault impact. The ACLC proposed in this paper not only ensures selectivity, but also improves its current limiting effect. Compared to before ACLC, the current amplitude decreased by 53.53%.

Under PTP fault, both positive and negative MMC start ACLC to suppress fault current. References^13,18 and the ACLC proposed in this paper reduced the fault current by 49.61%, 66.12%, and 56.84%, respectively, as shown in Fig. 27. In addition, it can be inferred that the ACLC proposed in this paper can handle different types of faults.

Verification of cooperation with DCCB

Set the PTG fault at point f₀ to verify the coordination between the proposed ACLC and DCCB. DCCB is a hybrid topology structure. The amplitude variation of the current flowing through CB12 and the energy absorption variation of the lightning arrester are shown in Figs. 28 and 29.

Fig. 28

DC side current.

Fig. 29

Energy absorption of lightning arrester.

In Fig. 28, it is evident that compared to before ACLC, the peak fault current during DCCB breaking has decreased by 51.6%, and the fault clearing time has reduced by 2.1 ms. As shown in Fig. 29, compared with before ACLC, the energy absorption of the lightning arrester is reduced by 84.15%. In summary, the combination of ACLC and DCCB proposed in this paper can reduce the peak breaking current and accelerate the fault isolation time. To a certain extent, it reduces the technical requirements of the DC power grid for DCCB and improves the economy of the DC power grid.

Adaptability verification of ACLC under different fault conditions

Fault resistance

Set PTG faults at point f₁, with fault resistances of 100 Ω, 200 Ω, and 300 Ω respectively. The calculated results for |k_ub(t)| is shown in Fig. 30.

Fig. 30

|k_ib(t)| at different fault resistances at f₁ fault.

As shown in Fig. 30, the fault resistance reduces the amplitude of |k_ib(t)|, but it does not affect the startup of the ACLC. Additionally, a PTG fault is set at f₀, f₁, and f₂ point, with fault resistances of 100, 200, and 300 Ω, respectively. The simulation results of |k_ub(t)| and ACLC start results are shown in Table 3.

Table 3 ACLC startup results at different fault locations.

According to Table 3, ACLC still recognizes the fault area and starts correctly under a fault resistance of 300 Ω.

To verify the effectiveness of ACLC under low resistance faults, PTG faults at line midpoint, with fault resistances of 25 Ω, 50 Ω, and 75 Ω respectively. The current limiting coefficient and DC side current are shown in Figs. 31 and 32.

Fig. 31

K_M at low fault resistances.

Fig. 32

DC side current at high fault resistances.

As shown in Figs. 31 and 32, under low-impedance faults, the ACLC proposed in this paper increases the current-limiting coefficient as the transition resistance rises, leading to a weakened current-limiting effect. However, when the fault resistance is relatively small, it still provides certain limitations on the fault current, facilitating faster fault isolation in conjunction with the DCCB.

To verify the effectiveness of ACLC under high resistance faults, PTG faults at line midpoint, with fault resistances of 100 Ω, 200 Ω, and 300 Ω respectively. The K_M is shown in Fig. 33 and the DC side current before and after ACLC is shown in Fig. 34.

Fig. 33

K_M at different fault resistances.

Fig. 34

DC side current at different fault resistances.

As shown in Fig. 33, with the increase of fault resistance, the K_M coefficient gradually increases and the current limiting effect weakens. It can be inferred that the proposed ACLC will not excessively suppress fault current under high resistance faults, as shown in Fig. 34. This enhances the adaptability of the ACLC to fault resistance, preventing any significant impact on the sensitivity of the line protection system.

Noise

In order to verify the proposed ACLC adaptability to noise, the PTP fault is set at f₃ point and Gaussian white noise with signal-to-noise (SNR) ratios of 50 dB and 40 dB is added to the sampled data. The calculation result of |k_ib (t)| is shown in Fig. 35.

Fig. 35

|k_ib(t)| at different SNR at f₃ fault.

Additionally, a PTP fault is set at f₀, f₁, and f₂ and add Gaussian white noise with SNR of 50 dB and 40 dB to the sampled signal. The simulation results of |k_ib(t)| and ACLC trigger results are shown in Table 4.

Table 4 ACLC startup results at different SNR.

According to Fig. 35 and Table 4, noise can cause changes in the value of |k_ib(t)|, but it does not affect the discrimination results of ACLC. When the SNR is 40 dB, ACLC can still identify the fault area and start ACLC.

In case of the PTP fault at f1, the K_M and DC side currents at different SNR levels are shown in Figs. 36 and 37.

Fig. 36

K_M at different SNR.

Fig. 37

DC side current at different SNR.

According to Fig. 36, noise will have a certain impact on the K_M value, but the impact is relatively small. Therefore, the impact of noise on the fault current limiting effect is relatively small, as shown in Fig. 37. In summary, the ACLC proposed in this paper has a certain adaptability to noise and can still selectively start and limit fault current even with an SNR of 40dB.

MMC capacitor voltage

Taking the metal fault at the midpoint of the line as an example, the capacitor voltage and total voltage of the SMs with and without ACLC after the fault are shown in Fig. 38.

Fig. 38

The capacitor voltage and total voltage of the SMs with and without ACLC.

As shown in Fig. 38, the voltage of the submodule capacitor drops instantly when the ACLC is not applied, releasing energy to the fault point and thus causing a large fault current. ACLC will change the working state of SMs. For the upper bridge arm, there are more SMs in the excised state. The removed SM is not into the circuit, and when most SMs are in the cut-off state after the ACLC, the capacitance of the SMs remains essentially unchanged, as shown in Fig. 38a. For the down bridge arm, there are more SMs in the engaged state. The SMs in the engaged state have two working modes: charging and discharging, with the specific mode determined by the direction of the bridge arm current. At this point, the direction of the bridge arm current causes more of the down bridge arm SMs to be in the charging state. As a result, the capacitor voltage of the SMs increases, as shown in Fig. 38b.

AC side current

Set a metallic PTG fault at f₀, and the AC side current is shown in Fig. 39.

Fig. 39

AC side current.

According to Fig. 39, the AC side current during without ACLC is [3.17 pu, − 3.02 pu], and after ACLC, the AC side current increases to [4.94 pu, − 4.74 pu]. Therefore, it can be concluded that ACLC will affect the AC side current, which is consistent with the above analysis. After switching the d-axis current inner loop control, the AC side current is limited to [4.28 pu, − 3.76 pu], which reduces the impact on the AC side current to a certain extent. Although ACLC may cause overcurrent on the AC side, it does not lead to mis-operation of the AC side protection. Because the DC side fault isolation time is shorter than the AC side²².

Bridge arm current of MMC

Set a metallic PTG fault at f₀, and the bridge arm current of MMC is shown in Fig. 40.

Fig. 40

MMC bridge arm current.

As shown in Fig. 40, activating the current inner loop control helps suppress the MMC bridge arm current, keeping it below the MMC block value during faults. This ensures the safety of the MMC and reduces the speed requirements for line protection.

MMC bridge arm voltage

The analysis of the examples in the text can be divided into three categories: metallic faults, presence of fault resistance, and presence of noise. Taking the upper bridge arm of MMC as an example, the following is an analysis of the bridge arm voltage under three different fault conditions.

Metallic fault

Set metal fault at the midpoint of the line. In order to observe the trend of bridge arm voltage more intuitively, the DCCB remained closed during the fault period. The reference voltage and actual voltage of the MMC bridge arm when ACLC is not triggered after the fault are shown in Fig. 41a. After the fault triggers ACLC, the reference voltage and actual voltage of the MMC bridge arm are shown in Fig. 41b.

Fig. 41

Bridge arm voltage under metallic fault.

According to Fig. 41a It can be seen that there was no significant change in the bridge arm voltage before and after the fault. Therefore, during the fault period, the SMs will continue to input, resulting in an increase in fault current. According to Fig. 41b It can be seen that ACLC will lower the bridge arm reference voltage of MMC, and modulation triggering will reduce the number of SMs. The actual voltage of the bridge arm decreases accordingly, reducing the fault current.

Fault resistance

Set PTG faults at the midpoint of the line, with fault resistances of 100 Ω and 300 Ω respectively. The reference voltage and actual voltage of the MMC bridge arm are shown in Fig. 42.

Fig. 42

Bridge arm voltage under fault resistances.

As shown in Fig. 41, when there is a fault resistance, the reference voltage of the bridge arm will hardly change. It will not further weaken the fault characteristics and affect the protection system. This further illustrates the adaptability of ACLC to fault resistance.

Noise

Set PTP faults at the midpoint of the line, and Gaussian white noise with SNR ratios of 50 dB and 40 dB is added to the sampled data. The reference voltage and actual voltage of the MMC bridge arm are shown in Fig. 43.

Fig. 43

Bridge arm voltage under fault resistances.

From Fig. 43, it can be seen that noise hardly affects the bridge arm reference voltage. Therefore, noise will not affect the fault current suppression effect.

DC bus voltage

A metallic PTG fault is set at the midpoint of Line 3, and the dynamic changes in DC bus voltage before and after the fault are shown in Fig. 44.

Fig. 44

The dynamic changes in DC bus voltage.

According to Fig. 44, after the fault occurs, the MMC at both ends of the faulty line starts ACLC to reduce the MMC voltage and suppress the fault current. After fault isolation, each MMC will experience overvoltage, but the overvoltage phenomenon of MMC that starts ACLC is more obvious, with a maximum of 1.25 pu. Compared to the overvoltage generated before ACLC, it is within an acceptable range. Secondly, there will be some fluctuations in the voltage of MMC that has not started ACLC, but voltage will eventually stabilize.

Comparison with existing current limiting control strategies

This section compares the ACLC proposed in this article with existing current limiting control strategies, as shown in Table 5.

Table 5 Comparison of ACLC schemes.

According to Table 5, compared to the existing ACLC, the ACLC proposed in this paper reasonably sets the startup criteria, which improves its selectivity. To avoid the impact of ACLC on power transmission at non-faulty ends and expand the scope of faults. Secondly, the current limiting start-up criteria and parameters in this article are not dependent on simulation and have a certain theoretical basis. In addition, this paper also considers the influence of fault resistance and noise on the current limiting starting criterion and the current limiting effect. Simulation results show that both have certain adaptability.

Conclusion

This paper proposes an ACLC for flexible DC power grids, which improves the selectivity and adaptability of ACLC and the conclusions are as follows.

• This paper determines the fault area based on backward TW and uses it as the starting criterion for ACLC, which has selectivity, certain ability to withstand fault resistance and noise. The setting of the startup threshold does not depend on simulation. It can avoid the problem of MMC’s ACLC strategy affecting power transmission at non faulty ends and expanding the scope of fault impact.

• The ACLC proposed in this paper is constructed based on the slope of backward TW and equipped with variable amplitude control to improve its adaptability. ACLC parameter selection does not depend on simulation. Secondly, switching the current inner loop control suppresses the MMC bridge arm current to ensure that the MMC does not block during the fault period.

• The combination of ACLC and DCCB can reduce the peak breaking current by 51% and the energy absorption of lightning arresters by 84.15%, effectively reducing the technical requirements for DCCB. At the same time, it improves the adaptability of ACLC to fault resistance.