Introduction

Snowpack profoundly influences hydrology, ecosystems, and agriculture, altering the energy and water balance between the Earth’s surface and the atmosphere1. Variations in snowpack depth induce changes in regional climate and environment and influence the climate change processes on a large scale or even globally2. As recorded in Essential Techniques for the Welfare of the People (also known as QIMIN Yaoshu), an ancient book on agriculture, snow water is the essence of all crops. Additionally, an old saying states, “Snow is an omen of a good year.” This underscores that snowpack is a critical element in agricultural production. Northeast China serves as a vital base for commercial grain production. The grain and commercial grain production of the three provinces in this region collectively contribute more than one-fifth of the nation’s grain production and about one-fourth of its commercial grain production, respectively3. The grain production in Northeast China directly influences China’s food security, impacting the healthy development of the economy and social stability4. The Sixth Assessment Report of the Intergovernmental Panel on Climate Change highlights that, with rising temperatures, global snowpack variation will accelerate5,6. The temperature increases in Northeast China are expected to be amongst the highest globally7,8. Thus, predictions about future snowpack depth variation are becoming increasingly crucial. These predictions will aid in understanding the characteristics of snowpack changes, providing scientific support to ensure China’s food security.

The Coupled Model Intercomparison Project has advanced to its sixth phase (CMIP6). CMIP6 not only enhances the climate models but also introduces a new climate scenario that integrates Representative Concentration Pathways (RCPs) and Shared Socioeconomic Pathways (SSPs), enabling more accurate predictions of future climate change9,10. Current studies focus on the spatiotemporal variation of snowpack depth under the SSPs-RCPs scenario based on CMIP6, primarily targeting the Northern Hemisphere, Arctic sea ice, and China. Results have shown that the snowpack depth in the Northern Hemisphere is experiencing a declining trend under the SSP1-2.6, SSP2-4.5, SSP3-7.0, and SSP5-8.5 scenarios during 2015–210011; the snowpack depth of Arctic sea ice is continuously decreasing under the SSP2-4.5 and SSP5-8.5 scenarios during 2025–209912; the snowpack depth in Xinjiang is significantly increasing during 2021–2100 under the SSPs-RCPs scenario13; a decrease in snowpack depth in the Qinghai-Tibet Plateau is observed under the scenarios of SSP1-2.6, SSP2-4.5, SSP3-7.0, and SSP5-8.5 during 2015–21007. Compared to the relatively stable snowpack areas of the Qinghai-Tibet Plateau and northern Xinjiang, more targeted research is necessary to investigate the variations in future snowpack depth in Northeast China.

In addition, with global warming, the East Asian summer monsoon will strengthen and have a longer duration. The duration is expected to increase by 1.6 pentads at 2 °C of global warming under a high radiative forcing scenario (SSP5-8.5), leading to increased precipitation in the East Asian monsoon region14,15. Therefore, this study analyzes the spatiotemporal variation of snowpack depth in winter under the SSP1-2.6, SSP2-4.5, and SSP5-8.5 scenarios during 2025–2100, and explores the influencing mechanisms of future snowpack depth, focusing on Northeast China as the study area. Specifically, the following four questions are addressed: (1) What are the spatiotemporal variation of snowpack depth under three different scenarios in the future? (2) As warming intensifies, what changes occur in snowpack depth under three distinct scenarios compared with the base period? And what are the differences in snowpack depth among these scenarios? (3) What are the main influencing factors (temperature, precipitation, atmospheric circulation and water vapor) driving the changes in snowpack depth under different scenarios in the future? The results will provide scientific references for a comprehensive understanding of the spatiotemporal variation of snowpack in the future.

Study area

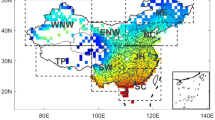
Northeast China, including the Heilongjiang, Jilin, and Liaoning provinces, represents the highest latitude region in China (38°43′N−53°33′N, 115°53′E−135°05′E, Fig. 1). It experiences a temperate monsoon climate and a continental climate. The summer season receives more precipitation, and daily temperature differences are notable. The winter is characterized by cold, long durations, and heavy snowfall, resulting in thick snow cover16. The study area encompasses 845,300 km2, with mountains and plains as its two primary landforms. The region possesses rich, fertile black soil, which makes it one of China’s critical commercial grain production bases17.

Fig. 1
figure 1

Overview of the three provinces in Northeast China. The symbol “•” shows the distribution of the 168 surface meteorological stations in Northeast China. (the figure was created by Arcgis10.8, https://www.esri.com/en-us/home ).

Full size image

Datasets

Data of snowpack

This study utilized the daily snow depth dataset of national surface meteorological stations in China for 1951–2017 to validate and select the CMIP6 models. The dataset was obtained from the China Meteorological Data Service Centre, available online at http://data.cma.cn/en. As this research focuses on winter (December, January, and February), only data from 1850 to 2014 is available (the CMIP6 historical simulations merely cover 1850–2014). The study selected a daily snow depth dataset of 168 stations in Northeast China (Heilongjiang, Jilin, and Liaoning provinces) for 1954–2014, including Mohe City, Tahe County, Huma County, Jiagedaqi district, and Aihui district, to validate the results of CMIP6.

Simulated data of CMIP6

CMIP6 was initiated, designed, and organized by the World Climate Research Programme. The variable of snow depth from 34 models and 18 models in CMIP6 was utilized for the historical simulation and the future projection under the three SSP-RCP scenarios, respectively. Hence, 18 models were selected from CMIP6: BCC-CSM2-MR, CanESM5, CanESM5-1, CAS-ESM2-0, CESM2-WACCM, CMCC-CM2-SR5, CMCC-ESM2, EC-Earth3, EC-Earth3-Veg, EC-Earth3-Veg-LR, FGOALS-f3-L, GFDL-ESM4, IPSL-CM6A-LR, MIROC6, MRI-ESM2-0, NorESM2-LM, NorESM2-MM, and TaiESM1, as listed in Table 1. Both historical simulations and three future scenarios, SSP1-2.6 (low vulnerability with low challenges for mitigation as well as a low radiative forcing signal), SSP2-4.5 (intermediate societal vulnerability with an intermediate radiative forcing level), and SSP5-8.5 (high societal vulnerability with a high radiative forcing level) from CMIP6, were adopted18. For the historical periods, output data on mean winter snowpack depth, temperature, precipitation, geopotential height, and others were utilized ( https://esgf-node.lnl.gov/search/cmip6/ ) and downscaled to a unified resolution of 0.25°×0.25°. The historical scenario period spans from 1850 to 2014, and the future scenario period ranges from 2015 to 2100. In this study, data from the base period (winter of 1985–2014) and the future period (winter of 2025–2100) are selected. The periods 1985–2014, 2025–2049, 2050–2074, and 2075–2099 were defined as base, near-term, mid-term, and long-term periods using the divide and average method.

Table 1 Basic information on 18 models of CMIP6.
Full size table

Methods

Mann-Kendall mutation test and anomaly

The Mann-Kendall mutation test is recognized by the World Meteorological Organization and is widely employed to analyze meteorological and hydrological trends19,20. In this study, the Mann-Kendall mutation test is utilized to determine the mutation years of future snowpack depth in Northeast China under different emission scenarios, and the anomaly method is combined for judgment.

Bilinear interpolation

Considering the differences in spatial resolution among models and observed data, for easier comparison with observed data, bilinear interpolation was first employed to process snowpack data in CMIP6 into a horizontal resolution of 0.25°×0.25°[21,22, unifying the resolutions of 18 models to 0.25°×0.25°. Bilinear interpolation is a technique to estimate a new pixel value within a two-dimensional array using the four nearest pixel values (the distance-weighted average of the four closest pixels). The formulas are shown below23:

First, this study successively performs a single linear interpolation in the x- and y-directions as follows:

$$\:f\left({R}_{1}\right)=\frac{{x}_{2}-x}{{x}_{2}-{x}_{1}}f\left({Q}_{11}\right)+\frac{{x}_{2}-x}{{x}_{2}-{x}_{1}}f\left({Q}_{21}\right)$$
(1)
$$\:f\left({R}_{2}\right)=\frac{{x}_{2}-x}{{x}_{2}-{x}_{1}}f\left({Q}_{12}\right)+\frac{{x}_{2}-x}{{x}_{2}-{x}_{1}}f\left({Q}_{22}\right)$$
(2)
$$\:f\left(P\right)=\frac{{y}_{2}-y}{{y}_{2}-{y}_{1}}f\left({R}_{1}\right)+\frac{y-{y}_{1}}{{y}_{2}-{y}_{1}}f\left({R}_{2}\right)$$
(3)

where \(\:{x}_{1}\) and \(\:{x}_{2}\) are x-coordinates, \(\:x\) is the x-coordinate of the point to be solved; \(\:{y}_{1}\) and \(\:{y}_{2}\) are y-coordinates, and \(\:y\) is the y-coordinate of the point to be solved; \(\:f\left({Q}_{ij}\right)\) is the function value of the known point, \(\:f\left(P\right)\) is the result of unilinear interpolation in the y-direction for \(\:f\left({R}_{1}\right)\) and \(\:f\left({R}_{2}\right)\).

The following is derived by substituting Eqs. (1) and (2) into Eq. (3).

$$\:{M}_{1}=\frac{f\left({Q}_{11}\right)}{{(x}_{2}-{x}_{1})-({y}_{2}-{y}_{1})}\left({x}_{2}-x\right)\left({y}_{2}-y\right)$$
(4)
$$\:{M}_{2}=\frac{f\left({Q}_{21}\right)}{{(x}_{2}-{x}_{1})-({y}_{2}-{y}_{1})}\left(x-{x}_{2}\right)\left({y}_{2}-y\right)$$
(5)
$$\:{M}_{3}=\frac{f\left({Q}_{12}\right)}{{(x}_{2}-{x}_{1})-({y}_{2}-{y}_{1})}\left({x}_{2}-x\right)\left(y-{y}_{1}\right)$$
(6)
$$\:f\left(x,y\right)={M}_{1}+{M}_{2}+{M}_{3}$$
(7)

where \(\:{M}_{1}\), \(\:{M}_{2}\), and \(\:{M}_{3}\) are the weighting values of different terms, and \(\:f\left(x,y\right)\) is the sum of these values.

Assessment of model simulation capabilities

This study adopts the skill score (\(\:S\)) introduced to quantitatively evaluate the simulation capabilities of different models for snowpack depth in Northeast China24. The formula is as follows:

$$\:S=\frac{4{(1+R)}^{4}}{(\frac{{\sigma\:}_{m}}{{\sigma\:}_{o}}-\frac{{\sigma\:}_{o}}{{\sigma\:}_{m}}){(1+{R}_{0})}^{4}}$$
(8)

where \(\:R\) is the correlation coefficient between simulation and observation; \(\:{R}_{0}\) is the maximum \(\:R\); \(\:{\sigma\:}_{o}\) and \(\:{\sigma\:}_{m}\) are the standard deviations between simulations and between observations, respectively; \(\:S\) is defined as the skill score of the simulation, ranging from 0 to 1. The larger the value, the stronger the simulation capacity.

\(\:S\)was first calculated using two indicators, the spatial correlation coefficient and standard deviation, for 18 individual models in CMIP6. The simulation capacity of all the models was ranked from top to bottom. Then, an equal-weight pooled average was adopted for the first two, first three, and up to the first 18 models25,26, resulting in 17 preferred model aggregate averages. The spatial correlation coefficient and standard deviation were utilized again to calculate S, and these results were ranked alongside those of the 18 individual models to obtain the final maximum S. The corresponding number of models was recognized as the optimal model for subsequent future snowpack depth simulations.

Taylor diagram

Taylor described the correlation coefficient of simulation and observation (R), standardized standard deviation (STD), Root Mean Square Error (RMSE), and others in one diagram, which is known as the Taylor diagram24. The larger the R, the smaller the RMSE. The closer the ratio of the STD of the model to the observation is to 1, the closer the simulation point is to the observation point, which indicates a stronger model’s capacity in simulation.

Model accuracy testing

Based on altitude, the research area is categorized into low altitude zones (0–500 m), middle altitude zones (500–1500 m), and high altitude zones (above 1500 m). To assess the simulation accuracy of the model in relation to the data and observed data within these different altitude regions, the Posterior Difference Ratio \(\:C\) and the Small Error Probability \(\:P\) were employed. The specific calculation formulas are as follows:

$$\:C={S}_{2}/{S}_{1}\:;\:P=P\left\{\left|{\epsilon\:}_{i}-\epsilon\:\right|<0.6745{S}_{1}\right\};\:{S}_{1}=\sqrt{\frac{\sum\:_{i=1}^{n}{\left({X}_{i}-\overline{X}\right)}^{2}}{n-1}},\:\overline{X}=\frac{1}{n}\sum\:_{i=1}^{n}{X}_{i};$$
(9)
$$\:{S}_{2}=\sqrt{\frac{\sum\:_{i=1}^{n}\:{\left({\epsilon\:}_{{i}_{i}}-\stackrel{-}{\epsilon\:}\right)}^{2}}{n-1}\:};\:{\epsilon\:}_{i}={X}_{i}-{Y}_{i};\:\stackrel{-}{\epsilon\:}=\frac{1}{n}+{\sum\:}_{i=1}^{n}{\epsilon\:}_{i};$$
(10)

where, n is the number of samples;\(\:{\:X}_{i}\): observed value; \(\:{Y}_{i}\): analog value; when \(\:C\) < 0.35, \(\:P\) > 0.95, the first-order precision is “good”; when \(\:C\)<0.50, \(\:P\)>0.80, for the second level accuracy “qualified”; when \(\:C\)<0.65, \(\:P\)>0.70, the result is rated as “barely acceptable”; when \(\:C\)≥0.65, \(\:P\)≤0.70, “failed” will be displayed.

Water vapor transport

The water vapor input through each boundary of the Songhua River Basin (42°–54°N, 119°–135°E) is calculated to analyze the contribution of the basin’s water vapor transport and budget to its future precipitation27. The calculation formula is as follows:

The vertically integrated water vapor flux can be represented as:

$$\:Q={Q}_{\lambda\:}i+{Q}_{\phi\:}j$$
(11)

Where the zonal component is:

$$\:{Q}_{\lambda\:}=-\frac{1}{g}{\int\:}_{{p}_{s}}^{{p}_{t}}qudp$$
(12)

The meridional component is:

$$\:{Q}_{\phi\:}=-\frac{1}{g}{\int\:}_{{p}_{s}}^{{p}_{t}}qvdp$$
(13)

Therefore, the water vapor flux through the eastern boundary is:

$$\:{Q}_{E}=-{\int\:}_{{\phi\:}_{S}}^{{\phi\:}_{N}}{Q}_{{\lambda\:}_{E}}ad\phi\:$$
(14)

The water vapor flux through the western boundary is:

$$\:{Q}_{W}={\int\:}_{{\phi\:}_{S}}^{{\phi\:}_{N}}{Q}_{{\lambda\:}_{W}}ad\phi\:$$
(15)

The water vapor flux through the southern boundary is:

$$\:{Q}_{S}={\int\:}_{{\lambda\:}_{W}}^{{\lambda\:}_{E}}{Q}_{{\phi\:}_{S}}a{cos}{\phi\:}_{S}d\lambda\:$$
(16)

The water vapor flux through the northern boundary is:

$$\:{Q}_{N}=-{\int\:}_{{\lambda\:}_{W}}^{{\lambda\:}_{E}}{Q}_{{\phi\:}_{N}}a{cos}{\phi\:}_{N}d\lambda\:$$
(17)

where g is the acceleration of gravity (9.8065 m/s2 in this paper), \(\:q\) is the specific humidity, u and v are the zonal wind and the meridional wind respectively, and the vertical integral level is 1000-300 hPa. When \(\:{Q}_{S}\) and \(\:{Q}_{W}\) are positive (negative), water vapor input (output); when \(\:{Q}_{E}\) and \(\:{Q}_{N}\) are positive (negative), water vapor output (input).

Results

Evaluation of capacities of CMIP6 models in simulating snowpack depth in Northeast China during 1954–2013

Figure 2 depicts the Taylor diagram of snowpack depth based on the simulation results of the 18 individual models or combined model ensembles. In the 18 individual model simulations, R for snowpack depth ranges from 0.6 to 0.8, and STD and RMSE are 0.7–1.9 cm and 0.6–1.1 cm, respectively. This shows that most models perform well in simulating snowpack depth in winter in Northeast China. Eighteen models, such as BCC-CSM2-MR, CAS-ESM2-0, CESM2-WACCM, and CMCC-CM2-SR5, were comprehensively assessed and ranked to quantify the simulation capacity of the CMIP6 models. Based on the averaged optimal model ensembles, S was computed again after arithmetic averaging the combined models and ranked with individual models to select the best-performing models. Results exhibited that the arithmetic average of the top four models, CESM2-WACCM, NorESM2-MM, TaiESM1, and NorESM2-LM, outperformed that of the individual models, with an S of 0.99, ranking first.

Fig. 2
figure 2

Taylor diagram of observed and averaged simulation results by 18 CMIP6 models of snowpack depth in Northeast China for the period of 1954−2013.

Full size image

The average snowpack depth of the four models is 5.86 cm, while that of observation is 4.95 cm. The two values are quite close (Fig. 3). The spatial distribution of winter snowpack depth in Northeast China, as simulated by the averaged optimal model ensemble, is examined to better analyze the spatial simulation of snowpack depth by the CMIP6 ensemble model in the study area. Figure 4a and b display the observed and ensemble-averaged winter snowpack depth distribution in Northeast China during 1954−2013, respectively. The snowpack depth decreases from south to north and west to east, with high-value areas concentrated in the region’s southeast, north, and northwest parts. Compared with the observed values, the results generated by the ensemble models demonstrate a more accurate simulation of the variation trend in the spatial distribution of snowpack depth than those of the individual models, although it overestimates the range of the snowpack depth by over 40.39% in most parts of the three provinces (Fig. 4c). Considering that the focus is mainly on the variation trend of snowpack depth and that the model ensemble has advantages in simulating future trends, the model ensemble is ultimately chosen.

Fig. 3
figure 3

Comparison of average snow depth observed and multi-model sets in the winter in Northeast China during the period of 1954−2013.

Full size image
Fig. 4
figure 4

Spatial distribution of mean winter snow depth based on the averaged ensemble in Northeast China from 1954 to 2013 (a) Observed values; (b) Mean winter snowpack depth simulated by CMIP6; (c) Differences between simulated and actual values.

Full size image

Spatiotemporal distribution and variation of snowpack depth in Northeast China during 2025−2099

Two perspectives must be considered to describe the future spatiotemporal variation of snowpack depth in Northeast China: comparison to the base period and analysis of future snowpack depth variations under three scenarios.

Temporal variation of snowpack depth

Comparison with the base period

Based on the characteristics of CMIP6, 1985−2014 is defined as the base period. Figure 5a illustrates the distribution of snowpack depth in Northeast China during 2025–2099 for the three scenarios of SSP1-2.6, SSP2-4.5, and SSP5-8.5, as well as the observed snow depth during the base period. It indicates that the snowpack depths for SSP1-2.6, SSP2-4.5, and SSP5-8.5 are 7.46, 7.34, and 6.76 cm, respectively, compared to a snow depth during the base period of 7.83 cm. This demonstrates that the snowpack depth in the three scenarios decreases by 0.37, 0.49, and 1.07 cm, respectively, accounting for 4.73%, 6.26%, and 13.67% of the base period. It is evident that as emissions increase, the reduction in snowpack depth also increases. Variance analysis results are displayed in Fig. 5b. A significant difference from the base period (p < 0.05) can be observed in the high-emission scenario (SSP5-8.5), while no significant difference is found in the moderate- and low-emission scenarios (SSP2-4.5 and SSP1-2.6). Accordingly, the results indicate that future snowpack depth in Northeast China from 2025 to 2099 will decrease compared to the base period, but only the high-emission scenario shows a significant decrease. This also indicates that temperature increases can influence snowpack depth in the region, with a sharp variation occurring when the temperature reaches a certain threshold. In the high-emission scenario, snowpack depth experiences a significant decrease of 15%.

Fig. 5
figure 5

Comparison of winter snow depth of future scenarios in Northeast China to that of the base period during 2025–2099.

Full size image

As previously introduced, 2025−2049, 2050−2074, and 2075−2099 are defined as near-term, mid-term, and long-term periods, respectively. Figure 6 compares winter snowpack depths in Northeast China in the near-, mid-, and long-term periods with the base period. It indicates that snowpack depths in the near-, mid-, and long-term periods for all three scenarios are below the base period. Variance analysis results show a significant difference between snowpack depths in different periods and those of the base period in the high-emission scenario (p < 0.05), while no significant variation is observed in the other two scenarios. Under all three scenarios, long-term snowpack depths show an apparent difference (p < 0.05). These findings indicate that the influence of high emissions on snowpack depth in Northeast China begins to appear in the near-term period, increases over time, and becomes more pronounced in the long term. In the low-, moderate-, and high-emission scenarios during 2075–2099, snowpack depth decreases by 0.49 cm (6.23%), 0.46 cm (5.86%), and 1.87 cm (23.89%), respectively, compared to the base period.

Fig. 6
figure 6

Averaged near-, mid-, long-term, and base-period winter snowpack depth of Northeast China for the three scenarios during 2025−2099.

Full size image

Variation trends

Figure 5a demonstrates that the variation rates of winter snowpack depth in Northeast China during 2025−2099 under the scenarios of SSP1-2.6, SSP2-4.5, and SSP5-8.5 are − 0.10 cm/10a (p > 0.05), 0.02 cm/10a (p > 0.05), and − 0.30 cm/10a (p < 0.05), respectively. This indicates that no obvious changes are found in the moderate- and low-emission scenarios, but the high-emission scenario experiences a significant decrease. The snowpack depth in the study area under the SSP5-8.5 scenario is expected to decrease to 4.50 cm by the end of the 21st century, with a reduction of 2.25 cm from the winter average. Compared to the first ten years of the 21st century (7.79 cm), the snowpack depth experiences a decrease of 42.23%. (Rounding is performed in the calculation) Variance analysis further indicates a significant difference between the high-emission scenario and the moderate- and low-emission scenarios (p < 0.05), but no significant difference is observed between the latter two (Fig. 7). This analysis exhibits that different scenarios have varying degrees of influence on snowpack depth in Northeast China, with the most considerable impact occurring in the high-emission scenario. Based on the Mann-Kendall (M-K) mutation test and anomaly results (Fig. 8), the only mutation is found in 2065 under SSP5-8.5, with a continuous decreasing trend. This shows that climate warming will considerably affect mid- and late-21st-century snowpack depth.

Fig. 7
figure 7

The average winter snowpack depth in Northeast China under three scenarios during 2025−2099.

Full size image
Fig. 8
figure 8

Mann-Kendall mutation and anomaly under three scenarios for Northeast China in winter during 2025−2099.

Full size image

Spatial variation of snowpack depths

Comparison with base period

Figure 9a and c show the snowpack depth’s spatial distribution and difference values under the SSP1-2.6, SSP2-4.5, and SSP5-8.5 scenarios for 2025−2099 in the study area. It reveals that future snowpack depths in Northeast China present a similar variation trend under the three scenarios, first decreasing and then increasing from southeast to northwest. Specifically, the areas with the highest decrease are concentrated in the southeast, while those with the largest increase are in the northwest. However, the scope and extent of the increase/decrease differ among the various scenarios (Table 2). Table 2 shows that the increased areas under the SSP1-2.6, SSP2-4.5, and SSP5-8.5 scenarios account for 36.50%, 31.58%, and 17.15% of the whole region, while the decreased areas occupy 68.80%, 68.41%, and 82.85% of the total, respectively. Compared to the base period, the area with decreased snowpack depth in Northeast China under the three scenarios is larger than the area with increased depth. As emissions increase, the reduced area continuously grows. Under the SSP5-8.5 scenario, the decreased area exceeds 80%. The variations in snowpack depths under the SSP1-2.6, SSP2-4.5, and SSP5-8.5 scenarios are − 2.72 to 0.76 cm, − 3.12 to 1.17 cm, and − 4.21 to 1.26 cm, respectively, compared to the base period. This indicates that increased emissions will lead to greater heterogeneity in the spatial distribution of snowpack depths in Northeast China in the future.

Fig. 9
figure 9

Characteristics of the spatial distribution of difference values of winter snowpack depth of three scenarios in Northeast China during the winter of 2025−2099 with the base period. Blue represents a positive trend, whereas red shows a negative trend.

Full size image
Table 2 Changes in the Spatial area of winter snowpack depth in Northeast China under three future scenarios compared to the base period and corresponding proportions (%).
Full size table

The spatial variation coefficients of winter snowpack depth in Northeast China from 2025 to 2099 under SSP1-2.6, SSP2-4.5, and SSP5-8.5 scenarios were calculated to better analyze the changes in spatial heterogeneity. Figure 10a and c show that in the future, under these three scenarios, the winter snow depth in Northeast China has a spatial distribution where the variation coefficient is lower in the north and east and higher in the center and southwest. There are differences in the spatial variation coefficients of snowpack depth among different scenarios. Under SSP1-2.6, SSP2-4.5, and SSP5-8.5 scenarios, the maximum variation coefficients of snowpack depth in Northeast China are 1.07, 1.26, and 1.89, respectively. The variation coefficient of snowpack depth gradually increases. Hence, as the emission scenarios intensify, the inter-annual variation of snowpack depth significantly increases, and the stability decreases.

Fig. 10
figure 10

Spatial distribution of the coefficient of variation of mean winter snowpack depth of three scenarios in Northeast China during the winter of 2025−2099.

Full size image

Characteristics of spatial variation

Spatial variations in winter snowpack depth in Northeast China under the three emission scenarios during 2025−2099 are depicted in Fig. 11. The number of areas with a significant increase can be observed in all the three scenarios. Areas with significant decreases under the SSP1-2.6, SSP2-4.5, and SSP5-8.5 scenarios account for 5.6%, 0.9%, and 60.5% of the total area, respectively. This indicates that, with increasing emissions, the areas with significant decreases in snowpack depth have been rapidly expanding. In the high-emission scenario, the areas with significant decreases can exceed 60% and are primarily concentrated in the central-southern part of Northeast China, with a variation rate ranging from − 1 to 0 cm/10a and the largest area distributed in the southeast. The snowpack depth in southern Northeast China would reduce by 6.98 cm at this rate by the end of the 21st century.

Fig. 11
figure 11

Spatial variation of winter snowpack depth in Northeast China from 2025 to 2099 under three future scenarios. units: cm/10a; The symbol “•” is that it passes the significance level of 0.05.

Full size image

Mechanisms for future variations in snowpack depth in Northeast China

Influences of temperature variation on the snowpack depth

Based on these results, snowpack depth in Northeast China during 2025–2099 is expected to decrease compared to the base period (Fig. 12). The reduction increases as emissions intensify, but considerable differences are only evident in the high-emission scenario. Therefore, the temperature distribution in the base period and under the three scenarios with different emission levels is analyzed. Based on statistics, the average temperature in Northeast China during the winter of 2014 was − 15.45℃, while under the SSP1-2.6, SSP2-4.5, and SSP5-8.5 scenarios during 2025–2099, the average temperatures are expected to be − 13.20, − 12.30, and − 10.41℃, respectively, all higher than during the base period. As emissions intensify, temperatures rise further. The variance analysis illustrated in Fig. 3 indicates significant differences between the average winter temperatures under the three future scenarios and the base period (p < 0.05). This indicates that average winter temperatures under the three scenarios are significantly higher than during the base period. The results reveal that the higher the temperature, the greater the decrease in snowpack depth. In addition, snowpack depth is only considerably affected when warmer temperatures reach a certain threshold. The winter average temperatures under the SSP1-2.6 and SSP2-4.5 scenarios are 2.23 and 3.13℃ higher than the base period, respectively. Under these circumstances, no significant difference between future snowpack depth and the base period is found. However, based on the Student’s t-test, a significant difference (p < 0.05) in temperature and snowpack depth is only observed under the SSP5-8.5 scenario. A considerable difference in snowpack depth is evident when the future winter average temperature is 5.02 °C higher than during the base period by calculating the difference between the average temperature for the high-emission scenario and that of the base period. The correlation coefficients between annual average temperatures and snowpack depth in Northeast China under the three scenarios during 2025–2099 are − 0.38 (p < 0.05), − 0.23 (p < 0.05), and − 0.58 (p < 0.05), respectively. This demonstrates a negative correlation between temperature and snowpack depth, indicating that as temperatures increase, snowpack depth decreases, with greater decreases occurring as temperatures rise further. Hence, the most significant decrease in snowpack depth is found under the SSP5-8.5 scenario.

Fig. 12
figure 12

Comparison of winter temperatures in Northeast China under three future scenarios to that of the base period during 2025−2099.

Full size image

Accordingly, winter snowpack depth in Northeast China remains relatively stable during 2025−2099 in the low and moderate emission scenarios while decreasing in the high-emission scenario. The variation rates under the SSP1-2.6, SSP2-4.5, and SSP5-8.5 scenarios are 0.01 (p < 0.05), 0.32 (p < 0.05), and 0.99℃/10a (p < 0.05), respectively, all showing significant increasing trends, with the highest variation rate under SSP5-8.5 (Table 3). This illustrates that within a given time scale, a significant decrease in snowpack depth only occurs when the annual average temperature increases significantly, and the extent of the decrease also increases as time progresses.

Table 3 Changes in winter average temperatures in Northeast China during 2025−2099.
Full size table

In addition, winter temperature variations in Northeast China under the three scenarios during 2025–2099 are depicted in Fig. 13. Areas with considerable temperature variations in SSP1-2.6, SSP2-4.5, and SSP5-8.5 account for 79.29%, 100%, and 100% of the total area, respectively. Except for the northwest part of the study area under SSP1-2.6, which shows no obvious change, winter average temperatures in all other regions under the three future scenarios exhibit a significant increasing trend. The spatial distribution of correlation coefficients between winter snowpack depth and temperature for the three future scenarios is further calculated and displayed in Fig. 14. The northwest part of the study area shows no notable correlation under any of the three scenarios, while the central and southern parts exhibit a significant negative relationship. The proportions of areas with a significant negative relationship are 86.02%, 67.25%, and 87.57% under SSP1-2.6, SSP2-4.5, and SSP5-8.5, respectively. Compared to Fig. 11, as emissions increase, the areas with a significant decrease in snowpack depth also increase rapidly, reaching more than 60% of the total in SSP5-8.5. This indicates that the extremely large variation in snowpack depth in the central and southern parts of Northeast China is closely connected to the significantly increased temperature. In SSP2-4.5 and SSP5-8.5, although apparent warming is observed in the northwest part, no significant decrease in snowpack depth is captured, likely because the northwest is mainly forested. There is no significant correlation between temperature and snowpack depth in the northwestern region under most scenarios. On one hand, the northwest parts of Northeast China is a high-value snowfall area, mainly affected by snowfall. However, the northeast is also a snowy region, and there is a significant correlation between temperature and snowpack depth under different scenarios, which on the other hand may be related to the simulation accuracy.

Fig. 13
figure 13

Spatial variation of winter average temperature in Northeast China from 2025 to 2099 under three future scenarios. The symbol “•” is that it passes the significance level of 0.05.

Full size image
Fig. 14
figure 14

Spatial correlation coefficients between winter snowpack depth and temperature for three future scenarios in Northeast China during 2025−2099. The symbol “•” is that it passes the significance level of 0.05.

Full size image

This paper concludes that in the future, temperature will increase significantly under the three emission scenarios, while snow depth will decrease significantly only under the high emission scenario. Under these scenarios, future snowfall in Northeast China has no significant difference or increasing trend. The significant snow depth decrease under the high emission scenario despite unchanged snowfall may be related to snow melting. So, the paper further calculates the number of days with daily maximum temperature > 0℃ in Northeast China under three models. Results show that the change rates of such days from 2025 to 2099 under the three scenarios are 1.00d/10a (p < 0.05), 2.29d/10a (p < 0.05) and 3.67d/10a (p < 0.05) respectively, with a significant increasing trend. The highest change rate is in the high-emission scenario (Table 4). Analysis of variance reveals significant differences between high- and low-emission scenarios. This indicates that even the average winter temperature remain cold, an increase in the number of days with maximum temperatures above zero may bring a small amount of winter rainfall or more winter snowmelt.

Table 4 Variations in winter maximum temperature > 0℃ for the three future scenarios in Northeast China during the winter of 2025−2099.
Full size table

Influence of snowfall variation on the snowpack depth

The snowfall in Northeast China under the three scenarios during 2025–2099 is shown in Table 5. The winter average snowfall under SSP1-2.6, SSP2-4.5, and SSP5-8.5 during the period is 72.16, 74.06, and 71.37 mm, with variation rates of 0.02, − 0.81, and − 0.89 mm/10a, respectively (p > 0.05), indicating no significant variation. As temperatures rise, there was no significant change in snowfall. The correlation coefficients between annual average snowfall and snowpack depth for SSP1-2.6, SSP2-4.5, and SSP5-8.5 are 0.71, 0.51, and 0.53, all with p < 0.05, indicating a significant positive correlation.

Table 5 Variations in average snowfall for the three future scenarios in Northeast China during the winter of 2025−2099.
Full size table

Figure 15 illustrates the spatial distribution of correlation coefficients between winter snowpack depth and snowfall under the three future scenarios. A significant positive relationship is observed across nearly the entire study area, except in central Liaoning under SSP2-4.5, with proportions of 99.29%, 80.26%, and 99.94% under SSP1-2.6, SSP2-4.5, and SSP5-8.5, respectively. As emissions increase, the northern and southern parts of the study region show declining correlation coefficients. Compared to Fig. 10, the results explain the increasing snowpack depth in the northern and southern parts of Northeast China.

Fig. 15
figure 15

Spatial correlation coefficients between winter snowpack depth and snowfall for three future scenarios in Northeast China during 2025−2099. The symbol “•” is that it passes the significance level of 0.05.

Full size image

Influence of changes in atmospheric circulation on snowfall

Changes in atmospheric circulation are a crucial factor influencing precipitation in East Asia. The response of atmospheric circulation in Northeast Asia in winter to climate change directly leads to variations in snowfall in Northeast China. Figure 16 shows the differences in geopotential height at 500 hPa for different periods under the three future scenarios relative to the base period. The overall performance in Northeast Asia at 500 hPa under the three scenarios is higher than in the base period, characterized by a “positive anomaly” with its main center to the east of the Sea of Japan and another relatively weak one at the Aleutian Islands. Differences exist in the increase in geopotential height under the three scenarios. In SSP1-2.6, the most significant positive anomaly in geopotential height is observed at Northeast Asia’s mid- and high-latitude areas (30°–45° N), with its center located east of the Sea of Japan. The anomaly from Baikal to the Aleutian Islands and the South China Sea region is relatively weak, with its center at the Aleutian Islands. The intensity of the anomaly center strengthens with global warming, and the geopotential height anomaly also intensifies (Fig. 16). A significant increase in geopotential height in Northeast Asia is observed as emissions intensify, with the most significant positive anomaly to the east of the Sea of Japan (Fig. 16d and i). These phenomena indicate that climate warming intensifies the positive anomaly in geopotential height to the east of the Sea of Japan in winter. In addition to the relatively low increase rate of the anomaly near Baikal, the distribution of geopotential height anomalies in Northeast Asia is characterized as “low in the west and high in the east.” This distribution of atmospheric circulation can facilitate the entry of water vapor from the Sea of Japan, benefiting the increase in snowfall in Northeast China during winter.

Fig. 16
figure 16

Spatial distribution of differences between 500 hPa geopotential height (unit: gpm) under SSP1-2.6, SSP2-4.5, and SSP5-8.5 scenarios and the base period in a multi-model ensemble simulation.

Full size image

Influence of changes in water vapor on snowfall

Water vapor transport and budget are important factors influencing precipitation variation. Considering the variation of water vapor flux, the Songhua River basin in Northeast China is chosen for calculation. Figure 17 illustrates the changes in water vapor transport during the winter in Songhua River basin across different periods under the three scenarios. All three scenarios show a positive water vapor balance compared to the base period under global warming. The water source and budget for the short, middle, and long terms under SSP1-2.6 and SSP2-4.5 are relatively stable. In terms of the water vapor sources and budgets in the near, medium and long terms in the future, there are differences among different emission scenarios. The southern and eastern sides of the basin experience vapor income, whereas the western and northern sides exhibit output, resulting in a positive balance overall. Under SSP1-2.6 and SSP2-4.5, the relative contribution rates of water vapor to the net water vapor budget in the southern (eastern) parts of Songhua River basin account for 60% (40%), 61% (39%), and 60% (40%) in the short, middle, and long terms, respectively, as well as 62% (38%), 64% (36%), and 70% (30%). However, under SSP5-8.5, different water vapor balances are observed between the short- to middle-term and the long-term horizons In shorter terms, income is found in the southern and eastern basins, while output occurs in the western and northern basins (Fig. 17g and h). In the longer term, output is primarily distributed in the eastern basin (Fig. 17i). And the proportions are 61% (39%) and 74% (26%) in the short and middle terms, while in the long term, the contribution rates of southern, western, and northern water vapor are 75%, 19%, and 6%, respectively. Based on the above data, with the increase of emission degree, not only will the direction of water vapor source change, but also the water vapor transport in the southern part of Songhua River basin in winter will continue to increase, which is the main reason for the projected increase in snowfall in the future. Specifically, an anomalous southeasterly flow on the western side of an anomalous anticyclonic circulation to the east of the Sea of Japan transports moisture to Songhua River basin, leading to increased winter snowfall in the region.

Fig. 17
figure 17

The difference between winter water vapor transport (unit: 108 g/s/m) by multi-mode ensemble simulation under the SSP1-2.6, SSP2-4.5, and SSP5-8.5 scenarios and the base period in Songhua River basin (error bars represent the maximum and minimum values of CMIP6 model) in the short, middle, and long terms.

Full size image

Discussion

Based on CMIP6 models, Zou et al. (2022) analyzed the spatiotemporal variation of snow depths in three regions with stable snowpack areas in China under SSP1-2.6, SSP2-4.5, SSP3-7.0, and SSP5-8.5 scenarios, revealing that snowpack depth in Northeast China decreases across all four scenarios8. The most pronounced decrease is found under SSP5-8.5, this is consistent with the paper’s conclusions. The results show that under the SSP5-8.5 scenario, the future snow depth will decrease significantly at a rate of −0.30 cm/10a from 2025 to 2099. It further indicates that if the temperature continues to rise in the future, the snow depth in northeast China will be significantly reduced. Zou et al. (2022) proposed that under the SSPs585 scenario, 58% of spatial areas in the northeast region significantly reduced (p < 0.05), with the high-value reduction area in the northern northeast, which is inconsistent with this paper’s conclusion. This paper forecasts snow depth by comparing with the base period and predicting the future trend, and holds that the southeast of Northeast China will see the most significant decrease in the future.

Shi et al. (2010) used the RegCM3 model to simulate the spatio-temporal variation of snow depth in China under the SRES A2 scenario (equivalent to the SSP5-8.5 scenario) during 2071 − 2100, and found that compared with measured values during 1961 − 1990, the snow depth in northeast China will decrease by 13.6% in the future, with the greatest decrease in the southeastern region28. The spatial area of snow depth reduction under the SSP5-8.5 scenario is the same as in this paper. In conclusion, whether using the CMIP6 model or the RegCM3 model, in the high-emission scenario, the snow depth in northeast China will decrease in the future, and the decrease area is more likely to be in the southeast.

Under climate warming, the future variation of snowpack depth is listed in Table 6. Most regions witness a decrease in snowpack depth, while a few show an increase. Shi (2020) found that the snowpack depth in the Northern Hemisphere decreases in four scenarios: SSP1-2.7, SSP2-4.5, SSP3-7.0, and SSP5-8.5. With increasing emissions, the decreasing trend amplifies. Under SSP5-8.5, the snowpack depth in the Northern Hemisphere will reduce to less than 0.04 m, only half of that in 2014 (Shi, 2020). Based on Zhang and Che (2019), future snowpack depth in Eurasia slowly declines or even levels off under all the selected scenarios, except for the high-emission scenario, which displays an evident and rapid decrease29. The snow depth at the end of the 21st century can be reduced to twice that of the mid-century30. indicate that snowpack depth in the Arctic from 2002 to 2100 continuously decreased, accelerating with increasing emissions, reaching − 0.20 cm/a under SSP5-8.5. Other researchers also demonstrate a decrease in snowpack depth in China under SRE, RCP, and SSPs-RCP28,31. Studies focusing on the Qinghai-Tibet Plateau32, the upper reaches of the Yangtze River33, northern Xinjiang34, and Northeast China (this study) reach the same conclusion. Some others have indicated that despite global warming, snowpack depth tends to increase in high-latitude and high-altitude areas35. Zhang et al. (2021a) show the increasing trend of snowpack depth in northern Xinjiang during 2021 − 2100 under seven SSPs-RCP scenarios. Li et al. (2019) study the variation of snowpack depth in northeastern Central Asia and indicate an increasing trend under 1.5 and 2 °C climate warming conditions. Theoretically, snowpack depth tends to decrease extensively due to the reduction in solid precipitation resulting from global warming36,37. In actual cases, increasing temperature can bring more water vapor. In regions that are largely affected by water vapor but do not exhibit an obvious warming trend, an increasing trend in snowpack depth is possible.

Table 6 Comparison of the future variation of snowpack depth in Northeast China and other areas.
Full size table

Although there have been few studies on the future variation trend of snowpack depth in Northeast China, many researchers have focused on the mechanisms in the past. Zhou et al. (2021) reported that snowpack depth in Northeast China during the winter half-year from 1961 to 2017 was more sensitive to precipitation (especially effective precipitation) than to the average temperature under the comprehensive influences of temperature, precipitation, altitude, latitude, and others41. Lu et al. (2018) believe that the weakening of the subtropical high in the Northern Hemisphere during winter from 1979 to 2014 is an essential factor leading to increased snowpack depth in Northeast China42. Based on Liu (2021), the closest correlation between snowpack depth and precipitation is found in all three regions with stable snowpack in China43. This study demonstrates that future snowpack depth variation results from temperature, snowfall, atmospheric circulation, and water vapor changes. Through comprehensive analysis, the following conclusions can be drawn: the future snow depth in Northeast China shows a significantly negative relationship with temperature (p < 0.05) and a significantly positive correlation with snowfall (p < 0.05). In other words, with climate warming, snowpack depth decreases. However, atmospheric circulation and water vapor affect the geopotential height anomaly caused by abnormal circulation distribution in Northeast Asia, characterized by lower heights in the west and higher heights in the east. This pattern facilitates the import of water vapor from the Sea of Japan, increasing winter snowfall in Northeast China. This conclusion contrasts with earlier findings. Therefore, atmospheric circulation and water vapor can lead to more snowfall under global warming. However, as temperatures rise, they can play a dominant role in snowfall patterns and snowmelt, potentially moderating the magnitude of snowfall increases. The effect of temperature on future snowpack depth will be greater than that of increased atmospheric circulation and water vapor.

We selected sampling points in different altitude areas. The posterior difference ratio (C) and the small error probability (P) were adopted to evaluate the simulation accuracy of the data series and observational data within different altitude segments of the model. The C values for the low, middle and high altitude regions were 0.63, 0.38 and 0.35 respectively, and the corresponding P values were 0.70, 0.90 and 0.99. The simulation accuracies were rated as “barely acceptable”, “qualified” and “good” respectively. The CMIP6 model shows relatively good spatial accuracy in simulating snow depth in the middle and high altitude zones. However, due to its relatively low model resolution, it fails to capture the detailed climatic nuances. In addition, compared with the low altitude areas, the scarcity of on-site measurement data in the middle and high altitude areas also poses a challenge. To address this problem, the Kriging interpolation method was used in this study to fill in the data gaps, but this inevitably led to differences in accuracy among different altitudes, which in turn affected the model selection process. Future research will involve using multi-source data for comparative analyses and improving the model resolution to enhance the accuracy of model evaluation.

Previous research shows CMIP6 model overestimates simulated snow depth and there are large discrepancies among different models44,45. This paper makes a deeper comparison. As shown in the figure, simulated values exceed measured ones. Since the focus is on analyzing future snow depth trend, correlation coefficients, RMSE and STD are used to optimize the model. To reduce randomness of a single model, top four optimal models are selected. Some scholars propose bilinear interpolation downscaling for meteorological elements. This paper uses bilinear interpolation method. But snowpack depth is related to factors like temperature, wind speed, altitude and minor topographical irregularities. Future work plans to enhance model resolution using snowpack depth downscaling method. Snow water equivalent (SWE) plays a crucial role in determining the availability of agricultural water. Typically, SWE is computed by multiplying the snowpack depth by the snow density. The CMIP6 model provides outputs of snow water equivalent, yet it does not offer snow density data. This brings some limitations to forecasting. Owing to the absence of future high-resolution snow density data, this paper contends that high-spatial-resolution snow density data is pivotal for converting snowpack depth into SWE.

Conclusions

  1. (1)

    Based on the simulation, the trend in snowpack depth in winter in Northeast China decreases during 2025 − 2099 under the scenarios of SSP1-2.6, SSP2-4.5, and SSP5-8.5, with the most significant variation under SSP5-8.5 (− 0.30 cm/10a). Compared to the base period, the snowpack depth is reduced by 6.76 cm (13.67%). In the other two scenarios, little change is observed. Under SSP5-8.5, a continuous significant decrease in snowpack depth is projected compared to historical records. The snowpack depth is expected to reduce to 5 cm (by 2.1 cm) by the end of the 21st century, with a reduction amplitude of 26.82%.

  2. (2)

    Regarding spatial distribution, snowpack depth decreases in most parts of Northeast China but increases in a few areas. With rising temperatures, the area with decreasing snowpack depth expands, with larger spatial differences. Regarding spatial variation, snowpack depth in Northeast China tends to decrease. Specifically, most of the study area demonstrates a significant decreasing trend. The conclusion can be summarized by analyzing both aspects as follows: due to the higher reduction rate of future snow depth in the central and southern parts, snow depth in these areas declines compared to the base period. In contrast, in the northwest part, snow depth increases due to a slower decrease rate.

  3. (3)

    Future snow depth variation in winter in Northeast China during 2025 − 2099 is jointly affected by temperature, snowfall, atmospheric circulation, and water vapor. The snowpack depth tends to decrease as temperatures rise. However, as a geopotential height anomaly of “low in the west, high in the east” forms in Northeast Asia, it becomes easier for water vapor from the Sea of Japan to enter this area, which can result in more snowfall in winter. With intensified global warming, the influence of the combination of these meteorological factors also increases. Considering the overall decreasing trend of snowpack depth, the effect of temperature on snowpack in the future is expected to be larger than that of the other three factors.