Introduction

Prefabricated construction represents a pivotal measure for the building industry to implement national requirements for green, environmentally friendly, and low-carbon development. It is also a major transformation in construction methods in China, aligning with the principles of green building development and holding great significance for achieving the goals of “carbon peaking and carbon neutrality”1,2,3,4. Concrete composite slabs, as prefabricated structural elements composed of precast concrete base slabs and cast-in-place concrete, are an essential component of prefabricated buildings5. However, the traditional concrete composite slabs have limitations, such as a small span and the presence of extended reinforcement at slab edges (commonly referred to as “anchor bars”), which reduce construction efficiency, increase procedures, and elevate production and material costs. These issues contradict the core concepts of prefabricated design6,7. Additionally, traditional designs fall short of meeting higher demands for building environments, functionality, and quality. Modern housing layouts are trending toward simplified arrangements of columns and beams, featuring larger column grids and fewer beams, to facilitate flexible spatial division while ensuring thermal insulation and soundproofing functions8.

To address issues such as extended reinforcement at the edges of precast concrete base slabs and the limited span of composite slabs, scholars have proposed solutions, including eliminating extended reinforcement from precast base slabs and employing prestressed reinforcement or lightweight core inserts to reduce slab weight and improve rigidity, thus achieving longer spans.

Zhang Xuefeng et al.9,10 conducted full-scale loading tests and in-situ loading tests on bidirectional reinforced truss composite slabs with no edge reinforcement and tight side connections. Their results demonstrated the effectiveness of directly placing additional reinforcement on the precast base slab, thereby eliminating the need for anchor bars at the joints. Lin Yan et al.11,12 proposed two types of tight-joint groove designs for edge connections: integrated and intermittent. Through experimental studies and numerical simulations, they validated the rationality of using groove connections with additional reinforcement in edge-tight prefabricated base slabs without extended reinforcement. Jiang Haihua13 investigated the structural connection of prefabricated concrete base slabs without extended reinforcement and cast-in-place beams using additional reinforcement through experimental research and ABAQUS finite element simulations, demonstrating the feasibility of eliminating edge reinforcement from precast base slabs. Yang Yue14, Nie Xin et al.6,15 proposed a grooved composite slab design and construction method, where the edge of the precast slab is grooved, and additional reinforcement is placed. Through static loading tests and ABAQUS finite element simulations, they confirmed the design’s rationality. Wu Fangbo et al.16 proposed a prestressed hollow composite slab design featuring tubular cores. By incorporating prestressed reinforcement into the precast concrete base slab and placing tubular cores within the composite slab, they verified that the structural performance of the slab satisfies safety requirements. Their study further proved that prestressed and hollow designs can meet the design needs of concrete composite slabs. Luo Bin17 introduced a composite slab design incorporating lightweight autoclaved aerated concrete (AAC) blocks. He conducted research on the structural performance of composite slabs with varying parameters and identified key factors influencing their mechanical properties. However, embedding AAC blocks in precast base slabs reduces production efficiency.

Based on the current research on floor slabs, this study addresses issues such as the short span, heavy weight, and absence of reinforcement extending from the sides of concrete composite slabs, Chen Xudong et al.18 proposed a steel truss reinforced hollow composite slab design, as illustrated in Fig. 1. By systematically placing hollow thin-walled boxes within the precast concrete base slab, the design reduces the slab’s self-weight and improves rigidity, enabling longer spans. The floor slab has the following notable features: (1) The steel reinforcement of the internal truss enhances the stiffness of the prefabricated bottom slab, effectively improving the shear strength at the interface between the new and old concrete composite. (2) The hollow thin-walled box gap inside the board forms longitudinal and transverse hidden beams, reducing weight by 18.37% and facilitating the integration of pipelines, installation of underfloor heating and other facilities. (3) Prefabricated bottom slab edges without steel reinforcement extension improve production efficiency, simplify transportation and installation processes, and reduce transportation damage. (4) In large-span column grid structures, reducing the height of the structure while eliminating secondary beams allows for more flexible spatial layout.This meets the demand for large spans and open spaces in modern architecture, offering extensive application prospects in floor slabs for large-span buildings, basement roofs, parking garage floors, and bridge decks.

Fig. 1
figure 1

Structural diagram of hollow composite slab. (Note: This figure is from SketchUp software 2016 version, and the corresponding graphic link is: https://pan.baidu.com/s/1WFuiXpe2KpO_Y8LQehbB7Q?pwd=gwqm Extract code: gwqm ).

Full size image

This study conducted static loading tests on two unidirectional hollow composite slab specimens and one unidirectional hollow cast-in-place slab specimen. The test comparisons demonstrated that the hollow composite slabs meet the design requirements. Building on these experimental studies, this paper employs finite element numerical simulations to analyze the structural performance and critical parameters of hollow composite slab specimens (specimens DKB1-1 and DKB2-1) and cast-in-place hollow slab specimens (specimen XJKB), providing references for engineering design and application.

Experimental overview

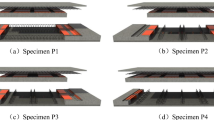
The experiment involved the design of three hollow slab specimens with different structural forms. Specimens DKB1-1 and DKB2-1 were hollow composite slabs, while specimen XJKB was a hollow cast-in-place slab. According to the relevant provisions for composite slabs in the Technical Specification for Prefabricated Concrete Structures (JGJ1-2014)19, the overall dimensions of the specimens in the tests were 4200 mm × 1400 mm, with thicknesses of 180 mm and 200 mm, respectively. The thickness of the precast bottom slab was uniformly 50 mm.The hollow thin-walled boxes had a planar dimension of 450 mm × 450 mm and thicknesses of 80 mm and 100 mm, respectively.For reinforcement, HRB400 steel meshes with a diameter of 8 mm and a spacing of 100 mm were placed in both the precast layer and the cast-in-place layer. The upper and lower chords of the trusses used HRB400 steel bars with a diameter of 8 mm, while the web bars of the trusses were HPB300 steel bars with a diameter of 6 mm. Three rows of truss reinforcement were arranged in each slab.The hollow composite slabs were designed as simply supported components subjected to secondary pouring and simultaneous loading. The composite surfaces of the slabs were manually roughened along the longitudinal direction to a depth of no less than 4 mm20.The primary parameters of the specimens are presented in Table 1, while the geometric dimensions of the specimens are illustrated in Fig. 2 (using specimen DKB2-1 as an example).

Fig. 2
figure 2

Specimen dimensions and reinforcement details (Units: mm).

Full size image
Table 1 Basic parameters of specimens.
Full size table

H represents the thickness of the slab, l₁ × b₁ denotes the planar dimensions of the hollow thin-walled box, and h₁ represents the thickness of the hollow thin-walled box.

The experiment employed the three-point loading method21, with an effective span of 4020 mm. The experimental loading setup is illustrated in Fig. 3. The two ends of the hollow composite slab specimens were supported by simple supports composed of circular steel rods and 10 mm thick steel plates. To ensure proper functioning of the data acquisition instruments, preloading was conducted before the formal loading process.During formal loading, before the specimens exhibited cracking, the load increment at each stage was 2 kN. After cracking, the load increment was increased to 4 kN per stage. Loading continued beyond the standard load value until the specimens reached the ultimate failure state, at which point loading was further increased until the concrete in the compression zone was crushed22.The test results showed that all specimens exhibited typical flexural failure characteristics in the normal section. The vertical crack distribution on the sides of specimens DKB1-1 and XJKB was relatively consistent. Under ultimate load, transverse cracks appeared in the composite layer at the mid-span region of the hollow composite slabs, as illustrated in Fig. 4.

Fig. 3
figure 3

Experimental loading setup (Units: mm).

Full size image
Fig. 4
figure 4

Side crack diagram of the specimen.

Full size image

The experimental results indicated that all specimens exhibited the failure characteristics of flexural members. The load-displacement curves of specimens DKB1-1 and XJKB showed similar behavior, with the load versus mid-span displacement curves presented in Fig. 5. The cracking loads for specimens DKB1-1 and XJKB were 36.40 kN and 30.10 kN, respectively, while the ultimate loads were 141.91 kN and 144.77 kN, respectively. These results suggest that the composite layer in the hollow composite slab had minimal impact on the mechanical performance of the specimens.

Fig. 5
figure 5

Load-midspan displacement curves.

Full size image

Finite element model

The hollow composite slab model was developed based on the design parameters described earlier, using the finite element analysis software ABAQUS to establish a representative model.

Model development

Concrete and bearing pads were modeled using 8-node linear reduced-integration solid elements (C3D8R).Truss reinforcement and steel mesh reinforcement were modeled using 2-node linear 3D truss elements (T3D2).Reinforcement Embedding: The reinforcement in the precast base slab, cast-in-place top slab, and truss bars were embedded into the concrete solid elements using the Embedded Region method. This ensured that the reinforcement interacted appropriately with the surrounding concrete.A uniform mesh size of 30 mm was used to achieve structured and regular mesh generation23.

The boundary conditions of the finite element model were set to be identical to those in the experiment. To prevent deformation or displacement of the bearing pads and loading pads during the loading process, rigid pads were employed.Four reference points (RP1 ~ RP4) were established at the centers of the loading and support pads.The degrees of freedom of the pads were fully coupled to their respective reference points, representing the force and deformation of the loading and support pads.The final specimen model, including the loading setup and boundary conditions, is illustrated in Fig. 6.

Fig. 6
figure 6

Finite element model of specimen. (Note: (a) is from ABAQUS software version 2020, and the corresponding graphic link is: https://pan.baidu.com/s/1WnLbJKUfDc5jeYpwxNgsNg?pwd=murh Extract code: murh).

Full size image

Material constitutive models

The concrete material properties were modeled using the Concrete Damaged Plasticity (CDP) model provided in ABAQUS. The stress-strain relationship for concrete was defined according to the constitutive model described in Appendix C of GB50010-2010: Code for Design of Concrete Structures24.

The stress-strain relationship of concrete under uniaxial compression is expressed as:

$$\sigma = (1 - d_{c} )E_{c} \varepsilon$$
(1)

Among them: \(d_{c} = \left\{ {\begin{array}{*{20}l} {1 - \frac{{\rho _{c} n}}{{n - 1 + x^{n} }}} \hfill & {x \le 1} \hfill \\ {1 - \frac{{\rho _{c} }}{{\alpha _{c} (x - 1)^{2} + x}}} \hfill & {x > 1} \hfill \\ \end{array} } \right.\)

\(\rho _{c} = \frac{{f_{{c,r}} }}{{E_{c} \varepsilon _{{c,r}} }},n = \frac{{E_{c} \varepsilon _{{c,r}} }}{{E_{c} \varepsilon _{{c,r}} - f_{{c,r}} }},x = \frac{\varepsilon }{{\varepsilon _{{c,r}} }}\)

Where: dc is the damage evolution parameter for concrete under uniaxial compression, Ec is the elastic modulus of concrete, αc is the parameter for the descending branch of the stress-strain curve under uniaxial compression, fc,r is the uniaxial compressive strength of concrete, εc,r is the peak compressive strain corresponding to the uniaxial compressive strength of concrete.

The stress-strain relationship of concrete under uniaxial tension is expressed as:

$$\sigma = (1 - d_{t} )E_{c} \varepsilon$$
(2)

Among them: \(d_{t} = \left\{ {\begin{array}{*{20}l} {1 - \rho _{t} (1.2 - 0.2x^{5} )} \hfill & {x \le 1} \hfill \\ {1 - \frac{{\rho _{t} }}{{\alpha _{t} (x - 1)^{{1.7}} + x}}} \hfill & {x > 1} \hfill \\ \end{array} } \right.\)

\(\rho _{t} = \frac{{f_{{t,r}} }}{{E_{c} \varepsilon _{{t,r}} }},x = \frac{\varepsilon }{{\varepsilon _{{t,r}} }}\)

Where: dt is the damage evolution parameter for concrete under uniaxial tension, Ec is the elastic modulus of concrete, αt is the parameter for the descending branch of the stress-strain curve under uniaxial tension, ft,r is the uniaxial tensile strength of concrete, εt,r is the peak tensile strain corresponding to the uniaxial tensile strength of concrete.

According to existing research findings25,26,27, the key plasticity-related parameters for concrete are set as follows: The dilation angle is set to 30°,the eccentricity is set to 0.1, the biaxial-to-uniaxial compressive strength ratio is set to 1.16, the yield surface shape factor KKK is set to 0.6667, and the viscosity parameter is set to 0.0005.The damage factor d in the concrete plastic damage model can be calculated using the energy equivalence principle proposed by Sidoroff28,29.

The reinforcement material adopts an ideal elastic-plastic model. For the uniaxial stress-strain relationship of ordinary reinforcement in the specimens, a three-segment elastic-plastic hardening model24 was used. The material parameters for the reinforcement and concrete used in the experiment are shown in Tables 2 and 3, respectively.

Table 2 Results of reinforcement material properties test.
Full size table
Table 3 Results of concrete material properties test.
Full size table

Results and analysis

Load–displacement curves

The load-displacement (F-Δ) curves of specimens DKB1-1、XJKB and DKB2-1 were obtained through finite element analysis and compared with the experimental results, as shown in Fig. 7. Table 4 presents a comparison of the characteristic load values between the finite element analysis and experimental results for specimens DKB1-1, XJKB and DKB2-1.From Fig. 7; Table 4, the following observations can be made: The load-midspan displacement curves obtained from the finite element analysis closely match the experimental curves.After concrete cracking, during the elastic-plastic stage of the reinforcement, the load simulated by the finite element model is slightly higher than the experimental results.At the end of the elastic-plastic stage, the stiffness degradation in the finite element model is slower than that observed in the experiments. However, as the load increases, the two curves gradually converge.The numerical analysis errors between the yield bearing capacities of the specimens and the experimental values were all within 15%, and the errors for the ultimate bearing capacities were within 8%. This indicates that the finite element analysis model for the hollow slab specimens, based on the selected parameters, is reasonable and provides reliable results. Notably, the numerical simulation results for specimen DKB1-1 were closer to the experimental values compared to specimen XJKB, further verifying the consistency in performance between the hollow composite slabs and cast-in-place hollow slabs, as well as the accuracy of the model. Based on this, subsequent analyses, such as stress and damage evaluations, were conducted only on the DKB1-1 model.

Fig. 7
figure 7

Comparison of experimental and finite element simulation load-displacement curves.

Full size image
Table 4 Comparison of simulated and experimental characteristic load values for specimens.
Full size table

Combining the experimental results with the numerical simulation outcomes, it can be observed that the numerically simulated yield bearing capacities of the hollow composite slab specimens were generally higher than the experimental values, with errors ranging from 10 to 20%. However, the ultimate bearing capacities were generally close to the experimental values, with errors within 8%. This discrepancy may be attributed to several factors, including material variability in the hollow composite slab specimens, differences between the simplified model and the actual structure of the specimens, or inaccuracies in the constitutive relationship of concrete in describing the mechanical behavior of the hollow composite slabs under complex stress conditions.

Stress and damage

Figure 8 illustrates the deformation and crack distribution of the specimens, while Fig. 9 presents the plastic strain cloud diagrams of specimens DKB1-1 and DKB2-1 finite element models. The plastic strain cloud diagrams depict the crack development in the tensile zone of the concrete. The crack distribution shown in the figures aligns closely with the experimental results, exhibiting typical flexural failure characteristics of the normal section.The primary crack development in the tensile zone of the concrete bottom surface was concentrated in the pure bending segment at the mid-span of the specimens. As the load increased, cracks extended towards the bending-shear zone. The cracks on the sides of the specimens propagated upward through the composite layer towards the top surface. As a result, the slab deformation increased progressively, and the crushing of the concrete top slab was consistent with the experimental observations. This consistency between the finite element analysis model and the experimental results further validates the reliability of the finite element model.

Fig. 8
figure 8

Deformation and crack distribution of specimens.

Full size image
Fig. 9
figure 9

Plastic strain contour plots of the finite element models.

Full size image

Figure 10 shows the vertical displacement contour plots of the finite element models for specimens DKB1-1 and DKB2-1, while Fig. 11 presents the Mises stress contour plots for the reinforcement frameworks in specimens DKB1-1 and DKB2-1.From the figures, the following observations can be made: The vertical displacement and stress distribution of the tensile reinforcement in the bottom slab are consistent with the experimental results, with concentrations observed in the pure bending region at mid-span.The tensile stress of the bottom slab reinforcement exceeds the yield strength obtained from material tests.The truss reinforcement also participates in the load-bearing behavior of the specimens.The agreement between the finite element analysis results (vertical displacement and tensile stress distribution in the bottom slab reinforcement) and the experimental results further confirms the rationality and reliability of the finite element model.

Fig. 10
figure 10

Vertical displacement contour plots of finite element models.

Full size image
Fig. 11
figure 11

Mises stress contour plots of the reinforcement framework.

Full size image

Key parameter analysis

The finite element model described above was utilized for modeling and parameter analysis. Based on the DKB1-1 specimen model, the effects of various parameters, such as material properties, sectional dimensions, and internal configurations, on the mechanical performance of hollow composite slabs were further studied by modifying the model.

Effect of concrete strength

By keeping other parameters constant, the concrete strength grade in the DKB1-1 model was adjusted to C30 and C40, respectively. The load-midspan displacement curves for these models were compared with that of the original model using C35 concrete. Figure 12 shows the load-midspan displacement curves obtained from finite element analysis for models with the three different concrete strength grades. Table 5 lists the characteristic load values derived from finite element analysis for the models with different concrete strength grades.

Fig. 12
figure 12

Load-Midspan displacement curves from finite element analysis.

Full size image
Table 5 Characteristic load values from finite element analysis.
Full size table

From Fig. 12; Table 5, it can be observed that the load-midspan displacement curves of the specimen models corresponding to different concrete strength grades exhibit a similar development trend. As the concrete strength grade increases, the flexural load-bearing capacity and stiffness of the models improve to some extent, though the overall improvement is not significant.Comparing the yield load and ultimate load values: The yield load values increase by 5.76% and 10.50%, respectively, relative to the C30 concrete specimen.The ultimate load values increase by 2.32% and 4.63%, respectively, relative to the C30 concrete specimen.This indicates that changes in concrete strength grade have a certain impact on the flexural performance of hollow composite slabs. As the concrete strength grade increases, the load-bearing capacity of the specimens also gradually improves.

Effect of Hollow thin-walled box dimensions

By keeping other parameters constant, the dimensions of the hollow thin-walled box in the DKB1-1 model were adjusted from 450 mm × 450 mm to 450 mm × 500 mm and 450 mm × 600 mm, respectively. This adjustment effectively changes the width of the transverse ribs in the hollow layer of the composite slab from 180 mm to 120 mm and 0 mm.The load-midspan displacement curves for these models were compared with the original model with a hollow thin-walled box size of 450 mm × 450 mm. Figure 13 shows the load-midspan displacement curves obtained from finite element analysis for models with the three different hollow thin-walled box dimensions. Table 6 presents the characteristic load values from finite element analysis for the models with the three hollow thin-walled box dimensions.

Fig. 13
figure 13

Load–Midspan displacement curves from finite element analysis.

Full size image
Table 6 Characteristic load values from finite element analysis.
Full size table

From Fig. 13; Table 6, it can be observed that the load-midspan displacement curves of the specimen models corresponding to different hollow thin-walled box dimensions exhibit a similar development trend. As the dimensions of the hollow thin-walled box increase, i.e., as the transverse rib width of the hollow layer decreases, the load-bearing capacity and stiffness of the models during the flexural process decrease slightly, but the overall reduction is not significant.Comparing the yield load and ultimate load values: The yield load values decrease by 1.02% and 1.88%, respectively, relative to the specimen with a 450 mm × 450 mm hollow box.The ultimate load values decrease by 0.08% and 0.91%, respectively, relative to the specimen with a 450 mm × 450 mm hollow box.These results indicate that changes in the dimensions of the hollow thin-walled box have a certain impact on the flexural performance of hollow composite slabs. As the dimensions of the hollow thin-walled box increase, the load-bearing capacity of the specimens decreases gradually, but the impact is relatively minor. This further demonstrates that, during model optimization design, increasing the longitudinal size of the hollow thin-walled box (reducing the transverse rib width) can be considered. This approach not only maintains the structural performance of the specimen but also reduces concrete usage, achieving economic benefits.

Effect of specimen thickness

By keeping other parameters constant, the thickness of the DKB1-1 model was adjusted from 180 mm to 200 mm, which corresponds to an increase in the thickness of the cast-in-place top slab from 50 mm to 70 mm. This adjustment effectively increased the height of both the longitudinal and transverse ribs within the hollow composite slab.The load-midspan displacement curves for the two thickness variations were compared with the original model. Figure 14 shows the load-midspan displacement curves obtained from finite element analysis for the two different specimen thicknesses. Table 7 lists the characteristic load values derived from finite element analysis for models with different specimen thicknesses.

Fig. 14
figure 14

Load-Midspan displacement curves from finite element analysis.

Full size image
Table 7 Characteristic load values from finite element analysis.
Full size table

From Fig. 14; Table 7, it can be observed that the load-midspan displacement curves of models with different thicknesses exhibit a similar development trend. As the slab thickness increases, i.e., with an increase in the concrete thickness of the cast-in-place top slab, the load-bearing capacity and stiffness of the model during the flexural process show noticeable improvement.Comparing the yield load and ultimate load values: The yield load increases by 17.81%, and the ultimate load increases by 20.46% as the slab thickness increases.These results indicate that changes in slab thickness have a significant impact on the flexural performance of hollow composite slabs. With an increase in slab thickness, the load-bearing capacity and flexural stiffness of the hollow composite slab are significantly enhanced. This further suggests that, during model optimization design, appropriately increasing the sectional thickness of the specimen can effectively improve the overall flexural performance of the slab.

Effect of specimen span

By keeping other parameters constant, the span of the DKB1-1 model was adjusted from 4200 mm to 5460 mm and 6720 mm, respectively. This adjustment corresponds to increasing the length of the hollow composite slab by 2 and 4 groups of hollow thin-walled boxes and transverse ribs (each group measuring 450 mm + 180 mm). The number of hollow thin-walled boxes increased to 12, 16, and 20, respectively, and the hollow ratios for the three specimen groups were 16.53%, 18.84%, and 19.13%, respectively. Figure 15 shows the load-midspan displacement curves obtained from finite element analysis for models with the three different spans. Table 8 presents the characteristic load values derived from finite element analysis for models with the three different spans.

Fig. 15
figure 15

Load-Midspan displacement curves from finite element analysis.

Full size image
Table 8 Characteristic load values from finite element analysis.
Full size table

From Fig. 15; Table 8, it can be observed that the load-midspan displacement curves for models with different spans exhibit a similar development trend. As the span of the specimen increases, the load-bearing capacity and stiffness of the model during the flexural process decrease significantly.Comparing the yield load and ultimate load values: The yield load decreases by 28.85% and 40.44%, respectively, relative to the specimen with a span of 4200 mm.The ultimate load decreases by 28.05% and 42.09%, respectively, relative to the specimen with a span of 4200 mm.These results indicate that changes in specimen span have a significant impact on the flexural performance of hollow composite slabs. As the span increases, the load-bearing capacity and flexural stiffness of the hollow composite slab decrease significantly. This further highlights the importance of balancing the relationship between structural performance and span during the optimization design process. Overemphasis on increasing the span should not come at the expense of the mechanical performance requirements, such as load-bearing capacity and stiffness.

Conclusions

Based on the static loading tests of three reinforced truss hollow concrete slab specimens with different structural forms, nonlinear finite element analysis was performed, and the results were compared with the experimental findings. Additionally, the effects of concrete strength, hollow thin-walled box dimensions, slab thickness, and span on the flexural load-bearing capacity of hollow composite slabs were investigated. The following conclusions were drawn.

The experiments verified the consistency in mechanical performance and deformation characteristics between hollow composite slabs and cast-in-place hollow slabs. Using a nonlinear finite element model for material behavior, the crack distribution, flexural performance, and deformation characteristics of the hollow composite slabs were well simulated.

The change in the concrete strength grade has a certain impact on the flexural performance of hollow composite slabs. As the concrete strength grade increases, the bearing capacity of the specimens gradually improves. However, the overall improvement is relatively small. Therefore, under the premise of not compromising the structural performance, it is feasible to appropriately reduce the concrete grade to lower construction costs.

The dimensions of the hollow thin-walled boxes have a relatively small impact on the flexural performance of hollow composite slabs. During the optimization design process, the longitudinal dimensions of the hollow thin-walled boxes can be increased, thereby reducing the width of the transverse ribs. This approach maintains the structural performance of the specimens while reducing concrete consumption, achieving economic efficiency.This result highlights that the hidden beams formed by the truss reinforcement within the hollow composite slabs play a primary role in load-bearing. It also provides a basis for further research on hollow composite slabs with high void ratios.

Slab thickness has a significant effect on the flexural performance of hollow composite slabs. With increasing thickness, both the load-bearing capacity and flexural stiffness of the slabs improve significantly. This indicates that, during model optimization design, the slab’s sectional thickness can be appropriately increased, provided that it does not compromise functional and economic requirements, to enhance the overall flexural performance of the hollow composite slab.

Slab span has a pronounced impact on the flexural performance of hollow composite slabs. As the span increases, the load-bearing capacity and flexural stiffness of the slab decrease significantly. This underscores the need to balance the relationship between structural performance and span during model optimization design. Pursuing longer spans should not compromise critical mechanical properties, such as load-bearing capacity and stiffness.

The hollow composite slabs in this study demonstrated excellent static flexural performance. However, their mechanical behavior under dynamic cyclic loading and different support conditions requires further investigation.