An effectiveness assessment ensemble for transmission corridor mechanized construction schemes based on weighted itemset mining and factor criticality analysis

Abstract

A reasonable assessment of overall effective levels, incorporating dimensions such as risks, durations, and costs, will be salutary for the rational planning and better selection of optional transmission corridor mechanized construction schemes. With this motivation, this paper establishes an ensemble to address the issue of effective level diagnoses, and thus the hidden patterns and regularities between scheme features and effective levels can be explored. Based on the complex characteristics of input data, the Pearson correlation coefficient is deployed to handle the multidimensional data from multiple sources, and K-means clustering is then employed to classify scheme indicators into classes. The Weighted Itemset Mining (W-IM) model is proposed to identify the underlying key factors, to cope with the frequent omission of High Impact Low Probability (HILP) factors during the qualitative analysis stage. Next, the Factor Criticality Analysis (FCA) model is built to quantify the specific impact levels of these distinguished key elements. Finally, the significance proportion of individual features to the overall effectiveness can be determined and optimized according to the Entropy Impact Model (EIM) model. An empirical case study indicates that the proposed ensemble in this paper exhibits higher predictive accuracy along with better flexibility and comprehensiveness.

Introduction

Transmission corridors are pivotal for ensuring the safe and reliable operation of energy grids. The design and construction of these corridors necessitate meticulous assessment and determination of tower placement schemes. These schemes encompass the orientation of the corridors, the selection of tower bases, and the installation methodologies, integrating considerations such as engineering technology, land use, geological features, and environmental protection¹. This integration aims to guarantee the energy system’s safety, reliability, and cost-efficiency². With the advancement of mechanization, the construction methodologies for transmission corridors have evolved significantly from a traditional approach predominantly reliant on human labor to a fully mechanized process. However, human resources remain essential in practical applications. Mechanized construction of transmission corridors is characterized by extensive construction areas, dispersed work sites, complex environmental conditions, and heightened risks, thus exposing workers to substantial occupational health hazards³. Survey data frequently report severe safety incidents, including injuries from heavy objects and electrocutions. Furthermore, the implementation process often confronts challenges such as escalating costs, significant on-site execution difficulties, low construction efficiency, and indiscriminate selection of tower locations. Consequently, during the preliminary survey stage of mechanized construction, it is crucial to evaluate the construction schemes accurately. Effective planning and strategic layout not only enhance the safety index for construction personnel but also elevate the energy supply quality in high-voltage transmission corridors, preventing significant quality issues during subsequent operations. Construction schemes for transmission corridors exhibit considerable variability in terms of safety, duration, efficiency, and economic impact, leading to disparate levels of assessment outcomes⁴. The establishment of an integrated system for assessing the effectiveness of construction schemes holds profound significance. It supports the rational planning and scientific coordination of future construction projects and promotes the enhancement and optimization of these projects. Such systematic evaluations are essential for advancing construction methodologies and achieving higher standards of safety and efficiency in the development of transmission corridors.

The evaluation of engineering construction schemes’ effectiveness is currently a focal area of research. This involves methods such as the Network Hierarchical Analysis Method, the Fuzzy Comprehensive Evaluation Method, statistical methods, and other relevant algorithms. The literature presents various applications of these methodologies: References^5,6,7apply the fuzzy comprehensive evaluation method to assess the merits and demerits of large-scale construction project organizations. References^8,9utilize the analytic hierarchy process coupled with safety cost model theory to evaluate safety risks within construction projects. Reference¹⁰introduces a prediction method using a feedforward backpropagation neural network to analyze the significance of relevant variables in transmission corridor projects. Reference¹¹proposes a comprehensive robust planning model that addresses the uncertainties associated with the prolonged durations of transmission corridors, tailored to specific index requirements. References^12,13focus on optimizing the balance among accuracy, computational time, and reliability to identify reliable and effective optimal solutions for construction schemes in transmission corridors. Reference¹⁴integrates the Dijkstra algorithm with the ARG algorithm to devise cost-effective, efficient routing schemes. Reference¹⁵ develops a safety risk assessment model, which evaluates site layout planning schemes based on various factors, thereby facilitating pre-construction site safety management for builders. Finally, Reference proposes a model for sustainability-based risk assessment of infrastructure projects through global data.

Another methodological approach is based on data analytics, which employs relevant mining algorithms to explore patterns within multi-source datasets. The efficacy of evaluating mechanized construction schemes for transmission corridors hinges on the critical assessment of the importance of various feature factors and the organic integration of multi-source data. This facilitates an objective analysis and optimization of the feature factors’ weights. Itemset mining (IM)¹⁶ represents a pivotal branch within the field of data mining, dedicated to extracting information from datasets and identifying strongly correlated itemset¹⁷. Reference¹⁸applies IM to explore the intrinsic links among risk factors within schemes. Reference¹⁹utilizes IM to detect patterns among transformer status parameters, aiding in fault prediction. References^20,21employ an IM-based diagnostic approach to ascertain potential causes and key factors associated with faults in distribution networks. Reference²²leverages IM to discover association rules between risk factors of schemes and unsafe behaviors and implements a random forest algorithm to build a predictive model. Reference²³initially mines typical scheme risk indicators through correlation analysis and subsequently uses IM to identify associated risk factors, thereby assessing the effectiveness of corporate financial schemes. Reference²⁴introduces a multilevel IM model, based on K-means clustering and the Apriority algorithm, to analyze the causative factors of natural disasters such as flash floods. Reference²⁵constructs a quantitative analysis model based on IM to explore factors impacting residents’ quality of life, providing valuable insights for policymakers. Reference²⁶develops a safety assessment model using IM mining, which enhances the safety of distribution network transmission corridors through precise evaluation of influencing factors. Lastly, Reference²⁷ utilizes an IM model to analyze workers’ risk perception tendencies, which aids in targeted risk training.

This method has been effectively implemented across various fields, exemplifying its adaptability and reliability in diverse research settings. Based on our previous works, Reference^28,29have introduced a model that utilizes an importance-based fuzzy high-utility pattern recognition approach, designed for precise spatiotemporal forecasting of vulnerabilities within energy systems. Additionally, Reference³⁰ has developed a learning system employing fuzzy inference based on IM, aimed at accurately predicting the spatiotemporal distribution of deficiencies in energy systems. As demonstrated, the IM method can deliver relatively precise predictive evaluations, making it well-suited for assessing the effectiveness of mechanized construction schemes in transmission corridors. Presently, research into the effectiveness evaluations of such schemes is limited, especially when compared to the transient prediction of system failures in transmission corridors and the assessment of traditional construction schemes.

The research methodology presented in this paper differs from previous contributions in the field. Reference^31,32address the issue of generating a large number of candidates sets and the complexity of the mining process in traditional pattern mining, they utilize more effective data structures to handle incremental data, resulting in significant improvements in runtime and memory usage. Although reference³³ also considers the impact of different feature importances, the algorithmic improvements primarily affect the speed of execution and memory usage. Compared to speed and memory, the precise evaluation of the scheme is a more critical issue in this study. Therefore, this research focuses on data characteristics, designing an algorithm that is qualitative before quantitative, and then further optimized using an objective weighting method. This method can provide specific and targeted prevention support for potential risk hazards, offering a new solution to the difficulties and inaccuracies associated with relying on manual labor and experience to judge the construction effect levels. The specific improvements are as follows: Traditional itemset mining uses the same importance identification formula for the analysis of all feature factors, which often overlooks high-impact, low-probability feature factors during the qualitative analysis phase. The weighted itemset mining proposed in this paper takes into account high-risk, low-probability feature factors, thereby enhancing the accuracy of the assessment to some extent. Secondly, the weight of input features should be determined by the level of effectiveness they produce, rather than by appearance probability or data proportion. Therefore, this paper calculates the weight of feature factors based on the FCA method, which is more scientific and effective. Finally, Lastly, the output proportion of the impact of features on the overall solution effect is further optimized using the entropy weight method.

Addressing challenges identified in prior research, this paper introduces an integrated methodology for assessing the effectiveness of mechanized construction schemes in transmission corridors. This approach utilizes weighted itemset mining, factor importance analysis, and an information entropy theory model to evaluate the performance levels of each scheme. Specifically, it accounts for high-risk, rare feature factors, employing an entropy weighting method to reflect the utility values of these features, thereby establishing the weights of various components. The primary contributions of this study are as follows:

• To comprehensively evaluate the effectiveness levels of mechanized construction schemes for transmission corridors, this research leverages machine learning theories related to pattern recognition. It employs external environmental conditions and features of the construction schemes as inputs.

• Addressing the presence of high-impact, low-probability feature factors in multisource data, we developed the W-IM model. This model not only mines these factors but also proposes a set of variables, state-based assessment standards. The methods for calculating importance are designed according to the distribution of rare factors among features, using a conditional itemset scoring model to quantify the correlations between feature factors and the effectiveness levels of various schemes, thereby enabling a deeper exploration of potential key factors within rare datasets.

• Building upon FCA theory, this study introduces an enhanced methodology for computing the weights of key factors. Traditional approaches to weight calculation, which primarily rely on the probability of occurrence or the proportionality of data, often lack necessary optimization and adjustment throughout the analytical process. In contrast, the weighting of input feature factors should be governed by their efficacy in enhancing overall system performance. Consequently, this paper proposes a refined weight calculation method that meticulously considers the individual impact of each input feature factor, thus enabling a more accurate assessment of their respective weights in the system.

• Moreover, the EIM method is utilized to objectively assign and optimize weights. This approach adjusts the weights of individual features based on the differences and volatility in feature weights, thereby minimizing biases introduced by human factors and enhancing the credibility and precision of the resulting weights.

Conceptual framework

This paper establishes a detailed methodology for evaluating the effectiveness levels of multidimensional construction schemes in energy transmission corridors, utilizing multifactorial pattern recognition. The framework of the proposed method is illustrated in the figure provided.

The study initially engages in preprocessing multisource data. Each historical dataset of construction schemes encompasses multiple features, each composed of several feature factors. Interdependencies among data features are assessed using Pearson correlation coefficients, which facilitate the elimination of redundant features. Subsequent analysis employs K-means clustering to categorize each construction scheme into distinct effectiveness levels, considering dimensions of construction risk, duration, and cost. Moreover, the study introduces the W-IM method to identify rare feature factors that have strong associations with the effectiveness levels, addressing the conventional issue in IM where rare factors are discarded, potentially leading to evaluation errors. Following this, the influence of feature factors is quantified through weight adjustments based on the Theory of System Stable Structures and the FCA. Additionally, leveraging the EIM, the entropy weights of features are calculated, taking into account variations and volatilities in feature weights. Ultimately, the study computes an effectiveness index for the dataset using these optimized weights, and predicts outcomes on test data to evaluate the accuracy of the model. The framework diagram for the evaluation of the mechanized construction scheme of the energy transmission corridor is shown in Fig. 1 below.

Fig. 1

Framework diagram for the evaluation of mechanized construction schemes in energy transmission corridors.

Data pre-processing

Data collection

This study compiles historical data on mechanized construction schemes for transmission corridors within a specific region of Hunan. Each scheme is devised considering two primary aspects: external environmental features and construction technical features. The external environmental factors include the terrain, slope, and overburden thickness. The construction technique for each tower involves a series of steps: construction of access roads, land usage for construction, excavation of foundation pits, concrete pouring for foundations, and the assembly of iron towers, each characterized by distinct features. The efficiency of these construction operations is evaluated based on three key metrics: cost, duration, and risk. The dataset encompasses both continuous and categorical data types, providing a comprehensive basis for analyzing the mechanization of tower construction.

Feature dependency assessment

Due to the diversity in sources, types, and dimensions of features that influence construction efficiency, it is crucial to perform dimensionality reduction on multi-source data to mitigate the effects of redundant information. This process facilitates a more precise evaluation of the feature factors. The Pearson correlation coefficient serves as a statistical metric to evaluate the strength and direction of the relationship between two data sets. This coefficient ranges from − 1 to 1. Assuming the two feature data sets are denoted as $\:X$ and $\:Y$, the formula for calculating their Pearson correlation coefficient is as follows.

$${\rho _{X,Y}}=\frac{{\operatorname{cov} (X,Y)}}{{{\sigma _X}{\sigma _Y}}}=\frac{{E(XY) - E(X)(Y)}}{{\sqrt {E({X^2}) - {{(E(X))}^2}} \sqrt {E({Y^2}) - {{(E(Y))}^2}} }}=\frac{{n\sum\limits_{{i=1}}^{n} {{x_i}{y_i}} - \sum\limits_{{i=1}}^{n} {{x_i}\sum\limits_{{i=1}}^{n} {{y_i}} } }}{{\sqrt {n\sum\limits_{{i=1}}^{n} {x_{i}^{2} - (\sum\limits_{{i=1}}^{n} {{x_i}{)^2}} } } \sqrt {n\sum\limits_{{i=1}}^{n} {y_{i}^{2} - (\sum\limits_{{i=1}}^{n} {{y_i}{)^2}} } } }}$$

(1)

In the equation:$\:cov\left(X,Y\right)\:$denotes the covariance between $\:X$ and $\:Y$ ,$\:{\sigma\:}_{X}$ and $\:{\sigma\:}_{Y}\:$represent the standard deviations of $\:X$ and $\:Y$,respectively. A value of $\:{\rho\:}_{X,Y}\:$approaching 1indicates a stronger linear correlation between the two sets of feature data. By excluding data points with strong correlations from the two sets, a more representative dataset can be derived. The specific meaning of Pearson correlation coefficients is shown in Table 1.

Table 1 Specific meaning of pearson correlation coefficient.

Feature discretization

In construction project schemes, data often comprises a blend of discrete and continuous types. To address data imbalance and enhance model interpretability, it is essential to discretize the continuous data. The process of discretizing continuous data fundamentally involves determining the number of discrete values and dividing the data into several intervals based on their values. Each interval’s continuous data is then mapped to a specific discrete value. This method allows for the representation of all continuous data with a limited set of discrete values, thus facilitating more robust data analysis and interpretation.

K-means clustering is a prevalent unsupervised learning algorithm that organizes a set of data points into $\:k$ non-overlapping clusters. This algorithm achieves the optimal segmentation of data through a process of iterative optimization aimed at minimizing the sum of squared errors. Specifically, consider a dataset denoted by $\:X=\left\{{x}_{1},{x}_{2},{\cdots\:,x}_{N}\right\},{x}_{i}\in\:{R}^{D},i=\text{1,2},\cdots\:,N$. The K-means algorithm divides this dataset into $\:k$ clusters, with the centroid of each cluster represented as $\:({c}_{1},{c}_{2},\cdots\:,{c}_{k})$. The clusters generated post-clustering are denoted by $\:({M}_{1},{M}_{2},\cdots\:,{M}_{k})$. The algorithm secures the final clustering outcome by minimizing the distance between each data point and the centroid of its respective cluster, thus ensuring optimal cluster cohesion.

The Euclidean distance, which quantifies the distance between a data point and the centroid of its cluster, is represented as $\:dis(x,{c}_{i})$.

$$dis{(x,{c_i})^2}=\sum\limits_{{j=1}}^{n} {\parallel {x_j} - {c_i}{\parallel ^2}}$$

(2)

Accordingly, the objective function of the K-means algorithm is defined as follows:

$$SSE(x,c)=\sum\limits_{{i=1}}^{k} {dis(x,} {c_i}{)^2}$$

(3)

Identification and quantification of feature factor -target association patterns

System for identifying feature factor importance

Initially, it is crucial to accurately identify the feature factors that demonstrate a strong correlation with the efficacy levels of hallway construction schemes. This study focuses on developing a methodology for identifying significant factors based on the Importance Measure (IM) approach. By employing a dataset composed of various variables, this research utilizes two metrics, itemset frequency (IF) and rule strength (RS), to discern high-frequency variable sets and associated rules, thereby extracting key factors.

Itemset frequency is defined as the ratio of the dataset entries containing the itemset $\:M$ to the total number of dataset entries $\:O$. This measure is predominantly employed to mine high-frequency variable sets. For an association rule $\:M\to\:N$, the itemset frequency can be expressed as follows:

$$I{F_{\left( M \right)}}=[M]:[O]$$

(4)

Rule strength is defined as the ratio of the dataset entries that contain both itemset $\:M$ and $\:N$ to those containing only itemset $\:M$. This metric is primarily used for mining association rules. The rule strength for an association rule $\:M\to\:N$ can be represented as follows:

$$R{S_{\left( {M \Rightarrow N} \right)}}=[M,N]:[M]$$

(5)

In the above equation, $\:\left[M,N\right]\:$represents the number of data appearing simultaneously in itemset $\:M\:$and $\:N$, $\:\left[O\right]\:$represents the total number of data, and $\:\left[M\right]\:$represents the total number of data appearing in itemset $\:M$.

The customization of mechanized construction schemes for energy transmission corridors is subject to a multitude of influencing factors. In the implementation of these construction schemes, the frequent omission of high-impact, low-probability factors can significantly affect the evaluation of the scheme’s effectiveness. It is observed that traditional calculation formulas applied to the data records of these factors tend to underestimate their outcomes, resulting in the overlook of their critical impacts.

To enhance the accuracy in assessing the effectiveness of construction schemes for energy transmission corridors, it is imperative to account for the influences of such high-impact, low-probability feature factors. This paper improves the original importance assessment standard calculation formula by utilizing weighted itemset mining and proposes a set of variable state importance assessment standard calculation formulas. By applying this set of state importance assessment standard calculation formulas, records containing rare data in each feature will be separately identified and scored using the state importance assessment standard calculation formula specifically generated for that feature. The scores are then compared with the set threshold. This approach can derive frequent item sets and association rules based on the rare data in the feature. In this way, adjustments can be made in advance for high-impact, low-probability factors to ensure construction efficiency. For the historical records of effectiveness levels corresponding to transmission corridor construction schemes, assume $\:O=\left\{{t}_{1},{t}_{2},{\cdots\:,t}_{s}\right\}$ represents the input database containing records of construction schemes. Let $\:{f}_{i}\:$be a set containing all features of the construction schemes, where $\:\left\{{b}_{j,1},{b}_{j,2},\cdots\:{b}_{j,3},{\cdots\:,b}_{j,w}\right\}\:$represents any specific feature of a construction scheme, and $\:R=\left\{{R}_{1},{R}_{2},\cdots\:,{R}_{i},{\cdots\:,R}_{s}\right\}$ represents the vector of scheme effectiveness states for all construction schemes within the dataset.

The constructible matrix for scheme effectiveness assessment is denoted as $\:Q=\left[T\:B\:R\right]$,where $\:T={\left[{t}_{1},\cdots\:,{t}_{i},{\cdots\:,t}_{s}\right]}^{T}\:$represents the index of each construction scheme record; $\:B={\left({b}_{ij}\right)}_{s\times\:n}$, $\:{b}_{ij}\:$denotes a feature factor within each record of scheme effectiveness; $\:R={\left[{R}_{1\:}{R}_{2\:}{R}_{i\:}\cdots\:\:{R}_{s}\right]}^{T}$, $\:{R}_{i\:}$represents the final assessment level of effectiveness for each construction scheme.

A correlation rule between rare and common feature factors can be written as:

$${M^g}+{M^r} \to N$$

(6)

Among them, $\:{M}^{g}\:$and $\:{M}^{r}$ represent the common and rare variable sets, respectively. The diagnostic scores for improved rare variables are calculated as shown in Eqs. 7 and 8.

$$I{F_{{{\left( {{M^g}+{M^r}} \right)}_j}}}={A_{({M^g}\left| {{M^r}} \right.)}}:{A_{\left( {{M^r}} \right)}}$$

(7)

$$R{S_{{{\left( {{M^g}+{M^r} \Rightarrow N} \right)}_j}}}={A_{(({M^g}\left| {{M^r}} \right.) \Rightarrow N)}}:{A_{\left( {{M^r}} \right)}}$$

(8)

$${A_{({M^g}\left| {{M^r}} \right.)}}=\left[ {\begin{array}{*{20}{c}} {{t_i} \in Q(i,1)} \\ {{M^g} \subseteq Q(i,{E_g}) \ne \emptyset } \\ {Q(i,j) \in {M^r} \ne \emptyset } \end{array}} \right]$$

(9)

$${A_{(({M^g}\left| {{M^r}} \right.) \Rightarrow N)}}=\left[ \begin{gathered} \begin{array}{*{20}{c}} {{t_i} \in Q(i,1)} \\ {{M^g} \subseteq Q(i,{E_g}) \ne \emptyset } \\ {Q(i,j) \in {M^r} \ne \emptyset } \end{array} \hfill \\ Q(i,n+2)=R(o) \hfill \\ \end{gathered} \right]$$

(10)

$${A_{\left( {{M^r}} \right)}}=\left[ {\begin{array}{*{20}{c}} {{t_i} \in Q(i,1)} \\ {Q(i,j) \in {M^r} \ne \emptyset } \end{array}} \right]$$

(11)

In the equation, $\:i=\text{1,2},\cdots\:,s$ represents each sample number in the library, $\:j=\text{2,3},\cdots\:,n+1$ represents each column feature, $\:\left[\right]$represents the data values in $\:Q$ that meet the conditions in parentheses, $\:R\left(O\right)\:$represents the fault result, and $\:{E}_{g}\:$represents the numerical range from 2 to $\:\left(n+1\right)$.

Measurement of feature factor influence weights

Due to the varying degrees of correlation between different feature factors and the levels of scheme effectiveness, a quantitative analysis of the weights attributed to construction factors in corridors is essential. Traditional methods for calculating these weights typically rely on the proportion or frequency of feature factors within datasets. However, the actual correlation between feature factors and the levels of scheme effectiveness does not directly relate to their representation in datasets. Consequently, it is imperative to scientifically and accurately quantify the specific correlations between highly relevant construction feature factors and scheme effectiveness levels to determine their criticality.

Informed by the theory of system stability structure, this research constructs a model to assess the decrement in scheme effectiveness attributable to environmental elements. This model evaluates the trends and magnitudes of system failures induced by these elements, with the aim of comprehensively determining the weights of scheme effectiveness for each feature factor. Assuming $\:{Q}_{jr}$ represents a subset of$\:\:O$, and $\:{f}_{j}$ includes a collection of failure records for all rare factors within any given feature.

Considering the influence of both rare and common feature factors on the effectiveness, the weight of scheme effectiveness for an individual feature factor is defined as follows:

$${\gamma _j}=\gamma _{j}^{{(r)}}+\gamma _{j}^{{(g)}}$$

(12)

In the formula, $\:{\gamma\:}_{j}^{\left(g\right)}$and $\:{\gamma\:}_{j}^{\left(r\right)}$ represent the influence weights from common and rare feature factors, respectively. When $\:{b}_{j,k}$ is a common value in$\:{\:f}_{j}$, the effectiveness weight calculation formula is as follows:

$$\gamma _{j}^{{(g)}}=\sum\limits_{{j=1}}^{{\left[ {{t_i} \in O} \right]}} {\frac{{\left[ {Q(i,j)={b_{j,k}}} \right]}}{m}}$$

(13)

$\:\left[Q\left(i,j\right)={b}_{j,k}\right]\:$represents the number of fault samples containing the feature factor, and $\:m$ represents the total number of fault samples in database $\:Q$.

When dealing with rare feature factors, it is critical to accurately assess their impact on the effectiveness levels of construction schemes. This study utilizes the FCA method to evaluate the influence of rare feature factors on the effectiveness assessment of system schemes. The criticality analysis indicates the importance of components to system operations, primarily focusing on assessing the sensitivity and impact of components within the system. The IP derived from FCA quantifies the weight of feature factors in the system. The degree of a feature factor’s IP reflects the extent to which improvements in scheme effectiveness can maximize enhancements in system reliability. The calculation formula for IP is as follows:

$$I({b_{j,k}}\left| {{t_i}} \right.)=H({1_j},{p_{{t_i}}}) - H({p_{{t_i}}})$$

(14)

In the equation, $\:H\left({1}_{j},{p}_{{t}_{i}}\right)$ denotes the risk of fault $\:{t}_{i}$ occurring in the system when feature factor $\:{b}_{j,k}$ is definitively present, and $\:H\left({P}_{{t}_{i}}\right)$ indicates the general risk of failure $\:{t}_{i}$ occurring in the system. It can be inferred from this equation that the magnitude of the IP value reflects the extent of fluctuation in system risk attributable to the presence of the feature factor; specifically, a larger IP value signifies a more pronounced significance of that factor. In the practical evaluation of construction scheme effectiveness for energy transmission corridors, the degree of scheme effectiveness is collectively determined by the various feature factors that comprise the construction scheme. Changes in any one of these factors will influence the evaluation of the scheme’s effectiveness level. Consequently, the system is conceptualized as a series structure. If each feature factor within the system operates independently, the total scheme effectiveness of the system can be determined by calculating the product of the weights of the feature factors within the series. The formula for this calculation is as follows:

$$H({p_{{t_i}}})=\prod\limits_{{k=1}}^{n} {\left( {\sum\limits_{{i=2}}^{{\left[ {{t_i} \in {O_{jr}}} \right]}} {\frac{{\left[ {{t_i} \in Q\left( {i,1} \right);Q(i,j)={b_{j,k}};Q\left( {i,j} \right) \in {M^r}} \right]}}{{\left[ {{e_i} \in {Q_c}(i,1);Q(i,j) \in {f_j}} \right]}}} } \right)}$$

(15)

In summary, the formula representing the effect weight of rare factors can be articulated as follows:

$$\gamma _{j}^{{(r)}}=\sum\limits_{{i=2}}^{{\left[ {{t_i} \in {O_{jr}}} \right]}} {\frac{{\left[ {{t_i} \in Q\left( {i,1} \right);Q(i,j)={b_{j,k}};Q\left( {i,j} \right) \in {M^r}} \right]}}{{\left[ {{e_i} \in Q(i,1);Q(i,j) \in {f_j}} \right]}}} - \prod\limits_{{k=1}}^{n} {\left( {\sum\limits_{{i=2}}^{{\left[ {{t_i} \in {O_{jr}}} \right]}} {\frac{{\left[ {{t_i} \in Q\left( {i,1} \right);Q(i,j)={b_{j,k}};Q\left( {i,j} \right) \in {M^r}} \right]}}{{\left[ {{e_i} \in Q(i,1);Q(i,j) \in {f_j}} \right]}}} } \right)}$$

(16)

Feature weight optimization based on entropy impact model

The preceding analysis determined the weights of individual factors within the features of scheme effectiveness and assessed the impact of these factors on the effectiveness level of the system. It was noted that the contribution ratios of different features to the overall effectiveness level of the scheme vary. In response to this, the present study utilizes the EIM to objectively weight the features of various schemes, thereby refining the feature weights.

In the realm of information theory, entropy serves as a measure of uncertainty. This study quantifies the information content of known data and establishes the weights for feature indicators by computing the entropy values associated with these features. When the data values of a feature indicator exhibit substantial variation, the corresponding entropy value is lower, indicating that the feature provides a significant amount of useful information, which justifies a higher weight. In contrast, when there is minimal variation in the data values, the entropy value increases, suggesting that the feature contributes less useful information, thereby warranting a lower weight.

The EIM is an objective weighting technique that assigns weights to indicators based on the variability of their values. This approach mitigates biases associated with subjective factors, thus enhancing the credibility and accuracy of the derived weights compared to subjective weighting methods. The EIM is extensively utilized in various domains, including multi-criteria comprehensive evaluation, decision analysis, and system optimization. The main objective of this method is to compute the information entropy of each evaluation indicator to ascertain the contribution of each feature indicator to the comprehensive evaluation outcomes.

As indicated in Sect. 4.2, after optimization through the W-IM, the weight of an individual feature factor is denoted as $\:{\gamma\:}_{jk}$. With $\:s$ representing the sample size and $\:n$ the number of features, the weight matrix for the feature factors of the effectiveness of construction schemes for energy transmission corridors is designated as $\:H={\left({\gamma\:}_{jk}\right)}_{s\times\:n}$. Based on the optimization with EIM, the feature weight matrix of the scheme effectiveness is defined as $\:I={\left({i}_{jk}\right)}_{s\times\:n}$. The specific computational steps are detailed as follows:

• (1) The data was normalized using standardized formulas for profitability and cost indices, resulting in the normalized matrix $\:{H}^{{\prime\:}}={\left({\gamma\:}_{jk}^{{\prime\:}}\right)}_{s\times\:n}$.

• (2) The feature weights of the data for each feature factor within the normalized matrix were calculated. The weight of the k-the indicator for the j-the sample is given by the following formula:

$${l_{jk}}=\frac{{\gamma _{{jk}}^{\prime }}}{{\sum\limits_{{j=1}}^{s} {\gamma _{{jk}}^{\prime }} }}$$

(17)

• (3) Determine the entropy of the feature based on the definition of entropy and the values of the feature data, with the entropy calculation formula as follows:

$${e_k}= - \frac{1}{{\ln s}}\sum\limits_{{j=1}}^{s} {{l_{jk}}\ln ({l_{jk}})}$$

(18)

• (4) Calculate the entropy weights of the feature for each scheme using the entropy values obtained in step three.

$${w_k}=(1 - {e_k})/(n - \sum\limits_{{k=1}}^{n} {{e_k})}$$

(19)

• (5) In summary, the feature weight optimization matrix is as follows:

$$I={({i_{jk}})_{s \times n}}={({l_{jk}} \bullet {w_k})_{s{{ \times n}}}}$$

(20)

Flowchart for effectiveness level assessment based on W-IM-EIM

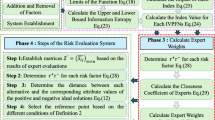
Based on the theoretical framework described previously, this study implements the proposed method for analyzing factor importance—termed the Weighted Itemset Mining and Entropy Influence Model (W-IM-EIM)—in assessing the effectiveness of mechanized construction schemes for transmission corridors. The specific procedure flow chart is shown in Fig. 2 below:

Fig. 2

Flowchart of scheme effectiveness evaluation based on W-IM-EIM.

The specific steps are as follows:

Step1.Initially, continuous data from multiple sources are labeled using K-means clustering. Subsequently, the Pearson correlation coefficient is employed to calculate the dependency of features, leading to the elimination of redundant features with high dependencies.

Step2.The effectiveness of each construction scheme is evaluated based on three criteria: cost, duration, and risk. This evaluation involves classifying the effectiveness levels through K-means clustering.

Step3.Feature factors in the input data are initially screened using traditional importance evaluation standards to distinguish between rare and common feature factors.

Step4.Sect. 4.1 describes the calculation of itemset frequency and rule strength for rare factors, thus determining the association between feature factors and various levels of scheme effectiveness. Steps 3 and 4 are repeated for each feature.

Step5.The FCA method, outlined in Sect. 4.2, is utilized to compute the effect weights for both common and rare feature factors.

Step6.Based on the effect weight matrix obtained from the previous step, the EIM method described in Sect. 4.3 is applied to compute the entropy weight of features for each scheme, resulting in an optimized matrix of scheme effect weights.

Step7.The scheme effect index for each scheme in the test dataset is calculated and compared with the actual outcomes to validate the predictive performance of the evaluation model.

Principles and advantages of the FP-Growth algorithm

Currently, most algorithms related to association rule mining focus on solving the issue of algorithm runtime. In the application of mechanized construction scheme effectiveness evaluation, we have ample time to ensure the correctness of the scheme selection, hence we do not prioritize reducing algorithm runtime. Addressing the issue of the generation of a large number of candidate item sets during the mining process of common association mining algorithms, this paper adopts the FP-Growth (Frequent Pattern Growth) algorithm as the association rule mining algorithm.

The FP-Growth algorithm is an algorithm used for mining frequent item sets, with its core idea being to transform the process of mining frequent item sets into constructing an FP-tree, and then mining frequent item sets through this tree. The main advantage of the FP-Growth algorithm is that it does not require the generation of candidate item sets, making it more efficient than the Apriori algorithm when dealing with large datasets.

The basic process of the FP-Growth algorithm is as follows:

(1) First, input the database. Calculate the score of each variable’s important diagnostic criteria and compare it with the preset threshold, sorting in descending order according to the score.

(2) Construct the FP-tree. Select the item with the highest score as the root node of the tree, and then scan the database again, adding each transaction to the FP-tree in order of item score.

(3) Mine high-frequency variable item sets. Extract the conditional pattern base from the FP-tree and recursively mine the corresponding high-frequency variable sets.

(4) Generate association rules. Based on the mined high-frequency variable sets, generate association rules using some measure (support, confidence).

The process of association rule mining can generally be summarized in two steps: ① Mine high-frequency item sets in the database using a preset support threshold; ② Based on the selected high-frequency item sets, filter out corresponding association rules using a preset confidence threshold. The support threshold set in this paper is 0.2, and the confidence threshold is 0.6.

Case study

In this study, we employed a dataset derived from the mechanized construction of 220 kV transmission towers within a specified region in Hunan Province for validation purposes. This dataset enabled the assessment of the actual effectiveness of the corridor construction scheme. Analysis of the scheme’s impact was conducted within the confines of the designated experimental area over a defined period. The dataset utilized consists of multisource data that encapsulate both external environmental features and specific features of the construction scheme. The results of the construction scheme were stratified into three levels: primary, secondary, and tertiary effects. The dataset was partitioned into training and testing subsets in a 3:1 ratio, facilitating an empirical evaluation.

Analysis of associations between feature factors

The study identified several key factors influencing the construction scheme for the transmission corridor towers, including external environmental conditions, construction road development and land use, pit excavation, foundation pouring, and tower assembly. These elements exhibit a certain degree of linear correlation. To quantitatively assess the interrelations among various construction features, the Pearson correlation coefficient was utilized. This statistical measure was applied to evaluate the relationships between the total length of features (item 1), specific feature length (item 2), area occupied by the tower base (item 3), area utilized for mechanized construction (item 4), volume of excavation (item 5), and the volume of soil transported externally (item 6). The resulting correlation matrix is described in Fig. 3 below:

Fig. 3

Feature correlation matrix.

Based on the relevance matrix, it is evident that the correlation coefficients between total length and length 1, as well as those between excavation volume and exported earth volume, exceed 0.8, indicating extremely strong correlations. Additionally, the sum of correlations of total length with other features is 0.39, for length 1 it is 0.46, for excavation volume it is 0.36, and for exported earth volume it is 0.62. Given these data, it is prudent to eliminate the features of length 1 and exported earth volume from further analysis. Moreover, the correlation coefficient between the base area of the tower and the area occupied by mechanized construction exceeds 0.6, signifying a strong correlation. The aggregate correlation with other features is 0.382 for the former and 0.572 for the latter, thus justifying the removal of the feature corresponding to the area occupied by mechanized construction.

In this study, the construction scheme data encompassed 37 distinct features. Pearson correlation coefficients were computed for the collected data, and features exhibiting a Pearson correlation coefficient greater than 0.5 were excluded. Consequently, 22 features were retained. These features were classified into several categories using K-means clustering, where each category represents a distinct label. The specific features and their constituent factors are depicted in Fig. 4:

Fig. 4

Summary of feature and feature factors.

Criteria for classification of scheme effectiveness levels

The environmental impacts of various construction factors differ significantly. Through a detailed investigation of different construction methodologies and their environmental repercussions, a radar chart as depicted in Fig. 5 was constructed. In this chart, each area quantitatively represents the environmental impact attributed to a specific construction factor. The chart reveals that activities such as laying foundation boxes and constructing new temporary access roads exert the most substantial environmental impact, while non-mechanized arrangements of construction sites have the minimal impact. Based on these findings and the practical needs for on-site decision-making, scenarios involving the laying of foundation boxes or the construction of new temporary roads are categorized as high-risk. In contrast, those involving non-mechanized site setups are categorized as low-risk, and scenarios that include mechanical excavation or mechanized site layouts are assigned a medium-risk category.

Furthermore, this study assesses the effectiveness of construction schemes based on three primary indicators: cost, duration, and risk. Given that the data pertaining to cost and duration are continuous, whereas risk is categorical, the continuous dataset was first subjected to clustering using the K-means algorithm, with the clustering results illustrated in Fig. 6. Integrating these clustering outcomes with the risk evaluations, the effectiveness levels of the construction schemes were comprehensively assessed and subsequently categorized, as detailed in Table 2. This methodological approach ensures a holistic evaluation of construction schemes, facilitating informed decision-making in construction management.

Fig. 5

Impact of construction factors on different environments.

Fig. 6

K-means clustering result.

Table 2 Classification of scheme effectiveness levels.

Analysis of associations between feature factors and effectiveness levels

By utilizing the W-IM computation described in Sect. 4.1 to evaluate the significance of feature factors, we can determine the importance of these factors across different levels of scheme effectiveness. Figure 7 presents the correlation between external environmental factors and various levels of scheme effectiveness. In contrast, Fig. 8 depicts the associations between construction factors and the effectiveness levels within different steps of the construction schemes. The analysis illustrated in Figs. 7 and 8 indicates an upward trend in the rule strength of both environmental and construction factors as the levels of scheme effectiveness increase. The strongest correlations are observed with the highest level of scheme effectiveness, Level Three, while the weakest associations occur with Level One. This phenomenon is attributable to the typical aim of construction schemes, which is to achieve high effectiveness, thereby accumulating a more substantial dataset for Level Three. In contrast, schemes associated with lower levels of effectiveness are less frequent, resulting in a paucity of feature factors that demonstrate significant relevance to Level One, due to the limited number of samples.

Fig. 7

Association between environmental feature factors and different effectiveness levels.

Fig. 8

Association between construction feature factors and different effectiveness levels.

Analysis of scheme effectiveness level assessment results

The confusion matrix is a widely utilized method for evaluating predictive models, primarily employed to assess a model’s performance on test datasets. This method is essential for contrasting the actual labels with the predictions made by the model. Consequently, it facilitates the calculation of four key statistical metrics: True Positives (TP), False Positives (FP), True Negatives (TN), and False Negatives (FN). These metrics are depicted in Fig. 9.

Fig. 9

Confusion matrix.

Given a designated threshold $\:T$, the evaluation probability of each sample dictates its classification: samples with probabilities exceeding $\:T$ are considered positive, while those below are deemed negative. The receiver operating characteristic (ROC) curve is utilized to assess the generalization performance of the model, as depicted in Fig. 10. The ROC curve’s horizontal axis represents the false positive rate—the likelihood that an actual positive is predicted as negative—while the vertical axis indicates the true positive rate—the probability that an actual positive is correctly predicted as such. The formula used is denoted as:

$$FPR=\frac{{FP}}{{FP+TN}}$$

(21)

$$TPR=\frac{{TP}}{{TP+FN}}$$

(22)

The higher the values of true positive rate (TPR) and 1 minus false positive rate (1 − FPR), the more effective the model evaluation. The area under the ROC curve (AUC) serves as a measure of the model’s predictive accuracy. This study categorizes the sample set based on the efficacy levels of three different intervention schemes for testing. When assessing the efficacy of one scheme, samples from the other two are treated as negative controls. The comparison involves three computational models: the traditional itemset mining model (IM), the weighted itemset mining model (W-IM), and the weighted itemset mining model based on an entropy impact model (W-IM-EIM). The ROC curves, illustrating the comparative effectiveness of these models based on the overall scheme performance, are shown in Fig. 11. Table 3 summarizes the performance indicators of different algorithm models.

Fig. 10

ROC curve explanation.

Table 3 Comparative data on evaluation effects.

Fig. 11

ROC curve comparison based on scheme effectiveness level evaluation.

Based on the comprehensive comparison of evaluation effect data from different algorithmic models and ROC curves, it is evident that the W-IM method, which takes into account the improved importance assessment criteria and scheme effect weight calculation methods, can more accurately evaluate the effectiveness levels of construction schemes compared to traditional IM. The reason is that traditional IM uses the same importance assessment method to calculate the importance of feature factors, neglecting the impact of high-influence, low-probability factors on the evaluation of scheme effectiveness levels. In contrast, the W-IM method employs a variable importance assessment approach, which not only mines high-influence, low-probability feature factors but also more accurately calculates their importance. Furthermore, the W-IM-EIM method, based on information entropy theory, further objectively improves the weights of features affecting the evaluation of construction scheme levels, enhancing the precision of the model evaluation method. As shown in the aforementioned figures, on average, when comparing the three scheme effectiveness levels, the W-IM-EWM method proposed in this paper has increased the AUC value of the ROC curve by 5.83% and 16.11% compared to the W-IM method and IM method, respectively; the SE value has increased by 9.2% and 21.2%, respectively; and the CI score has increased by 7.4% and 21.3%, respectively. Therefore, the W-IM-EIM method proposed in this paper significantly outperforms the traditional IM method in terms of accuracy in evaluating the effectiveness levels of transmission corridor construction schemes. Additionally, this method can mine high-influence, low-probability factors within construction schemes, providing specific and targeted support for potential scheme risks.

The results indicate that the three algorithm models have higher accuracy in assessing “Scheme Effect Level Three,” while their accuracy in assessing “Scheme Effect Level One” is relatively lower. The reason for this discrepancy lies in the fact that during the formulation of construction schemes, people tend to choose schemes with higher effect levels. These schemes achieve the highest comprehensive benefits and retain more detailed record data. In contrast, schemes with an effect level of one are less frequently formulated, resulting in fewer data records, which consequently affects the final assessment accuracy.

Conclusion

This study addresses an effectiveness level evaluation ensemble, where the weighted itemset mining, factor importance analysis, and information entropy theory models are combined, for transmission corridor construction schemes, through three dimensions including construction risks, durations, and costs. This framework can incorporate the HILP factors, and also emphasizes the entropy differences by components’ impact levels straightforwardly, yet frequency or proportion, which makes it more feasible and credible especially in complex data scenarios. The detailed works are structured as follows:

• Establishment of an importance identification system to distinguish impacting construction factors.

This system accounts for high-impact, low-probability factors typically overlooked by traditional itemset mining models. By refining the dynamic criteria for evaluating importance and utilizing a conditional itemset scoring model, the approach enables a deeper exploration of potential critical feature factors from rare datasets.

• Development of a multidimensional weight measurement model to measure their impact levels.

By employing factor importance analysis, this model optimizes the correlation assessment between construction factors and the scheme effectiveness. It provides a clear and precise measurement of the alterations of the overall system effectiveness generated via each individual feature factor rather than simply through their appearance frequency or data proportion, thus enhancing the credibility.

• Application of entropy impact model theory to determine the significance of each feature.

This model entails assessing the respective significance of each feature of the construction scheme to the overall effectiveness index of the scheme. By optimizing the weights of the scheme features and enhancing the accuracy of the predicted effectiveness index, a more reliable assessment can be produced. This methodology ensures a robust evaluation process that supports informed decision-making in scheme selection.

• An empirical case study is conducted.

Comparative analysis with historical data from specific corridor construction schemes in practical applications demonstrates that this method predicts the effectiveness level of scheme implementation, offering a solution to the challenges of operational difficulty and inaccuracies inherent in reliance on manual labor and experiential judgment in corridor construction.