Detection method of subgrade settlement for the road of ART in coastal tidal flat area based on Vehicle-mounted binocular stereo vision technology

Abstract

To address the problem present in current subgrade settlement detection methods, this paper proposes a nondestructive intelligent and dynamic detection method for subgrade settlement based on vehicle-mounted binocular stereo vision technology. This method aims to achieve all season, the whole road, long-term detection of subgrade settlement for Road of ART (Autonomous rail Rapid Transit) in coastal tidal flat areas. Firstly, improved Schneider encoding is adopted as the marker for subgrade settlement monitoring points. Binocular camera calibration and stereo rectification are performed using Zhang’s method and the Bouguet algorithm before acquiring the marker images at the monitoring points, followed by efficient capture of Schneider ring coding images by the vehicle-mounted binocular stereo vision system. Thirdly, OpenCV is employed to preprocess the images, which improve image quality, eliminate noise, and enhance the features of the ring coding markers. On this basis, an improved SGBM algorithm is utilized for binocular stereo matching. Finally, according to the principle of triangulation, the three-dimensional coordinates of the monitoring points are obtained, and the corresponding settlement values of each monitoring point are determined through decoding and matching. Experimental results indicate that, for a true settlement value of 60 mm, the proposed detection method achieves an average settlement value of 58.897 mm, with a relative error rate of 1.84%. In the same experimental environment, the relative error rate of using a monocular camera detection method is 10.3%. The vehicle-mounted binocular camera method, with lower relative error than the monocular camera, offers a more efficient and accurate solution for nondestructive subgrade settlement detection, enhancing its intelligence.

Introduction

Subgrade settlement has a profound impact on the structural stability of roads and the operational safety of ART, particularly in coastal tidal flat areas with complex geological conditions. In these areas, due to loose soil composition^1,2, frequent fluctuations in groundwater levels, and the effects of tidal forces, subgrade settlement are especially prominent. Subgrade settlement not only leads to reduced road surface smoothness and increased maintenance costs but also decreases passenger comfort and may even cause traffic accidents³. Therefore, accurate and efficient monitoring of subgrade settlement in coastal tidal flat area is crucial for the safe operation of ART.

Currently, subgrade settlement detection methods can be broadly categorized into traditional civil engineering detection methods and nondestructive testing methods. Traditional civil engineering methods are cost-effective, simple to operate, and easy to measure; however, they are highly influenced by subjective factors, have low operational efficiency, and are limited in their applicability. These methods can’t meet the requirements for efficient nondestructive measurement and dynamic monitoring. In contrast, nondestructive testing methods, which are characterized by high precision and real-time performance, provide superior capabilities, including dynamic measurement. Among these, fiber optic sensor measurement techniques provide high accuracy and the ability to perform long-distance measurements. However, fiber optic sensors are expensive, difficult to maintain, and have limited deformation detection capabilities⁴. As a result, its practical application in coastal tidal flat areas is restricted. Satellite remote sensing measurement method, while effective, is less sensitive to vertical displacement (settlement) and its data accuracy and stability are easily affected by many factors such as satellite geometric position and atmospheric disturbances⁵. Therefore, this method isn’t suitable for monitoring of the subgrade settlement of coastal tidal flat areas in where frequently experience foggy weather. In recent years, stereo vision measurement technology based on binocular cameras has been widely applied in fields such as surveying, transportation, and construction. For example, Chong et al.⁶ proposed a chain-based binocular camera 3D distance measurement algorithm for high-precision measurement of longitudinal displacement in seamless tracks. Hu et al.⁷ developed a new underwater vehicle distance measurement system based on semantic segmentation and binocular vision, meeting the needs for underwater target recognition and distance measurement. Zhang et al.⁸ designed a binocular vision-based method for measuring the volume of large materials, providing safety warning data for mining conveyor belts that exceed capacity limits. The core of binocular camera measurement lies in stereoscopic matching, which is crucial to the accuracy of the results. Consequently, researchers have conducted extensive studies to improve the precision of stereoscopic matching. Qiao et al.⁹ proposed a gradient-based adaptive window stereoscopic matching algorithm to address the problem of low matching accuracy caused by insufficient feature extraction in low-texture regions. Cao Yi et al.¹⁰ rearranged the traditional Census Transform window and combined it with a dynamic programming matching algorithm, improving stereo matching accuracy while effectively reducing complexity. To further reduce matching noise, Yoon et al.¹¹ applied a bilateral filtering algorithm to stereoscopic matching, which effectively preserves image edges but has high computational complexity and poor real-time performance. Hou et al.¹² proposed a stereoscopic matching algorithm based on texture filtering, using texture filtering methods for cost aggregation, highlighting image structure information, and smoothing internal textures.

Based on the existing research, it is evident that current studies utilizing binocular stereo measurement technology primarily focus on applications such as distance measurement, volume estimation, and pavement damage detection. However, there is a notable lack of research on subgrade settlement detection using binocular vision. In view of the limitations of existing detection methods for subgrade settlement, the complex natural environment and soil conditions of coastal tidal flat area, and the characteristics of actual road traffic loads (including the emerging medium-capacity public transportation system—ART, which are capable of unmanned driving, flexible formations, and a maximum speed of 70 km/h), as well as the applicability of detection methods, this paper proposed a novel subgrade settlement detection method for roads of ART in coastal tidal flat area, based on vehicle-mounted binocular stereo vision technology. The technology roadmap is shown in Fig. 1.

Fig. 1

Technology roadmap.

The complicated environment of the working site and the lack of sufficient features on the surfaces of the monitoring point markers pose challenges for binocular vision-based matching algorithms. To address these challenges, as illustrated in Fig. 1, the ring coding marker designed by Schneider C.T. is utilized as the marker for the monitoring points of subgrade settlement, with modifications tailored to practical applications. The modifications facilitate the acquisition of marker images and the subsequent decoding of the corresponding monitoring points. And then the binocular cameras are calibrated using the Zhang Zhengyou method to eliminate lens distortion and obtain accurate intrinsic and extrinsic camera parameters. After then, epipolar geometry constraints are applied to achieve stereo rectification, ensuring that the left and right views are coplanar and aligned for performing stereo matching. Building on this, the ring coding marker are efficient collected by the vehicle-mounted binocular stereo vision system and are performed images preprocessing. Preprocessing process involves an improved Otsu algorithm based on morphological closing operations to perform image binarization, thereby mitigating boundary effects and reducing the impact of image noise on subsequent stereoscopic matching. Additionally, Canny edge detection and Hough transform are employed to determine the center positions of the ring coding marker. The semi-global block matching (SGBM) algorithm is then used to calculate the disparity values between corresponding matching points in the left and right images, and generate a depth map. Post-processing of the disparity map is conducted by using multi-level mean filtering with integral images to remove noise and enhance detail, improving the accuracy and display effect of the disparity map. Finally, using the principles of triangulation in conjunction with the depth information and the center positions of the marker, the 3D coordinates of the monitoring points center are determined. The difference in the center coordinates of the monitoring point markers before and after settlement is computed through decoding and differential calculations, thereby obtains the settlement values at each monitoring point. This method enables to achieve precise quantification of subgrade settlement deformations.

Monitoring system for subgrade settlement

Construction of settlement monitoring system

The settlement monitoring system is shown in Fig. 2, which mainly includes two core parts: one is the marker module for monitoring subgrade settlement, another is the measurement system based on vehicle-mounted binocular stereo vision. Specifically, the monitoring system is equipped with improved Schneider C.T ring coding markers, used for the precise localization and monitoring of subgrade settlement, and the vehicle-mounted binocular camera device (Camera model D-455B, from Pixel XYZ brand). The measurement system of vehicle-mounted binocular stereo vision captures images of containing the Schneider C.T. ring coding markers. By decoding and analyzing these images, the system determines the central positions of the markers, and combines the depth information, it calculates the three-dimensional spatial coordinates of these points. By collecting positional data of the same marker at different monitoring intervals, the system can compute the vertical difference in the 3D coordinates between two acquisition periods. The effective monitoring and quantitative evaluation of the subgrade settlement can be realized by comparing and analyzing the height difference of the center point of the ring coding markers of the monitoring point.

Fig. 2

The monitoring system for the subgrade settlement.

However, in practical applications, it is challenging to ensure that the vehicle-mounted camera maintains a consistent pose angle when capturing the same monitoring marker across different time period. This inconsistency can lead to variations in the depth information between the camera and the markers, thereby affecting the accuracy of the 3D coordinate measurements. To address this problem, a DJI stabilizer (as shown in Fig. 3) is used as the connecting component between the detection vehicle and the binocular camera. The stabilizer helps maintain the camera’s posture, mitigate impact caused by changes in the camera’s posture angle. This ensures stable measurements of the monitoring points across different time period, thereby enhancing the accuracy and reliability of subgrade settlement monitoring.

Fig. 3

DJI stabilizer.

Generation and decoding of ring coding markers

Coding markers are an essential component in photogrammetry, with each marker corresponding to a unique code value, providing significant application value in image recognition. Coded markers can be categorized into several types, such as point distribution, concentric rings, and non-geometric features. To reduce subsequent processing computation, improve calculation speed, and meet the project’s coding quantity requirements, this study employs the ring coding markers designed by Schneider C.T. A program was developed to automatically generate, decode, and locate these coding markers, as illustrated in Fig. 4: (a) shows the Schneider-coded marker, (b) depicts the decoding of the marker, and (c) illustrates the locating of markers. The specific functions of the locating are further discussed in Sect. 2.3.

Fig. 4

Example of monitoring point marker based on Schneider coding.

Schneider code consists of a central circle and a concentric ring band encoded with binary data. These encoded bands are evenly divided into 10 segments, each referred to as a bright ring or a dark ring, corresponding to binary codes of 1 or 0 respectively.

Generation of ring coding markers

To ensure the continuity of Schneider codes across different decoding directions and positions, the method proposed by Forbes et al.¹³is adopted to improve the Schneider coding technique. The start position is sequentially shifted counterclockwise, generating multiple binary code values and their corresponding decimal numbers. All possible decimal values are then sorted to generate a code value lookup table. Each Schneider code is identified based on its position in this lookup Table¹⁴. The flowchart for generating the coding markers is shown in Fig. 5.

Fig. 5

Flowchart of generating ring coding markers.

Decoding of ring coding marker

First, a zero array matching the size of the binary image is created to serve as a mask. The outer and inner circles are then drawn onto this mask, filling the outer circle area with white and the inner circle area with black. A bitwise AND operation is applied to merge the binary image with the mask. Next, starting from the right above the image as the initial angle, sample points are taken at intervals corresponding to a 36° angular step. The grayscale value of each sampled point is compared to a threshold value; if it is greater than the threshold value, the output is “1”, otherwise, the output is “0”. This process converts the image information into a binary code. Finally, the binary code is converted into a decimal number, and the result is output within the image. The process is illustrated in Fig. 6.

Fig. 6

Flowchart of decoding for ring coding marker.

Affine transformation correction

Considering the potential distortions in the marker images caused by variations in the acquisition angle and other factors during actual image capture, errors in decoding may occur, negatively impacting the accuracy of subgrade settlement measurements. To address this, affine transformation is applied to correct the Schneider-coded marker images at monitoring points. This correction enhances the accuracy of the subgrade settlement monitoring system by refining the localization of the ring marker’s central point.

Affine transformation¹⁵ involves performing a linear transformation and a translation within a vector space, mapping it to another vector space. Its principle is illustrated in Fig. 7. To improve the recognizability of the image and facilitate subsequent corrections after affine transformation, this study optimizes the Schneider-coded markers. Specifically, an isosceles triangle with a base equal to one-seventeenth of the image width and a height equal to one-twelfth of the image width is placed in the white area between the central circle and the peripheral coded area, positioned directly to the left of the central circle, as shown within the red circle in Fig. 4(c).

The process begins with edge detection to identify the contour of the ring coding marker. The roundness and area of each contour are calculated, and contours that meet the specified criteria are screened out. Ellipse fitting is then implemented on the selected contour to obtain ellipse parameters. The ellipse region is cropped using the minimum bounding rectangle, followed by an affine transformation to adjust the ellipse into a perfect circle, which is then scaled to a fixed size. The transformed region is subsequently converted into a grayscale image and is binarized. The process of affine transformation correction is illustrated in Fig. 8.

Fig. 7

Schematic diagram of affine transformation.

Fig. 8

Process of Affine transformation correction.

As shown in Fig. 8, to extract the image after affine transformation, a series of preprocessing steps are first applied (detailed in Sect. 4), including gray scale processing, Gaussian filtering, and image binarization. These steps enhance the continuity of the image edges. Subsequently, Canny edge detection is used to extract the contours of the image after the affine transformation. The contours are then traversed to locate the isosceles triangle within the image. The direction from the triangle’s vertex to the midpoint of the base is taken as the positive direction, and the relationship between the triangle’s direction and the positive direction of the y-axis is determined, as shown in Eq. (1).

$$\alpha =\arctan \frac{{{D_x} - {A_x}}}{{{D_y} - {A_y}}}$$

(1)

Where, α represents the angle between the direction of the triangle and the positive direction of the y-axis, ${D_x},{A_x}$denote the x-axis coordinates of points D and A respectively, and${D_y},{A_y}$denote the y-axis coordinates of points D and A respectively.

To calculate the angle of rotation determined by which the positive direction of the y-axis rotate counterclockwise to align with the direction of the triangle, which represents the degree that the image has been rotated about its midpoint. Next, assess the triangle’s orientation relative to the center point: If the orientation is counterclockwise, the image has not undergone a symmetrical flip. If the orientation is clockwise, the image should be symmetrically flipped about the x-axis. Record both the rotation and symmetry operations. After performing the necessary affine transformation again, the corrected image is obtained. The effects before and after correction are shown in Fig. 9(a) and Fig. 9(b) respectively.

Fig. 9

Comparison of correction effect of the coding marker.

Calibration and rectification of binocular camera

Binocular camera calibration

During the production and assembly of cameras, various errors are introduced, preventing the stereo vision imaging model from achieving ideal results. Therefore, it is essential to calibrate the stereo camera system before image acquisition and use the obtained camera parameters for stereo rectification.

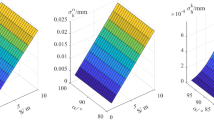
Considering the experimental environment and the precision requirements, the Zhang Zhengyou calibration method¹⁶ was adopted for stereo camera calibration, as shown in Fig. 10. A checkerboard calibration board with a square size of 10 mm was used, and 30 images were captured by varying the position and orientation of the board to calibrate the left and right cameras. The re-projection error of the calibration is shown in Fig. 11, and the spatial poses of the camera and the calibration board are depicted in Fig. 12. After removing images with significant errors and those that didn’t match the actual spatial distances, the average re-projection error was calculated to be 0.09 pixels. In practical applications, a re-projection error within 0.1 pixels is considered excellent; if the error is between 0.1 and 1.0 pixels, the calibration result is acceptable but may require further optimization depending on the specific application needs. Therefore, the calibration results obtained in this study are of high precision, ensuring the accuracy of subsequent stereo matching and depth calculations.

Fig. 10

Calibration procedure of binocular camera.

Fig. 11

Re-projection error of binocular camera calibration.

Fig. 12

Spatial pose of left and right cameras and calibration boards.

The intrinsic and extrinsic parameters obtained from calibration include the left and right camera matrices, distortion matrices, and the rotation and translation matrices of the right camera relative to the left camera. Using these parameters, stereo rectification of the left and right images can be achieved based on the principles of epipolar geometry¹⁷. Currently, the Bouguet al.gorithm is an effective method for stereo rectification. This algorithm decomposes the extrinsic matrix R into two parts${r_l},{r_r}$, applying each part to the rotation of the left and right cameras respectively, ensuring that the two views become coplanar. The specific steps of the Bouguet al.gorithm are as follows:

(1) To make the left and right views coplanar, each view is rotated by half of the angle$R$ . The relationship between the rotation matrices${r_l}$and${r_r}$is then given by Eq. (2):

$$\left\{ {\begin{array}{*{20}{c}} {R={r_l}r_{r}^{{ - 1}}} \\ {{r_l}{r_r}=E} \end{array}} \right.$$

(2)

Where, $E$ is the identity matrix, and after this operation, the two views will reach a coplanar state, as shown in Fig. 13.

Fig. 13

Position relationship between left view and right view after coplane.

As shown in Fig. 13, after performing the above operations, the two images achieve a coplanar state. At this point, the left and right images are rotated along the line connecting their principal points, achieving row alignment. The direction of this line corresponds to the calibrated translation vector T.

(2) The epipoles are the intersection points between the line connecting the origins of the two camera coordinate systems and the image planes. To place the epipoles at infinity (i.e., achieving row alignment), it is essential that the image planes of the two cameras are parallel to the line connecting the camera coordinate system origins. Therefore, a ${R_{rect}}$ (rectification rotation matrix) is constructed to position the epipoles at infinity, and this matrix is decomposed along the three coordinate axes as follows Eq. (3):

$${R_{rect}}=\left[ {\begin{array}{*{20}{c}} {{e_1}^{T}} \\ {{e_2}^{T}} \\ {{e_3}^{T}} \end{array}} \right]$$

(3)

Where ${e_1},{e_2}{\text{ and }}{e_3}$ are the decomposition components of ${R_{rect}}$, which are used to describe the rotation of matrix ${R_{rect}}$ in all directions. The forms are as follows Eq. (4):

$$\begin{gathered} {e_1}=\frac{T}{{\left\| T \right\|}} \hfill \\ {e_2}=\frac{1}{{\sqrt {T_{x}^{2}+T_{y}^{2}} }}{( - {T_y},{T_x},0)^T} \hfill \\ {e_3}={e_1} \times {e_2} \hfill \\ \end{gathered}$$

(4)

Where, ${T_x},{T_y}$ are the components of the translation parameter T in the direction of x and y axes respectively.

Obtain${R_{rect}}$matrix, multiply${R_{rect}}$with ${r_l}$and${r_r}$respectively, then obtain stereoscopic correction rotation matrix(${R_l}$,${R_r}$), and finally make the left and right views meet the requirements of coplanar line alignment, as shown in Eq. (5):

$$\begin{gathered} {R_l}={R_{rect}}{r_l} \hfill \\ {R_r}={R_{rect}}{r_r} \hfill \\ \end{gathered}$$

(5)

Using Eq. (3) to (5), stereo rectification can be completed, achieving coplanarity and row alignment of the left and right views. The rectified left and right images are shown in Fig. 14, where the matching points are located along the collinear epipolar lines.

Fig. 14

Rectification effect of left and right images.

Image preprocessing and center localization of the encoding markers

Image preprocessing

When capturing images of encoding markers using a stereo camera, various factors such as camera characteristics and external environmental conditions often introduce noise and other interferences, which can affect the accuracy of subsequent image matching. Additionally, the initial captured images typically suffer from deficiencies in detail and edge definition, increasing the difficulty of feature matching.

In practical applications, it is found that a single preprocessing method cannot simultaneously address all these issues. Therefore, this study employs a combined preprocessing approach for the captured encoding marker images, as illustrated in Fig. 15.

Fig. 15

Preprocessing process for captured marker images.

Image grayscale conversion

The original images captured by the vehicle-mounted stereo vision system are in color. Processing color images requires substantial computational effort, so in digital image processing, it is common practice to convert color images into grayscale images, which have lower computational demands. There are three main methods for grayscale conversion: the maximum value method, the average value method, and the weighted average method¹⁸.

Given that the human eye is most sensitive to green and least sensitive to blue, the weighted average method takes advantage of this characteristic by applying weighted averages to the R, G, and B components, resulting in a grayscale image that better aligns with human visual perception. This method considers spatial relationships between pixels and can perform local operations on the grayscale values of each pixel, thereby enhancing the image’s edges and textures. In contrast, the maximum value and average value methods tend to lose some details and texture information. The weighted average method is straightforward to implement, requires less computation, and operates relatively quickly, making it suitable for real-time image processing and large-scale image data applications. Therefore, in this project, the weighted average method is used for grayscale conversion.

Smooth filtering

The primary purpose of image smooth filtering is to reduce noise in the image and smooth the edges of objects. Filtering methods include both linear and nonlinear approaches. Linear smoothing filters include mean filtering and Gaussian filtering, while the most common nonlinear filtering algorithms are median filtering and adaptive median filtering. To determine the most suitable filtering method, images are processed using mean filtering, Gaussian filtering, median filtering, and adaptive median filtering, and the comparative results are shown in Fig. 16.

Fig. 16

The comparison of different filtering algorithms.

Based on Fig. 16, it can be observed that the image processed with mean filtering has poor performance in edge and texture areas, resulting in an overall blurry effect. The image processed with Gaussian filtering retains better detail features and effectively reduces Gaussian noise. The image after median filtering appears clearer overall, with good handling of salt-and-pepper noise. However, adaptive median filtering tends to focus on extracting image contours, leaving some residual salt-and-pepper noise in the image. Considering the filtering effects and the fact that Gaussian noise is more prevalent due to varying lighting conditions during image acquisition, the Gaussian filtering algorithm is chosen for denoising the images.

Image binarization with an improved Otsu algorithm

The Otsu algorithm, also known as the maximum between-class variance method, is a grayscale-based method for segmenting objects from the background. The larger the between-class variance, the more distinct the difference between the background and the foreground¹⁹. Therefore, a larger between-class variance indicates a lower probability of segmentation error. The segmentation threshold between the foreground and background is denoted as the optimal threshold T, and the between-class variance is denoted as g. The total average grayscale value of the image is denoted as µ, as shown in Eq. (6):

$$\mu ={\omega _0}{\mu _0}+{\omega _1}{\mu _1}$$

(6)

Where ω₀ represents the foreground pixel proportion; µ₀ represents the foreground average gray level; ω₁ represents the proportion of background pixels; µ₁ represents the background average gray level.

The between-class variance formula is shown in Eq. (7):

$$\begin{gathered} g={\omega _0}{({\mu _0} - \mu )^2}+{\omega _1}{({\mu _1} - \mu )^2} \hfill \\ g={\omega _0} \times {\omega _1} \times {({\mu _0} - {\mu _1})^2} \hfill \\ \end{gathered}$$

(7)

The larger the g value, the lower the probability of segmentation errors. The threshold T that maximizes g is selected as the optimal segmentation threshold.

The traditional Otsu algorithm may encounter boundary effects and has a relatively long computation time when determining the threshold²⁰. Therefore, an improved algorithm is proposed by incorporating image morphology. The most basic morphological operations are erosion and dilation, and common morphological operators with different characteristics are listed in Table 1. The improved algorithm combines morphological operations with block-based Otsu processing. First, the Otsu threshold is used to segment each part of the block-processed image. Then, the image is reassembled based on the original segmentation positions. Finally, digital morphological closing operations are applied to refine the edges and eliminate boundary effects, resulting in the final processed image.

Table 1 Characteristics of morphological operators.

The improved Otsu algorithm can effectively handle images with uneven lighting by applying morphological closing operations, which eliminates boundary effects and prevents the generation of interference points at the boundaries. Figure 17 shows a comparison of the results between the traditional Otsu algorithm and the improved Otsu algorithm.

Fig. 17

Effect comparison of Otsu algorithm before and after improvement.

Edge detection in images

Edges in an image are formed by a set of connected pixels where there is a significant change in grayscale, representing the fundamental features of the image. Edge detection techniques should preserve edge details while removing unnecessary information. Sobel and Laplacian edge detection algorithms detect edges through differentiation, and while they are stable and efficient, they do not fully utilize the gradient direction of the edges, and the resulting image is not binarized. The Canny edge detection algorithm, on the other hand, extracts image edges using hysteresis thresholding with high and low thresholds, resulting in more detailed detection and precise edge localization. To illustrate this more clearly, the binarized images were processed with Sobel, Laplacian, and Canny edge detection methods, as shown in Fig. 18. The original image, after Canny edge detection, produced more detailed edge images with more distinct contours. In contrast, the results from Sobel and Laplacian edge detection were more blurred in terms of details. Therefore, to improve precision, Canny edge detection was chosen for processing.

Fig. 18

Effect comparison of edge detection operators.

Hough transformation

The Hough Transformation²¹ connects edge pixels into a closed region by leveraging global features and converts the curves in the original image into peaks in the parameter space. In the Hough Transformation, the coordinates in the original image must satisfy the following Eq. (8):

$$y=mx+n$$

(8)

Where, m represents the slope of the line and n represents the intercept.

The Hough transformation is applied to the image, and the bold white outline in the image represents the outline of the central ellipse, as depicted in Fig. 19.

Fig. 19

The center circle in a marker obtained by Hough transformation.

Positioning monitoring point center

After performing image preprocessing and affine transformation, the center of the monitoring point can be accurately located. The position of this center can be determined using the six-point circle-fitting method²², as illustrated in Fig. 20(a). Six positioning points (A-F) are located on the imaging edge of the target point. By applying a least-squares circle fitting to these six points, the circle’s center is calculated, which approximates the imaging center, as shown in Fig. 20(b).

Fig. 20

Schematic diagram of the six-point method.

Stereo matching and settlement value calculation

Stereo matching

Stereo matching is a critical step in binocular stereo vision measurement. Its purpose is to identify corresponding points, known as homologous points, in the left and right images captured by the stereo cameras, thereby constructing a disparity map. The depth information of a point can then be calculated based on its disparity. According to the research of Scharstein²³, the stereo matching process can be divided into local matching and global matching, differentiated by whether a global energy optimization function is constructed. Considering factors such as matching speed and accuracy, the Semi-Global Block Matching (SGBM) algorithm was chosen. This algorithm optimizes the dynamic programming method, maintaining low computational complexity while offering high algorithmic robustness. The processes are illustrated in Fig. 21.

Fig. 21

The process of binocular stereo matching.

The main steps of binocular stereo matching are as follows:

Cost computation

The cost computation involves two parts as follows: First, the BT (Birchfield-Tomasi) cost is calculated for the gradient image obtained after preprocessing. Second, the BT cost is calculated for the original image. These two costs are then summed together. Finally, the resulting cost cube is summed within a rectangular window, as shown in Eq. (9).

$$C=C_{{original}}^{{BT}}+C_{{sobel}}^{{BT}}$$

(9)

After traversing all pixels, a three-dimensional cost space (C) of size W×H×D is obtained. Each element in C represents the matching cost value of each pixel in the left image at each disparity within the specified disparity range.

Cost aggregation

Since the matching cost obtained from the initial cost computation is not sufficiently accurate, cost aggregation is required to more precisely reflect the correlation between corresponding points and improve the accuracy of the cost computation. This process involves taking the preliminary cost data C obtained from the cost computation and performing cost aggregation to ultimately obtain the aggregated cost space S.

The path cost for a pixel p along a certain path r is calculated using the method shown in Eq. (10).

$${L_r}(p,d)=C(p,d)+\hbox{min} \left\{ {\begin{array}{*{20}{c}} {{L_r}(p - r,d)} \\ {{L_r}(p - r,d - 1)+{p_1}} \\ {{L_r}(p - r,d+1)+{p_1}} \\ {\mathop {\hbox{min} }\limits_{i} {L_r}(p - r,i)+{p_2}} \end{array}} \right\} - \mathop {\hbox{min} }\limits_{i} {L_r}(p - r,i)$$

(10)

Where, C represents the data item (matching cost); The second term is a smoothing term, which penalizes all pixels q in the vicinity of pixel p; The third item is to ensure that the new path generation value ${L_r}$doesn’t exceed a certain limit, that is${L_r} \leqslant {C_{\hbox{max} }}+{p_2}$; p-r represents adjacent pixels to the left (aggregated from left to right) or to the right (aggregated from right to left) of pixel p; ${L_r}(p - r,d)$ represents the aggregate generation value when parallax is d in path r, and $\mathop {\hbox{min} }\limits_{i} {L_r}(p - r,i)$ represents the minimum value of all costs in path r, as well as p₁ and p₂ are penalty coefficients.

The calculation formula of aggregate generation value S of a pixel is shown in Eq. (11). The path aggregation is shown in Fig. 22:

$$S(p,d)=\sum {{L_r}(p,d)}$$

(11)

Fig. 22

Schematic diagram of path aggregation.

Disparity computation

The disparity computation is performed by traversing all cost values within the disparity range and using the Winner-Takes-All (WTA) algorithm to determine the disparity value with the minimum cost²⁴, as shown in Fig. 23. The calculation is presented in Eq. (12).

$${d^*}=\arg \hbox{min} S(p,d)$$

(12)

Where, ${d^*}$is the optimal disparity value, $\arg \hbox{min}$is the parameter value when solving to minimize the function, and $S(p,d)$is the cost value matrix.

Fig. 23

Winner-takes-all.

Disparity refinement

Common disparity refinement methods include uniqueness verification, sub-pixel fitting, and left-right consistency check²⁵. To achieve higher sub-pixel accuracy, quadratic interpolation is typically used to refine the pixels, thereby realizing sub-pixel fitting. As shown in Fig. 24, let the minimum cost detected by the WTA algorithm for a certain pixel and the corresponding optimal disparity be denoted as (C₀,d), with the preceding and following costs represented by (C₁,d-1) and (C₂,d + 1) respectively. According to Eq. (13), the sub-pixel fitting of the optimal disparity can be performed, thereby obtaining the sub-pixel parallax d_sub.

$${d_{sub}}=d+\frac{{{C_1} - {C_2}}}{{2({C_1}+{C_2} - 2{C_0})}}$$

(13)

Fig. 24

Sub-pixel fitting for disparity refinement.

Evaluation of stereo matching accuracy

After obtaining the disparity map, various metrics such as edge contrast and depth map smoothness can be utilized to analyze and quantitatively assess the performance of the matching algorithm. Edge Contrast Index is employed to measure the intensity of disparity variations in the edge regions of the disparity map or depth map. Edge Contrast Index of a disparity map typically does not have a fixed range; a higher index indicates that the algorithm accurately captures disparity changes in edge regions. A high-quality disparity map should exhibit significant contrast variations at object edges while maintaining smoothness in flat regions. The relevant formulas are shown in Eqs. (14) and (15).

$$G(x,y)=\sqrt {{{\left( {\frac{{\partial D}}{{\partial x}}} \right)}^2}+{{\left( {\frac{{\partial D}}{{\partial y}}} \right)}^2}}$$

(14)

$$EdgeContrastIndex=\tfrac{{\sum\nolimits_{{x,y}} {G(x,y)\cdot E(x,y)} }}{{\sum\nolimits_{{x,y}} {E(x,y)} }}$$

(15)

In the formulas, D represents the pixel value of the disparity map, $\frac{{\partial D}}{{\partial x}}$ denotes the horizontal gradient of the depth map, $\frac{{\partial D}}{{\partial y}}$ represents the vertical gradient of the depth map, and $G(x,y)$indicates the gradient magnitude at position (x, y). $E(x,y)$ represents the value of the detected edge map at position (x, y).

Depth Map Smoothness Index is commonly used to evaluate the degree of variation in depth values within the depth map, overall smoothness, and the handling of noise and details. A smaller smoothness index indicates better smoothness of the depth map, with no significant noise or errors. The corresponding calculation is provided in Eq. (16).

$$SmoothnessIndex=\frac{1}{N}\sum\nolimits_{{i=1}}^{N} {\sum\nolimits_{{j \in \eta (i)}} {\left| {D(i) - D(j)} \right|} }$$

(16)

Where, N represents the total number of pixels in the depth map, $\eta (i)$ denotes the neighborhood set of pixel i, $D(i)$is the depth value of pixel i, and $D(i) - D(j)$ represents the depth difference between pixel i and its neighboring pixel j.

Stereo matching optimization based on multi-level mean filtering using integral images

Multi-level mean filtering using integral images

After the initial disparity map is generated, a multi-level mean filtering process based on integral images is introduced for post-processing the disparity map. The goal is to bring the depth coordinates formed by the target plane points as close to each other as possible, thereby enhancing smoothness and consistency, reducing errors, and producing a higher quality disparity map.

The integral image algorithm is a method used for rapidly computing the sum and the sum of squares of pixel values within an image region²⁶. It creates an integral image lookup table for each image, which is then used during processing to perform quick lookups, enabling linear-time computation of the mean convolution. This makes the execution time of the convolution operation independent of the window size. The detailed explanation of the integral image is as follows:

The integral image I of an image P is defined such that, for a point $(x,y)$ in I, its value I$(x,y)$is equal to the sum of pixel values of all points inside the upper left rectangular area of point $(x,y)$ in P, as shown in Eq. (17)

$$I(x,y)=\sum\limits_{{i \leqslant x,j \leqslant y}} {P(i,j)}$$

(17)

Where $P(i,j)$ represents the pixel value of $(i,j)$ point in the image.

By combining the integral term of the Eq. (17) with the coordinate coefficients, the generalized integral image can be obtained, as shown in Eq. (18).

$$I(x,y)=\sum\limits_{{i \leqslant x,j \leqslant y}} {f(x,y)P(i,j)}$$

(18)

Where $f(x,y)$is a weighting function associated with the coordinate $(x,y)$, representing the weighting of pixel values when calculating an integral image.

Intuitively, an image can be viewed as a rectangle, where the integral value of each pixel within this rectangle is the sum of all elements within the rectangular region extending from the top-left corner of the image to that pixel. As illustrated in Fig. 25(a), the integral value at point $(x,y)$ is the sum of all pixels within the rectangular region (including point $(x,y)$ itself). In practical integral images, it is generally unnecessary to recompute the sum of all elements within the rectangular region for each pixel. Instead, the integral values within the neighborhood are used for quick calculations to enhance computational efficiency. As shown in Fig. 25(b), the integral value at point$(x,y)$ can be computed using the sum of the integral values at points $(x - 1,y)$ and $(x,y - 1)$, subtracting the overlapping region, which is the integral value at point $(x - 1,y - 1)$, and finally adding the pixel value at point $(x,y)$ to obtain the integral value at point $(x,y)$.

Fig. 25

Solving integral value.

Specific Operations are as follows: First, an integral image is constructed, and integral calculations are performed on the entire image, preserving the count of nonzero pixels for each gradient value. A multilevel mean filtering approach is then applied. Initially, a larger window is used for mean filtering to fill large gaps. The window size is then halved, and the integral image is refiltered to fill smaller gaps and cover original values. Filtering ends when the window size is reduced to 3 × 3, resulting in a disparity map that fills gaps without excessive smoothing. Using the characteristics of the integral image to calculate the mean can avoid redundant operations. At the same time, by constantly adjusting the filter window size according to the size of the gap, large gaps are gradually filled, while smaller gaps are refined, preventing the images from overall excessive smoothing and ensuring both effective gap filling and detail preservation.

Comparison analysis for optimization effect

To demonstrate the optimization effect of multi-level mean filtering using integral images on the SGBM stereo matching algorithm, a comparison of the depth images before and after filtering is first conducted, as shown in Fig. 26. It is evident from Fig. 26(b) that the original depth image performs poorly, necessitating optimization of the disparity map to achieve better depth map results. Figure 26(c) shows the results after using OpenCV’s WLS filtering method, which yields a visually smooth depth image with uniform color. However, when compared to the original image in Fig. 26(a), it is clear that the background behind the main target in the original image exhibits varying colors due to differences in distance (depth). After WLS filtering, the colors become uniform, indicating that the distant detail information is lost. In contrast, the depth map optimized using multilevel mean filtering with integral images is shown in Fig. 26(d). The optimized depth map not only restores the depth variations of objects at different distances and recovers detail from the original image lost by depth map without filtering and WLS filtering map, but also smooths areas with significant color changes, ensuring the reasonableness of depth transitions in the target area. This approach avoids unreasonable depth jumps in the map and effectively fills missing gaps, reducing calculation errors.

Fig. 26

Filtering method and comparison before and after filtering.

On the basis of the qualitative analysis above, the disparity and depth maps before and after optimization using the proposed multi-level mean filtering with integral images are quantitatively evaluated using the edge contrast index and depth map smoothness index. The evaluation results are shown in Table 2.

Table 2 Evaluation of stereo matching effect before and after different filtering.

As shown in Table 2, after applying the multilevel mean filtering with integral images, the quality of the depth map was improved significantly. The edge contrast index increased by 34.14 compared to the original disparity map and by 32.55 compared to the WLS filtering, reaching a value of 95.12. This improvement indicates that the multi-level mean filtering algorithm outperforms both the WLS filtering algorithm and the original SGBM-generated disparity map. The optimized depth map more accurately captures disparity variations in edge regions, preserving finer details and rendering object contours more clearly. Additionally, compared to the original depth map, the depth smoothness index decreased by 13.21 after WLS filtering, and by 22.61 after the multi-level mean filtering algorithm, showing a much larger reduction. This suggests that the depth map processed by the multi-level mean filtering algorithm exhibits superior smoothness, effectively reducing noise and errors, presenting a more uniform depth transition. The lower smoothness index also highlights better detail handling, minimizing fluctuations in depth values, thereby enhancing overall image quality and reliability.

D coordinate calculation of the monitoring point’s center

By identifying the monitoring point’s encoded center position in the image (as described in Sect. 4.2), its corresponding location in the depth map can be automatically determined. As shown in Fig. 27, the red marker (indicated by the red arrow) is the automatically located center of the monitoring point. The 3D coordinates of this center can then be calculated using the depth map obtained from stereo matching and the principles of triangulation.

Fig. 27

The position of the center point in marker image identified in the depth map.

Next, the coordinates in the camera coordinate system are transformed into the world coordinate system. Let the external parameters of the camera be the rotation matrix R and the translation vector t, the coordinates in the world coordinate system can be calculated as shown in Eq. (19).

$$\left[ \begin{gathered} \mathop X\nolimits_{W} \hfill \\ \mathop Y\nolimits_{W} \hfill \\ \mathop Z\nolimits_{W} \hfill \\ 1 \hfill \\ \end{gathered} \right]={\left[ {\begin{array}{*{20}{c}} R&t \\ {{0^T}}&1 \end{array}} \right]^{ - 1}}\left[ \begin{gathered} \mathop X\nolimits_{C} \hfill \\ \mathop Y\nolimits_{C} \hfill \\ \mathop Z\nolimits_{C} \hfill \\ 1 \hfill \\ \end{gathered} \right]$$

(19)

In the equation, $({X_W},{Y_W},{Z_W})$ represents the 3D coordinates of the center of the monitoring point’s circular marker in the world coordinate system, and $({X_C},{Y_C},{Z_C})$ represents the 3D coordinates in the camera coordinate system.

Thus, the vertical coordinate y₁ of the monitoring point relative to the ground can be obtained. When conducting a second measurement of the roadbed subsidence, the same process is repeated to obtain y₂, allowing the calculation of the subsidence amount ${y_s}=\left| {{y_1} - {y_2}} \right|$.

Experimental results analysis

Analysis for subgrade settlement detection

Due to the depth camera mode of the utilized camera, depth images of the detected points can be obtained directly, as shown in Fig. 28(a). This depth image retains more detail and edge information, giving the image a sharper appearance. However, this sharpness also introduces noticeable noise and ghosting artifacts, which negatively impact image quality and can adversely affect subsequent experiments. In contrast, the depth image generated from the disparity map after multi-level mean filtering of the integral image, as depicted in Fig. 28(b), exhibits reduced noise and a smoother overall appearance, with more reasonable depth variations in the target areas.

Fig. 28

Comparison of the depth maps obtained by two methods.

To validate the accuracy and practical applicability of the subgrade settlement detection method based on vehicle-mounted binocular stereo vision, a series of simulated experiments were conducted. The experimental setup is as follows: first, the markers are placed as monitoring points. The calibrated and rectified binocular camera is fixed on the experimental vehicle using a gimbal. The vehicle is then driven along the road, during which the binocular camera captures the markers for the first time. After processing the captured data according to the methods described in this paper, the initial Y coordinate data of the detection point is obtained. Next, the monitoring point marker is manually lowered to simulate subgrade settlement. The binocular camera is used to capture the markers again, yielding the Y coordinate data of the second measurement. By analyzing the difference between the two Y values, the settlement values can be determined. In the experiment, the height of the monitoring point marker was manually reduced by 6 cm to simulate a real-world subgrade settlement of 6 cm. Four key frames were extracted from the video data captured before and after the height reduction, and the average Y value was calculated to determine the settlement values. The experimental data is presented in Tables 3 and 4 respectively. Tables 3 and 4 present a comparison of the effects of multi-level mean filtering of integral images and camera depth mode on the measurement results of roadbed settlement, along with an error analysis. Case (a) refers to the measurements obtained using multi-level mean filtering of the integral image, case (b) indicates the results without this filtering, and case (c) reflects the measurements derived from the camera’s built-in depth map. The data in the tables clearly demonstrate that the application of multi-level mean filtering of integral images yields the best results, significantly reducing experimental errors.

Table 3 Comparison of the influence of multilevel mean filtering on the measurement results of the subgrade settlement.

Table 4 Comparison of measurement results errors for the subgrade settlement based on multilevel mean filtering with integral diagram.

The average measurement result of the settlement detected using the vehicle-mounted binocular stereo vision measurement system is 5.8968 cm, compared to the known set settlement value of 6 cm, resulting in a relative error rate of 1.84%. This error is significantly lower than that obtained without using multi-level mean filtering of the integral image, and it also shows a 4.72% reduction in error compared to the coordinates derived from the camera depth mode. These findings indicate that the system demonstrates high precision in quantifying settlement changes.

Verification by comparative analysis

To further validate the measurement performance, a monocular camera detection system based on the pinhole imaging principle was used for comparison under the same conditions. The Y values of height difference in the monitoring points before and after settlement was measured.

Distance measurement of monocular camera relies on the principle of triangular similarity. By measuring the distance between specific points in the image and their real-world size, the depth information of the object in the camera coordinate system can be determined. The conversion relationship is as follows Eq. (20):

$$(\frac{f}{L})^2=\frac{s}{s_1}$$

(20)

Where $\:f$ is the focal length of the camera; $\:{S}_{1}$is the pixel area of the current object; $\:S\:$is the area of the object; $\:L$ is the distance of the object from the camera.

Fig. 29

Geometric diagram of imaging principle.

As shown in Fig. 29, point A represents the camera’s center, AB denotes the camera’s focal length $\:f$, AD represents the previously calculated object distance from the camera $\:L$, BC indicates the height of the object in the image h, and DE corresponds to the actual height of the object H (i.e., the object’s y-axis coordinate). Based on the principle of similar triangles, the following Eq. (21) and Eq. (22) can be established:

$$\frac{{AB}}{{AD}}=\frac{{BC}}{{DE}}$$

(21)

$$\frac{f}{L}=\frac{h}{H}$$

(22)

The depth information $\:L$, obtained from Eq. (22), can be used to calculate the object’s y-axis coordinate in the image based on the principle of similar triangles, thereby determining the object’s three-dimensional coordinates. Both monocular and binocular detection methods were used for multiple sets of simulation experiments, and a representative set of experimental data was selected for comparative analysis. The experimental comparison data are shown in Table 5. The settlement measured by the monocular camera was 5.3823 cm, with a corresponding relative error rate of 10.3%, which is significantly higher than the relative error level of the binocular camera.

Table 5 Result comparison of settlement detection of monocular and binocular camera detection systems.

The comprehensive comparative analysis results from the different experimental stages indicate that the proposed binocular stereo vision-based subgrade settlement detection method not only demonstrates good consistency and stability in practical applications, but also significantly outperforms monocular camera detection methods in terms of measurement accuracy. This strongly supports the superiority and practicality of binocular vision technology in subgrade settlement monitoring, offering a more precise and efficient solution for future nondestructive subgrade detection technology.

Conclusion

This paper addresses the practical need for monitoring the subgrade settlement of Road of ART in coastal tidal flat areas by proposing a nondestructive binocular stereo vision-based subgrade settlement measurement technique. Schneider code were used as the markers and optimized to ensure their recognizability and stability. The accuracy of stereo matching, which is a key step based on binocular stereo vision technology, is ensured by the combined preprocessing of the captured marker images, including image gray scale processing, denoising, edge extraction and enhancement. Furthermore, the integral image multi-level mean filtering algorithm was applied to improve the OpenCV-based SGBM stereo matching algorithm, enhancing disparity map quality, reducing matching errors, and generating high-quality disparity and depth maps, thus providing reliable data for subsequent three-dimensional coordinate calculations. Based on the principle of triangulation, the three-dimensional space coordinates of the monitoring points are calculated, and the dynamic measurement of subgrade settlement is realized. By comparing and analyzing the obtained three-dimensional coordinate data, the accurate quantification of the subgrade settlement of the road of ART in coastal tidal flat area is realized. The experimental results show that the proposed binocular stereo vision-based subgrade settlement measurement system offers high measurement precision and performs stably and reliably in practical applications.

In summary, the binocular stereo vision-based subgrade settlement detection technology proposed in this study is innovative in theory and demonstrates its effectiveness and feasibility in practice. The successful application of this method not only provides a new technical means for monitoring subgrade settlement of the roads in coastal tidal flat area, but also offers a reference solution for similar subgrade monitoring challenges, with broad prospects for promotion and application. Future work could involve further optimization of the algorithms and hardware configurations to enhance system real-time performance and intelligence, thereby meeting more complex monitoring environments and higher measurement requirements.