Legendre based neural networks integrated with heuristic algorithms for the analysis of Lorenz chaotic model: an intelligent and comparative study

Abstract

The optimal control methods for managing Lorenz model are achieved using an innovative intelligent computing framework that integrates artificial neural networks with stochastic unsupervised learning-based optimizers, specifically Firefly (FA) and Archimedes algorithm (AOA). The hyper parameters (weights & biases) of unsupervised neural networks are refined through Legendre polynomials Artificial Neural Networks (LENN) optimized with global search techniques, including FA-AOA collectively referred to as LENN-FA-AOA. This design approach is employed to Lorenz model across three (3) different scenarios using various step sizes and input intervals. The study’s findings reveal that to minimize the computational cost to find the solution of nonlinear chaotic systems by intelligence strategies. The absolute errors values from LENN-FA-AOA with reference solution are being ranged from 3.22 × 10⁻⁵ to 3.06 × 10⁻⁷, 4.56 × 10⁻⁵ to 7.27 × 10⁻⁸ and 5.17 × 10⁻⁵ to 2.11 v 10⁻⁷. Data validation through extensive graphical simulations confirms the effectiveness and robustness of the proposed intelligent solver. The LENN-FA-AOA solver is tested under different initial conditions of Lorenz model to assess its reliability, safety, and tolerance. Through this advanced LENN intelligent design framework, an objective/fitness optimization function is developed within a feedforward neural network. The hybrid FA-AOA optimization is also investigated to verify the LENN model accuracy and reliability. Mean square error (MSE) and TIC graphs are constructed to evaluate the proposed method integrity and efficiency.

Introduction

Chaos theory is a field of mathematics that analyze the effect of nonlinear dynamic systems, which are extremely sensitive to their initial conditions. This sensitivity results in dynamics that appear random, a phenomenon known as chaos. Chaotic systems have been studied in various domains such as mathematics, engineering’s (chemical, biological and mechanical), physics, and other sciences due to its non-linear nature. Scientists and engineers have formulated several approaches to understand and control the chaotic dynamics, such as bifurcation theory. These methodologies have been utilized to various systems, like electrical, biological and mechanical. Chaotic systems are a very significant area of research in various domains, with the potential to enhance our understanding of nature and its applications.

Nonlinear differential equations (NLDEs) have become a standard model for representing chaotic systems. Kudryashov¹ explored analytical solutions to the Lorenz system that have been found and further classified all exact solutions. Algaba et al.² used Poincare sections to study the global connections developed by the subcritical Hopf bifurcation in the Lorenz system. Barrio and Serrano³ conducted a theoretical and numerical investigation of the conventional Lorenz model, identifying the region where each positive semi-orbit converges to equilibrium and establishing constraints for the chaotic zone. Wu and Zhang⁴ characterized all rational integrals and Darboux polynomials for Lorenz systems. Algaba et al.⁵ conducted numerical analysis to find bifurcations in the Lorenz system. Eusebius Doedel et al. illustrated preturbulence in the three-dimensional space of the Lorenz system⁶. The Krishnan et al.⁷ utilized the laplace homotopy method (LHM) to determine the solution of Lorenz differential equations (LDEs). Klöwer et al.⁸ found that non-periodic simulations utilizing deterministic finite-precision result in periodic orbits.

The theory of nonlinear systems can be applied to solution of problems in various fields, including economics, astronomy, nerve physiology, chemistry, heartbeat control, cryptography, electronic circuits, and many others. Most systems in the modern world are by nature nonlinear^9,10. Furthermore, many researchers have been interested in nonlinear oscillations because most vibration problems are nonlinear. Thus, the nonlinear differential equations (NLDEs) were very useful in understanding scientific and engineering problems, which often take the form of nonlinear types. The significance of mathematical computations was emphasized in numerous research studies and literature works that deal with NLDEs that arise in a variety of scientific and engineering fields¹¹. While a large number of NLDEs can be numerically studied, very few of them can be solved directly. Several approximation schemes have been utilized in existing literature to investigate the correlation between the frequency and amplitude of the nonlinear oscillators (NOSs) such as Homotopy perturbation technique^12,13, Variational iteration method¹⁴, energy balance approach and others^15,16, Akbari Ganji method¹⁷, Adomain decomposition technique¹⁸ and many others.

In recent hot area of research, there has also been a lot of research on the use of artificial neural networks (ANNs) to solve nonlinear differential equations. Yang et al.¹⁹ proposed physics-informed generative adversarial networks as one data-driven method for handling stochastic differential equations (SDEs) using sparse observations. Raissi²⁰ investigated the application of deep learning methods for solving coupled SDEs. Mattheakis et al.²¹ constructed neural networks based on physics phenomena to analyze the DEs that describe the dynamic behavior of systems. The NN integrates the Hamiltonian formulation utilizing a loss function, which ensures the energy efficiency of the solutions. The predictions made by the network are used to build this loss function in its entirety, no outside data is required. Piscopo et al.²² studied for determining fully differentiable solutions for ordinary, partial (PDEs/ODEs) equations for analytical results. They investigated various network architectures and found that even very small networks achieved remarkable outcomes. Hagge et al.²³ introduced a system capable of estimating unknown functions or variable in iterated differential equations with suitable accuracy and sensitivity analysis for equations. This approach training the parameters of ANN for differential equation solvers at every time step, enabling faster backpropagation. Similarly, Mattheakis et al.²⁴ employed an artificial neural network (ANN) to solve nonlinear differential equations while ensuring energy conservation and velocity. They designed a symplectic neural network that adheres to energy conservation principles using the concept ANN. Raissi et al.²⁵ proposed the concept of physics-informed neural networks (PINNs), which are ANN trained to perform supervised learning tasks while complying with the nonlinear partial differential equations (PDEs/ODEs) dictated by physical laws. However, the challenge of addressing the “curse of dimensionality” has posed difficulties in developing algorithms for high-dimensional PDEs/ODEs. To address this, Han and Jentzen²⁶ presented a deep learning (DL) based method for solving high-dimensional PDEs/ODEs. Their approach involves transforming PDEs into stochastic differential equations (SDEs) and using neural networks to approximate the gradient of unknown solutions, a method comparable to deep reinforcement learning where the gradient acts as the policy function. In recent years, swarm intelligence (SI) has emerged as a popular method for solving optimization problems. Buhl et al.²⁷ highlighted how agents in SI interact with one another and their environment. Additionally, research by Blum and Li²⁸ demonstrated that many machine learning algorithms draw inspiration from the collective behavior of natural systems, such as ant colonies, animal herds, and bird flocks. The firefly algorithm (FA) is a global algorithm developed by Yang and Karamanoglu²⁹ that was inspired by the bioluminescent communication and flickering motion of fireflies. Yang³⁰ created the Firefly Algorithm based on these concepts, fireflies are unisexual, meaning that they become attracted to one another independent of sex, and the strength of this attraction is directly correlated with the brightness of each firefly’s lights. However, the attraction reduces as the two fireflies get farther apart. When two fireflies are equally bright, they will fly in opposing directions. Note that the firefly intensity should correspond to the objective function of the task. Because of their attraction, fireflies can divide into smaller groups, and each group eventually settles on a single optimum solution. This feature, according to Apostolopoulos and Vlachos³¹, makes the Firefly Algorithm especially helpful for optimization challenges. The mathematical and logical processes that make up an algorithm must be as simple as feasible in the field of applied mathematics. Due to its natural simplicity, FA behavior is ideally suitable for the solution of continuous mathematical functions. Based on statistical analyses utilizing simple stochastic test functions³², FA outperforms other widely used algorithms, gaining plaudits for its effectiveness. To solve optimization problems in complicated systems³³, researchers have employed the FA technique.

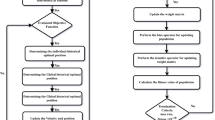
The traditional approach fails to find solutions for nonlinear systems. To address this issue, a more effective method is needed. In this research, we use the Legendre polynomial as an activation function to handle nonlinearity and achieve an optimal solution for the Lorenz model.The modelling and prediction of intricate patterns that would be challenging to investigate using traditional methods, is made possible by ANNs ability to capture the complicated relationships and nonlinearity found in these problems. The ability of artificial neural networks (ANNs) to capture complicated nonlinear interactions within a data set inspired them to tackle the challenges of nonlinear oscillator modelling. In this paper, we use LENN-FA-AOA to optimize parameters, improve accuracy and speed up simulations for nonlinear oscillators. This study aims to investigate how the accuracy of ANN models can be enhanced by combining the heuristic algorithms. The design methodology represents in Fig. 1.

Fig. 1

Design Methodology of the proposed LENN-FA-AOA.

Key features of this study include

• Application of the LENN-FA-AOA approach to analyze the chaotic Lorenz model.

• Reliable combined outcomes from FA-AOA and the Adams numerical method as a reference solution indicate the proposed approach accuracy.

• Validation of the LENN-FA-AOA model statistical performance across multiple runs for nonlinear dynamics using various statistical metrics.

• Comparison with reference solutions for Lorenz model shows that the LENN-FA-AOA results are accurate, stable, precise, and convergent.

• Further validation of the LENN-FA-AOA model performance is provided by quantitative metrics, including mean square error (MSE) and Theil’s inequality coefficient (TIC). The use of LENN offers a logical sequence of solutions across the entire training and learning region, making the proposed stochastic intelligent computational solver efficient and stable.

Problem formulation

The non-linear chaotic system consists of three nonlinear differential equations that characterize the behavior of a dynamical system. The system of nonlinear Lorenz equation expressed as follow³⁴:

$$\begin{array}{*{20}c} {\frac{dx}{{dt}} = \rho \left( {y\left( t \right) - x\left( t \right)} \right)} \\ {\frac{dy}{{dt}} = \sigma x\left( t \right) - y\left( t \right) - x\left( t \right)z\left( t \right)} \\ {\frac{dz}{{dt}} = x\left( t \right)y\left( t \right) - Rz\left( t \right)} \\ {t \in \left[ {0,T} \right]} \\ \end{array}$$

(1)

where t represents time and T denotes the final value of time and initial conditions are given as,

$$x\left(0\right)={a}_{1}, y\left(0\right)={a}_{2},z\left(0\right)={a}_{3}$$

In this given Lorenz model, the variables x(t), y(t) and z(t) are considered as three-dimensional coordinates. The dynamic of the chaotic system is analyze using these parameters, $\rho ,\sigma$ and R, which demonstrate the intensity of non-linear interactions across the variables.

Methodology: Legendre neural network

There are two stages to the suggested approach for resolving the governing mathematical model of Lorenz differential equation. The initial stage involves designing Legendre neural networks (LeNN) based on polynomials. The second phase demonstrate the optimizing unknown weights in the LeNN structure using the built network to determine the fitness value in an unsupervised manner.

Design of Le-NN model

The architecture of a single-layer Legendre Neural Network (LeNN), which is made up of a functional expansion block based on Legendre polynomials as well as an input and one output layer. To eliminate the hidden layer, the input pattern is transformed to a higher dimension using Legendre polynomials³⁵. They are orthogonal across [− 1, 1] and belong to the set of orthogonal polynomials. The first ten Legendre polynomials are listed in Table 1.

Table 1 Legendre polynomials’.

To construct high-order Legendre polynomials, use the recursive formula given Eq. (2):

$${L}_{n+1}\left(\xi \right)=\frac{1}{n+1}\left[\left(2n+1\right)\xi {L}_{n}\left(\xi \right)-{nL}_{n-1}\left(\xi \right)\right].$$

(2)

The problem’s mathematical model is represented by the series solution, which includes input, hidden, and output layers.

The solution $f(\xi )$ and its higher derivatives can be expressed as Eqs. (3), (4), (5), (6), (7).

$$\widehat{f}\left(t\right)=\sum_{p=1}^{q}{\phi }_{p}L\left({\omega }_{p}t+{\beta }_{p}\right),$$

(3)

$${\widehat{f}}{\prime}\left(t\right)=\sum_{p=1}^{q}{\phi }_{p}{L}{\prime}\left({\omega }_{p}t+{\beta }_{p}\right),$$

(4)

$${\widehat{f}}^{{\prime}{\prime}}\left(t\right)=\sum_{p=1}^{q}{\phi }_{p}{L}{\prime}{\prime}\left({\omega }_{p}t+{\beta }_{p}\right),$$

(5)

$${\widehat{f}}^{{\prime}{\prime}{\prime}}\left(t\right)=\sum_{p=1}^{q}{\phi }_{p}{L}{\prime}{\prime}{\prime}\left({\omega }_{p}t+{\beta }_{p}\right),$$

(6)

$${\widehat{f}}^{iv}\left(t\right)=\sum_{p=1}^{q}{\phi }_{p}{L}^{iv}\left({\omega }_{p}t+{\beta }_{p}\right).$$

(7)

$\phi =\left[{\phi }_{1},{\phi }_{2},{\phi }_{3},\dots {\phi }_{n}\right],\omega =\left[{\omega }_{1},{\omega }_{2},{\omega }_{3},\dots {\omega }_{n}\right]$ and $\beta =\left[{\beta }_{1},{\beta }_{2},{\beta }_{3},\dots {\beta }_{n}\right]$ are represented the real-valued vectors and bounded. Where L denotes the Legendre polynomials, n represents the order of polynomial and p demonstrates the number of neurons in the proposed structure. Table 1 presents the formulation of Legendre polynomials.

LENN based fitness function

The fitness function is designed for the proposed problem with initial conditions in term of mean square error (MSE) are given in Eq. (8).

$$E={e}_{1}+{e}_{2}+{e}_{3}+{e}_{4}$$

(8)

The fitness functions for the non-linear Lorenz model are in Eqs. (9), (10), (11), (12),

$${e}_{1}=\frac{1}{Q}\sum_{P=1}^{Q}{(\frac{d\widehat{x}}{dt}-(\rho \widehat{y}\left(t\right)+\widehat{x}\left(t\right)))}^{2}$$

(9)

$${e}_{2}=\frac{1}{Q}{\sum_{p=1}^{Q} (\frac{d\widehat{y}}{dt}-\sigma \widehat{x}\left(t\right)+\widehat{y}\left(t\right)+\widehat{x}\left(t\right)\widehat{z}\left(t\right))}^{2}$$

(10)

$${e}_{3}=\frac{1}{Q}{\sum_{p=1}^{Q} (\frac{d\widehat{z}}{dt}-\widehat{x}\left(t\right)\widehat{y}\left(t\right)+R\widehat{z}(t)}^{2}$$

(11)

$${e}_{4}=\frac{1}{3}({x\left(u\right)-a)}^{2}+{y\left(v\right)-b)}^{2}+{z\left(w\right)-c)}^{2}$$

(12)

The purpose of developing fitness functions for Lorenz attractor analysis is to find weights in the LENN structure that minimize error. The proposed technique accurately approximates the exact solution for the given problem when the fitness function value approaches zero.

Meta‑heuristic optimization algorithms

Heuristic schemes have played a crucial role in handling a broad variety of optimization problems, both unconstrained and constrained, across diverse engineering fields. These schemes were developed to provide approximate/optimal solutions to problems that typical optimization approaches cannot solve due to the difficulty or nonlinearity of the function involved. In the past years, researchers have designed various heuristics algorithms, with unique methodology. Several algorithms have made major contributions to engineering, including genetic algorithm GA, PSO, FA, WCA, GGO^36,37, ABC, and many others.

Firefly algorithm

Fireflies (FA) are bioluminescent insects emitting light from their abdomen without ultraviolet frequencies. They use this light to attract mates, lure prey, and warn predators, aiding in protection. The attraction of firefly $j$ to firefly i is determined by two factors: the firefly brightness $i$ and the distance across firefly $j$ and firefly $i$, as shown in Eq. (13).

$$I\left(r\right)=\frac{{I}_{s}}{{r}^{2}}$$

(13)

For n fireflies, ${x}_{i}$ represents each firefly’s solution, with brightness I determined by the objective function $f({x}_{i})$, reflecting its fitness value

$${I}_{i}=f({z}_{i})$$

(14)

Fireflies reduced brightness are attracted to brighter ones, each having a unique attraction rating $\beta$, which varies with distance, as defined by the Eq. (15).

$$\beta \left(r\right)={\beta }_{0}{e}^{{{-\gamma }{r}^{2}}}$$

(15)

where ${\beta }_{0}$ indicates the initial attraction value of a firefly at $r=0$, and $\gamma$ is the coefficient of absorption of light in the medium that surrounds it. The following equation to analyze how a firefly $(i)$ at position ${z}_{i}$ transitions to a brighter firefly $(j)$ at position ${z}_{j}$.

$${z}_{i}\left(t+1\right)={z}_{i}\left(t\right)+{\beta }_{0}{e}^{{{-\gamma }{r}^{2}}}\left({z}_{i}-{z}_{j}\right)+\alpha {\epsilon }_{i}$$

(16)

where ${\beta }_{0}{e}^{{{-\gamma }{r}^{2}}}$ denotes the attraction of firefly ${z}_{j}$ and $\alpha {\epsilon }_{i}$ indicates the random parameters. When ${\beta }_{0}=0$, the movement becomes a random process. The algorithm relocates the firefly if the new position has higher attractiveness; otherwise, it stays put. The termination condition for the firefly algorithm can be based on iterations or fitness values. The equation for the randomized movement of the brightest firefly is in Eq. (17).

$${z}_{i}\left(t+1\right)={z}_{i}\left(t\right)+\alpha {\epsilon }_{i}$$

(17)

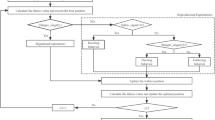
Archimedes optimization algorithm

Hashim et al.³⁸ proposed the new Archimedes Optimization Algorithm (AOA) that, inspired by Archimedes’ principles of buoyancy and floating bodies. The heuristic algorithm combines local search and global exploration to refine potential solutions based on their fitness values^39,40. By simulating buoyancy, it assigns higher weights to more effective solutions, enhancing optimization efficiency. The proposed optimization algorithm continuously improves potential solutions through the combination of local search techniques such as gradient descent or global exploration approach like crossover. This technique aims to find a balance across exploitation and exploration, utilizing both local and global knowledge to rapidly identify optimal or nearly perfect solutions. The Archimedes method has successfully solved optimization problems in various fields, particularly in engineering, data analysis, and logistics. This study aims to evaluate the effectiveness of the Archimedes optimization approach for a specific optimization problem. We aim to analyze its efficacy, advantages, and challenges, and compare it to other meta-heuristic methods. Our study aims to contribute to the understanding of optimization strategies and their applications. Suppose there are multiple objects, each attempting to reach a state of equilibrium. The acceleration of submerged things varies based on their density and volume. If the buoyant force ${F}_{b}$ and weight ${W}_{0}$ are equal, the object is in equilibrium.

$${F}_{b}={W}_{0}$$

(18)

$${P}_{b}{\nu }_{b}{a}_{b}={P}_{0}{\nu }_{0}{a}_{0}$$

(19)

In the equations above, subscripts $b$ and $o$ represent fluid and submerged items. $P$ indicates the density, $a$ denotes the gravity/acceleration, and $v$ is the volume. If the item is influenced by another force, like a collision with a neighboring object $r$, the equilibrium state will change that represents in Eqs. (20), (21).

$${F}_{b}-{W}_{r}={W}_{0}$$

(20)

$${P}_{b}{\nu }_{b}{a}_{b}-{P}_{r}{\nu }_{r}{a}_{r}={P}_{0}{\nu }_{0}{a}_{0}$$

(21)

The AOA technique randomly populates the search space by random selected volumes, accelerations, and densities. After evaluating the initial population’s fitness, AOA iteratively updates each item’s density, volume, and speed until the termination condition is met, determining new locations based on these properties. Here is a mathematical description of the proposed algorithm phases.

$${O}_{j}=L{B}_{J}+{rand}^{*}\left(U{B}_{J}-L{B}_{J}\right) , j=\text{1,2},3, \dots , \dots M$$

(22)

where ${O}_{j}$ denotes the ${j}^{th}$ object between N total items. $L{B}_{J}$ and $U{B}_{J}$ indicate the lower and upper limitation of the search space. Initializes volume and density for every ${j}^{th}$ item using

$${den}_{j}=rand , {vol}_{j}=rand$$

(23)

rand is a D-dimensional vector that creates random numbers between 0 and 1. Initialize the acceleration of the ${j}^{th}$ item using Eq. (24).

$${acc}_{j}=L{B}_{J}+{rand}^{*}\left(U{B}_{J}-L{B}_{J}\right) , j=\text{1,2},3, \dots , \dots M$$

(24)

Evaluate the initial population and select the item with the higher fitness value. Specify the order of ${x}_{best} ,{den}_{best}, {vol}_{best}, and {accel}_{best}$. The density and volume of item $J$ are adjusted for iteration $t+1$ using the following Eqs. (25), (26):

$${den}_{j}^{t+1}={den}_{j}^{t}+{rand}^{*}({den}_{best}-{den}_{j}^{t})$$

(25)

$${vol}_{j}^{t+1}={vol}_{j}^{t}+{rand}^{*}({vol}_{best}-{vol}_{j}^{t})$$

(26)

The terms ${vol}_{best}$ and ${den}_{best}$ refer to the volume and density of the best item identified. The $rand$ variable indicates a uniformly distributed random number. Objects collide at first, but eventually strive for equilibrium. The proposed AOA algorithm uses the transfer operator (TF) to move the search from exploration to exploitation. The transfer operator transforms search behaviour, enhancing convergence to optimal solutions.

$${T}_{F}=exp\left(\frac{t-{t}_{max}}{{t}_{max}}\right)$$

(27)

In this case, the transfer ${T}_{F}$ increases eventually unless it reaches 1. The variables $t$ and ${t}_{max}$ indicate the iteration and maximum number, respectively. Furthermore, the density decreasing parameter d helps balance across the global and local searches. Equation (11) shows a decrease over time.

$${d}^{t+1}=exp\left[\left(\frac{t-{t}_{max}}{{t}_{max}}\right)-\frac{t}{{t}_{max}}\right]$$

(28)

The algorithm can converge to an already determined promising region when the value of ${d}^{t+1}$ reduces over time. A collision across objects is indicated by a transfer operator TF of 0.5 or less. To update an object’s acceleration for iteration t + 1, a random material $mr$ is selected and a specific technique in Eq. (29).

$${acc}_{j}^{t+1}=\frac{{den}_{mr}+{vol}_{mr}{acc}_{mr}}{{den}_{j}^{t+1}{vol}_{j}^{t+1}}$$

(29)

where ${den}_{mr},{vol}_{mr}, and {acc}_{mr}$ indicate the density, volume and acceleration of the random material. The TF value greater than 0.5 implies no collision across items. In that case, the item’s acceleration is adjusted for the next iteration (t + 1) utilizing a specific technique or formula.

$${acc}_{j}^{t+1}=\frac{{den}_{best}+{vol}_{best}{acc}_{best}}{{den}_{j}^{t+1}{vol}_{j}^{t+1}}$$

(30)

To determine the percentage of change, divide the acceleration by a reference value.

$${acc}_{j-norm}^{t+1}=u\left(\frac{{acc}_{j}^{t+1}-\text{min}(acc)}{\text{max}\left(acc\right)-\text{min}(acc)}\right)+l$$

(31)

The normalization ranges (u and l) are set at 0.9 and 0.1. Where ${acc}_{j-norm}^{t+1}$ specifies the percentage of each agent’s step change. If an object is placed distant from the global optimum, it will receive a greater acceleration value, showing it is in the exploration phase. If the item is close to the global optimum, it will receive a smaller acceleration value, demonstrating it is in the exploitation phase. This change from exploration to exploitation illustrates the way the search process evolves. When TF is below or equal to 0.5, it represents the exploration phase. The location of the ${j}^{th}$ item for the next iteration $(t+1)$ is computed utilizing the following Eqs. (32), (33).

$${{x}_{j}}^{i+1}={{x}_{j}}^{i}+{C}_{1} . rand . {acc}_{j-norm}^{t+1} .d .({x}_{rand}-{x}_{j}^{t})$$

(32)

When TF exceeds 0.5, showing the exploitation phase, the items update their locations with a constant value of ${C}_{1}$ is equal to zero.

$${{x}_{j}}^{i+1}={x}_{best}^{t}+F . {C}_{2}rand .{ acc}_{j-norm }^{t+1}. d . (T{x}_{best}-{{x}_{j}}^{i+1})$$

(33)

where ${C}_{1}$ is equal to 6, the variable T is increasing over time and is proportional to the transfer operator. Particularly, T can be expressed as $T={C}_{3}{T}_{F}T$, where ${C}_{1}$ indicates a constant value and T continuously increases with time over the range of ${[C}_{3}\times \text{0.3,1}]$. Initially, T selects a percentage from the best location. The parameter G is a flag utilized to change the direction of motion.

$$G= \left\{\begin{array}{c}1, if P\le 0.5\\ -1, if+>0.5\end{array}\right.$$

(34)

Here $P=2rand-{C}_{4}$. We apply the objective function $f$ to evaluate each object and track the optimal solution identified so far.

Performance indices

In this section, we presented the statistical technique for MSE and TIC to the nonlinear Lorenz model. The mathematical indices consist of MSE and TIC are demonstrated as given,

$$\left[\begin{array}{c}{MSE}_{x}\\ {MSE}_{y}\\ {MSE}_{z}\end{array}\right]=\left[\begin{array}{c}\sum_{\text{p}=1}^{q}{({x}_{p}-{\widehat{x}}_{p})}^{2}\\ \sum_{\text{p}=1}^{q}{({y}_{p}-{\widehat{y}}_{p})}^{2}\\ \sum_{\text{p}=1}^{q}{({z}_{p}-{\widehat{z}}_{p})}^{2}\end{array}\right]$$

(35)

$$\left[\begin{array}{c}{TIC}_{x}\\ {TIC}_{y}\\ {TIC}_{z}\end{array}\right]=\left[\begin{array}{c}\frac{\sqrt{\frac{1}{q}\sum_{p=1}^{q}{({x}_{p}-{\widehat{x}}_{p})}^{2}}}{\sqrt{\frac{1}{q}\sum_{p=1}^{q}{\left({x}_{p}\right)}^{2}}+\sqrt{\frac{1}{q}\sum_{p=1}^{q}{\left({\widehat{x}}_{p}\right)}^{2}}}\\ \frac{\sqrt{\frac{1}{q}\sum_{p=1}^{q}{({y}_{p}-{\widehat{y}}_{p})}^{2}}}{\sqrt{\frac{1}{q}\sum_{p=1}^{q}{\left({x}_{p}\right)}^{2}}+\sqrt{\frac{1}{q}\sum_{p=1}^{q}{\left({\widehat{x}}_{p}\right)}^{2}}}\\ \frac{\sqrt{\frac{1}{q}\sum_{p=1}^{q}{({z}_{p}-{\widehat{z}}_{p})}^{2}}}{\sqrt{\frac{1}{q}\sum_{p=1}^{q}{\left({x}_{p}\right)}^{2}}+\sqrt{\frac{1}{q}\sum_{p=1}^{q}{\left({\widehat{x}}_{p}\right)}^{2}}}\end{array}\right]$$

(37)

Result and discussion

Traditional methods for solving the Lorenz differential equations, such as analytical and numerical often face several limitations. These approaches require small time steps to maintain stability and accuracy, making them computationally intensive and time-consuming, especially for highly sensitive chaotic systems like the Lorenz equations. Furthermore, traditional methods may struggle to capture long-term dynamics due to the nonlinear chaotic systems of these differential equations, which can lead to cumulative errors that grow over time, distorting predictions. Intelligent based approaches especially physics informed machine learning to handle these issues by learning the dynamics more efficiently and generalizing across different scenarios.

This section presents a detailed discussion of the Lorenz model results. Statistical metrics used the LENNs based results to validate the reliability and suitability of the proposed approach. The suggested findings for addressing the Lorenz model with LENNs-FA-AOA are displayed through relevant graphical and numerical representations to assess convergence and accuracy. The feed-forward LENN variables for 10 neurons are determined by applying FA and AOA coding across multiple runs in the Lorenz model. We are tested the proposed LENN-FA-AOA intelligent method for three (03) distinct scenarios. The fitness/ error function are evaluated through one hundred cycles to check the reliability convergence; the best values of each runs are presented in Fig. 2 for each scenario.

Fig. 2

Convergence analysis of fitness function for three different scenarios with 10 neurons of LENN-FA-AOA.

Figures 3, 4, 5 illustrates the optimal LENN parameters ${[w}_{x}, {w}_{y},{w}_{z},{\beta }_{x},{\beta }_{y},{\beta }_{z},{\phi }_{x},{\phi }_{y},{\phi }_{z}]$ generated by FA-AOA within the range − 10 to 10. All of which are used in the fitness value to represent quantitative measurements for $x\left(t\right), y\left(t\right)\text{and} z\left(t\right)$ among ten neurons to generate the outcomes of the Lorenz model. Figures 6, 7, 8 present the graphical representations of reference solution that obtained from Adam numerical approach and best and mean results based on LENN-FA-AOA across 100 independent runs, incorporating 10 neurons.

Fig. 3

Optimized hyper parameters of LENN through FA-AOA for scenario 1.

Fig. 4

Optimized hyper parameters of LENN through FA-AOA for scenario 2.

Fig. 5

Optimized hyper parameters of LENN through FA-AOA for scenario 3.

Fig. 6

Comparative analysis between the reference and LENN-FA-AOA solutions for scenario 1.

Fig. 7

Comparative analysis between the reference and LENN-FA-AOA solutions for scenario 2.

Fig. 8

Comparative analysis between the reference and LENN-FA-AOA solutions for scenario 3.

Tables 2, 3, 4 provide absolute error (AE) that compares reference results with LENN-FA-AOA for $x\left(t\right), y\left(t\right)\text{ and} z(t)$. In scenario 1, 2 and 3 the initial condition and constant of the Lorenz model are $\left[\rho =0.1, \sigma =0.2, R=-0.3,x\left(0\right)=0.5, y\left(0\right)=0.5, z\left(0\right)=0.5 \right],\left[\rho =-0.4, \sigma =0.2, R=0.3,x\left(0\right)=0.4, y\left(0\right)=0.4, z\left(0\right)=0.4\right]$ and $\left[\rho =-0.4, \sigma =0.2, R=0.3,x\left(0\right)=0.3, y\left(0\right)=0.3, z\left(0\right)=0.3\right]$. In scenario 1, the AE values are suitable for all class of model $(x\left(t\right), y\left(t\right) \text{and} z(t))$ range between $3.22\times 1 {0}^{-5}$ to $3.97\times 1 {0}^{-6}$, $2.47\times 1 {0}^{-5}$ to $3.06\times 1 {0}^{-7}$ and $4.24\times 1 {0}^{-5}$ to $6.82\times 1 {0}^{-7}$. The AE values for scenario 2 are ranging between $1.26\times 1 {0}^{-5}$ to $7.27\times 1 {0}^{-7}$, $1.26\times 1 {0}^{-5}$ to $7.27\times 1 {0}^{-8}$ and $4.56\times 1 {0}^{-5}$ to $1.04\times 1 {0}^{-6}$. The AE are ranging between $1.75\times 1 {0}^{-5}$ to $2.11\times 1 {0}^{-7}$, $5.17\times 1{0}^{-5}$ to $2.59\times 1 {0}^{-6}$ and $3.83\times 1 {0}^{-5}$ to $4.63\times 1 {0}^{-7}$ for Lorenz model scenario 3. The results obtained from LENN-FA-AOA that showed the proposed approach is convergence and efficient (Figs. 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26).

Table 2 Comparative analysis with absolute error of $x\left(t\right), y\left(t\right)\text{and} z(t)$ between reference and LENN-FA-AOA solution for scenario 1.

Table 3 Comparative analysis with absolute error of $x\left(t\right), y\left(t\right)\text{and} z(t)$ between reference and LENN-FA-AOA solution for scenario 2.

Table 4 Comparative analysis with absolute error of $x\left(t\right), y\left(t\right)\text{and} z(t)$ between reference and LENN-FA-AOA solution for scenario 3.

Fig. 9

Convergence analysis of MSE for scenarios 1 with 10 neurons of LENN-FA-AOA.

Fig. 10

Convergence analysis of TIC for scenarios 1 with 10 neurons of LENN-FA-AOA.

Fig. 11

Convergence value of MSE for $x(t), y(t) \text{and} z(t)$ with 10 neurons of LENN-FA-AOA of scenario 1.

Fig. 12

Convergence value of TIC for $x(t), y(t) \text{and} z(t)$ with 10 neurons of LENN-FA-AOA of scenario 1.

Fig. 13

Convergence value of MSE through histogram across multiple runs for $x(t), y(t) \text{and} z(t)$ with 10 neurons of LENN-FA-AOA of scenario 1.

Fig. 14

Convergence value of TIC through histogram across multiple runs for $x(t), y(t) \text{and} z(t)$ with 10 neurons of LENN-FA-AOA of scenario 1.

Fig. 15

Convergence analysis of MSE for scenarios 2 with 10 neurons of LENN-FA-AOA.

Fig. 16

Convergence analysis of TIC for scenarios 2 with 10 neurons of LENN-FA-AOA.

Fig. 17

Convergence value of MSE for $x(t), y(t) \text{and} z(t)$ with 10 neurons of LENN-FA-AOA of scenario 2.

Fig. 18

Convergence value of TIC for $x(t), y(t) \text{and} z(t)$ with 10 neurons of LENN-FA-AOA of scenario 2.

Fig. 19

Convergence value of MSE through histogram across multiple runs for $x(t), y(t) \text{and} z(t)$ with 10 neurons of LENN-FA-AOA of scenario 2.

Fig. 20

Convergence value of TIC through histogram across multiple runs for $x(t), y(t) \text{and} z(t)$ with 10 neurons of LENN-FA-AOA of scenario 2.

Fig. 21

Convergence analysis of MSE for scenarios 3 with 10 neurons of LENN-FA-AOA.

Fig. 22

Convergence analysis of TIC for scenarios 3 with 10 neurons of LENN-FA-AOA.

Fig. 23

Convergence value of MSE for $x(t), y(t) \text{and} z(t)$ with 10 neurons of LENN-FA-AOA of scenario 3.

Fig. 24

Convergence value of TIC for $x(t), y(t) \text{and} z(t)$ with 10 neurons of LENN-FA-AOA of scenario 3.

Fig. 25

Convergence value of MSE through histogram across multiple runs for $x(t), y(t) \text{and} z(t)$ with 10 neurons of LENN-FA-AOA of scenario 3.

Fig. 26

Convergence value of TIC through histogram across multiple runs for $x(t), y(t) \text{and} z(t)$ with 10 neurons of LENN-FA-AOA of scenario 3.

Furthermore, to check the deep understanding of the convergence and efficiency for proposed LENN-FA-AOA methodology to compute mean square error (MSE) and Theil’s inequality coefficient (TIC). Figures 9, 15, 21 show the convergence results of MSE for all model dependent parameters using LENN-FA-AOA. For convergence, MSE values range approximately between $1{0}^{-6}$ and $1{0}^{-9}$ for $x(t)$, $1{0}^{-6}$ and $1{0}^{-9}$ for $y(t)$, $1{0}^{-6}$ and $1{0}^{-9}$ for $z(t)$, respectively. The MSE values across multiple cycles/runs are illustrated in Figs. 11, 17, 23 for different scenarios and the ranging of MSE normal distributions are from $1{0}^{-6}$ to $1{0}^{-7}$ approximately and are represented in Figs. 12, 18, 24 for all scenarios.

Figures 10, 16, 22 show the convergence results of TIC for all model classes using LENN-FA-AOA. For convergence, TIC values range approximately between $1{0}^{-4}$ and $1{0}^{-6}$ for $x(t)$, $1{0}^{-4}$ and $1{0}^{-6}$ for $y(t)$, $1{0}^{-4}$ and $1{0}^{-6}$ for $z(t)$, respectively. The TIC values across multiple cycles/runs are illustrated in Figs. 12, 18, 24 for different scenarios and the ranging of MSE normal distributions are from $1{0}^{-3}$ to $1{0}^{-4}$ approximately and are represented in Figs. 13, 19, 25 for all scenarios. The intelligent unsupervised learning approach LENN-FA-AOA is used to train the weights of LENN through a FA-AOA hybrid scheme, assessing time of execution, generations/iterations, and function counts in the Lorenz model solution using 10 neurons. Figures 14, 20, 26 present the convergence value of TIC using histograms for x(t),y(t) and z(t) with 10 neurons of LENN-FA-AOA for all three scenarios. The statistical analysis was conducted across multiple runs to evaluate the maximum, average, minimum, and standard deviation values, as tabulated in Tables 5, 6, 7, for $x(t), y(t) \text{and} z(t)$ for scenario 1. This analysis provides a comprehensive assessment of the variability and performance trends across different conditions. Furthermore, the optimization of LeNN hyperparameters, specifically the weights and biases, was carried out using various optimizers and comparative evaluation of these optimizers, highlighting their tuning effectiveness, is presented in Table 8.

Table 5 Statistical analysis of absolute error of $x\left(t\right)$ between reference and LENN-FA-AOA solution for scenario 1 across multiple runs.

Table 6 Statistical analysis of absolute error of $y\left(t\right)$ between reference and LENN-FA-AOA solution for scenario 1 across multiple runs.

Table 7 Statistical analysis of absolute error of $z\left(t\right)$ between reference and LENN-FA-AOA solution for scenario 1 across multiple runs.

Table 8 Comparison of different optimizers.

Conclusion

LENN-FA-AOA is an innovative stochastic numerical solution based on a Legendre polynomials artificial neural network, enhanced by heuristic optimization algorithms. This proposed LENN-FA-AOA approach converges quickly and is capable of addressing a wide range of chaotic systems, including linear/nonlinear, singular/nonsingular, and stiff systems. The quantitative effectiveness of LENN-FA-AOA is validated through numerical testing, achieving a high level of precision that confirms the robustness of the proposed mathematical framework. By combining FA optimization hybrid with AOA used for the model predictive accuracy is enhanced, providing an effective tool for analysing the Lorenz model. Utilized neural networks with ten neurons, the proposed LENN-FA-AOA statistical approach efficiently examined the performance of the proposed method. The absolute errors values obtained from LENN-FA-AOA with reference solution ranging from $3.22\times 1 {0}^{-5}$ to $3.06\times 1 {0}^{-7}$, $4.56\times 1 {0}^{-5}$ to $7.27\times 1 {0}^{-8}$ and $5.17\times 1{0}^{-5}$ to $2.11\times 1 {0}^{-7}$ In one hundred independent trials/runs, statistical measures including the absolute error, mean square mean and TIC values further validate the reliability of the LENN-FA-AOA method. The limitation of the proposed approach is reduced prediction accuracy when the chaotic model has a high dimensionality like 5D, 6D and 7D.

Future work

In figure the proposed hybrid algorithm will be used for cyber security analysis based on differential equations. Also, various neuro-evolutionary intelligent computing paradigms will be developed to analyze fractional differential order based Lorenz system. Additionally to be used the quantum algorithms to enhance the accuracy of the Lorenz model.