Abstract
In the research on consensus tracking control for Lower Limb Rehabilitation Robotic Systems (LLRRS), it is crucial to ensure that all state variables of the LLRRS, including initial state, angle, and angular velocity, converge towards a consensus. This paper addresses the motion tracking control issue of LLRRS in scenarios with initial state deviations. Firstly, a dynamic mathematical model of the LLRRS is established, and the target motion trajectory is determined. To tackle the challenges posed by initial state deviation, a closed-loop PD-type accelerated iterative learning controller with initial state learning is designed, utilizing only the output measurements of the system and a variable learning gain factor. The applicability of this controller for achieving consensus tracking control of the LLRRS state variables is verified through mathematical analysis and simulation. Finally, the feasibility and effectiveness of the proposed algorithm are corroborated through experimental prototype testing. The experimental results demonstrate that the maximum tracking error for the hip joint angle of the LLRRS is 7.14°, and the maximum tracking error for the knee joint angle is 5.74°.
Similar content being viewed by others
Introduction
The rising number of patients with lower limb dysfunction is attributed to population aging, as well as the increasing prevalence of cardiovascular and cerebrovascular diseases, spinal cord injuries, traumatic brain injuries, and other diseases1,2. Despite the beneficial effects of traditional rehabilitation treatments in restoring certain functions to a limited extent, these approaches often face challenges related to insufficient training intensity, poor reproducibility, and limited therapeutic efficacy3. Hence, it is crucial to identify a more effective and precise rehabilitation treatment method4. The advent of lower limb rehabilitation robots offers a novel approach to addressing the aforementioned issues5. The system enables precise control and training of lower limb motion function through integration of advanced mechanical structure, sensor technology, motion control system and intelligent algorithm. It is becoming a research focus in the field of rehabilitation medicine6.
With regard to the mechanical structure, Hong et al.7 devised an ankle spring configuration for a lower limb exoskeleton robot, based on foam core sandwich structural composites (FCSC). The structure facilitates enhanced motion assistance through an elastic energy storage and release mechanism, thereby reducing the necessity for additional sensors. Concurrently, Shin et al.8 concentrated on the optimization of the knee joint structure of a lower limb wearable robot, devising a multilink structure incorporating a four-rod and six-rod mechanism. This design not only accurately simulates the natural motion pattern of the human knee joint, but also effectively improves the naturalness of motion assistance and the overall operational efficiency of the system by achieving a predetermined transmission ratio. Furthermore, Song et al.9 examined a compact crank-slider series elastic actuator (CS-SEA) structure. This structure incorporates a crank-slider mechanism with a built-in linear spring pack. The objective of this design is to address the issue of torque assistance in lower limb exoskeletons, while simultaneously achieving highly compliant physical interactions.
In terms of sensor technology, Francelino et al.10 developed an accurate estimation system for human continuous body segment posture and joint angle, which can achieve precise assessment using only two sensors: an accelerometer and a gyroscope. Concurrently, Zhang et al.11 proposed a dynamic adaptive neural network (GA-DANN) algorithm, which ingeniously incorporates the multidimensional attributes of surface electromyographic signals (sEMG) in the time domain, frequency domain, and sample entropy, and optimises the learning rate through genetic algorithms (GA) with the objective of enhancing the precision of lower limb movement intention recognition. Furthermore, Kim et al.12 devised a quantitative assessment methodology based on barometric sensors for real-time monitoring and quantifying the degree of misalignment between the exoskeleton robot and the wearer’s knee joint, improving the accuracy and objectivity of the assessment.
In the context of motion control systems, Xu et al.13 proposed an innovative framework for motion generation that combines dynamic motion primitives and impedance models. The framework has been developed with the objective of enabling the dynamic adjustment of the stiffness characteristics of a lower limb rehabilitation robot by means of real-time analysis of the surface electromyogram signal (sEMG). Meanwhile, Park et al.14 investigated the integration of hybrid control strategies with disturbance observers, real-time switching of controllers through adaptive modelling techniques, and the introduction of filter combinations to enhance the stability of lower limb exoskeleton systems. Moreover, Kenas et al.15 developed a seamless integration of model-free adaptive control, non-singular fast terminal sliding mode control and multilayer perceptron (MLP) neural network to optimise the rehabilitation motion control of a 10-degree-of-freedom lower limb exoskeleton.
With regard to intelligent algorithms, Sharifi et al.16 proposed an advanced control strategy for lower limb exoskeletons. This strategy employs an adaptive central pattern generator to facilitate human-robot interaction and an adaptive disturbance observer to adjust trajectory and tracking control in real time. On the other hand, Tsai et al.17 proposed the Adaptive Self-Organising Fuzzy Sliding Mode Controller (ASOFSMC), based on Pneumatic Artificial Muscle (PAM) 2-degree-of-freedom lower limb rehabilitation robot, with the objective of enhancing the precision of lower limb rehabilitation robot control. Furthermore, Laubscher et al.18 put forth a hybrid control strategy that integrates impedance and sliding mode to facilitate secure human-robot interaction.
However, most of these studies mentioned above did not consider the problem of initial state deviation between the patient and the lower limb rehabilitation robotic system, which has a significant impact on the patient’s rehabilitation outcome during the actual rehabilitation process19. Therefore, it is particularly important to choose a control scheme that can cope with the initial state deviation of the system. In the field of robotic systems, there have been research efforts aimed at solving similar challenges. For example, Liu et al.20 proposed an adaptive iterative learning control based on RBF neural network for hybrid robot trajectory tracking containing random initial error and full state constraints. The time-varying boundary layer error function is constructed, the initial conditions of iterative learning control are relaxed, and the tangential potential Lyapunov function is designed to ensure the state constraints. In addition, in the field of robotics, the application of Reinforcement Learning has become increasingly widespread. Nguyen et al.21 introduces an Off-policy algorithm tailored for spacecraft control systems, which aims to address the convergence issues of the Q-learning algorithm in time-varying linear Discrete-Time Systems under complete dynamic uncertainty. On the other hand, Dao et al.22 proposes both On-Policy and Off-Policy strategies for Bilateral Teleoperators systems characterized by variable time delays and dynamic uncertainties. These two strategies collectively address the conflict between synchronous control issues and optimal control performance for robots in unknown environments. Furthermore, Xue et al.23 presents a data-driven, model-free Inverse Reinforcement Learning algorithm specifically designed to solve the inverse H ∞ control problem in robotic systems. Additionally, Wang et al.24 introduces a model-free, Off-policy reinforcement learning algorithm that aims to tackle the Fully Cooperative consensus problem in nonlinear continuous-time Multiagent Systems. While Reinforcement Learning has found applications in the field of robotics, its learning efficiency still requires improvement (Cai et al.25). Therefore, this paper opts for the Iterative Learning Control algorithm.
Iterative learning control represents a methodology for enhancing the repetitive control performance of a system by leveraging the insights gleaned from past executions, with the objective of optimising the control accuracy and overall performance of the improved system26. Furthermore, Cheng et al.27 designed a variable gain iterative learning control strategy to address the challenges associated with the difficult dynamic modeling of hybrid robotic arms, as well as the issues of slow trajectory tracking and large positional errors encountered by traditional controllers. Further, Ye et al.28 put forth a distributed iterative learning control strategy for non-complete mobile robots, which addresses the issues of unknown control gains and the necessity for a predefined reference trajectory model. Furthermore, Maqsood et al.29 address the uncertainty of human dynamics by dividing the task space, combining adaptive impedance control with iterative trajectory learning, and dynamically adjusting the robot assistance to match the user’s motion. This enables the compensation for unintentional force deviations, thereby achieving stable and effective rehabilitation assistance. It can be seen that iterative learning provides a viable solution to the problem of controlling robotic systems.
Given the potential and feasibility of iterative learning control in enhancing robot system performance, this paper aims to utilize an iterative learning control scheme to address the consensus tracking problem in LLRRS with initial state deviations. The contributions of this paper are as follows:
-
1.
A closed-loop PD-type iterative learning control scheme with initial state learning is designed to effectively solve the motion trajectory tracking control problem of LLRRS in the presence of initial state deviations. This scheme only requires input and output data from the system.
-
2.
The initial state learning method designed by introducing the exponential variable gain factor. It accelerates the convergence speed of the state consistency of the LLRRS under the premise of effective consensus of the system state.
-
3.
Based on prototype experiments with LLRRS, the feasibility and effectiveness of the designed exponential variable gain closed-loop iterative learning control algorithm with initial state learning are verified, further expanding its practical application value.
The following sections of this paper are organized as follows: Firstly, the construction of the lower limb rehabilitation robot system model and the establishment of the target motion trajectory are introduced in details; Then the motion controller based on iterative learning control is designed, verifies its convergence behaviour and conducts simulation analysis; Then the system performance is evaluated through the test of the experimental prototype; Finally, a summary of the entire text is provided, and future research directions are proposed.
Lower limb rehabilitation robotic system model and target motion trajectory
To facilitate the analysis of the motion process of the Lower Limb Rehabilitation Robot System (LLRRS), it is necessary to establish a mathematical model, which is preceded by the following two assumptions:
Assumption 1
The LLRRS operates solely within the sagittal plane.
Assumption 2
The masses of both the thigh (calf) of the LLRRS are concentrated at their respective centers of mass.
Lower limb rehabilitation robotic system model
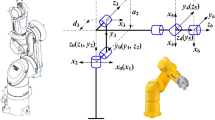
Since the normal gait of human walking is completed alternately by two legs, and the movements of both legs are completely consensus. Therefore, any single leg can be selected for modeling. The simplified model is shown in Fig. 1 below.
where point O is the hip joint, set as the origin of the coordinates; point N is the knee joint; point S is the ankle joint; the angle between the thigh link ON and the vertical line is defined as \({\theta _1}\), while the angle between the extension line of ON and the calf link NS is defined as \({\theta _2}\); l1 denotes the length of the thigh link ON, and l2 denotes the length of the calf link NS; the centre of mass coordinates of the thigh (calf) link are denoted as P(x1,y1) and Q(x2,y2) respectively; the thigh (calf) link masses are m1 and m2 respectively.
The kinetic equations of the LLRRS are derived from the Lagrange Equation30 as follows:
where \(u(t)\) represents the joint moment matrix, \(\theta\) is the lower limb joint angle, \(\dot {\theta }\) is the joint angular velocity, and \(\ddot {\theta }\) is the joint angular acceleration. \(D(\theta )\) is the inertia matrix, specified as:
\(H(\theta ,\dot {\theta })\) is the centrifugal and Coriolis force matrix, specified as:
\(G(\theta )\) is the gravity matrix, specifically:
\({T_d}\) is the system error and perturbation, specifically:
Letting \(A(t,\theta ,\dot {\theta })= - {D^{ - 1}}(\theta )\left[ {H(\theta ,\dot {\theta })\dot {\theta }+G(\theta )+{T_d}} \right]\), then Eq. (1) is written as:
Equation (2) can be further written in state space form, i.e.:
where\(\Phi (t,x(t))=\left[ \begin{gathered} {\dot {\theta }} \hfill \\ A(t,\theta ,\dot {\theta }) \hfill \\ \end{gathered} \right]\),\(M(t)=\left[ \begin{gathered} 0 \hfill \\ {D^{ - 1}}(\theta ) \hfill \\ \end{gathered} \right]\),\(x(t)=\left[ \begin{gathered} \theta \hfill \\ {\dot {\theta }} \hfill \\ \end{gathered} \right]\),\(C=\left[ {\begin{array}{*{20}{c}} 0&I \end{array}} \right]\).
Target motion trajectory of lower limb rehabilitation robot
In this study, normal human gait data are used as the target motion trajectory of the LLRRS. In order to facilitate the subsequent motion control of the LLRRS, the data are now fitted to a continuous function and the second order derivatives of the fitted function are ensured to be continuous. In this paper, a segmented 3rd order polynomial is used for fitting and its second order derivative is set to be:
where F is the function fitting coefficient, h is the fitting step, and \(\kappa\) is the discrete data. One obtains:
Further, due to \(\theta ^{\prime}({t_\kappa }+0)=\theta ^{\prime}({t_\kappa } - 0)\), one gets:
Letting \({d_k}=6\frac{{\theta [{t_\kappa },{t_{\kappa +1}}] - \theta [{t_{\kappa - 1}},{t_\kappa }]}}{{{h_{\kappa - 1}}+{h_\kappa }}}\), \({\alpha _i}=\frac{{{h_{\kappa - 1}}}}{{{h_{\kappa - 1}}+{h_\kappa }}}\), \(\beta =\frac{{{h_\kappa }}}{{{h_{\kappa - 1}}+{h_\kappa }}}\),then Eq. (6) is collapsed as:
The results of the function fitting are as follows:
where, \({\theta _{1fit}}\) and \({\theta _{2fit}}\) represent the motion trajectories of the hip and knee joints, respectively. The function curve is shown in Fig. 2, the red circle represents the data points collected by Real Gait DeLong Whole Body 3D Gait and Motion Analysis System, while the blue solid line represents the fitting function. It can be observed from the figure that the blue solid line and the red circle essentially overlap, which indicates that the fitting function obtained by using the segmented 3rd degree polynomial method has a satisfactory fitting effect.
Remark 1
In Fig. 2, the abscissa represents time, with units in seconds. The ordinate indicates the hip and knee joint angles of normal gait, with units in degrees.
The following error analysis is performed on the fitted function with the expression:
where err is the fitting error and Z is the sampling point.
The results of the function fitting error analysis indicate that the maximum fitting errors of both the hip and knee joints are within 1°, which is a satisfactory fit and thus can be used as the target motion trajectory of LLRRS.
Motion controller design for lower limb rehabilitation robotic system
In actual patient rehabilitation training, the initial state of the LLRRS is frequently shifted due to external disturbances or uncertainties, etc., resulting in the LLRRS being unable to maintain the desired initial state. This deviation may cause the LLRRS to fail to function properly. Therefore, this section aims to design the iterative learning controller with initial state learning for the initial position deviation problem of LLRRS.
Design of a closed-loop PD-type iterative learning controller based on initial state learning
To facilitate the description of the design process of the control algorithm, the following 2 assumptions are made:
Assumption 3
and C in the mathematical model (3) of the LLRRS are bounded; \(I+CM(t)L\) is invertible; and \(\Phi (t,{x_k}(t))\) satisfies the Lipschitz condition.
Assumption 4
There exists an optimal control input \({u_d}(t)\) to the LLRRS, an optimal state \({x_d}(t)\), and a target trajectory \({y_d}(t)\), which is continuous in \(t \in [0,T]\).
The iterative learning algorithm for the LLRRS equations is given by:
where k denotes the k-th iteration learning number of LLRRS.
The output error is:
The input control law uses a closed-loop PD-type iterative learning control algorithm:
where \({e_{k+1}}(t)\) and \({\dot {e}_{k+1}}(t)\) denote the tracking error and its error derivative for the k + 1-th iteration learning of LLRRS, respectively, and K and L are the iterative learning gain matrices to be determined.
The iterative learning control algorithm is also used to iteratively learn the initial state of the LLRRS, and its initial state control law is designed as:
where \({x_k}(0)\) is the initial state of the k-th iteration of the LLRRS and \({e_{k+1}}(0)\) is the initial value of the tracking error of the k + 1-th iteration of the LLRRS.
The control block diagram of LLRRS is shown in Fig. 3, which is mainly composed of two parts: initial value learning module and trajectory tracking module. Initial value learning module: this module learns the initial value deviation according to the initial state, initial deviation and learning rate of LLRRS.The module is capable of dynamically adjusting the initial state in order to reduce the initial deviation of LLRRS. Trajectory tracking module: this module performs estimated tracking learning based on the joint force learned in the previous iteration, the angular deviation in the current cycle, the rate of change of the angular deviation, and the learning rate. This module facilitates the dynamic tracking of the LLRRS trajectory. Following a sufficient number of iterations of learning, the initial state deviation of LLRRS is gradually reduced, thereby ensuring that the motion trajectory of LLRRS is gradually consensus with the target trajectory.
The following is pseudo-code for closed-loop PD-type iterative learning control based on initial learning:
Algorithm 1
Control of the operation of a robot for the rehabilitation of the lower limbs in the presence of an initial state deviation.

The following is an analysis of the convergence behaviour of a closed-loop PD-type iterative learning control based on initial state learning:
Lemma 1 31
Letting \(x(t)\), \(c(t)\) and \(a(t)\) (\(a(t) \geqslant 0\))be real-valued continuous functions on \(t \in [0,T]\). If \(x(t) \leqslant c(t)+\int_{0}^{t} {a(\tau )x(\tau )d\tau }\), then
Lemma 2 32
Assuming on \(t \in [0,T]\) that the operator \(Q:{C_r}[0,T] \to {C_r}[0,T]\) satisfies \(\left\| {Q(x)(t)} \right\| \leqslant M(q+\int_{0}^{t} {\left\| {x(s)} \right\|ds} )\;;\;\left\| {Q(x)(t) - Q(y)(t)} \right\| \leqslant M\int_{0}^{t} {\left\| {x(s) - y(s)} \right\|ds}\), where \(M \geqslant 0,q \geqslant 0\,\forall x,y \in {C_r}[0,T]\), the following conclusions follow:
(a1) \(\forall y \in {C_r}[0,T]\), there exists a unique \(\forall x \in {C_r}[0,T]\) such that
(a2) Define the operator Q to be \(\bar {Q}(y)(t)=Q(x)(t)\), \(\forall y \in {C_r}[0,T]\), where \(\forall x \in {C_r}[0,T]\) is the unique solution of (a1), then there exists a constant of \({M_1}>0\) such that
Lemma 3 33
Letting the sequence of constants \({\left\{ {{b_k}} \right\}_{k \geqslant 0}}({b_k} \geqslant 0)\) converge to zero and the operator Q satisfy \(\left\| {{Q_k}(u)(t)} \right\| \leqslant M({b_k}+\int_{0}^{t} {\left\| {u(s)} \right\|ds} )\), where the constant \(M \geqslant 1\), and the r-dimensional vectors of \({C_r}[0,T]\) take the maximum norm. Letting \(P(t)\) be a matrix of \(r \times r\) dimensional continuous functions, and \(P:{C_r}[0,T] \to {C_r}[0,T]\) be \(P(u)(t)=P(t)u(t)\). If the spectral radius of P is less than 1, then
holds consistently for t.
Theorem 1
If LLRRS (12) satisfies condition \(\rho [{(I+CM(t)L)^{ - 1}}]<1,t \in [0,T]\), then LLRRS in any initial state, one has:
where \({y_d}(t)\) is the target motion trajectory of LLRRS.
Proof
It can be derived from Eq. (12), Eqs. (14) and (15) in the previous section:
Meanwhile, the difference between the k + 1-th state and the k-th state of the LLRRS can be obtained as:
Taking simultaneous paradigms for both sides of the above Eq. (22), we have, according to the aforementioned Lemma 1:
where \(m=\mathop {\sup }\limits_{{t \in [0,T]}} \left\| {M(t)} \right\|\), \(l=\mathop {\sup }\limits_{{t \in [0,T]}} \left\| L \right\|\), \(k=\mathop {\sup }\limits_{{t \in [0,T]}} \left\| K \right\|\), \(n=\mathop {\sup }\limits_{{t \in [0,T]}} \left\| {\dot {M}(t)L} \right\|\), \({n_2}={n_1}+\varphi ml{e^{\varphi T}}+{n_1}\varphi T{e^{\varphi T}}\), \({n_1}=n+mk\).
From the aforementioned Eqs. (12) and (13), it can also be obtained:
Further, from Eqs. (24) and (22), the following equation also holds, viz.:
Letting \(Q(t)={\left[ {I+CM(t)L} \right]^{ - 1}}\) again, the operator can be defined as
Taking paradigms for both ends of Eq. (27) and estimating the operator \({S_{k+1}}\), there are:
where \({H_1}=hc{n_1}+hc\varphi ml+hc\varphi {n_2}T,{H_2}=\hbox{max} (1,{H_1})\), \(h=\mathop {\sup }\limits_{{t \in [0,T]}} \left\| {{{\left[ {I+CM(t)L} \right]}^{ - 1}}} \right\|\), \(c=\mathop {\sup }\limits_{{t \in [0,T]}} \left\| C \right\|\).
Furthermore, assuming \({e_{k+1}}(t), {e_k}(t) \in {C_r}[0,T]\), according to the aforementioned Lemma 2 we have
where \({\bar {S}_{k+1}}\) satisfies \(\left\| {\bar {Q}(y)(t)} \right\| \leqslant {M_1}(q+\int_{0}^{t} {\left\| {y(s)} \right\|ds} )\)
and define \({J_{k+1}}:{C_r}[0,T] \to {C_r}[0,T]\) as
\(\exists {N_2} \geqslant 1\), then we have
Finally, it follows from the previous Lemma 3 that if the spectral radius of \(Q(t)\) is less than 1, i.e., \(\rho [{(I+CM(t)L)^{ - 1}}]<1\), then
This completes the proof of Theorem 1.
Design of exponential variable gain type iterative learning controller based on initial state learning
Although the above proposed closed-loop PD-type iterative learning control algorithm based on initial state learning can effectively realize the trajectory tracking control of the LLRRS hip (knee) joint, its iterative learning efficiency is lower and its convergence speed is slower. The faster convergence speed often indicates that the system is better able to adapt to different initial conditions and environmental changes, and exhibits higher robustness. This is particularly important in systems operating in non-static or changing environments34. To further improve the convergence speed of the LLRRS trajectory tracking error, an exponential variable gain type accelerated iterative learning consensus control scheme based on initial state learning is designed in this subsection.
Based on the closed-loop PD iterative learning control law (Eq. 14), an exponential factor term is added to obtain the exponential variable gain type iterative learning control law for LLRRS, as shown below:
where \(\lambda (t){\text{=}}{e^{\alpha t}}\) and \(\alpha\) is the exponential learning factor with the value range (0,1). Meanwhile, the initial state learning control law based on the aforementioned Eq. (15) is also adjusted to:
The process of analyzing the convergence behaviour of the exponential variable gain type iterative learning control algorithm based on initial state learning is similar to that of the closed-loop PD-type iterative learning control based on initial state learning in previous section, and will not be repeated here. It is finally concluded that if LLRRS Eq. (12) satisfies condition
then LLRRS in any initial state, one has: the actual output converges to the desired objective.
Next, a theoretical proof that an exponential variable gain type iterative learning control algorithm based on initial state learning converges faster than a closed-loop PD type iterative learning control algorithm based on initial state learning is given.
Define
where let \({\rho _{PD}}\) denote the spectral radius of the closed-loop PD type iterative learning control system, and \({\rho _{EXP}}\) represent the spectral radius of the exponential variable gain iterative learning control system.
Theorem 2
It is known that both \({\rho _{PD}}\) and \({\rho _{EXP}}\) are less than 1, If satisfies condition
Then it is shown that the exponential variable gain iterative learning control algorithm of LLRRS converges faster than the closed-loop PD-type iterative learning control algorithm in any initial state.
Proof
Utilizing the scaling method based on matrix norms, it can be obtained:
Given that both \({\rho _{PD}}\) and \({\rho _{EXP}}\) possess inverse matrices, obtain their respective inverses.
Define
Here, according to the properties of matrix norms, one obtains
where \(\left\| {CM(t)L} \right\|>0\), and \(\lambda (t)\; \geqslant 1\) (The equality sign holds if and only if t = 0). It can be obtained: \(H \leqslant 0\).
Finally, one obtains
This completes the proof of Theorem 2.
Design of exponential variable gain type iterative learning controller based on initial state learning
Simulation analysis of closed-loop PD-type iterative learning control based on initial state learning
The target motion trajectory of the LLRRS has been given above. The mathematical model of the LLRRS adopts the aforementioned Eq. (12), with a simulation cycle length of 2 s, a sampling time of 0.01 s, and an initial value of the target motion trajectory:
The initial value of LLRRS is:
The iterative learning control gain matrix is taken:
Calculating the spectral radius \({\rho _{PD}}\), we have
The convergence condition is satisfied.
The tracking iterative control process of the hip and knee joints of the LLRRS is shown in Fig. 4. In the first iterative learning stage (a and e), it can be observed that there exists a significant deviation between the target curve (red dashed line) and the actual curve (blue solid line), which indicates that the hip (knee) joints of the LLRRS fail to track the target trajectory effectively, and that it needs further improvement. In the third iterative learning stage (b and f), although some deviation still exists, this deviation has been significantly reduced relative to the initial learning result, indicating the effectiveness of the iterative learning process and the trend of tracking error decreasing gradually. Subsequently, in the 17th iteration learning stage (c and g) and the 20th iteration learning stage (d and h), the actual curves basically coincide with the target curves, indicating that the hip (knee) joint of the LLRRS has been able to track the target trajectory effectively. In summary, the closed-loop PD-type iterative learning control algorithm with initial state learning shows good results in the LLRRS, successfully solves the initial state deviation problem, and achieves accurate tracking of the motion trajectory.
Remark 2
In Fig. 4, the abscissa represents time, with units in seconds. The ordinate of subplots (a)-(d) indicates the hip joint angle of the LLRRS, and the ordinate of subplots (e)-(h) indicates the knee joint angle of the LLRRS, both with units in degrees.
Remark 3
In Fig. 5, the abscissa represents the number of iterations for the closed-loop PD type iterative learning control of the LLRRS, with units in times. The ordinate indicates the maximum angular error of the hip (knee) joint of the LLRRS, with units in degrees.
As shown in Fig. 5, the maximum angular tracking error of the hip (knee) joint of the LLRRS during iterative learning is shown, where the red line with stars represents the hip joint and the blue line with circles represents the knee joint. From the global perspective, both the red line with stars and the blue line with circles show a decreasing trend, and the blue line with circles decreases faster, which indicates that the closed-loop PD-type iterative learning control algorithm with initial state learning can effectively reduce the angular tracking error of the hip (knee) joints of the LLRRS, and in particular the angular tracking error of the knee joints decreases more significantly. From the local perspective, after 18 iterations of learning, the errors of both knee and hip joints are reduced to lower values, below 0.2°. The variation graph of this maximum error argues the effectiveness of the closed-loop PD-type iterative learning control algorithm with initial state learning and shows that it can effectively control the motion trajectory tracking of the LLRRS.
The 20th iteration learning results, as shown in Fig. 6, demonstrate the LLRRS hip (knee) joint trajectory tracking errors. The red solid line represents the hip joint and the blue solid line represents the knee joint. It can be observed that the tracking error of the hip joint is maintained within 0.15°, while the error of the knee joint is controlled within 0.05°, both of which are relatively small. The effectiveness of the closed-loop PD-type iterative learning control algorithm with initial state learning in realising LLRRS motion trajectory tracking is thus verified from the error perspective.
Remark 4
In Fig. 6, the abscissa represents time, with units in seconds. The ordinate indicates the angular error of the hip (knee) joint of the LLRRS under the 20th iteration of the closed-loop PD type iterative learning control, with units in degrees.
According to the 20th iteration learning results shown in Fig. 7, the joint angular velocities and angular velocity errors are demonstrated as described below: in (a), the red dashed line represents the target angular velocity of the hip joint, and the blue solid line represents the actual angular velocity; and in (b), the red dashed line represents the target angular velocity of the knee joint, and the blue solid line represents the actual angular velocity, in which the red lines in the two figures originate from Eq. (8) and Eq. (9) of the target derivatives of the angular curves. It is observed that the blue solid lines in (a) and (b) basically coincide with the red dashed lines, which indicates that the angular velocity of the hip (knee) joint of the LLRRS can effectively track the target angular velocity. Figure (c) demonstrates the tracking error of the hip joint angular velocity, with the maximum error within 2.96°/s; while Figure (d) presents the tracking error of the knee joint angular velocity, with the maximum error within 0.7°/s. The small angular velocity tracking error indicates that the smooth and stable movement process of the LLRRS helps to ensure the life safety of the patients and reduces the risk of secondary injuries to the patients during the rehabilitation process.
Remark 5
In Fig. 7, the abscissa represents time, with units in seconds. Under the 20th iteration of the closed-loop PD type iterative learning control for the LLRRS, the ordinate of (a) and (b) indicates the angular velocity of the hip (knee) joint, while the ordinate of (c) and (d) indicates the angular velocity error of the hip (knee) joint, both with units in degrees per second.
Simulation analysis of exponential variable gain type iterative learning control based on initial state learning
The parameters K and L of the system control law of Eq. (34) take the same values as in Eq. (45), and the exponential learning factor takes the value of 0.8.
The results shown in Fig. 8, the maximum angular tracking error of the LLRRS under the control of the exponential variable gain type iterative learning algorithm based on initial state learning is demonstrated as follows: the red line with a star represents the hip joint, and the blue line with a circle represents the knee joint. Observed on the global perspective, the two curves gradually converge to 0, which indicates that the algorithm is able to gradually reduce the angular error of the LLRRS hip (knee) joint. From a local perspective, after 20 iterations of learning, the maximum tracking errors of the hip (knee) joint angles are all controlled within 0.1°, indicating that the angle tracking errors are relatively small.
Compared with Fig. 5, the closed-loop PD iterative learning algorithm based on initial state learning needs 18 iterations to converge, while the exponential variable gain iterative learning algorithm based on initial state learning needs only 9 iterations to converge. It can be seen that the exponential variable gain iterative learning algorithm converges significantly faster than the closed-loop PD iterative learning algorithm.
Remark 6
In Fig. 8, the abscissa represents the number of iterations for the exponential variable gain iterative learning control of the LLRRS, with units in times. The ordinate indicates the maximum angular error of the hip (knee) joint of the LLRRS, with units in degrees.
Figure 9 illustrates the tracking errors of the hip (knee) joints for the exponential variable gain type iterative learning control algorithm based on initial state learning in the 20th iteration of learning. The red solid line represents the hip joint and the blue solid line represents the knee joint. It is observed that the maximum errors of the hip (knee) joints are all less than 0.02°, indicating that the tracking errors are small. Compared with Fig. 6, the hip (knee) joint angle tracking errors in Fig. 9 are all significantly reduced, which indicates that the exponential variable gain iterative learning control algorithm based on initial state learning has a better control effect compared with the closed-loop PD iterative learning control algorithm.
Remark 7
In Fig. 9, the abscissa represents time, with units in seconds. The ordinate indicates the angular error of the hip (knee) joint of the LLRRS under the 20th iteration of the exponential variable gain iterative learning control, with units in degrees.
Remark 8
In Fig. 10, the abscissa represents time, with units in seconds. Under the 20th iteration of the exponential variable gain iterative learning control for the LLRRS, the ordinate of (a) and (b) indicates the angular velocity of the hip (knee) joint, while the ordinate of (c) and (d) indicates the angular velocity error of the hip (knee) joint, both with units in degrees per second.
Based on the results shown in Fig. 10, the angular velocity and angular velocity errors of the exponential variable gain type iterative learning control for the LLRRS hip (knee) joints in the 20th iteration of learning are demonstrated as follows: in (a), the red dashed line represents the desired angular velocity of the hip joint, and the blue solid line represents the actual angular velocity; whereas, in (b), the red dashed line represents the desired angular velocity of the knee joint, and the blue solid line represents the actual angular velocity. It is observed that the red dashed line basically coincides with the blue solid line, which indicates that the hip (knee) joint can effectively track the desired angular velocity under the exponential variable gain type iterative learning control. In (c), the hip joint angular velocity error is demonstrated, with a maximum error of 2.09°/s, while in (d), the knee joint angular velocity error is demonstrated, with a maximum error of 0.45°/s. Compared with the results in Fig. 8 (the maximum error of 2.96°/s for the hip joint and the maximum error of 0.7°/s for the knee joint), the angular velocity control of the hip (knee) joint is smoother and more stable. The exponential variable gain type iterative learning control is proved to be better than the closed-loop PD type iterative learning control in terms of joint angular velocity and angular velocity error.
Experimental prototype testing of a lower limb rehabilitation robotic system
The study was approved by the Hezhou University and was carried out in accordance with the approved guidelines. Written informed consent was provided by all participants.
The LLRRS experimental prototype test platform is shown in Fig. 11, which operates in a flat ground environment. The parameters of the Joint are specified in Table 1. Hip drive motors with a rated speed of 27 RPM, a rated torque of 133 N∙m, and a peak torque of 194 N∙m; and knee drive motors with a rated speed of 35 RPM, a rated torque of 107 N∙m, and a peak torque of 169 N∙m. These motors provide the necessary power and agility for the movement of the LLRRS. The motors use 17-bit encoders for position feedback and communicate via a CAN bus to ensure efficient control and data transfer. The experimental prototype platform is supplied with 48 V to ensure stable operation and sufficient power output of the system. The motor drive control core adopts the STM32F407 chip, which has powerful processing capability and rich peripheral interfaces and is suitable for real-time control. The upper layer of the exponential variable gain iterative learning control algorithm running platform adopts PC to implement the complex control algorithm and data processing tasks.
The target motion trajectory previously determined is adopted as the desired motion trajectory of the LLRRS. Subsequently, an exponential variable gain type iterative learning control algorithm based on initial state learning is run to achieve the motion control of the LLRRS. During the experimental process, the motion of the LLRRS is closely observed, including the intuitive effects in terms of the smoothness, accuracy and stability of its motion. At the same time, the data of the hip (knee) joint of LLRRS were collected, including the joint angle, joint angular velocity and other data. By quantitatively analyzing these data, the motor performance and control effect of the LLRRS in performing the rehabilitation tasks were assessed, including the precision of the LLRRS movement, the coverage of the range of motion, and the smoothness of the joint movement, so as to have a comprehensive understanding of the performance and effect of the LLRRS in the rehabilitation tasks.
Figure 12 shows the process of walking training by a volunteer wearing the LLRRS experimental prototype. Specifically, Figure (a) depicts the volunteer wearing the LLRRS device and in a static standing position assisted by the use of crutches, with the left leg in front and the right leg behind. Subsequently, in (b) to (d), the complete process of the LLRRS driving the volunteer’s right leg to perform a forward-striding movement by activating the drive motors in its hip (and knee) joints until it successfully lands is demonstrated. Figure (e) reflects the steps in which the crutches are synchronized to move forward to maintain balance. Immediately thereafter, in (f) to (h), the system again activates the hip (knee) drive motors to guide the left leg to perform a similar stepping and landing action, thus realizing a walking cycle of alternating, continuous forward movement of both legs assisted by the motors.
Remark 9
In Fig. 13, the abscissa represents time, with units in seconds. The ordinate indicates the angle of the hip (knee) joint, with units in degrees.
Remark 10
In Fig. 14, the abscissa represents time, with units in seconds. The ordinate indicates the angular error of the hip (knee) joint, with units in degrees.
Figure 13 demonstrates the joint angle curves of the hip (knee) joint of one leg during walking experiments with the LLRRS experimental prototype. (a) and (b) represent the hip and knee joints, respectively. In both figures, the red dashed line represents the desired joint angle, while the blue solid line represents the actual joint angle of the LLRRS during movement. Observed from a global perspective, the trend of the red dashed line and the blue solid line are basically the same, indicating the effectiveness of the exponential variable gain type iterative learning control algorithm based on initial state learning. However, observed from a local perspective, there are some deviations between the red dashed line and the blue solid line. The specific deviations can be observed in Fig. 14, where the red solid line represents the hip joint angle deviation and the blue solid line represents the knee joint angle deviation, and the maximum angle tracking error of the hip joint is 7.14° and the maximum angle tracking error of the knee joint is within 5.74°. Compared with the simulation results Fig. 9, there is a certain gap in the tracking effect of the LLRRS hip (knee) joint. This may be due to the following reasons: firstly, in modelling, only the motion of the lower limb in the sagittal plane is considered, while in reality, the LLRRS moves in three-dimensional space; secondly, the consideration of the systematic interference term in Eq. (1) is not precise enough, resulting in certain error in the modelling of the LLRRS. However, the intuitive effect of the walking experiments with the experimental prototype of the LLRRS shows that the walking training can be be carried out normally, indicating that the exponential variable gain type iterative learning control algorithm based on initial state learning is effective and can achieve consensus tracking control of the hip (knee) joint with LLRRS.
Figure 15 illustrates the joint angular velocity profile and angular velocity error profile of the LLRRS experimental prototype at the single leg hip (knee) joint during the walking experiment. Where, figure (a) represents the hip joint and figure (b) represents the knee joint. In both figures, the red dashed line represents the desired angular velocity, while the blue solid line represents the hip (knee) joint angular velocity of the LLRRS during operation. From the global observation, the red dashed line and the blue solid line have basically the same trend, indicating that the hip (knee) joint angular velocity of the LLRRS can track the desired curve. However, local observation reveals that there is some deviation between the blue solid line and the red dashed line. The specific deviations can be observed in (c) and (d), in which the maximum deviation of hip joint angular velocity is 36.24°/s and the maximum deviation of knee joint angular velocity is 33.02°/s. There is a lack of smoothness in the motion process of the LLRRS as observed from the aspect of angular velocity. The reason for this may be that the current mode control parameters of the motor are not set appropriately, resulting in insufficient accuracy and timely response. Therefore, the smoothness of the LLRRS needs to be further optimised in the future to improve its motion rehabilitation effect.
Remark 11
In Fig. 15, the abscissa represents time, with units in seconds. The ordinate of (a) and (b) indicates the angular velocity of the hip (knee) joint, while the ordinate of (c) and (d) indicates the angular velocity error of the hip (knee) joint, both with units in degrees per second.
Subsequently, the experimental results are compared with those of previous studies to further explore their significance and implications. Specifically, when compared to Model-free adaptive variable impedance control35, in the presence of initial state deviations, the LLRRS under the action of the controller designed in this paper exhibits lower trajectory tracking errors and demonstrates enhanced robustness. Furthermore, in contrast to A model-free deep reinforcement learning36, the controller designed in this study boasts higher learning efficiency, enabling it to achieve the desired control effect more rapidly and with smaller trajectory tracking errors.
Conclusions
This paper focuses on the motion trajectory tracking control problem of a lower limb rehabilitation robotic system (LLRRS) in case of initial state deviation. Firstly, the motion trajectory data of the normal human lower limbs were fitted with functions to serve as the desired motion trajectory for the LLRRS. Subsequently, the LLRRS was modelled, and a PD-type iterative learning control algorithm incorporating initial state learning was proposed to control the motion trajectory tracking of the LLRRS. Meanwhile, a detailed mathematical analysis of the convergence conditions of the algorithm was conducted, and the control effectiveness of the algorithm was verified by simulation experiments. Furthermore, addressing the issue of the slow convergence speed of the PD-type iterative learning control algorithm, an exponential variable gain type iterative learning control algorithm with initial state learning was proposed, and its improved convergence speed was mathematically proven. In addition, the experimental prototype validated the effectiveness of the algorithm, demonstrating its ability to achieve the motion trajectory tracking control of the LLRRS under the condition of initial state deviation. Although there were certain deviations in the experimental results, they did not adversely affect the walking training.
These findings are of profound significance for the design and application of LLRRS, and this paper contributes valuable references and insights for further research in this field. Nonetheless, the paper also acknowledges certain limitations, including the need for further reduction in experimental errors and enhancement of the operational smoothness of LLRRS. In the future, the algorithm can be further improved to enhance the control accuracy and operational smoothness of LLRRS.
Data availability
The data presented in this study are available on request from the corresponding author.
References
Wang, D. J., Wu, Y. H. & Yu, H. L. State of the Art of brain function detection technologies in Robot-Assisted lower limb rehabilitation. Brain Connect. 14, 401–417 (2024).
Zhou, L. et al. The burden of heat-related stroke mortality under climate change scenarios in 22 East Asian cities. Environ. Int. 170, 107602 (2022).
Li, M., Li, H. & Yu, H. L. Research status of lower limb exoskeleton rehabilitation robot. J. Biomed. Eng. 41, 833–839 (2024).
Khan, M. U. A., Ali, A., Muneer, R. & Faisal, M. Pneumatic artificial muscle-based stroke rehabilitation device for upper and lower limbs. Intel. Serv. Robot. 17, 33–42 (2024).
Yang, Y., Dong, X. C., Wu, Z. Q., Liu, X. & Huang, D. Q. Disturbance-observer-based neural sliding mode repetitive learning control of hydraulic rehabilitation exoskeleton knee joint with input saturation. Int. J. Control Autom. Syst. 20, 4026–4036 (2022).
Lu, Z. X., Zhang, J., Yao, L. G., Chen, J. S. & Luo, H. B. The Human-Machine interaction methods and strategies for upper and lower extremity rehabilitation robots: A review. IEEE Sens. J. 24, 13773–13787 (2024).
Hong, H. et al. Prediction of ground reaction forces using the artificial neural network from capacitive self-sensing values of composite ankle springs for exo-robots. Compos. Struct. 301, 116233 (2022).
Shin, Y. J., Kim, G. T. & Kim, Y. Optimal design of multi-linked knee joint for lower limb wearable robot. Int. J. Precis. Eng. Manuf. 24, 967–976 (2023).
Song, J. Y., Zhu, A. B., Tu, Y., Zhang, X. D. & Cao, G. Z. Novel design and control of a crank-slider series elastic actuated knee exoskeleton for compliant human–robot interaction. IEEE-ASME Trans. Mechatronics. 28, 531–542 (2022).
Francelino, E. et al. Markov system with self-aligning joint constraint to estimate attitude and joint angles between two consecutive segments. J. Intell. Robotic Syst. 104, 43 (2023).
Zhang, P., Zhang, J. X. & Elsabbagh, A. Lower limb motion intention recognition based on sEMG fusion features. IEEE Sens. J. 22, 7005–7014 (2022).
Kim, T., Jeong, M. & Kong, K. Bioinspired knee joint of a lower-limb exoskeleton for misalignment reduction. IEEE-ASME Trans. Mechatronics. 27, 1223–1232 (2021).
Xu, J. J., Xu, L. S., Ji, A. H., Li, Y. F. & Cao, K. A DMP-based motion generation scheme for robotic mirror therapy. IEEE-ASME Trans. Mechatronics. 28, 3120–3131 (2023).
Park, K. W., Choi, J. & Kong, K. Hybrid filtered disturbance observer for precise motion generation of a powered exoskeleton. IEEE Trans. Industr. Electron. 70, 646–656 (2022).
Kenas, F., Saadia, N., Ababou, A. & Ababou, N. Model-free based adaptive finite time control with multilayer perceptron neural network Estimation for a 10 DOF lower limb exoskeleton. Int. J. Adapt. Control Signal Process. 38, 696–730 (2024).
Sharifi, M., Mehr, J. K., Mushahwar, V. K. & Tavakoli, M. Autonomous locomotion trajectory shaping and nonlinear control for lower limb exoskeletons. IEEE-ASME Trans. Mechatronics. 27, 645–655 (2022).
Tsai, T. C. & Chiang, M. H. A lower limb rehabilitation assistance training robot system driven by an innovative pneumatic artificial muscle system. Soft Rob. 10, 1–16 (2023).
Laubscher, C. A., Goo, A., Farris, R. J. & Sawicki, J. T. Hybrid impedance-sliding mode switching control of the Indego explorer lower-limb exoskeleton in able-bodied walking. J. Intell. Robotic Syst. 104, 76 (2022).
Tian, J., Yuan, L., Xiao, W. D., Ran, T. & He, L. Trajectory following control of lower limb exoskeleton robot based on Udwadia–Kalaba theory. J. Vib. Control. 28, 3383–3396 (2022).
Liu, Q. P., Zhang, Z. R., Li, J. K., Bu, X. H. & Hanajima, N. Adaptive neural network iterative learning control of long-stroke hybrid robots with initial errors and full state constraints. Measurement and Control, Early Access, (2024).
Nguyen, H., Dang, H. & Dao, P. On-policy and off-policy Q-learning strategies for spacecraft systems: an approach for time-varying discrete-time without controllability assumption of augmented system. Aerosp. Sci. Technol. 146, 108972 (2024).
Dao, P., Nguyen, V. & Duc, H. Nonlinear RISE based integral reinforcement learning algorithms for perturbed bilateral teleoperators with variable time delay. Neurocomputing 605, 128355 (2024).
Xue, W. et al. Model-free inverse H-infinity control for imitation learning. IEEE Trans. Autom. Sci. Eng., (2024).
Wang, H. & Li, M. Model-free reinforcement learning for fully cooperative consensus problem of nonlinear multiagent systems. IEEE Trans. Neural Networks Learn. Syst. 33, 1482–1491 (2020).
Cai, Z. et al. Framework and Algorithm for Human-Robot Collaboration Based on Multimodal Reinforcement Learning. Computational Intelligence and Neuroscience, : 2341898 (2022). (2022).
Wang, C., Zhou, Z. P., Dai, X. S. & Liu, X. F. Iterative learning approach for consensus tracking of partial difference multi-agent systems with control delay under switching topology. ISA Trans. 136, 46–60 (2023).
Cheng, Z., Songxiao, L. & Zhuo, Z. Industrial robot arm dynamic modeling simulation and variable-gain iterative learning control strategy design. J. Mech. Sci. Technol. 38, 3729–3739 (2024).
Ye, X., Wen, B. Y., Zhang, H. Y. & Xue, F. Z. Leader-following consensus control of multiple nonholomomic mobile robots: an iterative learning adaptive control scheme. J. Franklin Inst. 359, 1018–1040 (2022).
Maqsood, K., Luo, J., Yang, C. G., Ren, Q. Y. & Li, Y. N. Iterative learning-based path control for robot-assisted upper-limb rehabilitation. Neural Comput. Appl. 35, 23329–23341 (2023).
Shi, D., Zhang, W. X., Zhang, W., Ju, L. H. & Ding, X. L. Human-centred adaptive control of lower limb rehabilitation robot based on human–robot interaction dynamic model. Mech. Mach. Theory. 162, 104340 (2021).
Xu, J. H., Li, D. Z. & Zhang, J. H. Extended state observer based dynamic iterative learning for trajectory tracking control of a six-degrees-of-freedom manipulator. ISA Trans. 143, 630–646 (2023).
Zhang, C., Li, S. X. & Zhang, Z. Industrial robot arm dynamic modeling simulation and variable-gain iterative learning control strategy design. J. Mech. Sci. Technol. 38, 3729–3739 (2024).
Pierallini, M. et al. Iterative learning control for compliant underactuated arms. IEEE Trans. Syst. Man. Cybernetics-Systems. 53, 3810–3822 (2023).
Wang, C., Zhou, Z. P. & Liu, X. F. Closed-loop consensus control of partial difference multi-agent systems via variable gain iterative learning. Int. J. Robust Nonlinear Control. 33, 2549–2569 (2022).
Bakhtiari, M., Haghjoo, M. R. & Taghizadeh, M. Model-free adaptive variable impedance control of gait rehabilitation exoskeleton. J. Brazilian Soc. Mech. Sci. Eng. 46, 557 (2024).
Rose, L., Bazzocchi, M. C. F. & Nejat, G. A model-free deep reinforcement learning approach for control of exoskeleton gait patterns. Robotica 40, 2189–2214 (2022).
Acknowledgements
This research was funded by the Sichuan Provincial Regional Innovation Cooperation Project, grant number 2023YFQ0092; the Sichuan Provincial Regional Innovation Cooperation Project, grant number 2024YFHZ0209; Project for Enhancing Young and Middle aged Teacher’s Research Basis Ability in Colleges of Guangxi, grant number 2024KY0723; the Sichuan Natural Science Foundation, grant number 2023NSFSC0368.
Author information
Authors and Affiliations
Contributions
Conceptualization, L.H. and M.Z.; methodology, L.H.; software, M.H.; validation, M.Z., J.D., and M.H.; formal analysis, L.H., J.D., and M.Z.; investigation, Y.G.; resources, L.H.; data curation, M.Z.; writing—original draft, M.Z., J.D., and M.H.; writing—review and editing, L.H., M.Z., and Y.G.; visualization, M.Z.; supervision, L.H. and Y.G.; project administration, M.Z. and M.H.; funding acquisition, L.H. and M.H. All authors have read and agreed to the published version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Huang, L., Zhang, M., He, M. et al. Closed loop iterative learning control for consistency tracking in lower limb rehabilitation robotic system with initial state deviations. Sci Rep 15, 9593 (2025). https://doi.org/10.1038/s41598-025-92197-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-92197-0