Introduction

Cerebral aneurysms, particularly those occurring in the middle cerebral artery (MCA), pose significant risks of rupture, often leading to catastrophic neurological consequences. Among the various treatment options available, endovascular coiling has emerged as a minimally invasive and effective method to mitigate these risks. This technique aims to reduce hemodynamic stress within the aneurysm sac by promoting thrombus formation and stabilizing the aneurysm wall. However, the relationship between aneurysm size, hemodynamic behavior, and the effectiveness of coiling remains underexplored, particularly from a computational fluid dynamics (CFD) perspective1,2,3.

Despite previous studies focusing on the efficacy of endovascular coiling, a detailed numerical investigation of the hemodynamic factors influencing aneurysm rupture risk, especially with respect to varying aneurysm sizes, has not been fully addressed4,5. In fact, theoretical techniques are widely developed for the recognition and treatment of patients with different types of aneurysems6,7,−8. Understanding how size impacts the hemodynamic efficiency of coiling is crucial to optimizing treatment strategies and predicting patient outcomes. Such insights can assist surgeons in tailoring interventions for patient-specific cases, ultimately enhancing the safety and efficacy of coiling procedures9,10,−11.

This study presents a computational analysis of the hemodynamic performance of endovascular coiling in both original and scaled-down patient-specific MCA aneurysm models12,13. By employing the Casson non-Newtonian model to simulate blood flow dynamics and incorporating a porous medium to represent the coiling, the research investigates critical hemodynamic factors such as wall shear stress (WSS), oscillatory shear index (OSI), and pressure distribution14,15. The findings provide valuable insights into the influence of aneurysm size on treatment outcomes and identify high-risk regions that remain prone to rupture even after coiling16,17. These results aim to bridge the knowledge gap in computational evaluations of endovascular techniques, offering a comprehensive understanding of their efficacy in mitigating rupture risks18,19,20.

Although previous scientists focused on endovascular coiling performance21,22,23, the computational fluid dynamic did not thoroughly study the evaluation of this technique. In this work, the endovascular coiling of the MCA aneurysm has been investigated in real and modified scale to disclose how the hemorrhage risk of the MCA aneurysm is changed during the evolution of the aneurysms. Meanwhile, the critical regions with high potential for rupture are also investigated to offer valuable insight for surgeons and scholars to find efficient treatments for patients.

Computational approach and governing equations

The blood hemodynamic factors in cerebral aneurysms have been modeled via computational fluid dynamics24,25,26. The simulations have been performed by solving Navier-stocks equations while the blood stream is presumed laminar, incompressible, and periodic27,28,29.

$$\:\frac{\partial\:\rho\:}{\partial\:t}+\nabla\:\cdot\left(\rho\:\:\varvec{u}\right)=0$$
(1)
$$\:\rho\:\left[\frac{\partial\:\varvec{u}}{\partial\:t}+\left(\varvec{u}\cdot\:\nabla\:\right)\varvec{u}\right]=-\nabla\:p+\nabla\:\cdot\varvec{\tau\:}$$
(2)
$$\mu = 0 \cdot 1\left( {\left[ {\sqrt \eta + \sqrt {\tau _{\gamma } \left( {\frac{{1 - e^{{ - m^{{\dot{\gamma }}} }} }}{{\left| {\dot{\gamma }} \right|}}} \right)} } \right]^{2} } \right)\;and\;\tau _{\gamma } = \left( {0.625H} \right)^{3}$$
(3)

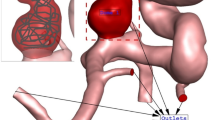
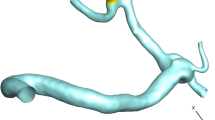
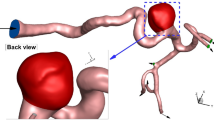
ANSYS-Fluent software is used for the computational modeling of the blood flow inside cerebral aneurysms30. The three-dimensional shape of the selected MCA aneurysm is demonstrated in Fig. 1. The selected unruptured MCA aneurysm is related to a Patient with a 67 years old and this model is obtained from the Aneurisk project31. The type of aneurysm is Saccular with a Terminal direction. The applied periodic cycle at the inlet and outlet of the patient-specific MCA case is demonstrated in Fig. 2. The normal Hematocrit Range of Men is within 0.38–0.50 and the applied hematocrit value is 0.44 and the time step for the computational study is 1.5 ms. Simulation has been performed for two cardiac cycles and the Heart Cycle length is 0.54 s as illustrated in Fig. 2. The mass flow rate of the blood flow varies between 3800 mg/s and 6600 mg/s.

Fig. 1
figure 1

The chosen patient-specific MCA.

Full size image
Fig. 2
figure 2

Applied cardiac cycle at inlet and outlet.

Full size image

The coiling technique is implemented via a porous domain in our chosen sac region of the MCA case. The details of the equivalent coiling are calculated based on the real coil with length and diameter of 300 mm and 0.25 mm, respectively. The porosity is calculated by the Kozeny correlation and the assumed porosity is 0.7 in this investigation. Table 1 displays the size of the sac in real and modified geometry and the calculated permeability of the coiling in real and modified cases.

Table 1 Details of the real and modified aneurysms.
Full size table

Figure 3 illustrates the produced grid for the chosen geometry of the MCA case. The grid size is nearly identical inside the sac while the density of the grid near the wall is higher due to the importance of this region for the calculation of the hemodynamic factors. The grid analyses have been done by comparison of the mean wall shear stress over the sac region for different generated grids and the final grid has 591,000 cells with a minimum size of 0.05 mm near the wall. In this work three main factors of Wall Shear stress (WSS), pressure and OSI are compared in different temporal and operational conditions. OSI is calculated, via following equation:

Fig. 3
figure 3

The grid generation.

Full size image
$$\:WSS=\mu\:{\left(\frac{\partial\:u}{\partial\:y}\right)}_{y=0}$$
(4)
$$\:OSI=\frac{1}{2}\:\left(1-\frac{\left|{\int\:}_{0}^{T}{WSS}_{i}\:dt\right|}{{\int\:}_{0}^{T}\left|{WSS}_{i}\right|\:dt}\right)$$
(5)

Where u is tangential velocity, t is time, and T is the duration of the cycle.

Results and discussion

The contour of wall shear stress (WSS) for the real patient-specific MCA aneurysm is compared with the coiled aneurysm in Fig. 4. The evaluation of the aneurysm in real and coiled condition demonstrates how the use of the coiling would reduce the shear stress on the sac surface. The results of the blood hemodynamic in the initial stages of the aneurysm growth where the size of the sac is small are also presented in this figure. The contour of the scale-down aneurysm with/without the use of coiling also demonstrates how the mechanism of the coiling is effective on the reduction of the shear stress over the sac surface. Comparison of the coiling performance in the real and scale-down geometry of MCA aneurysms indicates that the region with a high risk of rupture is effectively limited after coiling implementation in the scaled-down size. Although a significant reduction in the size of the high-potential region is noticed, the region for possible rupture is not changed as demonstrated in Fig. 4.

Fig. 4
figure 4

Contour of Wall Shear stress in real and modified conditions.

Full size image

Comparison of the pressure over the sac surface is also compared for both real and scale-down models in the presence of coiling, and the results of our modeling at peak systolic are illustrated in Fig. 5. The contour of the pressure demonstrates the change of the pressure under the influence of the coiling in real and scale-down models. In the real case, the high-pressure region is expanded after coiling. However, the change of the pressure in the scale-down case would not change after coiling implementations.

Fig. 5
figure 5

contour of pressure.

Full size image

Figure 6 illustrates the change of the mean velocity at the ostium section where blood flow enters to sac region. The effects of the endovascular coiling on the velocity change at the ostium region at the stage of peak systolic are illustrated in the figure. The velocity profile is sharper in the presence of coiling at the ostium section while the flow enters to sac with smoother shape in real geometry. Besides, the effects of the coiling are more noticeable in the scale-down geometry. In fact, the coiling could meaningfully decrease the mean velocity at the inlet of the ostium section.

Fig. 6
figure 6

Velocity profile at inlet.

Full size image

The oscillatory index is known as a significant parameter for the evaluation of the aneurysm rupture risk. Thus, the contour of the OSI which is obtained over the whole cardiac cycle in real and modified scale of the aneurysm is demonstrated in Fig. 7. As the results of the OSI contour demonstrated, the region near the ostium has more potential for rupture than the dome area. Indeed, the change of shear stream in this section is higher than in other regions and this region is more prone to shear stress change even when coiling is implemented. The size of this region is reduced in the scale-down model. The coiling technique in the scale-down model confirms this region is critical for the rupture.

Fig. 7
figure 7

OSI contour.

Full size image

The average WSS is also calculated over the sac surface for the whole of the cardiac cycle and the results of AWSS are also demonstrated in Fig. 8. The contour of the AWSS presents valuable insight into the change related to the geometry of the aneurysm and coiling technique. The change in the shear stress after coiling is limited since the blood flow has limited space for movement inside the sac region. Thus, it is expected to have fewer velocity changes near the sac surface after the implementation of the coiling. As the size of the aneurysm is scale-downed, the entered blood flow could move into the sac surface with higher velocity, and consequently, wall shear stress is higher. The use of the coiling reduces this high critical zone as demonstrated in Fig. 8.

Fig. 8
figure 8

Average WSS in real and modified aneurysm.

Full size image

Conclusion

The present paper investigates the hemodynamic factors related to the rupture risk of cerebral aneurysm by the change of the MCA sac volume. The computational technique of CFD is employed for the simulation of the bloodstream inside the aneurysm. The effects of coiling on the hemodynamic factors are also examined while the coiling is modeled by the porous condition inside the sac region. The original and scale-down models of the real patient-specific MCA aneurysm are simulated to recognize the region with a high risk of rupture in the evolution of the aneurysm. The modeling of the blood flow is conducted by Casson non-Newtonian model. The results of hemodynamic studies indicate that the use of the coiling could efficiently decrease the shear stress on the surface of the sac. The pressure changes were also compared and the results also show that the effects of coiling on the pressure changes over the sac region are not significant.