Introduction

Our brain is a complex neural network composed of numerous interconnected structures and functional regions1,2,3. The structural connectivity (SC) of the brain, in conjunction with other factors, shapes neurophysiological activity and thus affects the functional connectivity (FC) between neuronal populations and brain regions4. SC reflects the connections between physical white matter regions in the brain, which can be obtained through diffusion tensor imaging (DTI), while FC describes the temporal co-activation of activity between these regions, typically constructed by functional magnetic resonance imaging (fMRI)5,6,7. Multiple studies have shown that brain diseases can disrupt normal brain networks8,9,10,11,12. For example, in many brain diseases such as epilepsy, schizophrenia, and brain tumors, a series of abnormal connectivity or network characteristics have been found13,14,15,16,17,18,19. Therefore, analyzing large-scale brain networks helps to reveal the pathological and physiological mechanisms of brain diseases.

The relationship between structural connectivity and functional connectivity (known as SC-FC coupling) has been studied at the overall level of brain diseases20,21. SC-FC coupling describes the functional dynamics of the brain from the perspective of structural topology, and more sensitively detects subtle brain changes caused by diseases than any single imaging method22,23. Currently, some learning-based methods have been proposed to explore the relationship between SC and FC. For example, Popp et al.24 used a network communication model to capture SC-FC coupling in different regions of the brain, thereby proving that SC-FC coupling is related to human cognitive ability. Dan et al.25 proposed a physically guided deep model to reveal the mechanistic role of SC-FC coupling changes in disease progression. Sarwar et al.26trained a deep neural network to predict brain functional connectivity based on structural connectivity groups. In addition, SC-FC coupling plays an important role in various brain diseases and is currently a key biomarker for diagnosing and predicting disease progression27. Gu et al.28’s work has demonstrated that regional SC-FC coupling is a special feature of brain tissue and is influenced by genetic factors. Liao et al.29 proposed that SC-FC coupling is not only influenced by diseases, but also related to clinical manifestations. The research results of Chen et al.30 have shown that SC-FC coupling may serve as a valuable characteristic biomarker for the burden of Parkinson’s disease. Kong et al.31 found that SC-FC coupling exhibits significant changes in different stages of schizophrenia.

Fig. 1
figure 1

Illustration of our proposed brain disease analysis method, including (a) data pre-processing, (b) calculation SC-FC coupling, (c) feature selection and tree-based model, (d) counterfactual explanation based on tree ensemble.

Full size image

In the existing analyses of SC-FC coupling, various models have been employed to explore the relationship between brain structure and function. For example, statistical models evaluate SC-FC coupling by calculating the correlation between SC and FC32, biophysical models simulate the relationship between SC and FC based on biological mechanisms33, and network communication models use specific strategies based on neural communication to understand the SC-FC coupling mechanism34. In addition, computational models study the dynamic interactions between SC and FC through simulation and optimization methods35, while connectomics models focus on revealing the topological structure and functional connectivity patterns between different brain regions to gain a deeper understanding of the basis of SC and FC coupling36. Although these models reveal the complex relationship between SC and FC from different perspectives, there is still a lack of an interpretable auxiliary diagnostic tool. Counterfactual explanation provides an actionable and humane way of explanation to address this issue37,38. Cheng et al.39 introduced a classic example of counterfactuals: a person submitted a loan application but was rejected by the bank. If his credit score were 700 instead of 600, his loan application would have been approved.

Counterfactual explanations have been widely used in the field of disease diagnosis. For example, Singla et al.40 provided a BlackBox counterfactual interpreter aimed at explaining image classification models for medical applications. Richens et al.41 rephrased medical diagnosis as a counterfactual reasoning task by establishing a counterfactual causal diagnosis model, improving the effectiveness of machine learning in the field of medical diagnosis. Kim et al.42proposed a new generative network based on counterfactual explanation, which can effectively detect lesions. Currently, most existing counterfactual explanation methods usually rely on the differentiability of the model, which may not apply to non-differentiable models such as tree ensembles because they do not use gradient-based optimization procedures. However, compared with traditional counterfactual explanation models, the tree ensemble model can identify the most important features for brain disease diagnosis, which helps to generate more accurate counterfactual explanations43,44,45.

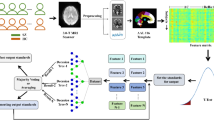
In this paper, we propose a novel brain disease analysis method that aims to reveal the potential impact of the coupling between SC and FC on brain diseases through counterfactual explanations. Unlike existing methods, we combine three tree-based ensemble models (i.e. Decision Tree, Random Forest, and Adaptive Boosting) to analyze and explain SC-FC coupling features and construct counterfactual examples to provide personalized explanations for patients. The schematic diagram of our proposed method is shown in Figure 1. Specifically, we first construct SC and FC matrices from preprocessed diffusion-weighted DTI and resting-state functional fMRI data. Then, we quantify the SC-FC coupling strength of each region and convert it into feature vectors. Subsequently, we select SC-FC coupling features that can reflect disease-related information and trained three tree-based models to analyze the predictive role of these coupling features for diseases. Finally, we design a tree ensemble counterfactual explanation model by fine-tuning the abnormal SC-FC coupling features of patients to generate a set of counterfactual examples that help us understand which feature changes have a significant impact on the predicted outcomes. We validate our proposed method on epilepsy and schizophrenia datasets, and the results show that our approach not only improved the interpretability of the model but also provided new insights into the analysis of brain diseases.

Materials and methods

Dataset

In this study, we use two datasets related to brain diseases: the epilepsy dataset and the schizophrenia dataset. It is worth noting that all subjects are right-handed. All patients in both datasets are diagnosed by experienced physicians to ensure the reliability and accuracy of the diagnostic results. All experiments are performed in accordance with relevant guidelines and regulations. All participants provide written informed consent prior to participation. The main details about the two datasets are as follows:

  • Epilepsy dataset: The patient group consists of two types of epilepsy: 103 patients with frontal lobe epilepsy (FLE) and 89 patients with temporal lobe epilepsy (TLE). Recruit 114 healthy volunteers who are age and gender matched as controls. According to the Pearson \({{\chi }^{2}}\) test, the gender p-value is 0.9601. The age p-value obtained from the one-way ANOVA test among the three groups is 0.2471. These results indicate that there are no significant differences in gender and age distribution among the groups. All participants are from Jinling Hospital of Nanjing University School of Medicine. The specific information of the participants is shown in Table 1.

  • Schizophrenia dataset: The participants included 26 patients with schizophrenia (SZ) and 28 age and gender matched healthy volunteers. The p-value for gender is 0.74, and the p-value for age is 0.8023, indicating that there are no significant differences in gender and age distribution among the groups. All participants are from Nanjing Medical University. The specific information of the participants is shown in Table 2.

Table 1 Epilepsy dataset.
Full size table
Table 2 Schizophrenia dataset.
Full size table

Data pre-processing

The detailed pre-processing process for epilepsy and schizophrenia datasets is described as follows:

  • Epilepsy dataset: The image acquisition is performed by a Siemens Trio 3T scanner from Nanjing Jinling Hospital. Use foam pads to minimize head movement for all subjects. Use a single gradient recall echo plane imaging sequence to obtain functional scans. The scanning parameters are as follows: repetition time = 2000 ms; echo time = 30 ms; flip angle = 90°; 30 transverse slices; field of view (FOV) = 240\(\times\)240 mm2; slice thickness = 4 ms; gap = 0.4 ms; voxel size = 3.75\(\times\)3.75\(\times\)3.75 mm3; obtain DTI scans using echo plane imaging sequences based on spin echoes. The scanning parameters are as follows: repetition time = 6100 ms; echo time = 93 ms; flip angle = 90°; field of view = 240\(\times\)240 mm2; matrix size = 256\(\times\)256; voxel size = 0.94\(\times\)0.94\(\times\)3 mm3; 45 slices; In addition, data is collected using 30 optimal nonlinear diffusion gradient directions with b = 1000 s/mm2 and a non-diffusion weighted volume. Repeat the entire sequence four times to improve the signal-to-noise ratio. The parameters for structural MRI T1 scan are as follows: repetition time = 2300 ms; echo time = 2.98 ms; flip angle = 90°; field of view = 240\(\times\)240 mm2; matrix size = 256\(\times\)256, zero padding and interpolation to 512\(\times\)512, slice thickness = 1 mm, no gap between slices, voxel size = 0.5\(\times\)0.5\(\times\)1 mm3 and 176 slices. It is worth noting that MRI data is only used during the data processing phase.

  • Schizophrenia dataset: The data is collected using a Siemens Trio 3T scanner. The scan parameters of rs-fMRI are as follows: TR = 2000 ms, TE = 21 ms, flipping angle = 90°, voxel size = 3.75\(\times\)3.75\(\times\)3.75 mm3; The scan parameters of DTI are as follows: TR = 7400 ms, TE = 21 ms, flip angle = 90°, voxel size = 0.94\(\times\)0.94\(\times\)0.94 mm3. Image pre-processing consistent with epilepsy dataset.

Brain network construction

We construct the structural network through DTI and the functional network through fMRI. Specifically, DTI data is processed using the PANDA suite. Firstly, use the FSL toolbox for DTI distortion correction (http://fsl.fmrib.ox.ac.uk/fsl/fslwiki). This tool can remove eddy current and extract brain masks from non-diffusion weighted images (B0 images). Then, we use TrackVis to obtain fiber images based on the anatomical regions defined by the automated anatomical labeling (AAL) convention on the T1 images of each subject, and employ deterministic tracking methods. Finally, the number of fibers can naturally be seen as the strength of the edges in the structural brain network. The fMRI data is processed using spm12 and executed in the DPARSF Toolbox version 2.046. The initial functional time series consists of slice time collection, correction, rearrangement, and normalization into EPI templates. Then, we perform trend removal to remove false sources of variance (i.e. six head motion parameters, average signals of cerebrospinal fluid and white matter, and global brain signals), and perform band-pass filtering on the time series (0.01–0.08Hz). The generated volume has 240 time points and is divided into 90 regions of interest (ROIs) using the AAL map47. Finally, the Pearson correlation between the entire network time processes is utilized to determine the weights of edges in the functional brain network.

Calculation of SC-FC coupling

We choose non-parametric Spearman correlation to quantify the coupling strength of structural and functional connectivity in a region, as it is an intuitive and easily interpretable measurement method. Importantly, it adapts to the non-Gaussian nature of entries in SC and FC28. As shown in Figure 1(b), SC-FC coupling is constructed by calculating the Spearman correlation coefficient between each row of the SC matrix and the corresponding row of the FC matrix. Analyzing the results of this step indicates that a vector with a length of 90 is obtained in each subject, representing the coupling strength of SC-FC in each of the 90 regions in the graph. We further construct the SC-FC feature matrix X for all subjects. Here, the dimension of X is \(n\times 90\), where n represents the number of subjects. Each subject contains a vector with a dimension of \(1\times 90\), reflecting the subject’s SC-FC coupling strength in 90 regions.

Feature selection and Tree-based model

To identify the most important SC-FC coupling features for brain disease diagnosis, we use the Lasso regression model for feature selection to remove unnecessary redundant information in matrix X48. After the above steps, we have a set of SC-FC coupling features \(\{({{{{\textbf {x}}}}_{{{\textbf {i}}}}},{{y}_{i}}),i=1,2,...,n\}\), where n is the number of subjects. Each \({{{{\textbf {x}}}}_{{{\textbf {i}}}}}=(x_{i}^{1},x_{i}^{2},...,x_{i}^{90})\in {{R}^{1\times 90}}\) is an SC-FC coupling vector, and \({{y}_{i}}\in R\) is its corresponding label for the i-th subject. We use matrix form \(X=[{{{{\textbf {x}}}}_{{{\textbf {1}}}}},{{{{\textbf {x}}}}_{{{\textbf {2}}}}},...,{{{{\textbf {x}}}}_{{{\textbf {n}}}}}]^{T}\in {{\mathbb {R}}^{n\times 90}}\) to represent the data and represent its corresponding labels as \(y={{({{y}_{1}},{{y}_{2}},...,{{y}_{n}})}^{T}}\in {{\mathbb {R}}^{n}}\). With this representation method, the Lasso regression model can be written as:

$$\begin{aligned} \omega =\arg {{\min }_{\omega }}||{y}-\omega X||_{2}^{2}+\xi ||\omega |{{|}_{1}} \end{aligned}$$
(1)

Among them, \(\omega\) is the coefficient vector and \(\xi\) is the regularization parameter. The selected SC-FC coupling feature matrix is represented as \(X'\in {{\mathbb {R}}^{n\times k}}\), where \(k\ll 90\).

Based on the selected feature matrix \(X'\), we train a series of machine learning models (i.e., \(f:X'\rightarrow y\)) for brain disease diagnosis. In this paper, we train three tree-based classification models, including Decision Tree (DT) (i.e., \({{f}_{DT}}\)), Random Forest (RF) (i.e., \({{f}_{RF}}\)), and Adaptive Boosting (AB) (i.e., \({{f}_{AB}}\)). Among them, Decision trees serve as the basic learner, integrating multiple decision trees to build a powerful predictive model, thereby improving the accuracy of brain disease diagnosis.

Fig. 2
figure 2

Simple decision tree \(T\) and its corresponding differentiable approximation tree \(\overset{\sim }{\mathop {T}}\).

Full size image

Counterfactual explanation based on tree ensemble

After the above steps, we use a tree ensemble counterfactual explanation model to adjust the patient’s SC-FC coupling features to make their state closer to that of a normal person. Specifically, the input of this model is the SC-FC coupling feature vector \({{{{\textbf {x}}}}_{{{\textbf {i}}}}}'\in {{R}^{1\times k}}\) of the i-th subject and a tree-based classifier f. The necessary condition for using this counterfactual explanation model to generate the best counterfactual example is that the input model f must satisfy the differentiable condition. Obviously, none of the three models we trained (i.e. \({{f}_{DT}}\), \({{f}_{RF}}\) and \({{f}_{AB}}\)) satisfy the differentiable condition. Therefore, we adopt the method of Lucic et al.49 to incorporate the differentiable approximation \(\overset{\sim }{\mathop {f}}\,\) of the non-differentiable model f into the gradient-based optimization framework. This method is achieved by replacing each partition in each tree with a sigmoid function, whose hyperparameter is \(\eta\), defined as:

$$\begin{aligned} sig(u)={{(1+\exp (\eta \cdot u))}^{-1}} \end{aligned}$$
(2)

where \(\eta \in {{\mathbb {Z}}_{>0}}\). The sigmoid function is incorporated into function \(\overset{\sim }{\mathop {{{m}_{q}}}}\,({{{{\textbf {x}}}}_{{{\textbf {i}}}}}')\), which is the \({{m}_{q}}({{{{\textbf {x}}}}_{{{\textbf {i}}}}}')\) function to approximates the activation of node q: \({{m}_{q}}({{{{\textbf {x}}}}_{{{\textbf {i}}}}}')\approx \overset{\sim }{\mathop {{{m}_{q}}}}\,({{{{\textbf {x}}}}_{{{\textbf {i}}}}}')\). The function is defined as follows:

$$\begin{aligned} \overset{\sim }{\mathop {{{m}_{q}}}}\,({{{\textbf {x}}}_{{\textbf {i}}}}')=\left\{ \begin{array}{*{35}{l}} 1, \quad \qquad \quad \qquad \qquad \quad \text { if }q\text { is the root,} \\ \overset{\sim }{\mathop {{{m}_{Q}}}}\,({{{\textbf {x}}}_{{\textbf {i}}}}')\cdot sig({{\theta }_{q}}-x_{i}^{j}),\text { if }q\text { is a left child,} \\ \overset{\sim }{\mathop {{{m}_{Q}}}}\,({{{\textbf {x}}}_{{\textbf {i}}}}')\cdot sig(x_{i}^{j}-{{\theta }_{q}}),\text { if }q\text { is a right child}\text {.} \\ \end{array} \right. \end{aligned}$$
(3)

where \({{\theta }_{q}}\) is a threshold for activation of node q, which is determined by the model’s determination of the optimal segmentation point during the training phase. For ease of explanation, we present a simple decision tree T and its corresponding differentiable approximation tree \(\overset{\sim }{\mathop {T}}\,\) in Figure 2. If the parent node Q of node q is activated and the j-th SC-FC coupling feature \(x_{i}^{j}(j\le k)>{{\theta }_{q}}\) of the i-th subject, then node q (left child node) is activated. If \(x_{i}^{j}<{{\theta }_{q}}\), then node \(\widehat{q}\) (right child node) is activated. The root node is always activated. Then, by approximating the activation of node q through the sigmoid function, the differentiable approximation tree \(\overset{\sim }{\mathop {T}}\,\) of a single decision tree T can be obtained. So the tree approximation can be defined as:

$$\begin{aligned} \overset{\sim }{\mathop {T}}\,({{y}_{i}}|{{{{\textbf {x}}}}_{{{\textbf {i}}}}}')=\sum \limits _{q\in {{\Omega }_{T}}}{\overset{\sim }{\mathop {{{m}_{q}}}}\,({{{{\textbf {x}}}}_{{{\textbf {i}}}}}')}\cdot T({{y}_{i}}|q) \end{aligned}$$
(4)

Among them, \({{\Omega }_{T}}\) is the set of leaf nodes in T, and each leaf node q has its own predicted distribution \(T({{y}_{i}}|q)\). From Figure 2, it can be seen that the approximate tree \(\overset{\sim }{\mathop {T}}\,\) and T has the same tree structure and threshold, but compared to tree T, its node activation mainly depends on the feature \(x_{i}^{j}\) and threshold \({{\theta }_{q}}\). Finally, this method replaces the maximum value operation of f with softmax function of temperature \(\lambda \in {{\mathbb {Z}}_{>0}}\), where f is an ensemble of L trees with weights \({{\rho }_{l}}\in \mathbb {Z}\). The approximate value \(\overset{\sim }{\mathop {f}}\,\) can be expressed as:

$$\begin{aligned} \overset{\sim }{\mathop {f}}\,({{y}_{i}}|{{{{\textbf {x}}}}_{{{\textbf {i}}}}}^{\prime })=\frac{\exp (\lambda \cdot \sum \limits _{l=1}^{L}{{{\rho }_{l}}\cdot \overset{\sim }{\mathop {{{T}_{l}}}}\,({{y}_{i}}|{{{{\textbf {x}}}}_{{{\textbf {i}}}}}^{\prime })})}{\sum \nolimits _{{{y}_{i}}^{\prime }}{\exp (\lambda \cdot \sum \limits _{l=1}^{L}{{{\rho }_{l}}\cdot }\overset{\sim }{\mathop {{{T}_{l}}}}\,({{y}_{i}}^{\prime }|{{{{\textbf {x}}}}_{{{\textbf {i}}}}}^{\prime }))}} \end{aligned}$$
(5)

where \({{y}_{i}}'\) is the predicted label. In our experiment, 0 corresponds to normal subjects and 1 corresponds to patients. We want to adjust the SC-FC coupling features of patients to make them closer to normal, so we usually set \({{y}_{i}}'\) to 0. After obtaining the approximate value \(\overset{\sim }{\mathop {f}}\,\) based on the original model f, we can obtain the optimal counterfactual example \(\overset{*}{\mathop {{{{{\textbf {x}}}}_{{{\textbf {i}}}}}}}\,'\):

$$\begin{aligned} \overset{*}{\mathop {{{{{\textbf {x}}}}_{{{\textbf {i}}}}}}}\,'=\arg \underset{\overline{{{{{\textbf {x}}}}_{{{\textbf {i}}}}}}'}{\mathop {\min }}\,\overset{\sim }{\mathop {f}}\,({{y}_{i}}'|{{{{\textbf {x}}}}_{{{\textbf {i}}}}}')+\alpha \cdot d({{{{\textbf {x}}}}_{{{\textbf {i}}}}}',\overline{{{{{\textbf {x}}}}_{{{\textbf {i}}}}}}') \end{aligned}$$
(6)

where weights \(\alpha \in {{\mathbb {Z}}_{>0}}\), \(\overline{{{{{\textbf {x}}}}_{{\textbf {i}}}}}'\) represent a perturbed version of the original example \({{{{\textbf {x}}}}_{{{\textbf {i}}}}}'\), and \(d(\cdot )\) is a differentiable distance function. In this paper, we use the Manhattan distance function. Further, derive its corresponding optimal counterfactual explanation \(\Delta {{x}^{*}}\):

$$\begin{aligned} \Delta {{x}^{*}}=\overset{*}{\mathop {{{{{\textbf {x}}}}_{{{\textbf {i}}}}}}}\,'-{{{{\textbf {x}}}}_{{{\textbf {i}}}}}' \end{aligned}$$
(7)

The optimal counterfactual explanation \(\Delta {{x}^{*}}\) reflects the minimum change that the original example \({{{{\textbf {x}}}}_{{{\textbf {i}}}}}'\) needs to make in order to change the model’s predictions.

Experiments and results

In the datasets of epilepsy (i.e. FLE vs. NC and TLE vs. NC tasks) and schizophrenia (i.e. SZ vs. NC tasks), we train tree-based classification models for brain disease diagnosis on 70% of each task: Decision Tree (DT), Random Forest (RF), and Adaptive Boosting (AB), with DT serving as the base learner. We use the remaining 30% to evaluate the model’s performance and generate counterfactual examples. We have a total of 9 models (3 tasks \(\times\) 3 tree-based models). It is worth noting that the hyperparameters may affect the model approximation \(\overset{\sim }{\mathop {f}}\,\), of f. For the selection of hyperparameters, we divide 10% of the training set as a validation set and determine the hyperparameters of the model through cross-validation. The hyperparameters we choose can produce a valid counterfactual example for each instance in the dataset and the minimum average distance between corresponding pairs \(({{\textbf{x}}_{\textbf{i}}}^{\prime },{{\overline{{{\textbf{x}}_{\textbf{i}}}}}^{\prime }})\).

We evaluate our model on two binary classification datasets: epilepsy (i.e., FLE vs. NC and TLE vs. NC tasks) and schizophrenia (i.e., SZ vs. NC tasks). We evaluate the model’s performance based on diagnostic accuracy (ACC), sensitivity (SEN), specificity (SPE), and area under the curve (AUC). Among them, SEN mainly refers to the proportion of correctly predicted patients in FLE vs. NC, TLE vs. NC, and SZ vs. NC tasks, while SPE mainly refers to the proportion of correctly predicted normal controls in FLE vs. NC, TLE vs. NC, and SZ vs. NC tasks. In addition, we also measure the average distance (\(dis{{t}_{\text {AVG}}}\)) between the counterfactual examples (i.e. SC-FC coupling features after patient conversion to normal) and the original examples (i.e. SC-FC coupling features of patients) in 9 models, which reflects the average similarity between the counterfactual examples and the original examples in the feature space. A smaller \(dis{{t}_{\text {AVG}}}\) means that the counterfactual examples are closer to the original examples in the feature space, making the model’s explanation of brain diseases more intuitive and easy to understand.

As shown in Table 3, we can observe that in the three tasks, regardless of which model, the \(dis{{t}_{\text {AVG}}}\) decreases with the increase of ACC. For example, in the FLE vs. NC task, the ACC of the RF model is better than AB, while the ACC of the DT model is better than RF, and their corresponding \(dis{{t}_{\text {AVG}}}\) gradually decreases. In the TLE vs. NC task, the ACC of the AB model is better than RF, while the ACC of the DT model is better than AB, and their corresponding \(dis{{t}_{\text {AVG}}}\) gradually decreases. In the SZ vs. NC task, the ACC of the AB model is better than that of the DT model, while the ACC of the DT model is better than RF, and their corresponding \(dis{{t}_{\text {AVG}}}\) gradually decreases. This result indicates that the higher the ACC of the model, the closer the generated counterfactual examples are to the original examples. This means that a highly ACC model can better capture the SC-FC coupling features of patient anomalies, thereby generating more accurate counterfactual examples. Furthermore, we find that models with higher ACC showed significant improvements in their corresponding SEN, SPE, or AUC compared to other models.

Table 3 Performance evaluation of 9 models. ACC: accuracy; SEN: sensitivity; SPE: specificity; AUC: area under the ROC curve; \(dis{{t}_{\text {AVG}}}\): the average distance between the counterfactual example and the original example.
Full size table
Fig. 3
figure 3

The selected brain regions for three tasks and the average perturbation of each brain region corresponding to 9 models.

Full size image

In Figure 3, we demonstrate the disease-related abnormal brain regions captured by our model in three tasks, as well as the average perturbation level of SC-FC coupling features measured in each brain region across the three models. The average disturbance mainly represents the average degree to which the SC-FC coupling features of each brain region are altered during the generation of counterfactual explanations. If the disturbance amplitude of certain brain regions is greater than that of other regions, it indicates that these brain regions have a greater impact on the prediction results of the model. From Figure 3, it can be seen that in all three tasks, regardless of which model, the overall amplitude of the average disturbance shows the same trend. For example, in the FLE vs. NC task, the average disturbance amplitude of the ORBsup.L (Superior frontal gyrus, orbital part) and SPG (Superior parietal gyrus) brain regions is greater than that of the other regions in all three models, and the average disturbance of the ORBmid.R (Middle frontal gyrus, orbital part) region is the lowest in all three models. Similar situations are also observed in TLE vs. NC and SZ vs. NC tasks. This result further demonstrates the accuracy of the counterfactual examples generated by our model, providing strong support for our understanding of the impact of brain diseases on different brain regions. In addition, most of the brain regions we capture have shown associations with brain diseases in existing studies. For example, studies by Luo et al.50 and O’Muircheartaigh et al.51 indicate that FLE patients exhibit abnormalities in the left superior frontal gyrus, which corresponds to the SFGdor.L (Superior frontal gyrus, dorsolateral) and ORBsup.L regions captured in the FLE vs. NC task. Secondly, Binding et al.52 point out that the SMA.L (Supplementary motor area) region is associated with language disorders in TLE patients, while Chabardes et al.53 point out that TLE attacks tend to preferentially spread to the STG (Superior temporal gyrus) region. These areas are all captured in our model. This result is further validated in the schizophrenia dataset. For example, for the PCL.L (Paracentral lobule) region, Zhang et al.54 find that SC-FC coupling in SZ patients is higher in this brain region than in other regions. Besides, Ferro et al.55 first point out abnormalities in the PoCG (Postcentral gyrus) region of SZ patients, and our model also captured this region.

Fig. 4
figure 4

Left: The distribution of the distances (\(dist\)) between the counterfactual examples generated by FLE, TLE, and SZ patients and the original examples in the 9 models. The black cross in the middle of each box plot indicates the average value of the distance (\(dist_{\text {AVG}}\)). Right: Counterfactual examples generated for randomly selected FLE, TLE and SZ patients in the test set.

Full size image

To illustrate how the perturbations of different brain regions differ between different subjects, we plot a box plot as shown in Figure 4 (left), which shows the distribution of the distance (dist) between the counterfactual examples generated by FLE, TLE and SZ patients and the original examples in 9 models. From this figure, it can be seen that different models perform differently in generating counterfactuals in the three tasks, and dist fluctuates significantly between models. Specifically, in the FLE vs. NC task, the dist distribution of the counterfactual examples of FLE patients in the three models is concentrated between 0.6 and 0.9, which shows that the model has a strong ability to explain FLE disease and the generated results are relatively consistent. In the TLE vs. NC task, the dist distribution of TLE patients on the AB and DT models is tighter than that of the RF model, which shows that the RF model may have some challenges in handling the interpretation task of TLE disease, which may be due to the higher pathological complexity of TLE disease, resulting in longer dist of the generated counterfactual examples. In the SZ vs. NC task, the dist distribution on the AB and DT models is smaller than that of the RF model, which means that the RF model has a poor interpretation effect on SZ patients. In addition, from the performance evaluation results of the models in Table 3, it can be seen that the performance of the 9 models is consistent with the above analysis. We show the counterfactual examples generated for FLE, TLE and SZ patients randomly selected from the test set in Figure 4(right). It is worth noting that this set of examples is selected based on the model with high accuracy. In the FLE vs. NC task, to bring the FLE patient to a normal state, we need to adjust its SC-FC coupling in the PreCG.L (Precental gyrus) region from −0.060 to 0.000, the SC-FC coupling in the SFGdor.L (Superior frontal gyrus, dorsolateral) region from 0.115 to 0.113, the SC-FC coupling in the IFGoperc.R (Inferior frontal gyrus, opercular part) region from 0.091 to 0.096, and the SC-FC coupling in the SPG.L (Superior parietal gyrus) region from −0.030to 0.000. In the TLE vs. NC task, we only need to adjust the SC-FC coupling of the TLE patient in the REC.R (Gyrus rectus) region from 0.230 to 0.235 to transition it to a normal state. In the SZ vs. NC task, to bring the SZ patient to a normal state, adjusting his SC-FC coupling in the ORBinf.R (Inferior frontal gyrus, orbital part) region from 0.026 to 0.019 and the ITG.R (Inferior temporal gyrus) region from 0.266 to 0.273 is necessary. The counterfactual explanation reveals the minimum changes required for input data to achieve different results56. It is not difficult to see that compared to the original SC-FC coupling features, the counterfactual examples we generated only make minor changes to the SC-FC coupling features. This fine-tuning, although subtle, is crucial and has great significance in the diagnosis of brain diseases.

Discussion

We explore three tree ensemble models (i.e. Decision Tree, Random Forest, and Adaptive Boosting) for the counterfactual explanation of SC-FC coupling, and to demonstrate the effectiveness of our method, we not only validate it on the epilepsy dataset, but also further empirically test it on the schizophrenia dataset. Our results show that the abnormal SC-FC coupling exhibited by patients is mainly concentrated in specific brain regions, which is consistent with the phenomenon of local abnormal connectivity in brain networks of patients with brain diseases mentioned in earlier studies. For example, the study by Chiang et al. shows that SC-FC coupling is dynamic and regulated by the duration of epilepsy57. Huang et al. and Liu et al. find significant differences in SC-FC coupling between TLE patients and normal subjects58,59. Similarly, for schizophrenia, previous studies show that the SC-FC coupling values in SZ patients are significantly higher than those in normal subjects in different brain regions60,61. In addition, Although previous studies have revealed the relationship between specific brain regions and their structural and functional connectivity, there is still a lack of an interpretable auxiliary diagnostic tool in the diagnosis of brain diseases. Our model can capture the brain regions where patients show abnormal SC-FC coupling and fine-tune the SC-FC coupling of the abnormal brain regions to generate counterfactual examples for the patients. To generate accurate counterfactual examples, we create an approximately differentiable version \(\overset{\sim }{\mathop {f}}\,\) of the original model f, rather than replacing f with \(\overset{\sim }{\mathop {f}}\,\) as in the traditional approach. This analytical method provides a useful reference for diagnosing brain diseases and offers a new perspective for understanding the nature of SC-FC coupling impairments.

However, current research still has several limitations. Firstly, we only use AAL templates to define brain regions. For future work, we will use different templates to evaluate the robustness of our proposed method62. Secondly, we only calculate the SC-FC coupling between each region. In future research, we will consider the impact of more factors on SC-FC coupling and conduct in-depth analysis of specific patterns or network structures in each region. Finally, for the generation of counterfactual explanations, in our experiment, only one explanatory result (one-to-one explanatory behavior) is generated for patients. We consider the possibility of generating diverse counterfactual explanations (one to many counterfactual explanations) for patients in the future.

Conclusions

In this paper, we propose a novel method for analyzing brain diseases. The existing brain disease analysis methods can only provide a simple explanation for the differences in specific brain regions between the patient group and the normal control group through statistical analysis, and cannot explain the relationship between the altered SC-FC coupling and brain diseases. Therefore, we explore three tree ensemble models (i.e. Decision Tree, Random Forest, and Adaptive Boosting) for the counterfactual explanation of SC-FC coupling. We validate the effectiveness of our approach on real epilepsy and schizophrenia datasets, and results suggest that our method can be used as a tool to assist in the diagnosis of brain diseases and provide a valuable reference for understanding the nature of SC-FC coupling impairments in these diseases.