MPPT of solar PV systems using PSO memetic algorithm considering the effect of change in tilt angle

Abstract

Tracking the peak power output of solar photovoltaic modules poses a significant challenge in contemporary times, that too under variable climatic conditions. Despite the availability of various Maximum Power Point Tracking (MPPT) methods, each method carries its own set of limitations. Many of these constraints can be effectively addressed by leveraging a suitable metaheuristic algorithm. In this context, a Particle Swarm Optimization Memetic Algorithm (PSOMA) is proposed as a powerful tool for accelerating convergence towards the maximum power point and enhancing the tracking process. Furthermore, the proposed algorithm incorporates the impact of changes in tilt angle, thereby augmenting its efficacy. Simulation results demonstrate that the proposed method exhibits superior tracking capabilities compared to conventional MPPT methods and various other MPPT algorithms. The convergence time is also greatly reduced by the proposed method. An efficiency of 99.91% and a convergence time of 8.5 ms is achieved by this algorithm. The efficiency remains almost constant for different irradiance levels which is demonstrated by simulation results. Additionally, hardware experimentation validates the robustness of the developed algorithm.

Introduction

The demand for electricity continues to surge steadily, driven by the expansion of industries, commercial buildings, and domestic loads. Consequently, there’s a growing need to expand existing power generation infrastructure and install new facilities. However, alongside this expansion, it’s imperative to consider the environmental impact of conventional power generation methods. Hence, there’s a pressing need to transition to renewable energy resources that are environmentally sustainable.

Solar energy stands out as a dependable and eco-friendly energy source, derived from the sun. Among the various methods of harnessing solar energy, one prominent approach is through solar photovoltaic (PV) systems. The PV systems are capable of producing electricity directly from the sunlight. The electricity is generated during the daytime and supplied to the load. Simultaneously, it is also stored in the battery for use at nighttime. Practically, the maximum power from the solar PV module is not obtained most of the time due to various factors. Thus, it’s crucial to employ techniques capable of extracting the maximum power from solar photovoltaic modules, especially under dynamic operating conditions. These specialized techniques, known as Maximum Power Point Tracking (MPPT) methods, play a pivotal role in optimizing energy capture from photovoltaic modules. But there are many challenges in the implementation process like temperature variations, irradiance changes, efficiency and tracking speed of the algorithm and cost of the tracking system. So, it becomes important to address these challenges when a method to track maximum power point is proposed and it is carried out in this literature.

A multitude of MPPT methods exist for effectively tracking the maximum power point of PV modules. Among these methods, the Perturb and Observe (P&O) technique and the incremental conductance (IC) method have been widely adopted. The P&O method operates by perturbing the voltage and monitoring the resulting power output of the PV module. If an increase in output power is detected, the voltage is perturbed further in the same direction; otherwise, the direction is reversed. However, a drawback of this method is its tendency for the operating point to oscillate even after reaching the maximum power point during steady-state operation^1,2,3,4,5,6. It will also take time to get stabilized after a sudden change in irradiance. To mitigate this limitation, hybrid approaches combine the P&O method with other tracking methods, enhancing overall tracking performance^4,5,6. In contrast, the incremental conductance method offers reduced steady-state oscillations. Additionally, it exhibits quicker response to changes in irradiance compared to the P&O method. Nevertheless, adjusting the step and threshold parameters in the incremental conductance method can prove challenging^7,8. The response of this method is slower for fast changes in irradiance. A small amount of power loss may be experienced as it can deviate from actual maximum power point even under steady state conditions.

To get around the limitations of traditional MPPT techniques, various optimization methods were proposed in various research papers like genetic algorithms and evolutionary algorithms. The PSO technique, which is simple in its structure and easy to implement, is a broadly used evolutionary algorithm for tracking the maximum power point^{9,10,11,12,13,14}. The time delay is large in standard PSO to reach the convergence as the particles in the swarm are randomly initialized. To overcome this drawback, Lagrange Interpolation (LI) formula is used along with PSO⁹ to increase the speed of convergence. The oscillation at steady state condition is also reduced in the approach when maximum power point (MPP) is reached. But this method needs an additional digital signal controller for its implementation.

An overarching distribution algorithm is employed in conjunction with PSO to enhance the precision of tracking the Maximum Power Point (MPP)¹⁰. This method facilitates swift convergence towards the global MPP, thereby expediting the tracking process. However, if the updated duty cycle falls beyond the predefined radius, it may prolong the time required to track the global MPP. To mitigate the expenses associated with employing multiple MPPT controllers for diverse arrays, a solution proposing the utilization of a single MPPT controller alongside PSO for all arrays has been introduced¹¹. While this method exhibited faster Maximum Power Point (MPP) tracking compared to traditional methods, it’s time to reach the MPP remains relatively high in comparison to modern methods. Additionally, the efficiency of the tracker was not validated in this approach.

The standard PSO method is adapted with modifications¹² to achieve Maximum Power Point Tracking (MPPT) under partial shading conditions. This approach demonstrates effective global point tracking with fewer iterations compared to alternative MPPT techniques. Moreover, it achieves a high success rate across a thousand different shading patterns, although its performance hinges on selecting suitable parameters for the PSO algorithm.

An enhanced PSO algorithm¹³ is employed for MPP tracking and compared against both standard PSO and fuzzy logic control (FLC). Simulation and prototype results indicate that the proposed method achieves faster global MPP tracking and higher tracking accuracy than the other two approaches. However, the termination strategy employed in this method may prematurely conclude the search process before reaching the global MPP.

Furthermore, the PSO method is optimized by integrating it with the Perturb and Observe (P&O) method¹⁴ to reduce the search region. This combined approach demonstrates faster convergence times, validated through simulations and experiments compared to standard PSO. Nonetheless, its comparative effectiveness against other enhanced PSO methods or hybrid MPPT techniques remains unexplored.

The impact of tilt angle on photovoltaic module power production is discussed in the literature to track maximum power point^15,16,17. While these studies emphasize tilt and azimuth angles, they generally do not integrate specific Maximum Power Point Tracking (MPPT) algorithms. Furthermore, these works do not demonstrate any measurable efficiency improvements.

The flying squirrel search optimization method is used to track the MPP¹⁸. From the results, it is observed that it attained a maximum efficiency of 99.99% but the time taken for tracking is 1.8 s. Even though the efficiency is high, the time taken for tracking is more in this approach. An adaptive sliding mode control technique is used with PSO method¹⁹ to track MPP. The MMP is reached at 0.215 s and an efficiency of 99.2% is attained in this method. A hybrid P&O algorithm which combines slow and fast sample-based computations²⁰ is used to track the maximum power point. The time taken to reach MPP is 0.35 s and efficiency attained is 99.68%. A dc–dc resonant converter with dual control²¹ is used and standard P&O method is used for MPP Tracking. The peak efficiency attained in this approach is 98.7% for 50% of the load. For other ranges of load, the efficiency obtained is less than this value. The time taken to reach MPP is not investigated in this approach.

The JAYA algorithm based on the Levy flight²² is used for tracking the MPP. Simulation results demonstrate that the proposed algorithm attains a maximum efficiency of 99.97% and the time taken for convergence ranges between 0.37 and 1.93 s for various iterations. The experimental results show that a maximum efficiency of 99.52% is attained and the associated tracking time is 2 s. The PSO algorithm is combined with P&O method (PSO + P&O) and IC method (PSO + IC)²³ to overcome the drawback of fixed step size. Simulation results demonstrate that the proposed (PSO + IC) approach attains a maximum efficiency of 99.07% with a tracking time of 43.4 ms. Experimental results are not available in this literature. The Grey Wolf Optimization (GWO) technique is used²⁴ to track the maximum power point from solar PV systems. In one of the shading patterns, a maximum efficiency of 99.92% is achieved by using this method but the tracking time is not mentioned in the literature. A Modified Grey Wolf Optimization (MGWO)²⁵ is proposed to track the MPP. The maximum efficiency obtained by this method is 99.763% with a tracking time of 2.85 s. The commonly seen drawbacks in these methods are increased tracking time and less efficiency under dynamic operating conditions. Moreover, some of the methods with high tracking efficiency take more tracking time which is again a drawback.

This paper proposes the particle swarm optimization memetic algorithm (PSOMA) for tracking the maximum power point which includes the effect of change in tilt angle. This method can perform the search process rapidly and reach the global maximum power point efficiently. Also, this literature provides the comparison between conventional P&O method, PSO method and the proposed PSOMA method which establishes the efficiency of the proposed algorithm. The method which is proposed in this literature is capable of effectively tracking MPP in a very less time which is verified by simulation results and an experimental design.

Overview of P&O, PSO and GWO algorithms

The most common method of MPPT is the P&O algorithm, while PSO can also be applied to monitor a PV module’s maximum power level. These methods are discussed in detail.

Overview of the P&O algorithm

The P&O method of tracking the point at which maximum power occurs involves the process of creating a perturbation in the voltage and measuring the PV module’s output power. The MPP is attained by following the Eq. (1) which is given by

$$\frac{dP}{{dV}} = 0$$

(1)

where dP is the change in power and dV is the change in voltage.

When the perturbation leads to an increase in value of power, the perturbation direction is maintained, otherwise it is reversed¹. Figure 1 shows the flowchart of P&O algorithm¹.

Fig. 1

Flowchart of P&O Algorithm¹.

Overview of the PSO algorithm

The PSO method is an optimization algorithm to find the global best solution. The method was developed by Eberhart and Kennedy for large scale optimization problems. In this method there are many particles which are grouped together to form a swarm. Each of these particles will be involved in the search operation and these particles can communicate with each other to share the best search value. The particles will either move towards the best solution or it will simply follow the particle which is performing well.

The particle swarm optimization approach can be best explained by the Eq. (2) and Eq. (3):

$$\begin{aligned} v_{i} \left( {k + 1} \right) & = \omega v_{i} \left( k \right) + c_{1} r_{1} \left( {p_{best,i} - x_{i} \left( k \right)} \right) \\ & \quad + c_{2} r_{2} \left( {g_{best} - x_{i} \left( k \right)} \right) \\ \end{aligned}$$

(2)

$$\begin{aligned} x_{i} \left( {k + 1} \right) & = x_{i} \left( k \right) + v_{i} \left( {k + 1} \right) \\ & {\text{i}} = {1},{2}, \ldots ,{\text{N}} \\ \end{aligned}$$

(3)

where $x_{i}$ represents ith particle position, ${\text{v}}_{{\text{i}}}$ represents velocity of ith particle, k represents iteration number, ω represents inertia weight, r₁ represents random variable 1, r₂ represents random variable 2, c₁ represents cognitive coefficient, c₂ represents social coefficient, p_best,i is the best position found by ith particle, g_best,i is the global best position.

The flow chart for the PSO algorithm is shown in Fig. 2¹². The following steps explains the standard particle swarm optimization:

Fig. 2

Flowchart of PSO Algorithm¹².

Steps:

• 1. The position of the particle and its velocity are randomly initialized.

• 2. Evaluate the objective function.

• 3. The particle’s best position and the global best position is evaluated.

• 4. Update the position of the particle and its velocity.

• 5. Repeat the steps from 2 to 4 until the search converges.

Overview of the GWO algorithm

The GWO Algorithm²⁴ is an optimization technique which is based on the natural hunting pattern of the grey wolves. These wolves have a social network among them and follow hierarchy in their pack to organize themselves in hunting. There are four categories in their hierarchy such as alpha, beta, delta and omega. The topmost leader in the pack is called the alpha wolf which leads the pack and takes the role of commander in the hunting process. The beta and delta wolves act like subordinates in executing the command. They also provide suggestions to the alpha wolf in hunting and decision-making process. The omega wolves are like workers, and they have to obey their leaders.

The hunting process of the grey wolves involves chasing and tracking the prey, encircling the prey and attacking them. The same process is adopted in the GWO for getting optimized solution. In tracking the MPP, the search process is done by the wolves, and they find the best solution. As the alpha wolf is the leader which dominates the wolf society and it knows the exact location of the prey, its value is taken as the best value of solution. This is directly linked with the duty cycle, which will be held constant when the optimum value is reached. This enables reduced oscillations and leads to an increase in efficiency. The equations governing the search process and the flow chart are mentioned in the literature²⁴.

Overview of the proposed algorithm

The proposed particle swarm optimization memetic algorithm (PSOMA) overcomes the drawbacks of the convention PSO algorithm. The added advantage in the proposed algorithm is that it also incorporates the changes in tilt angle which is important in tracking the maximum power point.

The flow chart for the proposed PSOMA algorithm is shown in Fig. 3. The following steps explains the proposed PSOMA algorithm:

Fig. 3

Flowchart of Proposed PSOMA Algorithm.

Steps:

• 1. The position of the particle and its velocity are randomly initialized.

• 2. Evaluate the objective function.

• 3. Evaluate the best position found by the particle and the global best position.

• 4. Update the position of the particle and its velocity.

• 5. Change the tilt angle and repeat the steps from 1 to 4 and refurbish the position of the particle and its velocity again.

• 6. Compare the global best position value obtained with the global best position value of previous tilt angle.

• 7. If the present value is better than the previous value, then update the value of g_best, if not change the angle of PV module in opposite direction and continue the process until optimum value is obtained.

• 8. The entire process is repeated when the change in insolation value exceeds the preset value.

Modeling and system design

PV module modeling

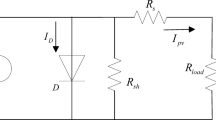
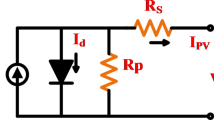
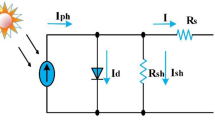
The single diode model of the solar PV module is shown in Fig. 4²⁶.

Fig. 4

Single diode model of a PV cell²⁶.

The photovoltaic current from the cell is given by the Eq. (4):

$$I_{PV} = I_{g} - I_{s} \left( {exp\left( {\frac{{q\left( {V_{PV} + I_{PV} .R_{s} } \right)}}{nkT}} \right) - 1} \right)$$

(4)

where n is the ideality factor of diode, k is the Boltzmann’s constant, q is the charge of electron, T is the temperature in Kelvin, R_s represents the equivalent value of resistance in series, I_s represents the saturation current, I_g represents the photocurrent.

DC-DC boost converter model

The solar photovoltaic module is connected to the load through a DC-DC boost converter. The duty cycle of the converter is controlled by the proposed PSOMA. This helps in tracking the maximum power point for continuously changing operating conditions. The Fig. 5, shows a DC-DC boost converter modeled with a MOSFET switch for the advantage of fast switching speed which is much needed in this application²⁷. The output voltage V_o is given by the following Eq. (5)²⁷:

$$V_{o} = \frac{{V_{i} }}{1 - D}$$

(5)

where V_i represents input voltage, D represents the duty cycle.

Fig. 5

A DC-DC boost converter circuit²⁷.

Simulation and hardware results

To substantiate the proposed algorithm, simulations are carried out in MATLAB software which consists of two series connected PV modules with two parallel strings, a boost converter and the MPPT controller. The operation of MOSFET switch in the boost converter is regulated by the PWM signal from the MPPT controller. The MPPT algorithm periodically updates the duty cycle of the MOSFET switch. Table 1 shows the parameters of the PV array used for simulation. The parameters of the boost converter used for simulation are mentioned in Table 2.

Table 1 Parameters of the PV module.

Table 2 Boost converter specifications.

The simulations were carried out in the developed simulation model to substantiate the efficiency and tracking time of the proposed algorithm. It is also juxtaposed with the responses of P & O algorithm, traditional PSO algorithm and GWO algorithm to demonstrate its superiority over the conventional algorithms.

The following parameters were used in the implementation of the PSO algorithm and in the proposed PSOMA algorithm as mentioned: c₁ = 0.2, c₂ = 1.0 and ω = 0.5. The number of particles used is five in both the algorithms. The convergence factor ‘a’ in GWO algorithm decreases linearly from 2 to 0. During the entire simulation time, the temperature is maintained constant at 25 °C for all the four algorithms. At first, the simulation starts with an irradiance value of 1000 W/m² and it is then varied to 200 W/m² and once again brought back to 1000 W/m² in all the implemented algorithms. This change in irradiance is incorporated in the simulation to demonstrate the tracking efficiency of the algorithms under investigation at various climatic conditions.

Initially, the developed system was simulated in MATLAB with the traditional P & O algorithm. The output power waveform of the P & O algorithm is shown in Fig. 6. From the waveform, it can be observed that the algorithm tracks the maximum power but still it’s deviating a lot from the ideal power. It takes 0.011 s to converge which is shown in Fig. 7. The efficiency of the P & O algorithm is depicted in Fig. 8. It can be noted from this waveform that the efficiency reached 98.55% when this algorithm is used.

Fig. 6

Output power waveform of P & O algorithm.

Fig. 7

Waveform showing convergence time of P & O algorithm.

Fig. 8

Efficiency waveform of P & O algorithm.

The traditional PSO algorithm is next implemented to track the point of maximum power. Figure 9 shows the output power waveform when this algorithm is implemented in the system. From the waveform, it can be noticed that the MPPT capability of this algorithm is better than the P & O method. Moreover, it converges around 0.0088 s, and it is shown in Fig. 10. The efficiency is 99.04%, which is also higher than the P & O method. It is evident from the waveform of efficiency which is shown in Fig. 11. The developed system is also tested with GWO algorithm, and the efficiency obtained by this algorithm is 99.52%.

Fig. 9

Output power waveform of PSO algorithm.

Fig. 10

Waveform showing convergence time of PSO algorithm.

Fig. 11

Efficiency waveform of PSO algorithm.

The output waveform when the proposed PSOMA algorithm is implemented is shown in Fig. 12. From the waveform, it can be clearly observed that the output power is very close to the ideal power which shows that it effectively tracked maximum power at various insolation values. The convergence time is around 0.0085 s when this algorithm is used which is superior when compared with the other three algorithms under investigation. This is very obvious from Fig. 13.

Fig. 12

Output power waveform of PSOMA algorithm.

Fig. 13

Waveform showing convergence time of PSOMA algorithm.

The efficiency of this algorithm is 99.91% which is far better when compared with P & O, PSO and GWO algorithms. The waveform for efficiency and its zoomed version is shown in Fig. 14. From Fig. 15, the power tracked at various irradiance values can be clearly seen, which shows the robustness of the proposed method. It is also evident from Fig. 16 that the proposed algorithm converges quickly and tracks the maximum power even when the irradiance values are suddenly changed. The efficiency of the PSOMA under various irradiance levels is shown in Fig. 17. From the figure it is evident that the efficiency of the proposed algorithm is not deviating much even under dynamic changes in climatic conditions.

Fig. 14

Efficiency waveform of PSOMA algorithm.

Fig. 15

Output power of PV module for sudden changes in irradiance with constant temperature of 25 °C—PSOMA method.

Fig. 16

Convergence of PSOMA under dynamic conditions (a) When insolation is 600 W/m² (b) When insolation is 800 W/m² (c) When insolation is 200 W/m² (d) When insolation is 400 W/m².

Fig. 17

Efficiency of PV module under dynamic environmental conditions using PSOMA method.

The convergence characteristics of the proposed method towards the global maximum power point (GMPP) is depicted in Fig. 18. It shows that the oscillations at the initial stages converge quickly and tracks the GMPP under various irradiance values. This further justifies the tracking efficiency of the proposed algorithm. The waveform for output voltage, current and the waveform for duty cycle when the proposed PSOMA algorithm is implemented is shown in Fig. 19. The duty cycle thus obtained is provided to the MOSFET in the DC-DC boost converter. The output power of the three algorithms under investigation and the proposed PSOMA algorithm are compared in Fig. 20. From the figure, it is evident that the proposed algorithm performs better in terms of tracking MPP and convergence time. The efficiency of the proposed algorithm is also superior when compared with other three methods and it is depicted in the bar chart in Fig. 21.

Fig. 18

Simulation result on PSOMA convergence characteristics.

Fig. 19

(a) Output voltage waveform (b) Output current waveform and (c) Duty cycle waveform of PSOMA algorithm.

Fig. 20

Comparison of output power of the four algorithms at various irradiance levels.

Fig. 21

Efficiency comparison of the four algorithms under investigation.

The efficiency and convergence time of various methods is compared with the proposed method, and it is graphically represented in Figs. 22 and Fig. 23 respectively. This is also explained in detail with the help of Table 3. From the comparison it is clear that the proposed method proves to be optimal in terms of both efficiency and convergence time.

Fig. 22

Comparison of efficiency between proposed method and existing MPPT methods.

Fig. 23

Comparison of convergence time between proposed method and existing MPPT methods.

Table 3 Comparison of various MPPT methods with proposed method.

The robustness of the proposed PSOMA algorithm is also verified by the developed prototype model which is shown in Fig. 24a and a small-scale solar PV module with a rated voltage of 2 V and a rated current of 550 mA is used in the prototype is shown in Fig. 24b. An adjustable table lamp is used as a light source. The irradiance of the lamp can be varied, and this will be the input for the solar PV module. A lamp is connected to the output of the converter which acts as a load. The measured voltage and current values are given as the input to the DSP controller in which the proposed algorithm is programmed. It will produce the pulse width modulated duty cycle which is given to the MOSFET in the boost converter.

Fig. 24

(a) Hardware setup of the developed system (b) Solar PV module used in the system.

The insolation value is continuously monitored with the help of a solar power meter. A DC servo motor is fitted with the solar PV module to change the tilt angle, and it is also controlled by the DSP controller. The direction of the lamp is also adjusted to verify the practical effectiveness of the proposed algorithm under various irradiance levels. The initial position of the tilt angle can be selected based on the geographic location where the system is being implemented for effective starting conditions in the tracking process. For real time operation, the reset command is used to bring the solar PV module back to its initial operating tilt angle at the end of the day to enable the module to be ready for the next day’s operation.

The value of output power of the solar PV module is measured by a digital oscilloscope and the waveform for output power is shown in Fig. 25. The PV module produces an output power of 1.099 W at an irradiance of 1000 W/m² which is also verified with a clamp meter. The efficiency thus obtained is 99.909% which is very close to the simulation result. Then the irradiance value is changed to 400 W/m² and the value of output power is found to be 0.438 W with an efficiency of 99.55% thus establishing the tracking efficiency of the proposed method. The convergence time from the hardware results is found to be 11.5 ms and it is shown in Fig. 26 which is slightly higher than the simulation result. From the results, it is evident that the proposed method proves its adaptability and robustness under dynamic conditions and ensures optimal operation of the PV system.

Fig. 25

Output power waveform of the proposed PSOMA.

Fig. 26

Convergence time of the proposed PSOMA.

Conclusion

This paper presents an efficient method for tracking the maximum power point (MPP) using the proposed PSOMA algorithm. With a maximum efficiency of 99.91%, the proposed method outperforms traditional MPPT algorithms investigated in this study. Additionally, it demonstrates a significantly shorter convergence time of 8.5 ms for the irradiance level of 1000 W/m², making it faster than many of the compared methods. Even under dynamic changes in the climatic conditions, the efficiency and convergence time does not change drastically. The proposed PSOMA method is shown to be superior in both efficiency and convergence time when compared to a range of existing MPPT techniques. MATLAB simulations validate the algorithm’s performance, confirming its high efficiency and rapid convergence even under varying irradiance conditions. Furthermore, experimental results from the developed prototype highlight the robustness of the proposed method, as the measured efficiency and convergence time closely matches the simulation results. The algorithm continues to perform optimally under dynamic environmental conditions, demonstrating its practical applicability and reliability in real-world scenarios.