Study on material point failure probability of complex jointed rock masses based on peridynamics

Abstract

In rock masses, the presence of numerous randomly distributed joints introduces uncertainty, making the prediction of failure paths challenging. Among these, key joints significantly influence rock mass fracturing. This study proposes a peridynamics (PD) method based on Monte Carlo simulation analysis, discussing the impact of joints with different dips in complex joint networks on rock mass failure probabilities. Efficient parallel computing programs have been developed, markedly enhancing the computational efficiency of large-scale Monte Carlo simulations for PD analysis. The concept of material point failure probability (PFP) is presented, investigating the variation of PFP contour maps after excluding specific joint dips. Grid-based PFP contour maps and Grid-based JAIC (Joint Angle Impact Coefficient) contour maps are created, enabling a quantitative assessment of rock mass failure probabilities. The study reveals the influence of joint dip angles on the failure probabilities of rock masses with complex joint networks. Additionally, the concept of key and non-key joint dip angles based on the grid is introduced. Statistical methods for identifying key and non-key joints in rock mass grid regions are established, providing new perspectives and tools for understanding and predicting the failure of rock masses with complex joint networks. This research contributes to the reliability study of rock mechanics and provides new theoretical guidance for geotechnical engineering.

Introduction

During their formation, rock masses undergo complex tectonic movements, resulting in the random distribution of structural planes, fractures, and other defects with varying characteristics^1,2. These defects form a random joint network within the rock mass, contributing to its discontinuity, heterogeneity, and anisotropy³. Among these, key joints significantly influence rock fracture and control the stability of geotechnical engineering, acting as critical structural weaknesses⁴. The initiation, propagation, and coalescence of joints lead to the ultimate failure of the rock mass⁵. The geometric parameters of joints, including density, thickness, dip angle, and aperture, are inherently uncertain, complicating the prediction of failure paths. Therefore, studying the characteristics of key joints and the expansion patterns of random joints within rock masses is of paramount importance.

In the research on the effects of a single joint dip angle, Su et al.⁶, Li et al.⁷, and others separately investigated the influence of weakly filled and unfilled joint dip angles on the dynamic mechanical properties and crack evolution patterns of sandstone. They found that as the angle increased, both the dynamic compressive strength and peak strain initially decreased and then increased. Moreover, specimens with weakly filled joint dip angles of 0°, 15°, and 30° exhibited stronger characteristics of plastic deformation. Cao et al.⁸ utilized Computed Tomography (CT) and acoustic emission techniques to investigate the influence of joint dip angle and connectivity on the fracture mechanics of specimens. Varma et al.⁹ explored the impact of joint dip angles on longitudinal wave velocity, revealing a pattern where the wave velocity decreases initially and then increases with the increasing joint dip angle. Qian et al.¹⁰ utilized acoustic emission and Digital Image Correlation (DIC) technologies to investigate the impact of the opening joint dip angle and moisture content on the fracture mechanics of coal rocks. They found that specimens with larger joint dip angles primarily undergo shear failure.

In the research on the effects of multiple joints dip angles, He et al.¹¹ studied the influence of bedding plane angles on the rock burst debris ejection velocity and sandstone shear strength. The results indicated that specimens are most prone to rock burst when the bedding plane angle is 60°, while rock burst is least likely to occur when the bedding plane is horizontal. Jin et al.⁵ conducted a series of studies employing Digital Image Correlation (DIC), Computed Tomography (CT), and acoustic emission techniques. Jin et al.⁴ constructed a random joint network based on Monte Carlo theory, and 7 kinds of joint specimens were prepared by 3D printing technology after eliminating a certain inclination angle. Chen et al.¹² conducted a study on the mechanical characteristics of sandstone using Acoustic Emission (AE). The experimental results indicated a transition in the crack propagation trend from shear fracture to tensile fracture in the central part of the specimen. The severity of fracture reached its maximum when the joint dip angle was 60°. Wang et al.¹³ conducted laboratory experiments and numerical simulations to explore the impact of bedding plane angles on the dynamic fracture behavior of shale. Their findings revealed that the bedding plane angle significantly influences the ability of crack propagation. Liu et al.¹⁴ investigated the influence of rough intersecting joint dip angles on rock strength, failure modes, and precursor damage characteristics. They summarized three types of failure modes along with their corresponding failure strength thresholds. Lin et al.¹⁵ explored the evolution of fractures and the failure mechanism in layered rock masses with joints. They analyzed the influence of joint dip angles and rock bridge angles on the mechanical properties and failure behavior of layered rock masses. Zhang et al.¹⁶ proposed a reliability analysis method that considers the uncertainty in the spatial distribution of joints.

Numerical methods, represented by the finite element method, have played an essential role in addressing problems in continuum mechanics. Derived from these methods are discontinuous deformation simulation techniques, such as the extended finite element method and cohesive zone modeling. However, these approaches rely on classical continuum mechanics theory, with governing equations being differential equations. When dealing with discontinuities caused by rock fractures, additional fracture criteria are needed to determine the initiation location and propagation direction of cracks. This dependence can lead to unreasonable predictions of crack propagation. Per the proposal by Silling¹⁷, peridynamics (PD) is a numerical computational method based on non-local thinking. It eliminates the need for differentiating displacement and instead describes material point forces by solving spatial integral equations. Consequently, it can address discontinuity issues without relying on external criteria, overcoming some drawbacks of traditional numerical methods in handling discontinuities. This method demonstrates outstanding performance in addressing discontinuous phenomena such as crack nucleation, propagation, and branching in solid structures.

In recent years, an increasing number of scholars have utilized PD theory to investigate the crack propagation in rocks, leveraging the advantages offered by PD theory in this regard^18,19,20. However, the majority of these studies have been confined to exploring the failure mechanisms of specimens with a limited number of specific cracks. The impact of the extensive presence of random joints in specimens and the influence of joint orientations on the rock failure have not been thoroughly investigated yet.

Some scholars have investigated the interaction between multiple cracks through the finite element method and the extended finite element method^21,22,23,24. Additionally, other researchers have employed PD theory to study the propagation of multiple cracks^25,26,27.

Recent studies have demonstrated the applicability of PD in simulating the mechanical behavior and failure mechanisms of jointed rock masses. For example, PD-based models have effectively captured various failure modes, such as sliding, splitting, and mixed failures, under different joint inclination angles, highlighting the V-shaped trend of peak loads with increasing joint angles and the influence of strength reduction coefficients²⁸. Additionally, advanced micropolar PD models have successfully simulated dynamic fracture processes by incorporating joint-specific parameters and stress-based failure criteria, further revealing the impact of joint geometry on failure characteristics²⁹. Moreover, PD has been employed to study crack propagation, bifurcation, and coalescence in brittle rocks, demonstrating excellent agreement with experimental results and confirming its potential for modeling complex fracture processes in jointed rock masses³⁰.

In summary, different dip angles of joints lead to distinct mechanical properties and failure modes in rock masses. However, existing research has mainly focused on the influence of dip angles in single joints, double joints, and bedding planes on the mechanical properties of rocks. There is limited research on the effects of dip angles in random joint networks, and the impact of “key joints” on the failure probability of rocks has been insufficiently studied. In engineering rock masses, complex joint networks are common, and the understanding of the influence of dip angles in different joints on the failure probability of rocks is still lacking. The transition from studying simple joint properties to complex joint networks is a challenge in the current stage of rock mechanics research, and the identification of key joint dip angles that play a decisive role in rock stability is essential for applying laboratory research to engineering practice. Therefore, it is necessary to conduct in-depth research on the effects of dip angles in complex joint networks, with a specific focus on the patterns of key joint dip angles influencing the final failure probability of rocks. Ultimately, establishing criteria based on dip angles for important joints and uncovering the relationship between rock failure probability and joint dip angles will allow for the statistical identification of key and non-key joints in various regions of rock masses. This statistical method and its findings can contribute to the study of rock engineering reliability, providing a means for the rapid assessment of vulnerable areas and the identification of key joints in different regions of rock masses.

Peridynamics theory

At any given moment, each point in the material corresponds to the position of a material particle, and the ensemble of these infinitely many particles (material points) constitutes a continuum. The PD theory discretizes the material into an infinite series of particles, each possessing mass and volume. By investigating the interactions between these material points and those within their defined range, with the assumption that interactions beyond this range are negligible³¹, the PD theory excels in representing discontinuities compared to classical continuum mechanics. It is a numerical computational model built on a non-local perspective, eliminating the need for displacement differentiation. Instead, it describes the magnitude and relationships of forces between material points by solving spatial integral equations³². Consequently, PD theory can handle both continuity and discontinuity issues. Moreover, it does not rely on external criteria, overcoming the drawbacks of traditional numerical methods that encounter singularities in simulating crack propagation. Hence, in addressing material crack propagation problems, PD theory possesses inherent advantages. This paper uses the bond-based PD theory for the study.

In classical continuum mechanics and local continuum mechanics, the governing equations for the motion of material points or elements within the computational domain can be expressed as:

$$\rho \user2{\ddot{u}}\left( {\varvec{x}} \right) = \nabla \cdot {\varvec{\sigma}}\left( {\varvec{x}} \right) + {\varvec{b}}\left( {\varvec{x}} \right),$$

(1)

where $\rho$ represents the density of the material; $\nabla \cdot {\varvec{\sigma}}$ is the divergence of the Cauchy stress tensor of material point ${\varvec{x}}$; ${\varvec{u}}$ represents the displacement vector of material point ${\varvec{x}}$, and ${\varvec{b}}$ represents the body force vector of material point $x$.

The fundamental expression for the motion equations in the bond-based PD theory model is:

$$\rho \user2{\ddot{u}}\left( {{\varvec{x}},t} \right) = \mathop \smallint \limits_{H} [{\varvec{T}}\left( {\user2{u^{\prime}} - {\varvec{u}},\user2{x^{\prime}} - {\varvec{x}},t} \right) - \user2{T^{\prime}}\left( {\user2{u^{\prime}} - {\varvec{u}},\user2{x^{\prime}} - {\varvec{x}},t} \right)]dH + {\varvec{b}}\left( {{\varvec{x}},t} \right),$$

(2)

where $H = H\left( {{\varvec{x}},\delta } \right) = \left\{ {\left| {\user2{x^{\prime}} - {\varvec{x}}} \right| \le \delta |{\varvec{x}}^{\prime } \in \Omega } \right\}$ represents the collection of material points within the spatial domain $\Omega$, centered around material point ${\varvec{x}}$ (all material points within the horizon of material point ${\varvec{x}}$), the interaction force between material points outside the horizon and ${\varvec{x}}$ is considered to be zero, $\delta$ represents the horizon radius. As shown in Fig. 1. $t$ represents a certain moment in time; $\user2{u^{\prime}}$ represents the displacement vector of material point $\user2{x^{\prime}}$; $T$ represents the force density vector acting on material point ${\varvec{x}}$. ${\varvec{T}}^{\prime }$ represents the force density vector at material point $\user2{x^{\prime}}$.

Fig. 1

Material points and their local region.

The force density vector ${\varvec{T}}$, which is of equal magnitude, is oriented parallel to the relative position vector in the deformed configuration and can be represented as:

$${\varvec{T}}\left( {\user2{u^{\prime}} - {\varvec{u}},\user2{x^{\prime}} - {\varvec{x}},t} \right) = \frac{1}{2}K\frac{{\varvec{\eta}}}{{\left| {\varvec{\eta}} \right|}},$$

(3)

where ${\varvec{\eta}}$ represents the relative displacement vector ${\varvec{\eta}} = \user2{u^{\prime}} - {\varvec{u}}$, and $K$ is an undetermined auxiliary parameter.

Substituting Eq. (3) into Eq. (2), we can obtain the bond-based PD motion equation for material point ${\varvec{x}}$:

$$\rho \user2{\ddot{u}}\left( {{\varvec{x}},t} \right) = \mathop \smallint \limits_{H} f\left( {\user2{u^{\prime}} - {\varvec{u}},\user2{x^{\prime}} - {\varvec{x}},t} \right)dH + {\varvec{b}}\left( {{\varvec{x}},t} \right),$$

(4)

where ${\varvec{f}}$ represents the interaction force function for the bonds associated with material point.

$${\varvec{f}}\left( {{\varvec{\eta}},{\varvec{\xi}}} \right) = \frac{{{\varvec{\eta}} + {\varvec{\xi}}}}{{\left| {{\varvec{\eta}} + {\varvec{\xi}}} \right|}}cs\mu \left( {t,{\varvec{\xi}}} \right),$$

(5)

where ${\varvec{\xi}}$ represents the relative position vector ${\varvec{\xi}} = \user2{x^{\prime}} - {\varvec{x}}$; $s$ represents the relative elongation between material points,$s = (\left| {{\varvec{\eta}} + {\varvec{\xi}}} \right| - \left| {\varvec{\xi}} \right|)/\left| {\varvec{\xi}} \right|$; $E$ is the elastic modulus; $\nu$ is the Poisson’s ratio; $c$ is the micro-modulus function, and for a three-dimensional problem, $c = 12E/\pi \delta^{4}$, when dealing with plane strain problems, $c = 12E/\pi \delta^{3} \left( {1 + \nu } \right)$, when addressing plane stress problems, $c = 6E/\pi \delta^{3} \left( {1 - \nu } \right)$.

When $s$ exceeds its critical relative elongation $s_{0}$, the bond between the material points is permanently broken and no force is applied thereafter, reflecting the entire fracture and failure process. Introducing a history-dependent scalar function $\mu \left( {{\varvec{\eta}},{\varvec{\xi}},t} \right)$ to describe the fracture of bonds:

$$\mu \left( {{\varvec{\eta}},{\varvec{\xi}},t} \right) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {if\quad s < s_{0} } \hfill \\ 0 \hfill & {otherwise} \hfill \\ \end{array} } \right.,$$

(6)

where $s_{0}$ is the critical relative elongation of the bond, and it is related to the fracture energy release rate in classical linear elastic fracture mechanics.

The critical relative elongation $s_{0}$ for the bond can be expressed as:

$$s_{0} = \left\{ {\begin{array}{*{20}l} {\sqrt {\frac{4\pi G}{{9E\delta }}} } \hfill & {2D} \hfill \\ {\sqrt {\frac{5G}{{6E\delta }}} } \hfill & {3D} \hfill \\ \end{array} } \right.,$$

(7)

where $G$ is the fracture energy of the material.

Silling and Askari³³ define damage in PD as the ratio $\varphi \left( {{\varvec{x}},t} \right)$ of the number of broken bonds within the horizon of a material point to the total number of bonds, to describe the path of crack propagation. The expression is given by:

$$\varphi \left( {{\varvec{x}},t} \right) = 1 - \frac{{\mathop \smallint \nolimits_{H} \mu \left( {{\varvec{x}},t,{\varvec{\xi}}} \right)dV_{{x^{\prime}}} }}{{\mathop \smallint \nolimits_{H} dV_{{x^{\prime}}} }},$$

(8)

where $0 \le \varphi \le 1$, $\varphi = 0$ indicates that the material point ${\varvec{x}}$ does not experience damage, while $\varphi = 1$ represents complete damage to that material point ${\varvec{x}}$.

Every point in the material denotes the location of a material particle, and these infinitely many material points (particles) constitute the continuum, within the horizon of a specific material point, there are multiple material points, each possessing physical properties such as volume, mass, displacement, acceleration, etc. For computational convenience, the material is discretized into finite, uniformly shaped, simple, and regularly arranged small cubes. The side length of these cubes is denoted as $\Delta x$, and their volume is $\left( {\Delta x} \right)^{3}$. The basic structural model of the analyzed object is formed by combining these cubes. This discretization approach eliminates the need for complex grid divisions as in the finite element method, while enjoying the advantages of a mesh-free method. The resulting structural elements are simple and regular³⁴.

The interaction between material point $x_{i}$ and other material points within its horizon $\delta$ can be discretely expressed in the motion equations of PD theory³⁴:

$$\rho_{i} \ddot{u}_{i} = \mathop \sum \limits_{j} f\left( {u_{j}^{n} - u_{i}^{n} ,x_{j} - x_{i} } \right)V_{j} + b_{i}^{n} ,$$

(9)

where $\rho_{i}$ represents the mass density of material point at location $i$; $n$ is the time step index, $u_{i}^{n}$ is the displacement of material point at location $i$ at time step $n$; $V_{j}$ is the volume of the material point’s cube at location $j$; $b_{i}^{n}$ is the body force density applied to material point at location $i$ at time step $n$.

A volume correction coefficient is introduced for material points located on the boundary of the horizon, which includes both parts inside and parts outside the horizon. The volume of material point at location $j$ is represented as:

$$V_{j} = \left\{ {\begin{array}{*{20}l} {\left( {\Delta x} \right)^{3} } \hfill & {\left| {\varvec{\xi}} \right| \le \delta - r} \hfill \\ {\frac{{\delta + r - \left| {\varvec{\xi}} \right|}}{2r}\left( {\Delta x} \right)^{3} } \hfill & {\delta - r < \left| {\varvec{\xi}} \right| \le \delta } \hfill \\ 0 \hfill & {other} \hfill \\ \end{array} } \right.,$$

(10)

where $\Delta x$ represents the side length of cubes;$\delta$ represents the horizon radius; $r = \Delta x/2$.

In the numerical model, constraint conditions, such as displacement and velocity, can be imposed on material points within a fictitious boundary region, which has a width approximately three times the grid spacing (δ ≈ $3\Delta x$). Similarly, external loads can be applied as body forces through a material layer with a width of Δx.. The time step length $\Delta t$ satisfies stability requirements according to the following Eq. ³⁵:

$$\Delta t < \sqrt {\frac{2\rho }{{\sum V_{k} \left| {C\left( {{\varvec{x}}_{k} - {\varvec{x}}_{i} } \right)} \right|}}} ,$$

(11)

where $V_{k}$ is the volume at material point at location $k$; $C$ is the elastic stiffness matrix.

The time integration of the PD equation of motion in Eq. (12) can be performed by using explicit forward and backward difference techniques, the calculation is performed according to the following expression:

$$\ddot{u}\left( {x_{i} ,t_{n + 1} } \right) = \frac{1}{\rho }\left[ {\mathop \sum \limits_{j} f\left( {u_{j} - u_{i} ,x_{j} - x_{i} ,t_{n} } \right)V_{j} + b\left( {x_{i} ,t_{n} } \right)} \right],$$

(12)

$$\dot{u}\left( {x_{i} ,t_{n + 1} } \right) = \dot{u}\left( {x_{i} + t_{n} } \right) + \ddot{u}\left( {x_{i} ,t_{n + 1} } \right)\Delta t,$$

(13)

$$u\left( {x_{i} ,t_{n + 1} } \right) = u\left( {x_{i} + t_{n} } \right) + \dot{u}\left( {x_{i} ,t_{n + 1} } \right)\Delta t,$$

(14)

where n represents the n-th time step, and $\Delta t$ is the time step length.

In the first step, the acceleration and velocity obtained at time step n can determine the velocity at time step n + 1, as shown in Eq. (13). In the second step, the displacement at time step n + 1 can be determined using the velocity obtained from Eq. (13) at time step n + 1 and the displacement at time step n, as shown in Eq. (14).

Generation of random joints in rock

Rock joints vary in size, and their distribution and orientation exhibit uncertainty to an extent that existing deterministic computational methods cannot capture and describe such complexity. However, the geometric parameters of the rock joint distribution follow certain probability distribution patterns³⁶. By introducing Monte Carlo simulation and establishing a probabilistic statistical model for relevant geometric parameters, stochastic simulation methods can be applied. Through large-sample Monte Carlo simulations, the interactions of random rock joints can be reproduced to simulate the failure and destruction path of rocks under random joint interactions.

In this paper, the geometric parameters of joints, including position, orientation, and length, are generated using a uniform distribution, denoted as $U\left( {a,b} \right)$.

The probability density function $f(x)$ of a uniform distribution $U\left( {a,b} \right)$ is defined as:

$$f(x) = \left\{ {\begin{array}{*{20}l} {\frac{1}{b - a}} \hfill & {a < x < b} \hfill \\ 0 \hfill & {other} \hfill \\ \end{array} } \right..$$

(15)

The distribution function $F\left( x \right)$ of a uniform distribution $U\left( {a,b} \right)$ is defined as follows:

$$F\left( x \right) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {x < a} \hfill \\ {\frac{x - a}{{b - a}}} \hfill & {a \le x \le b} \hfill \\ 1 \hfill & {x > b} \hfill \\ \end{array} } \right..$$

(16)

The position of joints is controlled by the coordinates of their center points. When describing the position of random joints, a specific region can be designated as the generation area for these joints.

In this paper, we assume the existence of mutually independent uniform distributions, whose distribution functions are denoted as $F_{1} \left( x \right)$, $F_{2} \left( x \right)$, $F_{3} \left( x \right)$, $F_{4} \left( x \right)$.

The center coordinates of random joints are represented as follows:

$$X_{c} = \left( { - l_{1} /2 + l_{1} \cdot F_{1} \left( x \right), - l_{2} /2 + l_{2} \cdot F_{2} \left( x \right)} \right),$$

(17)

where $F_{1} \left( x \right)$ and $F_{2} \left( x \right)$ are the distribution functions of two independent uniform distributions; $l_{1}$ and $l_{2}$ represent the length and width of the generated joint region, respectively, as shown in Fig. 2.

Fig. 2

Material points and their local region.

The description of the orientation of random joints is as follows:

$$X_{r} = \pi \cdot F_{3} \left( x \right),$$

(18)

where $F_{3} \left( x \right)$ is the distribution functions of an independent uniform distribution, and $\pi$ is in radians.

The description of the length of random joints is as follows:

$$X_{l} = l_{max} \cdot F_{4} \left( x \right).$$

(19)

where $F_{4} \left( x \right)$ is the distribution functions of an independent uniform distribution, and $l_{max}$ represents the maximum controlling length of the joint.

The geometric parameters of the random joints, including position, angle, and length, are generated using Eqs. (17), (18), and (19), respectively. These geometric parameters are further independent of each other, and their random generation can simulate the complex distribution of joints in rocks.

Material point failure probability (PFP) based on Monte Carlo simulation and the grid-averaged PFP statistical method

Material point failure probability (PFP) based on Monte Carlo simulation

Rocks, as natural materials, exhibit various complex internal joints. Analyzing and describing the failure probability of rocks require the introduction of probabilistic analysis methods and computational tools. In this work, the concept of Material Point Failure Probability (PFP) is introduced to quantify the failure probability at each material point within the rock masses^37,38.

The PD theory describes the crack propagation path through Eq. (8). When $\varphi_{e} > 0$, the material point starts to exhibit damage, and when $\varphi_{e} = 0$, the material point is undamaged. To statistically evaluate the frequency of material point failure in large-sample Monte Carlo simulations, the material point failure function $I_{e} (k)$ is introduced as follows:

$$I_{e} (k) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {{\text{if}}\;\;\varphi_{e} < \varphi_{t} } \hfill \\ 1 \hfill & {{\text{if}}\;\;\varphi_{e} \ge \varphi_{t} } \hfill \\ \end{array} } \right.,$$

(20)

where $\varphi_{e}$ represents the damage state of material point $e$; $\varphi_{t}$ represents the specified value when the damage value of the material point exceeds a critical threshold, typically ranging between 0.3 and 0.5; $k = \{ 1,2, \ldots ,N\}$, N represents the number of samples.

Material Point Failure Probability (PFP) is calculated using the following equation:

$${\text{PFP}}_{e} = \frac{1}{N}\mathop \sum \limits_{k = 1}^{N} I_{e} \left( k \right),$$

(21)

where ${\text{PFP}}_{e}$ represents the dimensionless PFP for material point e.

The grid-averaged PFP statistical method

To intuitively determine which angle of joints has a greater impact on the failure probability of rocks and quantitatively assess the PFP in each grid, this paper introduces the concept of “Grid-Averaged Material Point Failure Probability” as follows:

$${\text{PFP}}_{G} (i) = \frac{1}{{M_{i} }}\mathop \sum \limits_{q = 1}^{{M_{i} }} {\text{PFP}}_{e} \left( q \right),$$

(22)

where ${\text{PFP}}_{G} (i)$ is the Grid-Averaged Material Point Failure Probability of $i$ grid; $q = \{ 1,2, \ldots ,M_{i} \}$, $M_{i}$ is the number of material points within the $i$ grid.

The presence of joints in a rock mass affects the damage pattern of the rock mass, and in order to quantify the extent to which different angles of joints affect the damage pattern of the rock, this paper introduces the “Joint Angle Impact Coefficient” (JAIC). The JAIC is defined as the ratio of the Grid-Averaged PFP for the changed condition to the Grid-Averaged PFP for the initial condition.

$${\text{JAIC}}(i) = \frac{{{\text{PFP}}_{{{\text{G}}^{\prime } }} (i)}}{{{\text{PFP}}_{{\text{G}}} (i)}},$$

(23)

where ${\text{JAIC}}(i)$ is the JAIC of grid $i$; ${\text{PFP}}_{{{\text{G}}^{\prime } }} (i)$ is the Grid-Averaged PFP for the changed condition; ${\text{PFP}}_{{\text{G}}} (i)$ the Grid-Averaged PFP for the initial condition; When ${\text{JAIC}}(i)$ > 1, it indicates an enhanced destructive effect on the grid, and when ${\text{JAIC}}(i)$ < 1, it indicates the opposite.

In this work, the term ‘grid’ refers to a rectangular domain rather than the conventional meaning of a mesh. This definition is consistent throughout the manuscript."

Numerical flow of the PD method based on Monte Carlo simulation

The PD method based on Monte Carlo simulation is described in the following steps:

• (1) Parameter and matrix initialization, generation of material points and their coordinates, definition of the horizon, and application of initial and boundary conditions.

• (2) Generation of joint geometric parameters using Monte Carlo random numbers based on Eqs. (17), (18), and (19).

• (3) Iterative calculations using the PD solution method to obtain the damage status of each material point.

• (4) Calculation and statistics of Material Point Failure Probability (PFP) for multiple computational samples.

• (5) Plotting the Material Point Failure Probability (PFP) contour map.

• (6) Grid partitioning and calculation of the Grid-based PFP and Grid-based JAIC.

• (7) Plotting the path-'Grid-based PFP’ curves.

• (8) Statistical analysis of key joint dip angles in different regions.

Figure 3 shows the flowchart of the PD method based on Monte Carlo simulation. Figure 4 illustrates the comparison between the method proposed in this paper and traditional methods, as well as the schematic diagram of the Grid-Averaged Material Point Failure Probability method. The proposed method overcomes the limitations of traditional approaches, which neglect the uncertainty and complexity of rock joint distribution when studying rock failure modes and do not utilize uncertainty analysis methods. It provides an efficient technical route for quantitatively describing the uncertainty of rocks. By introducing Monte Carlo simulation and the concept of Material Point Failure Probability (PFP), this paper presents the Grid-Averaged Material Point Failure Probability. This innovative method calculates statistics by excluding different joint dip angles, intuitively revealing key and non-key joints in various regions of the rock mass.

Fig. 3

Flowchart of numerical calculation using the PD method based on Monte Carlo simulation.

Fig. 4

The comparison between the traditional method and the Method in This Paper.

Method verification and analytical methods

Method validation

Validation case 1

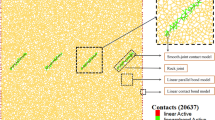
According to reference³⁹, the square rock model is configured as shown in Fig. 5a. Ten initial joints are pre-set, and the center coordinates, angles, and lengths of each joint are listed in Table 1.

Fig. 5

Comparison between PD method and extended finite element method: (a) Geometric model with preset cracks, (b) extended finite element method, and (c) PD method.

Table 1 Geometric parameter.

Figure 5b,c show the calculation results of the extended finite element method and the PD method, respectively. The PD crack propagation results are compared with the extended finite element results from reference³⁹, and they exhibit good consistency.

Validation case 2

According to the reference⁴⁰, the model parameters are set as follows: The upper and lower parts are subjected to tensile loads of 12 MPa, density is 2440 kg/m³, elastic modulus is 72 GPa, the pre-existing notch length is 50 mm, and the critical fracture energy density G₀ is 135 J/m², as shown in Fig. 6.

Fig. 6

Description of the problem setup for the crack branching study.

The calculation results from reference⁴⁰ are shown in Fig. 7a, and the results from the method proposed in this paper are shown in Fig. 7b, and the two sets of results coincide.

Fig. 7

The results from the literature and the results from this study: (a) The computational results from reference⁴⁰, and (b) The results obtained in this paper.

Impact of various dip angles in complex joint systems on failure modes

Model setup with random joints network

The joints in natural rock formations exhibit a random distribution, and the structurally weak planes that significantly influence failure and control the stability of engineering structures are referred to as key joints. To identify these key joints, this study investigates the dip angles of key joints. By introducing the Monte Carlo method, based on the principles of probability statistics, to effectively simulate the distribution characteristics of joints, combined with the advantages of the PD method in calculating fracture problems, we explore the influence of joints at various angles in complex joint systems on the failure probability. The aim is to identify the key joints in rocks.

To better study the influence of fractures with different dips on the failure probability in complex fractures, a complex joint zone was established in the right half of the model (Fig. 8a), based on the verification case in “Method validation” section with the computational model shown in Fig. 7.

Fig. 8

Complex joint Zone and Random complex joints: (a) Complex joint zones, and (b) Random complex joints.

First, based on Monte Carlo theory, we designed a random joint network in the complex joint zone with 7 types of joint dip angles (0°, 15°, 30°, 45°, 60°, 75°, and 90°). The joints were randomly distributed in position, and each type consisted of 4 joints, each 6 mm in length, as shown in Fig. 8b. Using this prototype joint network, we successively removed each specific dip angle, leaving the remaining 6 types to create 7 different joint network models⁴. Each joint network included 24 joints. In total, we constructed 8 fracture network models (without removing any joint dip angles). The flowchart for calculating the impact of different dip angles on failure modes is shown in Fig. 9.

Fig. 9

Flowchart for calculating the impact of different dip angles on failure modes.

Applying the same load as in Fig. 6 to the model with introduced random fractures, as shown in Fig. 10. Figure 11a represents one set of the preset random joint network, and the final failure mode for this set is shown in Fig. 11b. Comparing with the model without random fractures in Fig. 7 the distribution of fractures significantly impacts the failure mode, with fractures at different positions and angles exerting varying degrees of influence on the failure mode.

Fig. 10

Schematic of the numerical model.

Fig. 11

Complex joint network and its crack propagation: (a) Complex joint network, and (b) Crack propagation.

Determination of Monte Carlo simulation samples and computational efficiency

In order to stabilize the calculation results, large samples were computed for the randomly distributed fractures in the complex fracture region. We randomly selected 100 material points and plotted their sample size-PFP curves, as shown in Fig. 12. It can be observed that stability is reached at around 12,000 samples. In this paper, 20,000 Monte Carlo samples were used for the calculations.

Fig. 12

Sample size-PFP curves.

We developed an efficient parallel computing program that utilized 32 cores to process 20,000 samples in parallel. The total computation time was approximately 8.58 h, averaging 1.55 s per sample. This high computational efficiency was achieved through optimized program support, making the program suitable for large-scale Monte Carlo simulations.

PFP contour maps based on Monte Carlo simulation

This paper employs the PD method based on Monte Carlo simulations to calculate and statistically analyze eight PFP contour maps. These maps include joints with all angles, as well as maps where joints with dip angles of 0°, 15°, 30°, 45°, 60°, 75°, and 90° are excluded, as shown in Fig. 13.

Fig. 13

Removal of PFP contour maps for each joint dip angle and partition: (a) No removed angle, (b) Removed angle 0°, (c) Removed angle 15°, (d) Removed angle 30°, (e) Removed angle 45°, (f) Removed angle 60°, (g) Removed angle 75°, and (h) Removed angle 90°

From Fig. 13a–h, we observe significant differences between the PFP contour maps with all joint dip angles included and those with specific joint dip angles removed. The PFP contour map with all dip angles is relatively uniform, with generally higher PFP values compared to when specific dip angles are removed. This indicates that removing joint dip angles decreases the probability of damage in the region. The reduction in damage probability varies depending on which dip angles are removed, demonstrating that selectively removing joint dip angles can effectively lower the probability of damage in certain regions.

To facilitate a concise description of the changes in the PFP contour maps when different joint dip angles are removed, the PFP contour maps are divided into five regions based on the PFP values: I, II, III, A, and B, as illustrated in Fig. 13.

Comparing Fig. 13a–h, it is evident from the PFP contour maps for each removed joint dip angle that:

• (1) With the increase in the removed joint dip angle, the area of region II increases. This indicates that removing larger joint dip angles leads to a larger area in region II and a greater reduction in rock failure probability. In other words, larger joint dip angles have a relatively smaller impact on rock failure probability.

• (2) Comparing the PFP contour maps with and without removed joint dip angles, we observe that removing joint dip angles leads to a reduction in the areas of regions I and II, indicating that the presence of joint dip angles strengthens the rock failure probability.

• (3) The changes in the areas of regions I and III after removing joint dip angles are not significant, while the area of region II undergoes relatively larger changes.

• (4) As the number of excluded joint dip angles increases, the areas of regions A and B gradually enlarge. Notably, after removing the 45° joint dip angle, the areas of regions A and B are similar to those when no joint dip angles are excluded, indicating a similar impact on failure probability between removing the 45° joint dip angle and not removing any joint dip angles.

The values in the upper part of the PFP contour map are larger than those in the lower part. This is because the generated joint dip angles range from 0° to 90°, all inclined in the upper right direction. This orientation guides the path of crack propagation, leading to a higher probability of failure in the upper part compared to the lower part. Consequently, the distribution is not symmetric.

Grid-based PFP contour maps

To better understand the impact of each joint dip angle on the rock failure, and to quantify the PFP in each region more effectively, we introduce the “Grid-Averaged Material Point Failure Probability” proposed in “The grid-averaged PFP statistical method” section.

As shown in Fig. 14, the right half of the rock model is divided into grids, and the grids are categorized according to the specified direction. A total of 11 × 11 grids are set to statistically analyze the PFP contour maps under various conditions. According to Eq. (22), the average PFP for all material points in each grid region is calculated, resulting in the ${\text{PFP}}_{G}$ for each condition.

Fig. 14

Grid partition and its direction.

We selected 11 divisions for both the horizontal and vertical directions for grid partitioning. Compared to other partitioning methods, we believe that 11 divisions can better represent the damage probability of each region of the rock mass without causing a loss of accuracy due to large grid divisions, which would diminish the differences between regions. A denser grid partitioning would render the concept of ‘Grid-Averaged Material Point Failure Probability’ meaningless.

To describe any grid, 11 vertical partitions are designated by I–XI, with the positive direction from top to bottom, and 11 horizontal partitions are designated by A–K, with the positive direction from left to right, as shown in Fig. 14.

According to Eq. (22), calculate the ${\text{PFP}}_{G}$ for each grid region separately. Based on the calculation results and the grid partitioning rules (Fig. 14), draw the Grid-based PFP Contour Maps. The results are shown in Fig. 15.

Fig. 15

Grid-based PFP Contour Maps: (a) No removed angle, (b) Removed angle 0°, (c) Removed angle 15°, (d) Removed angle 30°, (e) Removed angle 45°, (f) Removed angle 60°, (g) Removed angle 75°, and (h) Removed angle 90°

The results in Fig. 15 provide the weighted average of the Material Point Failure Probability for each region (Grid-Averaged PFP), offering a clear visualization of the failure probability within those areas. However, when compared to the PFP contour maps in Fig. 13, it becomes less straightforward to intuitively discern the trends in Grid-Averaged PFP changes after removing joints with specific dip angles based solely on the contour colors.

Comparing Fig. 15a–h, it is evident from the PFP contour maps for each removed joint dip angle that:

• (1) Regions I–V exhibit higher rock failure probabilities than regions VI–XI. This is primarily because the selected joint dip angles (0°–90°) in the computational model guide the crack propagation direction toward the upper right section of the model.

• (2) In regions I–XI (excluding region V), the failure probability of the rock mass generally increases and then decreases along the left-to-right (A–K) direction, with the maximum values typically observed in the C-G region.

• (3) The rock mass failure probability exhibits a ring-shaped diffusion trend, gradually decreasing outward from region VI-A.

Grid-based JAIC contour maps

To quantify the impact of joints with different dip angles on rock failure patterns, the JAIC(i) was calculated according to Eq. (23). This ratio represents the Grid-based PFP for grid i after removing a specific joint dip angle, relative to the Grid-based PFP without removing any joints. Based on JAIC(i), we can determine the extent to which the presence of a specific joint dip angle strengthens or weakens the failure probability in grid i. When JAIC(i) > 1, the presence of the joint dip angle weakens the failure in grid i, and the larger the JAIC(i), the greater the weakening effect. Conversely, when JAIC(i) < 1, the presence of the joint dip angle strengthens the failure in grid i, and the smaller the JAIC(i), the greater the strengthening effect.

The JAIC(i) was calculated and statistically analyzed for the deletion of joint dip angles in seven cases ranging from 0° to 90°. The Grid-based JAIC contour maps were then drawn, as shown in Fig. 16.

Fig. 16

Grid-based JAIC Contour Maps, (a) Removed angle 0°, (b) Removed angle 15°, (c) Removed angle 30°, (d) Removed angle 45°, (e) Removed angle 60°, (f) Removed angle 75°, and (g) Removed angle 90°

By comparing Fig. 16a–g, we can observe the following from the Grid-based JAIC contour maps after removing different joint dip angles:

• (1) When 0°, 15°, 30°, and 45° joints are removed, the JAIC in grids VI-A and VI-B is greater than 1, indicating that the presence of joints with angles between 0° and 45° tends to weaken the failure in these grids. When 60°, 75°, and 90° joints are removed, the JAIC in all grids is less than or equal to 1, indicating that the presence of joints with angles between 60° and 90° tends to enhance the failure in all grid regions.

• (2) As more joint dip angles are removed, the number of grids with JAIC greater than 0.9 also increases. This suggests that removing joints with larger angles more closely resembles the failure pattern when no joints are removed. Larger joint dip angles lead to more uniform overall rock failure, as areas with PFP less than 0.9 gradually decrease.

• (3) When removing any joint dip angle from 0° to 90°, the number of grids with JAIC greater than 0.95 is roughly the same, with only slight variations in their locations.

• (4) The presence of any joint dip angle tends to enhance the failure of the rock.

Introducing paths to describe the grid-based PFP contour maps

To quantify the impact of joints with different dip angles on rock failure, paths were introduced to describe the Grid-based PFP contour maps, and relevant curve plots were drawn. As shown in Fig. 14, we designated A-K (from left to right) as the positive direction, and plotted the path-'Grid-based PFP’ curves for different joint dip angle removal scenarios, as shown in Fig. 17. Compared to the Grid-based PFP contour maps, these curve plots more intuitively illustrate the influence of each joint dip angle on rock failure, making it easier to observe the relationships between different scenarios. The plots clearly show the trend of Grid-based PFP changes in the positive direction of each region and reveal the relationship between Grid-based PFP and different rock regions.

Fig. 17

Path-‘Grid-based PFP’ curves, (a) Region I, (b) Region II, (c) Region III, (d) Region IV, (e) Region V, (f) Region VI, (g) Region VII, (h) Region VIII, (i) Region IX, (j) Region X, (k) Region XI.

By comparing Fig. 17a–k, the following observations can be made from the Path-'Grid-based PFP’ curves:

• (1) The Path-‘Grid-based PFP’ curves can be categorized into three types. Regions I–IV and VIII–XI exhibit a trend of initially increasing and then decreasing, with the maximum value near F. Regions V and VII show a similar trend, with the maximum value near C. Region VI consistently shows a decreasing trend.

• (2) The curves without removed joint dip angles consistently lie above those with removed joint dip angles, indicating that removing joint dip angles weakens the Grid-based PFP of the rock. The extent of this weakening effect varies depending on the specific joint dip angle removed.

• (3) The lower the curve relative to the one without removed joint dip angles, the greater the increase in the rock’s failure probability due to the presence of that joint dip angle. Therefore, the impact of joint dip angles on failure probability can be intuitively judged by comparing the differences in Grid-based PFP values between the curves. A larger difference indicates a greater impact of that joint dip angle on the rock’s failure probability.

• (4) From region I to region V, the distance between curves for each removed joint dip angle gradually decreases, while from region VII to region XI, this distance gradually increases. This indicates that from the upper and lower edges of the rock towards the centerline, the influence of each removed joint dip angle on the rock’s failure probability gradually decreases. In other words, the closer to the edges, the greater the difference in the impact of each joint dip angle on the rock’s failure probability.

• (5) The pattern of curve changes in regions II and X is generally similar to that in regions I and XI. The presence of joint dip angles at 75° and 90° has the smallest impact on the rock’s failure probability, while the influence of joint dip angles from 0° to 60° is essentially similar, with little variation among them.

Regional key joints

In “Introducing paths to describe the grid-based PFP contour maps” section introduces the path-‘Grid-based PFP’ curves. In regions III to IX, the influence of each joint dip angle on rock failure probability is not significantly different. A new statistical method is needed to assess the impact of each joint dip angle on rock failure in these regions.

According to Fig. 17, the Grid-based PFP after removing joint dip angles is generally lower than in the case without removal, indicating that removing joint dip angles tends to decrease the Grid-based PFP. Different joint dip angle removals result in different Grid-based PFP contour maps, with each grid corresponding to joint dip angles that have the maximum and minimum impact on its failure probability. The joint dip angle that has the maximum impact on the failure probability of a grid is considered the key joint dip angle for that grid, while the joint dip angle with the minimum impact is considered the non-key joint dip angle for that grid.

To clearly identify the key and non-key joint dip angles for each grid, we can statistically analyze the joint dip angles corresponding to the maximum and minimum impact on the Grid-based PFP of each grid. These key and non-key joint dip angles can then be marked on each grid. The concept of ‘Grid-based key joint dip angles’ is proposed. As shown in Fig. 18, Fig. 18a represents the joint dip angles whose removal results in the maximum Grid-based PFP (non-key joints), and Fig. 18b represents the joint dip angles whose removal results in the minimum Grid-based PFP (key joints).

Fig. 18

Key and Non-key Joints in the Grid, (a) Non-key Joints, (b) Key Joints.

Through Fig. 18, we can visually identify the key and non-key joint dip angles for each grid. In this paper, we use the grid shown in Fig. 14 for zoning. Readers can adjust the size of the grid based on the model’s dimensions and the desired level of accuracy to meet specific precision requirements.

Analyzing Fig. 18a,b, the following observations can be made:

• (1) In region VI, the key joints for grid areas A–F are mainly large-angle joints, while those for G–J are at a 15° angle. The non-key joint dip angles for A–E and J are small-angle joints in the range of 0°–15°, and for F–J, the non-key joint dip angle is 45°.

• (2) In regions I, II, X, and XI, the key joint dip angles are primarily horizontal joints ranging from 0° to 15°, all with relatively small angles. In region II, the key joint dip angles are 60° for grids A and C, 30° for grid D, and 90° for grid K. In region X, the key joint dip angles are 75° for grid A and 60° for grid K. The non-key joint dip angles are mainly vertical joints ranging from 75° to 90°, all with relatively large angles. Exceptions are grid K in region II and grid A in region X, which have non-key angles of 30°.

• (3) In regions III–V and VII–IX, key joint dip angles are distributed across various angles, primarily with small dips. Key joint dip angles with large dips are mainly located in the center-left position and the far-right edge, with a bias towards the upper side. Non-key joint dip angles are also distributed across various angles but are predominantly characterized by large dips. In regions VII–IX, the non-key joint dip angles tend to be smaller compared to their overall distribution in regions III–V.

• (4) The number of key joint dip angles with large dips in regions I–V is greater than in regions VII–XI. This is because the generated joint dip angles in this study range from 0° to 90°, influencing the direction of fracture propagation. In other words, the tendency of crack propagation is inclined to the upper right, naturally leading to a higher prevalence of large dip joint dip angles in the upper half.

Key joint dip angles significantly influence the stability and control of failures in engineering projects. We will focus on analyzing the key joint dip angles in the regions identified in Fig. 18b.

In regions I–V, there is a higher quantity of key joint dip angles with large angles compared to the right half of the area. Examining the distribution of key joint dip angles in regions I–V and VII–XI, in regions I–V, the key joint dip angles with large angles extend from the horizontal midline to the upper and lower sides, with a greater quantity in the upper part relative to the lower part. Moving from region I to region V, the quantity of key joint dip angles with large angles gradually decreases. In regions VII–XI, key joint dip angles near the right edge are primarily large-angle joint dip angles, while in the remaining areas, key joint dip angles are primarily small-angle joint dip angles.

Conclusion

In this paper, we explored the influence of joint dip angles on the failure probability of rocks under complex joint conditions using a PD method based on Monte Carlo simulation. The following is a summary of the main findings and contributions of the research:

We developed a parallel computing program based on Monte Carlo simulation on PD, selecting a sample size of 20,000 to ensure result stability and significantly improve the computational efficiency of large-sample Monte Carlo simulations. This approach provides low-cost samples for the large-scale training of fracture prediction AI models.

Based on the Material Point Failure Probability (PFP), PFP contour maps were generated, allowing for a quantitative analysis of rock failure probabilities. The introduction of Grid-based PFP contour maps provides a novel quantitative method for assessing failure probabilities in specific regions. Additionally, the incorporation of Grid-based JAIC contour maps quantifies the impact of removing specific joint dip angles on failure probabilities in different regions compared to the case without removal. The proposal of path-'Grid-based PFP’ curves enables statistical analysis of Grid-based PFP along paths, providing insights into the influence of different joint dip angles on rock failure probabilities at various locations.

The study investigated changes in Material Point Failure Probability (PFP) contour maps after removing specific joint dip angles, revealing the impact of each joint dip angle on the failure probability of complex jointed rock. The introduction of Grid-based JAIC contour maps quantifies the influence of removing specific joint dip angles on failure probabilities in different grids. The concept of ‘Grid-based key joint dip angles’ is proposed, offering visual representations of key and non-key joint dip angles in grid maps. This offers a statistical method for assessing engineering stability and provides an intuitive and rapid approach to identifying key and non-key joints in various grids.

In summary, this study introduces new perspectives and tools for understanding and predicting the failure behavior of complex jointed rocks, offering essential theoretical guidance for the reliability of geotechnical engineering. Future research should aim to incorporate the heterogeneity of rock masses, thereby providing more comprehensive theoretical references for depicting failure paths in rock formations.