Introduction

Social network analysis (SNA) is a powerful method to quantify inter-individual interactions and identify the social roles of each individual within a group1. The use of this method has become popular for studying the social dynamics within animal groups or populations and its application has increased considerably in recent years (e.g.,1,2,3). Previous studies on wild animals have, for example, shown the potential of SNA to detect temporal behaviour changes4 and to identify key individuals whose removal or introduction strongly impacts the dynamics of the group1,5,6. In addition, in zoo-housed populations, SNA can help to develop effective conservation strategies7 and improve welfare by reducing social stress8. In a social network, the individual animals are represented as nodes and are connected by edges. The edges can be direct when there is a clear initiator or receiver (e.g., in aggressive interactions), or indirect (e.g., during communal resting)9. Centrality metrics (e.g., degree, betweenness, eigenvector or clustering coefficient) describe the position of each individual within the network, representing different facets of behaviour such as connectivity or influence roles1. General network metrics (e.g., density, fragmentation, or radius) provide information about the overall network structure, such as the cohesion or the brokerage, and enable the comparison between different groups of similar sizes10,11.

Besides its application on wild and zoo animals, SNA is a promising method to gain knowledge about social interactions in farm animals, such as pigs (Sus scrofa domesticus), and to positively impact their welfare. A better comprehension of social interactions in pigs may open doors to new management or breeding strategies to improve their group functioning12. Changes in measures of centrality and cohesion could be used to predict the escalation of abnormal behaviours within groups of pigs. These changes could also help in decision-making to remove key individuals involved in the spread of these behaviours1,13. In addition, when pigs are transferred between production stages, they are subjected to repeated changes in group composition, which often destabilize the social structure and results in aggression14. SNA can guide management practices to reduce social stress and minimize the destabilizing of the social structure. For example, removing pigs with a high centrality from poorly interconnected groups is likely to have a negative impact by destabilizing the group, compared with removing animals from more cohesive groups1. SNA can also help to identify preferential affiliations and their drivers (e.g., sex, age, relatedness, dominance status)15,16,17 and manage groups to keep preferred affiliative partners together, as they may provide social buffering against stressful events18. Previous studies revealed that domestic pigs are highly social animals and may develop social preferences, expressed especially by close spatial proximity during rest19,20,21. The choice of lying partners has, therefore, been suggested as a potential indicator of affiliative preferences.

When performing SNA, researchers have to make a multitude of choices for data collection and analysis. Behavioural data can be collected in a variety of ways, including differences in the sampling method, the period of study, and the definition of the connections between individuals (i.e. edge definitions)4. Depending on the research question being addressed, the edges can be defined based on specific behavioural interactions (e.g., grooming, agonistic behaviours) or on spatial proximity. However, in the literature, there is no consensus on how spatial proximity is defined. In the context of lying, for example, Durell et al. defined spatial proximity as two growing pigs spending time in physical contact or in very close parallel contact19, whereas Li et al. specified a threshold for proximity of 50% of the pig’s body in contact with the other pig22. Goumon et al. considered growing pigs as lying in spatial proximity when they were within 30 cm of each other20, while Jowett and Amory used a threshold of 1 m in sows23. The definition of these thresholds may depend also on the size of the animals, on the environment in which they are housed, on the stocking density, and on the behaviour that is considered (for example lying in close proximity, versus exploring in close proximity)20.

Different spatial proximity definitions might significantly affect the network metrics, and the choice of a definition has therefore important implications for the conclusions that can be drawn from the network9. For example, using a smaller distance threshold to capture spatial proximity may result in a lower frequency of individuals captured as in close proximity, and, thus, a lower individual average degree and lower network density4. A few studies have tested the impact of different protocols on social networks, including the effect of the sampling methods4,24, or different social interactions and proximity techniques15,25. These studies demonstrated that using different methods significantly influences the results of the SNA. However, to our knowledge, the impact of different proximity definitions on proximity networks in pigs has not been investigated so far.

Apart from proximity definitions, sampling rates vary widely across SNA studies in pigs, with data collection periods ranging from one day26,27 to a few hours across several days22,28,29. For SNA based on proximity in pigs, some studies used instantaneous scan sampling, where observations are made by scanning videos at fixed time points (e.g., every 10 min22,30), while others record proximity continuously over a defined observation window (e.g., 30 min31). Most of the SNA studies are based on manual observations which are highly time-consuming and therefore limit sampling duration. However, large quantities of data across all possible interacting individuals are necessary to build a robust and accurate representation of the social network4. Insufficient sampling might result in missed connections between individuals and can have significant implications on social network structure9.

Recent advances in sensing technologies provide the opportunity to considerably increase the sampling rate of the data collection for SNA. Using such technologies, spatial positions of pigs may be investigated continuously at an individual level and over a long period. Location sensors, such as Global Positioning Systems (GPS), have been widely used in wild animals to assess contact patterns and study social networks based on spatial proximity32. These sensors are particularly well adapted to study behaviours of animals kept in large outdoor areas compared with cameras which have only a limited field of view. In farm animals, previous studies investigated the structure of the network of animals raised in relatively large areas (outdoor, free stall barn) with location sensors such as GPS15,33. However, the application of these sensors in dense groups of farm animals kept in relatively small areas is challenging as the quality of the data collected is limited by the accuracy of the sensor15,33, which might be insufficient to provide the correct distance between animals when all distances are relatively short (e.g., within 30 cm, as the threshold used in Goumon et al.20). In addition, such sensors are associated with high costs and often require regular maintenance and therefore are not optimal for applications in large-scale commercial farms32.

As an alternative to GPS, the use of computer vision algorithms is a non-invasive and relatively low-cost method that allows the collection of data at high sampling rates by providing the accurate location of individuals in each frame. Previous studies showed promising results of computer vision algorithms to track individual farm animals, such as cows34, laying hens35, and pigs36,37 in various environments. In pigs, these algorithms have been applied to measure individual activity38. By detecting the pig’s location in each frame, they also give the opportunity to calculate proximity to pen mates and location preferences. In previous studies, social interactions between animals have been extracted from computer vision tracking algorithms in different ways, such as identifying individuals that simultaneously occupy the same region of interest39 or using a combination of thresholds on close distance, orientation of the head and proximity duration40. However, the use of computer vision tracking algorithms to study social proximity has been limited and predominantly focused on small animals, such as mice and Drosophila. In addition, multiple options are also available here to define proximity, and therefore decisions need to be made on how to build the social networks. Furthermore, by giving information at the frame level, these algorithms generate a very large amount of data and may require a long computing time. Therefore, downsampling of camera frames is necessary to study social networks based on tracking algorithms, in order to reduce computing time and to make outputs accessible efficiently to researchers, breeders, or farmers.

Thus, computer vision algorithms allow for many proximity definitions and sampling rates. However, to the best of our knowledge, no research has investigated the effect of different proximity definitions and sampling rates on the social networks of livestock, including pigs, based on computer vision tracking. Therefore, this study aims to explore how different proximity definitions and sampling rates affect proximity social networks in inactive pigs based on tracking data using computer vision in two different housing conditions. We expect that both proximity definition and sampling rate crucially impact the structure of the network resulting in notable changes in the network metrics.

Material and methods

All methods complied with the European Directive 2010/63/EU and Dutch law on the protection of animals used for scientific purposes. The Animal Care and Use Committee of Wageningen University approved the experiment (AVD1040020186245). All methods applied in the study were performed in accordance with the ARRIVE guidelines and regulations41. No anesthesia was performed during the experiment and the pigs were not euthanized after use.

Animals and housing

The pigs used in this study were the same as those described in van der Zande et al.37 and Parois et al.42. The aim of these studies was to study resilience in pigs housed in different housing conditions. Hereto, pigs were subjected to several challenges between nine and 21 weeks of age. Pigs were 15 weeks of age when they were used for the current study. Three weeks before that, they had been exposed to a 2-h transport challenge with their pen mates42. Briefly, the experiment was carried out on 126 crossbred boars and gilts, equally divided into 3 different batches, and housed at CARUS research facility of Wageningen University and Research (Wageningen, the Netherlands) from 9 weeks of age. The pigs were grouped into 21 pens (n = 6 pigs per pen, balanced in sex) and kept in two different housing systems: 9 barren pens and 12 enriched pens. The unequal distribution of the pens across the two housing systems was due to technical issues with the cameras in the barren pens. In the barren system, the pigs were housed in pens with a partly slatted floor (1.2 × 4.7 m). The enriched pens were double in size (2.4 × 4.7 m) and the floor was covered with sawdust, straw, and peat, as bedding material, and several types of objects (toys, jute bags, rope, egg boxes) or substrate (hay, or alfalfa) were provided according to an alternating schedule. The temperature within the pens was recorded via temperature sensors during the three days of data collection. The temperature reached 23 °C during the first two days and 22 °C during the third day. Artificial light was provided between 07:00 and 19:00 h.

Data collection and computer vision algorithm

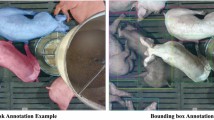
All pens were equipped with an RGB camera (Velleman: 1 lx/f2.0) mounted above the pen (top-down view) and plugged into electrics. Videos were recorded with a frame rate of 25 frames per second (FPS) and a resolution of 352 by 288 pixels. Videos were collected and analyzed on three consecutive days at 15 weeks of age using the computer vision algorithm for object detection and tracking described by van der Zande et al. (2021)37. This algorithm was trained on 4,000 annotated images spread across different days and pens. The algorithm You Only Look Once version 343, combined with Simple Online Realtime Tracking44 was used to detect and track the location of each pig by a bounding box. The tracking data was cleaned manually by removing false positive detections (detections of more than six individuals per pen) and the sequential bounding box ID was connected to the real ID of the animal. More details about false positive detections can be found in van der Zande et al. (2021)37.

Calculation and inactivity definition

To calculate proximity definitions during inactivity, we first needed to define when the pigs were inactive. Hereto, the distance moved by each pig in the three days was calculated by comparing the centroid of the bounding boxes of the same individual in two consecutive frames sampled at one frame per minute. Equation (1) from the Pythagorean theorem was used, where xt and yt are the coordinates of the centroid of the bounding boxes at frame \(t\), and \(x_{t+1}\) and \(y_{t+1}\) are the corresponding coordinates at frame \(t+1\). An individual was considered inactive when the \(distance\,moved\) between frame \(t\) and frame \(t+1\) was below 20 cm. This simple threshold was selected based on preliminary examinations of frames to capture instances when pigs were changing lying positions, such as transitioning between lateral and ventral lying, while filtering out pigs in locomotion.

$$distance\,moved = \sqrt {\left( {x_{t + 1} - x_{t} } \right)^{2} + \left( {y_{t + 1} - y_{t} } \right)^{2} }$$
(1)

Calculations of proximity definitions

The proximity between two pigs was only calculated when they were simultaneously inactive.

Distance between individuals

For each pair of pigs, the distance between the two individuals was calculated from the centroids of their bounding boxes within the same frame. The centroid of the bounding box corresponds to the point of intersection of its two diagonals. Equation (2) was used, where \({x}_{i{d}_{1}}\) and \({y}_{i{d}_{1}}\) are the coordinates of the centroid of the bounding box of pig \(i{d}_{1}\), and \({x}_{i{d}_{2}}\) and \({y}_{i{d}_{2}}\), the corresponding measure for pig \(i{d}_{2}\).

$$distanc{e}_{i{d}_{1}i{d}_{2}}= \sqrt{{\left({x}_{i{d}_{1}}-{x}_{i{d}_{2}}\right)}^{2}+{\left({y}_{i{d}_{1}}-{y}_{i{d}_{2}}\right)}^{2}}$$
(2)

Surface of overlap of the bounding boxes

The surface of overlap of two bounding boxes within the same frame (S) was calculated from the coordinates of the bounding boxes (Supplementary Fig. S1). The percentage of the overlap of the surface (surface overlap) was calculated as the surface of overlap divided by the sum of the areas of the two bounding boxes using Eq. (3).

$$surface\,overlap= \frac{S}{{S}_{1}+{S}_{2}} \times 100\%$$
(3)

Proximity definitions

Five different definitions of proximity were used to build the social networks (Table 1); four binary definitions based on the distance between the centroids and/or surface overlap of the bounding boxes, and a weighted proximity, being the inverse of the harmonic mean of the distances between two individuals. This approach was chosen, as it assigns more significance to differences in distance when pigs are in close proximity compared to when they are further apart. For instance, if there are three distance records for two pigs (0.5 m, 1 m, and 1.5 m), the mean distance is 1 m. However, the mean proximity is calculated as (1/0.5 + 1/1 + 1/1.5)/3, resulting in a value of 0.82. This value is smaller than the reciprocal of the mean distance (1/1 = 1), indicating that shorter distances (such as 0.5 m) have a more pronounced impact than longer distances (like 1.5 m). \({P}_{weig}\), the weighted proximity (cm) was calculated using Eq. (4), where \(distanc{e}_{i{d}_{1}i{d}_{2}}(k)\) is the distance between the centroids of the bounding boxes of pig \(i{d}_{1}\) and pig \(i{d}_{2}\) (calculated similarly to Eq. (2)) in the frame k, and n is the total number of frames in which the two individuals were simultaneously inactive. The thresholds of 20% and 50 cm were chosen by combining insights from existing literature (50 cm corresponding to the 30 cm as used in Goumon et al.20, with an additional 20 cm to account for the centroid of the bounding box, rather than the edge of the pig) and through preliminary examination of frames (Fig. 3).

Table 1 Proximity definitions used to construct the five different social networks.
Full size table
$${P}_{weig}=\frac{1}{n}\sum_{k=1}^{n}\frac{1}{distanc{e}_{i{d}_{1}i{d}_{2}}\left(k\right)}$$
(4)

Agreement between proximity definitions

The percentage of agreement was calculated for each pair of the binary proximity definitions and each pair of bounding boxes across time using Eq. (5). \(Agreement\) refers to the instances where pairs of bounding boxes were classified similarly by the two proximity definitions (either both in close proximity or both not in close proximity). \(Disagreement\) refers to the instances where one proximity definition categorized the bounding boxes as in close proximity while the other did not.

$$\%\,of\,agreement= \frac{Agreement}{Agreement+Disagreement} \times 100$$
(5)

Social network analysis

Construction of matrices for social network analysis

A matrix of proximity was generated for each pen and proximity definition. We filtered this matrix to keep only the associations when the individuals were simultaneously inactive and in close proximity (according to each definition). The edges of each network (for the four binary definitions) were built with a half weighted index (HWI)45 using Eq. (6), where \({{T}_{prox}}_{i{d}_{1}i{d}_{2}}\) is the total time during which pig \(i{d}_{1}\) and pig \(i{d}_{2}\) were simultaneously inactive and in close proximity according to one of the definitions, \({{T}_{id}}_{1}\) the total time pig \(i{d}_{1}\) spent inactive, and \({{T}_{id}}_{2}\) the total time pig \(i{d}_{2}\) spent inactive. This correction was necessary to account for variation in activity between pigs from the same pen. Otherwise, more active pigs might have appeared more central in a network simply due to their increased activity level, rather than their actual social preferences.

$$HWI= \frac{{{T}_{prox}}_{i{d}_{1}i{d}_{2}}}{{{(T}_{id}}_{1}+{{T}_{id}}_{2})/2}$$
(6)

Similarly, we calculated the HWI for the quantitative proximity definition (WEIG) using Eq. (7), where \({T}_{i{d}_{1}i{d}_{2}}\) is the total time during which pig \(i{d}_{1}\) and pig \(i{d}_{2}\) were simultaneously inactive.

$$HWI= \frac{{{{P}_{weig}\times T}}_{i{d}_{1}i{d}_{2}}}{\left.{{\left(T\right.}_{id}}_{1}+{{T}_{id}}_{2}\right)/2}$$
(7)

The HWI in Eq. (6) represents the proportion of time that two pigs were simultaneously inactive and in close proximity, adjusted for their individual inactivity durations. Similarly in Eq. (7), the HWI represents the proportion of time that two pigs were simultaneously inactive, adjusted for both individual inactivity duration and the proximity, defined as the average distance between the two pigs.

Construction of the complete and reduced networks

To estimate the effect of sampling rate on social networks, we compared a complete network to networks built with different sampling rates. For each proximity definition, the complete network was built using a frame rate of 0.5 FPS (corresponding to one frame every two seconds) to reduce potential noise due to micro-movements of the bounding boxes38. For each proximity definition, networks were built using different sampling rates, by using different sampling intervals (i.e. the interval between frames) ranging from one frame per 10 s to one frame per hour. From here on, we will refer to these networks as reduced networks, to distinguish them from the complete network (with one frame per 2 s).

Network visualization

Undirected social networks were visualized with R (version 4.1.2, R Foundation, Vienna, Austria), using the package “igraph”46 where nodes represent individuals, and edges the HWI.

Network metrics

For each network, we calculated four different network metrics (Table 2 and Fig. 1) that measure different aspects of the network, both at individual and group level, based on direct and indirect connections. These metrics were selected based on their widespread use and established biological relevance1. They measure different aspects of the network and were therefore used as a representative case to illustrate the impact of proximity definitions and sampling rates on the network. Their characteristics are summarized in Table 2 and examples are given in Fig. 1. Direct/indirect relates to whether a metric measures properties using only immediate relationships (direct) or considers more complex network structures or relationships (indirect). Local/global, on the other hand, refers to whether a metric provides information about the network as a whole structure (global) or about the micro-structure of the network (local). Degree and eigenvector centrality reflect the prominence of a node, the degree centrality serving as an indicator of animals that are well connected with others and the eigenvector centrality as an indicator of influential animals47. In the context of the study, a pig with a high degree centrality is lying in proximity to many of its pen mates, whereas a pig with a high eigenvector centrality is lying in proximity to other pigs that are themselves lying in proximity to many of their pen mates. Clustering coefficient and radius evaluate the cohesiveness and the strength of bonds in a group10,11. The clustering coefficient evaluates the cohesiveness between the neighbours of a specific node (pen mates it lies close to) and the radius between all group members. A pig with a high clustering coefficient is part of a closely connected group, where its neighbours frequently lie in proximity to each other. A low radius value indicates that most of the pigs are lying in proximity to most of their pen mates.

Table 2 Description of the network metrics.
Full size table
Fig. 1
figure 1

Examples of networks (a–c) and their metrics. Individual level metrics are shown only for network a.

Full size image

Comparison of social network metrics

A Mann–Whitney U test was used to assess whether the metric of the enriched pens (n = 12) differed significantly from the metric of the barren pens (n = 9) within each proximity definition. This non-parametric statistical test was used because the data were not normally distributed.

A bivariate linear model was fitted in ASReml 4.249 to estimate the correlation between the same metric for pairs of proximity definitions or pairs of sampling rates (Eq. 8),

$$\left[\begin{array}{c}{\mathbf{y}}_{1}\\ {\mathbf{y}}_{2}\end{array}\right]= \left[\begin{array}{cc}{\mathbf{X}}_{1}& 0\\ 0& {\mathbf{X}}_{2}\end{array}\right] \left[\begin{array}{c}{{\boldsymbol{\upbeta}}}_{1}\\ {{\boldsymbol{\upbeta}}}_{2}\end{array}\right] + \left[\begin{array}{c}{{\boldsymbol{\upvarepsilon}}}_{1}\\ {{\boldsymbol{\upvarepsilon}}}_{2}\end{array}\right]$$
(8)

where \({\mathbf{y}}_{1}\) and \({\mathbf{y}}_{2}\) are the response vectors for the first and second trait, respectively, \({\mathbf{X}}_{1}\) and \({\mathbf{X}}_{2}\) are the design matrices for the vectors of fixed effects \({{\boldsymbol{\upbeta}}}_{1}\) and \({{\boldsymbol{\upbeta}}}_{2}\), and \({{\boldsymbol{\upvarepsilon}}}_{1}\) and \({\varepsilon }_{2}\) are the vectors of residuals. Traits 1 and 2 were either the metrics of a pair of proximity definitions, or the metrics of a pair of sampling rates. When analyzing sampling rates, trait 1 was always the metric of the complete network and trait 2 the metric of the reduced network. The fixed effects included housing and sex for the individual level metrics, and housing for the pen level metric (radius). The normality of the residuals was assessed for each univariate model by visual inspections (histograms and QQ-plots) and a Shapiro–Wilk test. A log transformation was applied to the radius, as the residuals of the models built with radius and DIST and DIST_SURF were not normally distributed. Residuals follow a bivariate normal distribution with (co)variance matrix:

$$var\left[ {\begin{array}{*{20}c} {{{\boldsymbol{\upvarepsilon}}}_{1} } \\ {{{\boldsymbol{\upvarepsilon}}}_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\sigma_{{\varepsilon_{1} }}^{2} } & {\rho_{12} \sigma_{{\varepsilon_{1} }} \sigma_{{\varepsilon_{2} }} } \\ {\rho_{12} \sigma_{{\varepsilon_{1} }} \sigma_{{\varepsilon_{2} }} } & {\sigma_{{\varepsilon_{2} }}^{2} } \\ \end{array} } \right] \otimes {\mathbf{I}}$$

where \(\otimes\) denotes the Kronecker product of two matrices and I is an identity matrix. The \(\rho_{12}\) is the parameter of interest i.e. the correlation between the metrics for trait 1 and trait 2. Hence, correlations were estimated after the correction of response variables for the fixed effects.

To assess the significance of the correlations, we calculated the Z-score by dividing the correlation coefficient by the standard error.

Results

Data description

Distribution of the distance and surface overlap of bounding boxes

Figure 2a shows the distribution of the distance between the centroids of bounding boxes among all possible pairs of individuals when both were inactive. In enriched pens, the average distance between bounding box centroids was 202.9 ± 96.6 cm (mean ± standard error), whereas, in barren pens, it was 129.9 ± 88.4 cm. Note that the enriched pens were twice as large as the barren pens. In enriched pens, the distribution was right-skewed without clear peaks (Fig. 2a). In barren pens, the distribution was more complex, with three local maxima. In addition, in the enriched pens, 2.3% of the pairs of bounding boxes were in close proximity based on their distance (< 50 cm), whereas in the barren pens, this was 11.3% (Fig. 2a).

Fig. 2
figure 2

Distributions of the distance between the centroids of pairs of bounding boxes (a) and the percentage of overlap of the surfaces of pairs of overlapping bounding boxes (b), separated for enriched and barren housing conditions. These distributions are based on n = 21 pens (12 enriched, 9 barrens), each pen containing 15 pairs of bounding boxes (for 6 individuals) at each time point (FPS = 0.5) and over 3 days. Note that panel b starts at values greater than 0% to focus on cases where bounding boxes overlap.

Full size image

Figure 2b shows the distribution of the percentage of overlap, between pairs of bounding boxes with more than 0% overlap. In total, 15.9% of the pairs of bounding boxes overlapped in enriched pens and 32.3% in barren pens (Fig. 2b). For both housing conditions, the distribution followed a right-skewed decreasing trend, with a higher probability for a small overlap than a large overlap. The probability of an overlap greater than ~ 60% was almost zero. Within the pairs that showed overlap, the percentage of overlap was smaller in enriched pens than in barren pens. In addition, in the enriched pens, 5.2% of the pairs of bounding boxes were in close proximity based on their overlap (> 20%), whereas in the barren pens this was 14.4% (Fig. 2b).

Agreement between proximity definitions

Table 3 shows the percentage of agreement of the four binary proximity definitions. The agreement varied from 81.9% between DIST_SURF and OVER to 98.9% between DIST and DIST_SURF (Table 3). The lowest agreements were found between OVER and the other definitions, and the highest between DIST_SURF and the two definitions DIST and SURF (Table 3).

Table 3 Percentage of agreement between the four binary proximity definitions.
Full size table

Figure 3 shows four cropped frames with the bounding boxes of two pigs, illustrating agreement (Fig. 3a) and disagreement between the binary proximity definitions (Fig. 3b–d). As an example, we concentrate our result description on DIST and DIST_SURF. In Fig. 3b, the two pigs adopted a parallel ventral position, resulting in a short distance between the centroids of their bounding boxes (DIST criterion for proximity satisfied) but a limited surface overlap (SURF proximity criterion rejected). In Fig. 3c, d, only the SURF criterion was met and not DIST. This occurred for example, when the two pigs faced each other, with a portion of their body aligned in parallel (Fig. 3c), or when the two pigs lay at an angle (Fig. 3d).

Fig. 3
figure 3

Examples of cropped frames showing detected pairs of pigs with bounding boxes (a–d). In blue and yellow the bounding boxes and their respective centroids are highlighted. Below the frames, the distance between the centroids of the bounding boxes and surface overlap of the bounding boxes are given. The table indicates whether the pigs fulfil each proximity definition (marked by a green check) or not (indicated by a red cross). DIST: Distance between centroids of bounding boxes < 50 cm, SURF: Overlap of bounding boxes > 20%, DIST_SURF: Combination of DIST and SURF, OVER: Presence of overlap between bounding boxes.

Full size image

Consequences of the proximity definitions for the network

The results reveal significant differences between enriched and barren pens for some of the network metrics (Table 4). Within the same proximity definition, barren pens exhibited a higher degree centrality, clustering coefficient and radius compared to the enriched pens (Table 4). This result indicates denser connectivity within the network of the barren pens in line with the distribution of the distance and surface overlap (Fig. 2).

Table 4 Comparison of four network metrics (mean ± standard deviation) per housing condition (Barren vs. Enriched) built with different proximity definitions.
Full size table

Figure 4 shows the correlations, estimated by a bivariate model, of the complete networks built with the five different proximity definitions for each of the four metrics studied. All correlations were highly significant (Z > 3.29, p < 0.001), indicating strong associations for the same network metric across different proximity definitions. Overall, positive correlations were observed but the strength of these correlations varied largely. Strong correlation coefficients were observed for the direct metric degree centrality, ranging from 0.66 to 0.99 (Fig. 4). However, these correlations were lower for indirect metrics with values decreasing to 0.39 for eigenvector centrality and 0.35 for clustering coefficient. For the indirect metrics, the correlations were found to be weaker for the local metric clustering coefficient than the global metric eigenvector centrality. At the network level, the radius metric showed both weak and strong correlations, ranging from 0.52 to 0.96 (Fig. 4).

Fig. 4
figure 4

Comparison of network metrics built with different proximity definitions. (a) Degree centrality, (b) Eigenvector centrality, (c) Clustering coefficient, (d) Radius. The network metrics are calculated based on the tracking data with a sampling rate of 0.5 FPS. The lower off-diagonal shows scatter plots with the linear fit in black and the correlation coefficients calculated from the bivariate model. All the correlations were significant (p < 0.001). The correlations coefficients for the radius were estimated with a log-transformation, due to the non-normal distribution of the residuals. The scatter plot and distribution of the radius values are plotted with the original data. Proximity between two pigs is defined with DIST: Distance between centroids of bounding boxes < 50 cm, SURF: Overlap of bounding boxes > 20%, DIST_SURF: Combination of DIST and SURF, OVER: Presence of overlap between bounding boxes, WEIG: harmonic mean of the distance between the centroids of the bounding boxes.

Full size image

Among the binary proximity definitions, there was a trend to stronger correlations between the metrics when the proximity definition was built using the same geometric measure (Fig. 4). For instance, there were higher correlations between the metrics, when proximity was based on bounding box centroid distance (DIST and DIST_SURF) or between the ones based on surface overlap (SURF and OVER). On the other hand, correlations tended to be lower when comparing different geometric measures; particularly between DIST_SURF and OVER (correlation coefficients < 0.66).(Interestingly, the correlations between the proximity definition WEIG and the other four definitions differed largely depending on which metric was considered. The correlations between a metric of a pair of proximity definitions were particularly high with degree centrality and lower with the other metrics (Fig. 4).

A case study of an enriched pen

To illustrate the influence of the choice of a proximity definition on the network, a case study of an enriched pen is presented in Fig. 5. The DIST, DIST_SURF, and SURF networks show variations in edge strengths between different nodes within the network. These variations suggest that certain pairs of individuals spent more time in close proximity compared to other pairs (Fig. 5). In contrast, in the OVER and WEIG networks, all individuals appeared to be nearly equally connected within the network, suggesting a more uniform distribution of proximity across the group. This contrast between the networks is also reflected by the network metrics, with higher variations between the metrics values for different nodes in DIST, DIST_SURF, and SURF than in OVER and WEIG. The high connectivity between all pairs of individuals in OVER and WEIG is reflected by the higher clustering coefficient for both OVER and WEIG compared with DIST, DIST_SURF, and SURF (Fig. 5).

Fig. 5
figure 5

An example of the structure of the networks for an enriched pen based on the different proximity definitions. The network metrics are calculated based on the tracking data with a sampling rate of 0.5 FPS. The width of the edge is proportional to the strength of the proximity. The degree centrality shown in this plot has been normalized by dividing the value by the average degree centrality of each proximity definition. The normalization was applied to the degree centrality to facilitate the comparison across different networks. In contrast, normalization was not necessary for eigenvector centrality and clustering coefficient, as these metrics are already bounded between 0 and 1. Proximity between two pigs is defined with DIST: Distance between centroids of bounding boxes < 50 cm, SURF: Overlap of bounding boxes > 20%, DIST_SURF: Combination of DIST and SURF, OVER: Presence of overlap between bounding boxes, WEIG: harmonic mean of the distance between the centroids of the bounding boxes.

Full size image

Furthermore, certain edges (e.g., 4–6 and 1–5) exhibited consistent strength levels across all networks, whereas others displayed varying strength between the five different networks (Fig. 5). For example, edge 3–4 was characterized by weak strength in OVER, SURF, and WEIG, but high strength in DIST and DIST-SURF (Fig. 5). As a result, we observed that pigs were ranked differently across networks, according to the network metrics. For example, in DIST and DIST_SURF, Pig 3 exhibited a noticeably high centrality (according to average degree and eigenvector) whereas Pig 1 had a low centrality (Fig. 5). This position was, however, not consistent across the five network definitions.

Consequences of downsampling for each network metric and proximity definition.

The impact of downsampling the tracking data for the two housing conditions combined is shown in Fig. 6 and presented separately for enriched and barred pens in Supplementary Figure S2. The impact of downsampling varied across network metrics (Fig. 6). Overall, the degree, eigenvector centrality, and radius were minimally impacted by downsampling. Especially for the degree centrality, the correlations with the complete network (1 frame every 2 s) remained high (> 0.90) even after reducing the sampling rate to 1 frame every hour (Fig. 6). Lower correlations between the reduced networks and the complete network were found for the clustering coefficient. To maintain high correlations for all the network metrics (> 0.90) without considering the housing conditions, the downsampling should not go beyond 1 frame every 6 min (Fig. 6). However, in barren pens, a larger sampling rate (1 frame every 25 min) would be sufficient to maintain high correlations for all network metrics, whereas in enriched pens, the downsampling should not go beyond 1 frame every 6 min (Supplementary Fig. S2).

Fig. 6
figure 6

Correlations between the metrics of the reduced network (built with different sampling intervals) and the metrics of the complete network (2 s sampling interval), for the degree centrality, eigenvector centrality, clustering coefficient, and radius. Note that the y-axis scale differs between panels. These plots show the results for both enriched and barren environments combined.

Full size image

The impact of downsampling on the network metrics varied across proximity definitions. For the networks built with WEIG, the metrics of the reduced networks maintained strong correlations with the complete network (ranging from 0.86 for clustering coefficient to 0.98 for degree centrality at a 1 frame per hour sampling rate, Fig. 6). For degree centrality and radius, the choice for a binary proximity definition seems to have less impact on the effect of downsampling on the correlations. For degree centrality, for example, the maximum difference between the lowest and highest correlations for different proximity definitions was 0.05 (observed at a sampling rate of 1 frame per 45 min). In contrast, the choice of a binary proximity definition has a clear impact on the effect of downsampling on the clustering coefficient. For the clustering coefficient, the maximum difference between the lowest and highest correlations for different proximity definitions was 0.55 (achieved with 1 frame per hour, Fig. 6). The clustering coefficient of the networks DIST and DIST_SURF were more sensitive to downsampling than the clustering coefficient of OVER and SURF.

Discussion

This study aimed to explore how different proximity definitions and sampling rates affect social network metrics of inactive pigs. Clear differences between networks, at both the individual and the network level, were revealed when using different proximity definitions. Network metrics differed in their sensitivity to downsampling, and this sensitivity was also affected by the chosen proximity definition.

In previous studies on spatial proximity in pigs with manual observation, lying in spatial proximity was defined in different ways19,20,22,23. The definition seems to depend on the interpretation of the observer whether two pigs are in proximity or not. Given the absence of one unique proximity definition, the goal of this study was not to identify the best definition for validating the detection of proximity. However, observers likely agree that pigs are in close proximity when there is full-body contact (as captured by DIST definition, see Fig. 3a, b). In contrast, part-body contact (captured by definition based on the overlap of bounding boxes, i.e. SURF and OVER, see Fig. 3c, d) is more likely to result in interobserver discrepancies, for example in the case when pigs are tail-to-tail.

The downside of DIST, SURF and DIST_SURF, the latter definition combining distance and overlap, is that the experimenter needs to decide on a minimal threshold that distinguishes whether pigs are in close proximity or not. The decision on this threshold might be arbitrary, as the ‘ideal’ distance is currently unknown50. This threshold needs to be decided carefully as a larger threshold, for example, may include more pairs of individuals considered as in close spatial proximity, resulting in a higher degree centrality4. The dependency of the results on the definition of the threshold also hampers comparisons of studies. In this study, we set thresholds for two definitions: DIST with a threshold of 50 cm distance between the centroids of two bounding boxes, and SURF with a threshold of 20% overlap of the surface of bounding boxes. DIST depends on the size of the animal, and the threshold should therefore be higher with larger pigs. SURF already takes into account the size of the animal, which makes it possible to use the same threshold for older pigs. An alternative to defining the threshold by an experimenter may utilize the size of the bounding box for the threshold.

Two of our definitions, OVER and WEIG, did not rely on a threshold set by the experimenter. OVER, i.e. the presence of overlap between two bounding boxes, might have included pigs that did not have any kind of contact. This definition can be relevant for a large population in a large area, but it may not be so suitable for pigs kept in relatively small pens. WEIG, the quantitative definition of proximity, was defined as the harmonic mean proximity between pigs and calculated as the average of the reciprocals of their distances. This definition assigns more significance to differences in distance when pigs are in close proximity compared to when they are further apart. As this approach includes all the distances, we expect it to be more powerful in distinguishing between certain pairs of individuals—for example, in distinguishing one pair that does not meet a binary definition of proximity but is often slightly above the threshold to another pair that consistently remains far apart.

At the individual level, changes in proximity definition had a minor effect on the direct metric degree centrality, whereas the indirect metrics (eigenvector centrality and clustering coefficients) were considerably affected. Degree centrality only considers a node’s immediate connections, making it less sensitive to changes in the network4 induced by different proximity definitions, compared with indirect metrics which consider the importance of a node based not only on its own connections but also on the connections of its neighbours1. A different proximity definition could result in changes in the weight of the edge and neighbouring nodes, potentially causing a cascading effect throughout the entire network structure and leading to significant shifts in the values of the indirect metric. In line with this result, Castles et al. (2014), who compared baboon networks based on three different proximity definitions (distance rule, chain rule, and nearest neighbour) also observed that the direct metrics degree and closeness were less affected by the chosen proximity definition than the indirect metric betweenness (another indirect metric that quantifies the extent to which a node serves as an intermediary between other nodes in a network)25.

The local metric clustering coefficient was more affected by the choice of proximity definition than the global metric eigenvector centrality. The clustering coefficient is based on micro-level patterns within the network, whereas eigenvector centrality takes into account a node’s influence on the entire network and captures larger network patterns that may remain more consistent across proximity definitions. This could explain the lower correlation coefficients found between clustering coefficient metrics based on different proximity definitions and suggests that the networks based on the five different proximity definitions share more common information at a global network level, but may not align as closely at a local level.

Degree centrality, eigenvector centrality, and radius were also less impacted by downsampling than the clustering coefficient. For most of the proximity definitions (except DIST and DIST_SURF), downsampled tracking data still provided robust information (i.e. correlations between the yielded metrics and complete network remained > 0.90) on the positions of individuals within the network. These results agree with Davis et al. (2018), who found that low levels of sampling (10 samples/individual) can provide the same information as high levels of sampling (> 64 samples/individual in the same period) for social networks based on proximity in baboons4. Furthermore, downsampling had a negligible impact on the WEIG networks across various network metrics, compared with the binary definitions. This distinction lies in the nature of the proximity definition: WEIG integrates proximity between individuals in each frame, whereas the binary definitions consider individuals in proximity in a given frame only if they meet the specific condition. Downsampling increases the probability of missing a frame where this specific condition is met. Within the binary definitions, DIST and DIST_SURF were particularly affected by downsampling, given their restrictive condition occurring less frequently than OVER and SURF. Networks built with DIST and DIST_SURF require therefore a higher sampling rate to produce networks that reflect the social patterns on the complete period.

To produce networks that reflect similar social patterns as a high sampling rate, while reducing the data processing time, the downsampling should not go beyond 1 frame every 6 min in inactive pigs. A larger sampling interval may be sufficient when studying animals in limited space. In comparison, Larsen et al.51 recommended a sampling interval of 1 frame every 30 s for assessing feeding duration in pigs. When investigating social networks based on proximity, longer sampling intervals remain reliable, given the higher frequency of proximity occurrences compared to feeding events and the focus on network metrics and not directly on duration.

The different values of the metrics across networks might also be a consequence of different types of proximity captured by the definitions. Although we found a high percentage of agreement between the binary proximity definitions, especially between DIST, SURF, and DIST_SURF, when examining specific frames, these definitions appear to relate to distinct types of proximity. DIST seems to capture spatial proximity in cases where both individuals engaged in full-body contact, while SURF seems to capture situations where individuals were in part-body contact. In addition, OVER seems to capture both full-body and part-body contacts, including very small body contacts and even the absence of body contact.

It is unknown why a pig decides to be in full-body contact (as captured by DIST) or in part-body contact (as captured by SURF) with another pig, and which of these choices more accurately represents having a social preference for that other pig. The preference for full-body contact may be partially attributed to the pig’s thermoregulatory needs52,53. However, in our study, the temperature was within the thermoneutral zone (22 °C and 23 °C), which reduced the likelihood of associations being driven by thermoregulation54. In addition, lying together for thermoregulation is more prevalent among newborns than among older pigs as used in this study52,55. In contrast, part-body contact, such as head-to-head, might mean being engaged in more specific social behaviours (e.g., nosing). In this study, no differentiation could be made between various body parts and information regarding the orientation of the pigs could not be considered. SURF might have captured part-body contact with all parts of the pig’s body, including head-to-head or tail-to-tail contact, each potentially being driven by completely different motivations. Including the detection of specific key body points in the computer vision algorithm, for example, by detecting the head and the tail, could help to identify the direction of the pigs and to make the distinction between lying in close proximity head-to-head versus tail-to-tail. In a previous study, Wutke et al.56 showed the potential of using key point detection to build networks based on specific contacts (head-to-head and head-to-tail).

In our study, we examined proximity during inactive periods, defined as instances where the distance moved between two frames one minute apart was less than 20 cm. We assumed that when inactive, pigs were predominantly in a lying posture, taking into account that fattening pigs spend the major part of their time lying57. However, our method could not distinguish between lying and standing pigs, therefore inactive defined pigs may have also included pigs that were standing still in the same location, for instance, when pigs in enriched environments were exploring straw. This method is therefore not suitable to assess welfare based on activity, as behaviours that are beneficial to pig’s welfare, such as exploration of straw58,59,60,61, are misclassified as inactivity. Additionally, our definition might have excluded pigs that were moving while lying, for example changing from lateral to sternal postures. We intentionally opted for a simple definition, as the main focus of our paper was on defining proximity and not on inactivity. Nevertheless, for research focused on networks based on spatial proximity during lying periods, more sophisticated criteria (such as analyzing consecutive active frames) or using alternative algorithms to differentiate between postures, could be investigated.

We observed a greater number of pairs of individuals with smaller distances and with larger overlapping values of their bounding box surfaces in barren pens compared to enriched pens. This suggests that when more space is given to the pigs, they do not choose to stay as close as in smaller environments. This questions the biological relevance of using spatial proximity to investigate social preferences in pigs kept under intensive housing conditions. Limited space allowance may inhibit the ability to express social preferences and maintain individual relationships reflected by spatial proximity19,22. In contrast, it has been shown that pigs with access to outdoor areas, generally characterized by more space, exhibited non-random social preferences in their lying behaviour20. Therefore, specific pro-social behaviours, such as play or social nosing contacts might be more relevant when investigating social preferences in restricted space62,63. Gan et al.64 developed an algorithm based on convolutional neural networks to identify social behaviours between piglets (snout-snout, snout-body and play behaviour). However, data collection methods to study SNA based on an algorithm for such specific social behaviours and how the choice of one method affects the network metrics still have to be investigated.

In conclusion, computer vision algorithms based on tracking allow for the collection of data on location of individuals at a high sampling rate and are therefore useful to characterize social networks based on proximity. However, our results demonstrate that social network characteristics are influenced by both proximity definition and sampling rate and that their impact varies for different network metrics. Moreover, the effect of the sampling rate on network structure and the position of individuals within the network depends on the proximity definition chosen. This means that proximity definitions and sampling rates need to be selected carefully when using computer vision algorithms for social network analysis.