Abstract
Artificial Intelligence (AI) based energy management systems utilize sophisticated AI algorithms to improve and control the consumption of energy in various sectors, such as power utilities, industrial systems, and smart buildings. These systems support real-time analysis of data, predictive analytics, and automatic adjustments to improve energy efficiency, reduce expenses, and lower environmental footprints. This research introduces a new method of AI-based energy management through the creation of advanced mathematical aggregation operators under the theory of hesitant bipolar complex fuzzy sets (HBCFSs). The generalized HBCFS theory is a complete decision-making model that can efficiently deal with uncertainties, hesitancy, and bipolar information in a complex setting. To solve the intrinsic difficulties of energy management decision-making, we propose a series of new HBCF Hamacher power aggregation operators. These operators improve the precision and stability of multi-attribute decision-making (MADM) processes by using the Hamacher t-norm and power aggregation rules to represent intricate interactions among decision attributes. Further, a comparative study is conducted to highlight the strength and superiority of the proposed aggregation operators that significantly contribute to AI energy management systems. The results establish that the method developed significantly improves the accuracy and reliability of decisions, warranting application in energy distribution and usage optimization.
Similar content being viewed by others
Introduction
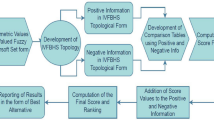
The implementation of AI technology for energy optimization and efficiency enhancement serves different sectors such as homes industrial facilities and commercial buildings. This innovative solution employs prediction analytics together with machine learning algorithms and data analytics insights to track manage and optimize energy consumption patterns. Through AI-driven energy management systems organizations can make data-based decisions as well as predict energy consumption and detect anomalies while minimizing energy waste. These solution methods will eventually establish themselves as cost-effective systems with minimal carbon emissions and represent an ideal way of consuming energy. AI-controlled energy management stands as one of its essential attributes because it processes large datasets immediately. The combination of AI algorithms enables analysis of data streams from sensors and Internet of Things (IoT) devices and smart meters to detect energy use patterns that help locate areas for better energy efficiency control. The described insights enable enterprises to decide on proper energy source utilization windows which reduce expenses while improving operational efficiency. Through forecasting energy use peaks AI algorithms present solutions to minimize the demand peaks thus protecting both the system resources and maximizing efficiency. AI-based energy management provides and anticipates preventative maintenance strategies for maintaining energy systems. AI algorithms detect equipment performance issues and system inefficiencies or breakdowns by constantly monitoring components and running performance analyses to prevent energy loss from occurring. Predictive maintenance allows the lifespan of equipment to grow longer while decreasing downtime along with improving energy usage performance. Modern AI systems employ earlier data and climate forecasting capabilities to produce predictions about renewable power generation. The importance of AI-driven energy management systems can be understood through the analysis of the presented graphs in Figs. 1, 2, and 3.
Role of HBCFSs in MADM
HBCFSs are an essential component in AI-based energy management systems due to their capability to improve decision-making accuracy under uncertain and dynamic conditions. When applied to multi-attribute decision-making (MADM), they manage hesitation, bipolarity, and complex uncertainty efficiently and therefore are significant for energy optimization issues. The incorporation of HBCF Hamacher power aggregation operators enhances decision-making further by providing a more flexible and credible aggregation of various attributes. The operators effectively rank various energy management approaches by accounting for positive and negative membership degrees with hesitation, providing a more thorough evaluation. HBCF framework is better than conventional fuzzy methods in offering better adaptability with changing energy requirements, stability of the grid, and integration of renewable energy. Their implementation in AI-based models enables real-time optimization, predictive analysis, and sound decision support. The sophisticated framework supports the choice of best energy policies, enhances efficiency, and alleviates uncertainties in energy distribution.
Study framework
The research is organized into various sections to methodically introduce the research for an easy and logical flow of information. The sections are systematic, with each one building on the other, beginning with basic concepts and moving towards advanced methodology, applications, and comparative studies. This structure enables a thorough understanding of the proposed approach.
Below Fig. 4 shows the section-wise study of the proposed research.
Motivation and contributions
The growing complexity and uncertainty in energy management systems require sophisticated decision-making models that can process imprecise and changing data. Conventional fuzzy methods tend to neglect hesitation and bipolarity in decision-making, resulting in less precise energy optimization. The combination of AI with HBCF logic improves the accuracy and flexibility of energy management strategies. The new tentative HBCF Hamacher power aggregation operators supply a solid background for MADM with certain guarantees, achieving better ranking and prioritization for energy solutions. The objective of this research is discussed as;
-
Optimizing energy management systems remains essential to support the rising global energy demand to achieve efficiency alongside sustainability and reduced costs. Decision-making processes in complex energy systems become better through intelligent automation and optimization delivered by AI-driven solutions.
-
Tools within energy systems experience various uncertainties because of changing consumer behavior renewable integration and market price variability. The combination of various uncertainties in traditional fuzzy models requires an HBCF framework for better decision precision.
-
Energy management decisions need comparisons of several contradictory attributes including cost management and dependability and ecological concerns. The HBCF Hamacher power aggregation operators establish a strong mathematical system to deal with ambiguity in MADM thus enabling precise priority decisions.
-
Traditional fuzzy aggregation systems (Einstein, Frank, and Aczel-Alsina operators) lack sufficient capabilities to address decision-making hesitation together with bipolarity conditions. The recently developed Hamacher power aggregation operators create a flexible and realistic method to enhance decision reliability within artificial intelligence systems controlling energy management.
-
AI-driven energy management needs adaptive capabilities to support smart grids together with IoT-based energy monitoring and real-time control systems. The proposed methodology manages to deliver enhanced scalability to dynamic large-scale systems.
-
The implementation of AI approaches together with HBCF logic creates stronger decision-making capabilities for energy management by incorporating data analytics with uncertain data modeling capabilities. The hybrid approach results in enhanced automation alongside increased efficiency and predictive accuracy when operating energy systems.
These objectives and motivations drive the need for a novel AI-driven energy management system that integrates HBCF Hamacher power aggregation operators within the MADM framework to enhance precision, robustness, and scalability in modern energy solutions.
Contributions
In this study, we introduce an AI-driven energy management system based on HBCF Hamacher power aggregation operators within the MADM framework. The key contributions of our research are as follows;
-
(a)
We propose a new set of aggregation operators under the HBCF framework, incorporating the Hamacher power function to enhance decision-making capabilities. The introduced operators are;
-
HBCF Hamacher power averaging (HBCFHPA) operator.
-
HBCF Hamacher power weighted averaging (HBCFHPWA) operator.
-
HBCF Hamacher power ordered weighted averaging (HBCFHPOWA) operator.
-
HBCF Hamacher power geometric (HBCFHPG) operator.
-
HBCF Hamacher power weighted geometric (HBCFHPWG) operator.
-
HBCF Hamacher power ordered weighted geometric (HBCFHPOWG) operator.
-
-
(b)
The MADM methodology receives MADM extension through the implementation of HBCF-Hamacher power aggregation operators which help achieve effective alternative prioritizing in complex decision-making conditions.
-
(c)
The HBCF-MADM framework gets applied to a real energy management system that demonstrates its capability to optimize energy distribution together with efficiency increases and sustainable decision support capabilities.
-
(d)
Our research performs extensive comparative evaluations that test both the proposed HBCF-Hamacher power aggregation operators together with present approaches to demonstrate their ability to manage uncertain energy management choices.
Through such contributions, our research enhances decision-making techniques through the provision of a more adaptable, accurate, and smart way of managing energy through AI and HBCF logic.
Literature review
Ali et al.1 discussed AI innovations in building energy management systems and noted their prospective application areas and savings in energy consumption. Their article focused on applying AI methods toward energy optimization to improve efficiency within smart buildings. Hadi et al.2 also discussed AI-aided energy management methods to enhance network durability in wireless sensor networks, projecting the contribution of AI in the longevity extension of a network by strategic energy distribution. Varghese3 analyzed AI-enabled solutions for energy optimization and environmental protection, highlighting their application in digital business landscapes to attain sustainable energy use. Long4 suggested an AI-enabled model for energy-efficient building envelope prediction and optimization, which helped improve intelligent energy management for architectural use. The theory of fuzzy logic, developed by Zadeh5, provided the basis for numerous fuzzy-based decision-making approaches. Merigo and Casanovas6 further developed this notion by developing fuzzy generalized hybrid aggregation operators, which are used extensively in fuzzy decision-making. Torra7 presented hesitant fuzzy sets so that decision-makers can make use of hesitation when evaluating various criteria. Zhang8 and Xia et al.9 further made contributions toward hesitant fuzzy aggregation operators, building models for multiple attribute decision-making (MADM) under uncertainty. Tan et al.10 generalized hesitant fuzzy methods by introducing Hamacher aggregation operators for multicriteria decision-making. Xia and Xu11 and Qian et al.12 further developed hesitant fuzzy information aggregation methods, making them more applicable in complicated decision-making situations. Qin et al.13 proposed Frank aggregation operators in hesitant fuzzy MADM, offering a strong framework for dealing with multiple attributes of different importance levels. Zhang14 came up with bipolar fuzzy sets, in the process opening up the research of bipolar fuzzy logic for decision-making. Wei et al.15 took this a step further by creating bipolar fuzzy Hamacher aggregation operators for use in MADM. Jana et al.16 suggested bipolar fuzzy Dombi prioritized aggregation operators, enhancing the effectiveness of decision-making systems. Chen et al.17 used bipolar fuzzy multi-criteria decision-making methods with probability aggregation operators for the selection of AI frameworks, whereas Garg et al.18 used Aczel-Alsina power aggregation operators in bipolar fuzzy MADM for quantum computing purposes. Riaz and Tehrim19 generalized the VIKOR method for bipolar fuzzy sets by using connection numbers in SPA theory-based metric spaces. Tchangani20 proposed a bipolar aggregation approach to fuzzy nominal classification using weighted cardinal fuzzy measures. Mandal and Ranadive21 presented hesitant bipolar-valued fuzzy sets, enriching multi-attribute group decision-making techniques. Gao et al.22 utilized dual hesitant bipolar fuzzy Hamacher aggregation operators in MADM situations and proved that they are useful for dealing with uncertainty. Wei et al.23 introduced hesitant bipolar fuzzy aggregation operators for multi-attribute decision-making, broadening the application of hesitant bipolar fuzzy logic. Mahmood and Ur Rehman24 introduced bipolar complex fuzzy sets for generalized similarity measures, adding to sophisticated fuzzy modeling. Mahmood et al.25 categorized aggregation operators based on bipolar complex fuzzy settings for decision support systems, and Mahmood et al.26 presented bipolar complex fuzzy Hamacher aggregation operators for MADM problems. Mahmood and Rehman27 advanced MADM methods by combining Dombi aggregation operators based on bipolar complex fuzzy information. Aslam et al.28 employed HBCF Dombi aggregation operators to choose cloud service providers using MADM techniques. Waqas et al.29 used the MABAC method with hesitant bipolar complex fuzzy data for choosing cloud security, showcasing the increasing applicability of AI-based MADM techniques in cybersecurity and cloud computing fields. Subsequent research has then extended the scope of hesitant bipolar complex fuzzy MADM approaches further.
Table 1 shows the overall abbreviations and their meanings used in this manuscript.
Table 2 shows the overall mathematical notations and their meanings.
Fundamentals
In this section, we discuss some basic notions of HFSs and HBCFSs with their related operations.
Definition 1
7 A HFS \(\underline {\text{B}}\) is categorized by \(\underline {\text{B}} = \left\{ {\left\langle {{\upnu },{{ \upbeta }}_{{\underline {\text{B}}}} \left( {\upnu } \right)} \right\rangle |{\upnu } \in {\mathbb{U}}} \right\}\) under the universal set \({\mathbb{U}}\). Where \({\upbeta }_{{\underline {\text{B}}}} \left( {\upnu } \right)\) is the set of finite values in \(\left[ {0,1} \right]\), which shows the possible membership grades of each \({\upnu } \in {\mathbb{U}}\). For easiness \(\underline {\text{B}} = {\upbeta }_{{\underline {\text{B}}}} \left( {\upnu } \right)\) denotes a hesitant fuzzy number (HFN).
Definition 2
7 For three HFNs \(\underline {\text{B}}_{1} ,\underline {\text{B}}_{2}\) and \(\underline {\text{B}}_{3}\) and if \({\uplambda } > 0,\) then the following holds.
-
1.
\(\underline {\text{B}}_{1} \cup \underline {\text{B}}_{2} = \mathop \cup \limits_{{\xi_{1} \in \underline {\text{B}}_{1} ,\;\xi_{2} \in \underline {\text{B}}_{2} }} {\text{max}}\left\{ {\xi_{1} ,\;\xi_{2} } \right\}\)
-
2.
\(\underline {\text{B}}_{1} \cap \underline {\text{B}}_{2} = \mathop \cup \limits_{{\xi_{1} \in \underline {\text{B}}_{1} ,\;\xi_{2} \in \underline {\text{B}}_{2} }} {\text{min}}\left\{ {\xi_{1} ,\;\xi_{2} } \right\}\)
-
3.
\(\underline {\text{B}}_{1} \oplus \underline {\text{B}}_{2} = \mathop \cup \limits_{{\xi_{1} \in \underline {\text{B}}_{1} ,\;\xi_{2} \in \underline {\text{B}}_{2} }} \left\{ {\xi_{1} + \xi_{2} - \xi_{1} \xi_{2} } \right\}\)
-
4.
\({{\uplambda \underline {{\text{B}}} }} = \mathop \cup \limits_{{\xi \in \underline {\text{B}}}} \left\{ {1 - \left( {1 - \xi } \right)^{{\uplambda }} } \right\}\)
-
5.
\(\underline {\text{B}}_{1} \otimes \underline {\text{B}}_{2} = \mathop \cup \limits_{{\xi_{1} \in \underline {\text{B}}_{1} ,\;\xi_{2} \in \underline {\text{B}}_{2} }} \left\{ {\xi_{1} \xi_{2} } \right\}\)
-
6.
\(\underline {\text{B}}^{{\uplambda }} = \mathop \cup \limits_{{\xi \in \underline {\text{B}}}} \left\{ {\xi^{{\uplambda }} } \right\}\)
Definition 3
28 A HBCFS \(\underline {\text{B}}\) under the universal set \({\mathbb{U}}\) is categorized by;
where, \({\upbeta }_{{\underline {\text{B}}}}^{ + } \left( {\upnu } \right) = \left\{ {\xi_{{\underline {\text{B}}_{{\text{j}}} }}^{{ + \left( {{\text{Re}}} \right)}} \left( {\upnu } \right) + {\upiota }\xi_{{\underline {\text{B}}_{{\text{j}}} }}^{{ + \left( {{\text{Im}}} \right)}} \left( {\upnu } \right),\quad {\text{j}} = 1,2, \ldots {\text{m}}} \right\}\) and \({\upbeta }_{{\underline {\text{B}}}}^{ - } \left( {\upnu } \right) = \left\{ {\xi_{{\underline {\text{B}}_{{\text{k}}} }}^{{ - \left( {{\text{Re}}} \right)}} \left( {\upnu } \right) + {\upiota }\xi_{{\underline {\text{B}}_{{\text{k}}} }}^{{ - \left( {{\text{Im}}} \right)}} \left( {\upnu } \right),\quad {\text{k}} = 1,2, \ldots {\text{n}}} \right\}\) are the set of finite values that lies in the unit square of a complex plane denotes the positive and negative part of the membership grades for each \({\upnu } \in {\mathbb{U}}\). For easiness, the hesitant bipolar complex fuzzy number (HBCFN) is symbolized by \(\underline {\text{B}} = \left( {{\upbeta }^{ + } ,\;{\upbeta }^{ - } } \right) = \left( {\xi^{{ + \left( {{\text{Re}}} \right)}} + {\upiota }\xi^{{ + \left( {{\text{Im}}} \right)}} ,\xi^{{ - \left( {{\text{Re}}} \right)}} + {\upiota }\xi^{{ - \left( {{\text{Im}}} \right)}} } \right)\).
Definition 4
28 Let us assume that the \(\underline {\text{B}} = \left( {{\upbeta }^{ + } ,\;{\upbeta }^{ - } } \right) = \left( {\xi^{{ + \left( {{\text{Re}}} \right)}} + {\upiota }\xi^{{ + \left( {{\text{Im}}} \right)}} ,\xi^{{ - \left( {{\text{Re}}} \right)}} + {\upiota }\xi^{{ - \left( {{\text{Im}}} \right)}} } \right),\) \(\underline {\text{B}}_{1} = \left( {{\upbeta }_{1}^{ + } ,{{ \upbeta }}_{1}^{ - } } \right) = \left( {\xi_{1}^{{ + \left( {{\text{Re}}} \right)}} + {\upiota }\xi_{1}^{{ + \left( {{\text{Im}}} \right)}} ,\xi_{1}^{{ - \left( {{\text{Re}}} \right)}} + {\upiota }\xi_{1}^{{ - \left( {{\text{Im}}} \right)}} } \right)\) and \(\underline {\text{B}}_{2} = \left( {{\upbeta }_{2}^{ + } ,{{ \upbeta }}_{2}^{ - } } \right) = \left( {\xi_{2}^{{ + \left( {{\text{Re}}} \right)}} + {\upiota }\xi_{2}^{{ + \left( {{\text{Im}}} \right)}} ,\xi_{2}^{{ - \left( {{\text{Re}}} \right)}} + {\upiota }\xi_{2}^{{ - \left( {{\text{Im}}} \right)}} } \right)\) are three HBCFNs then, the following holds.
-
1.
\(\underline {\text{B}}^{{\text{c}}} = \left( {\mathop \cup \limits_{{\xi^{ + } \in {\upbeta }^{ + } }} \left\{ {\left( {1 - \xi^{{ + \left( {{\text{Re}}} \right)}} } \right) + {\upiota }\left( {1 - \xi^{{ + \left( {{\text{Im}}} \right)}} } \right)} \right\},\mathop \cup \limits_{{\xi^{ - } \in {\upbeta }^{ - } }} \left\{ {\left( { - 1 - \xi^{{ - \left( {{\text{Re}}} \right)}} } \right) + {\upiota }\left( { - 1 - \xi^{{ - \left( {{\text{Im}}} \right)}} } \right)} \right\}} \right)\)
-
2.
\(\underline {\text{B}}_{1} \cup \underline {\text{B}}_{2} = \left( {\begin{array}{*{20}c} {\mathop \cup \limits_{{\xi_{1}^{ + } \in {\upbeta }_{1}^{ + } ,\xi_{2}^{ + } \in {\upbeta }_{2}^{ + } }} \left\{ {\max \left( {\xi_{1}^{{ + \left( {{\text{Re}}} \right)}} ,\xi_{2}^{{ + \left( {{\text{Re}}} \right)}} } \right) + {\upiota }\max \left( {\xi_{1}^{{ + \left( {{\text{Im}}} \right)}} ,\xi_{2}^{{ + \left( {{\text{Im}}} \right)}} } \right)} \right\},} \\ {\mathop \cup \limits_{{\xi_{1}^{ - } \in {\upbeta }_{1}^{ - } ,\xi_{2}^{ - } \in {\upbeta }_{2}^{ - } }} \left\{ {\min \left( {\xi_{1}^{{ - \left( {{\text{Re}}} \right)}} ,\xi_{2}^{{ - \left( {{\text{Re}}} \right)}} } \right) + {\upiota }\min \left( {\xi_{1}^{{ - \left( {{\text{Im}}} \right)}} ,\xi_{2}^{{ - \left( {{\text{Im}}} \right)}} } \right)} \right\}} \\ \end{array} } \right)\)
-
3.
\(\underline {\text{B}}_{1} \cap \underline {\text{B}}_{2} = \left( {\begin{array}{*{20}c} {\mathop \cup \limits_{{\xi_{1}^{ + } \in {\upbeta }_{1}^{ + } ,\xi_{2}^{ + } \in {\upbeta }_{2}^{ + } }} \left\{ {\min \left( {\xi_{1}^{{ + \left( {{\text{Re}}} \right)}} ,\xi_{2}^{{ + \left( {{\text{Re}}} \right)}} } \right) + {\upiota }\min \left( {\xi_{1}^{{ + \left( {{\text{Im}}} \right)}} ,\xi_{2}^{{ + \left( {{\text{Im}}} \right)}} } \right)} \right\},} \\ {\mathop \cup \limits_{{\xi_{1}^{ - } \in {\upbeta }_{1}^{ - } ,\xi_{2}^{ - } \in {\upbeta }_{2}^{ - } }} \left\{ {\max \left( {\xi_{1}^{{ - \left( {{\text{Re}}} \right)}} ,\xi_{2}^{{ - \left( {{\text{Re}}} \right)}} } \right) + {\upiota }\max \left( {\xi_{1}^{{ - \left( {{\text{Im}}} \right)}} ,\xi_{2}^{{ - \left( {{\text{Im}}} \right)}} } \right)} \right\}} \\ \end{array} } \right)\)
Definition 5
28 Let \(\underline {\text{B}}\), \(\underline {\text{B}}_{1}\) and \(\underline {\text{B}}_{2}\) be three HBCFNs and \({\uplambda } > 0\) then,
-
1.
\(\underline {\text{B}}_{1} \oplus \underline {\text{B}}_{2} = \left( {\begin{array}{*{20}c} {\mathop \cup \limits_{{\xi_{1}^{ + } \in {\upbeta }_{1}^{ + } ,\xi_{2}^{ + } \in {\upbeta }_{2}^{ + } }} \left\{ {\begin{array}{*{20}c} {\left( {\xi_{1}^{{ + \left( {{\text{Re}}} \right)}} + \xi_{2}^{{ + \left( {{\text{Re}}} \right)}} - \xi_{1}^{{ + {\text{Re}}}} \xi_{2}^{{ + {\text{Re}}}} } \right)} \\ { + \upiota \left( {\xi_{1}^{{ + \left( {{\text{Im}}} \right)}} + \xi_{2}^{{ + \left( {{\text{Im}}} \right)}} - \xi_{1}^{{ + \left( {{\text{Im}}} \right)}} \xi_{2}^{{ + \left( {{\text{Im}}} \right)}} } \right)} \\ \end{array} } \right\},} \\ {\mathop \cup \limits_{{\xi_{1}^{ - } \in {\upbeta }_{1}^{ - } ,\xi_{2}^{ - } \in {\upbeta }_{2}^{ - } }} \left\{ {\left( { - \xi_{1}^{{ - \left( {{\text{Re}}} \right)}} \xi_{2}^{{ - \left( {{\text{Re}}} \right)}} } \right) + {\upiota }\left( { - \xi_{1}^{{ - \left( {{\text{Im}}} \right)}} \xi_{2}^{{ - \left( {{\text{Im}}} \right)}} } \right)} \right\}} \\ \end{array} } \right)\)
-
2.
\(\underline {\text{B}}_{1} \otimes \underline {\text{B}}_{2} = \left( {\begin{array}{*{20}c} {\mathop \cup \limits_{{\xi_{1}^{ + } \in {\upbeta }_{1}^{ + } ,\xi_{2}^{ + } \in {\upbeta }_{2}^{ + } }} \left\{ {\left( {\xi_{1}^{{ + \left( {{\text{Re}}} \right)}} \xi_{2}^{{ + \left( {{\text{Re}}} \right)}} } \right) + {\upiota }\left( {\xi_{1}^{{ + \left( {{\text{Im}}} \right)}} \xi_{2}^{{ + \left( {{\text{Im}}} \right)}} } \right)} \right\},} \\ {\mathop \cup \limits_{{\xi_{1}^{ - } \in {\upbeta }_{1}^{ - } ,\xi_{2}^{ - } \in {\upbeta }_{2}^{ - } }} \left\{ {\begin{array}{*{20}c} {\left( {\xi_{1}^{{ - \left( {{\text{Re}}} \right)}} + \xi_{2}^{{ - \left( {{\text{Re}}} \right)}} + \xi_{1}^{{ - \left( {{\text{Re}}} \right)}} \xi_{2}^{{ - \left( {{\text{Re}}} \right)}} } \right)} \\ { + \upiota \left( {\xi_{1}^{{ - \left( {{\text{Im}}} \right)}} + \xi_{2}^{{ - \left( {{\text{Im}}} \right)}} + \xi_{1}^{{ - \left( {{\text{Im}}} \right)}} \xi_{2}^{{ - \left( {{\text{Im}}} \right)}} } \right)} \\ \end{array} } \right\}} \\ \end{array} } \right)\)
-
3.
\(\underline {\text{B}}^{{\uplambda }} = \left( {\mathop \cup \limits_{{\xi^{ + } \in {\upbeta }^{ + } }} \left\{ {\left( {\left( {\xi^{{ + \left( {{\text{Re}}} \right)}} } \right)^{{\uplambda }} } \right) + {\upiota }\left( {\left( {\xi^{{ + \left( {{\text{Im}}} \right)}} } \right)^{{\uplambda }} } \right)} \right\},\mathop \cup \limits_{{\xi^{ - } \in {\upbeta }^{ - } }} \left\{ {\begin{array}{*{20}c} {\left( { - 1 + \left( {1 + \xi^{{ - \left( {{\text{Re}}} \right)}} } \right)^{{\uplambda }} } \right)} \\ { + \upiota \left( { - 1 + \left( {1 + \xi^{{ - \left( {{\text{Im}}} \right)}} } \right)^{{\uplambda }} } \right)} \\ \end{array} } \right\}} \right)\)
-
4.
\({{\uplambda \underline {{\text{B}}} }} = \left( {\mathop \cup \limits_{{\xi^{ + } \in {\upbeta }^{ + } }} \left\{ {\begin{array}{*{20}c} {\left( {1 - \left( {1 - \xi^{{ + \left( {{\text{Re}}} \right)}} } \right)^{{\uplambda }} } \right)} \\ { + \upiota \left( {1 - \left( {1 - \xi^{{ + \left( {{\text{Im}}} \right)}} } \right)^{{\uplambda }} } \right)} \\ \end{array} } \right\},\mathop \cup \limits_{{\xi^{ - } \in {\upbeta }^{ - } }} \left\{ {\left( { - \left| {\xi^{{ - \left( {{\text{Re}}} \right)}} } \right|^{{\uplambda }} } \right) + {\upiota }\left( { - \left| {\xi^{{ - \left( {{\text{Im}}} \right)}} } \right|^{{\uplambda }} } \right)} \right\}} \right)\)
Definition 6
28 Let \(\underline {\text{B}}\) be a HBCFN then the score and accuracy function are defined as;
Definition 7
30 Let \(\upphi_{1} ,\upphi_{2} \in \left[ {0,1} \right],\aleph > 0\) then Hamacher t-norm and t-conorms are defined as;
Definition 8
Let \(\underline {\text{B}}\), \(\underline {\text{B}}_{1}\) and \(\underline {\text{B}}_{2}\) be three HBCFNs and \({\uplambda } > 0\) then,
-
1.
\(\underline {\text{B}}_{1} \oplus_{\text{H}} \underline {\text{B}}_{2} = \left( \begin{gathered} \mathop \cup \limits_{{\xi_{1}^{ + } \in {\upbeta }_{1}^{ + } ,\xi_{2}^{ + } \in {\upbeta }_{2}^{ + } }} \left\{ {\begin{array}{*{20}c} {\left( {\frac{{\left( {\xi_{1}^{{ + \left( {{\text{Re}}} \right)}} + \xi_{2}^{{ + \left( {{\text{Re}}} \right)}} - \xi_{1}^{{ + \left( {{\text{Re}}} \right)}} \xi_{2}^{{ + \left( {{\text{Re}}} \right)}} } \right) - \left( {1 - \aleph } \right)\xi_{1}^{{ + \left( {{\text{Re}}} \right)}} \xi_{2}^{{ + \left( {{\text{Re}}} \right)}} }}{{1 - \left( {1 - \aleph } \right)\xi_{1}^{{ + \left( {{\text{Re}}} \right)}} \xi_{2}^{{ + \left( {{\text{Re}}} \right)}} }}} \right)} \\ { +\upiota \left( {\frac{{\left( {\xi_{1}^{{ + \left( {{\text{Im}}} \right)}} + \xi_{2}^{{ + \left( {{\text{Im}}} \right)}} - \xi_{1}^{{ + \left( {{\text{Im}}} \right)}} \xi_{2}^{{ + \left( {{\text{Im}}} \right)}} } \right) - \left( {1 - \aleph } \right)\xi_{1}^{{ + \left( {{\text{Im}}} \right)}} \xi_{2}^{{ + \left( {{\text{Im}}} \right)}} }}{{1 - \left( {1 - \aleph } \right)\xi_{1}^{{ + \left( {{\text{Re}}} \right)}} \xi_{2}^{{ + \left( {{\text{Re}}} \right)}} }}} \right)} \\ \end{array} } \right\}, \hfill \\ \mathop \cup \limits_{{\xi_{1}^{ - } \in {\upbeta }_{1}^{ - } ,\xi_{2}^{ - } \in {\upbeta }_{2}^{ - } }} \left\{ {\begin{array}{*{20}c} {\left( {\frac{{ - \left( {\xi_{1}^{{ - \left( {{\text{Re}}} \right)}} \xi_{2}^{{ - \left( {{\text{Re}}} \right)}} } \right)}}{{\aleph - \left( {1 - \aleph } \right)\left( {\xi_{1}^{{ - \left( {{\text{Re}}} \right)}} + \xi_{2}^{{ - \left( {{\text{Re}}} \right)}} + \xi_{1}^{{ - \left( {{\text{Re}}} \right)}} \xi_{2}^{{ - \left( {{\text{Re}}} \right)}} } \right)}}} \right)} \\ { +\upiota \left( {\frac{{ - \left( {\xi_{1}^{{ - \left( {{\text{Im}}} \right)}} \xi_{2}^{{ - \left( {{\text{Im}}} \right)}} } \right)}}{{\aleph - \left( {1 - \aleph } \right)\left( {\xi_{1}^{{ - \left( {{\text{Im}}} \right)}} + \xi_{2}^{{ - \left( {{\text{Im}}} \right)}} + \xi_{1}^{{ - \left( {{\text{Im}}} \right)}} \xi_{2}^{{ - \left( {{\text{Im}}} \right)}} } \right)}}} \right)} \\ \end{array} } \right\} \hfill \\ \end{gathered} \right)\)
-
2.
\(\underline {\text{B}}_{1} \otimes_{\text{H}} \underline {\text{B}}_{2} = \left( \begin{gathered} \mathop \cup \limits_{{\xi_{1}^{ + } \in {\upbeta }_{1}^{ + } ,\xi_{2}^{ + } \in {\upbeta }_{2}^{ + } }} \left\{ {\begin{array}{*{20}c} {\left( {\frac{{\xi_{1}^{{ + \left( {{\text{Re}}} \right)}} \xi_{2}^{{ + \left( {{\text{Re}}} \right)}} }}{{\aleph + \left( {1 - \aleph } \right)\left( {\xi_{1}^{{ + \left( {{\text{Re}}} \right)}} + \xi_{2}^{{ + \left( {{\text{Re}}} \right)}} - \xi_{1}^{{ + \left( {{\text{Re}}} \right)}} \xi_{2}^{{ + \left( {{\text{Re}}} \right)}} } \right)}}} \right)} \\ { +\upiota \left( {\frac{{\xi_{1}^{{ + \left( {{\text{Im}}} \right)}} \xi_{2}^{{ + \left( {{\text{Im}}} \right)}} }}{{\aleph + \left( {1 - \aleph } \right)\left( {\xi_{1}^{{ + \left( {{\text{Im}}} \right)}} + \xi_{2}^{{ + \left( {{\text{Im}}} \right)}} - \xi_{1}^{{ + \left( {{\text{Im}}} \right)}} \xi_{2}^{{ + \left( {{\text{Im}}} \right)}} } \right)}}} \right)} \\ \end{array} } \right\}, \hfill \\ \mathop \cup \limits_{{\xi_{1}^{ - } \in {\upbeta }_{1}^{ - } ,\xi_{2}^{ - } \in {\upbeta }_{2}^{ - } }} \left\{ {\begin{array}{*{20}c} {\left( {\frac{{\left( {\xi_{1}^{{ - \left( {{\text{Re}}} \right)}} + \xi_{2}^{{ - \left( {{\text{Re}}} \right)}} + \xi_{1}^{{ - \left( {{\text{Re}}} \right)}} \xi_{2}^{{ - \left( {{\text{Re}}} \right)}} } \right) + \left( {1 - \aleph } \right)\xi_{1}^{{ - \left( {{\text{Re}}} \right)}} \xi_{2}^{{ - \left( {{\text{Re}}} \right)}} }}{{1 - \left( {1 - \aleph } \right)\xi_{1}^{{ - \left( {{\text{Re}}} \right)}} \xi_{2}^{{ - \left( {{\text{Re}}} \right)}} }}} \right)} \\ { +\upiota \left( {\frac{{\left( {\xi_{1}^{{ - \left( {{\text{Im}}} \right)}} + \xi_{2}^{{ - \left( {{\text{Im}}} \right)}} + \xi_{1}^{{ - \left( {{\text{Im}}} \right)}} \xi_{2}^{{ - \left( {{\text{Im}}} \right)}} } \right) + \left( {1 - \aleph } \right)\xi_{1}^{{ - \left( {{\text{Im}}} \right)}} \xi_{2}^{{ - \left( {{\text{Im}}} \right)}} }}{{1 - \left( {1 - \aleph } \right)\xi_{1}^{{ - \left( {{\text{Im}}} \right)}} \xi_{2}^{{ - \left( {{\text{Im}}} \right)}} }}} \right)} \\ \end{array} } \right\} \hfill \\ \end{gathered} \right)\)
-
3.
\({{\uplambda \underline {{\text{B}}} }} = \left( \begin{gathered} \mathop \cup \limits_{{\xi^{ + } \in {\upbeta }^{ + } }} \left\{ {\begin{array}{*{20}c} {\left( {\frac{{\left( {1 + \left( {\aleph - 1} \right)\xi^{{ + \left( {{\text{Re}}} \right)}} } \right)^{{\uplambda }} - \left( {1 - \xi^{{ + \left( {{\text{Re}}} \right)}} } \right)^{{\uplambda }} }}{{\left( {1 + \left( {\aleph - 1} \right)\xi^{{ + \left( {{\text{Re}}} \right)}} } \right)^{{\uplambda }} + \left( {\aleph - 1} \right)\left( {1 - \xi^{{ + \left( {{\text{Re}}} \right)}} } \right)^{{\uplambda }} }}} \right)} \\ { +\upiota \left( {\frac{{\left( {1 + \left( {\aleph - 1} \right)\xi^{{ + \left( {{\text{Im}}} \right)}} } \right)^{{\uplambda }} - \left( {1 - \xi^{{ + \left( {{\text{Im}}} \right)}} } \right)^{{\uplambda }} }}{{\left( {1 + \left( {\aleph - 1} \right)\xi^{{ + \left( {{\text{Im}}} \right)}} } \right)^{{\uplambda }} + \left( {\aleph - 1} \right)\left( {1 - \xi^{{ + \left( {{\text{Im}}} \right)}} } \right)^{{\uplambda }} }}} \right)} \\ \end{array} } \right\}, \hfill \\ \mathop \cup \limits_{{\xi^{ - } \in {\upbeta }^{ - } }} \left\{ {\begin{array}{*{20}c} {\left( {\frac{{ - \aleph \left| {\xi^{{ - \left( {{\text{Re}}} \right)}} } \right|^{{\uplambda }} }}{{\left( {1 + \left( {\aleph - 1} \right)\left( {1 + \xi^{{ - \left( {{\text{Re}}} \right)}} } \right)} \right)^{{\uplambda }} + \left( {\aleph - 1} \right)\left| {\xi^{{ - \left( {{\text{Re}}} \right)}} } \right|^{{\uplambda }} }}} \right)} \\ { +\upiota \left( {\frac{{ - \aleph \left| {\xi^{{ - \left( {{\text{Im}}} \right)}} } \right|^{{\uplambda }} }}{{\left( {1 + \left( {\aleph - 1} \right)\left( {1 + \xi^{{ - \left( {{\text{Im}}} \right)}} } \right)} \right)^{{\uplambda }} + \left( {\aleph - 1} \right)\left| {\xi^{{ - \left( {{\text{Im}}} \right)}} } \right|^{{\uplambda }} }}} \right)} \\ \end{array} } \right\} \hfill \\ \end{gathered} \right)\)
-
4.
\(\underline {\text{B}}^{{\uplambda }} = \left( \begin{gathered} \mathop \cup \limits_{{\xi^{ + } \in {\upbeta }^{ + } }} \left\{ {\begin{array}{*{20}c} {\left( {\frac{{\aleph \left( {\xi^{{ + \left( {{\text{Re}}} \right)}} } \right)^{{\uplambda }} }}{{\left( {1 + \left( {\aleph - 1} \right)\left( {1 - \xi^{{ + \left( {{\text{Re}}} \right)}} } \right)} \right)^{{\uplambda }} + \left( {\aleph - 1} \right)\left( {\xi^{{ + \left( {{\text{Re}}} \right)}} } \right)^{{\uplambda }} }}} \right)} \\ { +\upiota \left( {\frac{{\aleph \left( {\xi^{{ + \left( {{\text{Im}}} \right)}} } \right)^{{\uplambda }} }}{{\left( {1 + \left( {\aleph - 1} \right)\left( {1 - \xi^{{ + \left( {{\text{Im}}} \right)}} } \right)} \right)^{{\uplambda }} + \left( {\aleph - 1} \right)\left( {\xi^{{ + \left( {{\text{Im}}} \right)}} } \right)^{{\uplambda }} }}} \right)} \\ \end{array} } \right\}, \hfill \\ \mathop \cup \limits_{{\xi^{ - } \in {\upbeta }^{ - } }} \left\{ {\begin{array}{*{20}c} { - \left( {\frac{{\left( {1 + \left( {\aleph - 1} \right)\left| {\xi^{{ - \left( {{\text{Re}}} \right)}} } \right|} \right)^{{\uplambda }} - \left( {1 + \xi^{{ - \left( {{\text{Re}}} \right)}} } \right)^{{\uplambda }} }}{{\left( {1 + \left( {\aleph - 1} \right)\left| {\xi^{{ - \left( {{\text{Re}}} \right)}} } \right|} \right)^{{\uplambda }} + \left( {\aleph - 1} \right)\left( {1 + \xi^{{ - \left( {{\text{Re}}} \right)}} } \right)^{{\uplambda }} }}} \right)} \\ { +\upiota \left( { - \frac{{\left( {1 + \left( {\aleph - 1} \right)\left| {\xi^{{ - \left( {{\text{Im}}} \right)}} } \right|} \right)^{{\uplambda }} - \left( {1 + \xi^{{ - \left( {{\text{Im}}} \right)}} } \right)^{{\uplambda }} }}{{\left( {1 + \left( {\aleph - 1} \right)\left| {\xi^{{ - \left( {{\text{Im}}} \right)}} } \right|} \right)^{{\uplambda }} + \left( {\aleph - 1} \right)\left( {1 + \xi^{{ - \left( {{\text{Im}}} \right)}} } \right)^{{\uplambda }} }}} \right)} \\ \end{array} } \right\} \hfill \\ \end{gathered} \right)\)
Theorem 1
Let \(\underline {\text{B}}\), \(\underline {\text{B}}_{1}\) and \(\underline {\text{B}}_{2}\) be three HBCFNs and \({\uplambda } > 0\) then, the following holds;
-
(a)
\(\underline {\text{B}}_{1} \oplus \underline {\text{B}}_{2} = \underline {\text{B}}_{2} \oplus \underline {\text{B}}_{1}\)
-
(b)
\(\underline {\text{B}}_{1} \otimes \underline {\text{B}}_{2} = \underline {\text{B}}_{2} \otimes \underline {\text{B}}_{1}\)
-
(c)
\(\left( {\underline {\text{B}}_{1} \cap \underline {\text{B}}_{2} } \right)^{{\text{c}}} = \underline {\text{B}}_{1}^{{\text{c}}} \cup \underline {\text{B}}_{2}^{{\text{c}}}\)
-
(d)
\(\left( {\underline {\text{B}}_{1} \cup \underline {\text{B}}_{2} } \right)^{{\text{c}}} = \underline {\text{B}}_{1}^{{\text{c}}} \cap \underline {\text{B}}_{2}^{{\text{c}}}\)
-
(e)
\(\left( {\underline {\text{B}}_{1} \otimes \underline {\text{B}}_{2} } \right)^{{\uplambda }} = \underline {\text{B}}_{1}^{{\uplambda }} \otimes \underline {\text{B}}_{2}^{{\uplambda }}\)
HBCF Hamacher power aggregation operators
In this section of the article, we developed some new Hamacher power average and geometric aggregation operators.
Definition 9
Let \(\underline {\text{B}}_{{\upalpha }} = \left( {{\upbeta }_{{\upalpha }}^{ + } ,{{ \upbeta }}_{{\upalpha }}^{ - } } \right) = \left( {\xi_{{\upalpha }}^{{ + \left( {{\text{Re}}} \right)}} + {\upiota }\xi_{{\upalpha }}^{{ + \left( {{\text{Im}}} \right)}} ,\xi_{{\upalpha }}^{{ - \left( {{\text{Re}}} \right)}} + {\upiota }\xi_{{\upalpha }}^{{ - \left( {{\text{Im}}} \right)}} } \right)\left( {{\upalpha } = 1,2,3, \ldots ,{\updelta }} \right)\) be the collection of HBCFNs, then the HBCFHWA operator is a function of \({\text{HBCFHPA}}:\underline {\text{B}}^{{\updelta }} \to \underline {\text{B}}\) and defined as;
where, \(^\circ\!{\text{F}}\left( {\underline {\text{B}}_{{\upalpha }} } \right) = \mathop \sum \nolimits_{{\begin{array}{*{20}c} {\upalpha ,{\mathbf{\varsigma }} = 1} \\ {{\mathbf{\varsigma }} \ne \upalpha } \\ \end{array} }}^{{\updelta }} {\text{sup}}\left( {\underline {\text{B}}_{{\upalpha }} ,\underline {\text{B}}_{{\mathbf{\varsigma }}} } \right)\) and \({\text{sup}}\left( {\underline {\text{B}}_{{\upalpha }} ,\underline {\text{B}}_{{\mathbf{\varsigma }}} } \right)\) implies that the support between two HBCFNs \(\underline {\text{B}}_{{\upalpha }}\) and \(\underline {\text{B}}_{{\mathbf{\varsigma }}}\). Then the following conditions holds.
-
\({\text{sup}}\left( {\underline {\text{B}}_{{\upalpha }} ,\underline {\text{B}}_{{\mathbf{\varsigma }}} } \right) \in \left[ {0,1} \right].\)
-
\({\text{sup}}\left( {\underline {\text{B}}_{{\upalpha }} ,\underline {\text{B}}_{{\mathbf{\varsigma }}} } \right) = {\text{sup}}\left( {\underline {\text{B}}_{{\mathbf{\varsigma }}} ,\underline {\text{B}}_{{\upalpha }} } \right)\).
-
\({\text{sup}}\left( {\underline {\text{B}}_{{\upalpha }} ,\underline {\text{B}}_{{\mathbf{\varsigma }}} } \right) \ge {\text{sup}}\left( {\underline {\text{B}}_{{{{\upalpha^{\prime}}}}} ,\underline {\text{B}}_{{{\mathbf{\varsigma^{\prime}}}}} } \right),\) if \({\Upsilon }\left( {\underline {\text{B}}_{{\upalpha }} ,\underline {\text{B}}_{{\mathbf{\varsigma }}} } \right) < {\Upsilon }\left( {\underline {\text{B}}_{{{{\upalpha^{\prime}}}}} ,\underline {\text{B}}_{{{\mathbf{\varsigma^{\prime}}}}} } \right){\Upsilon }\) is the distance measure.
Theorem 2
Let \(\underline {\text{B}}_{{\upalpha }}\) be the collection of HBCFNs, then by (2), we get the following.
HBCFHPA aggregation operator satisfies below cases.
Particular cases We discussed two different particular cases of HBCFHPA operators as follows:
-
1.
When \(\aleph = 1,\) then the HBCFHPA operator reduces to the hesitant bipolar complex fuzzy power averaging (HBCFPA) operator.
$${\text{HBCFPA}}\left( {\underline {\text{B}}_{1} ,\underline {\text{B}}_{2} , \ldots ,\underline {\text{B}}_{{\updelta }} } \right) = \begin{array}{*{20}c} {\updelta } \\ \oplus \\ {{\upalpha } = 1} \\ \end{array} \left( {\frac{{\left( {1 +^\circ\!{\text{F}}\left( {\underline {\text{B}}_{{\upalpha }} } \right)} \right)}}{{\mathop \sum \nolimits_{{{\upalpha } = 1}}^{{\updelta }} \left( {1 +^\circ\!{\text{F}}\left( {\underline {\text{B}}_{{\upalpha }} } \right)} \right)}}\underline {\text{B}}_{{\upalpha }} } \right)$$$$\ = \left( \begin{gathered} \mathop \cup \limits_{{\xi_{1}^{ + } \in {\upbeta }_{1}^{ + } ,\ldots,\xi_{{\updelta }}^{ + } \in {\upbeta }_{{\updelta }}^{ + } }} \left\{ {\left( {1 - \mathop \prod \limits_{{{\upalpha } = 1}}^{{\updelta }} \left( {1 - \xi_{{\upalpha }}^{{ + \left( {{\text{Re}}} \right)}} } \right)^{{\frac{{\left( {1 +^\circ\!{\text{F}}\left( {\underline {\text{B}}_{{\upalpha }} } \right)} \right)}}{{\mathop \sum \nolimits_{{{\upalpha } = 1}}^{{\updelta }} \left( {1 +^\circ\!{\text{F}}\left( {\underline {\text{B}}_{{\upalpha }} } \right)} \right)}}}} } \right) + {\upiota }\left( {1 - \mathop \prod \limits_{{{\upalpha } = 1}}^{{\updelta }} \left( {1 - \xi_{{\upalpha }}^{{ + \left( {{\text{Im}}} \right)}} } \right)^{{\frac{{\left( {1 +^\circ\!{\text{F}}\left( {\underline {\text{B}}_{{\upalpha }} } \right)} \right)}}{{\mathop \sum \nolimits_{{{\upalpha } = 1}}^{{\updelta }} \left( {1 + ^\circ\!{\text{F}}\left( {\underline {\text{B}}_{{\upalpha }} } \right)} \right)}}}} } \right)} \right\}, \hfill \\ \mathop \cup \limits_{{\xi_{1}^{ - } \in {\upbeta }_{1}^{ - } ,\ldots,\xi_{{\updelta }}^{ - } \in {\upbeta }_{{\updelta }}^{ - } }} \left\{ {\left( { - \mathop \prod \limits_{{{\upalpha } = 1}}^{{\updelta }} \left| {\xi_{{\upalpha }}^{{ - \left( {{\text{Re}}} \right)}} } \right|^{{\frac{{\left( {1 +^\circ\!{\text{F}}\left( {\underline {\text{B}}_{{\upalpha }} } \right)} \right)}}{{\mathop \sum \nolimits_{{{\upalpha } = 1}}^{{\updelta }} \left( {1 +^\circ\!{\text{F}}\left( {\underline {\text{B}}_{{\upalpha }} } \right)} \right)}}}} } \right) + {\upiota }\left( { - \mathop \prod \limits_{{{\upalpha } = 1}}^{{\updelta }} \left| {\xi_{{\upalpha }}^{{ - \left( {{\text{Im}}} \right)}} } \right|^{{\frac{{\left( {1 +^\circ\!{\text{F}}\left( {\underline {\text{B}}_{{\upalpha }} } \right)} \right)}}{{\mathop \sum \nolimits_{{{\upalpha } = 1}}^{{\updelta }} \left( {1 +^\circ\!{\text{F}}\left( {\underline {\text{B}}_{{\upalpha }} } \right)} \right)}}}} } \right)} \right\} \hfill \\ \end{gathered} \right)$$ -
2.
When \(\aleph = 2,\) then the HBCFHPA operator reduces to the HBCF Einstein power averaging (HBCFEPA) operator.
$${\text{HBCFEPA}}\left( {\underline {\text{B}}_{1} ,\underline {\text{B}}_{2} , \ldots ,\underline {\text{B}}_{{\updelta }} } \right) = \begin{array}{*{20}c} {\updelta } \\ \oplus \\ {{\upalpha } = 1} \\ \end{array} \left( {\frac{{\left( {1 +^\circ\!{\text{F}}\left( {\underline {\text{B}}_{{\upalpha }} } \right)} \right)}}{{\mathop \sum \nolimits_{{{\upalpha } = 1}}^{{\updelta }} \left( {1 +^\circ\!{\text{F}}\left( {\underline {\text{B}}_{{\upalpha }} } \right)} \right)}}\underline {\text{B}}_{{\upalpha }} } \right)$$$$= \left( \begin{gathered} \bigcup\limits_{{\xi _{1}^{ + } \in \upbeta _{1}^{ + } , \ldots ,\xi _{\updelta }^{ + } \in \upbeta _{\updelta }^{ + } }} {\left\{ \begin{gathered} \left( {\frac{{\mathop \prod \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + \xi _{\upalpha }^{{ + \left( {\text{Re} } \right)}} } \right)^{{\frac{{\left( {1 + ^\circ\!{\text{F}}\left( {{\underline {\text{B}}}_{\upalpha } } \right)} \right)}}{{\mathop \sum \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + ^\circ\!{\text{F}}\left( {{\underline {\text{B}}}_{\upalpha } } \right)} \right)}}}} - \mathop \prod \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 - \xi _{\upalpha }^{{ + \left( {\text{Re} } \right)}} } \right)^{{\frac{{\left( {1 + ^\circ\!{\text{F}}\left( {{\underline {\text{B}}}_{\upalpha } } \right)} \right)}}{{\mathop \sum \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + ^\circ\!{\text{F}}\left( {{\underline {\text{B}}}_{\upalpha } } \right)} \right)}}}} }}{{\mathop \prod \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + \xi _{\upalpha }^{{ + \left( {\text{Re} } \right)}} } \right)^{{\frac{{\left( {1 + ^\circ\!{\text{F}}\left( {{\underline {\text{B}}}_{\upalpha } } \right)} \right)}}{{\mathop \sum \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + ^\circ\!{\text{F}}\left( {{\underline {\text{B}}}_{\upalpha } } \right)} \right)}}}} + \mathop \prod \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 - \xi _{\upalpha }^{{ + \left( {\text{Re} } \right)}} } \right)^{{\frac{{\left( {1 + ^\circ\,{\text{F}}\left( {{\underline {\text{B}}}_{\upalpha } } \right)} \right)}}{{\mathop \sum \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + ^\circ\!{\text{F}}\left( {{\underline {\text{B}}}_{\upalpha } } \right)} \right)}}}} }}} \right) \hfill \\ + \upiota \left( {\frac{{\mathop \prod \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + \xi _{\upalpha }^{{ + \left( {\text{Im} } \right)}} } \right)^{{\frac{{\left( {1 + ^\circ\!{\text{F}}\left( {{\underline {\text{B}}}_{\upalpha } } \right)} \right)}}{{\mathop \sum \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + ^\circ\!{\text{F}}\left( {{\underline {\text{B}}}_{\upalpha } } \right)} \right)}}}} - \mathop \prod \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 - \xi _{\upalpha }^{{ + \left( {\text{Im} } \right)}} } \right)^{{\frac{{\left( {1 + ^\circ\!{\text{F}}\left( {{\underline {\text{B}}}_{\upalpha } } \right)} \right)}}{{\mathop \sum \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + ^\circ\!{\text{F}}\left( {{\underline {\text{B}}}_{\upalpha } } \right)} \right)}}}} }}{{\mathop \prod \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + \xi _{\upalpha }^{{ + \left( {\text{Im} } \right)}} } \right)^{{\frac{{\left( {1 + ^\circ\!{\text{F}}\left( {{\underline {\text{B}}}_{\upalpha } } \right)} \right)}}{{\mathop \sum \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + ^\circ\!{\text{F}}\left( {{\underline {\text{B}}}_{\upalpha } } \right)} \right)}}}} + \mathop \prod \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 - \xi _{\upalpha }^{{ + \left( {\text{Im} } \right)}} } \right)^{{\frac{{\left( {1 + ^\circ\!{\text{F}}\left( {{\underline {\text{B}}}_{\upalpha } } \right)} \right)}}{{\mathop \sum \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + ^\circ\!{\text{F}}\left( {{\underline {\text{B}}}_{\upalpha } } \right)} \right)}}}} }}} \right) \hfill \\ \end{gathered} \right\}} , \hfill \\ \bigcup\limits_{{\xi _{1}^{ - } \in \upbeta _{1}^{ - } , \ldots ,\xi _{\updelta }^{ - } \in \upbeta _{\updelta }^{ - } }} {\left\{ \begin{gathered} \left( {\frac{{ - 2\mathop \prod \nolimits_{{\upalpha = 1}}^{\updelta } \left| {\xi _{\upalpha }^{{ - \left( {\text{Re} } \right)}} } \right|^{{\frac{{\left( {1 + ^\circ\!{\text{F}}\left( {{\underline {\text{B}}}_{\upalpha } } \right)} \right)}}{{\mathop \sum \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + ^\circ\!{\text{F}}\left( {{\underline {\text{B}}}_{\upalpha } } \right)} \right)}}}} }}{{\mathop \prod \nolimits_{{\upalpha = 1}}^{\updelta } \left( {2 + \xi _{\upalpha }^{{ - \left( {\text{Re} } \right)}} } \right)^{{\frac{{\left( {1 + ^\circ\!{\text{F}}\left( {{\underline {\text{B}}}_{\upalpha } } \right)} \right)}}{{\mathop \sum \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + ^\circ\!{\text{F}}\left( {{\underline {\text{B}}}_{\upalpha } } \right)} \right)}}}} + \mathop \prod \nolimits_{{\upalpha = 1}}^{\updelta } \left| {\xi _{\upalpha }^{{ - \left( {\text{Re} } \right)}} } \right|^{{\frac{{\left( {1 + ^\circ\!{\text{F}}\left( {{\underline {\text{B}}}_{\upalpha } } \right)} \right)}}{{\mathop \sum \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + ^\circ\!{\text{F}}\left( {{\underline {\text{B}}}_{\upalpha } } \right)} \right)}}}} }}} \right) \hfill \\ + \upiota \left( {\frac{{ - 2\mathop \prod \nolimits_{{\upalpha = 1}}^{\updelta } \left| {\xi _{\upalpha }^{{ - \left( {\text{Im} } \right)}} } \right|^{{\frac{{\left( {1 + ^\circ\!{\text{F}}\left( {{\underline {\text{B}}}_{\upalpha } } \right)} \right)}}{{\mathop \sum \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + ^\circ\!{\text{F}}\left( {{\underline {\text{B}}}_{\upalpha } } \right)} \right)}}}} }}{{\mathop \prod \nolimits_{{\upalpha = 1}}^{\updelta } \left( {2 + \xi _{\upalpha }^{{ - \left( {\text{Im} } \right)}} } \right)^{{\frac{{\left( {1 + ^\circ\!{\text{F}}\left( {{\underline {\text{B}}}_{\upalpha } } \right)} \right)}}{{\mathop \sum \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + ^\circ\!{\text{F}}\left( {{\underline {\text{B}}}_{\upalpha } } \right)} \right)}}}} + \mathop \prod \nolimits_{{\upalpha = 1}}^{\updelta } \left| {\xi _{\upalpha }^{{ - \left( {\text{Im} } \right)}} } \right|^{{\frac{{\left( {1 + ^\circ\!{\text{F}}\left( {{\underline {\text{B}}}_{\upalpha } } \right)} \right)}}{{\mathop \sum \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + ^\circ\!{\text{F}}\left( {{\underline {\text{B}}}_{\upalpha } } \right)} \right)}}}} }}} \right) \hfill \\ \end{gathered} \right\}} \hfill \\ \end{gathered} \right)$$
Definition 10
Let \(\underline {\text{B}}_{{\upalpha }}\) be the collection of HBCFNs, then the HBCFHPWA operator is a function of \({\text{HBCFHPWA}}:\underline {\text{B}}^{{\updelta }} \to \underline {\text{B}}\) defines by;
where, \({\underline {\upomega } }_{{\upalpha }} = \left( {{\underline {\upomega } }_{1} ,{\underline {\upomega } }_{2} , \ldots ,{\underline {\upomega } }_{{\updelta }} } \right)\) is a weight vector, \({\underline {\upomega } }_{{\upalpha }} \in \left[ {0,1} \right]\) and \(\mathop \sum \nolimits_{{{\upalpha } = 1}}^{{\updelta }} {\underline {\upomega } }_{{\upalpha }} = 1.\)
Theorem 3
Let \(\underline {\text{B}}_{{\upalpha }}\) be a collection of HBCFNs, then by (4), we get the HBCFN and;
Definition 11
Let \(\underline {\text{B}}_{{\upalpha }}\) be a collection of HBCFNs, then HBCFHPOWA operator is a function \({\text{HBCFHPOWA}}:\underline {\text{B}}^{{\updelta }} \to \underline {\text{B}}\) such that.
where, \({\underline {\upomega } }_{{\upalpha }} = \left( {{\underline {\upomega } }_{1} ,{\underline {\upomega } }_{2} , \ldots ,{\underline {\upomega } }_{{\updelta }} } \right)\) is a weight vector, \({\underline {\upomega } }_{{\upalpha }} \in \left[ {0,1} \right]\forall {{ \upalpha }}\) and \(\mathop \sum \nolimits_{{{\upalpha } = 1}}^{{\updelta }} {\underline {\upomega } }_{{\upalpha }} = 1\) and \({\Gamma }\left( 1 \right),{\Gamma }\left( 2 \right),{\Gamma }\left( 3 \right), \ldots ,{\Gamma }\left( {\updelta } \right)\) are the permutation of \({\Gamma }\left( {\upalpha } \right)\left( {{\upalpha } = 1,2,3, \ldots ,{\updelta }} \right)\) such that \(\underline {\text{B}}_{{{\Gamma }\left( {{\upalpha } - 1} \right)}} \ge \underline {\text{B}}_{{{\Gamma }\left( {\upalpha } \right)}} \;\forall {\upalpha }.\)
Theorem 4
Let \(\underline {\text{B}}_{{\upalpha }}\) be a collection of HBCFNs, then by (6), we have the HBCFN and
Definition 12
Let \(\underline {\text{B}}_{{\upalpha }}\) be a collection of HBCFNs, then the HBCFHPG operator is a function \({\text{HBCFHWG}}:\underline {\text{B}}^{{\updelta }} \to \underline {\text{B}}\) presented as;
where, \(\ ^\circ\!{\text{F}}\left( {\underline {\text{B}}_{{\upalpha }} } \right) = \mathop \sum \nolimits_{{\begin{array}{*{20}c} {\upalpha ,{\mathbf{\varsigma }} = 1} \\ {{\mathbf{\varsigma }} \ne \upalpha } \\ \end{array} }}^{{\updelta }} {\text{sup}}\left( {\underline {\text{B}}_{{\upalpha }} ,\underline {\text{B}}_{{\mathbf{\varsigma }}} } \right)\) and \({\text{sup}}\left( {\underline {\text{B}}_{{\upalpha }} ,\underline {\text{B}}_{{\mathbf{\varsigma }}} } \right)\) implies that the support between two HBCFNs \(\underline {\text{B}}_{{\upalpha }}\) and \(\underline {\text{B}}_{{\mathbf{\varsigma }}}\) and also satisfy;
-
\({\text{sup}}\left( {\underline {\text{B}}_{{\upalpha }} ,\underline {\text{B}}_{{\mathbf{\varsigma }}} } \right) \in \left[ {0,1} \right],\)
-
\({\text{sup}}\left( {\underline {\text{B}}_{{\upalpha }} ,\underline {\text{B}}_{{\mathbf{\varsigma }}} } \right) = {\text{sup}}\left( {\underline {\text{B}}_{{\mathbf{\varsigma }}} ,\underline {\text{B}}_{{\upalpha }} } \right)\)
-
\({\text{sup}}\left( {\underline {\text{B}}_{{\upalpha }} ,\underline {\text{B}}_{{\mathbf{\varsigma }}} } \right) \ge {\text{sup}}\left( {\underline {\text{B}}_{{{{\upalpha^{\prime}}}}} ,\underline {\text{B}}_{{{\mathbf{\varsigma^{\prime}}}}} } \right),\) if \(\Upsilon \left( {\underline {\text{B}}_{{\upalpha }} ,\underline {\text{B}}_{{\mathbf{\varsigma }}} } \right) < {\Upsilon }\left( {\underline {\text{B}}_{{{{\upalpha^{\prime}}}}} ,\underline {\text{B}}_{{{\mathbf{\varsigma^{\prime}}}}} } \right).\) Where \({\Upsilon }\) is the distance measure.
Theorem 5
Let \(\underline {\text{B}}_{{\upalpha }}\) be a collection of HBCFNs, then by (8), we have;
Particular cases We discussed two different particular cases of \(\text{HBCFHPG}\) operators as follows:
-
1.
When \({\aleph } = 1,\) then the HBCFHPG operator reduces into the hesitant bipolar complex fuzzy power geometric (HBCFPG) operator as;
$${\text{HBCFPG}}\left( {\underline {\text{B}}_{1} ,\underline {\text{B}}_{2} , \ldots ,\underline {\text{B}}_{{\updelta }} } \right) = \begin{array}{*{20}c} {\updelta } \\ \otimes \\ {{\upalpha } = 1} \\ \end{array} \left( {\underline {\text{B}}_{{\upalpha }} } \right)^{{\frac{{\left( {1 +^\circ\!{\text{F}}\left( {\underline {\text{B}}_{{\upalpha }} } \right)} \right)}}{{\mathop \sum \nolimits_{{{\upalpha } = 1}}^{{\updelta }} \left( {1 +^\circ\!{\text{F}}\left( {\underline {\text{B}}_{{\upalpha }} } \right)} \right)}}}}$$$$= \left( \begin{gathered} \mathop \cup \limits_{{\xi_{1}^{ + } \in {\upbeta }_{1}^{ + } , \ldots ,\xi_{{\updelta }}^{ + } \in {\upbeta }_{{\updelta }}^{ + } }} \left\{ {\left( {\mathop \prod \limits_{{{\upalpha } = 1}}^{{\updelta }} \left( {\xi_{{\upalpha }}^{{ + \left( {{\text{Re}}} \right)}} } \right)^{{\frac{{\left( {1 +^\circ\!{\text{F}}\left( {\underline {\text{B}}_{{\upalpha }} } \right)} \right)}}{{\mathop \sum \nolimits_{{{\upalpha } = 1}}^{{\updelta }} \left( {1 +^\circ\!{\text{F}}\left( {\underline {\text{B}}_{{\upalpha }} } \right)} \right)}}}} } \right) + {\upiota }\left( {\mathop \prod \limits_{{{\upalpha } = 1}}^{{\updelta }} \left( {\xi_{{\upalpha }}^{{ + \left( {{\text{Re}}} \right)}} } \right)^{{\frac{{\left( {1 +^\circ\!{\text{F}}\left( {\underline {\text{B}}_{{\upalpha }} } \right)} \right)}}{{\mathop \sum \nolimits_{{{\upalpha } = 1}}^{{\updelta }} \left( {1 +^\circ\!{\text{F}}\left( {\underline {\text{B}}_{{\upalpha }} } \right)} \right)}}}} } \right)} \right\}, \hfill \\ \mathop \cup \limits_{{\xi_{1}^{ - } \in {\upbeta }_{1}^{ - } , \ldots ,\xi_{{\updelta }}^{ - } \in {\upbeta }_{{\updelta }}^{ - } }} \left\{ {\left( { - 1 + \mathop \prod \limits_{{{\upalpha } = 1}}^{{\updelta }} \left( {1 + \xi_{{\upalpha }}^{{ - \left( {{\text{Im}}} \right)}} } \right)^{{\frac{{\left( {1 +^\circ\!{\text{F}}\left( {\underline {\text{B}}_{{\upalpha }} } \right)} \right)}}{{\mathop \sum \nolimits_{{{\upalpha } = 1}}^{{\updelta }} \left( {1 +^\circ\!{\text{F}}\left( {\underline {\text{B}}_{{\upalpha }} } \right)} \right)}}}} } \right) + {\upiota }\left( { - 1 + \mathop \prod \limits_{{{\upalpha } = 1}}^{{\updelta }} \left( {1 + \xi_{{\upalpha }}^{{ - \left( {{\text{Im}}} \right)}} } \right)^{{\frac{{\left( {1 +^\circ\!{\text{F}}\left( {\underline {\text{B}}_{{\upalpha }} } \right)} \right)}}{{\mathop \sum \nolimits_{{{\upalpha } = 1}}^{{\updelta }} \left( {1 +^\circ\!{\text{F}}\left( {\underline {\text{B}}_{{\upalpha }} } \right)} \right)}}}} } \right)} \right\} \hfill \\ \end{gathered} \right)$$ -
2.
When \(\aleph = 2,\) then the HBCFHPG operator reduces into the hesitant bipolar complex fuzzy Einstein power geometric (HBCFEPG) operator.
$${\text{HBCFEPG}}\left( {\underline {\text{B}}_{1} ,\underline {\text{B}}_{2} , \ldots ,\underline {\text{B}}_{{\updelta }} } \right) = \begin{array}{*{20}c} {\updelta } \\ \otimes \\ {{\upalpha } = 1} \\ \end{array} \left( {\underline {\text{B}}_{{\upalpha }} } \right)^{{\frac{{\left( {1 +^\circ\!{\text{F}}\left( {\underline {\text{B}}_{{\upalpha }} } \right)} \right)}}{{\mathop \sum \nolimits_{{{\upalpha } = 1}}^{{\updelta }} \left( {1 +^\circ\!{\text{F}}\left( {\underline {\text{B}}_{{\upalpha }} } \right)} \right)}}}}$$$$= \left( \begin{gathered} \bigcup\limits_{{\xi _{1}^{ + } \in \upbeta _{1}^{ + } , \ldots ,\xi _{\updelta }^{ + } \in \upbeta _{\updelta }^{ + } }} {\left\{ \begin{gathered} \left( {\frac{{2\mathop \prod \nolimits_{{\upalpha = 1}}^{\updelta } \left( {\xi _{\upalpha }^{{ + \left( {\text{Re} } \right)}} } \right)^{{\frac{{\left( {1 + ^\circ\!{\text{F}}\left( {\underline {\text{B}}_{\upalpha } } \right)} \right)}}{{\mathop \sum \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + ^\circ\!{\text{F}}\left( {\underline {\text{B}}_{\upalpha } } \right)} \right)}}}} }}{{\mathop \prod \nolimits_{{\upalpha = 1}}^{\updelta } \left( {2 - \xi _{\upalpha }^{{ + \left( {\text{Re} } \right)}} } \right)^{{\frac{{\left( {1 + ^\circ\!{\text{F}}\left( {\underline {\text{B}}_{\upalpha } } \right)} \right)}}{{\mathop \sum \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + ^\circ\!{\text{F}}\left( {\underline {\text{B}}_{\upalpha } } \right)} \right)}}}} + \mathop \prod \nolimits_{{\upalpha = 1}}^{\updelta } \left( {\xi _{\upalpha }^{{ + \left( {\text{Re} } \right)}} } \right)^{{\frac{{\left( {1 + ^\circ\!{\text{F}}\left( {\underline {\text{B}}_{\upalpha } } \right)} \right)}}{{\mathop \sum \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + ^\circ\!{\text{F}}\left( {\underline {\text{B}}_{\upalpha } } \right)} \right)}}}} }}} \right) \hfill \\ + \upiota \left( {\frac{{2\mathop \prod \nolimits_{{\upalpha = 1}}^{\updelta } \left( {\xi _{\upalpha }^{{ + \left( {\text{Im} } \right)}} } \right)^{{\frac{{\left( {1 + ^\circ\!{\text{F}}\left( {\underline {\text{B}}_{\upalpha } } \right)} \right)}}{{\mathop \sum \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + ^\circ\!{\text{F}}\left( {\underline {\text{B}}_{\upalpha } } \right)} \right)}}}} }}{{\mathop \prod \nolimits_{{\upalpha = 1}}^{\updelta } \left( {2 - \xi _{\upalpha }^{{ + \left( {\text{Im} } \right)}} } \right)^{{\frac{{\left( {1 + ^\circ\!{\text{F}}\left( {\underline {\text{B}}_{\upalpha } } \right)} \right)}}{{\mathop \sum \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + ^\circ\!{\text{F}}\left( {\underline {\text{B}}_{\upalpha } } \right)} \right)}}}} + \mathop \prod \nolimits_{{\upalpha = 1}}^{\updelta } \left( {\xi _{\upalpha }^{{ + \left( {\text{Im} } \right)}} } \right)^{{\frac{{\left( {1 + ^\circ\!{\text{F}}\left( {\underline {\text{B}}_{\upalpha } } \right)} \right)}}{{\mathop \sum \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + ^\circ\!{\text{F}}\left( {\underline {\text{B}}_{\upalpha } } \right)} \right)}}}} }}} \right) \hfill \\ \end{gathered} \right\}} \hfill \\ \bigcup\limits_{{\xi _{1}^{ - } \in \upbeta _{1}^{ - } , \ldots ,\xi _{\updelta }^{ - } \in \upbeta _{\updelta }^{ - } }} {\left\{ \begin{gathered} \left( { - \frac{{\mathop \prod \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + \left| {\xi _{\upalpha }^{{ - \left( {\text{Re} } \right)}} } \right|} \right)^{{\frac{{\left( {1 + ^\circ\!{\text{F}}\left( {\underline {\text{B}} } \right)} \right)}}{{\mathop \sum \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + ^\circ\!{\text{F}}\left( {\underline {\text{B}}_{\upalpha } } \right)} \right)}}}} - \mathop \prod \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + \xi _{\upalpha }^{{ - \left( {\text{Re} } \right)}} } \right)^{{\frac{{\left( {1 + ^\circ\!{\text{F}}\left( {\underline {\text{B}}_{\upalpha } } \right)} \right)}}{{\mathop \sum \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + ^\circ\!{\text{F}}\left( {\underline {\text{B}}_{\upalpha } } \right)} \right)}}}} }}{{\mathop \prod \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + \left| {\xi _{\upalpha }^{{ - \left( {\text{Re} } \right)}} } \right|} \right)^{{\frac{{\left( {1 + ^\circ\!{\text{F}}\left( {\underline {\text{B}}_{\upalpha } } \right)} \right)}}{{\mathop \sum \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + ^\circ\!{\text{F}}\left( {\underline {\text{B}}_{\upalpha } } \right)} \right)}}}} + \mathop \prod \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + \xi _{\upalpha }^{{ - \left( {\text{Re} } \right)}} } \right)^{{\frac{{\left( {1 + ^\circ\!{\text{F}}\left( {\underline {\text{B}}_{\upalpha } } \right)} \right)}}{{\mathop \sum \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + ^\circ\!{\text{F}}\left( {\underline {\text{B}}_{\upalpha } } \right)} \right)}}}} }}} \right) \hfill \\ + \upiota \left( { - \frac{{\mathop \prod \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + \left| {\xi _{\upalpha }^{{ - \left( {\text{Im} } \right)}} } \right|} \right)^{{\frac{{\left( {1 + ^\circ\!{\text{F}}\left( {\underline {\text{B}}_{\upalpha } } \right)} \right)}}{{\mathop \sum \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + ^\circ\!{\text{F}}\left( {\underline {\text{B}}_{\upalpha } } \right)} \right)}}}} - \mathop \prod \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + \xi _{\upalpha }^{{ - \left( {\text{Im} } \right)}} } \right)^{{\frac{{\left( {1 + ^\circ\!{\text{F}}\left( {\underline {\text{B}}_{\upalpha } } \right)} \right)}}{{\mathop \sum \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + ^\circ\!{\text{F}}\left( {\underline {\text{B}}_{\upalpha } } \right)} \right)}}}} }}{{\mathop \prod \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + \left| {\xi _{\upalpha }^{{ - \left( {\text{Im} } \right)}} } \right|} \right)^{{\frac{{\left( {1 + ^\circ\!{\text{F}}\left( {\underline {\text{B}}_{\upalpha } } \right)} \right)}}{{\mathop \sum \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + ^\circ\!{\text{F}}\left( {\underline {\text{B}}_{\upalpha } } \right)} \right)}}}} + \mathop \prod \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + \xi _{\upalpha }^{{ - \left( {\text{Im} } \right)}} } \right)^{{\frac{{\left( {1 + ^\circ\!{\text{F}}\left( {\underline {\text{B}}_{\upalpha } } \right)} \right)}}{{\mathop \sum \nolimits_{{\upalpha = 1}}^{\updelta } \left( {1 + ^\circ\!{\text{F}}\left( {\underline {\text{B}}_{\upalpha } } \right)} \right)}}}} }}} \right) \hfill \\ \end{gathered} \right\}} \hfill \\ \end{gathered} \right)$$
Definition 13
Let \(\underline {\text{B}}_{{\upalpha }}\) be a collection of HBCFNs, then the HBCFHPWG operator is a function of \({\text{HBCFHPWG}}:\underline {\text{B}}^{{\updelta }} \to \underline {\text{B}}\) presented as;
where, \({\underline {\upomega } }_{{\upalpha }} = \left( {{\underline {\upomega } }_{1} ,{\underline {\upomega } }_{2} , \ldots ,{\underline {\upomega } }_{{\updelta }} } \right)\) is a weight vector, \({\underline {\upomega } }_{{\upalpha }} \in \left[ {0,1} \right]\;\forall {\upalpha }\) and \(\mathop \sum \nolimits_{{{\upalpha } = 1}}^{{\updelta }} {\underline {\upomega } }_{{\upalpha }} = 1.\)
Theorem 6
Let \({\underline {\rm B} }_{{\upalpha }}\) be the collection of HBCFNs, then by (10), we get the HBCFN and;
Definition 14
Let \(\underline {\text{B}}_{{\upalpha }}\) be a collection of HBCFNs, then the HBCFHPOWG operator is a function \({\text{HBCFHPOWG}}:\underline {\text{B}}^{{\updelta }} \to \underline {\text{B}}\) such that;
where \({\underline {\upomega } }_{{\upalpha }} = \left( {{\underline {\upomega } }_{1} ,{\underline {\upomega } }_{2} , \ldots ,{\underline {\upomega } }_{{\updelta }} } \right)\) is a weight vector, \({\underline {\upomega } }_{{\upalpha }} \in \left[ {0,1} \right]\quad \forall \;{\upalpha }\) and \(\mathop \sum \nolimits_{{{\upalpha } = 1}}^{{\updelta }} {\underline {\upomega } }_{{\upalpha }} = 1\) and \({\Gamma }\left( 1 \right),{\Gamma }\left( 2 \right),{\Gamma }\left( 3 \right), \ldots ,{\Gamma }\left( {\updelta } \right)\) are the permutation of \({\Gamma }\left( {\upalpha } \right)\left( {{\upalpha } = 1,2,3, \ldots ,{\updelta }} \right)\) such that \(\underline {\text{B}}_{{{\Gamma }\left( {{\upalpha } - 1} \right)}} \ge \underline {\text{B}}_{{{\Gamma }\left( {\upalpha } \right)}} \;\forall {\upalpha }.\)
Theorem 7
Let \(\underline {\text{B}}_{{\upalpha }}\) be a collection of HBCFNs, then by (12), we have the HBCFN and;
All the above defined operators hold must holds the properties of idempotency, monotonicity and boundedness.
HBCF-MADM
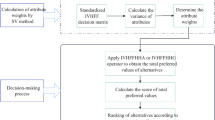
In this section, we propose a MADM approach based on the proposed operators and in the environment of HBCFNs. Let us assume that there are \({\upmu }\) alternatives signified by \({\Delta } = \left\{ {{\Delta }_{1} ,{\Delta }_{2} , \ldots ,{\Delta }_{{\upmu }} } \right\}\) and \(\upvartheta\) attributes signified by \({\text{\AA}} = \left\{ {{\text{\AA}}_{1} ,{\text{\AA}}_{2} ,{\text{\AA}}_{2} , \ldots ,{\text{\AA}}_{\upvartheta } } \right\}\). Let \({\underline {\upomega } } = \left( {{\underline {\upomega } }_{1} ,{\underline {\upomega } }_{2} ,{\underline {\upomega } }_{3} , \ldots ,{\underline {\upomega } }_{\upvartheta } } \right)\) be the weight vector of attributes with \({\underline {\upomega } }_{{\upalpha }} \in \left[ {0,1} \right],{\upalpha } = \left( {1,2,3, \ldots ,\upvartheta } \right)\) and \(\mathop \sum \nolimits_{{{\upalpha } = 1}}^{\upvartheta } {\underline {\upomega } }_{{\upalpha }} = 1\). Now we supposed \({\text{M}} = \left( {\underline {\text{B}}_{{{{\upalpha \upeta }}}} } \right)_{{{\upmu } \times \upvartheta }} = \left( {{\upbeta }_{{{{\upalpha \upeta }}}}^{ + } ,{{ \upbeta }}_{{{{\upalpha \upeta }}}}^{ - } } \right)_{{{\upmu } \times \upvartheta }} = \left( {\xi_{{{{\upalpha \upeta }}}}^{{ + \left( {{\text{Re}}} \right)}} + {\upiota }\xi_{{{{\upalpha \upeta }}}}^{{ + \left( {{\text{Im}}} \right)}} ,\xi_{{{{\upalpha \upeta }}}}^{{ - \left( {{\text{Re}}} \right)}} + {\upiota }\xi_{{{{\upalpha \upeta }}}}^{{ - \left( {{\text{Im}}} \right)}} } \right)_{{{\upmu } \times \upvartheta }}\) be a HBCF decision matrix. Also, note that \(\xi_{{{{\upalpha \upeta }}}}^{{ + \left( {{\text{Re}}} \right)}} + {\upiota }\xi_{{{{\upalpha \upeta }}}}^{{ + \left( {{\text{Im}}} \right)}} \in \left[ {0,1} \right],\xi_{{{{\upalpha \upeta }}}}^{{ - \left( {{\text{Re}}} \right)}} + {\upiota }\xi_{{{{\upalpha \upeta }}}}^{{ - \left( {{\text{Im}}} \right)}} \in \left[ { - 1,0} \right]\). Next, we have the following algorithm steps;
Step-1 In each MADM process, the attribute may be in two types, one is benefit type and the second is cost type. In any MADM procedure if the attributes are given in the form of cost type, then we use the following formula to make it benefit type:
Step-2 In this step we find out the support as:
Note that the Eq. (14) holds the condition of support. Furthermore, to determine \({\Upsilon }\left( {\underline {\text{B}}_{{{{\upalpha \upeta }}}} ,\underline {\text{B}}_{{{\upalpha }\aleph }} } \right)\) we have the following underneath distance formula.
Step-3 In this step we find out the
where \({\upalpha } = 1,2,3, \ldots ,{\upmu },{{ \upeta }},{{\varsigma }} = 1,2,3, \ldots ,\upvartheta\) and \({\upeta } \ne {{\varsigma }}.\)
Step-4 Determine the corelated weight using following:
where, \({\mathbb{R}}_{{{{\upalpha \upeta }}}} \in \left[ {0,1} \right]\) for each \({\upalpha },{{ \upeta }}\) and \(\mathop \sum \nolimits_{{{\upeta } = 1}}^{\upvartheta } {\mathbb{R}}_{{{{\upalpha \upeta }}}} = 1,\)\({\upalpha } = 1,2,3, \ldots ,{\upmu }.\)
Step-5 In this step, we utilize one of the proposed operators HBCFHPA or HBCFHPG operators to aggregate the expert’s decision matrix.
Step-6 The score values of the aggregated outcome would be determined using score value or accuracy value format.
Step-7 Rank all the finding values to choose the best alternative.
Case study
The energy management responsibilities of ABC Energy Management Company rest upon achieving maximum energy efficiency and waste reduction through AI-based methodology. The company intends to use AI to optimize energy usage while boosting operational efficiency and reducing costs along with sustainability promotion. Energy management complexity forces ABC Energy Management Company to examine different strategies until they select the best solution according to performance characteristics.
The company has the following alternatives;
\({{\varvec{\Delta}}}_{1}\): Machine learning-based strategy (MLBS)
The system computes energy consumption patterns through sophisticated machine-learning models that evaluate records. This strategy ensures top-level accuracy in real-time energy optimization through its extensive costs at setup. The strategic use of these systems gives exact energy predictions though owning suitable hardware represents a substantial upfront expense.
\({{\varvec{\Delta}}}_{2}\): Internet of Things integration (IOTI)
The strategy implements IoT-enabled devices that serve as data collection sources for real-time monitoring and control functionalities. The system offers time-sensitive optimization along with adjustable features though it shows difficulties when implemented in extensive installations. This system performs very well with energy changes however extensive network elements are necessary.
\({{\varvec{\Delta}}}_{3}\): Predictive analytics driven method (PADM)
The system calculates future power requirements with AI-powered models while it enhances power consumption efficiency patterns. The system provides high scalability and cost-effectiveness however accurate predictions depend on reliable data quality. These techniques work well for proactive power management with accuracy levels that differ from case to case.
\({{\varvec{\Delta}}}_{4}\): Hybrid AI algorithm strategy (HAAS)
The system uses machine learning with IoT devices alongside predictive analytics for maximizing operational results. This approach balances accuracy parallel with scalability besides adaptability though it needs additional expertise and resources. The system provides complete energy management although its implementation requires advanced complexity.
For further evaluation, the company has the following criteria.
\(\text{\AA}_{1}\): Accuracy: The measure determines both the predictive accuracy for energy usage along the reduction of unnecessary resources. The level of precision in predictions works to increase operational efficiency and distribute energy in real-time. This decision-making tool needs sophisticated computational abilities although it provides very accurate results.
\(\text{\AA}_{2}\): Adaptability: It evaluates how effectively the strategy responds to transformations in environment and technology. Changing approaches create ongoing efficiency even when operating through changing situations. The system requires adaptations during future periods for ongoing protection against obsolescence.
\(\text{\AA}_{3}\): Scalability: The strategy needs to demonstrate its capacity to support higher energy requirements and expand business operations. A scalable system allows organizations to grow their operation without encountering any performance decline. Sustainability for the long run demands this approach yet demands elevated infrastructure costs.
\(\text{\AA}_{4}\): Cost-Effectiveness: The assessment analyzes how efficient operations relate to the expenses needed for implementation and operations. Such a method produces superior energy conservation results with spending maintained at a minimum level. Financial viability should be maintained through this approach as it does not reduce overall performance.
The company experts have the following decision matrix based on HBCF information given in Table 3.
Step-1 The given data in Table 1 is benefit type so there is no need to normalize it.
Step-2 The supports are;
For \({\upalpha } = 1\)
For \({\upalpha } = 2\)
For \({\upalpha } = 3\)
For \({\upalpha } = 4\)
Step-3 In this step we have:
Step-4 We have the following corelated weights:
If we have the following weight vectors \(\left( {0.34,0.14,0.32,0.25} \right)\), then the corelated weights are;
Step-5 The aggregated value after utilizing the HBCFHPA, HBCFHPWA, HBCFHPG, HBCFHPWG operators are;
HBCFHPA;
HBCFHPWA;
HBCFHPG;
HBCFHPWG;
Step-6 The score values of the aggregated outcome are discussed in Table 4.
Step-7 Rank all the finding values for choosing best is discussed in Table 5.
Based on the above Table 3 we exactly observe that by using all the proposed operators like HBCFHPA, HBCFHPWA, HBCFHPG and HBCFHPWG we conclude that \({\Delta }_{3}\) is the best alternative.
The graphical representation of ranking different alternatives is discussed in Figs. 5, 6, 7 and 8.
Comparative analysis
To highlight the benefits and standards of the newly proposed theory, we compare newly developed work with earlier published results. This is because each newly developed work must be compared to truly understand its relevance and effectiveness. We cannot discriminate between the superior and inferior without comparison. We select a few ideas that have been published before for this. Next, we include all of these ideas in the proposed theory and monitor the results, which are shown in below Table 6. First, we suppose the following theories of different authors and then discuss their limitations.
-
The theory of hesitant fuzzy Hamacher aggregation operators (HFHAOs) by Tan et al.10.
-
The theory of hesitant fuzzy Frank aggregation operators (HFFAOs) by Qin et al.13.
-
The theory of bipolar fuzzy Hamacher aggregation operators (BFHAOs) by Wei et al.15.
-
The theory of bipolar fuzzy Dombi prioritized aggregation operators (BFDPAOs) by Jana et al.16.
-
The theory of bipolar complex fuzzy Hamacher aggregation operators (BCFHAOs) and their applications in MADM by Mahmood et al.26.
All above supposed theories are mostly basic theories including their AOs. We try to solve the HBCF information or data using different frameworks. In this comparison we take different values that are defined in Table 3 and try to solve with different supposed AOs and the coming results are discussed in below Table 6.
The above-given Table 6 is the resultant table. Overall observation in the above table is discussed step by step. First of all, we take the theory of HFHAOs by Tan et al.10 and try to solve HBCF information using the proposed AOs defined in this theory. However, we observe that the theory of HFHAOs by Tan et al.10 can only solve fuzzy data, which means this theory can only solve the membership value of any object and cannot solve both positive and negative grades at the same time. Similarly, the theory of HFFAOs by Qin et al.13 is also only a fuzzy-based theory and can only solve fuzzy information and cannot be capable of solving our HBCF information. Next, we suppose that the theories of BFHAOs by Wei et al.15 and BFDPAOs by Jana et al.16. Both theories are bipolar-based theories that can deal easily with positive and negative aspects of any object at the same time and their aggregation tools can also solve and handle any decision in the form of bipolar information. But we closely note that aggregation of bipolar theories like BF Hamacher and BF Dombi prioritized AOs cannot solve the HBF information. All the above bipolar theories are very close to our work but our information has many qualities at the same time like handling positive and negative aspects of any information i.e. bipolarity, extra informative terms in the form of iota, and also hesitancy. Bipolar can solve only one quality of positive and negative of our information but hesitancy and complex terms are not solved with bipolar. So, we conclude that our theory is superior then all other theories. In the end, we suppose that the theory of BCFHAOs and their applications in MADM by Mahmood et al.26. This theory is closer to our theory and our work is an extension of this theory. So, because our data has the following characteristics of hesitancy, bipolarity, complex numerical data, and two-dimensional situations the above theory cannot solve the hesitancy fact of our proposed work. So, that’s why our work is superior to all other supposed approaches.
Possible managerial implications
Our research on HBCFSs and MADM techniques has important managerial results which can be applied as follows:
-
Decision-making becomes enhanced by the method which enables precise flexible complex alternative evaluation while allowing managers to base their choices on accurate data.
-
The framework functions across various industry sectors by enabling its use in energy management and cloud security systems and smart charging infrastructure development and climate impact assessment to achieve improved resource optimization and enhanced efficiency.
-
The model serves organizations that need to process imprecise and hesitant or conflicting data through its effective approach to adding uncertainty in decision-making processes.
-
Policymakers should utilize the results to construct well-rounded approaches regarding sustainable development combined with smart infrastructure and industrial automation for lasting results.
-
The developed aggregation operators enable systematic assessment of different techniques models or technologies that helps managers make better investment and operational choices.
Limitations
The results of the work with HBCFSs have some restrictions. One of the main difficulties is the computational complexity of calculations that takes much longer, particularly for large data sets or in real-world applications. Second, the nature of HBCFSs is tailored to accommodate hesitancy, bipolarity, and imaginary variables, which means it can be applied only to problems showing these properties. Other uncertainty representation models, like neutrosophic sets, soft sets, or rough sets, are not completely accessible through HBCFSs since every model has its domain and restrictions. These constraints exhibit the necessity to conduct more research to spread the applicability of HBCFSs into more frameworks.
Conclusion
AI energy management is an emerging technology that exploits AI technologies such as data analytics, predictive modeling, and machine learning to reduce energy consumption in different sectors like homes, businesses, and industries. We present in this manuscript a new framework for managing and choosing AI-based energy management systems based on sophisticated aggregation operators. We have created several aggregation tools for processing HBCF data efficiently, thus making AI-based energy decision-making effective. The aggregation operators proposed are HBCFHPA, HBCFHPWA, HBCFHPOWA, HBCFHPG, HBCFHPWG, and HBCFHPOWG operators. A numerical case study is presented to illustrate their use in choosing the most appropriate AI-based energy management strategy. In addition, we compare our suggested approach with other existing methodologies to prove its efficacy and superiority. Future research avenues involve applying this framework to other mathematical models, i.e.31,32,33,34,35,36,37,38.
The key findings are;
-
Predictive analytics together with machine learning support AI-driven energy management systems to boost overall energy efficiency.
-
The proposal presents an innovative approach to identifying the most suitable AI-powered energy management system.
-
This research develops new aggregation operators named HBCFHPA and HBCFHPWA as well as their variants HBCFHPOWA HBCFHPG and HBCFHPWG and HBCFHPOWG.
-
A numerical illustration in this study demonstrates how the proposed method works effectively.
-
The proposed framework demonstrates superiority compared to existing methods during collaborative examination.
Data availability
The data will be available on reasonable request to the corresponding author or anyone can use the data by just citing the article.
References
Ali, D. M. T. E., Motuzienė, V. & Džiugaitė-Tumėnienė, R. Ai-driven innovations in building energy management systems: A review of potential applications and energy savings. Energies 17(17), 4277 (2024).
Hadi, A. S. A. A., Wahab, A. A. B. A., Hamzah, F. M. & Veena, B. S. AI-driven energy management techniques for enhancing network longevity in wireless sensor networks. J. Robot. Control (JRC) 6(1), 246–261 (2025).
Varghese, A. AI-driven solutions for energy optimization and environmental conservation in digital business environments. Asia Pac. J. Energy Environ. 9(1), 49–60 (2022).
Long, L. D. An AI-driven model for predicting and optimizing energy-efficient building envelopes. Alex. Eng. J. 79, 480–501 (2023).
Zadeh, L. A. Fuzzy sets. Inf. Control 8(3), 338–353 (1965).
Merigo, J. M. & Casanovas, M. Fuzzy generalized hybrid aggregation operators and its application in fuzzy decision making. Int. J. Fuzzy Syst. 12(1) (2010).
Torra, V. Hesitant fuzzy sets. Int. J. Intell. Syst. 25(6), 529–539 (2010).
Zhang, Z. Hesitant fuzzy power aggregation operators and their application to multiple (2013)
Xia, M., Xu, Z. & Chen, N. Some hesitant fuzzy aggregation operators with their application in group decision making. Group Decis. Negot. 22, 259–279 (2013).
Tan, C., Yi, W. & Chen, X. Hesitant fuzzy Hamacher aggregation operators for multicriteria decision making. Appl. Soft Comput. 26, 325–349 (2015).
Xia, M. & Xu, Z. Hesitant fuzzy information aggregation in decision making. Int. J. Approx. Reason. 52(3), 395–407 (2011).
Qian, G., Wang, H. & Feng, X. Generalized hesitant fuzzy sets and their application in decision support system. Knowl.-Based Syst. 37, 357–365 (2013).
Qin, J., Liu, X. & Pedrycz, W. Frank aggregation operators and their application to hesitant fuzzy multiple attribute decision making. Appl. Soft Comput. 41, 428–452 (2016).
Zhang, W. R. (Yin)(Yang) bipolar fuzzy sets. In 1998 IEEE International Conference on Fuzzy Systems Proceedings. IEEE World Congress on Computational Intelligence (Cat. No. 98CH36228) Vol. 1, 835–840 (IEEE, 1998).
Wei, G., Alsaadi, F. E., Hayat, T. & Alsaedi, A. Bipolar fuzzy Hamacher aggregation operators in multiple attribute decision making. Int. J. Fuzzy Syst. 20, 1–12 (2018).
Jana, C., Pal, M. & Wang, J. Q. Bipolar fuzzy Dombi prioritized aggregation operators in multiple attribute decision making. Soft. Comput. 24, 3631–3646 (2020).
Chen, Y., Rehman, U. U. & Mahmood, T. Bipolar fuzzy multi-criteria decision-making technique based on probability aggregation operators for selection of optimal artificial intelligence framework. Symmetry 15(11), 2045 (2023).
Garg, H., Mahmood, T., ur Rehman, U. & Nguyen, G. N. Multi-attribute decision-making approach based on Aczel-Alsina power aggregation operators under bipolar fuzzy information & its application to quantum computing. Alex. Eng. J. 82, 248–259 (2023).
Riaz, M. & Tehrim, S. T. A robust extension of VIKOR method for bipolar fuzzy sets using connection numbers of SPA theory based metric spaces. Artif. Intell. Rev. 54, 561–591 (2021).
Tchangani, A. Bipolar aggregation method for fuzzy nominal classification using weighted cardinal fuzzy measure (WCFM). J. Uncertain Syst. 7, 138 (2013).
Mandal, P. & Ranadive, A. S. Hesitant bipolar-valued fuzzy sets and bipolar-valued hesitant fuzzy sets and their applications in multi-attribute group decision making. Granul. Comput. 4(3), 559–583 (2019).
Gao, H., Lu, M. & Wei, Y. Dual hesitant bipolar fuzzy hamacher aggregation operators and their applications to multiple attribute decision making. J. Intell. Fuzzy Syst. 37(4), 5755–5766 (2019).
Wei, G., Alsaadi, F. E., Hayat, T. & Alsaedi, A. Hesitant bipolar fuzzy aggregation operators in multiple attribute decision making. J. Intell. Fuzzy Syst. 33(2), 1119–1128 (2017).
Mahmood, T. & Ur Rehman, U. A novel approach towards bipolar complex fuzzy sets and their applications in generalized similarity measures. Int. J. Intell. Syst. 37(1), 535–567 (2022).
Mahmood, T., Rehman, U. U., Ali, Z., Aslam, M. & Chinram, R. Identification and classification of aggregation operators using bipolar complex fuzzy settings and their application in decision support systems. Mathematics 10(10), 1726 (2022).
Mahmood, T., Rehman, U. U., Ahmmad, J. & Santos-García, G. Bipolar complex fuzzy Hamacher aggregation operators and their applications in multi-attribute decision making. Mathematics 10(1), 23 (2021).
Mahmood, T. & Rehman, U. U. A method to multi-attribute decision making technique based on Dombi aggregation operators under bipolar complex fuzzy information. Comput. Appl. Math. 41(1), 47 (2022).
Aslam, M., Waqas, H. M., Rehman, U. U. & Mahmood, T. Selection of cloud services provider by utilizing multi-attribute decision-making based on hesitant bipolar complex fuzzy Dombi aggregation operators. IEEE Access 12(35417–35447), 2024 (2024).
Waqas, H. M., Emam, W., Mahmood, T., Rehman, U. U. & Yin, S. Selection of cloud security by employing MABAC technique in the environment of hesitant bipolar complex fuzzy information. IEEE Access 12(123127–123148), 2024 (2024).
Hamacher, H. ber logische Verknpfungen unscharfer Aussagen und deren zugehrige Bewertungsfunktionen. In Progress in Cybernetics and Systems Research Vol. 2 (eds Trappl, R. & de Hanika P.) 276 (1975).
Li, Y., Bu, F., Li, Y. & Long, C. Optimal scheduling of island integrated energy systems considering multi-uncertainties and hydrothermal simultaneous transmission: A deep reinforcement learning approach. Appl. Energy 333, 120540 (2023).
Sen, S., Sahoo, L. & Ghosh, S. L. Lifetime extension of wireless sensor networks by perceptive selection of cluster head using K-means and Einstein weighted averaging aggregation operator under uncertainty. J. Ind. Intell. 2(1), 54–62 (2024).
Hussain, I. & Alam, L. Adaptive road crack detection and segmentation using Einstein operators and ANFIS for real-time applications. J. Intell Syst. Control 3(4), 213–226 (2024).
Duško, T. & Bozanic, D. Optimizing military decision-making: Application of the FUCOM–EWAA–COPRAS-G MCDM model. Acadlore Trans. Appl Math. Stat 1(3), 148–160 (2023).
Puška, A., Hodžić, I., Štilić, A. & Murtič, S. Evaluating European Union countries on climate change management: A fuzzy MABAC approach to the climate change performance index. J. Green Econ. Low-Carbon Dev. 3(1), 15–25 (2024).
Tešić, D., Božanić, D. & Khalilzadeh, M. Enhancement of the defining interrelationships between ranked criteria II method using interval grey numbers for application in the grey-rough MCDM Model. Int. J. Knowl. Innov. Stud. 2(2), 81–91 (2024).
Mahalakshmi, P., Vimala, J., Jeevitha, K. & Nithya Sri, S. Advancing cybersecurity strategies for multinational corporations: Novel distance measures in q-rung orthopair multi-fuzzy systems. J. Oper. Strateg. Anal. 2(1), 49–55 (2024).
Riaz, M. & Farid, H. M. A. Enhancing green supply chain efficiency through linear Diophantine fuzzy soft-max aggregation operators. J. Ind. Intell. 1(1), 8–29 (2023).
Acknowledgements
The study was funded by Researchers Supporting Project number (RSPD2025R749), King Saud University, Riyadh, Saudi Arabia.
Author information
Authors and Affiliations
Contributions
Hafiz Muhammad Waqas and Ubaid Ur Rehman wrote the main manuscript, while Walid Emam and Tahir Mahmood proofread the manuscript, validate the results and made the corrections wherever needed. Further Dragan Pamucar prepared the revision of the manuscript as per the journal and reviewers requirements.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Ethics approval
The authors state that this is their original work and it is neither submitted nor under consideration in any other journal simultaneously.
Human and animal participants
This article does not contain any studies with human participants or animals performed by any of the authors.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Emam, W., Waqas, H.M., Mahmood, T. et al. AI-driven energy management system based on hesitant bipolar complex fuzzy Hamacher power aggregation operators and their applications in MADM. Sci Rep 15, 13083 (2025). https://doi.org/10.1038/s41598-025-94340-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-94340-3