Introduction

As the water demand in Northwest China increases annually, the water supply capacity of existing channels and pipelines can no longer meet the water consumption requirements of industry and residents. To protect local economic development and address the water supply demand of people, the reasonable and accurate design of a new water supply project has become an effective method1,2. Along with the construction and operation of water supply pipeline projects, a series of difficult problems arise in the filling of soil and the placement of pipelines, such as the selection of materials for filling the soil, the thickness of the single-layer filling, the selection of the internal water pressure, and the spacing of the double-line pipelines, which have an impact on the safety of the project and the mechanical properties of the pipelines3,4,5. Therefore, investigating the effects of the single-layer filling thickness and internal water pressure under pulverized sandstone on the mechanical properties of double-line pipelines to ensure the normal operation of water supply pipelines is highly important.

The safety of pipeline structures is highly important for buried pipeline engineering. At present, scholars at home and abroad have made many achievements in buried pipeline engineering. Robert et al.6 used model tests and numerical simulation methods to establish a three-dimensional finite element model and used field-measured data to compare and verify the model to investigate the effect of the wall thickness of a buried pipeline on the maximum stress of the pipeline under the action of vehicular and hydraulic loading. Katebi et al.7 used numerical simulation methods to investigate the effects of lateral soil confining forces on buried pipelines at different depths of burial and concluded that the forces on buried pipelines increase with increasing burial depth. McCarron8, to analyze the effect of resistance to pipeline‒soil lateral interactions, used the finite element method to simulate the lateral breakout resistance of a buried pipeline on undrained clayey soils. Neya et al.9 used a numerical simulation to analyze the effects of different vehicle loads and soil parameters on the dynamic stresses of buried steel pipes, and the results revealed that the maximum principal stresses of buried pipes decreased with increasing vehicle speed and elastic modulus of the surrounding soil. Lv et al.10, based on buried pipeline engineering, used model tests and numerical simulations to investigate the effect of cyclic axial loading on the axial force of buried pipelines connected by corrugated pipe joints. The results show that bellows connections can significantly reduce the axial force of the pipe joint system and improve its deformation capacity. Therefore, the current research on buried pipelines focuses more on the influence of different parameters on the structural safety of pipelines, whereas the influence of the construction process of filling on the mechanical properties of buried pipelines has not been explored.

At present, scholars worldwide are more inclined to study the mechanical properties of tunnel and pipeline engineering under the action of internal water pressure. Meng et al.11, based on the Dianzhong diversion tunnel project, used numerical simulation to establish a composite lining model to investigate the mechanical properties of a double-layer lining under the action of internal water pressure and reported that the internal water pressure has a greater effect on the bending moment of the lining joints. Zhu12 used a numerical simulation method to analyze the change rule of tunnel pipe lining under internal water pressure and concluded that the pipe lining deforms outward under internal water pressure, and the stress tends to be tensile. Mo et al.13 analyzed the stress state of a single-layer lining under the action of internal pressure based on the in situ observation tests and numerical simulation methods and obtained the limit values of the internal and external pressures of the single-layer lining under different surrounding rocks. In summary, to ensure the safety of single-lane tunnel pipelines, the internal water pressure borne by the pipeline lining in the single-lane tunnel project will be transferred to the surrounding rock strata, and the force situation of the double-lane water supply buried pipelines is more complicated than that of single-lane pipelines. Additionally, the double-lane pipelines must bear the internal pressure of themselves as well as the stress transferred by the other pipeline at the same time.

Therefore, to investigate the mechanical properties of double-lane water supply buried pipelines during the construction and operation periods, this study takes the Sun Mountain Water Supply Project in the Ningxia Hui Autonomous Region as the research object. We then establish a three-dimensional finite element model integrating a “double-lane pipeline-artificial fill-foundation,” and investigates the mechanical properties of double-lane buried pipelines with different single-layer fill thicknesses and internal water pressures. The results can provide theoretical references for the evaluation of the operational safety of similar water supply buried pipeline projects. The results of this study can provide a theoretical reference for the operation safety evaluation of similar water supply buried pipeline projects.

Basic theory

Tube‒soil interaction theory

The study of the interaction between pipe and soil can be traced back to the 1990s, when Marston14 established a calculation model of the overburden pressure on a rigid pipe and proposed the relationship between the load on the pipe and the total weight of the filled soil along the trench wall. Spangler15 found that although the stiffness of flexible pipe is lower than that of rigid pipe, it can play a better role in tube-to-soil coupling. Burns and Richard16, Höeg17, Einstein and Schwartz18 studied the elastoplastic solution of buried pipelines, and Moore established an elastoplastic model of pipeline soil loading based on previous studies.

As the working conditions of the project become more and more complex, the above model can not meet the requirements of the pipeline design of the existing project. Li Xin et al.19 used the two-dimensional finite element method to analyze the response of continuously buried pipeline under dynamic load, and studied the influence of input wave frequency, input wave amplitude, buried depth of pipeline, soil type, tube-soil friction coefficient and other factors on the dynamic response of buried pipeline. Wu Xiaogang et al.20, based on the Eular Bernoulli elastic foundation beam stress model of the pipeline under traffic load, proposed an analytical solution for calculating the coupling response when system parameters change with time. Vorster et al.21 further verified the solution through centrifuge experiments on the basis of assuming a continuous medium, and Klar et al.22 provided a more accurate solution on the basis of the above work.

Numerical modeling of the water supply pipe

Project overview

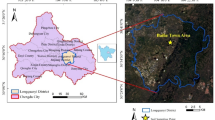
The Sun Mountain Water Supply Project is in Wuzhong city, Ningxia Province, China, and is a water conservancy project that focuses mainly on industrial and residential water supplies with irrigation functions. The Sun Mountain Water Supply Project uses a C15 concrete pipeline with a diameter of 800 mm for water transmission, with a spacing of 800 mm between the two lines of the pipeline, an excavation elevation of 1391.90 m, a center elevation of the pipeline of 1387.00 m, a bottom elevation of 1386.20 m, and an excavation slope ratio of 1:1. The solidification grouting layer is made of C20 concrete material, with a length of 2.9 m and a height of 1.6 m.

Simulation modeling

This study focuses on a section of the typical pressurized water supply pipeline, characterized by a substantial siltstone layer, within the Sun Mountain Project (pile numbers: A + 2330 to A + 2340). A three-dimensional finite element model representing the ‘double-line pipeline—artificial filling—foundation’ system has been developed, as illustrated in Fig. 1. The simulation model of the water supply pipeline adopts three-dimensional solid units for the pipeline, a consolidation grouting layer, and a foundation. The finite element model extends one excavation length to the left and one excavation depth to the right23. The dimensions of the model are 42 m long, 10 m wide, and 11.2 m high. The double-line pipe inner and outer diameters are 0.68 m, 0.8 m, the double-line pipeline spacing is 0.8 m, the consolidation grouting layer lengths are 2.9 m and 1.6 m, and the model overall width is 10 m. To reduce the stress generated by the force transfer in the calculation, the model is used as a three-dimensional solid unit. The overall width of the model is selected as 10 m. To reduce the stress concentration phenomenon generated by the force transfer in the calculation, the model grid is mainly divided into regular hexahedral cells, and the whole model is divided into 51,105 cells with 56,544 nodes. The boundary conditions of the model are as follows: the left and right boundaries are x-displacement constraints, the front and rear boundaries are y-displacement constraints, and the bottom boundary is completely fixed.

Fig. 1
figure 1

Three-dimensional finite element model of a typical water supply pipeline.

Full size image

Material parameters

In the model, the Mohr‒Coulomb yield criterion constitutive model is used for the foundation and artificial fill layer, and the linear elastic constitutive model is used for the pipeline and consolidation grouting layer. C15 concrete is used for the pipe material. C20 concrete is used for the consolidation grouting layer. The main parameters are shown in Table 1. The interaction between the pipe and the consolidation grouting layer, the consolidation grouting layer and the artificial fill layer and the foundation, and the artificial fill layer and the foundation is simulated by the surface-to-surface contact in the model. The normal direction is defined as a hard contact, which permits the separation of contacting surfaces, the tangential direction obeys Coulomb’s law of friction and permits the slip of the tangential stress after reaching a critical value, and the friction is defined as a hard contact; it reaches a critical value that allows slip to occur, and the friction coefficient is taken as 0.524.

Table 1 Main material physical and mechanical parameters.
Full size table

Simulation and loading process

In the numerical calculation and analysis, to ensure the correctness of the initial geostress state at the grassroots level, the foundation is first subjected to geostress balance simulation of the initial geostress field. The application of artificial fill during the simulated construction process is simulated, and the inner surface of the double-line pipeline is subjected to an unevenly distributed internal water pressure along the direction of the height, with an increment of 0.2 MPa/step, and the maximum internal pressure is set to 1.0 MPa. The specific working conditions are shown in Table 2.

Table 2 Working condition table.
Full size table

Validation of the water supply pipe model

Modal characterization

To verify the validity of the three-dimensional finite element model of the “double-line pipeline-artificial fill-foundation”, this paper analyzes the prototype monitoring data of the pipeline vibration signals, adopts a signal processing method based on the improved variational modal decomposition of dispersive entropy, extracts the modal parameters of the double-line water supply pipeline, and then analyzes the self-oscillation frequency of the pipeline compared with the results of the finite element coupling model. The identified self-oscillation frequency of the pipeline is compared and analyzed with the results of the finite element coupling model to verify the validity of the three-dimensional finite element model of the “double-line pipeline-artificial fill-foundation” as a whole25,26. The first 4-order formation diagram of the water supply pipe is shown in Fig. 2, the measured time course diagram of the pipe and the power spectrum of the dynamically fused signal are summarized in Fig. 3, and the comparison results are shown in Table 3.

Fig. 2
figure 2

Modal self-oscillation frequency of water supply pipe.

Full size image
Fig. 3
figure 3

Signal time chart and power spectra.

Full size image
Table 3 Identification results of the dam modal parameters.
Full size table

As shown in Table 3, the finite element model calculation results are closer to the first four orders of the original view data calculated via the feature system implementation algorithm, and the maximum error of the data is 1.55%. Therefore, the constructed finite element model can effectively simulate the real operating conditions of the double-line water supply pipeline structure.

Grid convergence verification

Theoretically, the results of the finite element solution are related to the mesh division, in which the finer the mesh division is, the higher the solution accuracy. For the actual project used to calculate the working conditions, the time of finite element calculation is highly dependent on the performance of the computer because the sharp increase in the number of model meshes leads to a substantial increase in the time cost of the calculation, and when the number of meshes reaches a certain number, the improvement in the calculation accuracy is not obvious27. A length of 10 m “double line pipe—artificial fill—foundation” was used for the integration of a three-dimensional finite element model for grid convergence verification, and mesh sizes of 1 m, 0.66 m, 0.5 m, 0.4 m, and 0.2 m for the mechanical properties of the double line water supply pipeline were used to compare the accuracy of the results. The calculation conditions of a single-layer filling thickness of 0.3 m and an internal water pressure of 0 MPa are selected, and the finite element results for extracting the maximum displacement, tensile stress and compressive stress of the double-line water supply pipeline at the completion of soil filling are shown in Table 4.

Table 4 Mechanical characteristics of the double-line pipeline under different grid sizes.
Full size table

As shown in Table 4, when the grid size of the finite element model is gradually reduced, the maximum displacement and tensile stress of the bilinear water supply pipe are basically unchanged, and the maximum compressive stress gradually decreases with decreasing grid size. When the grid size is reduced by 5×, the maximum compressive stress is reduced by 0.0046%. Therefore, the accuracy of the finite element solution results can ignore the error caused by the grid size.

Mechanical characterization of water supply pipes with different fill laying thicknesses

Analysis of the influence of stratified thickness on surface settlement

To analyze the effect of the soil filling process on the settlement change process, a single-layer filling thickness of 0.3 m is selected for the calculation of the working condition, and settlement cloud diagrams are extracted for filling thicknesses of 0.6 m, 1.5 m, 2.4 m and 4 m, as shown in Fig. 4. As shown in the figure, the maximum vertical settlement displacement increases with increasing soil filling thickness, and the maximum values are 3.783 mm, 6.133 mm, 8.626 mm and 13.32 mm, respectively. The maximum settlement area occurs in the soil at the bottom of the double-line pipeline, the consolidation grouting layer and the consolidation grouting layer, which is due mainly to the increase in the thickness of the soil filling. The soil pressure continues to increase owing to the increase in the thickness of the soil fill and acts directly on the consolidation grouting layer, whereas the pipe and the consolidation grouting layer have different stiffnesses from the soil body, which leads to a sudden change in the displacement at this location. Therefore, the pipeline and consolidation grouting layer should be monitored during the construction process.

Fig. 4
figure 4

Vertical settlement cloud map for single layer filling with a thickness of 0.3 m.

Full size image

To further explore the influence of the single-layer filling thickness on the surface settlement change rule, the water supply pipeline construction excavation at the end of the surface cross-section vertical settlement curve is drawn, as shown in Fig. 5. As shown in the figure, under different working conditions, the surface settlement displacement with the lateral measurement point from the axis distance first increases, then becomes smooth, and finally decreases. The maximum displacement of the region appears in the double-line pipeline and consolidation grouting layer, which is also due to the double-line pipeline and the consolidation grouting layer under the greatest soil pressure. When the single-layer filling thickness gradually increased, the surface monitoring cross-section closer to the axis increased, and the amount of surface settlement increased. When the thickness of single-layer filling gradually increases, the closer the surface monitoring section is to the axis and the greater the amount of surface settlement is, the greater the maximum displacements of surface settlement are 12.23 mm, 12.28 mm, 12.31 mm, and 12.35 mm, respectively. When the thickness of single-layer filling is 1.2 m, compared with when the thickness of single-layer filling is 0.3 m, the amount of surface settlement is increased by 0.98%.

Fig. 5
figure 5

Surface settlement displacement and lateral measurement point variation curve at the end of filling.

Full size image

Effect of delamination thickness on pipe displacement

To analyze the effect of the soil-filling process on the vertical displacement change rule of the double-line pipe, limited to the length of a single layer with a filling thickness of 0.3 m for the calculation of the working condition, the filling thicknesses of 0.6 m, 1.5 m, 2.4 m and 4 m for the vertical displacement of the cloud are extracted, as shown in Fig. 6. As shown in the figure, under different soil filling thicknesses, the trend of the change in vertical displacement of the double-line pipeline is basically the same, and the double-line pipeline moves downward as a whole. The main reason for this phenomenon is that, owing to the small stiffness of the foundation, the self-gravitational stress generated by the pipeline, the consolidation grouting layer and the soil body are not enough to support when the soil body is filled, resulting in overall downward movement. With increasing soil filling thickness, the maximum vertical displacement of the double-line pipeline increased, with maximum values of 3.725 mm, 5.853 mm, 8.088 mm, and 12.24 mm, respectively, and the maximum settlement areas appeared at 45° for the left-line pipeline and 135° for the right-line pipeline. Therefore, it is more important to pay attention to 45° of the left pipeline and 135° of the right pipeline during construction monitoring.

Fig. 6
figure 6

Vertical displacement cloud map of double line pipeline with a single layer filling thickness of 0.3 m.

Full size image

The variation curves of the vertical displacement of the double-line pipe with the number of fillings under different single-layer filling thicknesses are shown in Fig. 7. The figure shows that the vertical displacement of the double line pipe increases with increasing number of soil fillings. When the thickness of the single layer filling is small, the vertical displacement of the double line pipe tends to change more slowly. As the thickness of the single layer filling gradually increases, the vertical displacement of the double line pipe increases more obviously. The vertical displacement of the double-line pipeline under different working conditions is shown in Fig. 8. The figure shows that the maximum vertical displacement of the double-line pipeline is 12.24 mm, 12.21 mm, 12.16 mm and 12.11 mm, respectively, and the vertical displacement of the double-line pipeline is reduced by 1.07% compared with the single-layer filling thickness of 1.2 m compared with the single-layer filling thickness of 0.3 m, indicating that the vertical displacement of the pipeline remains unchanged with increasing single-layer filling thickness, but the vertical displacement of the pipeline increases when the single-layer filling thickness increases. Therefore, to consider the normal and stable operation of the double-line pipeline, the thickness of the single-layer filling should be reduced in actual engineering construction.

Fig. 7
figure 7

Curve of vertical displacement variation of double line pipeline with the number of soil filling times.

Full size image
Fig. 8
figure 8

Variation curves of soil filling times and vertical displacements of double-line pipes.

Full size image

Effect of delamination thickness on pipe stresses

To analyze the effect of the soil filling process on the double-line pipe stress change rule, limited to the length of a single layer with a filling thickness of 0.3 m under the calculation conditions, the filling thicknesses of 1.5 m and 4 m of the tensile and compressive stress maps, respectively, are extracted, as shown in Fig. 9. As shown in the figure, under different soil-filling thicknesses, the stress maps of the double-line pipe basically have the same trend, and the tensile regions of the left and right line pipes are on the inner side of the arch bottom, whereas the compressive region appears on the inner side of the left gang of the left line pipe and on the inner side of the right gang of the right line pipe. The maximum tensile and compressive stresses of the double-line pipe increase with increasing filling thickness of the soil body, the maximum tensile stresses are 0.053 MPa and 0.130 MPa, the maximum compressive stresses are 0.053 MPa and 0.130 MPa, and the maximum compressive stresses are 0.130 MPa. The maximum tensile stresses are 0.053 MPa and 0.130 MPa, and the maximum compressive stresses are 0.263 MPa and 0.565 MPa, which are lower than the standard values of C15 concrete tensile and compressive strengths of 1.27 MPa, 10.0 MPa, and 10.0 MPa, respectively.

Fig. 9
figure 9

Stress cloud map of double line pipeline with a single layer filling thickness of 0.3 m.

Full size image

The variation curve of the relationship between the amount of soil filling and the stress of the bilinear pipe is shown in Fig. 10. As shown in Fig. 10a, the tensile stress of the double-line pipe increases with an increasing number of soil fillings. When the thickness of single-layer filling is 0.3 m, the tensile stress of the pipe tends to increase with the increasing number of fillings, and the maximum values of the tensile stress of the pipe under different single-layer filling thicknesses are 0.13 MPa, 0.138 MPa, 0.144 MPa and 0.148 MPa. When the number of soil layers is the same, the tensile stress of the pipe sheet increases more obviously with increasing single-layer filling thickness. As shown in Fig. 10b, the compressive stress of the double-line pipe increases with an increasing number of soil fillings. When the thickness of the single-layer filling is 0.3 m, the trend of the increase in the compressive stress of the pipe with the increasing number of fillings is slower, and the maximum values of the tensile stress of the pipe under different thicknesses of single-layer filling are 0.565 MPa, 0.567 MPa, 0.568 MPa and 0.567 MPa. When the number of soil layers is the same, the compressive stress of the pipe sheet increases more obviously with increasing single-layer filling thickness. When the filling thickness is certain, the tensile and compressive stresses of the pipe are essentially the same, but the growth rates are different. Therefore, to consider the normal and stable operation of the double-line pipeline, a suitable thickness of single-layer filling should be selected in actual engineering construction.

Fig. 10
figure 10

Relationship between soil filling times and stress of double line pipeline.

Full size image

Mechanical characterization of pipes with different internal water pressures

To investigate the mechanical properties of the double-line pipeline structure under the action of internal water pressure and the influence of different internal water pressures on the mechanical properties of the double-line pipeline structure, a single-layer filling thickness of 0.3 m is selected for the calculation of the case, and the stresses and displacements at the inner and outer locations of the double-line pipeline are extracted. To eliminate the influence of the boundary effect on the results, this paper extracts only the middle position of the pipeline model. The order of data extraction points of the double-line pipeline is in the clockwise direction, which is in the order of the right gang (0°), the top of the arch (90°), the left gang (180°), the bottom of the arch (270°), and the right gang (360°). The specific diagram is shown in Fig. 11.

Fig. 11
figure 11

Schematic diagram of the extraction locations for dual-line pipelines.

Full size image

Effect of internal water pressure on pipe displacement

When the internal water pressure is 0.6 MPa, the vertical displacement of the inner and outer surfaces of the middle part of the double-line pipeline is as shown in Fig. 12. The figure shows that the vertical displacement of the inner and outer surfaces of the whole double-line pipeline is negative and that the pipeline experiences settlement deformation. The overall deformation size of the double-line pipeline is basically the same, but in the interval of 270°–90°, the left-line pipeline is slightly larger than the right-line pipeline is, and in the interval of 90°–270°, the right-line pipeline is slightly larger than the left-line pipeline is. The maximum deformation area appears in the right gang of the left line and the left gang of the right line. This indicates that the maximum deformation area occurs at the right gang of the left line and the left gang of the right line, suggesting that the distance between the two lines of pipelines can affect the deformation of pipelines to a certain extent.

Fig. 12
figure 12

Vertical displacement inside and outside the double-line pipeline.

Full size image

The results of the vertical displacement of the middle part of the double-line pipe under different internal water pressures are shown in Fig. 13. As shown in the figure, with increasing internal water pressure, the overall displacement of the double-line pipeline first decreases but then increases. When the internal water pressure is 0.2 MPa, the overall settlement of the pipeline is the smallest, whereas when the internal water pressure settlement deformation is 0.02 mm greater than the internal water pressure of 1 MPa, the settlement deformation is 0.03 mm greater. The internal water pressure resisted a part of the filling soil pressure on the structure of the double-line pipeline, but with increasing internal pressure, the pipeline arch needed to bear most of the load. However, with increasing internal water pressure, the pipe arch bottom needs to bear most of the load, resulting in an increase in settlement deformation.

Fig. 13
figure 13

Maximum displacement internal water pressure relationship curve of the dual-line pipeline.

Full size image

Effect of the internal water pressure on the pipe stress

The tensile stress distributions of the pipeline on the inner and outer surfaces of the middle part of the double-line pipeline when the internal water pressure is 0.6 MPa are shown in Fig. 14. The figure shows that the maximum tensile stress of the double-line pipeline appears in the inner part of the left and right line pipelines, and the maximum values of tensile stress are 1.498 MPa and 1.511 MPa, respectively, of which the left line pipeline appears mainly in the intervals of 90°–150° and 210°–270°, whereas the right line pipeline appears mainly in the intervals of 30°–70° and 285°–330°. The tensile stresses in the inner and outer annular directions of the left and right line pipelines basically exhibit the same trend, and the outer tensile stress is lower than the inner tensile stress. The trend of change is basically the same: the outer tensile stress is smaller than the inner tensile stress, which is reduced by 25% and 20.1%, respectively, indicating that the inner side of the pipeline is the most likely to experience plastic damage when the double-line pipeline is subjected to a certain external load. However, owing to the small spacing of the double-line pipeline, the tensile stress does not appear to suddenly change in the bottom of the arch or the top of the arch. Therefore, the maximum tensile stress of the double-line pipeline should be monitored in the later operation of the structure.

Fig. 14
figure 14

Distribution of the maximum tensile stress in the inner and outer circumferential directions of dual-line pipelines.

Full size image

The maximum tensile stress in the middle part of the double-line pipe under different internal water pressures is shown in Fig. 15. The figure shows that the maximum tensile stress on the double-line pipe increases gradually with increasing internal water pressure, and the maximum tensile stresses on the single-layer filling thickness of the 0.3 m pipe under different internal water pressures are 0.130 MPa, 0.453 MPa, 0.791 MPa, 1.141 MPa, 1.511 MPa, and 1.882 MPa. This is 13.4× greater than that under the action of no internal water pressure. The maximum tensile stress of the single-layer pipe was 0.148 MPa, 0.481 MPa, 0.819 MPa, 1.173 MPa, 1.543 MPa, and 1.913 MPa, respectively. This was 11.9× greater than that under the action of no internal water pressure. The maximum tensile stress on the pipe sheet when the internal water pressure is 0.8 MPa is 1.511 MPa, which exceeds 18.9% of the standard value of the C15 concrete tensile strength of 1.27 MPa. Therefore, in actual projects, we should choose the appropriate internal water pressure and focus on monitoring the tensile stress of the double-line pipeline in an environment with high internal water pressure.

Fig. 15
figure 15

Maximum tensile stress internal water pressure relationship curve for dual-line pipelines.

Full size image

The distribution of pipeline compressive stresses on the inner and outer surfaces of the middle part of the double-line pipeline when the internal water pressure is 0.6 MPa is shown in Fig. 16. The trends of the inner and outer circumferential compressive stresses in the left and right pipelines are basically the same, and the outer compressive stress is smaller than the inner compressive stress, which is reduced by 16% and 18.2%, respectively. The maximum values of the compressive stresses are 0.763 MPa and 0.769 MPa, which are mainly in the left gang of the left line pipeline and the right gang of the right line pipeline. Therefore, in actual projects, the compressive stress on the inner side of the pipeline should be monitored when the double-line pipeline is in operation.

Fig. 16
figure 16

Distribution of the maximum compressive stress in the inner and outer circumferential directions of dual-line pipelines.

Full size image

The maximum compressive stress in the middle part of the double-line pipeline under different internal water pressures is shown in Fig. 17. As shown in the figure, with increasing internal water pressure, the compressive stress on the double-line pipe tends to decrease but then increases, with a single layer with a filling thickness of 0.3 m. For example, the maximum compressive stresses on the pipe are 0.565 MPa, 0.306 MPa, 0.392 MPa, 0.58 MPa, 0.769 MPa, and 0.957 MPa, which are lower than the standard compressive strength of C15 concrete, which is 10 MPa. The main reason for this phenomenon is that when the internal water pressure is 0 MPa, the left and right arches of the pipe are in a pressurized state, and with increasing internal water pressure, part of the soil load is offset by the internal water pressure, resulting in a reduction in the pipe compressive stress. With increasing single-layer filling, the pipe compressive stress is basically unchanged, and the maximum compressive stresses of the pipe when the internal water pressure is 1 MPa are 0.957 MPa, 0.958 MPa, 0.959 MPa, and 0.960 MPa. The compressive stress of the double-line pipe is the smallest when the internal water pressure is 0.2 MPa, and the compressive stress decreases by 45.8% compared with the compressive stress without the action of internal water pressure and decreases by 45.8% compared with the compressive stress under the action of an internal water pressure of 1 MPa. The pressure of 1 MPa under the action of compressive stress increased by 68%. Therefore, to ensure the safe and stable operation of double-line pipelines in actual projects, the appropriate internal water pressure should be selected.

Fig. 17
figure 17

Maximum compressive stress internal water pressure relationship curve for dual-line pipelines.

Full size image

Conclusion

Taking the typical pipeline section of the Sun Mountain Water Supply Project (Pile No. A + 2330–A + 2340) as the research object, a three-dimensional finite element model integrating a “double-line pipeline-artificial fill-foundation” is established to investigate the mechanical properties of a double-line pipeline with different thicknesses of single-layer fill and internal water pressure. The following conclusions are drawn.

  1. (1)

    A three-dimensional finite element model integrating the double-line pipeline, artificial fill and foundation is established, the inherent modes are calculated and analyzed, and the first four modal frequencies of the pipeline are 2.61 Hz, 3.28 Hz, 3.80 Hz, and 4.06 Hz. A comparison of the simulation results with the frequencies identified by the DVMD reveals that the maximum relative error is 1.55%, which confirms the validity of the finite element model and the calculation results accuracy.

  2. (2)

    An increase in the amount of soil filling and an increase in the thickness of single-layer filling increase the vertical displacement of the double-line pipeline, and an increase in the thickness of single-layer filling increases the rate of increase in the vertical displacement of the double-line pipeline. The vertical displacement of the double line pipe is reduced by 1.07% when the single layer thickness is 1.2 m compared to the single layer thickness of 0.3 m.With an increasing number of soil fillings, the tensile and compressive stresses of the double-line pipeline gradually increased, and the maximum values were 0.148 MPa and 0.568 MPa, respectively. When the number of soil layers was the same, the tensile and compressive stresses of the pipe sheet increased with increasing single-layer filling thickness.

  3. (3)

    When the internal water pressure is 0.6 MPa, the trends of the inner and outer circumferential deformation and tensile and compressive stresses of the pipe in the left and right lines are basically the same. The outer stresses are lower than the inner stresses, of which the tensile stresses are reduced by 25% and 20.1%, respectively, and the compressive stresses are reduced by 16% and 18.2%, respectively. Under the joint action of soil pressure and internal water pressure, the internal water pressure increases, the deformation and compressive stress of the double-line pipeline decreases and then increases, and the tensile stress gradually increases, as does the thickness of the single-layer filling. For example, the settlement deformation is reduced by 0.02 mm, the tensile stress is increased by 13.4×, and the compressive stress is reduced by 45.8% compared with that without the action of the internal water pressure.

  4. (4)

    The influence of the internal water pressure on the safety and stability of the double-line water supply pipeline is greater than that of the single-layer filling thickness. At the same time, the internal water pressure increases the stress value of the inner side of the pipeline, which easily leads to the occurrence of phenomena such as pipe bursts in the water supply project. The stress value of the inner side of the pipeline should be monitored to achieve a better pipeline safety operation effect.