Generalizing the similitude approach for laboratory astrophysics through equivalence symmetries for the example of radiative waves

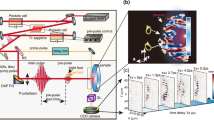
Abstract

For decades, scaling laws have served as the cornerstone of laboratory astrophysics, enabling quantitative comparisons between astrophysical phenomena and laboratory experiments. However, the lack of observational data and some experimental limitations has limited our ability to validate certain theoretical and numerical models when studying some of the most extreme phenomena in the universe. In this work, we present a theoretical framework for a new class of laboratory astrophysics experiments that leverage existing high-power laser facilities to investigate supersonic radiation-dominated waves. By extending Lie symmetry theory, we demonstrate that the stringent constraints imposed by traditional scaling laws can be relaxed. This approach enables the study of astrophysical phenomena in the laboratory, even when the ratio of radiation energy density to thermal energy and the micro-physics of the systems differ. These equivalence symmetry concepts are illustrated through simulations under conditions relevant to Type-I X-ray bursts and through the design of a first equivalent laboratory experiment. These findings pave the way for a broader range of astrophysical systems to be explored using laboratory experiments, marking the birth of a new innovative approach in laboratory astrophysics.

Introduction

Similarity transformations have been used for over a century, becoming progressively the pillar of current laboratory astrophysics¹ by creating a theoretical link between the astrophysical and laboratory scales^2,3. More precisely, the theoretical model of both systems is the same after application of the scaling transformations, whereas the scales they describe can differ. This is classically referred as absolute invariance¹ in which only the macroscopic properties of the plasmas are modified. Recently, a first step towards more generality was made by introducing global invariance⁴ that is now allowing the microscopic properties of the systems, such as the equation of state, to be scaled.

This development expanded the potential for studying a broader range of astrophysical systems on a laboratory scale and enhanced the precision in categorizing the associated experiments⁵. Among this classification first stands the “identity experiments”, in which the exact astrophysical conditions can be reproduced in the laboratory. In this case, the GEKKO XII laser⁶ allowed to study a photoionisation mechanism thought to happen around compact objects like Cygnus X-3 or Vela X-1^7,8. However, it is generally the case that the temporal and spatial scales of astrophysical phenomena cannot be directly replicated in laboratory settings. Then, the “similitude” approach is required^9,10. The constraints now differ and take the form of a dimensionless numbers conservation^11,12, each characterizing an aspect of the physical regime of the systems. Moreover, fundamental properties of plasmas, such as their equation of state, must also be conserved by the scaling transformations. This is often inconceivable during laboratory experiments and can lead to the emergence of scaling effects¹³. The next step towards a more generalized invariance is the “resemblance” concept, among which lies partial similarity¹⁴. This category also includes parametric invariance¹⁵ which have been successfully applied in the context of POLAR experiments¹⁶. These examples merely demonstrate that physics can be studied qualitatively across two different scales, though without explicitly linking the variables between the scales as achieved through scaling laws. The last category of experiments are “analogies” that we will discuss in the last section.

The main difference between those concepts is that identity and similarity transformations can be systemically obtained through analysis of the theoretical model under consideration. In particular, scaling laws have been shown to be explicitly part of the set of Lie symmetries^17,18,19 of a system. However, resemblance transformations and analogies cannot be derived as simply. The present work finds its roots within the idea that a natural extension of similitude concepts could lead to a generalization of scaling laws as resemblance transformations. Thus, we aim to provide a systematic method for deriving resemblance transformations based on Lie theory. As going from absolute to global invariance led to account for a change in the microphysics of the system, the equivalence concept¹⁹ seems to be the natural generalization of Lie symmetries. Recently, we unveiled the equivalence symmetries of supersonic radiatively driven heat waves²⁰ (in short, radiative waves) in the context of the interaction between a Type-I X-ray burst and the accretion disk around a neutron star^21,22. In particular, we showed that dimensionless numbers, the Boltzmann (Bo) and Mihalas (R) numbers, conserved by the similitude approach, were able to be modified, as well as the equation of state and opacity law between astrophysics and the laboratory scale. However, neither the method to obtain this set of transformations nor the amount of possibilities they bring was detailed in that study²⁰.

Here, we detail the method of deriving a set of equivalence symmetries for a given theoretical model, applied to radiative waves. This work aims to offer a consistent and systematic framework for physicists seeking potential resemblance transformations between systems. It addresses the need for an algorithm capable of deriving generalized transformations that account for both microphysical details and deviations in dimensionless numbers. We will then shed light on the benefits of this approach such as validating numerical models in experimentally unreachable regimes. Finally, we propose a first experimental design capable of producing a radiative wave on a laboratory scale that enables the investigation of equivalent phenomena relevant to the most extreme radiative environments in the universe.

Methods: lie symmetries

A symmetry is a transformation that leaves an equation invariant. This transformation consists of a change of variable which leaves the form of the equations studied unchanged. Lie symmetries¹⁷ depend continuously on a parameter and can even allow, for example, to develop particular solutions of differential equations²³. However, unveiling Lie symmetries of a physical model also allows to obtain a set of changes of variables that encompass similitude transformations, or, in other words, scaling laws.

The process of determining Lie symmetries of differential equations can be tedious in different situations, but relies on one analytical development that has now been widely addressed by many authors^17,18,19,23. In this work, we will mainly follow the notations introduced by Coggeshall & Axford²³ and remind of the principal stages of the method that introduce the main principles we need. First, let us consider a differential equation of arbitrary order n over a function f that we write as:

$$\begin{aligned} F\left( \textbf{x},f(\textbf{x}),\frac{\partial f(\textbf{x})}{\partial x_1}, ... , \frac{\partial ^n f(\textbf{x})}{\partial x_N^n}\right) = 0 \end{aligned}$$

(1)

where $\textbf{x} = x_{i_{1 \le i \le N}}$ is a vector of N independent variables and $f(\textbf{x})$ is a dependent variable. For most of the differential equations in physics, the independent variables are the space and time variables, whereas the dependent variables can be the density or temperature for example. The objective of the method is to obtain transformations acting on these variables that can conserve the structure of the differential Eq. (1). When the transformation laws do not explicitly use the derivatives of the dependent variables, we call those point symmetries. These will be the focus of this work, as they allow to keep the physical consistency of the variables from one equation to another. We note that certain types of transformations, such as contact transformations¹⁸ and Lie-Bäcklund symmetries²⁴, also involve modifying the derivatives of the dependent variables. However, these transformations are often of limited relevance in physical applications. The point transformations of interest here can therefore be expressed in the following form:

$$\begin{aligned} \hat{x}_i = \Phi _i(\textbf{x},f,a), \quad \hat{f} = \Psi (\textbf{x},f,a), \quad \forall i \in [1,N], \end{aligned}$$

(2)

with a the parameter associated with the transformations, and under the assumption that there exists a group invariant $a=a_0$ for which these transformations act only as an identity. The notion of group is of primary importance as the complete set of Lie symmetries, together with the commutative operation, constitutes what is called a Lie group¹⁹. This means that any combination of these symmetries stays within this group, and, by definition, is also a symmetry for the differential equation studied. Now, the power of Lie’s approach resides in the assumption that we can search for transformations in the vicinity of $a_0$, so for a parameter $a = a_0 + \delta a$ with $\delta a$ arbitrary small. By doing this, it is then possible to obtain²³:

$$\begin{aligned} F(\hat{\textbf{x}},\hat{f}) = F(\textbf{x},f) + \delta a \left[ \sum _{i=1}^N \xi _i \frac{\partial F}{\partial x_i} + \eta \frac{\partial F}{\partial f}\right] + \mathscr {O}\left( \delta a \right) = 0 \end{aligned}$$

(3)

where the functions $\xi _i$ and $\eta$ are called the coordinate functions associated with the independent variable $x_i$ and the dependent variable f respectively. They represent the infinitesimal displacement between the starting and ending variables in their respective spaces and are given by:

$$\begin{aligned} \xi _i(\textbf{x},f) = \left. \frac{d \Phi _i(\textbf{x},f,a)}{da}\right| _{a=a_0}, \eta (\textbf{x},f) = \left. \frac{d \Psi (\textbf{x},f,a)}{da}\right| _{a=a_0}. \end{aligned}$$

(4)

The formulation (3) introduces an operator called the infinitesimal generator, given by:

$$\begin{aligned} G = \left[ \sum _{i=1}^N \xi _i \frac{\partial }{\partial x_i} + \eta \frac{\partial }{\partial f}\right] . \end{aligned}$$

(5)

This leads to the straightforward so-called invariant condition for a differential equation:

$$\begin{aligned} GF(\textbf{x},f) = 0 \quad \text {when} \quad F(\textbf{x},f) = 0 \end{aligned}$$

(6)

which gives a set of conditions to determine the functions $\xi _i$ and $\eta$. However, differential equations also feature the derivatives of the function f with respect to $x_i$. The relevance of the point symmetries is that the transformations on the derivatives of the dependent variable f are completely determined by the transformation law of this function. Indeed, one can show that, for the first and second order derivatives of a dependent variable indicated by the suffix “1”, one can respectively obtain:

$$\begin{aligned} & \frac{\partial \hat{f}}{\partial \hat{x}_i} = \frac{\partial f}{\partial x_i} + \pi _{1i} \delta a , \quad \pi _{1i} = \frac{d \eta }{dx_i} - \sum _{j=1}^N \frac{\partial f}{\partial x_j} \frac{d\xi _j}{d x_i} \end{aligned}$$

(7)

$$\begin{aligned} & \frac{\partial ^2 \hat{f}}{\partial \hat{x}_i \partial \hat{x}_j} = \frac{\partial ^2 f}{\partial x_i \partial x_j} + \kappa _{1ij} \delta a , \quad \kappa _{1ij} = \frac{d \pi _{1i}}{dx_j} - \sum _{k=1}^N \frac{\partial ^2 f}{\partial x_i \partial x_k} \frac{d \xi _k}{d x_i} \end{aligned}$$

(8)

By applying the infinitesimal transformations to the complete differential equation with its derivatives of arbitrary order n as in (1), we obtain:

$$\begin{aligned} G^{(n)}F = 0 \quad \text {when} \quad F = 0, \quad G^{(n)} = G + \sum _{i=1}^N \pi _{1i} \frac{\partial }{\partial f_{x_i}} + \sum _{j=1}^N \kappa _{1ij} \frac{\partial }{\partial f_{x_i x_j}} + ... \end{aligned}$$

(9)

with $G^{(n)}$ being the extended infinitesimal generator at order n. The notation $f_{x_i}$ denotes the derivative of the dependent variable f with respect to the independent variable $x_i$. Similarly, the second derivative of f with respect to the variables $x_i$ and $x_j$ is represented as $f_{x_i x_j}$. The invariance condition (9) then allows us to obtain a system of linear differential equations on the coordinate functions $\varvec{\xi }$ and $\eta$. We note that this analysis can be easily generalized to the case of a system of differential equations involving several dependent variables^23,25.

Lie symmetries of radiative waves

Radiatively driven heat waves, also referred as radiative waves or Marshak waves^26,27, have been studied extensively in the last decades, ranging from astrophysics^20,28 to laboratory experiments^29,30,31. A theoretical model for the supersonic phase of radiative waves propagation (in which the density $\rho _0$ is considered constant) can be developed by considering the diffusion approximation³² for radiative transport:

$$\begin{aligned} \frac{\partial E(T)}{\partial t} = \frac{4 a_R c}{3} \frac{\partial }{\partial x} \left[ \lambda _R(T) T^3 \frac{\partial T}{\partial x} \right] \end{aligned}$$

(10)

where $E(T) = \rho _0 e(T) + a_R T^4$ is the total energy density of the system, with e(T) the specific internal energy of the plasma, $a_R \simeq 7.56 \times 10^{-15}$ erg.$\hbox {cm}^{-3}.\hbox {K}^{-4}$ the radiative constant, $c \simeq 3 \times 10^8~\hbox {cm.s}^{-1}$ the speed of light, and where $\lambda _R(T)$ is the photon mean free path of the material. We note that, in the supersonic approximation, these functions only depend on the temperature T. From this theoretical model can be derived two dimensionless numbers usually conserved by similarity transformations⁴, namely the Boltzmann number $Bo = \rho _0 e(T) c_s / F_{rad}$ and the Mihalas number $R = \rho e(T) / a_R T^4$, with $c_s$ the sound speed of the medium, typically estimated as $\sqrt{\gamma P/rho}$, with the temperature taken at the boundary from which the radiation originates. We can define the optical thickness of the medium as $\tau = L/\lambda _R$ with L the characteristic size of the system. For the diffusion approximation to be applicable, this parameter is expected to satisfy the condition $\tau > 1$.

For this model, the system has two independent variables that are space x and time t, and one dependent variable, the temperature T(x, t). The infinitesimal generator can thus be written as:

$$\begin{aligned} G = \xi (x,t,T) \frac{\partial }{\partial x} + \tau (x,t,T) \frac{\partial }{\partial t} + \eta (x,t,T) \frac{\partial }{\partial T} \end{aligned}$$

(11)

where $\xi$, $\tau$, $\eta$ are the coordinate functions associated with the two dependent variables x, t and the dependent variable T(x, t) respectively. The radiative wave model (10) involves at most second-order derivatives of the dependent variable, allowing the invariance condition to be expressed as:

$$\begin{aligned} & G^{(2)} F = 0, \quad \text {when} \quad F = T_t - \frac{4 a_R c}{3 E_T} \left[ \left( \lambda _{R_T} T^3 + 3 T^2 \lambda _R \right) T_x^2 + \lambda _R T^3 T_{xx}\right] = 0, \nonumber \\ & \quad G^{(2)} = G + \pi _{11} \frac{\partial }{\partial {T_x}} + \pi _{12} \frac{\partial }{\partial T_t} + \kappa _{111} \frac{\partial }{\partial {T_{xx}}} \end{aligned}$$

(12)

where we introduced derivatives as indices ($\partial T/\partial t \equiv$ $T_t$) for convenience. This condition leads to seven determining equations for the functions $\xi$, $\tau$ and $\eta$ that can be written in the form:

$$\begin{aligned} & \xi _T = 0 , \quad \tau _T = 0, \quad \tau _x = 0, \quad E_T\eta _t = \frac{4a_R c}{3} \lambda _R T^3 \eta _{xx}, \quad -E_T\xi _t = \frac{4a_R c}{3}\left[ 2 \left( \lambda _R T^3 \eta _x \right) _T - \lambda _R T^3 \xi _{xx}\right] , \end{aligned}$$

(13)

$$\begin{aligned} & \left[ \frac{E_{TT}}{E_T} \eta + \left( 2 \xi _x - \tau _t \right) \right] \left( \lambda _R T^3 \right) _T = \left( \eta \lambda _R T^3\right) _{TT}, \quad \eta \left[ \left( \lambda _R T^3 \right) _T-\frac{\lambda _R T^3 E_{TT}}{E_T}\right] = \lambda _R T^3 \left[ 2\xi _x-\tau _t \right] , \end{aligned}$$

(14)

$$\begin{aligned} & \text {with} \quad D(T) = \frac{4 a_R c}{3} \left[ \frac{\lambda _R T^3}{E_T} \right] \end{aligned}$$

(15)

It is worth noting that the Lie analysis naturally leads to the introduction of a diffusion coefficient D(T), which depends on the equation of state and the opacity law of the material under study. This parameter basically controls the form of the Lie symmetries of radiative waves. Three cases can be inferred, depending of the form of the function D(T) and are summed up in Table 1. The mathematical formulation of the symmetries involves a total of six real parameters $\gamma _i$, which represent the degrees of freedom of the transformations. Depending on the form of the parameter D(T), the number of independent parameters ranges from three to six, with the maximum occurring when D(T) is a constant coefficient. Notably, in the specific case where $D(T) = D_0$, an additional infinitesimal generator can be recovered, corresponding to the infinite symmetry of the linear heat equation³³, which is of relatively little interest in this study.

We see that for non-analytical functions E(T) and $\lambda _R(T)$, as it is generally the case for laboratory materials, only three symmetries exist. These transformations do not even act on the temperature variable, as only a scaling of space and time is allowed at best. Now, some freedom can be gained by choosing a particular form for the equation of state and opacity law. For example, we can write E(T) and $\lambda _R(T)$ as power laws of the form:

$$\begin{aligned} E(T) = e_0 T^{\beta } \quad \text {and} \quad \lambda _R(T) = \lambda _0 T^{\alpha } \end{aligned}$$

(16)

One striking constraint that arises from the Lie symmetries of radiative waves is the conservation of the exponents $\alpha$ and $\beta$, as in radiation hydrodynamics scaling laws⁴. However, here the constants $e_0$ and $\lambda _0$ still remain the same, showing a clear separation from global invariance theory, and highlighting the limits of classical Lie theory to derive similitude or resemblance transformations. That being said, Lie symmetries of radiation waves presented in Table 1 can still be used to derive analytical solutions of the model (10) or even as additional transformation laws in some particular cases.

Table 1 Lie generators and symmetries of radiative waves described by Eq. (10) under different assumptions for the functions E(T) and $\lambda _R(T)$.

Methods: lie equivalence symmetries

As stated in the introduction, Lie symmetries assume a certain form for the functions defining the plasma under consideration, such as the equation of state and opacity law for radiation hydrodynamics. In order to cope with this missing piece in the theory, these so-called arbitrary elements or functions must be included in the algorithm defined in the previous section, which leads us to introduce the notion of equivalence symmetries^18,25. So, we now consider the differential equation (1), where we account for the existence of M arbitrary functions $\textbf{g} = g_{i_{1\le i \le M}}(f)$ explicitly depending on the previous dependent variable f. We can define a class for this differential equation which can be defined as the set formed by the differential equation:

$$\begin{aligned} F\left( \textbf{x},f(\textbf{x}), ..., g_1(f), ..., g_M(f), \frac{\partial {g_1(f)}}{\partial f}, ...., \frac{\partial {g_M(f)}}{\partial {f}}\right) = 0 \end{aligned}$$

(17)

as well as the equations defining the dependence of the arbitrary elements $g_{i_{1\le i\le M}}$, given here by:

$$\begin{aligned} \frac{\partial g_i}{\partial x_j} = 0, \quad 1 \le i \le M, \quad 1 \le j \le N \quad (A) \end{aligned}$$

(18)

The system of equations (A) is called an auxiliary system. We treat here the case of arbitrary functions depending only on the variable f, which will be used for our application. In practice, the dependence of arbitrary functions can be any. Moreover, we restrict ourselves to the presence of derivatives of order 1 for these arbitrary derivatives, the generalization to the case of derivatives of order n being immediate. Considering the invariance of such a class of equations allows to modify the arbitrary functions $g_i$, but not their dependencies. This is called the principle of strong equivalence, as opposed to weak equivalence³⁴ where the conservation of the dependence of the arbitrary functions is no longer guaranteed. It is on this concept of strong equivalence that our attention is naturally focused, in order to preserve a physical coherence for the arbitrary functions.

In this case, we now consider that the arbitrary elements are dependent variables. It introduces some modifications to the classical Lie method presented earlier. First, when searching for transformations as in Eq. (2), we now allow the arbitrary functions to be modified as well, giving:

$$\begin{aligned} \hat{\textbf{g}} = \varvec{\zeta }(\textbf{x},f,\textbf{g},a), \quad \text {with} \quad \frac{d \varvec{\zeta }}{da} = \varvec{\epsilon }(\hat{\textbf{x}},\hat{f},\hat{\textbf{g}}) \end{aligned}$$

(19)

with $\varvec{\epsilon }$ being the coordinate functions associated with the arbitrary elements $\textbf{g}$. The invariance condition (6) stays the same as long as we account for the following modification of the infinitesimal generator (5):

$$\begin{aligned} G = \left[ \sum _{i=1}^N \xi _i \frac{\partial }{\partial x_i} + \eta \frac{\partial }{\partial f} + \sum _{j=1}^M \epsilon _j \frac{\partial }{\partial g_j}\right] \end{aligned}$$

(20)

The derivatives of arbitrary elements can also be present in the differential equation, as derivatives of a dependent variable now. In the context of finding equivalence point symmetries, the infinitesimal equivalence transformations again induce infinitesimal transformations on these derivatives. In the case of derivatives of order 1, these transformations take, as for Eq. (7), the following form:

$$\begin{aligned} \frac{\partial \hat{g}_j}{\partial f} = \frac{\partial g_j}{\partial f} + \pi _{j3} \delta a, \quad \pi _{j3} = \frac{d \epsilon _j}{df} - \frac{\partial g_j}{\partial f} \left[ \frac{\partial \eta }{\partial T} + \sum _{i=1}^N\frac{\partial f}{\partial x_i} \frac{d \xi _i}{df} \right] \end{aligned}$$

(21)

The notation j3 corresponds to the arbitrary function (considered as a dependent variable) number j and the variable it depends of (f here) which can be considered as a third independent variable. We note that, in this framework, f is considered as a dependent variable with regards to $\textbf{x}$ but as an independent variable with regards to $\textbf{g}$. The equivalence generator extended to order 1 is now written as follows:

$$\begin{aligned} G^{(1)} = G + \sum _{j=1}^M \pi _{j3} \frac{\partial }{\partial g_{j_f}} \end{aligned}$$

(22)

where $g_{j_f} \equiv \partial g_j / \partial f$. This analysis can be generalized directly to the case of derivatives of order n, as for the Lie analysis of the first section, but also to the case of a system of differential equations³⁵. The invariance condition (9) modified with the new infinitesimal generator then leads to a system of linear differential equations on the coordinate functions $\varvec{\xi }$, $\eta$ and $\varvec{\epsilon }$.

Lie equivalence symmetries of radiative waves

The class of radiative waves can be defined as follows:

$$\begin{aligned} E_T T_t = \frac{4 a_R c}{3} \left[ T_x^2 \left( \lambda _{R_T} T^3 + 3 \lambda _R T^2 \right) + \lambda _R T^3 T_{xx} \right] \quad \text {with} \quad E = E(T) \quad \text {and} \quad \lambda _R = \lambda _R(T) \end{aligned}$$

(23)

in which the auxiliary system is the mathematical formulation of the assessment that the functions E and $\lambda _R$ only depend on the dependent variable T. We can then write the infinitesimal generator of Lie equivalence point symmetries as:

$$\begin{aligned} G = \xi (x,t,T) \frac{\partial }{\partial x} + \tau (x,t,T) \frac{\partial }{\partial t} + \eta (x,t,T) \frac{\partial }{\partial T} + \epsilon _1\left( x,t,T,E,\lambda _R \right) \frac{\partial }{\partial E} + \epsilon _2\left( x,t,T,E,\lambda _R \right) \frac{\partial }{\partial \lambda _R} \end{aligned}$$

(24)

where $\epsilon _1$ and $\epsilon _2$ are the new coordinate functions associated with the arbitrary elements E and $\lambda _R$ respectively. As for classical Lie symmetries, a set of determining equations can now be derived, that can be separated in polynomials of the dependent variables derivatives of which the coordinate functions cannot depend. This leads us to obtain a general form for these functions, given by:

$$\begin{aligned} \xi (x) = b_1 + (b_3 + b_4 + b_5) x, \quad \tau (t) = b_2 + 2b_3 t, \quad \eta = \eta (T), \quad \epsilon _1(E) = -2 b_4 E, \quad \epsilon _2(T,\lambda _R) = \lambda _R \left( 2b_5 - \left[ \eta _T + 3 \frac{\eta }{T}\right] \right) \end{aligned}$$

(25)

in which the five $b_i$ parameters are independent. Interestingly, we see that the constraints on E(T) and $\lambda _R(T)$ from the previous analysis do not remain. In particular, the D(T) coefficient is not appearing in the analysis at all, which can be explained by the fact that E(T) and $\lambda _R(T)$ are now dependent variables which can be modified by the symmetries. Finally, the coordinate function associated with temperature $\eta$ is now only constrained by its dependence with T which introduces another degree of freedom for the transformations. Ultimately, we now obtained six degrees of freedom which can be translated as six Lie equivalence generators, each associated with one symmetry, all given in Table 2.

Table 2 Equivalence generators and symmetries of radiative waves described by Eq. (10).

By composing these transformations, redefining $a_x = \gamma _3 \gamma _4 \gamma _5$ and $a_t = \gamma _3^2$ to define clear spatial and temporal scaling factors, we get:

$$\begin{aligned} {\left\{ \begin{array}{ll} \hat{x} = a_x \left( x+\gamma _1\right) \\ \hat{t} = a_t \left( t+\gamma _2 \right) \\ \hat{T} = \phi (T,\gamma _6) \\ \hat{E}(\hat{T}) = \frac{a_t \gamma _5^2}{a_x^2} E(T) \\ \hat{\lambda }_R(\hat{T}) = \gamma _5^2 \lambda _R \left( \frac{T}{\hat{T}}\right) ^3 \frac{dT}{d\hat{T}} \end{array}\right. } \end{aligned}$$

(26)

Such transformations have been shown²⁰ to degenerate into the radiation hydrodynamics scaling laws⁴ in the static limit for a particular choice of parameters. This shows how the equivalence tends to generalize the similitude approach by increasing the number of degrees of freedom initially allowed by the similarity transformations. We even see that it can lead to more complex transformations modifying deeply the plasma properties. In essence, we now have a set of symmetries that allows us to explicitly link systems evolving in different radiative regimes with fundamentally different microscopic properties. According to the classification introduced earlier, we jumped from similitude to resemblance transformations. Thus, the importance of being able to modify the functions E(T) and $\lambda _R(T)$ between two scales cannot be emphasized enough. More particularly, the application of the equivalence symmetries (26) allows to join these two quantities in the form of a new dimensionless parameter²⁰. Modifying the energy balance in the system is now allowed, while being absorbed by modifying accordingly the balance of the fluxes.

Results: application to numerical model validation

In a previous work²⁰, we showed that equivalence could be reached between an astrophysical system simulated with RAMSES-RT^36,37,38 and an equivalent laboratory system simulated with the FCI2 code^39,40. However, this example was using a particular function for the opacity law of the laboratory material while simulations were performed with unfrozen dynamics which led to a departure from equivalence. To illustrate both the vast range of possibilities offered by these new concepts and their additional value in assessing the validity of numerical models for extremely radiative environments, we present here a new example. In this case, we explicitly link an extremely radiative wave (R$\le$ 1) to a laboratory wave in an experimentally accessible regime ($\hat{R} \simeq 25$), where numerical model validation is feasible. No hydrodynamic motion of the plasma is allowed, and we use a description of an equation of state relevant to actual laboratory materials. In particular, we used typical metallic foam fittings from Cohen et al.⁴¹ to obtain a range of parameters representative of laboratory materials microscopic properties. In this case, the energy density distributions of the initial and transformed systems take the following forms:

$$\begin{aligned} E(T) = \rho _0 e(T) + a_R T^4, \quad \hat{E}(\hat{T}) = \hat{\rho }_0 \hat{e}(\hat{T}) \end{aligned}$$

(27)

We aim to model the first instants of a X-ray burst and accretion disk interaction that can be described²⁰ by a perfect gas law, giving an internal energy function $e(T) = c_v T$ as well as a Thomson dominated opacity law, which allows to use a constant mean free path $\lambda _R(T) = \lambda _0$. Furthermore, we consider the case of a medium with density $\rho _0 = 10^{-4}\hbox {g.cm}^{-3}$ and initial temperature $T_0 = 1$ eV. The boundary condition is a burst going from 50 eV to a maximum temperature $T_R = 250$ eV reached at a time of 0.05 s.

Now, assuming that the function $\hat{E}(\hat{T}) = \rho _0 e(T)$ for the laboratory scale material can be put in the form of a power law as in Eq.(16) over the temperature intervals considered, we can obtain a transformation law for the temperature field and the laboratory mean free path as:

$$\begin{aligned} \hat{T} = \left( \frac{a_t \gamma _5^2}{a_x^2} \frac{1}{\hat{e}_0}\right) ^ \frac{1}{\hat{\beta }} \left[ \rho _0 c_v T+a_R T^4 \right] ^{\frac{1}{\hat{\beta }}}, \quad \hat{\lambda }_R(T) = \gamma _5^2 \lambda _0 \hat{\beta } T^3 \frac{\left( \frac{a_t \gamma _5^2}{a_x^2} \frac{1}{\hat{e}_0} \left[ \rho _0 c_v T+a_R T^4 \right] \right) ^{1-\frac{4}{\hat{\beta }}}}{\left( \frac{a_t \gamma _5^2}{a_x^2} \frac{1}{\hat{e}_0} \left[ \rho _0 c_v +4a_R T^3 \right] \right) } \end{aligned}$$

(28)

We note that there is an explicit form for $\hat{\lambda }_R(T)$, which is not the case for $\hat{\lambda }_R(\hat{T})$. The analytical determination of the function $\hat{\lambda }_R(\hat{T})$ would require to be able to invert the relation (28) for any value of $\hat{\beta }$. This can be done numerically in order to also apply equivalence transformations to systems whose equations of state and opacity laws are not known theoretically.

Table 3 Values of the defining variables of the astrophysical and laboratory (with a hat on) systems along with equivalence parameters.

The different free parameters determining the laboratory system are presented in Table 3. The internal energy evolution is set to lie in the interval of data provided by Cohen et al.⁴¹. These particular choices allow to obtain, at a laboratory scale, a physical regime described by a Mihalas number $\hat{\text {R}} \simeq 25 \gg 1$. Finally, we used a fitted function for the laboratory mean free path on the considered temperature interval ($0 \rightarrow 250$ eV) to provide FCI2 with an analytical opacity law. The resulting values together with the internal energy of the laboratory plasma are presented on the left panel of Fig. 1.

We can see that the variation of the internal energy density is indeed increasing with temperature, which is not the case for the average mean free path $\hat{\lambda }_R(\hat{T})$ over the whole temperature range. Indeed, this function is decreasing for temperatures above 40 eV, which is a behavior not usually observed for typical laboratory materials. However, this form of mean free path is imposed by the equivalence to counterbalance the change of physical regime between the astrophysical and the laboratory scale. We see here a limitation of the equivalence symmetries that do not naturally conserve the physical interpretation of the arbitrary functions E(T) and $\lambda _R(T)$ between the two scales. This example remains particularly valuable for numerical purposes, as simulating this physically unconventional system enables the study of a physically significant situation that is challenging to compute numerically with RAMSES-RT due to the unverified extremely radiative regimes involved. The simulation of the laboratory system is presented on the right panel of Fig. 1.

We obtain temperature profiles extremely different from those we used to see in terms of wavefront concavity in laboratory systems. This seems to be due to the particular shape of the photon mean free path $\hat{\lambda }_R(\hat{T})$, which is decreasing over most of the considered temperature interval. On the astrophysical scale, this is due to the relative importance of radiative energy compared to internal energy, the latter varying way slower with respect to temperature. In order to obtain such a theoretical material, a solution would be to completely control the microphysics of the laboratory system governing the behavior of the equation of state and opacity law. This could theoretically allow us to verify the equivalence relations perfectly. However, the science of metamaterials⁴² remains far from fully developed, as current manufacturing techniques would be unable to precisely replicate the desired microphysical properties. For now, there will inevitably be deviations from the perfect equivalence scenario which have to be taken into account in the design of a laboratory experiment which will be the subject of the last section.

Fig. 1

Left panel: Functions $\hat{\rho }\hat{e}(\hat{T})$ (in solid lines, chosen arbitrarily) and $\hat{\lambda }_R(\hat{T})$ (in dotted lines, fixed by the equivalence) of the laboratory system. The photon mean free path fit function is represented in blue circles, with a correlation coefficient $r^2 \simeq 0.99$. Right panel: FCI2 simulation of the laboratory equivalent system for different times that correspond to the astrophysical equivalent ones.

Apart from these considerations, one of the major interest of these transformations resides in the link created between different physical regimes and scales. The astrophysical system featuring a supersonic, highly radiative wave can be simulated using RAMSES-RT, albeit without any guarantee that the obtained solution is accurate, in particular in an unverified extremely radiative regime. The lack of analytical validation or the impossibility to rely on observational data to validate such simulations could potentially be solved by the use of equivalence transformations. As a practical demonstration, we simulated the astrophysical system with RAMSES-RT whose results are shown on the left panel of Fig. 2. The radiative wave concavity is much closer to the expected classical picture of Marshak waves²⁷, and we can see that the temporal and spatial scales greatly differ from the FCI2 simulations previously shown by $a_t$ and $a_x$ factors respectively. In order to compare this astrophysical radiative wave to the laboratory validated one, we then apply the equivalence symmetries (26) to the numerical solutions. The results are shown on the right panel of Fig. 2.

Fig. 2

Left panel: RAMSES-RT simulation of the astrophysical system for different times that correspond to the laboratory equivalent ones. Right panel: Superposition of the spatial temperature profiles of the astrophysical system (RAMSES-RT, in red shaded dotted lines) and the transformed equivalent laboratory system (FCI2, in black shaded straight lines) after applying the equivalence transformation on temperature (28). The different time and spatial scales are indicated to emphasize the scaling embedded in the equivalence transformations (26).

After application of the equivalence transformations, the simulation of the astrophysical system corresponds exactly to that of the equivalent laboratory system. Despite their non-similar physical regimes ($\text {R} \le 1 \ll \hat{\text {R}}$), fundamentally different microscopic behaviors ($\lambda _R$, $\hat{\lambda }_R$), and very distant spatial and temporal scales ($a_x = 2 \times 10^{-8}$, $a_t = 2 \times 10^{-7}$), we succeeded in linking explicitly these two systems. From an experimentally validated weakly radiative regime on a laboratory scale to an extremely radiative setup on an astrophysical scale, the equivalence symmetries of radiative waves have been successfully applied. This gives us confidence in the way RAMSES-RT solves radiative transport in extremely radiative regimes and paves the way to more model validation using equivalence symmetries or more generalized transformations. For now, the main limitation resides in being able to take into consideration real material properties in the definition of the functions E(T) and $\lambda _R(T)$ in order to design an actual experiment.

Results: a first experimental design

After demonstrating the usefulness of the equivalence approach in 1D using a theoretical material, we now detail the analysis carried out in an 2D axisymmetric geometry, for a real foam material: $\hbox {Ta}_2 \hbox {O}_5$. This material has been chosen for its high Z, allowing to reach a diffusive regime easily. We used this tabulated foam opacity as a given data. Thus, the application of the equivalence transformations (26) together with experimental requirements constrain the function $\phi$, the internal energy density law $\hat{\rho }\hat{e}(\hat{T})$ of the material and the $\gamma _5$ and $\gamma _6$ parameters. The experimental dimensions must respect the constraints of a feasible design allowing the implementation of spatial and temporal diagnostics. In practice, we tried to obtain systems of size $\hat{L} \in [0.1,0.3]$ cm and characteristic time scale $\hat{t} \in [2,10]$ ns. We also chose $a_t = 2 \times 10^{-7}$ to study the first milliseconds of burst-disk interaction at the astrophysical scale. The only remaining parameter thus is $a_x$, meaning that the choice of a proper spatial extension for the experiment has to be optimized. We found that $a_x = 2.24 \times 10^{-8}$ corresponds to the closest correlation between the real and equivalent energy densities on the timescale of 5 ns. This leads to a laboratory length reaching at least 0.19 cm, falling into the expected interval. The different parameters defining the astrophysical and laboratory systems are gathered in Table 4.

Table 4 Values of the defining variables of the astrophysical and laboratory (with a hat on) systems along with equivalence parameters.

This choice of material and density has been found to be one of the best compromise attainable for classical foams used in radiative waves experiments and for the application of equivalence to the astrophysical system studied. Using this, we now present a first design based on Megajoule lasers capabilities (LMJ and NIF), aiming at producing supersonic radiative waves equivalent to those propagating in accretion disks around neutron stars. The experimental configuration is presented on the right panel of Fig. 3. It consists of a gold cavity used to convert laser energy into X-rays, uniformly irradiating the low density $\hbox {Ta}_2\hbox {O}_5$ foam described earlier. A hard X-ray imager diagnostic is placed on the side of the tube to study the density perturbations inside the foam. It looks at the radiation transmitted from an outside X-ray source using a Scandium back lighter. A soft X-ray imager, temporally resolved, is placed at the end of the tube in order to analyze the radiation coming out of it. We do not present in details this diagnostic here as we only discuss focus primarily on the application to equivalence.

The required laser energy on 10 ns is of the order of $E_L \sim 600$ kJ. The laser configuration is essential to obtain the desired foam attack temperature $T_S(t)$. In our experiments, we need a temperature rise in the form of a ramp of at least ten nanoseconds duration. This temperature increase stops at about 250 eV. Moreover, in order to obtain a temperature rise corresponding to that imposed by the equivalence, it is necessary to progressively increase the laser power delivered. The evolution of the laser power deposited on the walls of the cavity, as well as that of the temperature of the radiation in the cavity, can be obtained with the help of a time-resolved broadband X-ray spectrometer (DMX on the LMJ or DANTE on the NIF). From FCI2 simulations, we simulated the radiation seen by the DMX, which we present on the left panel of Fig. 3.

Fig. 3

Left panel: Simulation of the temperature measured by the DMX in the conversion cavity. Right panel: 3D Representation of the experimental setup with a gold cavity and the tube containing the foam. The different diagnostics are indicated on the side.

Unlike the parameter $a_x$, the choice of the parameter $a_t$ is not completely independent of the other parameters in the system. In particular, the choice of a new timescale directly modified the form of the jump $\hat{T}_S (\hat{t})$ that constitutes the boundary condition in the laboratory. This constraint set the form of the radiation source presented on the left panel of Fig. 3. For the laboratory system, the goal was first to remain in the supersonic approximation, meaning that high temperatures were required in order to maintain the supersonic assumption over long enough timescales to be diagnostically relevant. Thus, we chose a maximum temperature $\hat{T} = 250, \text {eV}$, consistent with the possibilities offered by the most energetic current laser facilities (NIF, LMJ) on the considered timescales. We note that other temperature choices can be made, leading to modifications in the equivalence application parameters. In any case, the boundary condition designed for the equivalent laboratory experiment introduces another constraint to satisfy the equivalence relations and, in this case, sets the values of two equivalence parameters..

We then performed 2D axisymmetric FCI2 simulations of this setup, which results are presented on the left panel of Fig. 4. We can see the propagation of a radiative front curved by the absorption of radiation at the walls. This curvature intensifies with time and impacts more and more the zones close to the center of the foam. This is partly due to radiation propagating inside the tube being absorbed at its walls, which tends to bend the radiative front (albedo effect)^43,44 and slow it down. For this setup, we found that a typical diameter of $D=0.4$ cm is sufficient to prevent both of these effects from reaching the center of the tube during the equivalence application frame. It would be possible to reduce the CHON tube albedo by, for example, switching to a gold tube and incorporating a slit to perform diagnostics, or even further optimizing the equivalence symmetry parameters to achieve an alternative experimental configuration that would eliminate the need for this specific diameter. Such considerations should be explored in future experiments. After 5 ns, we can see that in more than two thirds of the tube the radiative wave is propagating unaltered by these edge effects. At 10 ns, this result is only valid for one third of the tube and the position of the radiative front at the tube is very different from the unaltered one at the center of the foam. The radiative Mach number is about Ma = $v_f/c_s$ $\simeq 2$, which characterizes a supersonic regime. Indeed, we can see that the density maximum at the center of the foam, which can be characterized as the place where the acoustic perturbations accumulate, is well upstream of the radiative front, and present density ratios about 2 times lower than those necessary for the creation of a shock. However, the propagation of density perturbations close to the tube walls is also visible, in particular at 10 ns, where a shock starts to propagate within the foam, which will inevitably alter the experiment supposed to take place in the supersonic regime. We can see that these perturbations, around 10 ns, impact only half of the foam, leaving the center unaltered. Thus, the temperature evolution at the center of the tube is the relevant quantity to be experimentally obtained and the expected results are shown in blue on the right panel of Fig. 4.

Fig. 4

Left panel: Radiation intensity and scaled density map within the $\hbox {Ta}_2\hbox {O}_5$ foam for $t=5$ ns and $t=10$ ns. The effects of radiation absorption at the walls are visible on the simulations where the tube is represented in yellow. The density is scaled by 4 times the initial density of the foam, characteristic of the onset of a strong shock. We can observe both the ablation of the tube and the accumulation of acoustic perturbations following the propagation of the radiative wave without creating a hydrodynamic separation shock. Right panel: Spatial temperature profiles for $\hat{t} = 4$ ns and $\hat{t} = 8$ ns. The RAMSES-RT 1D simulations are in red straight lines. The 1D FCI2 simulations are in dotted blue lines, and the $\pm 10 \%$ uncertainty 2D runs in black dashed lines, all after applying the equivalence transformations. The results are both shown on the astrophysical scale along with the scaled confidence interval in yellow.

This Fig. also shows the effect of uncertainties in the properties of the synthesized foams⁴⁵, as well as uncertainties in the temperature reached in the cavity. We think it is important to at least address the modifications that such uncertainties can bring to the experiments. Thus, we performed additional simulations, allowing three parameters to vary by $10 \%$ in amplitude: the density $\rho _{0}$ of the foam, the deposited laser energy $E_L$ and the mean free path of the plasma $\lambda _R$. This would correspond to experimental uncertainties for the foam density⁴⁶ for example but can be seen as low estimations in most experiments for the laser energy and plasma mean free path. The results of the simulations taking into considerations all these uncertainties are presented in yellow and black on the right panel of Fig. 4. It is particularly interesting to see how experimental uncertainties actually propagate to the astrophysical scale after using the equivalence transformations. As expected the uncertainty interval grows with time as uncertainties accumulate. During the relevant 10 ns for equivalence theory to be applied, the RAMSES radiative front position, in red, stays within the uncertainty interval.

This observation is particularly interesting as, in practice, additional measurements of the foam properties can redefine the initial system within this confidence interval. Then, modifying the equivalence transformations accordingly, it is possible to absorb these differences to reduce these temperature disparities. This is allowed by the fact that this specific design is far enough from the breaking point of the supersonic and optically thick hypothesis. In general, as long as the core physical principles remain valid within the confidence interval, the flexibility of equivalence transformations can be leveraged to accommodate deviations in material properties. Interestingly, on the flip side, experiments of this nature could also serve to test the characterization of the governing behavioral laws of the propagation medium, including the equation of state and opacity law.⁴⁷.

Concluding remarks

We showed here that the equivalence approach can allow to generalize scaling laws and explicitly link extremely radiative astrophysical waves to experimentally reachable regimes. We presented for the first time a design of a resemblance experiment that shows an explicit relation between the macroscopic properties of supersonic radiative waves. The versatility of these symmetries also allowed us to use them for numerical model validation, an example that could be generalized to different systems. Even though the strengths of this approach allowed to go beyond similarity, several limitations persist. The major constraint is that the equation of state and opacity law of the transformed system are linked, making it difficult to associate both with experimentally relevant materials. An improvement could potentially be realized by exploring the use of metamaterials⁴², which, in theory, would enable more precise control over the internal properties of materials, thus moving closer to meeting the theoretical requirements set by equivalence.

Now, to go further beyond this approach, we can look back at the classification discussed in the introduction⁵. Ahead of resemblance lies the analogy category, in which a system can be modeled by apparently completely different physics. Some analogies appear naturally, such as the electronic circuit and harmonic oscillator⁴⁸. Others required inventiveness in theoretical developments such as the acoustic black holes analogy⁴⁹. The latter was even used in recent experiments that led to observe Hawking radiation in Bose Einstein condensates⁵⁰. As equivalence appeared as the solution to systematically search for resemblance transformations, mapping techniques⁵¹ could become a standard method to derive analogies between systems^52,53.