Abstract
In recent years, integrating trigonometric techniques into probability models has garnered significant interest. This paper presents a novel trigonometric generator based on the Arc cosine function, referred to as the Arc cos-\(\Psi\) distribution. The proposed distribution demonstrates unique and flexible patterns in its probability density function (PDF) and hazard rate function (HRF), showcasing its ability to effectively model both symmetrical and asymmetrical data behaviors. Key mathematical properties of the distribution are thoroughly investigated, including moments, extremum behavior of the PDF and HRF, incomplete moments, quantile function, and entropies. Parameter estimation is carried out using various methods, and their performance is assessed through comprehensive numerical studies. Additionally, a simulation study is conducted to further validate the distribution’s properties and estimation techniques. The practical utility and adaptability of the model are demonstrated using two real-world datasets, including COVID-19 data, where the distribution provides an exceptional fit and reveals unique data characteristics. This underscores its potential for modeling complex datasets with intricate structures, making it a valuable addition to the statistical toolkit.
Similar content being viewed by others
Introduction
The COVID-19 pandemic, caused by the novel coronavirus SARS-CoV-2, has profoundly impacted global health and socio-economic systems. Since its emergence in late 2019, the pandemic has highlighted the importance of accurate statistical modeling for understanding and predicting the progression of infectious diseases. Reliable models are crucial for evaluating trends, analyzing the efficacy of interventions, and guiding public health decisions. In this context, probability distributions have played a pivotal role in analyzing COVID-19 data, as they offer versatile tools for capturing the variability and patterns inherent in such datasets. Motivated by the complex nature of COVID-19 data, this study introduces a novel generator of probability distributions based on inverse trigonometric functions. The new generator is designed to enhance flexibility and provide a better fit for real-world data with varying characteristics, such as heavy tails, skewness, or multimodality. Trigonometric function-based probability generators offer a robust framework to address complex data patterns, including those observed during the pandemic. These generators provide flexibility and precision, enabling researchers to uncover nuanced insights from diverse datasets. Using the proposed generator, we derive a novel distribution that is applied to two COVID-19-related datasets. This innovative distribution demonstrates enhanced adaptability and efficiency in data modeling, providing superior fits compared to existing models. Overall, the use of trigonometric function-based generators represents a significant advancement in statistical modeling. It equips researchers with powerful tools to address intricate data analysis challenges, fostering discoveries and improving our ability to analyze diverse datasets across various scientific domains.
The following are some derived families of distributions: SS-transformation based on trigonometric functions is proposed by Kumar et al.1, Al Babtain et al.2, Chesneau et al.3, Mahmood and Chesneau4, Souza et al.5, Jammal et al.6, Luciano Souza et al.7, Lone et al.8, Anwar et al.9, Muzamil et al.10, Odhah et al.11, Alomair et al.12, Heydari et al.13, Alghamdi et al.14, Omalsad et al.15, Wang et al.16, Zhu et al.17 and Aijaz et al.18,19,20,21,22.
Aijaz et al.23, recently proposed a new cosine generator considering Weibull distribution as an illustration; the cdf of this generator is stated as.
In the literature of probability distribution theory, a new arctan-generator family was formulated by Aijaz et al.24 to enhance the efficacy of the conventional distributions. The CDF of the arctan-generator is stated as.
In this research, we present an innovative probability generator rooted in the arc cosine function, engineered to amplify adaptability in intricate data analysis. The core significance of this generator is its capacity to deliver enhanced flexibility without the need for supplementary parameters. Utilizing the Weibull distribution as the foundational framework for the generator, we observe from its probability density function (PDF) plot that this distribution can manifest a variety of shapes, including symmetric, left-skewed, right-skewed, L-shaped, and long-tailed configurations. Moreover, its hazard rate function exhibits both decreasing and increasing trends, thereby broadening its utility in diverse modeling contexts. This study addresses the critical research question of how to develop a probability generator that offers superior adaptability and versatility in modeling complex data without complicating the model with additional parameters. The motivation behind this work is to provide a robust tool that can seamlessly integrate into various analytical frameworks, offering a significant advancement in the field of probability modeling.The mathematical formulation of this generator is defined as follows.
Defination
Let \(F(z;\xi )\) symbolize the cumulative distribution function (CDF) and \(f(z;\xi )\) signify the related probability density function (PDF) for a random variable Z. The cumulative distribution function of the novel arc cosine-\(\Psi (z;\xi )\) class of distribution can be described as such.
The probability density function for Eq. (1) is formatted as
The function \(\Psi (z;\xi )\) represents the baseline cumulative distribution function, where its characteristics are governed by the parameter vector \(\xi\). Moreover, the derivative of \(\Psi (z;\xi )\) with respect to z is denoted as \(\psi (z;\xi )\) and \(\bar{\Psi }(z;\xi )=1-\Psi (z;\xi )\).
In reliability analysis, several key functions are established to describe system behavior. The survival function, represented as \(R(z;\xi ),\) provides the probability of a system functioning beyond time z. The hazard rate function, \(h(z;\xi ),\) reflects the instantaneous failure rate at time z. Similarly, the reverse hazard rate function,\(h(z;\xi ),\) indicates the rate of failure when approaching from larger values of z. Finally, the cumulative hazard rate function \(H(z;\xi ),\) accumulates the hazard rate over time, offering insights into the total failure risk up to time z.
The examination of the PDF and HRF shapes, including points of maxima, minima, and inflection, provides valuable insights. Maxima indicate the most likely values of the random variable, while minima suggest regions of least likelihood. Inflection points signal changes in the concavity of the distribution, helping to understand transitions in the failure rates or risk behaviors across different time intervals. These characteristics are crucial in reliability modeling and risk assessment.Now, we analyze the behavior of the probability density function (PDF) and hazard rate function (HRF) for the proposed generator. Through logarithmic differentiation of the PDF, we obtain the following expression:
We aim to determine if the PDF reaches a maximum, minimum, or inflection point at the critical values, denoted by \(z_{0}\), found by solving \(\frac{d}{dz}\log (f(z;\xi ))=0\). To achieve this, we assess the behavior of the function using the second derivative at these critical points indicated as \(\beta _{1}=\left\{ \frac{d^{2}}{dz^{2}}\log (f(z;\xi ))\right\} _{z_{0}}\) if \(\beta _{1}>0\) then The point represents a local minimum, if \(\beta _{1}<0\) the point is a local maximum and if \(\beta _{1}=0\) it represents point of inflection. In analyzing the hazard rate function (HRF), we utilize a comparable approach. By calculating the first derivative of the HRF, we derive the following expression.
Similarly, we analyze the behavior of the hazard rate function (HRF) by first setting the derivative of the logarithm of the hazard rate, \(\frac{d}{dz}\log (h(z;\xi ))=0\). This step helps us identify the critical points, denoted as \(z_{*}\), where changes in the HRF occur. At these critical points, we aim to determine whether the HRF reaches a maximum, minimum, or inflection point. To achieve this, we proceed by computing the second derivative. \(\beta _{2}=\left\{ \frac{d^{2}}{dz^{2}}\log (h(z;\xi ))\right\} _{z_{*}}\). if \(\beta _{2}>0\) implies a minimum, \(\beta _{2}<0\) suggests a maximum, and \(\beta _{2}=0,\) signifies a inflection point at crucial points.
Linear representation of CDF
By applying the arc cosine expansion to the cumulative distribution function (CDF) in Eq. (1), we obtain the following modified expression, leading to a restructured form of the CDF.
Since we know that \(\left( 1-u\right) ^{a}=\sum _{q=0}^{\infty } (-1)^{q} {a \atopwithdelims ()q} u^{q},\) using this expansion in Eq. (2), we have
Now, we make the use of the following expansion in Eq. (3), and we have
Now
Where
Now the associated PDF of Eq. (4) can be yied by differentiating it
Where
The Weibull distribution is extensively used in survival analysis, reliability engineering, and various scientific fields due to its adaptability in modeling diverse data types. In the context of COVID-19, it provides significant insights into the patterns of disease spread, infection duration, and recovery times. By estimating parameters like the duration of infection or mortality risk, the Weibull distribution aids in understanding the temporal dynamics of the pandemic. Its shape and scale parameters allow for a nuanced representation of the pandemic’s progression, capturing both increasing and decreasing hazard rates. This flexibility means it can effectively model changes in infection or fatality rates over time, adapting to shifts in public health trends or interventions. The Weibull distribution’s hazard rate function is particularly valuable in assessing how the risk of infection or death evolves throughout the pandemic. For example, an increasing hazard rate could indicate worsening conditions, while a decreasing rate suggests improvements or the effectiveness of public health measures. Overall, its versatility and the ability to model varying hazard rates make the Weibull distribution an ideal tool for analyzing COVID-19 data, supporting effective decision-making in public health policy and planning. The cumulative distribution function (CDF) of the Weibull distribution further aids in predicting the probability of recovery or death over time, contributing to a more comprehensive understanding of the disease’s impact.
Novel Arc cosine-Weibull distribution
In the following, we consider the Weibull distribution as the baseline for developing a new generator. This leads to the formulation of a novel distribution called the new arc Cosine-Weibull distribution (NACWD). We will derive and explore several properties of this newly defined NACWD. Employing Eq. (6) in (1), we yield the cumulative distribution function (CDF) of the NACWD, which is expressed as follows:
Figure 1 demonstrates the varied forms of the cumulative distribution function (CDF) across different parameter settings, highlighting that the curves consistently remain within the interval (0,1). This confirms that the formulated NACWD adheres to the fundamental properties of a CDF.
The related PDF is stated as
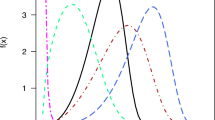
Figure 2 demonstrates the varied forms of the probability density function (PDF) under different parameter settings. When both the scale and shape parameters are increased, it yields a left-skewed symmetric shape. Conversely, reducing the scale parameter while increasing the shape parameter results in a symmetric distribution. When the scale and shape parameters are set equal, it produces a long-tailed distribution. On the other hand, increasing the scale parameter while decreasing the shape parameter generates a reverse J-shaped curve. This versatility highlights the distribution’s capacity to model both symmetric and asymmetric patterns, enabling it to effectively represent a broad spectrum of datasets with diverse characteristics. Such adaptability makes it an ideal choice for capturing the intricacies of complex real-world phenomena.
Statistical properties
In this section, we thoroughly explore the statistical properties of the proposed generator, focusing on the application of the Weibull distribution as the baseline model. Recognized for its flexibility in modeling various data types, the Weibull distribution is particularly useful for analyzing the generator’s behavior using COVID-19 data. We apply real-world COVID-19 datasets to estimate the parameters of the arc cosine-Weibull distribution, assess its goodness of fit, and evaluate its effectiveness. The model’s validity is further confirmed through simulation studies. This method aims to offer a detailed understanding of the generator’s statistical performance, reliability, and applicability in the context of pandemic data analysis.
Moments
Let us suppose \(Z\sim \text {NACWD}\) denotes a random variable, then the \(k^{th}\) moment is derived as
Employing Eq. (5) in Eq. (10), we have
On substitution \(\gamma _{1}(r+1)z^{\gamma _{2}}=y,\) so that \(0<y<\infty\), we have
On integrating, we obtain
Where \(\Gamma (.)\) represents the gamma function.
The moment generating function of the distribution denoted by \(M_{Z}(v)\) is describe as
Incomplete moments
Incomplete moments are used in economics and statistics to study income distribution, mean deviation, and inequality measures like Lorenz curves. They capture the behavior of data over a limited range, offering insights into partial data moments, which help in assessing variability and central tendencies in specific segments. The \(u^{th}\) incomplete moment of the NACWD can be expressed as
On substitution \(\gamma _{1}(t+1)z^{\gamma _{2}}=y,\) so that \(0<y<\gamma _{1}(t+1)u^{\gamma _{2}}\), we have
After simplification, we yield
Where \(\gamma (d,w)=\int _{0}^{w} x^{d-1}e^{-x}dx\) denotes the lower incomplete gamma function. The conditional moments are defined as
Now
After simplification, we yield
Therefore, using Eq. (12) in (11), we have
Similarly, the Lorenz and Bonferroni curves can be derived by employing the following statements.
and
Where \(\mu =\mu _{1}^{\prime }\)
Quantile function
The quantile function plays a crucial role in characterizing the distribution of a random variable. It is particularly valuable for generating random numbers and is instrumental in calculating key statistical measures such as the median, skewness, and kurtosis. Let z be a random variable with CDF defined in Eq. (8). The quantile function of the NACWD can be obtained by reversing the cumulative distribution function (CDF) as follows.
As the function cannot be represented in a simplified form, we can leverage advanced mathematical software tools like Mathematica, MATLAB, R, and Python to obtain the required outcomes. By substituting \(q=u\) and \(u\in (0,1),\) We acquire the NACWD’s random number generation function.
Entropy evaluations
Uncertainty, randomness, and chaos are pervasive phenomena but can be efficiently quantified by employing entropy statistics. Entropy has been extensively applied across diverse disciplines, including engineering, physics, geophysics, computer science, and many others. Its versatility makes it a powerful tool for assessing disorder and unpredictability in various systems.
Rényi entropy
Where \(\rho >0\) and \(\rho \ne 1\)
Now, we solve the following integral.
We utilize the following generalized bionomial expression.
We employ the following expression.
we have
With the aid of the following expression, we have
Where
Now, considering Weibull distribution as base line distribution in the Eq. (15), we have
After simplification, we yield
Utilizing Eq. (16) in Eq. (14), we acquire the Rényi entropy as
Harvada and charvat entropy
Where \(\rho >0\) and \(\rho \ne 1\)
Utilizing Eq. (16) in (17), we yield Harvada and Charvat entropy as
Arimoto entropy
Where \(\rho >0\) and \(\rho \ne 1\)
Utilizing Eq. (16) in (18), we yield Arimoto entropy as
Reliability indicators
This section focuses on different reliability indicators.
Survival function
In survival analysis, the survival function plays a pivotal role in understanding the distribution of survival times or durations, such as the period until recovery, the time until severe symptoms develop, or the duration until a critical event occurs in COVID-19 patients. It offers valuable insights into the probability of survival beyond various time points, aiding in the assessment of disease progression and recovery likelihood in affected individuals. Let us suppose Z be a random variable with CDF F(z). Then, its survival function is defined as
Therefore, the survival function for NTWD is stated as
Cumulative hazard rate function
The cumulative hazard rate function of a random variable z is given as
Differentiating Eq. (20), we acquire the hazard rate function as
Figure 3 illustrates the varying shapes of the hazard rate function, which exhibit both increasing and decreasing trends, depending on the choice of parameters. This flexibility allows the model to accommodate distinct datasets, capturing different behaviors such as rising or falling hazard rates over time. The diverse patterns of the hazard rate function demonstrate the model’s versatility in adapting to a wide range of data characteristics.
Reverse hazard rate function
The reverse hazard rate function of a random variable z is stated as
Therefore, the reverse hazard rate function for NACWD is stated as
Mean residual function
The mean residual lifetime represents the expected remaining duration or average time until an event (e.g., recovery, severe progression, or death) occurs for a COVID-19 patient who has surpassed a specific stage or day z of illness. This measure is particularly significant in studies focused on COVID-19 prognosis and patient recovery.
The mean residual function of random z variable can be obtained as
On substitution \(\gamma _{1}(t+1)v^{\gamma _{2}}=y,\) so that \(\gamma _{1}(t+1)z^{\gamma _{2}}<y<\infty,\) we have
On performing the integral, we get
where \(\Gamma (.)\) denotes the upper incomplete gamma function.
Inference
Inference in probability involves concluding a population based on sample data, using probabilistic methods to make predictions or estimate parameters.
Maximum likelihood function
The likelihood function represents the joint probability of observing the data, given the parameters \(\xi\). When considering a dataset of observations \(Z_{1},Z_{2},Z_{3},..., Z_{n}\) and assuming these data points are independent and identically distributed (i.i.d.), the likelihood function can be expressed as:
The log-likelihood function is given as
The partial derivatives of the log-likelihood function with respect \(\gamma _{1}\) and \(\gamma _{2}\) are as follows
To derive the estimators for \(\gamma _{1}\) and \(\gamma _{2},\) set Eqs. (22) and (23) to 0. Nevertheless, considering these equations are nonlinear and complex to evaluate through conventional approaches, we resort to iterative techniques. The Newton-Raphson approach, the secant method, and the Regula-Falsi method are often employed in these settings to find parameter estimators.
Another technique, referred to as Anderson-Darling estimation (\(E_2\)), entails minimizing the following equation:
In the estimation of Cramér-von Mises (\(E_3\)), the objective is to minimize the following equation for improved statistical analysis.
The maximum product of spacings estimation (\(E_4\)) is achieved by maximizing the following equation, which is commonly used in statistical analysis for parameter estimation.
In contrast, least-squares estimation (\(E_5\)) seeks to minimize the equation by reducing the sum of square differences between observed and expected values to achieve the best fit.
Analogously, in the weighted least squares estimation (\(E_6\)), the goal is to minimize the equation by applying weights to reduce the influence of certain data points on the overall estimation process.
Simulation
In this section of the paper, we conduct a simulation study designed to rigorously examine the performance of multiple estimation methods across different sample sizes, denoted as \(n=50,100,250.350,400,450.\) These sample sizes have been carefully chosen, with each undergoing \(N=500\) iterations under a range of parameter settings. Random samples from the NACWD can be generated using the Eq. (13): The simulation results are comprehensively presented in Tables 1, 2, 3, 4, and 5, where we examine bias, mean squared error (MSE), and mean relative error (MRE), alongside their corresponding rankings. Furthermore, an overview of these rankings is encapsulated in Table 6.
-
As the sample size grows, it becomes apparent that these estimation metrics stabilize and converge toward the true parameter values. Significantly, both bias and mean squared error (MSE) decrease with larger sample sizes, as shown in Tables 1, 2, 3, 4, and 5. This highlights that increased sample sizes produce accurate and dependable parameter estimates.
-
Examining the rankings and simulation outcomes in Table 6, it is evident that the maximum product spacing estimation method consistently outperforms other approaches in accurately estimating the relevant parameters.
Data aanalysis
This section evaluates the flexibility and effectiveness of the NTWD distribution by analyzing its performance using real-world COVID-19 data. The adaptability of the NACWD distribution is assessed by comparing its suitability against several established distributions, including the novel arctan Fréchet distribution (NATD) introduced by Aijaz et al.24, new cosine-Weibull distribution (NCWD) introduced by Aijaz et al.23, Weibull distribution (WD), additive Weibull distribution (AWD), and Kumaraswamy power Fréchet distribution (KPFD) introduced by Najwan et al.25, Fréchet distribution (FD), Inverse Burr distribution (IBD), Lomax distribution (LD) and exponentiated exponential distribution (EED).
To assess the flexibility of the NACWD distribution, a range of statistical evaluation measures are utilized. These encompass the Akaike Information Criterion (AIC), Consistent Akaike Information Criterion (CAIC), Bayesian Information Criterion (BIC), Hannan-Quinn Information Criterion (HQIC), as well as the Kolmogorov-Smirnov test (K-S), Anderson-Darling test (A*), and Cramér-von Mises test (W*), along with their corresponding p-values. A distribution is deemed highly versatile and efficient if it achieves the smallest values across these metrics when applied to the dataset while also demonstrating higher p-values. This comprehensive comparison highlights the NACWD distribution’s capability in accurately modeling complex data patterns associated with COVID-19. Tables 7 and 10 present a comprehensive overview of the datasets, while Tables 8 and 11 offer detailed information on the estimates along with their respective standard errors. Furthermore, Tables 9 and 12 deliver valuable insights into the evaluation metrics and goodness-of-fit statistics for the datasets.
Data set I: The first dataset analyzed in this study consists of COVID-19 data from Italy, covering a period of 172 days, spanning from March 1 to August 20, 2020. The details of this dataset are as follows:
0.0107, 0.0490, 0.0601, 0.0460, 0.0533, 0.0630, 0.0297, 0.0885, 0.0540, 0.1720, 0.0847, 0.0713, 0.0989, 0.0495, 0.1025, 0.1079, 0.0984, 0.1124, 0.0807, 0.1044, 0.1212,0.1167, 0.1255, 0.1416, 0.1315, 0.1073, 0.1629, 0.1485, 0.1453, 0.2000, 0.2070, 0.1520, 0.1628, 0.1666, 0.1417, 0.1221, 0.1767, 0.1987, 0.1408, 0.1456, 0.1443, 0.1319, 0.1053,0.1789, 0.2032, 0.2167, 0.1387, 0.1646, 0.1375, 0.1421, 0.2012, 0.1957, 0.1297, 0.1754, 0.1390, 0.1761, 0.1119, 0.1915, 0.1827, 0.1548, 0.1522, 0.1369, 0.2495, 0.1253, 0.1597,0.2195, 0.2555, 0.1956, 0.1831, 0.1791, 0.2057, 0.2406, 0.1227, 0.2196, 0.2641, 0.3067, 0.1749, 0.2148, 0.2195, 0.1993, 0.2421, 0.2430, 0.1994, 0.1779, 0.0942, 0.3067, 0.1965,0.2003, 0.1180, 0.1686, 0.2668, 0.2113, 0.3371, 0.1730, 0.2212, 0.4972, 0.1641, 0.2667, 0.2690, 0.2321, 0.2792, 0.3515, 0.1398, 0.3436, 0.2254, 0.1302, 0.0864, 0.1619, 0.1311,0.1994, 0.3176, 0.1856, 0.1071, 0.1041, 0.1593, 0.0537, 0.1149, 0.1176, 0.0457, 0.1264, 0.0476, 0.1620, 0.1154, 0.1493, 0.0673, 0.0894, 0.0365, 0.0385, 0.2190, 0.0777, 0.0561,0.0435, 0.0372, 0.0385, 0.0769, 0.1491, 0.0802, 0.0870, 0.0476, 0.0562, 0.0138, 0.0684, 0.1172, 0.0321, 0.0327, 0.0198, 0.0182, 0.0197, 0.0298, 0.0545, 0.0208, 0.0079, 0.0237,0.0169, 0.0336, 0.0755, 0.0263, 0.0260, 0.0150, 0.0054, 0.0375, 0.0043, 0.0154, 0.0146, 0.0210, 0.0115, 0.0052, 0.2512, 0.0084, 0.0125, 0.0125, 0.0109, 0.0071.
The Fig. 4 illustrates the uses of various graphical tools, including the fitted histogram, empirical cumulative distribution function (CDF), survival function, P-P plot, Q-Q plot, and T-T plot, to analyze Dataset I.
Data set II: The second dataset analyzed COVID-19 data pertains to Italy and spans a period of 111 days, from April 1 to July 20, 2020. It comprises the daily ratio of new deaths to new cases recorded during this timeframe The data are available at (https://covid19.who.int/). The data points are as follows:
0.2070, 0.1520, 0.1628, 0.1666, 0.1417, 0.1221, 0.1767, 0.1987, 0.1408, 0.1456, 0.1443,0.1319, 0.1053, 0.1789, 0.2032, 0.2167, 0.1387, 0.1646, 0.1375, 0.1421, 0.2012, 0.1957, 0.1297,0.1754, 0.1390, 0.1761, 0.1119, 0.1915, 0.1827, 0.1548, 0.1522, 0.1369, 0.2495, 0.1253, 0.1597,0.2195, 0.2555, 0.1956, 0.1831, 0.1791, 0.2057, 0.2406, 0.1227, 0.2196, 0.2641, 0.3067, 0.1749,0.2148, 0.2195, 0.1993, 0.2421, 0.2430, 0.1994, 0.1779, 0.0942, 0.3067, 0.1965, 0.2003, 0.1180,0.1686, 0.2668, 0.2113, 0.3371, 0.1730, 0.2212, 0.4972, 0.1641, 0.2667, 0.2690, 0.2321, 0.2792,0.3515, 0.1398, 0.3436, 0.2254, 0.1302, 0.0864, 0.1619, 0.1311, 0.1994, 0.3176, 0.1856, 0.1071,0.1041, 0.1593, 0.0537, 0.1149, 0.1176, 0.0457, 0.1264, 0.0476, 0.1620, 0.1154, 0.1493, 0.0673,0.0894, 0.0365, 0.0385, 0.2190, 0.0777, 0.0561, 0.0435, 0.0372, 0.0385, 0.0769, 0.1491, 0.0802,0.0870, 0.0476, 0.0562, 0.0138.
The Fig. 5 illustrates the uses of various graphical tools, including the fitted histogram, empirical cumulative distribution function (CDF), survival function, P-P plot, Q-Q plot, and T-T plot, to analyze Dataset II.
Figure 6 depicts the visual representation of the estimated probability density functions (PDFs) for the fitted models applied to Dataset I (left) and Dataset II (right), showcasing the comparative distribution patterns across both datasets.
Conclusion
In this study, we introduced and examined a novel category of trigonometric distributions known as the Arc Cos-\(\Psi\) family, with a particular emphasis on a new lifetime model within this category, termed the Arc Cos-Weibull Distribution (ACWD). The research offered an in-depth analysis of the statistical characteristics of the ACWD, encompassing moments, moment-generating functions, incomplete moments, entropies, and reliability analysis. Model parameters were estimated using several classical estimation techniques, and their efficacy was evaluated through a comprehensive simulation study. The measures of Bias, MSE, and MRE are detailed in Tables 1, 2, 3, 4 and 5, with the corresponding partial and overall rankings of all estimation methods for the proposed distribution under various parameter values presented in Table 7. This table demonstrates that the maximum product spacing estimation method consistently surpasses other approaches in accurately estimating the relevant parameters. Utilizing two real-life datasets, including COVID-19 data, the ACWD model exhibited superior performance compared to competing models based on a variety of goodness-of-fit criteria such as AIC, BIC, AICC, HQIC, the Kolmogorov-Smirnov (K-S) test, Anderson Darling test (A*) and Cramer von mises test (W*). supported by significant p-values, as shown in Tables 8 and 11, which provide detailed information on the estimates and their corresponding standard errors for the datasets. Additionally, Tables 9 and 12 offer insights into the comparison criteria and goodness-of-fit statistics for the datasets. Notably, the model demonstrated flexibility in capturing both symmetric and asymmetric data patterns, as evidenced by the distinct shapes of its probability density function (pdf) and hazard rate function (hrf). These attributes highlight its adaptability to a broad spectrum of practical applications, particularly in analyzing pandemic data characterized by diverse patterns and irregularities. Specific submodels within the Arc Cos-G family can be explored in greater detail, especially to address various real-world datasets. Beyond COVID-19 data, the model could be applied to datasets from other fields, such as engineering reliability, biomedical studies, and environmental science, to further validate its robustness and versatility.
Data availability
The data that supports the findings of this study are available within the article.
References
Kumar, D., Singh, U. & Singh, S. new distribution using sine function its application to bladder cancer patients data. J. Stat. Probab. 4(3), 417–427 (2015).
Babtain -Al, A. A., Elbatal, I., & Chesneau et al. Sine Toop-Leone-G family of distributions. Theory and applicationsDe Gruyter, 575-577 (2020).
Chesneau, C., Bakouch, H. S. & Hussian, T. A new class of probability distributions via cosine and sine functions with applications. Commun. Stat.-Simul. Comput. 48(8), 2287–2300 (2019).
Mahood, Z., & Chesneau, C. A new sine-G family of distributions properties and applications. hal-:1-20 (2019).
Souza, L. et al. General properties of cos-G class of distributions with applications. Eurasian Bull. Math 2, 63–79 (2019).
Jamal, F. & Chesneau, C. A new family of polyno-trigonometric distributions with applications. Infin. Dimens. Anal. Quantum Probab. Relat. Top. 22(4), 1950027 (2020).
Souza, L. et al. Tan-G class of trigonometric distributions and its applications. CUBO Math. J. 23(1), 1–20 (2021).
Murtaza, L., Ishfaq, H. D. & Tariq, R. J. A new method for generating distributions with an application to Weibull distribution. Relabil. Theory Appl. 1(67), 223–239 (2022).
Anwar, H., Ishfaq, H. D. & Murtaza, L. A novel family of generating distributions based on trigonometric functions with an application to exponential distribution. J. Sci. Res. 65(2), 173–179 (2021).
Muzamil, J., Aijaz, A. & Rajnee, T. Weibull-Power Rayleigh distribution with applications related to distinct fields of science. Reliabil. Theory Appl. 17, 272–290 (2022).
Odhah, H. O., Alshanari, H. M., Ahmad, Z., Khan, F. & El-Bagoury, A. A novel probailistic approach based on trigonometric function: Model theory with practical applications. Symmetry 15(8), 1528 (2023).
Alomair, M. A. et al. A new trigonometric modification of the Weibull distribution: Control chart and applications in quality control. PLoS ONE 18(7), e0286593 (2023).
Heydari, T., Zare, K., Shokri, S., Khodadadi, Z. & Almaspoor, Z. A New Sine Based Probabilistic Approach: Theory and Monte Carlo Simulation with Reliability Application (J. Math. Univ, Tokushima, 2024).
Alghamdi, A. S. & Abd El-Raouf, M. M. A new alpha power cosine-Weibull model with applications to hydrological and engineering data. Mathematics 11(3), 673 (2023).
Omalsad, H. O., Olayan, A. & Huda, M. A. A new trigonometric-oriented distributional method: Model, theory, and practical applications. Alex. Eng. J. 25, 1–12 (2025).
Wang, Y., Lv, S., Zhuang, Z., Albalawi, O. & Alshanbari, H. M. A novel probabilistic model: Simulation and modeling the time duration in musical education and engineering. Alex. Eng. J. 106, 392–402 (2024).
Zhu, J. et al. A new sine-arisen probabilistic model and artificial neural network methods for statistical modeling of the music engineering and reliability data. Alex. Eng. J. 101, 108–117 (2024).
Aijaz, A., Mujamil, J. & Afaq, A. A novel approach for constracting distributions with an example of the Rayleigh distribution. Reliab. Theory Appl. 17, 42–64 (2022).
Aijaz, A., Qurat ul-Ain, S., Afaq, A. & Rajnee, T. Inverse Weibull-Rayleigh distribution characterisation with applications related to cancer data. Reliab. Theory Appl. 4(65), 364–382 (2021).
Ahmad, A., Rather, A.A., Tashkady, Y.A., Bakr, M.E., El-Din, M.M.M., et al. Deriving the new cotangent frechet distribution with real data analysis.Alexandria Eng. J. 100, 12-24 (2024).
Ahmad, A. et al. Novel sin-G class of distributions with an illustration of Lomex distribution: Properties and data analysis. AIP Adv. 14, 035132-1–17 (2024).
Ahmad, A., Alsadat, N., Atchade, M. N., ul-Ain, S. Q., Gemeay, A. M., Meraou, M. A., et al. A new hyperbolic sine-generator with an example of Rayleigh distribution: Simulation and data analysis in industry. Alex. Eng. J., 73, 415–426 (2023).
Ahmad, A., Jallal, M. & Mubarak, S. A. M. New cosine-generator with an example of Weibull distribution: Simulation and application related to banking sector. Reliab. Theory Appl. 18(72), 133–145 (2023).
Ahmad, A. et al. New arctan-generator family of distribution with an example of frechet distribution; simulation and analysis to strength of glass carbon fiber. Alex. Eng. J. 100, 42–52 (2024).
Najwan, A. et al. The novel Kumaraswamy power Frechetdistribution with data analysis related todiverse scientific areas. Alex. Eng. J. 70, 651–664 (2023).
Acknowledgements
Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R734), Princess Nourah bint Abdulrahman University, Riyadh,Saudi Arabia
Author information
Authors and Affiliations
Contributions
Authors have worked equally to write and review the manuscript.
Corresponding author
Ethics declarations
Competing interest
The authors declare no conflict of interest.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Ahmad, A., Rather, A.A., Alqasem, O.A. et al. Introducing novel arc cosine-\(\Psi\) class of distribution with theory and data evaluation related to coronavirus. Sci Rep 15, 13069 (2025). https://doi.org/10.1038/s41598-025-95084-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-95084-w